 Примеры циклических четырехугольников.
Примеры циклических четырехугольников. В евклидовой геометрии, вписанный четырехугольник или вписанный четырехугольник - это четырехугольник, вершины которого лежат на одной окружности. Этот круг называется описанной окружностью или описанной окружностью, а вершины называются конциклическими. Центр окружности и ее радиус называются центром описанной окружности и радиусом описанной окружности соответственно. Другие названия этих четырехугольников: конциклический четырехугольник и хордовый четырехугольник, последнее, поскольку стороны четырехугольника являются хордами описанной окружности. Обычно четырехугольник считается выпуклым, но бывают также скрещенные вписанные четырехугольники. Приведенные ниже формулы и свойства справедливы в выпуклом случае.
Слово циклическое происходит от древнегреческого κύκλος (куклос), что означает «круг» или «колесо».
Все треугольники имеют описанную окружность, но не все четырехугольники. Примером четырехугольника, который не может быть вписанным, является неквадратный ромб. В разделе характеристики ниже указано, каким необходимым и достаточным условиям должен удовлетворять четырехугольник, чтобы он имел описанную окружность.
Любой квадрат, прямоугольник, равнобедренная трапеция или антипараллелограмм является циклическим. воздушный змей является циклическим тогда и только тогда, когда имеет два прямых угла. Бицентрический четырехугольник - это вписанный четырехугольник, который также является тангенциальным, а экс-бицентрический четырехугольник - это циклический четырехугольник, который также экс-тангенциальный. Гармонический четырехугольник - это вписанный четырехугольник, в котором произведения длин противоположных сторон равны.
 Вциклический четырехугольник ABCD
Вциклический четырехугольник ABCD Выпуклый четырехугольник является циклическим тогда и только тогда, когда четыре перпендикуляра биссектрисы стороны параллельны. Эта общая точка - центр описанной окружности.
Выпуклый четырехугольник ABCD является циклическим тогда и только тогда, когда его противоположные углы являются дополнительными, то есть

Прямая теорема была предложением 22 в книге 3 из Евклида Элементы. Эквивалентно выпуклый четырехугольник является вписанным тогда и только тогда, когда каждый внешний угол равен противоположному внутреннему углу.
В 1836 году Дункан Грегори обобщил этот результат следующим образом: Для любого выпуклого циклического 2n-угольника, то каждая из двух сумм чередующихся внутренних углов равна (n-1) 
Выпуклый четырехугольник ABCD является вписанным, если и только если угол между стороной и диагональю равен углу между противоположной стороной и другой диагональю. Это, например,

 ABCD - это циклический четырехугольник. E - точка пересечения диагоналей, а F - точка пересечения продолжений сторон BC и AD.
ABCD - это циклический четырехугольник. E - точка пересечения диагоналей, а F - точка пересечения продолжений сторон BC и AD.  - круг, диаметр которого равен отрезку EF. P и Q - это точки Паскаля, образованные окружностью
- круг, диаметр которого равен отрезку EF. P и Q - это точки Паскаля, образованные окружностью  .
.Еще одно необходимое и достаточное условие для того, чтобы выпуклый четырехугольник ABCD был цикличным: пусть E - точка пересечения диагоналей, пусть F - точка пересечения продолжений сторон AD и BC, пусть 


Если две прямые, одна из которых содержит сегмент AC, а другая - сегмент BD, пересекаются в точке P, то четыре точки A, B, C, D совпадают, если и только если

Пересечение P может быть внутренним или внешним по отношению к окружности. В первом случае вписанный четырехугольник - это ABCD, а во втором - вписанный четырехугольник - ABDC. Когда пересечение является внутренним, равенство утверждает, что произведение длин сегментов, на которые P делит одну диагональ, равно произведению длины другой диагонали. Это известно как теорема о пересечении хорд, поскольку диагонали вписанного четырехугольника являются хордами описанной окружности.
Теорема Птолемея выражает произведение длин двух диагоналей e и f циклического четырехугольника как равное сумме произведений противоположных сторон:

обратное также верно. То есть, если этому уравнению удовлетворяет выпуклый четырехугольник, то образуется вписанный четырехугольник.
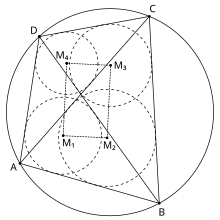
 ABCD - вписанный четырехугольник. EFG - диагональный треугольник ABCD. Точка T пересечения бимедианов ABCD принадлежит девятиточечной окружности EFG.
ABCD - вписанный четырехугольник. EFG - диагональный треугольник ABCD. Точка T пересечения бимедианов ABCD принадлежит девятиточечной окружности EFG. В выпуклом четырехугольнике ABCD пусть EFG будет диагональным треугольником ABCD и 

.
Выпуклый четырехугольник ABCD является циклическим тогда и только тогда, когда

площадь K вписанного четырехугольника со сторонами a, b, c, d определяется по формуле Брахмагупты

где s, полупериметр, равно s = 1/2 ( а + б + в + г). Это следствие формулы Бретшнайдера для общего четырехугольника, поскольку противоположные углы являются дополнительными в циклическом случае. Если также d = 0, циклический четырехугольник становится треугольником, и формула сокращается до формулы Герона.
У циклического четырехугольника максимальная площадь среди всех четырехугольников с одинаковой длиной сторон (независимо от последовательности). Это еще одно следствие формулы Бретшнайдера. Это также можно доказать с помощью исчисления.
Четыре неравных длины, каждая из которых меньше суммы трех других, являются сторонами каждого из трех несовпадающих циклических четырехугольников, которые по формуле Брахмагупты имеют одинаковую площадь. В частности, для сторон a, b, c и d сторона a может быть противоположной любой из стороны b, стороны c или стороны d.
Площадь вписанного четырехугольника с последовательными сторонами a, b, c, d и углом B между сторонами a и b можно выразить как

or

где θ - это любой угол между диагоналями. Если угол A не является прямым, площадь также можно выразить как

Другая формула:

, где R - радиус описанной окружности . Как прямое следствие,

, где равенство имеет место тогда и только тогда, когда четырехугольник является квадратом.
В циклическом четырехугольнике с последовательными вершинами A, B, C, D и сторонами a = AB, b = BC, c = CD и d = DA длины диагонали p = AC и q = BD могут быть выражены через стороны как
 и
и 
таким образом показывая теорему Птолемея

Согласно второй теореме Птолемея,

с использованием тех же обозначений, что и выше.
Для суммы диагоналей имеем неравенство

Равенство сохраняется тогда и только тогда, когда диагонали имеют одинаковую длину, что можно доказать с помощью Неравенство AM-GM.
Более того,

В любом выпуклом четырехугольнике две диагонали вместе разделяют четырехугольник на четыре треугольника; в круговом четырехугольнике противоположные пары этих четырех треугольников подобны друг другу.
Если M и N являются серединами диагоналей AC и BD, то

где E и F - точки пересечения продолжений противоположных сторон.
Если ABCD - вписанный четырехугольник, где AC пересекает BD в точке E, то

Набор сторон, которые могут образовывать циклический четырехугольник может быть расположен в любой из трех различных последовательностей, каждая из которых может образовывать циклический четырехугольник одной и той же площади в одной описанной окружности (площади совпадают в соответствии с формулой площади Брахмагупты). Любые два из этих циклических четырехугольников имеют общую длину диагонали.
Для циклического четырехугольника с последовательными сторонами a, b, c, d, полупериметр s, и угол A между сторонами a и d, тригонометрические функции матрицы A задаются выражением



Угол θ между диагонали удовлетворяет

Если расширения противоположные стороны a и c пересекаются под углом φ, тогда

где s - полупериметр.
Циклический четырехугольник с последовательными сторонами a, b, c, d и полупериметр s имеет радиус описанной окружности ( радиус описанной окружности ), заданный как

Это было получено индийским математиком Ватассери Парамешварой в 15 веке.
Используя формулу Брахмагупты, формулу Парамешвары можно переформулировать как

где K - площадь вписанного четырехугольника.
Четыре отрезка прямых, каждый перпендикулярный одной стороне циклического четырехугольника и проходящий через середину противоположной стороны, равны одновременно. Эти линейные сегменты называются солодыми, что является аббревиатурой от средней высоты над уровнем моря. Их точка пересечения называется антицентром. Он имеет свойство быть отражением центра описанной окружности в "центроиде вершины". Таким образом, в циклическом четырехугольнике центр описанной окружности, «центр тяжести вершины» и антицентр являются коллинеарными.
Если диагонали циклического четырехугольника пересекаются в точке P, а середины диагоналей равны M и N, тогда антицентр четырехугольника - это ортоцентр треугольника MNP.
 Японская теорема
Японская теорема A Четырехугольник Брахмагупты - это вписанный четырехугольник с целыми сторонами, целыми диагоналями, и целая область. Все четырехугольники Брахмагупты со сторонами a, b, c, d, диагоналями e, f, площадью K и радиусом описанной окружности R могут быть получены очисткой знаменателей из следующих выражений, содержащих рациональные параметры t, u и v:
![a = [t (u + v) + (1-uv)] [u + vt (1-uv)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9cd163fbbbaa9656bd5676b09a171e5cbbb85e5b)





![K = uv [2t (1-uv) - (u + v) (1-t ^ {2})] [2 (u + v) t + (1-uv) (1-t ^ {2})]](https://wikimedia.org/api/rest_v1/media/math/render/svg/093f0b615f9b1a926b92deb5fb486cc82281c53d)

Для вписанного четырехугольника, который также является ортодиагональным (имеет перпендикулярные диагонали), предположим, что пересечение диагоналей делит одну диагональ на сегменты длиной p 1 и p 2 и делит другую диагональ на сегменты длиной q 1 и q 2. Тогда (первое равенство - это предложение 11 в Архимед 'Книга лемм )

где D - диаметр описанной окружности. выполняется, потому что диагонали перпендикулярны хордам окружности. Из этих уравнений следует, что описанный радиус R может быть выражен как

или, в терминах сторон четырехугольника, как

Отсюда также следует, что

Таким образом, согласно теореме Эйлера о четырехугольнике, радиус описанной окружности может быть выражен через t Диагонали p и q, а расстояние x между серединами диагоналей как

Формула для площади K циклического ортодиагонального четырехугольника в терминах четырех сторон получается непосредственно при объединении теоремы Птолемея и формулы для площади ортодиагонального четырехугольника. Результат:

В сферической геометрии сферический четырехугольник, образованный из четырех пересекающихся больших окружностей, является циклическим тогда и только тогда, когда суммы противоположных углов равны, т. е. α + γ = β + δ для последовательных углов α, β, γ, δ четырехугольника. Одно направление этой теоремы было доказано И. А. Лекселлом в 1786 году. Лекселл показал, что в сферическом четырехугольнике, вписанном в малый круг сферы, суммы противоположных углов равны, а в описанном четырехугольнике суммы противоположных сторон равны. Первая из этих теорем является сферическим аналогом теоремы о плоскости, а вторая теорема двойственная к ней, то есть результат перестановки больших окружностей и их полюсов. Кипер и др. доказал обратное теореме: если суммы противоположных сторон равны в сферическом четырехугольнике, то существует вписывающая окружность для этого четырехугольника.