Произведение (математика)

редактировать

В математике произведение является результатом умножения или выражение, определяющее множители для умножения. Например, 30 - это произведение 6 и 5 (результат умножения), а $x ⋅ (2 + x) {\ displaystyle x \ cdot (2 + x)}$ $x \ cdot (2 + x)$ - произведение из $x {\ displaystyle x}$ $x$ и $(2 + x) {\ displaystyle (2 + x)}$ $(2 + x)$ (что указывает на то, что эти два множителя следует умножить вместе).

Порядок, в котором действительные или комплексные числа умножаются, не имеет отношения к произведению; это известно как коммутативный закон умножения. Когда матрицы или члены различных других ассоциативных алгебр умножаются, произведение обычно зависит от порядка факторов. Например, умножение матриц некоммутативно, как и умножение в других алгебрах в целом.

В математике существует множество различных видов произведений: помимо умножения простых чисел, многочленов или матриц, можно также определять продукты на множестве различных алгебраических структур.

Содержание

1 Продукт двух чисел
- 1.1 Произведение двух натуральных чисел
- 1.2 Произведение двух целых чисел
- 1.3 Произведение двух дробей
- 1.4 Произведение двух действительных чисел
- 1.5 Произведение двух комплексных чисел
  - 1.5.1 Геометрический смысл комплексного умножения
- 1.6 Произведение двух кватернионов
2 Произведение последовательностей
3 Коммутативные кольца
- 3.1 Остаточные классы целых чисел
- 3.2 Свертка
- 3.3 Полиномиальные кольца
4 Произведения в линейной алгебре
- 4.1 Скалярное умножение
- 4.2 Скалярное произведение
- 4.3 Перекрестное произведение в 3-мерном пространстве
- 4.4 Композиция линейных отображений
- 4.5 Произведение двух матриц
- 4.6 Композиция линейные функции как матричное произведение
- 4.7 Тензорное произведение векторных пространств
- 4.8 Класс всех объектов с тензором product
- 4.9 Другие продукты в линейной алгебре
5 Декартово произведение
6 Пустое произведение
7 Произведения над другими алгебраическими структурами
8 Продукты в теории категорий
9 Другие продукты
10 См. также
11 Примечания
12 Ссылки
13 Библиография
14 Внешние ссылки

Произведение двух чисел

Произведение двух натуральных чисел

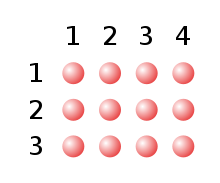
3 на 4 равно 12

Если поместить несколько камней в прямоугольный узор с $r {\ displaystyle r}$ $r$ строками и $s {\ displaystyle s}$ $s$ столбцами, получим

r ⋅ s = ∑ я знак равно 1 sr знак равно р + р + ⋯ + р ⏟ s раз = ∑ j = 1 rs = s + s + ⋯ + s ⏟ r раз {\ displaystyle r \ cdot s = \ sum _ {i = 1} ^ {s} r = \ underbrace {r + r + \ cdots + r} _ {s {\ text {times}}} = \ sum _ {j = 1} ^ {r} s = \ underbrace {s + s + \ cdots + s} _ {r {\ text {times}}}}

{\ displaystyle r \ cdot s = \ sum _ {i = 1} ^ {s } r = \ underbrace {r + r + \ cdots + r} _ {s {\ text {times}}} = \ sum _ {j = 1} ^ {r} s = \ underbrace {s + s + \ cdots + s } _{р {\ text {times}}}}

камней.

Произведение двух целых чисел

Целые числа допускают положительные и отрицательные числа. Их продукт определяется произведением их положительных сумм в сочетании со знаком, полученным из следующего правила:

⋅ - + - + - + - + {\ displaystyle {\ begin {array} {| c | cc |} \ hline \ cdot - + \\\ hline - + - \\ + - + \\\ hline \ end {array}}}

{\ displaystyle { \ begin {array} {| c | cc |} \ hline \ cdot - + \\\ hline - + - \\ + - + \\\ hline \ end {array}}}

(Это правило является необходимым следствием требования (дистрибутивность умножения над сложением и не является дополнительным правилом.)

На словах мы имеем:

Минус, умноженный на минус, дает Плюс
Минус раз, Плюс дает Минус
Плюс, умноженный на Минус, дает Минус
Плюс, умноженный на Плюс, дает Плюс

Произведение двух дробей

Две дроби можно умножить, умножив их числители и знаменатели:

zn ⋅ z ′ n ′ знак равно z ⋅ z ′ n ⋅ n ′ {\ displaystyle {\ frac {z} {n}} \ cdot {\ frac {z '} {n'}} = {\ frac {z \ cdot z ' } {n \ cdot n '}}}

\frac{z}{n} \cdot \frac{z'}{n'} = \frac{z\cdot z'}{n\cdot n'}

Произведение двух действительных чисел

Для точного определения произведения двух действительных чисел см. Построение действительных чисел.

Формулы

Теорема - Предположим, что>0 и b>0. Если 1 < p < ∞ and q := p/p - 1 then

ab = min0 < t < ∞ t a /p + t b /q.

Доказательство -
Определите действительную функцию f на положительных действительных числах с помощью
f (t): = ta / p + tb / q
для каждого t>0, а затем вычислить его минимум.
Произведение двух комплексных чисел
Два комплексных числа можно умножить по закону распределения и тому факту, что $i 2 = - 1 {\ displaystyle i ^ {2} = - 1}$ ${\ displaystyle i ^ {2} = - 1}$ следующим образом:
$(a + bi) ⋅ (c + di) = a ⋅ c + a ⋅ di + b ⋅ ci + b ⋅ d ⋅ i 2 = (a ⋅ c - b ⋅ d) + (a ⋅ d + б ⋅ с) я {\ Displaystyle {\ begin {выровнено} (а + b \, я) \ cdot (с + d \, я) = а \ cdot c + a \ cdot d \, i + b \ cdot c \, i + b \ cdot d \ cdot i ^ {2} \\ = (a \ cdot cb \ cdot d) + (a \ cdot d + b \ cdot c) \, i \ end {align}}}$ ${\ displaystyle {\ begin {align} (a + b \, i) \ cdot (c + d \, i) = a \ cdot c + a \ cdot d \, i + b \ cdot c \, i + b \ cdot d \ cdot i ^ {2} \\ = (a \ cdot cb \ cdot d) + (a \ cdot d + b \ cdot c) \, я \ конец {выровнен}}}$
Геометрический смысл комплексного умножения
Комплексное число в полярных координатах.
Комплексные числа могут быть записаны в полярных координатах :
$a + bi = r ⋅ ( соз ⁡ (φ) + я грех ⁡ (φ)) знак равно р ⋅ еi φ {\ Displaystyle а + Ь \, я = г \ CDOT (\ соз (\ varphi) + я \ грех (\ varphi)) = г \ cdot e ^ {я \ varphi}}$ ${\ displaystyle a + b \, i = r \ cdot (\ cos (\ varphi) + i \ sin (\ varphi)) = r \ cdot e ^ {i \ varphi}}$
Кроме того,
$c + di = s ⋅ (cos ⁡ (ψ) + i sin ⁡ (ψ)) = s ⋅ ei ψ, {\ displaystyle c + d \, i = s \ cdot (\ cos (\ psi) + i \ sin (\ psi)) = s \ cdot e ^ {i \ psi},}$ ${\ displaystyle c + d \, i = s \ cdot (\ cos ( \ psi) + я \ грех (\ psi)) = s \ cdot e ^ {i \ psi},}$
, из которого получается
$(a ⋅ c - б ⋅ г) + (а ⋅ г + б ⋅ с) i = r ⋅ s ⋅ e i (φ + ψ). {\ displaystyle (a \ cdot cb \ cdot d) + (a \ cdot d + b \ cdot c) я = r \ cdot s \ cdot e ^ {i (\ varphi + \ psi)}.}$ ${\ displaystyle (a \ cdot cb \ cdot d) + (a \ cdot d + b \ cdot c) я = r \ cdot s \ cdot e ^ {я (\ varphi + \ psi)}.}$
геометрический смысл состоит в том, что величины умножаются и аргументы складываются.
Произведение двух кватернионов
Произведение двух кватернионов можно найти в статье о кватернионах. Обратите внимание, что в данном случае $a ⋅ b {\ displaystyle a \ cdot b}$ $a \ cdot b$ и $b ⋅ a {\ displaystyle b \ cdot a}$ $b \ cdot a$ находятся в вообще разные.
Произведение последовательностей
Оператор произведения для произведения последовательности обозначается заглавной греческой буквой пи ∏ (по аналогии с использование заглавной буквы Sigma ∑ в качестве символа суммирования ). Например, выражение $∏ i = 1 6 i 2 {\ displaystyle \ textstyle \ prod _ {i = 1} ^ {6} i ^ {2}}$ ${\ displaystyle \ textstyle \ prod _ {i = 1} ^ {6} i ^ {2}}$ является другим способом написания $1 ⋅ 4 ⋅ 9 ⋅ 16 ⋅ 25 ⋅ 36 {\ displaystyle 1 \ cdot 4 \ cdot 9 \ cdot 16 \ cdot 25 \ cdot 36}$ ${\ displaystyle 1 \ cdot 4 \ cdot 9 \ cdot 16 \ cdot 25 \ cdot 36}$ .

Продукт последовательности, состоящей только из одного числа, и есть это число сам; произведение вообще без факторов известно как пустое произведение и равно 1.
Коммутативные кольца
Коммутативные кольца имеют операцию произведения.
Классы остатков целых чисел
Классы остатков в кольцах $Z / NZ {\ displaystyle \ mathbb {Z} / N \ mathbb {Z}}$ $\ Z / N \ Z$ могут быть добавлено:
$(a + NZ) + (b + NZ) = a + b + NZ {\ displaystyle (a + N \ mathbb {Z}) + (b + N \ mathbb {Z}) = a + b + N \ mathbb {Z}}$ ${\ displaystyle (a + N \ mathbb { Z}) + (b + N \ mathbb {Z}) = a + b + N \ mathbb {Z}}$
и умножаем:
$(a + NZ) ⋅ (b + NZ) = a ⋅ b + NZ {\ displaystyle (a + N \ mathbb {Z}) \ cdot (b + N \ mathbb {Z}) = a \ cdot b + N \ mathbb {Z}}$ ${\ displaystyle (a + N \ mathbb {Z}) \ cdot (b + N \ mathbb {Z}) = a \ cdot b + N \ mathbb {Z}}$
Свертка
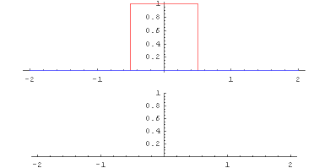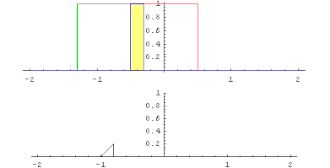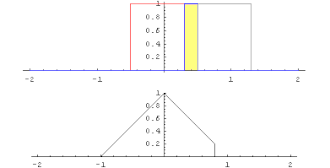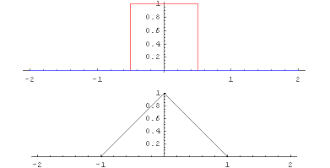
Свертка прямоугольной волны с самой собой дает треугольную функцию
Две функции от действительных чисел к себе можно перемножить другим способом, называемым сверткой .

Если
$∫ - ∞ ∞ | f (t) | dt < ∞ and ∫ − ∞ ∞ | g ( t) | d t < ∞, {\displaystyle \int \limits _{-\infty }^{\infty }|f(t)|\,\mathrm {d} t<\infty \qquad {\t_dv{and}}\qquad \int \limits _{-\infty }^{\infty }|g(t)|\,\mathrm {d} t<\infty,}$ ${\ displaystyle \ int \ limits _ {- \ infty} ^ {\ infty} | f (t) | \, \ mathrm {d} t <\ infty \ qquad {\ t_dv {and}} \ qquad \ int \ limits _ {- \ infty} ^ {\ infty} | g (t) | \, \ mathrm {d} t <\ infty,}$
, тогда интеграл
$(f ∗ g) (t): = ∫ - ∞ ∞ f (τ) ⋅ g (t - τ) d τ {\ displaystyle (f * g) (t) \; : = \ int \ limits _ {- \ infty} ^ {\ infty} f (\ tau) \ cdot g (t- \ tau) \, \ mathrm {d} \ tau}$ ${ \ Displaystyle (е * г) (т) \;: = \ int \ limits _ {- \ infty} ^ {\ infty} f (\ tau) \ cdot g (t- \ tau) \, \ mathrm {d} \ tau}$
хорошо определено и называется свертка.

При преобразовании Фурье свертка становится точечным умножением функций.
Кольца многочленов
Произведение двух многочленов определяется следующим образом:
$(∑ i = 0 nai X i) ⋅ (∑ j = 0 mbj X j) = ∑ k Знак равно 0 N + mck Икс К {\ displaystyle \ left (\ sum _ {i = 0} ^ {n} a_ {i} X ^ {i} \ right) \ cdot \ left (\ sum _ {j = 0} ^ {m} b_ {j} X ^ {j} \ right) = \ sum _ {k = 0} ^ {n + m} c_ {k} X ^ {k}}$ ${\ displaystyle \ left (\ sum _ { i = 0} ^ {n} a_ {i} X ^ {i} \ right) \ cdot \ left (\ sum _ {j = 0} ^ {m} b_ {j} X ^ {j} \ right) = \ sum _ {k = 0} ^ {n + m} c_ {k} X ^ {k}}$
с
$ck = ∑ я + j = кай ⋅ bj {\ displaystyle c_ {k} = \ sum _ {i + j = k} a_ {i} \ cdot b_ {j}}$ $c_k = \ сумма_ {я + J = к} a_i \ cdot b_j$
Продукты в линейной алгебре
В линейной алгебре есть много разных видов произведений. Некоторые из них имеют сходные до степени смешения имена (внешний продукт, внешний продукт ) с очень разными значениями, в то время как другие имеют очень разные названия (внешний продукт, тензорный продукт, продукт Кронекера) и все же передают по сути та же идея. Краткий обзор этого дается в следующих разделах.
Скалярное умножение
По самому определению векторного пространства можно сформировать произведение любого скаляра с любым вектором, давая карту $R × V → V {\ displaystyle \ mathbb {R} \ times V \ rightarrow V}$ ${\ Displaystyle \ mathbb {R} \ times V \ rightarrow V}$ .
Скалярное произведение
A скалярное произведение - это билинейное отображение:
$⋅: V × V → R {\ displaystyle \ cdot: V \ times V \ rightarrow \ mathbb {R}}$ ${\ displaystyle \ cdot: V \ times V \ rightarrow \ mathbb {R}}$
со следующими условиями, что $v ⋅ v>0 {\ displaystyle v \ cdot v>0}$ $v\cdot v>0$ для всех $0 ≠ v ∈ V {\ displaystyle 0 \ not = v \ in V}$ ${\ displaystyle 0 \ not = v \ in V}$ .

Из скалярного произведения можно определить норму, положив $‖ v ‖: = v ⋅ v {\ displaystyle \ | v \ |: = { \ sqrt {v \ cdot v}}}$ ${\ displaystyle \ | v \ |: = {\ sqrt {v \ cdot v}}}$ .

Скалярное произведение также позволяет определить угол между двумя векторами:
$cos ⁡ ∠ (v, w) = v ⋅ w ‖ v ‖ ⋅ ‖ w ‖ { \ displaystyle \ cos \ angle (v, w) = {\ frac {v \ cdot w} {\ | v \ | \ cdot \ | w \ |}}}$ ${\ displaystyle \ cos \ angle (v, w) = {\ frac {v \ cdot w} {\ | v \ | \ cdot \ | w \ |}}}$
In $n {\ disp laystyle n}$ $n$ -мерное евклидово пространство, стандартное скалярное произведение (называемое скалярным произведением ) определяется как:
$(∑ i = 1 n α iei) ⋅ (∑ i Знак равно 1 N β iei) знак равно ∑ я знак равно 1 N α я β я {\ Displaystyle \ влево (\ сумма _ {я = 1} ^ {п} \ альфа _ {я} е_ {я} \ вправо) \ CDOT \ left (\ sum _ {i = 1} ^ {n} \ beta _ {i} e_ {i} \ right) = \ sum _ {i = 1} ^ {n} \ alpha _ {i} \, \ beta _ {i}}$ ${\ displaystyle \ left (\ sum _ {i = 1} ^ {n} \ alpha _ {i} e_ {i} \ right) \ cdot \ left (\ sum _ {i = 1} ^ {n} \ beta _ {я} е_ {я} \ право) = \ сумма _ {я = 1} ^ {п} \ альфа _ {я} \, \ бета _ {я}}$
Перекрестное произведение в трехмерном пространстве
Перекрестное произведение двух векторов в трехмерном пространстве - это вектор, перпендикулярный двум факторам, с длиной, равной площадь параллелограмма, образованная двумя факторами.

Перекрестное произведение также может быть выражено как формальный определитель :
$u × v = | i j k u 1 u 2 u 3 v 1 v 2 v 3 | {\ displaystyle \ mathbf {u \ times v} = {\ begin {vmatrix} \ mathbf {i} \ mathbf {j} \ mathbf {k} \\ u_ {1} u_ {2} u_ {3} \ \ v_ {1} v_ {2} v_ {3} \\\ end {vmatrix}}}$ ${\ displaystyle \ mathbf { u \ times v} = {\ begin {vmatrix} \ mathbf {i} \ mathbf {j} \ mathbf {k} \\ u_ {1} u_ {2} u_ {3} \\ v_ {1} v_ {2} v_ {3} \\\ конец {vmatrix}}}$
Композиция линейных отображений
Линейное отображение можно определить как функцию f между двумя векторными пространствами V и W с нижележащим полем F, удовлетворяющим
$f (t 1 x 1 + t 2 x 2) = t 1 f (x 1) + t 2 f (x 2), ∀ x 1, x 2 ∈ V, ∀ t 1, t 2 ∈ F. {\ Displaystyle f (t_ {1} x_ {1} + t_ {2} x_ {2}) = t_ {1} f (x_ {1}) + t_ {2} f (x_ {2}), \ forall x_ {1}, x_ {2} \ in V, \ forall t_ {1}, t_ {2} \ in \ mathbb {F}.}$ ${\ displaystyle f (t_ {1} x_ {1} + t_ {2} x_ {2})) = t_ {1} f (x_ {1}) + t_ {2} f (x_ {2}), \ forall x_ {1}, x_ {2} \ in V, \ forall t_ {1}, t_ { 2} \ in \ mathbb {F}.}$
Если рассматривать только конечномерные векторные пространства, то
$f (v) знак равно е (виб В я) знак равно vif (б В я) = fijvib W J, {\ Displaystyle F (\ mathbf {v}) = е \ влево (v_ {я} \ mathbf {b_ {V}} ^ {i} \ right) = v_ {i} f \ left (\ mathbf {b_ {V}} ^ {i} \ right) = {f ^ {i}} _ {j} v_ {i} \ mathbf { b_ {W}} ^ {j},}$ ${\ displaystyle f (\ mathbf {v}) = f \ left ( v_ {i} \ mathbf {b_ {V}} ^ {i} \ right) = v_ {i} f \ left (\ mathbf {b_ {V}} ^ {i} \ right) = {f ^ {i} } _ {j} v_ {i} \ mathbf {b_ {W}} ^ {j},}$
, в которых bVи bWобозначают основания V и W, а v i обозначает компонент из v на bV, и соглашение о суммировании Эйнштейна.

Теперь мы рассмотрим композицию двух линейных отображений между конечномерными векторными пространствами. Пусть линейное отображение f отображает V в W, а линейное отображение g отображает W в U. Тогда можно получить
$g ∘ f (v) = g (f i j v i b W j) = g j k f i j v i b U k. {\ displaystyle g \ circ е (\ mathbf {v}) = g \ left ({f ^ {i}} _ {j} v_ {i} \ mathbf {b_ {W}} ^ {j} \ right) = {g ^ {j}} _ {k} {f ^ {i}} _ {j} v_ {i} \ mathbf {b_ {U}} ^ {k}.}$ ${\ displaystyle g \ circ f (\ mathbf {v}) = g \ left ({f ^ {i}} _ {j} v_ {i} \ mathbf {b_ {W}} ^ {j} \ right) = {g ^ {j}} _ {k} {f ^ {i}} _ {j} v_ {i} \ mathbf {b_ {U}} ^ {k}.}$
Или в матричной форме:
$g ∘ е (v) = GF v, {\ displaystyle g \ circ f (\ mathbf {v}) = \ mathbf {G} \ mathbf {F} \ mathbf {v},}$ $g \ circ f (\ mathbf {v}) = \ mathbf {G} \ mathbf { F} \ mathbf {v},$
в котором i -row, элемент j-столбца F, обозначенный F ij, это f i, и G ij=gi.

Состав более двух линейных отображений аналогично можно представить цепочкой умножения матриц.
Произведение двух матриц
Даны две матрицы
$A = (a i, j) i = 1… s; j = 1… r ∈ R s × r {\ displaystyle A = (a_ {i, j}) _ {i = 1 \ ldots s; j = 1 \ ldots r} \ in \ mathbb {R} ^ {s \ умножить на r}}$ ${\ displaystyle A = ( a_ {я, j}) _ {я = 1 \ ldots s; j = 1 \ ldots r} \ in \ mathbb {R} ^ {s \ times r}}$ и $B = (bj, k) j = 1… r; к знак равно 1… t ∈ р р × t {\ displaystyle B = (b_ {j, k}) _ {j = 1 \ ldots r; k = 1 \ ldots t} \ in \ mathbb {R} ^ {r \ раз t}}$ ${\ displaystyle B = (b_ {j, k }) _ {j = 1 \ ldots r; k = 1 \ ldots t} \ in \ mathbb {R} ^ {r \ times t}}$
их произведение определяется как
$B ⋅ A = (∑ j = 1 rai, j ⋅ bj, k) i = 1… s; К знак равно 1… T ∈ R s × T {\ Displaystyle B \ cdot A = \ left (\ sum _ {j = 1} ^ {r} a_ {i, j} \ cdot b_ {j, k} \ right) _ {i = 1 \ ldots s; k = 1 \ ldots t} \; \ in \ mathbb {R} ^ {s \ times t}}$ ${\ displaystyle B \ cdot A = \ left (\ sum _ {j = 1} ^ {r} a_ {i, j} \ cdot b_ {j, k} \ right) _ {i = 1 \ ldots s; k = 1 \ ldots t} \; \ in \ mathbb { R} ^ {s \ times t}}$
Составление линейных функций в виде матричного произведения
Там это отношение между композицией линейных функций и произведением двух матриц. Чтобы увидеть это, пусть r = dim (U), s = dim (V) и t = dim (W) - (конечные) размерности векторных пространств U, V и W. Пусть $U = {u 1,…, ur} {\ displaystyle {\ mathcal {U}} = \ {u_ {1}, \ ldots, u_ {r} \}}$ ${\ displaystyle {\ mathcal {U}} = \ {u_ {1}, \ ldots, u_ {r} \}}$ быть базисом из U, $V = {v 1,…, vs} {\ displaystyle {\ mathcal {V}} = \ {v_ {1}, \ ldots, v_ {s} \}}$ ${\ displaystyle {\ mathcal {V}} = \ {v_ {1}, \ ldots, v_ {s} \}}$ быть основой V и $W = {w 1,…, wt} {\ displaystyle {\ mathcal {W}} = \ {w_ {1}, \ ldots, w_ {t} \}}$ ${\ displaystyle {\ mathcal {W}} = \ {w_ {1}, \ ldots, w_ {t} \}}$ быть базисом W. В терминах этого базиса пусть $A = MVU (f) ∈ R s × r {\ displaystyle A = M _ {\ mathcal {V}} ^ {\ mathcal {U}} (f) \ in \ mathbb {R} ^ {s \ times r}}$ ${\ displaystyle A = M _ {\ mathcal {V}} ^ {\ mathcal {U}} (f) \ in \ mathbb {R} ^ { s \ times r}}$ - матрица, представляющая f: U → V и $B = MWV (g) ∈ R r × t {\ displaystyle B = M _ {\ mathcal {W}} ^ {\ mathcal {V}} (g) \ in \ mathbb {R} ^ {r \ times t}}$ ${\ displaystyle B = M _ {\ mathcal {W}} ^ {\ mathcal {V}} (g) \ in \ mathbb {R} ^ {r \ times t} }$ - матрица представляющий g: V → W. Тогда
$B ⋅ A = MWU (g ∘ f) ∈ R s × t {\ displaystyle B \ cdot A = M _ {\ mathcal {W}} ^ {\ mathcal {U}} (g \ circ f) \ in \ mathbb {R} ^ {s \ times t}}$ ${\ displaystyle B \ cdot A = M _ {\ mathcal {W}} ^ {\ mathcal {U}} (g \ circ f) \ in \ mathbb {R} ^ {s \ times t}}$
- это матрица, представляющая $g ∘ f: U → W {\ displaystyle g \ circ f: U \ rightarrow W}$ ${\ displaystyle g \ circ f: U \ rightarrow W}$ .

Другими словами: матричное произведение - это описание в координатах композиции линейных функций.
Тензорное произведение векторных пространств
Для двух конечномерных векторных пространств V и W их тензорное произведение может быть определено как (2,0) -тензор, удовлетворяющий:
$V ⊗ W (v, m) знак равно V (v) W (w), ∀ v ∈ V ∗, ∀ w ∈ W ∗, {\ displaystyle V \ otimes W (v, m) = V (v) W (w), \ forall v \ in V ^ {*}, \ forall w \ in W ^ {*},}$ ${\ displaystyle V \ otimes W (v, m) = V (v) W (w), \ forall v \ in V ^ {*}, \ для всех w \ in W ^ {*},}$
где V и W обозначают двойные пространства к V и W.

Для бесконечномерных векторных пространств также есть:
Тензорное произведение гильбертовых пространств
Топологическое тензорное произведение.
Тензорное произведение, внешнее произведение и произведение Кронекера Все передают одну и ту же общую идею. Различия между ними заключаются в том, что произведение Кронекера - это просто тензорное произведение матриц по отношению к ранее фиксированному базису, тогда как тензорное произведение обычно дается в его внутреннем определении. Внешний продукт - это просто произведение Кронекера, ограниченное векторами (вместо матриц).
Класс всех объектов с тензорным произведением
В общем, если у одного есть два математических объекта, которые можно комбинировать таким образом, чтобы вести себя как тензор линейной алгебры продукт, то его можно наиболее широко понимать как внутренний продукт из моноидальной категории. То есть моноидальная категория точно передает смысл тензорного произведения; он точно отражает понятие того, почему тензорные произведения ведут себя именно так. Точнее, моноидальная категория - это класс всех вещей (заданного типа ), которые имеют тензорное произведение.
Другие продукты линейной алгебры
Другие виды продуктов линейной алгебры включают:
произведение Адамара
произведение Кронекера
произведение тензоров :
Клин продукт или внешний продукт
Интерьерный продукт
Внешний продукт
Тензорный продукт
декартово произведение
В теории множеств декартово произведение математическая операция , которая возвращает набор (или набор продуктов ) из нескольких наборов. То есть для множеств A и B декартово произведение A × B - это множество всех упорядоченных пар (a, b), где a ∈ A и b ∈ B.

класс всех вещей (заданного типа ), которые имеют декартовы произведения, называется декартовой категорией. Многие из них являются декартовыми замкнутыми категориями. Наборы являются примером таких объектов.
Пустое произведение
Пустое произведение для чисел и большинства алгебраических структур имеет значение 1 (тождественный элемент умножения), как и пустая сумма имеет значение 0 (тождественный элемент сложения). Однако концепция пустого продукта является более общей и требует специального рассмотрения в логике, теории множеств, компьютерном программировании и теории категорий.
Продукты над другими алгебраическими структурами
Продукты над другими видами алгебраических структур включают:
декартово произведение наборов
прямое произведение групп, а также полупрямое произведение, вязанное произведение и сплетение
свободное произведение групп
произведение колец
произведение идеалов
произведение топологических пространств
произведение Вика случайных переменные
крышка, чашка, Massey и наклонное произведение в алгебраической топологии
произведение разрушения и сумма клина (иногда называемая произведением клина) в гомотопии
Некоторые из приведенных выше продуктов являются примерами общего понятия внутреннего продукта в категории моноидальных ; остальные описываются общим понятием продукта в теории категорий.
Продукты в теории категорий
Все предыдущие примеры являются частными случаями или примерами общего понятия продукта. Для общей трактовки концепции продукта см. продукт (теория категорий), где описывается, как объединить два объекта какого-либо типа для создания объекта, возможно, другого типа.. Но также, в теории категорий, есть:
продукт из волокна или откат,
категория продукта, категория, которая является продуктом категорий.
сверхпродукт, в теории моделей.
внутренний продукт из моноидальной категории, который отражает суть тензорное произведение.
Другие продукты
Функциональное произведение интеграла (как непрерывный эквивалент произведения последовательности или как мультипликативная версия нормального / стандартного / аддитивного интеграла. Интеграл произведения равен также известный как «непрерывный продукт» или «множественный».
Комплексное умножение, теория эллиптических кривых.
См. также
тензорное произведение Делиня абелевых категорий
Неопределенное произведение
Бесконечное product
Итерированная двоичная операция
Умножение - Арифметическая операция
Примечания
Ссылки
Библиография
Jarchow, Hans (1981). Локально выпуклые пространства. Штутгарт : BG Teubner. ISBN 978-3-519-02224-4. OCLC 8210342.
Внешние ссылки
«Продукт». PlanetMath.