Радиан

редактировать

Производная единица измерения угла в СИ

Радиан
Система единиц	Производная единица СИ
Единица измерения	Угол
Символ	рад или
В единицах	Безразмерный с длиной дуги, равной радиусу, то есть 1 м / м
Преобразования
1 рад дюйм...	... равно...

миллирадианам	1000 мрад
оборотов	1 / 2π поворота
градусов	180 / π ≈ 57,296 °
градиентов	200 / π ≈ 63,662

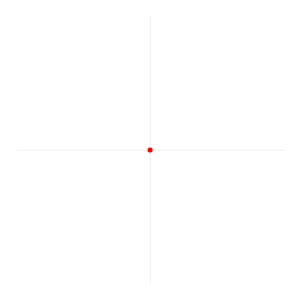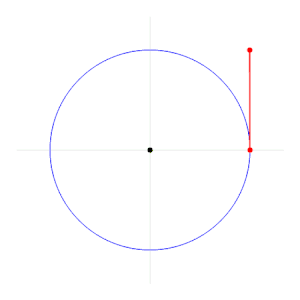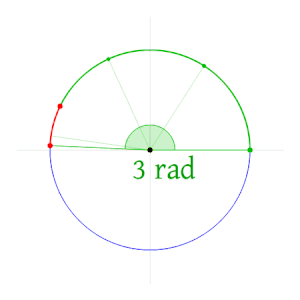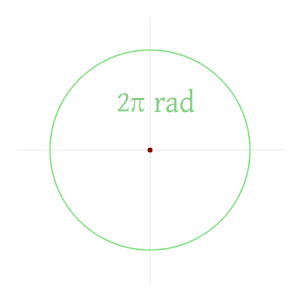Дуга окружности той же длины, что и радиус этой окружности, образует угол в 1 радиан. Окружность образует угол 2 π радиан.

радиан, обозначается символом $rad {\ displaystyle {\ text {rad}}}$ ${\ displaystyle {\ text {rad} }}$ , это единица СИ для измерения углов и стандартная единица измерения угла, используемая во многих областях математики. Длина дуги единичной окружности численно равна измерению в радианах угла , который он охватывает ; один радиан равен 180 / π градусов или чуть меньше 57,3 °. Ранее эта единица была дополнительной единицей СИ (до того, как эта категория была отменена в 1995 г.), а радиан теперь считается производной единицей СИ. Радиан определяется в СИ как безразмерное значение, и его символ, соответственно, часто опускается, особенно в математической письменной форме.

Содержание

1 Определение
2 История
3 Символ единицы
4 Преобразования
- 4.1 Преобразование радиан в градусы
  - 4.1.1 Выведение из радиана в градусы
- 4.2 Преобразование между радианами и градианами
5 Преимущества измерения в радианах
6 Анализ размеров
7 Использование в физике
8 кратных единиц СИ
9 См. также
10 Примечания и ссылки
11 Внешний links

Определение

Радиан описывает плоскость angle , соединенную окружностью дугой, как длину дуги, деленную на радиус дуги. Один радиан - это угол, образуемый в центре окружности дугой , которая по длине равна радиусу окружности. В более общем смысле, величина в радианах такого вытянутого угла равна отношению длины дуги к радиусу круга; то есть θ = s / r, где θ - угол наклона в радианах, s - длина дуги, а r - радиус. И наоборот, длина замкнутой дуги равна радиусу, умноженному на величину угла в радианах; то есть s = rθ.

Хотя обычно утверждают, что как отношение двух длин радиан является «чистым числом », хотя Мор и Филлипс оспаривают это утверждение. Однако в математическом письме символ «рад» почти всегда опускается. При количественном определении угла в отсутствие какого-либо символа используются радианы, а когда подразумеваются градусы, используется знак градуса °. Радиан определяется как 1. Существуют разногласия относительно того, является ли удовлетворительным в SI рассмотрение углов безразмерными. Это может привести к путанице при рассмотрении единиц частоты и постоянной Планка.

Полный оборот составляет 2π радиан (здесь показан круг с радиусом один и, следовательно, длина окружности 2π).

Это Из этого следует, что величина в радианах одного полного оборота (360 градусов) равна длине всей окружности, деленной на радиус, или 2 π r / r, или 2π. Таким образом, 2π радиан равняется 360 градусам, что означает, что один радиан равен 180 / π градусам.

Соотношение 2π рад = 360 ° может быть получено с использованием формулы для длины дуги. Взяв формулу для длины дуги, или $ℓ arc = 2 π r (θ 360 ∘) {\ displaystyle \ ell _ {arc} = 2 \ pi r \ left ({\ tfrac {\ theta} {360 ^ { \ circ}}} \ right)}$ ${\ displaystyle \ ell _ {arc} = 2 \ pi r \ left ({\ tfrac {\ theta} {360 ^ {\ circ }}} \ right)}$ . Предполагая единичный круг; радиус, следовательно, равен 1. Поскольку радиан - это мера угла, образующего дугу длиной, равной радиусу круга, $1 = 2 π (1 рад 360 ∘) {\ displaystyle 1 = 2 \ pi \ left ({\ tfrac {1 {\ text {rad}}} {360 ^ {\ circ}}} \ right)}$ ${\ displaystyle 1 = 2 \ pi \ left ({\ tfrac {1 {\ text {rad}}} {360 ^ {\ circ}}} \ right)}$ . Это можно упростить до $1 = 2 π rad 360 ∘ {\ displaystyle 1 = {\ tfrac {2 \ pi {\ text {rad}}} {360 ^ {\ circ}}}}}$ ${\ displaystyle 1 = {\ tfrac {2 \ pi {\ text {rad}}} {360 ^ {\ circ}}}}$ . Умножение обеих сторон на 360 ° дает 360 ° = 2π рад.

История

Концепция радиана, в отличие от градуса угла, обычно приписывается Роджеру Котсу в 1714 году. Он описал радиан во всем, кроме имя, и признал его естественность как единица угловой меры. До того, как термин радиан стал широко распространенным, эту единицу измерения обычно называли круговой мерой угла.

Идея измерения углов по длине дуги уже использовалась другими математиками. Например, аль-Каши (ок. 1400) использовал так называемые части диаметра в качестве единиц измерения, где одна часть диаметра составляла 1/60 радиана. Они также использовали шестидесятеричные единицы диаметра.

Термин радиан впервые появился в печати 5 июня 1873 г. в экзаменационных вопросах, заданных Джеймсом Томсоном (братом лорда Кельвина ) в Королевском колледже, Белфаст. Он использовал этот термин еще в 1871 году, в то время как в 1869 году Томас Мьюир, тогда из Университета Сент-Эндрюс, колебался между терминами рад, радиал и радиан. В 1874 году, после консультации с Джеймсом Томсоном, Мюр принял радиан. Некоторое время после этого название радиан не было общепринятым. В 1890 году тригонометрия школы Лонгмана все еще называлась радианной круговой мерой.

Обозначение единицы

Международное бюро мер и весов и Международная организация по стандартизации укажите rad как символ радиана. Альтернативные символы, использовавшиеся 100 лет назад, - это (верхняя буква c, обозначающая «круговая мера»), буква r или верхний индекс, но эти варианты используются нечасто, поскольку их можно принять за градусный символ (°) или радиус (r). Следовательно, значение 1,2 радиана обычно записывается как 1,2 рад; другие обозначения включают 1.2 r, 1.2, 1.2 или 1.2.

Преобразования

График для преобразования между градусами и радианами

Преобразование общих углов
Повороты	Радианы	Градусы	Градианы или гононы
0	0	0 °	0
1/24	π / 12	15 °	16 + 2/3
1/12	π / 6	30 °	33 + 1/3
1/10	π / 5	36 °	40
1/8	π / 4	45 °	50
1 / 2π	1	c.57,3 °	c.63,7
1/6	π / 3	60 °	66 + 2/3
1/5	2π / 5	72 °	80
1/4	π / 2	90 °	100
1/3	2π / 3	120 °	133 + 1 / 3
2/5	4π / 5	144 °	160
1/2	π	180 °	200
3/4	3π / 2	270 °	300
1	2π	360 °	400

Преобразование радианов в градусы

Как указано, один радиан равен 180 / π градусов. Таким образом, чтобы преобразовать радианы в градусы, умножьте на 180 / π.

угол в градусах = угол в радианах ⋅ 180 ∘ π {\ displaystyle {\ text {угол в градусах}} = {\ text {угол в радианах}} \ cdot {\ frac {180 ^ {\ circ}} { \ pi}}}

{\ text {угол в градусах}} = { \ text {угол в радианах}} \ cdot {\ frac {180 ^ {\ circ}} {\ pi}}

Например:

1 рад = 1 ⋅ 180 ∘ π ≈ 57,2958 ∘ {\ displaystyle 1 {\ text {rad}} = 1 \ cdot {\ frac {180 ^ {\ circ} } {\ pi}} \ приблизительно 57,2958 ^ {\ circ}}

1 {\ text {rad}} = 1 \ cdot {\ frac {180 ^ {\ circ}} {\ pi}} \ приблизительно 57,2958 ^ {\ circ}

2,5 рад = 2,5 ⋅ 180 ∘ π ≈ 143,2394 ∘ {\ displaystyle 2,5 {\ text {rad}} = 2,5 \ cdot {\ frac {180 ^ {\ circ}} {\ pi}} \ приблизительно 143,2394 ^ {\ circ}}

2,5 {\ text {rad}} = 2,5 \ cdot {\ frac {180 ^ {\ circ}} {\ pi}} \ приблизительно 143,2394 ^ {\ circ}

π 3 рад = π 3 ⋅ 180 ∘ π = 60 ∘ {\ displaystyle {\ frac {\ pi} {3}} { \ text {rad}} = {\ frac {\ pi} {3}} \ cdot {\ frac {180 ^ {\ circ}} {\ pi}} = 60 ^ {\ circ}}

{\ frac {\ pi} {3}} {\ text {rad}} = {\ frac {\ pi} {3}} \ cdot {\ frac {180 ^ {\ circ}} {\ pi}} = 60 ^ {\ circ}

И наоборот, чтобы преобразовать из градусов в радианы, умножить на π / 180.

угол в радианах = угол в градусах ⋅ π 180 ∘ {\ displaystyle {\ text {угол в радианах}} = {\ text {угол в градусах}} \ cdot {\ frac {\ pi} {180 ^ {\ circ}}}}

{\ text {угол в радианах}} = {\ text {угол в градусах}} \ cdot {\ frac {\ pi} {180 ^ {\ circ}}}

Например:

1 ∘ = 1 ⋅ π 180 ∘ ≈ 0,0175 рад {\ displaystyle 1 ^ {\ circ} = 1 \ cdot {\ frac {\ pi} {180 ^ {\ circ}}} \ приблизительно 0,0175 {\ text {rad}}}

1 ^ {\ circ} = 1 \ cdot {\ frac {\ pi} {180 ^ {\ circ}}} \ приблизительно 0,0175 {\ text {rad}}

$23 ∘ = 23 ⋅ π 180 ∘ ≈ 0,4014 рад {\ displaystyle 23 ^ {\ circ} = 23 \ cdot {\ frac {\ pi} { 180 ^ {\ circ}}} \ приблизительно 0,4014 {\ text {rad}}}$ $23 ^ {\ circ} = 23 \ cdot {\ frac {\ pi} {180 ^ {\ circ}}} \ приблизительно 0,4014 {\ text {rad}}$

Радианы можно преобразовать в оборотов (полные обороты), разделив количество радианов на 2π.

Преобразование радиана в градусы

Длина окружности круга определяется как $2 π r {\ displaystyle 2 \ pi r}$ $2 \ pi r$ , где $r {\ displaystyle r}$ $r$ - радиус круга.

Итак, следующее эквивалентное соотношение верно:

$360 ∘ ⟺ 2 π r {\ displaystyle 360 ^ {\ circ} \ iff 2 \ pi r}$ $360 ^ {\ circ} \ iff 2 \ pi r$ [Поскольку a $360 ∘ {\ displaystyle 360 ^ {\ circ}}$ $360 ^ {\ circ}$ развертка необходима, чтобы нарисовать полный круг]

По определению радиана полный круг представляет:

2 π rr рад {\ displaystyle {\ frac {2 \ pi r} {r}} {\ text {rad}}}

{\ frac {2 \ пи r} {r}} {\ text {rad}}

= 2 π rad {\ displaystyle = 2 \ pi {\ text {rad}}}

= 2 \ pi {\ text {rad}}

Объединение обоих указанных выше соотношений:

2 π rad = 360 ∘ {\ displaystyle 2 \ pi {\ text {rad}} = 360 ^ {\ circ}}

2 \ pi {\ text {rad}} = 360 ^ {\ circ}

⇛ 1 rad = 360 ∘ 2 π {\ displaystyle \ Rrightarrow 1 {\ text {rad}} = {\ frac {360 ^ {\ circ}} {2 \ pi}}}

\ Rrightarrow 1 {\ text {rad}} = {\ frac {360 ^ {\ circ }} {2 \ pi}}

⇛ 1 рад = 180 ∘ π {\ displaystyle \ Rrightarrow 1 {\ text { rad}} = {\ frac {180 ^ {\ circ}} {\ pi}}}

\ Rrightarrow 1 {\ text {rad}} = {\ frac {180 ^ {\ circ}} {\ pi}}

Преобразование радианов в градусы

$2 π {\ displaystyle 2 \ pi}$ $2 \ pi$ радиан равняется единице поворот, который по определению равен 400 градусам (400 углам или 400). Итак, чтобы преобразовать радианы в градиенты, умножьте их на $200 / π {\ displaystyle 200 / \ pi}$ $200 / \ pi$ , а для преобразования из градианов в радианы умножьте на $π / 200 {\ displaystyle \ пи / 200}$ $\ pi / 200$ . Например,

1,2 рад = 1,2 ⋅ 200 г π ≈ 76,3944 г {\ displaystyle 1.2 {\ text {rad}} = 1,2 \ cdot {\ frac {200 ^ {\ text {g}}} {\ pi} } \ приблизительно 76,3944 ^ {\ text {g}}}

1.2 {\ text {rad}} = 1.2 \ cdot {\ frac {200 ^ { \ text {g}}} {\ pi}} \ приблизительно 76,3944 ^ {\ text {g}}

50 г = 50 ⋅ π 200 г ≈ 0,7854 рад {\ displaystyle 50 ^ {\ text {g}} = 50 \ cdot {\ frac {\ pi} {200 ^ {\ text {g}}}} \ приблизительно 0,7854 {\ text {rad}}}

50 ^ {\ text {g}} = 50 \ cdot {\ frac {\ pi} {200 ^ {\ text {g}}}} \ приблизительно 0,7854 {\ text {rad}}

Преимущества измерения в радианах

Некоторые общие углы, измеряемые в радианах. Все большие многоугольники на этой диаграмме являются правильными многоугольниками.

В исчислении и большинстве других разделов математики, выходящих за рамки практической геометрии, углы всегда измеряются в радианах. Это потому, что радианы обладают математической «естественностью», которая приводит к более элегантной формулировке ряда важных результатов.

В частности, результаты анализа, включающего тригонометрические функции, могут быть элегантно сформулированы, когда аргументы функций выражены в радианах. Например, использование радианов приводит к простой формуле limit

lim h → 0 sin ⁡ hh = 1, {\ displaystyle \ lim _ {h \ rightarrow 0} {\ frac {\ sin h} {h}} = 1,}

\ lim _ {h \ rightarrow 0} {\ frac {\ sin h} {h}} = 1,

который является основой многих других тождеств в математике, включая

ddx sin ⁡ x = cos ⁡ x {\ displaystyle {\ frac {d} {dx}} \ sin x = \ cos x}

{\ frac {d} {dx}} \ sin x = \ cos x

d 2 dx 2 sin ⁡ x = - sin ⁡ x. {\ displaystyle {\ frac {d ^ {2}} {dx ^ {2}}} \ sin x = - \ sin x.}

{\ frac {d ^ {2}} {dx ^ {2}}} \ sin x = - \ sin x.

Благодаря этим и другим свойствам тригонометрические функции появляются в решениях математических задач которые явно не связаны с геометрическим значением функций (например, решения дифференциального уравнения $d 2 ydx 2 = - y {\ displaystyle {\ tfrac {d ^ {2} y} {dx ^ {2 }}} = - y}$ ${\ displaystyle {\ tfrac {d ^ {2} y} {dx ^ {2}}} = - y}$ , вычисление интеграла $∫ dx 1 + x 2, {\ displaystyle \ textstyle \ int {\ frac {dx} {1 + x ^ {2} }},}$ ${\ displaystyle \ textstyle \ int {\ frac {dx} {1 + x ^ {2}}},}$ и так далее). Во всех таких случаях выясняется, что аргументы функций наиболее естественно записываются в форме, которая соответствует, в геометрическом контексте, измерению углов в радианах.

Тригонометрические функции также имеют простое и элегантное расширение рядов при использовании радианов. Например, когда x выражается в радианах, ряд Тейлора для sin x принимает следующий вид:

sin ⁡ x = x - x 3 3! + х 5 5! - х 7 7! + ⋯. {\ displaystyle \ sin x = x - {\ frac {x ^ {3}} {3!}} + {\ frac {x ^ {5}} {5!}} - {\ frac {x ^ {7} } {7!}} + \ Cdots.}

\ sin x = x - {\ frac {x ^ {3}} {3 !}} + {\ frac {x ^ {5}} {5!}} - {\ frac {x ^ {7}} {7!}} + \ cdots.

Если бы x был выражен в градусах, тогда ряд содержал бы беспорядочные множители, включающие степени π / 180: если x - это количество градусов, количество радиан равно y = πx / 180, поэтому

sin ⁡ xdeg = sin ⁡ yrad = π 180 x - (π 180) 3 x 3 3! + (π 180) 5 х 5 5! - (π 180) 7 х 7 7! + ⋯. {\ displaystyle \ sin x _ {\ mathrm {deg}} = \ sin y _ {\ mathrm {rad}} = {\ frac {\ pi} {180}} x- \ left ({\ frac {\ pi} {180 }} \ right) ^ {3} \ {\ frac {x ^ {3}} {3!}} + \ left ({\ frac {\ pi} {180}} \ right) ^ {5} \ {\ frac {x ^ {5}} {5!}} - \ left ({\ frac {\ pi} {180}} \ right) ^ {7} \ {\ frac {x ^ {7}} {7!} } + \ cdots.}

\ sin x _ {\ mathrm {deg}} = \ sin y _ {\ mathrm {rad}} = {\ frac {\ pi} {180}} x- \ left ({\ frac {\ pi} {180}} \ right) ^ {3} \ {\ frac { x ^ {3}} {3!}} + \ left ({\ frac {\ pi} {180}} \ right) ^ {5} \ {\ frac {x ^ {5}} {5!}} - \ left ({\ frac {\ pi} {180}} \ right) ^ {7} \ {\ frac {x ^ {7}} {7!}} + \ cdots.

В том же духе математически важные отношения между функциями синуса и косинуса и экспоненциальной функцией (см., например, формулу Эйлера ) могут быть элегантно сформулировано, когда аргументы функций выражены в радианах (в противном случае - беспорядочно).

Анализ размеров

Хотя радиан - это единица измерения, это безразмерная величина. Это видно из определения, данного ранее: угол в центре круга, измеренный в радианах, равен отношению длины заключенной дуги к длине радиуса круга. Поскольку единицы измерения отменяются, это соотношение безразмерно.

Хотя полярные и сферические координаты используют радианы для описания координат в двух и трех измерениях, единица измерения получается из координаты радиуса, поэтому мера угла по-прежнему безразмерна.

Использование в физике

Радиан широко используется в физике, когда требуются угловые измерения. Например, угловая скорость обычно измеряется в радианах в секунду (рад / с). Один оборот в секунду равен 2π радиан в секунду.

Аналогично, угловое ускорение часто измеряется в радианах в секунду в секунду (рад / с).

В целях анализа размеров единицами измерения угловой скорости и углового ускорения являются с и с соответственно.

Аналогично, разность фаз двух волн также может быть измерена в радианах. Например, если разность фаз двух волн составляет (k⋅2π) радиан, где k - целое число, они считаются в фазе, тогда как если разность фаз двух волн составляет (k (2π + π), где k - целое число, они считаются противофазными.

Множители СИ

Метрические префиксы имеют ограниченное использование с радианами и не используются в математике. миллирадиан (мрад) - это одна тысячная радиана, а микрорадиан (мкрад) - одна миллионная радиана, то есть 1 рад = 10 мрад = 10 мрад.

В круге 2 π × 1000 миллирадиан (≈ 6283,185 мрад). Таким образом, миллирадиан составляет чуть менее 1/6283 угла, образуемого полным кругом. Эта «настоящая» единица измерения угла круга используется производителями телескопических прицелов, использующих (стадиометрический) дальномер в сетках. расходимость лазерных лучей также обычно измеряется в миллирадианах.

Приближенное значение миллирадиана (0,001 рад) используется НАТО и другими военными организациями в артиллерийских установках и нацеливании на. Каждый угловой мил представляет 1/6400 окружности и на 15/8% или 1,875% меньше миллирадиана. Для малых углов, которые обычно встречаются при наведении на цель, удобство использования числа 6400 в расчетах перевешивает небольшие математические ошибки, которые оно вносит. В прошлом другие артиллерийские системы использовали другие приближения к 1 / 2000π; например, Швеция использовала полосу 1/6300, а СССР - 1/6000. Основываясь на миллирадианах, мила НАТО выступает примерно на 1 м на дальности 1000 м (при таких малых углах кривизна незначительна).

Меньшие единицы, такие как микрорадианы (мкрад) и нанорадианы (нрад), используются в астрономии, а также могут использоваться для измерения качества луча лазеров со сверхмалой расходимостью. Чаще всего это угловая секунда, что составляет π / 648000 рад (около 4,8481 микрорадиан). Точно так же префиксы меньше милли- потенциально полезны при измерении очень малых углов.

См. Также

Угловая частота
Минута и секунда дуги
Стерадиан, многомерный аналог радиана, который измеряет телесный угол
Тригонометрия

Примечания и ссылки

Внешние ссылки

В Викиучебниках есть книга по темам: Тригонометрия / радианы и меры в градусах

Поиск радиан в Wiktionary, бесплатный словарь.

Средства массовой информации, относящиеся к Radian на Викискладе