Аналитическое продолжение

Расширение области определения аналитической функции (математика)

В комплексном анализе, ветвь математики, аналитическое продолжение - это метод расширения области заданной аналитической функции. Аналитическое продолжение часто преуспевает в определении дополнительных значений функции, например, в новой области, где представление бесконечной серии, в терминах которого оно изначально определено, становится расходящимся.

Однако пошаговая техника продолжения может столкнуться с трудностями. Они могут иметь по существу топологический характер, приводя к несогласованности (определение более одного значения). В качестве альтернативы они могут иметь отношение к наличию особенностей. Случай нескольких комплексных переменных несколько отличается, поскольку сингулярности не обязательно должны быть изолированными точками, и его исследование стало основной причиной развития когомологий пучков.

• 1 Исходное обсуждение
• 2 Приложения
• 3 Рабочий пример
• 4 Формальное определение ростка
• 5 Топология множества ростков
• 6 Примеры аналитического продолжения
• 7 Естественная граница
  • 7.1 Пример I: функция с естественной границей в нуле (простая дзета-функция)
  • 7.2 Пример II: Типичный лакунарный ряд (естественная граница как подмножество единичной окружности)
• 8 Теорема монодромии
• 9 Разрыв Адамара теорема
• 10 Теорема Поли
• 11 Полезная теорема: достаточное условие для аналитического продолжения к целым неположительным числам
  • 11.1 Гипотезы теоремы
  • 11.2 Заключение теоремы
  • 11.3 Примеры
    • 11.3.1 Пример I. Связь дзета-функции Римана с числами Бернулли
    • 11.3.2 Пример II: Интерпретация Использование F как сумматорной функции для некоторой арифметической последовательности
• 12 См. также
• 13 Ссылки
• 14 Внешние ссылки

Аналитическое продолжение натурального логарифма (мнимая часть)

Предположим, что f является аналитической функцией, определенной на непустом открытом подмножестве U комплексной плоскости $C.\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{C\}.\}$Если V является большим открытым подмножеством $C,\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{C\},\}$содержит U и F аналитическая функция, определенная на V, такая, что

$F\; (z)\; =\; f\; (z)\; \forall \; z\; \in \; U,\; \{\backslash \; displaystyle\; F\; (z)\; =\; f\; (z)\; \backslash \; qquad\; \backslash \; forall\; z\; \backslash \; in\; U,\}$

тогда F называется аналитическим продолжением f. Другими словами, ограничение F на U - это функция f, с которой мы начали.

Аналитические продолжения уникальны в следующем смысле: если V является связанной областью двух аналитических функций F 1 и F 2 таких, что U содержится в V и для всех z в U

$F\; 1\; (z)\; =\; F\; 2\; (z)\; =\; f\; (z),\; \{\backslash \; displaystyle\; F\_\; \{1\}\; (z)\; =\; F\_\; \{2\}\; (z)\; =\; f\; (z),\}$

, затем

$F\; 1\; =\; F\; 2\; \{\backslash \; displaystyle\; F\_\; \{1\}\; =\; F\_\; \{2\}\}$

на всем V. Это потому, что F 1 - F 2 - аналитическая функция, которая обращается в нуль в открытой связной области U функции f и, следовательно, должна исчезать во всей своей области. Это непосредственно следует из теоремы тождества для голоморфных функций.

Обычный способ определения функций в комплексном анализе заключается в том, что сначала задается функция только в небольшой области, и затем расширив его аналитическим продолжением.

На практике это продолжение часто выполняется, сначала устанавливая некоторое функциональное уравнение для небольшой области, а затем используя это уравнение для расширения области. Примерами являются дзета-функция Римана и гамма-функция.

Концепция универсального покрытия была впервые разработана для определения естественной области для аналитического продолжения аналитическая функция. Идея найти максимальное аналитическое продолжение функции, в свою очередь, привело к развитию идеи римановых поверхностей.

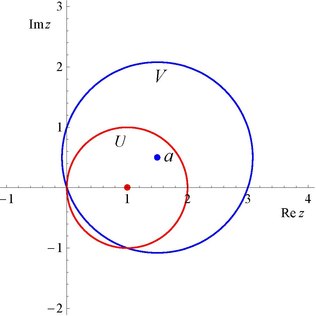
Аналитическое продолжение от U (с центром в 1) к V (с центром в a = (3 + i) / 2)

Начните с конкретной аналитической функции $f\; \{\backslash \; displaystyle\; f\}$. В этом случае он задается степенным рядом с центром в $z\; =\; 1\; \{\backslash \; displaystyle\; z\; =\; 1\}$:

$f\; (z)\; =\; \sum \; k\; =\; 0\; \infty \; (-\; 1)\; k\; (г\; -\; 1)\; к.\; \{\backslash \; displaystyle\; f\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; (-\; 1)\; ^\; \{k\}\; (z-1)\; ^\; \{k\}.\}$

Автор Коши– Теорема Адамара, ее радиус сходимости равен 1. То есть $f\; \{\backslash \; displaystyle\; f\}$определен и аналитичен на открытом множестве с границей $\partial \; U\; =\; \{|\; z\; -\; 1\; |\; Знак\; равно\; 1\}\; \{\backslash \; displaystyle\; \backslash \; partial\; U\; =\; \backslash \; \{|\; z-1\; |\; =\; 1\; \backslash \}\}$. Действительно, ряд расходится в точке $z\; =\; 0\; \in \; \partial \; U\; \{\backslash \; displaystyle\; z\; =\; 0\; \backslash \; in\; \backslash \; partial\; U\}$.

Представьте, что мы не знаем, что $f\; (z)\; =\; 1\; /\; z\; \{\backslash \; displaystyle\; f\; (z)\; =\; 1\; /\; z\}$и сосредоточить внимание на повторном центрировании степенного ряда в другой точке $a\; \in \; U\; \{\backslash \; displaystyle\; a\; \backslash \; in\; U\}$:

$f\; (z)\; =\; \sum \; k\; =\; 0\; \infty \; ak\; (z\; -\; a)\; k.\; \{\backslash \; displaystyle\; f\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; a\_\; \{k\}\; (za)\; ^\; \{k\}.\}$

Мы вычислим $ak\; \{\backslash \; displaystyle\; a\_\; \{k\}\}$и определить, сходится ли этот новый степенной ряд в открытом наборе $V\; \{\backslash \; displaystyle\; V\}$, который не содержится в $U\; \{\backslash \; стиль\; отображения\; U\}$. Если это так, мы продолжим аналитически $f\; \{\backslash \; displaystyle\; f\}$до области $U\; \cup \; V\; \{\backslash \; displaystyle\; U\; \backslash \; cup\; V\}$, которая строго больше чем $U\; \{\backslash \; displaystyle\; U\}$.

Расстояние от $a\; \{\backslash \; displaystyle\; a\}$до $\partial \; U\; \{\backslash \; displaystyle\; \backslash \; partial\; U\}$равно $\rho \; =\; 1\; -\; |\; а\; -\; 1\; |>0\; \{\backslash \; displaystyle\; \backslash \; rho\; =\; 1-\; |\; a-1\; |>0\}$. Возьмем ; пусть $D\; \{\backslash \; displaystyle\; D\}$будет диском радиуса $r\; \{\backslash \; displaystyle\; r\}$вокруг $a\; \{\backslash \; displaystyle\; a\}$; и пусть $\partial \; D\; \{\backslash \; displaystyle\; \backslash \; partial\; D\}$будет его границей. Тогда $D\; \cup \; \partial \; D\; \subset \; U\; \{\backslash \; displaystyle\; D\; \backslash \; cup\; \backslash \; partial\; D\; \backslash \; subset\; U\}$. Используя формулу дифференцирования Коши для вычисления новых коэффициентов,

$ak = f (k) (a) k! = 1 2 π i ∫ ∂ D f (ζ) d ζ (ζ - a) k + 1 = 1 2 π i ∫ ∂ D ∑ n = 0 ∞ (- 1) n (ζ - 1) nd ζ (ζ - a) k + 1 = 1 2 π i ∑ n = 0 ∞ (- 1) n ∫ ∂ D (ζ - 1) nd ζ (ζ - a) k + 1 = 1 2 π i ∑ n = 0 ∞ (- 1) n ∫ 0 2 π (a + rei θ - 1) nriei θ d θ (rei θ) k + 1 = 1 2 π ∑ n = 0 ∞ (- 1) n ∫ 0 2 π (a - 1 + rei θ) nd θ (rei θ) k = 1 2 π ∑ n = 0 ∞ (- 1) n ∫ 0 2 π ∑ m = 0 n ( нм) (a - 1) n - m (rei θ) md θ (rei θ) k = (- 1) ka - k - 1 {\ displaystyle {\ begin {align} a_ {k} = {\ frac { f ^ {(k)} (a)} {k!}} \\ = {\ frac {1} {2 \ pi i}} \ int _ {\ partial D} {\ frac {f (\ zeta) d \ zeta} {(\ zeta -a) ^ {k + 1}}} \\ = {\ frac {1} {2 \ pi i}} \ int _ {\ partial D} {\ frac {\ sum _ {n = 0} ^ {\ infty} (- 1) ^ {n} (\ zeta -1) ^ {n} d \ zeta} {(\ zeta -a) ^ {k + 1}}} \\ = {\ frac {1} {2 \ pi i}} \ sum _ {n = 0} ^ {\ infty} (- 1) ^ {n} \ int _ {\ partial D} {\ frac {(\ дзета -1) ^ {n} d \ zeta} {(\ zeta -a) ^ {k + 1}}} \\ = {\ frac {1} {2 \ pi i}} \ sum _ {n = 0} ^ {\ infty} (- 1) ^ {n} \ int _ {0} ^ {2 \ pi} {\ frac {(a + re ^ {i \ theta} -1) ^ {n} rie ^ {i \ theta} d \ theta} {(re ^ {i \ theta}) ^ {k + 1}}} \\ = {\ frac {1} {2 \ pi}} \ sum _ {n = 0 } ^ {\ infty} (- 1) ^ {n} \ int _ {0} ^ {2 \ pi} {\ frac {(a-1 + re ^ {i \ theta}) ^ {n} d \ theta } {(re ^ {i \ theta}) ^ {k}}} \\ = {\ frac {1} {2 \ pi}} \ sum _ {n = 0} ^ {\ infty} (- 1) ^ {n} \ int _ {0} ^ {2 \ pi} {\ frac {\ sum _ {m = 0} ^ {n} {\ binom {n} {m}} (a-1) ^ {nm } (re ^ {i \ theta}) ^ {m} d \ theta} {(re ^ {i \ theta}) ^ {k}}} \\ = (- 1) ^ {k} a ^ {- k-1} \ end {align}}}$

То есть

$f\; (z)\; =\; \sum \; k\; =\; 0\; \infty \; ak\; (z\; -\; a)\; k\; =\; \sum \; к\; знак\; равно\; 0\; \infty \; (-\; 1)\; ка\; -\; к\; -\; 1\; (z\; -\; а)\; к\; знак\; равно\; 1\; а\; \sum \; к\; =\; 0\; \infty \; (1\; -\; za)\; к,\; \{\backslash \; displaystyle\; f\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; a\_\; \{k\}\; (za)\; ^\; \{k\}\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; (-\; 1)\; ^\; \{k\}\; a\; ^\; \{-\; k-1\}\; (za)\; ^\; \{k\}\; =\; \{\backslash \; frac\; \{1\}\; \{a\}\}\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{z\}\; \{a\}\}\; \backslash \; right)\; ^\; \{k\},\; \}$

с радиусом схождения $|\; а\; |\; \{\backslash \; displaystyle\; |\; a\; |\}$и Если мы выберем $a\; \in \; U\; \{\backslash \; displaystyle\; a\; \backslash \; in\; U\}$с $|\; а\; |>1\; \{\backslash \; displaystyle\; |\; a\; |>1\}$, тогда $V\; \{\backslash \; displaystyle\; V\}$не является подмножеством $U\; \{\backslash \; displaystyle\; U\}$и фактически по площади больше, чем $U\; \{\backslash \; displaystyle\; U\}$. На графике показан результат для $a\; =\; 1\; 2\; (3\; +\; i).\; \{\backslash \; displaystyle\; a\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; (3\; +\; i).\}$

Мы можем продолжить процесс: выберите $b\; \in \; U\; \cup \; V\; \{\backslash \; displaystyle\; b\; \backslash \; in\; U\; \backslash \; cup\; V\}$, измените центр мощности ряд в $b\; \{\backslash \; displaystyle\; b\}$и определить, где сходится новый степенной ряд. Если область содержит точки, не входящие в $U\; \cup \; V\; \{\backslash \; displaystyle\; U\; \backslash \; cup\; V\}$, то мы продолжим аналитически $f\; \{\backslash \; displaystyle\; f\}$еще дальше. Этот конкретный $f\; \{\backslash \; displaystyle\; f\}$можно продолжить аналитически. на проколотую комплексную плоскость $C\; \setminus \; \{0\}.\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{C\}\; \backslash \; setminus\; \backslash \; \{0\; \backslash \}.\}$

Определенный ниже степенной ряд обобщен идеей ростка. Общая теория аналитического продолжения и ее обобщения известна как теория пучков. Пусть

$f\; (z)\; =\; \sum \; K\; =\; 0\; \infty \; \alpha \; K\; (z\; -\; z\; 0)\; k\; \{\backslash \; displaystyle\; f\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \backslash \; alpha\; \_\; \{k\}\; (z-z\_\; \{0\})\; ^\; \{k\}\}$

быть степенным рядом, сходящимся в диске Dr(z0), r>0, определяемым

.

Обратите внимание, что без ограничения общности здесь и ниже мы всегда будем предполагать, что было выбрано максимальное такое r, даже если это r равно ∞. Также обратите внимание, что было бы эквивалентно начать с аналитической функции, определенной на некотором небольшом открытом множестве. Мы говорим, что вектор

$g\; =\; (z\; 0,\; \alpha \; 0,\; \alpha \; 1,\; \alpha \; 2,\dots )\; \{\backslash \; displaystyle\; g\; =\; (z\_\; \{0\},\; \backslash \; alpha\; \_\; \{0\},\; \backslash \; alpha\; \_\; \{1\},\; \backslash \; alpha\; \_\; \{2\},\; \backslash \; ldots)\}$

- это росток f. Основание g 0 для g равно z 0, основа g - (α 0, α 1, α 2,...), а верхний g 1 g равен α 0. Вершина g - это значение f в точке z 0.

Любой вектор g = (z 0, α 0, α 1,...) является ростком, если он представляет собой степенной ряд аналитической функции около z 0 с некоторым радиусом сходимости r>0. Следовательно, мы можем смело говорить о наборе ростков $G\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\}$.

Пусть g и h равны микробы. Если где r - радиус сходимости g, и если степенной ряд, определяемый g и h, задает идентичные функции на пересечении двух областей, то мы говорим, что h порождается g (или совместим с ним), и мы напишите g ≥ h. Это условие совместимости не является ни транзитивным, ни симметричным, ни антисимметричным. Если мы расширим отношение на транзитивность, мы получим симметричное отношение, которое, следовательно, также будет отношением эквивалентности на ростках (но не упорядочением). Это расширение по транзитивности является одним из определений аналитического продолжения. Отношение эквивалентности будет обозначено $\cong \; \{\backslash \; displaystyle\; \backslash \; cong\}$.

. Мы можем определить топологию на $G\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\}$. Пусть r>0 и

Наборы U r (g) для всех r>0 и $g\; \in \; G\; \{\backslash \; displaystyle\; g\; \backslash \; in\; \{\backslash \; mathcal\; \{G\}\}\}$определяют основа открытых множеств для топологии на $G\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\}$.

A компонент связности из $G\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{\; G\}\}\}$(т. Е. Класс эквивалентности) называется связкой. Также отметим, что карта, определенная как $\varphi \; g\; (h)\; =\; h\; 0:\; U\; r\; (g)\; \to \; C,\; \{\backslash \; displaystyle\; \backslash \; phi\; \_\; \{g\}\; (h)\; =\; h\_\; \{0\}:\; U\_\; \{r\}\; (g)\; \backslash \; to\; \backslash \; mathbb\; \{C\},\}$, где r - радиус сходимости g, - это диаграмма. Набор таких диаграмм образует атлас для $G\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\}$, следовательно, $G\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\; \}\}\}$- это риманова поверхность. $G\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\}$иногда называют универсальной аналитической функцией.

$L\; (z)\; =\; \sum \; k\; =\; 1\; \infty \; (-\; 1)\; k\; +\; 1\; k\; (z\; -\; 1)\; k\; \{\backslash \; displaystyle\; L\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{k\; +\; 1\}\}\; \{k\}\}\; (z-1)\; ^\; \{k\}\}$

- степенной ряд, соответствующий натуральный логарифм около z = 1. Этот степенной ряд можно превратить в росток

$g\; =\; (1,\; 0,\; 1,\; -\; 1\; 2,\; 1\; 3,\; -\; 1\; 4,\; 1\; 5,\; -\; 1\; 6,\dots )\; \{\backslash \; displaystyle\; g\; =\; \backslash \; left\; (1,0,1,\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\},\; \{\backslash \; frac\; \{1\}\; \{3\}\},\; -\; \{\backslash \; frac\; \{1\}\; \{4\; \}\},\; \{\backslash \; frac\; \{1\}\; \{5\}\},\; -\; \{\backslash \; frac\; \{1\}\; \{6\}\},\; \backslash \; ldots\; \backslash \; right)\}$

Этот росток имеет радиус сходимости 1, поэтому существует связка S, соответствующая ему. Это пучок логарифмической функции.

Теорема единственности для аналитических функций распространяется также на пучки аналитических функций: если пучок аналитической функции содержит нулевой росток (то есть пучок равномерно равен нулю в некоторой окрестности), то весь пучок равен нулю. Вооружившись этим результатом, мы можем видеть, что если мы возьмем любой росток g пучка S логарифмической функции, как описано выше, и превратим его в степенной ряд f (z), то эта функция будет обладать тем свойством, что exp (f (z)) = z. Если бы мы решили использовать версию теоремы об обратной функции для аналитических функций, мы могли бы построить широкий спектр обратных функций для экспоненциального отображения, но мы бы обнаружили, что все они представлены некоторым ростком в S В этом смысле S является «истинным обратным» экспоненциальному отображению.

В более ранней литературе пучки аналитических функций назывались многозначными функциями. См. Общую концепцию связки.

Предположим, что степенной ряд имеет радиус сходимости r и определяет аналитическую функцию f внутри этого диска. Рассмотрим точки на круге сходимости. Точка, для которой существует окрестность, в которой f имеет аналитическое расширение, регулярна, иначе особа. Окружность является естественной границей, если все ее точки особые.

В более общем плане мы можем применить определение к любой открытой связной области, в которой f является аналитической, и классифицировать точки границы области как регулярные или особые: граница области тогда является естественной границей, если все точки являются особенными, и в этом случае область является областью голоморфности.

Пример I: функция с естественной границей в нуле (простая дзета-функция)

Для $\Re \; (s)>1\; \{\backslash \; displaystyle\; \backslash \; Re\; (s)>1\}$мы определяем так называемую простую дзета-функцию, $P\; (s)\; \{\backslash \; displaystyle\; P\; (s)\}$, быть

$P\; (s):\; =\; \sum \; p\; простое\; p\; -\; s.\; \{\backslash \; displaystyle\; P\; (s):\; =\; \backslash \; sum\; \_\; \{p\; \backslash \; \{\backslash \; text\; \{prime\}\}\}\; p\; ^\; \{-\; s\}.\}$

Эта функция аналогична суммирующей форме дзета-функции Римана, когда $\Re \; (s)>1\; \{\backslash \; displaystyle\; \backslash \; Re\; (s)>1\}$, поскольку это та же сумматорная функция, что и $\zeta \; (s)\; \{\backslash \; displaystyle\; \backslash \; zeta\; (s)\}$, за исключением индексов, ограниченных только простыми числами вместо взятия суммы по всем положительным натуральным числам. Простая дзета-функция имеет аналитическое продолжение на все комплексные s, такие что , факт, который следует из выражения $P\; (s)\; \{\backslash \; displaystyle\; P\; (s)\}$с помощью логарифмов дзета-функции Римана как

$P\; (s)\; =\; \sum \; n\; \ge \; 1\; \mu \; (n)\; log\; \; \zeta \; (ns)\; n.\; \{\backslash \; displaystyle\; P\; (s)\; =\; \backslash \; sum\; \_\; \{n\; \backslash \; geq\; 1\}\; \backslash \; mu\; (n)\; \{\backslash \; frac\; \{\backslash \; log\; \backslash \; zeta\; (ns)\}\; \{n\}\}.\}$

Поскольку $\zeta \; (s)\; \{\backslash \; displaystyle\; \backslash \; zeta\; (s)\}$имеет простой несъемный столб в $s:\; =\; 1\; \{\backslash \; displaystyle\; s:\; =\; 1\}$, тогда он может видно, что $P\; (s)\; \{\backslash \; displaystyle\; P\; (s)\}$имеет простой полюс в $s:\; =\; 1\; k,\; \forall \; k\; \in \; Z\; +\; \{\backslash \; displaystyle\; s:\; =\; \{\; \backslash \; tfrac\; \{1\}\; \{k\}\},\; \backslash \; forall\; k\; \backslash \; in\; \backslash \; mathbb\; \{Z\}\; ^\; \{+\}\}$. Поскольку набор точек

$Sing\; P:\; =\; \{k\; -\; 1:\; k\; \in \; Z\; +\}\; =\; \{1,\; 1\; 2,\; 1\; 3,\; 1\; 4,\dots \}\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Sing\}\; \_\; \{P\}:\; =\; \backslash \; left\; \backslash \; \{k\; ^\; \{-\; 1\}:\; k\; \backslash \; in\; \backslash \; mathbb\; \{Z\}\; ^\; \{+\}\; \backslash \; right\; \backslash \}\; =\; \backslash \; left\; \backslash \; \{1,\; \{\backslash \; frac\; \{1\}\; \{2\}\},\; \{\backslash \; frac\; \{\; 1\}\; \{3\}\},\; \{\backslash \; frac\; \{1\}\; \{4\}\},\; \backslash \; ldots\; \backslash \; right\; \backslash \}\}$

имеет точку накопления 0 (предел последовательности как $k\; \mapsto \; \infty \; \{\backslash \; displaystyle\; k\; \backslash \; mapsto\; \backslash \; infty\}$), мы видим, что ноль образует естественную границу для $P\; (s)\; \{\backslash \; displaystyle\; P\; (s)\}$. Это означает, что $P\; (s)\; \{\backslash \; displaystyle\; P\; (s)\}$не имеет аналитического продолжения для s слева от (или в) нуля, т.е. продолжение невозможно для $P\; (s)\; \{\backslash \; displaystyle\; P\; (s)\}$когда $0\; \ge \; \Re \; (s)\; \{\backslash \; displaystyle\; 0\; \backslash \; geq\; \backslash \; Re\; (s)\}$. В качестве примечания, этот факт может быть проблематичным, если мы выполняем комплексный контурный интеграл по интервалу, действительные части которого симметричны относительно нуля, скажем $IF\; \subseteq \; C,\; такой\; что\; \Re \; (s)\; \in \; (-\; C,\; C),\; \forall \; s\; \in \; ЕСЛИ\; \{\backslash \; Displaystyle\; I\_\; \{F\}\; \backslash \; substeq\; \backslash \; mathbb\; \{C\}\; \backslash \; \{\backslash \; text\; \{такой,\; что\}\}\; \backslash \; \backslash \; Re\; (s)\; \backslash \; in\; (-C,\; C),\; \backslash \; forall\; s\; \backslash \; in\; I\_\; \{F\}\; \}$для некоторых $C>0\; \{\backslash \; displaystyle\; C>0\}$, где подынтегральное выражение - это функция со знаменателем, который зависит от $P\; (s)\; \{\backslash \; displaystyle\; P\; (s)\}$существенным образом.

Пример II: Типичный лакунарный ряд (естественная граница как подмножество единичного круга)

Для целых чисел $c\; \ge \; 1\; \{\backslash \; displaystyle\; c\; \backslash \; geq\; 1\}$, мы определяем лакунарный ряд порядка c разложением в степенной ряд

Очевидно, поскольку $cn\; +\; 1\; =\; c\; \cdot \; cn\; \{\backslash \; displaystyle\; c\; ^\; \{n\; +\; 1\}\; =\; c\; \backslash \; cdot\; c\; ^\; \{n\}\}$существует функциональное уравнение для $L\; c\; (z)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; \_\; \{c\}\; (\; z)\}$для любого z, удовлетворяющего задается как $L\; c\; (z)\; =\; zc\; +\; L\; c\; (zc)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; \_\; \{c\}\; (z)\; =\; z\; ^\; \{c\}\; +\; \{\backslash \; mathcal\; \{L\; \}\}\; \_\; \{c\}\; (z\; ^\; \{c\})\}$. Также нетрудно увидеть, что для любого целого числа $m\; \ge \; 1\; \{\backslash \; displaystyle\; m\; \backslash \; geq\; 1\}$у нас есть другое функциональное уравнение для $L\; c\; (z)\; \{\backslash \; displaystyle\; \{\; \backslash \; mathcal\; \{L\}\}\; \_\; \{c\}\; (z)\}$определяется как

Для любых положительных натуральных чисел c функция лакунарного ряда имеет простой полюс в $z:\; =\; 1\; \{\backslash \; displaystyle\; z:\; =\; 1\}$. Мы рассматриваем вопрос аналитического продолжения $L\; c\; (z)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; \_\; \{c\}\; (z)\}$на другой комплексный z такой, что $|\; \Re \; (z)\; |>1.\; \{\backslash \; displaystyle\; |\; \backslash \; Re\; (z)\; |>1.\}$Как мы увидим, для любого $n\; \ge \; 1\; \{\backslash \; displaystyle\; n\; \backslash \; geq\; 1\}$, набор $cn\; \{\; \backslash \; displaystyle\; c\; ^\; \{n\}\}$корни -й степени из единицы накладывают естественную границу на функцию $L\; c\; (z)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; \_\; \{c\}\; (z)\}$. Следовательно, поскольку множество объединения всех таких корней из единицы над $n\; \ge \; 1\; \{\backslash \; displaystyle\; n\; \backslash \; geq\; 1\}$плотно на границе единичный круг, у нас нет возможного аналитического продолжения $L\; c\; (z)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; \_\; \{c\}\; (z)\}$до комплексного z, действительные части которого превышают один.

Доказательство этого факта обобщается на основе стандартного аргумента для случая, когда $c:\; =\; 2.\; \{\backslash \; displaystyle\; c:\; =\; 2.\}$А именно, для целых чисел $n\; \ge \; 1\; \{\backslash \; displaystyle\; n\; \backslash \; geq\; 1\}$, пусть

$R\; c,\; n:\; =\; \{z\; \in \; D\; \cup \; \partial \; D:\; zcn\; =\; 1\},\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{R\}\}\; \_\; \{c,\; n\}:\; =\; \backslash \; left\; \backslash \; \{z\; \backslash \; in\; \backslash \; mathbb\; \{D\}\; \backslash \; cup\; \backslash \; partial\; \{\backslash \; mathbb\; \{D\}\}:\; z\; ^\; \{c\; ^\; \{n\}\}\; =\; 1\; \backslash \; right\; \backslash \},\}$

где $D\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{D\}\}$обозначает открытый единичный диск в комплексной плоскости, а $|\; R\; c,\; n\; |\; =\; cn\; \{\backslash \; displaystyle\; |\; \{\backslash \; mathcal\; \{R\}\}\; \_\; \{c,\; n\}\; |\; =\; c\; ^\; \{n\}\}$, то есть есть $cn\; \{\backslash \; displaystyle\; c\; ^\; \{n\}\; \}$ различные комплексные числа z, лежащие внутри или внутри единичного круга, такие что $z\; c\; n\; =\; 1\; \{\backslash \; displaystyle\; z\; ^\; \{c\; ^\; \{n\}\}\; =\; 1\}$. Теперь ключевой частью доказательства является использование функционального уравнения для $L\; c\; (z)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; \_\; \{c\}\; (z)\}$при , чтобы показать, что

$\forall \; z\; \in \; R\; c,\; n,\; L\; c\; (z)\; =\; \sum \; i\; =\; 0\; cn\; -\; 1\; zci\; +\; L\; c\; (zcn)\; =\; \sum \; i\; =\; 0\; cn\; -\; 1\; zci\; +\; L\; c\; (\; 1)\; =\; +\; \infty .\; \{\backslash \; displaystyle\; \backslash \; forall\; z\; \backslash \; in\; \{\backslash \; mathcal\; \{R\}\}\; \_\; \{c,\; n\},\; \backslash \; qquad\; \{\backslash \; mathcal\; \{L\}\}\; \_\; \{c\}\; (z)\; =\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{c\; ^\; \{n\}\; -1\}\; z\; ^\; \{c\; ^\; \{i\}\}\; +\; \{\backslash \; mathcal\; \{L\}\}\; \_\; \{c\}\; (z\; ^\; \{c\; ^\; \{n\}\})\; =\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{\; c\; ^\; \{n\}\; -1\}\; z\; ^\; \{c\; ^\; \{i\}\}\; +\; \{\backslash \; mathcal\; \{L\}\}\; \_\; \{c\}\; (1)\; =\; +\; \backslash \; infty.\}$

Таким образом, для любой дуги на границе единичной окружности, существует бесконечное количество точек z внутри этой дуги, таких что $|\; L\; c\; (z)\; |\; Знак\; равно\; +\; \infty \; \{\backslash \; displaystyle\; |\; \{\backslash \; mathcal\; \{L\}\}\; \_\; \{c\}\; (z)\; |\; =\; +\; \backslash \; infty\}$. Это условие эквивалентно тому, что окружность $C\; 1:\; =\; \{z:\; |\; z\; |\; =\; 1\}\; \{\backslash \; displaystyle\; C\_\; \{1\}:\; =\; \backslash \; \{z:\; |\; z\; |\; =\; 1\; \backslash \}\}$образует естественную границу для функции $L\; c\; (z)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; \_\; \{c\}\; (z)\}$для любого фиксированного выбора $c\; \in \; Z\; +.\; \{\backslash \; displaystyle\; c\; \backslash \; in\; \backslash \; mathbb\; \{Z\}\; ^\; \{+\}.\}$Следовательно, для этих функций нет аналитического продолжения за пределы внутренней части единичной окружности.

Теорема монодромии дает достаточное условие для существования прямого аналитического продолжения (т. Е. Расширения аналитической функции до аналитической функции на большем множестве).

Предположим, что $D\; \subset \; C\; \{\backslash \; displaystyle\; D\; \backslash \; subset\; \backslash \; mathbb\; \{C\}\}$- открытое множество, а f - аналитическая функция на D. Если G - односвязная область, содержащая D, такая, что f имеет аналитическое продолжение вдоль каждого пути в G, начиная с некоторой фиксированной точки a в D, тогда f имеет прямое аналитическое продолжение на G.

На указанном выше языке это означает, что если G - односвязная область, а S - пучок, множество базовых точек которого содержит G, то существует аналитическая функция f на G, ростки которой принадлежат S.

Для степенного ряда

$f\; (z)\; =\; \sum \; k\; =\; 0\; \infty \; akznk\; \{\backslash \; displaystyle\; f\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; a\_\; \{k\}\; z\; ^\; \{n\_\; \{k\}\}\}$

с

$lim\; inf\; k\; \to \; \infty \; nk\; +\; 1\; nk>1\; \{\backslash \; displaystyle\; \backslash \; liminf\; \_\; \{k\; \backslash \; to\; \backslash \; infty\}\; \{\backslash \; frac\; \{n\_\; \{\; k\; +\; 1\}\}\; \{n\_\; \{k\}\}\}>1\}$

круг конвергенции естественная граница. Такой степенной ряд называется лакунарным. Эта теорема была существенно обобщена Ойгеном Фабри (см. теорему Фабри о разрыве ) и Джорджем Полиа.

Пусть

$f\; (z)\; =\; \sum \; k\; =\; 0\; \infty \; \alpha \; К\; (Z\; -\; Z\; 0)\; К\; \{\backslash \; Displaystyle\; f\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \backslash \; alpha\; \_\; \{k\}\; (z-z\_\; \{0\})\; ^\; \{k\}\; \}$

- степенной ряд, то существует ε k ∈ {−1, 1} такое, что

$f\; (z)\; =\; \sum \; k\; =\; 0\; \infty \; \epsilon \; k\; \alpha \; k\; (z\; -\; z\; 0)\; к\; \{\backslash \; displaystyle\; f\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \backslash \; varepsilon\; \_\; \{k\}\; \backslash \; alpha\; \_\; \{k\}\; (z-z\_\; \{0\})\; ^\; \{k\}\}$

имеет диск сходимости f вокруг z 0 в качестве естественной границы.

Доказательство этой теоремы использует теорему Адамара о разрыве.

В большинстве случаев, если аналитическое продолжение сложной функции существует, оно задается интегральной формулой. Следующая теорема, при условии, что ее гипотезы выполнены, обеспечивает достаточное условие, при котором мы можем продолжить аналитическую функцию от ее сходящихся точек вдоль положительных вещественных чисел до произвольных $s\; \in \; C\; \{\backslash \; displaystyle\; s\; \backslash \; in\; \backslash \; mathbb\; \{C\}\}$(за исключением конечного числа полюсов). Более того, формула дает явное представление значений продолжения неположительных целых чисел, выраженных в точности исходной функцией, получившей нулевое значение.

Гипотезы теоремы

Мы требуем, чтобы функция $F:\; R\; +\; \to \; C\; \{\backslash \; displaystyle\; F:\; \backslash \; mathbb\; \{R\}\; ^\; \{+\}\; \backslash \; to\; \backslash \; mathbb\; \{C\}\}$удовлетворяет следующим условиям для применения теоремы о продолжение этой функции, указанной ниже:

• (T-1). Функция должна иметь непрерывные производные всех порядков, т. е. $F\; \in \; C\; \infty \; (R\; +)\; \{\backslash \; displaystyle\; F\; \backslash \; in\; \{\backslash \; mathcal\; \{C\}\}\; ^\; \{\backslash \; infty\}\; (\backslash \; mathbb\; \{R\}\; ^\; \{+\})\}$. Другими словами, для любых целых чисел $j\; \ge \; 1\; \{\backslash \; displaystyle\; j\; \backslash \; geq\; 1\}$, целочисленный порядок $jth\; \{\backslash \; displaystyle\; j\; ^\; \{th\}\}$производная $F\; (j)\; (x)\; =\; d\; (j)\; dx\; (j)\; [F\; (x)]\; \{\backslash \; displaystyle\; F\; ^\; \{(j)\}\; (x)\; =\; \{\backslash \; frac\; \{d\; ^\; \{(j)\}\}\; \{dx\; ^\; \{(j)\}\}\}\; [F\; (x)]\}$должен существовать, быть непрерывным на $R\; +\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{R\}\; ^\; \{+\}\}$и сам быть дифференцируемым, так что все производные высшего порядка от F являются гладкими функциями x от положительных действительных чисел;
• (T-2 Мы требуем, чтобы функция F быстро убывала, чтобы для всех $n\; \in \; Z\; +\; \{\backslash \; displaystyle\; n\; \backslash \; in\; \backslash \; mathbb\; \{Z\}\; ^\; \{+\}\}$мы получили ограничивающее поведение, при котором $tn\; F\; (t)\; \to \; 0\; \{\backslash \; displaystyle\; t\; ^\; \{n\}\; F\; (t)\; \backslash \; to\; 0\}$, когда t становится неограниченным, стремящимся к бесконечности;
• (T- 3). (обратное гамма-масштабирование) преобразование Меллина функции F существует для всех сложных s таких, что $\Re \; (s)>0\; \{\backslash \; displaystyle\; \backslash \; Re\; (s)>0\}$за исключением $s\; \in \; \{\zeta \; 1\; (F),\; \zeta \; 2\; (F),\dots \; \zeta \; К\; (F)\}\; \{\backslash \; Displaystyle\; s\; \backslash \; в\; \backslash \; \{\backslash \; zeta\; \_\; \{1\}\; (F),\; \backslash \; zeta\; \_\; \{2\}\; (F),\; \backslash \; ldots,\; \backslash \; zeta\; \_\; \{k\}\; (F)\; \backslash \}\}$(или для всех s с положительными действительными частями, кроме, возможно, конечного числа исключительных полюсов):

$M\; ~\; [F]\; (s):\; =\; 1\; \Gamma \; (s)\; \int \; 0\; \infty \; ts\; F\; (\; t)\; dtt,\; |\; M\; ~\; [F]\; (s)\; |\; \in \; (-\; \infty ,\; +\; \infty ),\; s\; \in \; \{z\; \in \; C:\; \Re \; (z)>0\}\; \setminus \; \{\zeta \; 1\; (F),\dots ,\; \zeta \; k\; (F)\}.\; \{\backslash \; displaystyle\; \{\backslash \; widetilde\; \{\backslash \; mathcal\; \{M\}\}\}\; [F]\; (s):\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; Gamma\; (s)\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; t\; ^\; \{\; s\}\; F\; (t)\; \{\backslash \; frac\; \{dt\}\; \{t\}\},\; \backslash \; qquad\; \backslash \; left\; |\; \{\backslash \; widetilde\; \{\backslash \; mathcal\; \{M\}\}\}\; [F]\; (s)\; \backslash \; right\; |\; \backslash \; in\; (-\; \backslash \; infty,\; +\; \backslash \; infty),\; \backslash \; forall\; s\; \backslash \; in\; \backslash \; \{z\; \backslash \; in\; \backslash \; mathbb\; \{C\}:\; \backslash \; Re\; (z)>0\; \backslash \}\; \backslash \; setminus\; \backslash \; \{\backslash \; zeta\; \_\; \{1\}\; (F),\; \backslash \; ldots,\; \backslash \; zeta\; \_\; \{\; k\}\; (F)\; \backslash \}.\}$

Заключение теоремы

Пусть F - любая функция, определенная на положительных вещественных числах, которая удовлетворяет всем условиям (T1) - (T3) выше. Тогда интегральное представление масштабированного преобразования Меллина функции F в точке s, обозначенное $M\; ~\; [F]\; (s)\; \{\backslash \; displaystyle\; \{\backslash \; widetilde\; \{\backslash \; mathcal\; \{M\}\}\}\; [F]\; (s)\}$, имеет мероморфное продолжение до комплексная плоскость $C\; \setminus \; \{\zeta \; 1\; (F),\dots ,\; \zeta \; K\; (F)\}\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{C\}\; \backslash \; setminus\; \backslash \; \{\backslash \; zeta\; \_\; \{1\}\; (F),\; \backslash \; ldots,\; \backslash \; zeta\; \_\; \{k\}\; (F)\; \backslash \}\}$. Более того, у нас есть, что для любого неотрицательного $n\; \in \; Z\; \{\backslash \; displaystyle\; n\; \backslash \; in\; \backslash \; mathbb\; \{Z\}\}$продолжение F в точке $s:\; =\; -\; n\; \{\backslash \; displaystyle\; s:\; =\; -\; n\}$явно задается формулой

$M\; ~\; [F]\; (-\; n)\; =\; (-\; 1)\; n\; \times \; F\; (n)\; (0)\; \equiv \; (-\; 1)\; n\; \times \; \partial \; n\; \partial \; xn\; [F\; (x)]\; |\; х\; =\; 0.\; \{\backslash \; Displaystyle\; \{\backslash \; widetilde\; \{\backslash \; mathcal\; \{M\}\}\}\; [F]\; (-\; n)\; =\; (-\; 1)\; ^\; \{n\}\; \backslash \; times\; F\; ^\; \{(n)\}\; (0)\; \backslash \; Equiv\; (-1)\; ^\; \{\; n\}\; \backslash \; times\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{n\}\}\; \{\{\backslash \; partial\; x\}\; ^\; \{n\}\}\}\; \backslash \; left\; [F\; (x)\; \backslash \; right]\; |\; \_\; \{x\; =\; 0\}.\}$

Примеры

Пример I. Связь дзета-функции Римана с числами Бернулли

Мы можем применить теорему к функции

$F\; \zeta \; (x):\; =\; xex\; -\; 1\; =\; \sum \; n\; \ge \; 0\; B\; nxnn!,\; \{\backslash \; displaystyle\; F\; \_\; \{\backslash \; zeta\}\; (x):\; =\; \{\backslash \; frac\; \{x\}\; \{e\; ^\; \{x\}\; -1\}\}\; =\; \backslash \; sum\; \_\; \{n\; \backslash \; geq\; 0\}\; B\_\; \{n\}\; \{\backslash \; frac\; \{x\; ^\; \{n\}\}\; \{n!\}\},\}$

, что соответствует экспоненциальной производящей функции чисел Бернулли, $B\; n\; \{\backslash \; displaystyle\; B\_\; \{n\}\; \}$. Для $\Re \; (s)>1\; \{\backslash \; displaystyle\; \backslash \; Re\; (s)>1\}$, мы можем выразить $\zeta \; (s)\; =\; M\; ~\; [F\; \zeta ]\; (s)\; \{\backslash \; displaystyle\; \backslash \; zeta\; (s)\; =\; \{\; \backslash \; widetilde\; \{\backslash \; mathcal\; \{M\}\}\}\; [F\; \_\; \{\backslash \; zeta\}]\; (s)\}$, поскольку мы можем вычислить следующую интегральную формулу для обратных степеней целых чисел $n\; \ge \; 1\; \{\backslash \; displaystyle\; n\; \backslash \; geq\; 1\}$выполняется для s в этом диапазоне:

$1\; ns\; =\; 1\; \Gamma \; (s)\; \int \; 0\; +\; \infty \; ts\; -\; 1\; e\; -\; ntdt,\; \Re \; (s)>1.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{n\; ^\; \{s\}\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; Gamma\; (s)\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{+\; \backslash \; infty\}\; t\; ^\; \{s-1\; \}\; e\; ^\; \{-\; nt\}\; dt,\; \backslash \; Re\; (s)>1.\}$

Теперь, поскольку подынтегральное выражение последнего уравнения является равномерно непрерывной функцией t для каждого положительного целого числа n, мы имеем интегральное представление для $\zeta \; (s)\; \{\backslash \; displaystyle\; \backslash \; zeta\; (s)\}$всякий раз, когда $\Re \; (s)>1\; \{\backslash \; displaystyle\; \backslash \; Re\; (s)>1\}$задано

$\zeta \; (s)\; =\; \sum \; n\; \ge \; 1\; n\; -\; s\; =\; 1\; \Gamma \; (s)\; \int \; 0\; +\; \infty \; (\sum \; n\; \ge \; 1\; e\; -\; nt)\; ts\; -\; 1\; dt\; =\; 1\; \Gamma \; (s)\; \int \; 0\; \infty \; ts\; -\; 1\; F\; \zeta \; (t)\; tdt.\; \{\backslash \; displaystyle\; \backslash \; zeta\; (s)\; =\; \backslash \; sum\; \_\; \{n\; \backslash \; geq\; 1\}\; n\; ^\; \{-\; s\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; Gamma\; (s)\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{+\; \backslash \; infty\; \}\; \backslash \; left\; (\backslash \; sum\; \_\; \{n\; \backslash \; geq\; 1\}\; e\; ^\; \{-\; nt\}\; \backslash \; right)\; t\; ^\; \{s-1\}\; dt\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; Gamma\; (s)\}\}\; \backslash \; int\; \_\; \{0\; \}\; ^\; \{\backslash \; infty\}\; t\; ^\; \{s-1\}\; \{\backslash \; frac\; \{F\; \_\; \{\backslash \; zeta\}\; (t)\}\; \{t\}\}\; dt.\}$

Когда мы выполняем интегрирование по частям с преобразование Меллина интеграл для этого $F\; \zeta \; (x)\; \{\backslash \; displaystyle\; F\; \_\; \{\backslash \; zeta\}\; (x)\}$, мы также получаем соотношение, что

$\zeta \; (s)\; =\; 1\; (s\; -\; 1)\; M\; ~\; [F\; \zeta ]\; (s\; -\; 1).\; \{\backslash \; displaystyle\; \backslash \; zeta\; (s)\; =\; \{\backslash \; frac\; \{1\}\; \{(s-1)\}\}\; \{\backslash \; widetilde\; \{\backslash \; mathcal\; \{M\}\}\}\; [F\; \_\; \{\backslash \; zeta\}]\; (s-1).\}$

Более того, поскольку $et\; \gg \; tn\; \{\backslash \; displaystyle\; e\; ^\; \{t\}\; \backslash \; gg\; t\; ^\; \{n\}\}$для любой фиксированной целочисленной полиномиальной степени t, мы удовлетворяем гипотезе теоремы, которая требует что $lim\; t\; \to \; +\; \infty \; tn\; \cdot \; F\; \zeta \; (t),\; \forall \; n\; \in \; Z\; +\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{t\; \backslash \; to\; +\; \backslash \; infty\}\; t\; ^\; \{n\}\; \backslash \; cdot\; F\; \_\; \{\backslash \; zeta\}\; (t),\; \backslash \; forall\; n\; \backslash \; in\; \backslash \; mathbb\; \{Z\}\; ^\; \{+\}\}$. Стандартное применение теоремы Тейлора к обычной производящей функции чисел Бернулли показывает, что $F\; \zeta \; (n)\; (0)\; =\; B\; n\; n!\; \times \; п!\; =\; B\; n\; \{\backslash \; displaystyle\; F\; \_\; \{\backslash \; zeta\}\; ^\; \{(n)\}\; (0)\; =\; \{\backslash \; frac\; \{B\_\; \{n\}\}\; \{n!\}\}\; \backslash \; Times\; n!\; =\; B\_\; \{n\}\}$. В частности, с помощью наблюдения, сделанного выше для сдвига $s\; \mapsto \; s\; -\; 1\; \{\backslash \; displaystyle\; s\; \backslash \; mapsto\; s-1\}$, и этих замечаний, мы можем вычислить значения так называемого тривиальные нули дзета-функции Римана (для $\zeta \; (-\; 2\; n)\; \{\backslash \; displaystyle\; \backslash \; zeta\; (-2n)\}$) и рационального- оцененные отрицательные нечетные целочисленные константы порядка, $\zeta \; (-\; (2\; n\; +\; 1)),\; n\; \ge \; 0\; \{\backslash \; displaystyle\; \backslash \; zeta\; (-\; (2n\; +\; 1)),\; n\; \backslash \; geq\; 0\}$, согласно формуле

$\zeta \; (-\; n)\; =\; -\; 1\; n\; +\; 1\; M\; ~\; [F\; \zeta ]\; (-\; n\; -\; 1)\; =\; (-\; 1)\; nn\; +\; 1\; F\; \zeta \; (n\; +\; 1)\; (0)\; =\; \{\; -\; 1\; 2,\; n\; =\; 0;\; \infty ,\; n\; =\; 1;\; -\; В\; n\; +\; 1\; n\; +\; 1,\; n\; \ge \; 2.\; \{\backslash \; displaystyle\; \backslash \; zeta\; (-n)\; =\; -\; \{\backslash \; frac\; \{1\}\; \{n\; +\; 1\}\}\; \{\backslash \; widetilde\; \{\backslash \; mathcal\; \{M\}\}\}\; [F\_\; \{\; \backslash \; zeta\}]\; (-\; n-1)\; =\; \{\backslash \; frac\; \{(-1)\; ^\; \{n\}\}\; \{n\; +\; 1\}\}\; F\; \_\; \{\backslash \; zeta\}\; ^\; \{(n\; +\; 1)\}\; (0)\; =\; \{\backslash \; begin\; \{case\}\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\},\; n\; =\; 0;\; \backslash \backslash \backslash \; infty,\; n\; =\; 1;\; \backslash \backslash \; -\; \{\backslash \; frac\; \{B\_\; \{n\; +\; 1\}\}\; \{n\; +\; 1\}\},\; n\; \backslash \; geq\; 2.\; \backslash \; end\; \{ases\}\}\}$

Пример II: Интерпретация F как сумматорной функции для некоторой арифметической последовательности

Предположим, что F - гладкая, достаточно убывающая функция на положительных вещественных числах, удовлетворяющая дополнительное условие, что

$\Delta \; [F]\; (x\; -\; 1)\; =\; F\; (x)\; -\; F\; (x\; -\; 1)\; =:\; f\; (x),\; \forall \; x\; \in \; Z\; +.\; \{\backslash \; Displaystyle\; \backslash \; Delta\; [F]\; (x-1)\; =\; F\; (x)\; -F\; (x-1)\; =:\; f\; (x),\; \backslash \; forall\; x\; \backslash \; in\; \backslash \; mathbb\; \{Z\}\; ^\; \{+\}.\}$

Применительно к теоретико-числовым контекстам, мы рассматриваем такое F как суммирующую функцию арифметической функции f,

$F\; (x):\; =\; \sum \; N\; \ge \; x\; \prime \; f\; (n)\; \{\backslash \; displaystyle\; F\; (x):\; =\; \{\backslash \; sum\; \_\; \{n\; \backslash \; geq\; x\}\}\; ^\; \{\backslash \; prime\}\; f\; (n)\}$

где мы берем , а простое обозначение в предыдущей сумме соответствует стандартным соглашениям, используемым для формулировки теоремы Перрона :

$F\; f\; (x):\; =\; \sum \; n\; \le \; x\; \prime \; f\; (n)\; =\; \{\sum \; n\; \le \; [x]\; f\; (n),\; x\; \in \; R\; +\; \setminus \; Z;\; \sum \; n\; \le \; x\; f\; (n)\; -\; f\; (x)\; 2,\; x\; \in \; R\; +\; \cap \; Z.\; \{\backslash \; displaystyle\; F\_\; \{f\}\; (x):\; =\; \{\backslash \; sum\; \_\; \{n\; \backslash \; leq\; x\}\}\; ^\; \{\backslash \; prime\}\; f\; (n)\; =\; \{\backslash \; begin\; \{case\}\; \backslash \; sum\; \_\; \{n\; \backslash \; leq\; [x]\}\; f\; (n),\; x\; \backslash \; in\; \backslash \; mathbb\; \{R\}\; ^\; \{+\}\; \backslash \; setminus\; \backslash \; mathbb\; \{Z\};\; \backslash \backslash \backslash \; sum\; \_\; \{n\; \backslash \; leq\; x\}\; f\; (n)\; -\; \{\backslash \; frac\; \{f\; (x)\}\; \{2\}\},\; x\; \backslash \; in\; \backslash \; mathbb\; \{R\}\; ^\; \{+\}\; \backslash \; cap\; \backslash \; mathbb\; \{Z\}.\; \backslash \; End\; \{cases\}\}\}$

Нас интересует аналитическое продолжение DGF f, или, что эквивалентно, ряда Дирихле над f в s,

$D\; f\; (s):\; =\; \sum \; n\; \ge \; 1\; f\; (n)\; ns.\; \{\backslash \; displaystyle\; D\_\; \{f\}\; (s):\; =\; \backslash \; sum\; \_\; \{n\; \backslash \; geq\; 1\}\; \{\backslash \; frac\; \{f\; (n)\}\; \{n\; ^\; \{s\}\}\}.\}$

Как правило, у нас есть определенное значение абсциссы сходимости , $\sigma \; 0,\; f>0\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{0,\; f\}>0\}$, определяемый таким образом, что $D\; f\; (s)\; \{\backslash \; displaystyle\; D\_\; \{f\}\; (s)\}$абсолютно сходится для всех сложных s, удовлетворяющих $\Re \; (s)>\sigma \; 0,\; f\; \{\backslash \; displaystyle\; \backslash \; Re\; (s)>\backslash \; sigma\; \_\; \{0,\; f\}\; \}$, и где $D\; f\; (s)\; \{\backslash \; displaystyle\; D\_\; \{f\}\; (s)\}$предполагается иметь полюс в $s:\; =\; \pm \; \sigma \; 0,\; f\; \{\backslash \; displaystyle\; s:\; =\; \backslash \; pm\; \backslash \; sigma\; \_\; \{0,\; f\}\}$и так, чтобы исходный ряд Дирихле для $D\; f\; (s)\; \{\backslash \; displaystyle\; D\_\; \{f\}\; (\; s)\}$расходится для всех s таких, что $\Re \; (s)\; \le \; \sigma \; 0,\; е\; \{\backslash \; Displaystyle\; \backslash \; Re\; (s)\; \backslash \; Leq\; \backslash \; sigma\; \_\; \{0,\; f\}\}$. Известно, что существует связь между преобразованием Меллина сумматорной функции любого f и продолжением его DGF в $s\; \mapsto \; -\; s\; \{\backslash \; displaystyle\; s\; \backslash \; mapsto\; -s\}$формы:

$D\; f\; (s)\; =\; M\; [F]\; (-\; s)\; =\; \int \; 1\; \infty \; F\; f\; (s)\; xs\; +\; 1\; dx\; \{\backslash \; displaystyle\; D\_\; \{f\}\; (s)\; =\; \{\; \backslash \; mathcal\; \{M\}\}\; [F]\; (-\; s)\; =\; \backslash \; int\; \_\; \{1\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{F\_\; \{f\}\; (s)\}\; \{x\; ^\; \{s\; +\; 1\}\}\}\; dx\}$

То есть при условии, что $D\; f\; (s)\; \{\backslash \; displaystyle\; D\_\; \{f\}\; (s)\}$имеет продолжение на комплексную плоскость слева от начала координат, мы можем выразить Суммирующая функция любого f посредством DGF функции f продолжается до s с вещественными частями меньше нуля, как:

$F\; f\; (x)\; =\; M\; -\; 1\; [M\; [F\; f]\; (-\; s)]\; (x)\; =\; M\; -\; 1\; [D\; f\; (-\; s)]\; (x).\; \{\backslash \; displaystyle\; F\_\; \{f\}\; (x)\; =\; \{\backslash \; mathcal\; \{M\}\}\; ^\; \{-\; 1\}\; \backslash \; left\; [\{\backslash \; mathcal\; \{M\}\}\; [F\_\; \{f\}]\; (-\; s)\; \backslash \; right]\; (x)\; =\; \{\backslash \; mathcal\; \{M\}\}\; ^\; \{-\; 1\}\; [D\_\; \{f\}\; (-\; s)]\; (x).\}$

Мы можем сформировать DGF или производящую функцию Дирихле любой предписанной f для нашей гладкой целевой функции F путем выполнения суммирования по частям как

$D f (s) = 1 Γ (s) ∫ 0 + ∞ (∑ n ≥ 1 (F (n) - F ( n - 1)) e - nt) tsdt = 1 Γ (s) ∫ 0 ∞ lim N → ∞ [F (N) e - N t + ∑ k = 0 N - 1 F (k) e - kt (1 - e - t)] dt = 1 Γ (s) ∫ 0 ∞ ts - 1 (1 - e - t) ∫ 0 ∞ F (r / t) e - rdrdt = 1 Γ (s) ∫ 0 ∞ ts - 1 ( 1 - е - t) F ~ (1 t) dt = 1 Γ (s) ∫ 0 ∞ (1 - e - 1 / u) нас (1 - u) F (u 1 - u) du, {\ displaystyle { \ begin {align} D_ {f} (s) = {\ frac {1} {\ Gamma (s)}} \ int _ {0} ^ {+ \ infty} \ left (\ sum _ {n \ geq 1} (F (n) -F (n-1)) e ^ {- nt} \ right) t ^ {s} dt \\ = {\ frac {1} {\ Gamma (s)}} \ int _ {0} ^ {\ infty} \ lim _ {N \ to \ infty} \ left [F (N) e ^ {- Nt} + \ sum _ {k = 0} ^ {N-1} F (k) e ^ {- kt} \ left (1-e ^ {- t} \ right) \ right] dt \\ = {\ frac {1} {\ Gamma (s)}} \ int _ {0} ^ {\ inft y} t ^ {s-1} (1-e ^ {- t}) \ int _ {0} ^ {\ infty} F (r / t) e ^ {- r} drdt \\ = {\ frac {1} {\ Gamma (s)}} \ int _ {0} ^ {\ infty} t ^ {s-1} \ left (1-e ^ {- t} \ right) {\ widetilde {F}} \ left ({\ frac {1} {t}} \ right) dt \\ = {\ frac {1} {\ Gamma (s)}} \ int _ {0} ^ {\ infty} {\ frac { \ left (1-e ^ {- 1 / u} \ right)} {u ^ {s} (1-u)}} F \ left ({\ frac {u} {1-u}} \ right) du, \ end {align}}}$

где $F\; ^\; (x)\; \equiv \; L\; [F]\; (x)\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{F\}\}\; (x)\; \backslash \; Equiv\; \{\backslash \; mathcal\; \{L\}\}\; [F]\; (x)\}$- это преобразование Лапласа-Бореля F, которое, если

$F\; (z):\; =\; \sum \; n\; \ge \; 0\; fnn!\; zn\; \{\backslash \; displaystyle\; F\; (z):\; =\; \backslash \; sum\; \_\; \{n\; \backslash \; geq\; 0\}\; \{\backslash \; frac\; \{f\_\; \{n\}\}\; \{n!\}\}\; z\; ^\; \{n\}\}$

соответствует экспоненциальному , генерирующему функция некоторой последовательности, пронумерованной $fn\; /\; n!\; =\; F\; (п)\; (0)\; /\; п!\; \{\backslash \; displaystyle\; f\_\; \{n\}\; /\; n!\; =\; F\; ^\; \{(n)\}\; (0)\; /\; n!\}$(как предписано разложением F в ряд Тейлора около нуля), затем

$F\; ~\; (z)\; =\; \sum \; N\; \ge \; 0\; fnzn\; \{\backslash \; displaystyle\; \{\backslash \; widetilde\; \{F\}\}\; (z)\; =\; \backslash \; sum\; \_\; \{n\; \backslash \; geq\; 0\}\; f\_\; \{n\}\; z\; ^\; \{n\}\}$

- его обычное порождение форма функции над последовательностью, коэффициенты которой пронумерованы как $[zn]\; F\; ~\; (z)\; \equiv \; fn\; =\; F\; (n)\; (0)\; \{\backslash \; displaystyle\; [z\; ^\; \{n\}]\; \{\backslash \; widetilde\; \{F\}\}\; (z)\; \backslash \; Equiv\; f\_\; \{n\}\; =\; F\; ^\; \{(n)\}\; (0)\}$.

Отсюда следует, что если мы напишем

$GF\; (x):\; =\; x\; 1\; -\; x\; F\; (x\; 1\; -\; x)\; =\; \sum \; N\; \ge \; 0\; (\sum \; К\; знак\; равно\; 0\; N\; (nk)\; [zk]\; F\; (z))\; xn\; +\; 1,\; \{\backslash \; displaystyle\; G\_\; \{F\}\; (x):\; =\; \{\backslash \; frac\; \{x\}\; \{1-x\}\}\; F\; \backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{1-x\}\}\; \backslash \; right)\; =\; \backslash \; sum\; \_\; \{n\; \backslash \; geq\; 0\}\; \backslash \; left\; (\backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{n\}\; \{\backslash \; binom\; \{n\}\; \{\; k\}\}\; [z\; ^\; \{k\}]\; F\; (z)\; \backslash \; right)\; x\; ^\; \{n\; +\; 1\},\}$

поочередно интерпретируется как вариант со знаком биномиального преобразования F, тогда мы может выразить DGF как следующее преобразование Меллина в $-\; s\; \{\backslash \; displaystyle\; -s\}$:

$D\; f\; (s)\; =\; M\; [GF]\; (-\; s)\; M\; [1\; -\; e\; -\; 1\; /\; x]\; (-\; s)\; =\; M\; [GF]\; (-\; s)\; s\; -\; 1\; (1\; -\; \Gamma \; (\; s))\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; D\_\; \{f\}\; (s)\; =\; \{\backslash \; mathcal\; \{M\}\}\; [G\_\; \{F\}]\; (-\; s)\; \{\backslash \; mathcal\; \{M\}\}\; \backslash \; left\; [1-\; e\; ^\; \{-\; 1\; /\; x\}\; \backslash \; right]\; (-\; s)\; \backslash \backslash \; =\; \{\backslash \; frac\; \{\{\backslash \; mathcal\; \{M\}\}\; [G\_\; \{F\}]\; (-\; s)\}\; \{s-1\}\}\; \backslash \; left\; (\; 1-\; \backslash \; Gamma\; (s)\; \backslash \; right)\; \backslash \; end\; \{align\}\}\}$

Наконец, поскольку гамма-функция имеет мероморфное продолжение до $C\; \setminus \; N\; \{\; \backslash \; displaystyle\; \backslash \; mathbb\; \{C\}\; \backslash \; setminus\; \backslash \; mathbb\; \{N\}\}$, для всех $s\; \in \; C\; \setminus \; \{0,\; 1,\; 2,\dots \},\; \{\backslash \; displaystyle\; s\; \backslash \; in\; \backslash \; mathbb\; \{\; C\}\; \backslash \; setminus\; \backslash \; \{0,1,2,\; \backslash \; ldots\; \backslash \},\}$у нас есть аналитическое продолжение DGF для f at -s вида

$D\; f\; (-\; s)\; =\; -\; 1\; -\; \Gamma \; (-\; s)\; s\; +\; 1\; M\; [GF]\; (s),\; \{\backslash \; displaystyle\; D\_\; \{f\}\; (-\; s)\; =\; -\; \{\backslash \; frac\; \{1-\; \backslash \; Gamma\; (-s)\}\; \{s\; +\; 1\}\; \}\; \{\backslash \; mathcal\; \{M\}\}\; [G\_\; \{F\}]\; (s),\}$

где формула для $D\; f\; (-\; n)\; \{\backslash \; displaystyle\; D\_\; \{f\}\; (-\; n)\}$для неотрицательных целых чисел n задается согласно формуле теоремы как

$D\; f\; (-\; n)\; =\; (-\; 1)\; ndndxn\; [(1\; -\; e\; -\; 1\; /\; x)\; x\; 1\; -\; x\; F\; (\; х\; 1\; -\; х)]\; |\; х\; =\; 0.\; \{\backslash \; displaystyle\; D\_\; \{f\}\; (-\; n)\; =\; (-\; 1)\; ^\; \{n\}\; \{\backslash \; frac\; \{d\; ^\; \{n\}\}\; \{\{dx\}\; ^\; \{n\}\}\}\; \backslash \; left\; [\backslash \; left\; (1-e\; ^\; \{-1\; /\; x\}\; \backslash \; right)\; \{\backslash \; frac\; \{x\}\; \{1-x\}\}\; F\; \backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{1-x\}\}\; \backslash \; right)\; \backslash \; right]\; \{\backslash \; Biggr\; |\}\; \_\; \{\; x\; =\; 0\}.\}$

Более того, при условии, что арифметическая функция f удовлетворяет $f\; (1)\; \ne \; 1\; \{\backslash \; displaystyle\; f\; (1)\; \backslash \; neq\; 1\}$, так что ее обратная функция Дирихле существует, DGF $f\; -\; 1\; \{\backslash \; displaystyle\; f\; ^\; \{-\; 1\}\}$продолжается до любого $s\; \in \; C\; \cap \; \{z:\; \Re \; (z)\; \in \; (-\; \infty ,\; -\; \sigma \; 0,\; е)\; \cup \; (\sigma \; 0,\; е,\; +\; \infty )\}\; \{\backslash \; Displaystyle\; s\; \backslash \; in\; \backslash \; mathbb\; \{C\}\; \backslash \; cap\; \backslash \; \{z:\; \backslash \; Re\; (z)\; \backslash \; in\; (-\; \backslash \; infty,\; -\; \backslash \; sigma\; \_\; \{0,\; f\})\; \backslash \; cup\; (\backslash \; sigma\; \_\; \{0,\; f\},\; +\; \backslash \; infty)\; \backslash \}\}$, то есть любой комплекс s, за исключением s в f-определяемом или зависящем от приложения f- специфическая, так называемая критическая полоса между вертикальными линиями $z\; =\; \pm \; \sigma \; 0,\; f\; \{\backslash \; displaystyle\; z\; =\; \backslash \; pm\; \backslash \; sigma\; \_\; \{0,\; f\}\}$, и значение этой обратной функции DGF при определяется как

$D\; f\; -\; 1\; (-\; s)\; =\; \{0,\; n\; \in \; N;\; -\; s\; +\; 1\; 1\; -\; \Gamma \; (-\; s)\; M\; [G\; F\; -\; 1]\; (s)\; в\; противном\; случае.\; \{\backslash \; Displaystyle\; D\_\; \{е\; ^\; \{-\; 1\}\}\; (-\; s)\; =\; \{\backslash \; begin\; \{case\}\; 0,\; n\; \backslash \; in\; \backslash \; mathbb\; \{N\};\; \backslash \backslash \; -\; \{\backslash \; frac\; \{s\; +\; 1\}\; \{1-\; \backslash \; Gamma\; (-s)\}\}\; \{\backslash \; mathcal\; \{M\}\}\; [G\_\; \{F\}\; ^\; \{-\; 1\}]\; (s),\; \{\backslash \; text\; \{в\; противном\; случае.\}\}\; \backslash \; end\; \{cases\}\}\}$

Чтобы продолжить DGF функции Дирихле, обратной к s внутри этой f-определенной критической полосы, мы должны требовать некоторых знаний функционального уравнения для DGF, $D\; f\; (s)\; \{\backslash \; displaystyle\; D\_\; \{f\}\; (s)\}$, что позволяет нам связать s таким образом, что ряд Дирихле, который изначально определяет эту функцию, абсолютно сходится к значениям s внутри этой полосы - по сути, формула, обеспечивающая, что $D\; е\; (s)\; знак\; равно\; \xi \; е\; (s)\; \times \; D\; е\; (\sigma \; 0,\; f\; -\; s)\; \{\backslash \; displaystyle\; D\_\; \{f\}\; (s)\; =\; \backslash \; xi\; \_\; \{f\}\; (s)\; \backslash \; times\; D\_\; \{f\}\; (\; \backslash \; sigma\; \_\; \{0,\; f\}\; -s)\}$необходимо для определения DGF в этой полосе.

• звезда Миттаг-Леффлера
• Голоморфное функциональное исчисление

• Ларс Альфорс (1979). Комплексный анализ (3-е изд.). Макгроу-Хилл. С. 172, 284.
• Людвиг Бибербах (1955). Analytische Fortsetzung. Спрингер-Верлаг.
• П. Диенес (1957). Серия Тейлора: введение в теорию functions of a complex variable. New York: Dover Publications, Inc.

• , Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Analytic Continuation at MathPages
• Weisstein, Eric W. "Analytic Continuation". MathWorld.