Интегрирование по частям

В исчислении и в более общем плане в математическом анализе, интегрировании по частям или частичное интегрирование - это процесс, который находит интеграл от произведения функций в терминах интеграла от произведения их производной и первообразный. Он часто используется для преобразования первообразной произведения функций в первообразную, для которой легче найти решение. Правило можно рассматривать как интегральную версию правила произведения дифференциации.

Если $u\; =\; u\; (x)\; \{\backslash \; displaystyle\; u\; =\; u\; (x)\}$и $du\; =\; u\; \text{'}(x)\; dx\; \{\backslash \; displaystyle\; du\; =\; u\text{'}\; (x)\; \backslash ,\; dx\}$, а $v\; =\; v\; (x)\; \{\backslash \; displaystyle\; v\; =\; v\; (x)\}$и $dv\; =\; v\; \prime \; (x)\; dx\; \{\backslash \; displaystyle\; dv\; =\; v\; \text{'}(x)\; dx\}$, тогда формула интегрирования по частям указывает что

$\int \; abu\; (x)\; v\; \prime \; (x)\; dx\; =\; [u\; (x)\; v\; (x)]\; ab\; -\; \int \; abu\; \prime \; (x)\; v\; (x)\; dx\; =\; u\; (b)\; v\; (b)\; -\; u\; (а)\; v\; (a)\; -\; \int \; abu\; \prime \; (x)\; v\; (x)\; dx.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; u\; (x)\; v\; \text{'}(x)\; \backslash ,\; dx\; =\; \{\backslash \; Big\; [\}\; u\; (x)\; v\; (x)\; \{\backslash \; Big]\}\; \_\; \{a\}\; ^\; \{b\}\; -\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; u\; \text{'}(x)\; v\; (x)\; \backslash ,\; dx\; \backslash \backslash \; [6pt]\; =\; u\; (b)\; v\; (b)\; -u\; (a)\; v\; (a)\; -\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; u\; \text{'}(x)\; v\; (x)\; \backslash ,\; dx.\; \backslash \; end\; \{align\}\}\}$

Более компактно,

$\int \; udv\; =\; uv\; -\; \int \; vdu.\; \{\backslash \; displaystyle\; \backslash \; int\; u\; \backslash ,\; dv\; \backslash \; =\; \backslash \; uv-\; \backslash \; int\; v\; \backslash ,\; du.\}$

Математик Брук Тейлор обнаружил интеграцию по частям, впервые опубликовав идею в 1715. Более общие формулировки интегрирования по частям существуют для интегралов Римана – Стилтьеса и Лебега – Стилтьеса. Дискретный аналог для последовательностей называется суммированием по частям.

Содержание

• 1 Теорема
  • 1.1 Произведение двух функций
  • 1.2 Справедливость для менее гладких функций
  • 1.3 Произведение многих функций
• 2 Визуализация
• 3 Приложения
  • 3.1 Поиск первообразных
    • 3.1.1 Полиномы и тригонометрические функции
    • 3.1.2 Экспоненты и тригонометрические функции
    • 3.1.3 Функции, умноженные на единицу
    • 3.1.4 LIATE правило
  • 3.2 Произведение Уоллиса
  • 3.3 Тождество гамма-функции
  • 3.4 Использование в гармоническом анализе
    • 3.4.1 Преобразование Фурье производной
    • 3.4.2 Распад преобразования Фурье
  • 3.5 Использование в теории операторов
  • 3.6 Другие приложения
• 4 Многократное интегрирование по частям
  • 4.1 Табличное интегрирование по частям
• 5 Высшие измерения
  • 5.1 Первая идентичность Грина
• 6 См. Также
• 7 Примечания
• 8 Дополнительная литература
• 9 Внешние ссылки

Теорема

Произведение двух функций

Теорема может быть получена следующим образом. Для двух непрерывно дифференцируемых функций u (x) и v (x) правило произведения утверждает:

$(u\; (x)\; v\; (x))\; \prime \; =\; V\; (x)\; u\; \prime \; (x)\; +\; u\; (x)\; v\; \prime \; (x).\; \{\backslash \; displaystyle\; \{\backslash \; Big\; (\}\; u\; (x)\; v\; (x)\; \{\backslash \; Big)\}\; \text{'}\backslash \; =\; \backslash \; v\; (x)\; u\text{'}\; (x)\; +\; u\; (x)\; v\; \text{'}(x).\}$

Интегрирование обе стороны относительно x,

$\int \; (u\; (x)\; v\; (x))\; \prime \; dx\; =\; \int \; u\; \prime \; (x)\; v\; (x)\; dx\; +\; \int \; u\; (x)\; v\; \prime \; (x)\; dx,\; \{\backslash \; displaystyle\; \backslash \; int\; \{\backslash \; Big\; (\}\; u\; (x)\; v\; (x)\; \{\backslash \; Big)\}\; \text{'}\backslash ,\; dx\; \backslash \; =\; \backslash \; \backslash \; int\; u\text{'}\; (x)\; v\; (x)\; \backslash ,\; dx\; +\; \backslash \; int\; u\; (x)\; v\; \text{'}\; (x)\; \backslash ,\; dx,\}$

и отметив, что неопределенный интеграл является первообразной, дает

$u\; (x)\; v\; (x)\; =\; \int \; u\; \prime \; (x)\; v\; (x)\; dx\; +\; \int \; U\; (Икс)\; v\; \text{'}(Икс)\; dx,\; \{\backslash \; Displaystyle\; u\; (x)\; v\; (x)\; \backslash \; =\; \backslash \; \backslash \; int\; u\text{'}\; (x)\; v\; (x)\; \backslash ,\; dx\; +\; \backslash \; int\; u\; (x)\; v\; \text{'}(\; x)\; \backslash ,\; dx,\}$

где мы пренебрегаем записью константы интегрирования . Это дает формулу для интегрирования по частям :

$\int \; u\; (x)\; v\; \prime \; (x)\; dx\; =\; u\; (x)\; v\; (x)\; -\; \int \; u\; \prime \; (x)\; v\; (x)\; dx,\; \{\backslash \; displaystyle\; \backslash \; int\; u\; (x)\; v\; \text{'}(x)\; \backslash ,\; dx\; \backslash \; =\; \backslash \; u\; (x)\; v\; (x)\; -\; \backslash \; int\; u\text{'}\; (x)\; v\; (x)\; \backslash ,\; dx,\}$

или в терминах дифференциалы $du\; =\; u\; \prime \; (x)\; dx,\; dv\; =\; v\; \prime \; (x)\; dx,\; \{\backslash \; displaystyle\; \backslash \; du\; =\; u\; \text{'}(x)\; \backslash ,\; dx,\; \backslash \; \backslash \; dv\; =\; v\text{'}\; (\; х)\; \backslash ,\; dx,\; \backslash \; quad\}$

$\int \; u\; (x)\; dv\; =\; u\; (x)\; v\; (x)\; -\; \int \; v\; (x)\; du.\; \{\backslash \; displaystyle\; \backslash \; int\; u\; (x)\; \backslash ,\; dv\; \backslash \; =\; \backslash \; u\; (x)\; v\; (x)\; -\; \backslash \; int\; v\; (x)\; \backslash ,\; du.\}$

Это следует понимать как равенство функций с неопределенная константа добавляется к каждой стороне. Если взять разность каждой стороны между двумя значениями x = a и x = b и применить фундаментальную теорему исчисления, получится версия с определенным интегралом:

$\int \; abu\; (x)\; v\; \prime \; (x)\; dx\; =\; u\; (b)\; v\; (b)\; -\; u\; (a)\; v\; (a)\; -\; \int \; abu\; \prime \; (x)\; v\; (x)\; dx.\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; u\; (x)\; v\; \text{'}(x)\; \backslash ,\; dx\; \backslash \; =\; \backslash \; u\; (b)\; v\; (b)\; -u\; (a)\; v\; (a)\; -\; \backslash \; int\; \_\; \{\; a\}\; ^\; \{b\}\; u\; \text{'}(x)\; v\; (x)\; \backslash ,\; dx.\}$

Исходный интеграл ∫ uv ′ dx содержит производную v ′; чтобы применить теорему, нужно найти v, первообразную v ', а затем вычислить полученный интеграл ∫ vu ′ dx.

Действительность для менее гладких функций

Нет необходимости, чтобы u и v были непрерывно дифференцируемыми. Интегрирование по частям работает, если u абсолютно непрерывно, а функция, обозначенная v ′, интегрируема по Лебегу (но не обязательно непрерывна). (Если v 'имеет точку разрыва, тогда ее первообразная v может не иметь производной в этой точке.)

Если интервал интегрирования не компактный, то это не обязательно для u было абсолютно непрерывным во всем интервале или чтобы v ′ было интегрируемым по Лебегу в интервале, как покажет пара примеров (в которых u и v непрерывны и непрерывно дифференцируемы). Например, если

$u\; (x)\; =\; exp\; \; (x)\; /\; x\; 2,\; v\; \prime \; (x)\; =\; exp\; \; (-\; x)\; \{\backslash \; displaystyle\; u\; (x)\; =\; \backslash \; exp\; (x)\; /\; x\; ^\; \{\; 2\},\; \backslash ,\; v\; \text{'}(x)\; =\; \backslash \; exp\; (-x)\}$

u не является абсолютно непрерывным на интервале [1, ∞), но тем не менее

$\int \; 1\; \infty \; u\; (x)\; v\; \prime \; (\; Икс)\; dx\; знак\; равно\; [u\; (x)\; v\; (x)]\; 1\; \infty \; -\; \int \; 1\; \infty \; u\; \text{'}(x)\; v\; (x)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{1\}\; ^\; \{\backslash \; infty\}\; u\; (x)\; v\text{'}\; (x)\; \backslash ,\; dx\; =\; \{\backslash \; Big\; [\}\; u\; (x)\; v\; (x)\; \{\backslash \; Big]\}\; \_\; \{1\}\; ^\; \{\backslash \; infty\}\; -\; \backslash \; int\; \_\; \{1\}\; ^\; \{\backslash \; infty\}\; u\; \text{'}(x)\; v\; (x)\; \backslash ,\; dx\}$

, пока $[u\; (x)\; v\; (x)]\; 1\; \infty \; \{\backslash \; displaystyle\; \backslash \; left\; [u\; (x)\; v\; (x)\; \backslash \; right]\; \_\; \{1\; \}\; ^\; \{\backslash \; infty\}\}$означает предел $u\; (L)\; v\; (L)\; -\; u\; (1)\; v\; (1)\; \{\backslash \; displaystyle\; u\; (L)\; v\; (L)\; -u\; (1)\; v\; (1)\}$as $L\; \to \; \infty \; \{\backslash \; displaystyle\; L\; \backslash \; to\; \backslash \; infty\}$и пока два члена справа- стороны конечны. Это верно, только если мы выберем $v\; (x)\; =\; -\; exp\; \; (-\; x).\; \{\backslash \; displaystyle\; v\; (x)\; =\; -\; \backslash \; exp\; (-x).\}$Аналогично, если

$u\; (x)\; =\; exp\; \; (-\; x),\; v\; \prime \; (x)\; =\; x\; -\; 1\; sin\; \; (x)\; \{\backslash \; displaystyle\; u\; (x)\; =\; \backslash \; exp\; (-x),\; \backslash ,\; v\; \text{'}(x)\; =\; x\; ^\; \{-\; 1\}\; \backslash \; sin\; (x)\}$

v ′ не интегрируется по Лебегу на интервал [1, ∞), но тем не менее

$\int \; 1\; \infty \; u\; (x)\; v\; \prime \; (x)\; dx\; =\; [u\; (x)\; v\; (x)]\; 1\; \infty \; -\; \int \; 1\; \infty \; u\; \prime \; (x)\; v\; (\; х)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{1\}\; ^\; \{\backslash \; infty\}\; u\; (x)\; v\; \text{'}(x)\; \backslash ,\; dx\; =\; \{\backslash \; Big\; [\}\; u\; (x)\; v\; (x)\; \{\backslash \; Big]\}\; \_\; \{\; 1\}\; ^\; \{\backslash \; infty\}\; -\; \backslash \; int\; \_\; \{1\}\; ^\; \{\backslash \; infty\}\; u\; \text{'}(x)\; v\; (x)\; \backslash ,\; dx\}$

с той же интерпретацией.

Можно также легко найти аналогичные примеры, в которых u и v не являются непрерывно дифференцируемыми.

Далее, если $f\; (x)\; \{\backslash \; displaystyle\; f\; (x)\}$является функцией ограниченной вариации на отрезке $[a,\; b],\; \{\backslash \; displaystyle\; [a,\; b],\}$и $\phi \; (x)\; \{\backslash \; displaystyle\; \backslash \; varphi\; (x)\}$дифференцируем на $[a,\; b],\; \{\; \backslash \; displaystyle\; [a,\; b],\}$, затем

$\int \; abf\; (x)\; \phi \; \prime \; (x)\; dx\; =\; -\; \int \; -\; \infty \; \infty \; \phi \; ~\; (x)\; d\; (\chi \; ~\; [a,\; b]\; (х)\; е\; ~\; (х)),\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; е\; (х)\; \backslash \; varphi\; \text{'}(x)\; \backslash ,\; dx\; =\; -\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\; \}\; \{\backslash \; widetilde\; \{\backslash \; varphi\}\}\; (x)\; \backslash ,\; d\; (\{\backslash \; widetilde\; \{\backslash \; chi\}\}\; \_\; \{[a,\; b]\}\; (x)\; \{\backslash \; widetilde\; \{f\}\}\; (x)),\}$

где $d\; (\chi \; [a,\; b]\; (x)\; f\; ~\; (x))\; \{\backslash \; displaystyle\; d\; (\backslash \; chi\; \_\; \{[a,\; b]\}\; (x)\; \{\backslash \; widetilde\; \{f\}\}\; (x))\}$обозначает знаковую меру, соответствующую функции ограниченной вариации $\chi \; [a,\; b]\; (x)\; f\; (x)\; \{\backslash \; displaystyle\; \backslash \; chi\; \_\; \{[a,\; b]\}\; (x)\; f\; (x)\}$, а функции $f\; ~,\; \phi \; ~\; \{\backslash \; displaystyle\; \{\backslash \; widetilde\; \{f\}\},\; \{\backslash \; widetilde\; \{\backslash \; varphi\}\}\}$являются расширения $f,\; \phi \; \{\backslash \; displaystyle\; f,\; \backslash \; varphi\}$до $R,\; \{\backslash \; d\; isplaystyle\; \backslash \; mathbb\; \{R\},\}$которые соответственно имеют ограниченную вариацию и дифференцируемы.

Произведение многих функций

Интегрирование правила произведения для трех умноженных функций u ( x), v (x), w (x) дает аналогичный результат:

$\int \; abuvdw\; =\; [uvw]\; ab\; -\; \int \; abuwdv\; -\; \int \; abvwdu.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; uv\; \backslash ,\; dw\; \backslash \; =\; \backslash \; \{\backslash \; Big\; [\}\; uvw\; \{\backslash \; Big]\}\; \_\; \{a\}\; ^\; \{b\}\; -\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; uw\; \backslash ,\; dv-\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; vw\; \backslash ,\; du.\}$

В общем, для n факторов

$(\prod \; i\; =\; 1\; nui\; (x))\; \prime \; =\; \sum \; j\; =\; 1\; nuj\; \text{'}(Икс)\; \prod \; я\; \ne \; jnui\; (Икс),\; \{\backslash \; Displaystyle\; \backslash \; left\; (\backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; u\_\; \{i\}\; (x)\; \backslash \; right)\text{'}\; \backslash \; =\; \backslash \; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; u\_\; \{j\}\; \text{'}(x)\; \backslash \; prod\; \_\; \{i\; \backslash \; neq\; j\}\; ^\; \{n\}\; u\_\; \{i\}\; (x),\}$

, что приводит к

$[\prod \; i\; =\; 1\; nui\; (x)]\; ab\; =\; \sum \; j\; =\; 1\; n\; abuj\; \prime \; (x)\; \prod \; i\; \ne \; jnui\; (x).\; \{\backslash \; displaystyle\; \backslash \; left\; [\backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; u\_\; \{i\}\; (x)\; \backslash \; right]\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; =\; \backslash \; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\; \}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; u\_\; \{j\}\; \text{'}(x)\; \backslash \; prod\; \_\; \{i\; \backslash \; neq\; j\}\; ^\; \{n\}\; u\_\; \{i\}\; (x).\}$

Визуализация

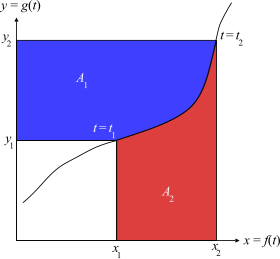
Графическая интерпретация теоремы. Изображенная кривая параметризуется переменной t.

Рассмотрим параметрическую кривую как (x, y) = (f (t), g (t)). Предполагая, что кривая локально взаимно однозначно и интегрируема, мы можем определить

$x\; (y)\; =\; f\; (g\; -\; 1\; (y))\; \{\backslash \; displaystyle\; x\; (Y)\; знак\; равно\; е\; (г\; ^\; \{-\; 1\}\; (у))\}$

$у\; (х)\; =\; г\; (е\; -\; 1\; (х))\; \{\backslash \; Displaystyle\; у\; (х)\; =\; г\; (е\; ^\; \{-\; 1\}\; (x))\}$

Площадь синей области равна

$A\; 1\; =\; \int \; y\; 1\; y\; 2\; x\; (y)\; dy\; \{\backslash \; displaystyle\; A\_\; \{1\}\; =\; \backslash \; int\; \_\; \{y\_\; \{1\}\}\; ^\; \{\; y\_\; \{2\}\}\; x\; (y)\; \backslash ,\; dy\}$

Аналогично, площадь красной области равна

$A\; 2\; =\; \int \; x\; 1\; x\; 2\; y\; (x)\; dx\; \{\backslash \; displaystyle\; A\_\; \{2\}\; =\; \backslash \; int\; \_\; \{x\_\; \{1\}\}\; ^\; \{x\_\; \{2\}\}\; y\; (x)\; \backslash ,\; dx\}$

Общая площадь A 1 + A 2 равна площадь большего прямоугольника, x 2y2, минус площадь меньшего, x 1y1:

$\int \; y\; 1\; y\; 2\; x\; (y)\; dy\; ⏞\; A\; 1\; +\; \int \; x\; 1\; x\; 2\; y\; (x)\; dx\; ⏞\; A\; 2\; =\; x\; \cdot \; y\; (x)\; |\; х\; 1\; х\; 2\; =\; у\; \cdot \; х\; (у)\; |\; y\; 1\; y\; 2.\; \{\backslash \; displaystyle\; \backslash \; overbrace\; \{\backslash \; int\; \_\; \{y\_\; \{1\}\}\; ^\; \{y\_\; \{2\}\}\; x\; (y)\; \backslash ,\; dy\}\; ^\; \{A\_\; \{1\}\}\; +\; \backslash \; overbrace\; \{\backslash \; int\; \_\; \{x\_\; \{1\}\}\; ^\; \{x\_\; \{2\}\}\; y\; (x)\; \backslash ,\; dx\}\; ^\; \{A\_\; \{2\}\}\; \backslash \; =\; \backslash \; \{\backslash \; biggl.\}\; x\; \backslash \; cdot\; y\; (x)\; \{\backslash \; biggl\; |\}\; \_\; \{x\_\; \{1\}\}\; ^\; \{x\_\; \{2\}\}\; \backslash \; =\; \backslash \; \{\backslash \; biggl.\}\; y\; \backslash \; cdot\; x\; (y)\; \{\backslash \; biggl\; |\}\; \_\; \{y\_\; \{1\}\}\; ^\; \{y\_\; \{2\}\}.\}$

Или, в терминах t,

$\int \; t\; 1\; t\; 2\; x\; (t)\; dy\; (t)\; +\; \int \; t\; 1\; t\; 2\; y\; (t)\; dx\; (t)\; =\; x\; (t)\; y\; (t)\; |\; t\; 1\; t\; 2\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{t\_\; \{1\}\}\; ^\; \{t\_\; \{2\}\}\; x\; (t)\; \backslash ,\; dy\; (t)\; +\; \backslash \; int\; \_\; \{t\_\; \{1\}\}\; ^\; \{t\_\; \{2\}\}\; y\; (t)\; \backslash ,\; dx\; (t)\; \backslash \; =\; \backslash \; \{\backslash \; biggl.\}\; x\; (t)\; y\; (t)\; \{\backslash \; biggl\; |\}\; \_\; \{t\_\; \{1\}\}\; ^\; \{t\_\; \{2\}\}\}$

Или в терминах неопределенных интегралов это можно записать как

$\int \; xdy\; +\; \int \; ydx\; =\; xy\; \{\backslash \; displaystyle\; \backslash \; int\; x\; \backslash ,\; dy\; +\; \backslash \; int\; y\; \backslash ,\; dx\; \backslash \; =\; \backslash \; xy\}$

Перестановка:

$\int \; xdy\; =\; xy\; -\; \int \; ydx\; \{\backslash \; displaystyle\; \backslash \; int\; x\; \backslash ,\; dy\; \backslash \; =\; \backslash \; xy-\; \backslash \; int\; y\; \backslash ,\; dx\}$

Таким образом, интегрирование по частям можно рассматривать как получение площади синей области из области прямоугольников и красной области.

Эта визуализация также объясняет, почему интегрирование по частям может помочь найти интеграл от обратной функции f (x), если известен интеграл от функции f (x). В самом деле, функции x (y) и y (x) являются обратными, и интеграл x dy может быть вычислен, как указано выше, исходя из знания интеграла ∫ y dx. В частности, это объясняет использование интегрирования по частям для интегрирования логарифма и обратных тригонометрических функций. Фактически, если $f\; \{\backslash \; displaystyle\; f\}$является дифференцируемой взаимно-однозначной функцией на интервале, то интегрирование по частям может использоваться для вывода формулы для интеграла от $f\; -\; 1\; \{\backslash \; displaystyle\; f\; ^\; \{-\; 1\}\}$в терминах интеграла от $f\; \{\backslash \; displaystyle\; f\}$. Это продемонстрировано в статье Интеграл обратных функций.

Приложения

Поиск первообразных

Интеграция по частям - это эвристика, а не чисто механический процесс. для решения интегралов; учитывая единственную функцию, которую нужно интегрировать, типичная стратегия состоит в том, чтобы тщательно разделить эту единственную функцию на произведение двух функций u (x) v (x) так, чтобы остаточный интеграл от интегрирования по формуле частей было легче вычислить, чем единственную функцию. Следующая форма полезна для иллюстрации наилучшей стратегии:

$\int \; u\; v\; d\; x\; =\; u\; \int \; v\; d\; x\; -\; \int \; (u\; \prime \; \int \; v\; d\; x)\; d\; x.\; \{\backslash \; displaystyle\; \backslash \; int\; uv\; \backslash \; dx\; =\; u\; \backslash \; int\; v\; \backslash \; dx-\; \backslash \; int\; \backslash \; left\; (u\; \text{'}\backslash \; int\; v\; \backslash \; dx\; \backslash \; right)\; \backslash \; dx.\}$

В правой части дифференцируется u, а v интегрирован; следовательно, полезно выбрать u как функцию, которая упрощается при дифференцировании, или выбрать v как функцию, которая упрощается при интегрировании. В качестве простого примера рассмотрим:

$\int \; ln\; \; (x)\; x\; 2\; d\; x.\; \{\backslash \; displaystyle\; \backslash \; int\; \{\backslash \; frac\; \{\backslash \; ln\; (x)\}\; \{x\; ^\; \{2\}\}\}\; \backslash \; dx\; \backslash .\}$

Поскольку производная ln (x) равна 1 / x, получается (ln (x)) часть u; так как первообразная 1 / x равна −1 / x, получается 1 / x dx как часть dv. Теперь формула дает:

$\int \; ln\; \; (x)\; x\; 2\; d\; x\; =\; -\; ln\; \; (x)\; x\; -\; \int \; (1\; x)\; (-\; 1\; x)\; d\; x.\; \{\backslash \; displaystyle\; \backslash \; int\; \{\backslash \; frac\; \{\backslash \; ln\; (x)\}\; \{x\; ^\; \{2\}\}\}\; \backslash \; dx\; =\; -\; \{\backslash \; frac\; \{\backslash \; ln\; (x)\}\; \{x\}\}\; -\; \backslash \; int\; \{\backslash \; biggl\; (\}\; \{\; \backslash \; frac\; \{1\}\; \{x\}\}\; \{\backslash \; biggr)\}\; \{\backslash \; biggl\; (\}\; -\; \{\backslash \; frac\; \{1\}\; \{x\}\}\; \{\backslash \; biggr)\}\; \backslash \; dx\; \backslash .\}$

Первообразная от −1 / x можно найти с помощью правила мощности и составляет 1 / x.

В качестве альтернативы можно выбрать u и v таким образом, чтобы произведение u '(∫v dx) упрощалось из-за отмены. Например, предположим, что кто-то хочет интегрировать:

$\int \; sec\; 2\; \; (x)\; \cdot \; ln\; \; (|\; sin\; \; (x)\; |)\; d\; x.\; \{\backslash \; displaystyle\; \backslash \; int\; \backslash \; sec\; ^\; \{2\}\; (x)\; \backslash \; cdot\; \backslash \; ln\; \{\backslash \; Big\; (\}\; \{\backslash \; bigl\; |\}\; \backslash \; sin\; (x)\; \{\backslash \; bigr\; |\}\; \{\backslash \; Big)\}\; \backslash \; dx.\}$

Если мы выберем u (x) = ln (| sin (x) |) и v (x) = secx, то u дифференцируется до 1 / tan x с использованием цепного правила , а v интегрируется в tan x; поэтому формула дает:

$\int \; sec\; 2\; \; (x)\; \cdot \; ln\; \; (|\; sin\; \; (x)\; |)\; dx\; =\; tan\; \; (x)\; \cdot \; ln\; \; (|\; sin\; \; (x)\; |)\; -\; \int \; tan\; \; (х)\; \cdot \; 1\; загар\; \; (х)\; dx.\; \{\backslash \; displaystyle\; \backslash \; int\; \backslash \; sec\; ^\; \{2\}\; (x)\; \backslash \; cdot\; \backslash \; ln\; \{\backslash \; Big\; (\}\; \{\backslash \; bigl\; |\}\; \backslash \; sin\; (x)\; \{\backslash \; bigr\; |\}\; \{\backslash \; Big)\}\; \backslash \; dx\; =\; \backslash \; tan\; (x)\; \backslash \; cdot\; \backslash \; ln\; \{\backslash \; Big\; (\}\; \{\backslash \; bigl\; |\}\; \backslash \; sin\; (x)\; \{\backslash \; bigr\; |\}\; \{\backslash \; Big)\}\; -\; \backslash \; int\; \backslash \; tan\; (x)\; \backslash \; cdot\; \{\backslash \; frac\; \{1\}\; \{\backslash \; tan\; (\; x)\}\}\; \backslash ,\; dx\; \backslash .\}$

Подынтегральное выражение упрощается до 1, поэтому первообразная равна x. Поиск упрощающей комбинации часто требует экспериментов.

В некоторых приложениях может не быть необходимости гарантировать, что интеграл, полученный интеграцией по частям, имеет простую форму; например, в численном анализе может быть достаточно того, что он имеет небольшую величину и поэтому вносит лишь небольшой член ошибки. Некоторые другие специальные методы показаны в примерах ниже.

Полиномы и тригонометрические функции

Для вычисления

$I\; =\; \int \; x\; cos\; \; (x)\; dx,\; \{\backslash \; displaystyle\; I\; =\; \backslash \; int\; x\; \backslash \; cos\; (x)\; \backslash \; dx\; \backslash ,\}$

let:

$u\; =\; x\; \Rightarrow \; du\; =\; dx\; \{\backslash \; displaystyle\; u\; =\; x\; \backslash \; \backslash \; Rightarrow\; \backslash \; du\; =\; dx\}$

$dv\; =\; cos\; \; (x)\; dx\; \Rightarrow \; v\; =\; \int \; cos\; \; (x)\; dx\; =\; sin\; \; (x)\; \{\backslash \; displaystyle\; dv\; =\; \backslash \; cos\; (x)\; \backslash \; dx\; \backslash \; \backslash \; Rightarrow\; \backslash \; v\; =\; \backslash \; int\; \backslash \; cos\; (x)\; \backslash \; dx\; =\; \backslash \; sin\; (x)\}$

, затем:

$\int \; x\; cos\; \; (x)\; dx\; =\; \int \; udv\; =\; u\; \cdot \; v\; -\; \int \; vdu\; =\; x\; sin\; \; (x)\; -\; \int \; sin\; \; (x)\; dx\; =\; x\; sin\; \; (x)\; +\; cos\; \; (x)\; +\; C,\; \{\; \backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; int\; x\; \backslash \; cos\; (x)\; \backslash \; dx\; =\; \backslash \; int\; u\; \backslash \; dv\; \backslash \backslash \; =\; u\; \backslash \; cdot\; v-\; \backslash \; int\; v\; \backslash ,\; du\; \backslash \backslash \; =\; x\; \backslash \; sin\; (x)\; -\; \backslash \; int\; \backslash \; sin\; (x)\; \backslash \; dx\; \backslash \backslash \; =\; x\; \backslash \; sin\; (x)\; +\; \backslash \; cos\; (x)\; +\; C,\; \backslash \; end\; \{align\}\}\}$

где C - константа интегрирования .

Для высших степеней x в форме

$\int \; xnexdx,\; \int \; xn\; sin\; \; (x)\; dx,\; \int \; xn\; cos\; \; (x)\; dx,\; \{\backslash \; displaystyle\; \backslash \; int\; x\; ^\; \{n\}\; e\; ^\; \{x\}\; \backslash \; dx,\; \backslash \; \backslash \; int\; x\; ^\; \{n\}\; \backslash \; sin\; (x)\; \backslash \; dx,\; \backslash \; \backslash \; int\; x\; ^\; \{n\}\; \backslash \; cos\; (x)\; \backslash \; dx\; \backslash ,\}$

, многократно используя интегрирование по частям, можно вычислять такие интегралы; каждое применение теоремы понижает степень x на единицу.

Показатели и тригонометрические функции

Пример, обычно используемый для исследования работы интегрирования по частям, - это

$I\; =\; \int \; e\; x\; cos\; \; (x)\; d\; x.\; \{\backslash \; displaystyle\; I\; =\; \backslash \; int\; e\; ^\; \{x\}\; \backslash \; cos\; (x)\; \backslash \; dx.\}$

Здесь интегрирование по частям выполняется дважды. Пусть сначала

$u\; =\; соз\; \; (x)\; \Rightarrow \; du\; =\; -\; sin\; \; (x)\; dx\; \{\backslash \; displaystyle\; u\; =\; \backslash \; cos\; (x)\; \backslash \; \backslash \; Rightarrow\; \backslash \; du\; =\; -\; \backslash \; sin\; (x)\; \backslash \; dx\}$

$dv\; =\; exdx\; \Rightarrow \; v\; =\; \int \; exdx\; =\; ex\; \{\backslash \; displaystyle\; dv\; =\; e\; ^\; \{x\}\; \backslash \; dx\; \backslash \; \backslash \; Rightarrow\; \backslash \; v\; =\; \backslash \; int\; e\; ^\; \{x\}\; \backslash \; dx\; =\; e\; ^\; \{x\}\}$

тогда:

$ex\; cos\; \; (x)\; dx\; =\; ex\; cos\; \; (x)\; +\; \int \; ex\; sin\; \; (x)\; dx.\; \{\backslash \; displaystyle\; \backslash \; int\; e\; ^\; \{x\}\; \backslash \; cos\; (x)\; \backslash \; dx\; =\; e\; ^\; \{x\}\; \backslash \; cos\; (x)\; +\; \backslash \; int\; e\; ^\; \{x\}\; \backslash \; sin\; (x)\; \backslash \; dx.\}$

Теперь, чтобы вычислить оставшийся интеграл, мы снова используем интегрирование по частям:

$u\; =\; sin\; \; (x)\; \Rightarrow \; du\; =\; cos\; \; (x)\; dx\; \{\backslash \; displaystyle\; u\; =\; \backslash \; sin\; (x)\; \backslash \; \backslash \; Rightarrow\; \backslash \; du\; =\; \backslash \; cos\; (x)\; \backslash \; dx\}$

$dv\; =\; exdx\; \Rightarrow \; v\; =\; \int \; exdx\; =\; ex.\; \{\backslash \; displaystyle\; dv\; =\; e\; ^\; \{x\}\; \backslash \; dx\; \backslash \; \backslash \; Rightarrow\; \backslash \; v\; =\; \backslash \; int\; e\; ^\; \{x\}\; \backslash \; dx\; =\; e\; ^\; \{x\}.\}$

Тогда:

$\int \; ex\; sin\; \; (x)\; dx\; =\; ex\; sin\; \; (x)\; -\; \int \; ex\; cos\; \; (x)\; dx.\; \{\backslash \; displaystyle\; \backslash \; int\; e\; ^\; \{x\}\; \backslash \; sin\; (x)\; \backslash \; dx\; =\; e\; ^\; \{x\}\; \backslash \; sin\; (x)\; -\; \backslash \; int\; e\; ^\; \{x\}\; \backslash \; cos\; (x)\; \backslash \; dx.\}$

Положив эти вместе

$\int \; ex\; cos\; \; (x)\; dx\; =\; ex\; cos\; \; (x)\; +\; ex\; sin\; \; (x)\; -\; \int \; ex\; cos\; \; (x)\; dx.\; \{\backslash \; displaystyle\; \backslash \; int\; e\; ^\; \{x\}\; \backslash \; cos\; (x)\; \backslash \; dx\; =\; e\; ^\; \{x\}\; \backslash \; cos\; (x)\; +\; e\; ^\; \{x\}\; \backslash \; sin\; (x)\; -\; \backslash \; int\; e\; ^\; \{x\}\; \backslash \; cos\; (\; x)\; \backslash \; dx.\}$

Один и тот же интеграл появляется с обеих сторон этого уравнения. Интеграл можно просто добавить к обеим сторонам, чтобы получить

$2\; \int \; ex\; cos\; \; (x)\; dx\; =\; ex\; [sin\; \; (x)\; +\; cos\; \; (x)]\; +\; C,\; \{\backslash \; displaystyle\; 2\; \backslash \; int\; e\; ^\; \{\; x\}\; \backslash \; cos\; (x)\; \backslash \; dx\; =\; e\; ^\; \{x\}\; \{\backslash \; bigl\; [\}\; \backslash \; sin\; (x)\; +\; \backslash \; cos\; (x)\; \{\backslash \; bigr]\}\; +\; C,\}$

который преобразуется в

$\int \; ex\; cos\; \; (x)\; dx\; =\; 1\; 2\; ex\; [грех\; \; (x)\; +\; cos\; \; (x)]\; +\; C\; \prime \; \{\backslash \; displaystyle\; \backslash \; int\; e\; ^\; \{x\}\; \backslash \; cos\; (x)\; \backslash \; dx\; =\; \{\backslash \; frac\; \{1\; \}\; \{2\}\}\; e\; ^\; \{x\}\; \{\backslash \; bigl\; [\}\; \backslash \; sin\; (x)\; +\; \backslash \; cos\; (x)\; \{\backslash \; bigr]\}\; +\; C\; \text{'}\}$

где снова C (и C ′ = C / 2) является константой интегрирования.

Аналогичный метод используется для нахождения интеграла секущей в кубе.

Функции, умноженные на единицу

Два других хорошо известных примера: когда интегрирование по частям применяется к функции, выраженной как произведение 1 и самой себя. Это работает, если известна производная функции, а также известен интеграл от этой производной, умноженный на x.

Первый пример - ∫ ln (x) dx. Запишем это как:

$I\; =\; \int \; ln\; \; (x)\; \cdot \; 1\; d\; x.\; \{\backslash \; displaystyle\; I\; =\; \backslash \; int\; \backslash \; ln\; (x)\; \backslash \; cdot\; 1\; \backslash \; dx\; \backslash .\}$

Пусть:

$u\; =\; ln\; \; (x)\; \Rightarrow \; du\; =\; dxx\; \{\backslash \; displaystyle\; u\; =\; \backslash \; ln\; (x)\; \backslash \; \backslash \; Rightarrow\; \backslash \; du\; =\; \{\backslash \; frac\; \{dx\}\; \{x\}\}\}$

$dv\; =\; dx\; \Rightarrow \; v\; =\; x\; \{\backslash \; displaystyle\; dv\; =\; dx\; \backslash \; \backslash \; Rightarrow\; \backslash \; v\; =\; x\}$

, затем:

$\int \; ln\; \; (Икс)\; dx\; знак\; равно\; Икс\; пер\; \; (Икс)\; -\; \int \; Xxdx\; =\; Икс\; пер\; \; (Икс)\; -\; \int \; 1\; dx\; =\; Икс\; пер\; \; (Икс)\; -\; Икс\; +\; С\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{Выровнено\}\; \backslash \; int\; \backslash \; ln\; (x)\; \backslash \; dx\; =\; x\; \backslash \; ln\; (x)\; -\; \backslash \; int\; \{\backslash \; frac\; \{x\}\; \{x\}\}\; \backslash \; dx\; \backslash \backslash \; =\; x\; \backslash \; ln\; (x)\; -\; \backslash \; int\; 1\; \backslash \; dx\; \backslash \backslash \; =\; x\; \backslash \; ln\; (x)\; -x\; +\; C\; \backslash \; end\; \{align\}\}\}$

где C - константа интегрирования.

Второй пример - функция арктангенса arctan (x):

$Я\; =\; \int \; arctan\; \; (x)\; dx.\; \{\backslash \; displaystyle\; I\; =\; \backslash \; int\; \backslash \; arctan\; (x)\; \backslash \; dx.\}$

Перепишите это как

$\int \; arctan\; \; (x)\; \cdot \; 1\; d\; x.\; \{\backslash \; displaystyle\; \backslash \; int\; \backslash \; arctan\; (x)\; \backslash \; cdot\; 1\; \backslash \; dx.\}$

Теперь позвольте:

$u\; =\; arctan\; \; (x)\; \Rightarrow \; du\; =\; dx\; 1\; +\; x\; 2\; \{\backslash \; displaystyle\; u\; =\; \backslash \; arctan\; (x)\; \backslash \; \backslash \; Rightarrow\; \backslash \; du\; =\; \{\backslash \; frac\; \{dx\}\; \{1\; +\; x\; ^\; \{2\}\}\}\}$

$dv\; =\; dx\; \Rightarrow \; v\; =\; x\; \{\backslash \; displaystyle\; dv\; =\; dx\; \backslash \; \backslash \; Rightarrow\; \backslash \; v\; =\; x\}$

затем

$\int \; arctan\; \; (x)\; dx\; =\; x\; arctan\; \; (x)\; -\; \int \; x\; 1\; +\; x\; 2\; dx\; =\; x\; arctan\; \; (x)\; -\; ln\; \; (1\; +\; x\; 2)\; 2\; +\; C\; \{\backslash \; displaystyle\; \{\; \backslash \; begin\; \{align\}\; \backslash \; int\; \backslash \; arctan\; (x)\; \backslash \; dx\; =\; x\; \backslash \; arctan\; (x)\; -\; \backslash \; int\; \{\backslash \; frac\; \{x\}\; \{1\; +\; x\; ^\; \{2\}\}\}\; \backslash \; dx\; \backslash \backslash \; [8pt]\; =\; x\; \backslash \; arctan\; (x)\; -\; \{\backslash \; frac\; \{\backslash \; ln\; (1\; +\; x\; ^\; \{2\})\}\; \{2\}\}\; +\; C\; \backslash \; end\; \{align\}\}\}$

с использованием комбинации метода правила обратной цепочки и интегральное условие натурального логарифма.

правило LIATE

Было предложено практическое правило, состоящее в выборе в качестве u функции, которая стоит первой в следующем списке:

L– логарифмическая функции : $ln\; \; (x),\; log\; b\; \; (x),\; \{\backslash \; displaystyle\; \backslash \; ln\; (x),\; \backslash \; \backslash \; log\; \_\; \{b\}\; (x),\}$и т. д.

I– обратные тригонометрические функции : $arctan\; \; (x),\; arcsec\; \; (x),\; \{\backslash \; displaystyle\; \backslash \; arctan\; (x),\; \backslash \; \backslash \; ope\; ratorname\; \{arcsec\}\; (x),\}$и т. д.

A– алгебраические функции : $x\; 2,\; 3\; x\; 50,\; \{\backslash \; displaystyle\; x\; ^\; \{2\},\; \backslash \; 3x\; ^\; \{50\; \},\}$и т. Д.

T– тригонометрическиефункции : $грех\; \; (х),\; загар\; \; (х),\; \{\backslash \; displaystyle\; \backslash \; sin\; (x),\; \backslash \; \backslash \; tan\; (x),\}$и т. Д.

E– экспоненциальные функции : $ex,\; 19\; x,\; \{\backslash \; displaystyle\; e\; ^\; \{x\},\; \backslash \; 19\; ^\; \{x\},\}$и т. д.

Функция, которая является первообразными, имеют следующие функции в списке: расположенные ниже в списке, имеют более простые первообразные, чем функции над ними. Правило иногда обозначается как «ДЕТАЛИ», где D означает dv.

Чтобы использовать правило LIATE, рассмотрим интеграл

$x\; \cdot \; cos\; \; (x)\; d\; x.\; \{\backslash \; displaystyle\; \backslash \; int\; x\; \backslash \; cdot\; \backslash \; cos\; (x)\; \backslash ,\; dx.\}$

Следуя правилу LIATE, u = x и dv = cos (x) dx, следовательно, du = dx и v = sin (x), в результате чего интеграл становится

$x\; \cdot \; sin\; \; (x)\; -\; \int \; 1\; sin\; \; (x)\; dx,\; \{\backslash \; displaystyle\; x\; \backslash \; cdot\; \backslash \; sin\; (x)\; -\; \backslash \; int\; 1\; \backslash \; sin\; (x)\; \backslash ,\; dx,\}$

что равно

$x\; \cdot \; sin\; \; (x)\; +\; cos\; \; (x)\; +\; C.\; \{\backslash \; displaystyle\; x\; \backslash \; cdot\; \backslash \; sin\; (x)\; +\; \backslash \; cos\; (x)\; +\; C.\}$

В общем, каждый пытается выбрать u и dv так, чтобы du было проще, чем u, а dv было легко интегрировать. Если бы вместо этого cos (x) был выбран как u, а x dx как dv, мы имели бы интеграл

$x\; 2\; 2\; cos\; \; (x)\; +\; \int \; x\; 2\; 2\; sin\; \; (x)\; dx,\; \{\backslash \; displaystyle\; \{\; \backslash \; frac\; \{x\; ^\; \{2\}\}\; \{2\}\}\; \backslash \; cos\; (x)\; +\; \backslash \; int\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{2\}\}\; \backslash \; sin\; (x)\; \backslash ,\; dx,\}$

после рекурсивное применение формулы интегрирования по частям, очевидно, к бесконечной рекурсии и ни к чему не приведет.

Несмотря на полезное практическое правило, из правил LIATE есть исключение. Распространенной альтернативой рассмотрение правил в порядке «ILATE». Кроме того, в некоторых случаях полиномиальные члены необходимо разделить нетривиальным образом. Например, интегрировать

$\int \; x\; 3\; ex\; 2\; dx,\; \{\backslash \; displaystyle\; \backslash \; int\; x\; ^\; \{3\}\; e\; ^\; \{x\; ^\; \{2\}\}\; \backslash ,\; dx,\}$

, нужно установить

$u\; =\; x\; 2,\; dv\; =\; x\; \cdot \; ex\; 2\; dx,\; \{\backslash \; displaystyle\; u\; =\; x\; ^\; \{2\},\; \backslash \; quad\; dv\; =\; x\; \backslash \; cdot\; e\; ^\; \{x\; ^\; \{2\}\}\; \backslash ,\; dx,\}$

так что

$du\; =\; 2\; xdx,\; v\; =\; ex\; 2\; 2.\; \{\backslash \; displaystyle\; du\; =\; 2x\; \backslash ,\; dx,\; \backslash \; quad\; v\; =\; \{\backslash \; frac\; \{e\; ^\; \{x\; ^\; \{2\}\}\}\; \{2\}\}.\}$

Тогда

$x\; 3\; ex\; 2\; dx\; =\; \int \; (x\; 2)\; (xex\; 2)\; dx\; =\; \int \; udv\; =\; uv\; -\; \int \; vdu\; =\; x\; 2\; ex\; 2\; 2\; -\; xex\; 2\; dx.\; \{\backslash \; displaystyle\; \backslash \; int\; x\; ^\; \{3\}\; e\; ^\; \{x\; ^\; \{2\}\}\; \backslash ,\; dx\; =\; \backslash \; int\; (x\; ^\; \{2\})\; \backslash \; left\; (xe\; ^\; \{x\; ^\; \{2\}\}\; \backslash \; right)\; \backslash ,\; dx\; =\; \backslash \; int\; u\; \backslash ,\; dv\; =\; uv-\; \backslash \; int\; v\; \backslash ,\; du\; =\; \{\backslash \; frac\; \{x\; ^\; \{2\}\; e\; ^\; \{x\; ^\; \{2\}\}\}\; \{2\}\}\; -\; \backslash \; int\; xe\; ^\; \{x\; ^\; \{2\; \}\}\; \backslash ,\; dx.\}$

Наконец, это приводит к

$\int \; x\; 3\; ex\; 2\; dx\; =\; ex\; 2\; (x\; 2\; -\; 1)\; 2\; +\; C.\; \{\backslash \; displaystyle\; \backslash \; int\; x\; ^\; \{3\}\; e\; ^\; \{\; x\; ^\; \{2\}\}\; \backslash ,\; dx\; =\; \{\backslash \; frac\; \{e\; ^\; \{x\; ^\; \{2\}\}\; (x\; ^\; \{2\}\; -1)\}\; \{2\}\}\; +\; C.\}$

Интегрирование по частям часто используется как инструмент для доказательства теорем в математическом анализе.

произведение Уоллиса

Бесконечное произведение Уоллиса для $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$

$\pi \; 2\; =\; \prod \; n\; =\; 1\; \infty \; 4\; n\; 2\; 4\; n\; 2\; -\; 1\; знак\; равно\; \prod \; n\; =\; 1\; \infty \; (2\; n\; 2\; n\; -\; 1\; \cdot \; 2\; n\; 2\; n\; +\; 1)\; =\; (2\; 1\; \cdot \; 2\; 3)\; \cdot \; (4\; 3\; \cdot \; 4\; 5)\; \cdot \; (6\; 5\; \cdot \; 6\; 7)\; \cdot \; (8\; 7\; \cdot \; 8\; 9)\; \cdot \; \cdots \; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; =\; \backslash \; prod\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{4n\; ^\; \{2\}\}\; \{4n\; ^\; \{2\}\; -1\}\}\; =\; \backslash \; prod\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \backslash \; left\; (\{\backslash \; frac\; \{2n\}\; \{2n-1\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{2n\; \}\; \{2n\; +\; 1\}\}\; \backslash \; right)\; \backslash \backslash \; [6pt]\; =\; \{\backslash \; Big\; (\}\; \{\backslash \; frac\; \{2\}\; \{\; 1\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{2\}\; \{3\}\}\; \{\backslash \; Big)\}\; \backslash \; cdot\; \{\backslash \; Big\; (\}\; \{\backslash \; frac\; \{4\}\; \{3\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{4\}\; \{5\}\}\; \{\; \backslash \; Big)\}\; \backslash \; cdot\; \{\backslash \; Big\; (\}\; \{\backslash \; frac\; \{6\}\; \{5\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{6\}\; \{7\}\}\; \{\backslash \; Big)\}\; \backslash \; cdot\; \{\backslash \; Big\; (\}\; \{\backslash \; frac\; \{8\; \}\; \{7\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{8\}\; \{9\}\}\; \{\backslash \; Big)\}\; \backslash \; cdot\; \backslash ;\; \backslash \; cdots\; \backslash \; end\; \{align\}\}\}$

может быть получено с использованием интегрирования по частям.

Идентификатор гамма-функции

гамма-функция является примером специальной функции . n, особый как неправильный интеграл для $z>0\; \{\backslash \; displaystyle\; z>0\}$. Интегрирование по частям показывает, что это расширение факториальной функции:

$\Gamma \; (z)\; =\; \int \; \infty \; e\; -\; xxz\; -\; 1\; dx\; =\; -\; \int \; 0\; \infty \; xz\; -\; 1\; d\; (e\; -\; x)\; =\; -\; [e\; -\; xxz\; -\; 1]\; 0\; \infty \; +\; \int \; 0\; \infty \; e\; -\; xd\; (xz\; -\; 1)\; =\; 0\; +\; \int \; 0\; \infty \; (z\; -\; 1)\; xz\; -\; 2\; е\; -\; xdx\; знак\; равно\; (z\; -\; 1)\; \Gamma \; (z\; -\; 1).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; Gamma\; (z)\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\; \}\; e\; ^\; \{-\; x\}\; x\; ^\; \{z-1\}\; dx\; \backslash \backslash \; [6pt]\; =\; -\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; x\; ^\; \{z-1\}\; \backslash ,\; d\; \backslash \; left\; (e\; ^\; \{\; -\; x\}\; \backslash \; right)\; \backslash \backslash \; [6pt]\; =\; -\; \{\backslash \; Biggl\; [\}\; e\; ^\; \{-\; x\}\; x\; ^\; \{z-1\}\; \{\backslash \; Biggl]\}\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; +\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; e\; ^\; \{-\; x\}\; d\; \backslash \; left\; (x\; ^\; \{z-1\}\; \backslash \; right)\; \backslash \backslash \; [6pt]\; =\; 0+\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; \backslash \; left\; (z-1\; \backslash \; right)\; x\; ^\; \{z-2\}\; e\; ^\; \{-\; x\}\; dx\; \backslash \backslash \; [6pt]\; =\; (z-1)\; \backslash \; Gamma\; (z-1).\; \backslash \; End\; \{align\}\}\}$

<Форма 704>Γ (1) = ∫ 0 ∞ e - xdx Знак равно 1, {\ displaystyle \ Gamma (1) = \ int _ {0} ^ {\ infty} e ^ {- x} \, dx = 1,}

, когда $z\; \{\backslash \; displaystyle\; z\}$является естественным числом, то есть $z\; =\; n\; \in \; N\; \{\backslash \; displaystyle\; z\; =\; n\; \backslash \; in\; \backslash \; mathbb\; \{N\}\}$, многократное применение этой формулы дает факториал : $\Gamma \; (n\; +\; 1)\; =\; n!\; \{\backslash \; displaystyle\; \backslash \; Gamma\; (n\; +\; 1)\; =\; n!\}$

Использование в гармоническом анализе

Интегрирование по частям часто используется в гармоническом анализе, особенно в анализе Фурье, чтобы показать , что быстро осциллирующие интегралы с достаточно гладкими интегралами быстро затухают. Наиболее распространенным примером этого является использование для демонстрации того, что затухание функции преобразования зависит от гладкости этой функции.

Преобразование Фурье производной

Если fk-кратной непрерывно дифференцируемой функцией и все производные до k-й единицы убывают до нуля на бесконечности, то ее преобразование Фурье удовлетворяет

$(F\; е\; (к))\; (\xi )\; знак\; равно\; (2\; \pi \; я\; \xi )\; к\; F\; е\; (\xi ),\; \{\backslash \; displaystyle\; (\{\backslash \; mathcal\; \{F\}\}\; f\; ^\; \{(k)\})\; (\backslash \; xi)\; =\; (2\; \backslash \; pi\; i\; \backslash \; xi)\; ^\; \{k\}\; \{\backslash \; mathcal\; \{F\}\}\; f\; (\backslash \; xi),\}$

где f - k-я производная от f. (Точная константа справа от соглашения зависит от используемого преобразования Фурье.) Это доказывается тем, что

$ddye\; -\; 2\; \pi \; iy\; \xi \; =\; -\; 2\; \pi \; i\; \xi \; e\; -\; 2\; \pi \; iy\; \xi ,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dy\}\}\; e\; ^\; \{-\; 2\; \backslash \; pi\; iy\; \backslash \; xi\}\; =\; -\; 2\; \backslash \; pi\; i\; \backslash \; xi\; e\; ^\; \{-\; 2\; \backslash \; pi\; iy\; \backslash \; xi\},\}$

поэтому, используя интегрирование по частям на преобразовании Фурье производной, мы получаем

$(F\; f\; \prime )\; (\xi )\; =\; \int \; -\; \infty \; \infty \; e\; -\; 2\; \pi \; iy\; \xi \; f\; \prime \; (y)\; dy\; =\; [e\; -\; 2\; \pi \; iy\; \xi \; f\; (y)]\; -\; \infty \; \infty \; -\; \int \; -\; \infty \; \infty \; (-\; 2\; \pi \; i\; \xi \; e\; -\; 2\; \pi \; iy\; \xi )\; f\; (y)\; dy\; =\; 2\; \pi \; i\; \xi \; \int \; -\; \infty \; \infty \; e\; -\; 2\; \pi \; iy\; \xi \; f\; (y)\; dy\; =\; 2\; \pi \; i\; \xi \; F\; f\; (\xi ).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; (\{\backslash \; mathcal\; \{F\}\}\; f\; \text{'})\; (\backslash \; xi)\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; e\; ^\; \{-\; 2\; \backslash \; pi\; iy\; \backslash \; xi\}\; f\; \text{'}(y)\; \backslash ,\; dy\; \backslash \backslash \; =\; \backslash \; left\; [e\; ^\; \{-\; 2\; \backslash \; pi\; iy\; \backslash \; xi\}\; f\; (y)\; \backslash \; right]\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; -\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; (-\; 2\; \backslash \; pi\; i\; \backslash \; xi\; e\; ^\; \{-\; 2\; \backslash \; pi\; iy\; \backslash \; xi\})\; f\; (y)\; \backslash ,\; dy\; \backslash \backslash \; [5pt]\; =\; 2\; \backslash \; pi\; i\; \backslash \; xi\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; e\; ^\; \{-\; 2\; \backslash \; pi\; iy\; \backslash \; xi\}\; f\; (y)\; \backslash ,\; dy\; \backslash \backslash \; [5pt]\; =\; 2\; \backslash \; pi\; i\; \backslash \; xi\; \{\backslash \; mathcal\; \{F\}\}\; f\; (\backslash \; xi).\; \backslash \; end\; \{align\}\}\}$

Применение этого индуктивно дает результат для общего k. Аналогичный метод можно использовать для поиска преобразования Лапласа производной функции.

Затухание преобразования Фурье

Приведенный выше результат говорит нам о затухании преобразования Фурье, поскольку из него следует, что если f и f интегрируемы, то

$|\; F\; f\; (\xi )\; |\; \le \; I\; (f)\; 1\; +\; |\; 2\; \pi \; \xi \; |\; k,\; где\; I\; (f)\; =\; \int \; -\; \infty \; \infty \; (|\; f\; (y)\; |\; +\; |\; f\; (k)\; (y)\; |)\; d\; y.\; \{\backslash \; displaystyle\; \backslash \; vert\; \{\backslash \; mathcal\; \{F\}\}\; е\; (\backslash \; xi)\; \backslash \; vert\; \backslash \; leq\; \{\backslash \; frac\; \{I\; (f)\}\; \{1+\; \backslash \; vert\; 2\; \backslash \; pi\; \backslash \; xi\; \backslash \; vert\; ^\; \{k\}\}\},\; \{\; \backslash \; text\; \{where\}\}\; I\; (f)\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; Bigl\; (\}\; \backslash \; vert\; f\; (y)\; \backslash \; vert\; +\; \backslash \; vert\; f\; ^\; \{(k)\}\; (y)\; \backslash \; vert\; \{\backslash \; Bigr)\}\; \backslash ,\; dy.\}$

Другими словами, если удовлетворяет этим условиям, то его преобразование Фурье затухает на бесконечности по крайней мере так же быстро, как 1 / | ξ |. В частности, если k ≥ 2, то преобразование Фурье интегрируемо.

Доказательство использует тот факт, который непосредственно вытекает из определения преобразования Фурье, что

$|\; F\; f\; (\xi )\; |\; \le \; \int \; -\; \infty \; \infty \; |\; f\; (y)\; |\; д\; г\; \{\backslash \; displaystyle\; \backslash \; vert\; \{\backslash \; mathcal\; \{F\}\}\; f\; (\backslash \; xi)\; \backslash \; vert\; \backslash \; leq\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \backslash \; vert\; f\; (y)\; \backslash \; vert\; \backslash ,\; dy.\}$

Использование той же идеи, сформулированного в начале этого подраздела, дает

$|\; (2\; \pi \; i\; \xi )\; k\; F\; f\; (\xi )\; |\; \le \; \int \; -\; \infty \; \infty \; |\; f\; (k)\; (y)\; |\; д\; г\; \{\backslash \; displaystyle\; \backslash \; vert\; (2\; \backslash \; pi\; i\; \backslash \; xi)\; ^\; \{k\}\; \{\backslash \; mathcal\; \{F\}\}\; f\; (\backslash \; xi)\; \backslash \; vert\; \backslash \; leq\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \backslash \; vert\; f\; ^\; \{(k)\}\; (y)\; \backslash \; vert\; \backslash ,\; dy.\}$

Суммируя эти два неравенства и разделив их на 1 + | 2πξ | дает указанное неравенство.

Использование в теории операторов

Одно из применений интегрирования по частям в теории операторов состоит в том, что оно показывает, что −∆ (где ∆ - оператор Лапласа ) является положительным оператором на L (см. пробел L ). Если f гладкая и имеет компактный носитель, то, используя интегрирование по частям,

$⟨-\; ∆\; f,\; f⟩\; L\; 2\; =\; -\; \int \; -\; \infty \; \infty \; f\; ″\; (x)\; f\; (x)\; ¯\; dx\; =\; -\; [f\; \prime \; (x)\; f\; (x)\; ¯]\; -\; \infty \; \infty \; +\; \int \; -\; \infty \; \infty \; f\; \prime \; (x)\; f\; \prime \; (x)\; ¯\; dx\; =\; \int \; -\; \infty \; \infty \; |\; f\; \prime \; (x)\; |\; 2\; dx\; \ge \; 0.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; langle\; -\; \backslash \; Delta\; f,\; f\; \backslash \; rangle\; \_\; \{L\; ^\; \{2\}\}\; =\; -\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; f\; \text{'}\; \text{'}(x)\; \{\backslash \; overline\; \{f\; (x)\}\}\; \backslash ,\; dx\; \backslash \backslash \; [5pt]\; =\; -\; \backslash \; left\; [f\text{'}\; (x)\; \{\backslash \; overline\; \{f\; (x)\}\}\; \backslash \; right]\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; +\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; f\; \text{'}(x)\; \{\backslash \; overline\; \{f\text{'}\; (x)\}\}\; \backslash ,\; dx\; \backslash \backslash \; [5pt]\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \backslash \; vert\; f\; \text{'}(x)\; \backslash \; vert\; ^\; \{2\}\; \backslash ,\; dx\; \backslash \; geq\; 0.\; \backslash \; end\; \{align\}\}\}$

Другие приложения

• Определение границы условия в теории Штурма - Лиувилля
• Вывод уравнения Эйлера - Лагранжа в вариационном исчислении

Повторное интегрирование по частям

Рассмотрение производная от $v\; \{\backslash \; displaystyle\; v\}$в интеграле на левой стороне формулы интегрированного предположения повторного применения к интегралу на правой стороне:

$\int \; uv\; ″\; dx\; =\; uv\; \prime \; -\; \int \; u\; \prime \; v\; \prime \; dx\; =\; uv\; \prime \; -\; (u\; \prime \; v\; -\; \int \; u\; ″\; vdx).\; \{\backslash \; displaystyle\; \backslash \; int\; uv\; \text{'}\text{'}\; \backslash ,\; dx\; =\; uv\; \text{'}-\; \backslash \; int\; u\text{'}v\text{'}\; \backslash ,\; dx\; =\; uv\; \text{'}-\; \backslash \; left\; (u\text{'}v-\; \backslash \; int\; u\text{'}\text{'}v\; \backslash ,\; dx\; \backslash \; right).\}$

Распространение этой концепции повторного интегрирования в производственные степени n приводит к

$\int \; u\; (0)\; v\; (n)\; dx\; =\; u\; (0)\; v\; (n\; -\; 1)\; -\; u\; (1)\; v\; (n\; -\; 2))\; +\; u\; (2)\; v\; (n\; -\; 3)\; -\; \cdots \; +\; (-\; 1)\; n\; -\; 1\; u\; (n\; -\; 1)\; v\; (0)\; +\; (-\; 1)\; n\; \int \; u\; (n)\; v\; (0)\; dx.\; Знак\; равно\; \sum \; К\; знак\; равно\; 0\; N\; -\; 1\; (-\; 1)\; К\; U\; (K)\; v\; (N\; -\; 1\; -\; K)\; +\; (-\; 1)\; N\; \int \; U\; (N)\; v\; (0)\; d\; x.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; int\; u\; ^\; \{(0)\}\; v\; ^\; \{(n)\}\; \backslash ,\; dx\; =\; u\; ^\; \{(0)\}\; v\; ^\; \{(n-1)\}\; -\; u\; ^\; \{\; (1)\}\; v\; ^\; \{(n-2)\}\; +\; u\; ^\; \{(2)\}\; v\; ^\; \{(n-3)\}\; -\; \backslash \; cdots\; +\; (-\; 1)\; ^\; \{n-1\}\; u\; ^\; \{(n-\; 1)\}\; v\; ^\; \{(0)\}\; +\; (-\; 1)\; ^\; \{n\}\; \backslash \; int\; u\; ^\; \{(n)\}\; v\; ^\; \{(0)\}\; \backslash ,\; dx.\; \backslash \backslash \; [5pt]\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{n-1\}\; (-\; 1)\; ^\; \{k\}\; u\; ^\; \{(k)\}\; v\; ^\; \{(n-1-k)\}\; +\; (-\; 1)\; ^\; \{n\}\; \backslash \; int\; u\; ^\; \{(n)\}\; v\; ^\; \{(0)\}\; \backslash ,\; dx.\; \backslash \; end\; \{align\}\}\}$

Эта концепция может быть полезна, когда последовательные интегралы от $v\; (n)\; \{\backslash \; displaystyle\; v\; ^\; \{(n)\}\}$легко доступны (например, простые экспоненты или синус и косинус, как в Лапласе или преобразовании Фурье ), и когда n-я производная $u\; \{\backslash \; displaystyle\; u\}$исчезает (например, как полиномиальная функция со степенью $(n\; -\; 1)\; \{\backslash \; displaystyle\; (n-1)\}$). Последнее условие останавливает повторение частичного интегрирования, так как RHS-интеграл обращается в нуль.

В ходе вышеупомянутого повторения частичного интегрирования интегралы

$\int \; u\; (0)\; v\; (n)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; u\; ^\; \{(0)\}\; v\; ^\; \{(n)\}\; \backslash ,\; dx\; \backslash \; quad\; \}$и $\int \; u\; (\ell )\; v\; (n\; -\; \ell )\; dx\; \{\backslash \; displaystyle\; \backslash \; quad\; \backslash \; int\; u\; ^\; \{(\backslash \; ell)\}\; v\; ^\; \{(n-\; \backslash \; ell)\}\; \backslash ,\; dx\; \backslash \; quad\}$и $\int \; u\; (m)\; v\; (n\; -\; m)\; dx\; для\; 1\; \le \; m,\; \ell \; \le \; n\; \{\backslash \; displaystyle\; \backslash \; quad\; \backslash \; int\; u\; ^\; \{(m)\}\; v\; ^\; \{(nm)\}\; \backslash ,\; dx\; \backslash \; quad\; \{\backslash \; text\; \{for\}\}\; 1\; \backslash \; leq\; m,\; \backslash \; ell\; \backslash \; leq\; n\}$

связаны. Это можно интерпретировать как произвольное "смещение" производных между $v\; \{\backslash \; displaystyle\; v\}$и $u\; \{\backslash \; displaystyle\; u\}$внутри подынтегрального выражения, и оказывается полезным, тоже (см. формулу Родригеса ).

Табличное интегрирование по частям

Существенный процесс приведенной формулы выше можно резюмировать в таблице; полученный метод называется "табличное интегрирование" и был показан в фильме Стой и выполняй.

. Например, рассмотрим интеграл

$\int \; x\; 3\; cos\; \; xdx\; \{\backslash \; displaystyle\; \backslash \; int\; x\; ^\; \{3\}\; \backslash \; cos\; x\; \backslash ,\; dx\; \backslash \; quad\}$и возьмем $u\; (0)\; =\; x\; 3,\; v\; (n)\; =\; cos\; \; x.\; \{\backslash \; displaystyle\; \backslash \; quad\; u\; ^\; \{(0)\}\; =\; x\; ^\; \{3\},\; \backslash \; quad\; v\; ^\; \{(n)\}\; =\; \backslash \; cos\; x.\}$

Начните перечислять в столбце A функция $u\; (0)\; =\; x\; 3\; \{\backslash \; displaystyle\; u\; ^\; \{(0)\}\; =\; x\; ^\; \{3\}\}$и ее последующие производные $u\; (i)\; \{\backslash \; displaystyle\; u\; ^\; \{(i)\}\}$до достижения нуля. Затем перечислите в столбце B функцию $v\; (n)\; =\; cos\; \; x\; \{\backslash \; displaystyle\; v\; ^\; \{(n)\}\; =\; \backslash \; cos\; x\}$и ее последующие интегралы $v\; (n\; -\; i)\; \{\backslash \; displaystyle\; v\; ^\; \{(ni)\}\}$до тех пор, пока размер столбца B не станет таким же, как столбец A . Результат выглядит следующим образом:

# i	Sign	A: производные u	B: интегралы v
0	+	$x\; 3\; \{\backslash \; displaystyle\; x\; ^\; \{3\; \}\}$	$соз\; \; x\; \{\backslash \; displaystyle\; \backslash \; cos\; x\}$
1	−	$3\; x\; 2\; \{\backslash \; displaystyle\; 3x\; ^\; \{2\}\}$	$sin\; \; x\; \{\backslash \; displaystyle\; \backslash \; sin\; x\}$
2	+	$6\; x\; \{\backslash \; displaystyle\; 6x\}$	$-\; cos\; \; x\; \{\backslash \; displaystyle\; -\; \backslash \; cos\; x\}$
3	−	$6\; \{\backslash \; displaystyle\; 6\}$	$-\; sin\; \; x\; \{\backslash \; displaystyle\; -\; \backslash \; sin\; x\}$
4	+	$0\; \{\backslash \; displaystyle\; 0\; \}$	$cos\; \; x\; \{\backslash \; displaystyle\; \backslash \; cos\; x\}$

Произведение записей в строке i столбцов A и B вместе с соответствующим знаком дает соответствующий интегралы на шаге i при повторном интегрировании по частям. Шаг i = 0 дает исходный интеграл. Для получения полного результата на шаге i>0 i-й интеграл необходимо добавить ко всем предыдущим произведениям (0 ≤ j < i) of the jth entry of column A and the (j + 1)st entry of column B (i.e., multiply the 1st entry of column A with the 2nd entry of column B, the 2nd entry of column A with the 3rd entry of column B, etc....) with the given jth sign. This process comes to a natural halt, when the product, which yields the integral, is zero (i = 4 in the example). The complete result is the following (with the alternating signs in each term):

$(+\; 1)\; (x\; 3)\; (sin\; \; x)\; ⏟\; j\; =\; 0\; +\; (-\; 1)\; (\; 3\; x\; 2)\; (-\; cos\; \; x)\; ⏟\; j\; =\; 1\; +\; (+\; 1)\; (6\; x)\; (-\; sin\; \; x)\; ⏟\; j\; =\; 2\; +\; (-\; 1)\; (6)\; (cos\; \; x)\; ⏟\; j\; =\; 3\; +\; \int \; (+\; 1)\; (0)\; (соз\; \; Икс)\; dx\; ⏟\; я\; знак\; равно\; 4:\; \to \; С.\; \{\backslash \; Displaystyle\; \backslash \; Underbrace\; \{(+1)\; (х\; ^\; \{3\})\; (\backslash \; грех\; х)\}\; \_\; \{j\; =\; 0\}\; +\; \backslash \; underbrace\; \{(-1)\; (3x\; ^\; \{2\})\; (-\; \backslash \; cos\; x)\}\; \_\; \{j\; =\; 1\}\; +\; \backslash \; underbrace\; \{(+1)\; (6x)\; (-\; \backslash \; sin\; x)\}\; \_\; \{\; j\; =\; 2\}\; +\; \backslash \; underbrace\; \{(-1)\; (6)\; (\backslash \; cos\; x)\}\; \_\; \{j\; =\; 3\}\; +\; \backslash \; underbrace\; \{\backslash \; int\; (+1)\; (0)\; (\backslash \; cos\; x)\; \backslash ,\; dx\}\; \_\; \{i\; =\; 4:\; \backslash ;\; \backslash \; to\; \backslash ;\; C\}.\}$

Это дает

$\int \; x\; 3\; cos\; \; xdx\; ⏟\; step\; 0\; =\; x\; 3\; sin\; \; x\; +\; 3\; x\; 2\; cos\; \; x\; -\; 6\; x\; sin\; \; Икс\; -\; 6\; соз\; \; Икс\; +\; С.\; \{\backslash \; Displaystyle\; \backslash \; underbrace\; \{\backslash \; int\; х\; ^\; \{3\}\; \backslash \; соз\; х\; \backslash ,\; dx\}\; \_\; \{\backslash \; text\; \{step\; 0\}\}\; =\; х\; ^\; \{3\}\; \backslash \; sin\; x\; +\; 3x\; ^\; \{2\}\; \backslash \; cos\; x-6x\; \backslash \; sin\; x-6\; \backslash \; cos\; x\; +\; C.\}$

Повторное частичное интегрирование также оказывается полезным, когда в ходе соответственно дифференцирования и интегрирования функций $u\; (i)\; \{\backslash \; displaystyle\; u\; ^\; \{(i)\}\}$и $v\; (n\; -\; i)\; \{\backslash \; displaystyle\; v\; ^\; \{(n\; -i)\}\}$результат их произведения является кратным исходному подынтегральному выражению. В этом случае повторение также может быть прекращено с этим индексом i. Это может произойти, как ожидается, с экспонентами и тригонометрическими функциями. В качестве примера рассмотрим

$\int \; e\; x\; cos\; \; x\; d\; x.\; \{\backslash \; displaystyle\; \backslash \; int\; e\; ^\; \{x\}\; \backslash \; cos\; x\; \backslash ,\; dx.\}$

# i	Sign	A: производные u	B: интегралы v
0	+	$ex\; \{\backslash \; displaystyle\; e\; ^\; \{x\}\}$	$cos\; \; x\; \{\backslash \; displaystyle\; \backslash \; cos\; x\}$
1	−	$ex\; \{\backslash \; displaystyle\; e\; ^\; \{x\}\}$	$грех\; \; x\; \{\backslash \; displaystyle\; \backslash \; sin\; x\}$
2	+	$ex\; \{\backslash \; displaystyle\; e\; ^\; \{x\}\}$	$-\; cos\; \; x\; \{\backslash \; displaystyle\; -\; \backslash \; cos\; x\}$

В данном случае произведение терминов в столбцах A и B с соответствующим знаком для индекса i = 2 дает отрицательное значение исходного подынтегрального выражения (сравните строки i = 0 и i = 2).

$\int \; ex\; cos\; \; xdx\; ⏟\; step\; 0\; =\; (+\; 1)\; (ex)\; (sin\; \; x)\; ⏟\; j\; =\; 0\; +\; (-\; 1)\; (ex)\; (-\; cos\; \; x)\; ⏟\; j\; =\; 1\; +\; \int \; (+\; 1)\; (ex)\; (-\; cos\; \; x)\; dx\; ⏟\; i\; =\; 2.\; \{\backslash \; displaystyle\; \backslash \; underbrace\; \{\backslash \; int\; e\; ^\; \{x\}\; \backslash \; cos\; x\; \backslash ,\; dx\}\; \_\; \{\backslash \; text\; \{step\; 0\}\}\; =\; \backslash \; underbrace\; \{(+1)\; (e\; ^\; \{x\})\; (\backslash \; sin\; x)\}\; \_\; \{j\; =\; 0\}\; +\; \backslash \; underbrace\; \{(-1)\; (e\; ^\; \{x\})\; (-\; \backslash \; cos\; x)\}\; \_\; \{j\; =\; 1\}\; +\; \backslash \; underbrace\; \{\backslash \; int\; (+1)\; (e\; ^\; \{x\})\; (-\; \backslash \; cos\; x)\; \backslash ,\; dx\}\; \_\; \{i\; =\; 2\}.\}$

Заметим, что интеграл на правой стороне может иметь свою собственную постоянную интегрирования $C\; \prime \; \{\backslash \; displaystyle\; C\; \text{'}\}$и перенос абстрактного интеграла на другую сторону дает

$2\; \int \; ex\; cos\; \; xdx\; =\; ex\; sin\; \; x\; +\; ex\; cos\; \; x\; +\; C\; \text{'},\; \{\backslash \; displaystyle\; 2\; \backslash \; int\; e\; ^\; \{x\}\; \backslash \; cos\; x\; \backslash ,\; dx\; =\; e\; ^\; \{x\}\; \backslash \; sin\; x\; +\; e\; ^\; \{x\}\; \backslash \; cos\; x\; +\; C\; \text{'},\}$

и, наконец:

$\int \; ex\; cos\; \; xdx\; =\; 1\; 2\; (ex\; (sin\; \; Икс\; +\; соз\; \; Икс))\; +\; С,\; \{\backslash \; Displaystyle\; \backslash \; int\; e\; ^\; \{x\}\; \backslash \; соз\; х\; \backslash ,\; dx\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; (e\; ^\; \{x\}\; (\backslash \; sin\; x\; +\; \backslash \; cos\; x)\; \backslash \; right)\; +\; C,\}$

где C = C ′ / 2.

Высшие измерения

Интегрирование по частям можно расширить до функций нескольких переменных, применив версию фундаментальной теоремы исчисления к соответствующему правилу произведения. В многомерном исчислении возможно несколько таких пар, включающих скалярную функцию u и векторную функцию (векторное поле) V.

Правило произведения для дивергенции утверждает:

$\nabla \; \cdot \; (u\; V)\; =\; u\; \cdot \; V\; +\; \nabla \; u\; \cdot \; V.\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; cdot\; (u\; \backslash \; mathbf\; \{V\})\; \backslash \; =\; \backslash \; u\; \backslash ,\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{V\}\; \backslash \; +\; \backslash \; \backslash \; nabla\; u\; \backslash \; cdot\; \backslash \; mathbf\; \{V\}.\}$

Предположим, $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$является open ограниченным подмножеством из $R\; n\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{R\}\; ^\; \{n\}\; \}$с кусочно-гладкой границей $\Gamma \; =\; \partial \; \Omega \; \{\backslash \; displaystyle\; \backslash \; Gamma\; =\; \backslash \; partial\; \backslash \; Omega\}$. Интегрирование по $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$относительно стандартной формы объема $d\; \Omega \; \{\backslash \; displaystyle\; d\; \backslash \; Omega\}$и применение теорема о расходимости дает:

$\Gamma \; u\; V\; \cdot \; n\; ^\; d\; \Gamma \; =\; \int \; \Omega \; \nabla \; \cdot \; (u\; V)\; d\; \Omega \; =\; \int \; \Omega \; u\; \nabla \; \cdot \; V\; d\; \Omega \; +\; \int \; \Omega \; \nabla \; u\; \cdot \; V\; d\; \Omega ,\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\backslash \; Gamma\}\; u\; \backslash \; mathbf\; \{V\}\; \backslash \; cdot\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{n\}\}\}\; \backslash ,\; d\; \backslash \; Gamma\; \backslash \; =\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; \backslash \; nabla\; \backslash \; cdot\; (u\; \backslash \; mathbf\; \{V\})\; \backslash ,\; d\; \backslash \; Omega\; \backslash \; =\; \backslash \; \backslash \; int\; \_\; \{\backslash \; Omega\}\; u\; \backslash ,\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{V\}\; \backslash ,\; d\; \backslash \; Omega\; \backslash \; +\; \backslash \; \backslash \; int\; \_\; \{\backslash \; Omega\}\; \backslash \; nabla\; u\; \backslash \; cdot\; \backslash \; mathbf\; \{V\}\; \backslash ,\; d\; \backslash \; Omega,\}$

где $n\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{n\}\}\}\}$- нормальная единица измерения вектор к границе, интегрированный относительно его стандартной формы риманова объема $d\; \Gamma \; \{\backslash \; displaystyle\; d\; \backslash \; Gamma\}$. Перестановка дает:

$\int \; \Omega \; u\; \nabla \; \cdot \; V\; d\; \Omega \; =\; \int \; \Gamma \; u\; V\; \cdot \; n\; ^\; d\; \Gamma \; -\; \int \; \Omega \; \nabla \; u\; \cdot \; V\; d\; \Omega ,\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; u\; \backslash ,\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{V\}\; \backslash ,\; d\; \backslash \; Omega\; \backslash \; =\; \backslash \; \backslash \; int\; \_\; \{\backslash \; Gamma\}\; u\; \backslash \; mathbf\; \{V\}\; \backslash \; cdot\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{n\}\}\}\; \backslash ,\; d\; \backslash \; Gamma\; -\; \backslash \; int\; \_\; \{\; \backslash \; Omega\}\; \backslash \; nabla\; u\; \backslash \; cdot\; \backslash \; mathbf\; \{V\}\; \backslash ,\; d\; \backslash \; Omega,\}$

или, другими словами,

$\int \; \Omega \; u\; div\; \; (V)\; d\; \Omega \; =\; \int \; \Gamma \; u\; V\; \cdot \; n\; ^\; d\; \Gamma \; -\; \int \; \Omega \; grad\; \; (u)\; \cdot \; V\; d\; \Omega .\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; и\; \backslash ,\; \backslash \; operatorname\; \{div\}\; (\backslash \; mathbf\; \{V\})\; \backslash ,\; d\; \backslash \; Omega\; \backslash \; =\; \backslash \; \backslash \; int\; \_\; \{\backslash \; Gamma\}\; и\; \backslash \; mathbf\; \{V\}\; \backslash \; cdot\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{n\}\}\}\; \backslash ,\; d\; \backslash \; Gamma\; -\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; \backslash \; operatorname\; \{grad\}\; (u)\; \backslash \; cdot\; \backslash \; mathbf\; \{V\}\; \backslash ,\; d\; \backslash \; Omega.\}$

Регулярность требования теоремы можно ослабить. Например, граница $\Gamma \; =\; \partial \; \Omega \; \{\backslash \; displaystyle\; \backslash \; Gamma\; =\; \backslash \; partial\; \backslash \; Omega\}$должна быть только непрерывной по Липшицу, а функции u, v должны только лежать в пространстве Соболева H (Ω).

Первая идентичность Грина

Рассмотрим непрерывно дифференцируемые векторные поля $U\; =\; u\; 1\; e\; 1\; +\; \cdots \; +\; unen\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\}\; =\; u\_\; \{1\}\; \backslash \; mathbf\; \{\; e\}\; \_\; \{1\}\; +\; \backslash \; cdots\; +\; u\_\; \{n\}\; \backslash \; mathbf\; \{e\}\; \_\; \{n\}\}$и $ve\; 1,\dots ,\; ven\; \{\backslash \; displaystyle\; v\; \backslash \; mathbf\; \{e\}\; \_\; \{1\},\; \backslash \; ldots,\; v\; \backslash \; mathbf\; \{e\}\; \_\; \{n\}\}$, где $ei\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\}$- i-й стандартный базисный вектор для $i\; =\; 1,\dots ,\; n\; \{\backslash \; displaystyle\; i\; =\; 1,\; \backslash \; ldots,\; n\}$. Теперь примените указанное выше интегрирование по частям к каждому $ui\; \{\backslash \; displaystyle\; u\_\; \{i\}\}$, умноженному на векторное поле $vei\; \{\backslash \; displaystyle\; v\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\}$:

$\int \; \Omega \; ui\; \partial \; v\; \partial \; xid\; \Omega \; =\; \int \; \Gamma \; uivei\; \cdot \; n\; ^\; d\; \Gamma \; -\; \int \; \Omega \; \partial \; ui\; \partial \; xivd\; \Omega .\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; u\_\; \{i\}\; \{\backslash \; frac\; \{\backslash \; partial\; v\}\; \{\backslash \; partial\; x\_\; \{i\}\}\}\; \backslash ,\; d\; \backslash \; Omega\; \backslash \; =\; \backslash \; \backslash \; int\; \_\; \{\backslash \; Gamma\}\; u\_\; \{i\}\; v\; \backslash ,\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\; \backslash \; cdot\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{n\}\}\}\; \backslash ,\; d\; \backslash \; Gamma\; -\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; \{\backslash \; frac\; \{\backslash \; partial\; u\_\; \{i\}\}\; \{\; \backslash \; partial\; x\_\; \{i\}\}\}\; v\; \backslash ,\; d\; \backslash \; Omega.\}$

Суммирование по i дает новую формулу интегрирования по частям:

$\int \; \Omega \; U\; \cdot \; \nabla \; vd\; \Omega \; =\; \int \; \Gamma \; v\; U\; \cdot \; n\; ^\; d\; \Gamma \; -\; \int \; \Omega \; v\; \nabla \; \cdot \; U\; d\; \Omega .\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; \backslash \; mathbf\; \{U\}\; \backslash \; cdot\; \backslash \; nabla\; v\; \backslash ,\; d\; \backslash \; Omega\; \backslash \; =\; \backslash \; \backslash \; int\; \_\; \{\backslash \; Gamma\}\; v\; \backslash \; mathbf\; \{U\}\; \backslash \; cdot\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{\; n\}\}\}\; \backslash ,\; d\; \backslash \; Gamma\; -\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; v\; \backslash ,\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{U\}\; \backslash ,\; d\; \backslash \; Omega.\}$

Случай $U\; =\; \nabla \; u\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\}\; =\; \backslash \; nabla\; u\}$, где $u\; \in \; C\; 2\; (\Omega \; ¯)\; \{\backslash displaystyle\; u\backslash in\; C^\{2\}(\{\backslash bar\; \{\backslash Omega\; \}\})\}$, is known as the first of Green's identities :

$\int \; \Omega \; \nabla \; u\; \cdot \; \nabla \; v\; d\; \Omega \; =\; \int \; \Gamma \; v\; \nabla \; u\; \cdot \; n\; ^\; d\; \Gamma \; -\; \int \; \Omega \; v\; \nabla \; 2\; u\; d\; \Omega .\; \{\backslash displaystyle\; \backslash int\; \_\{\backslash Omega\; \}\backslash nabla\; u\backslash cdot\; \backslash nabla\; v\backslash ,d\backslash Omega\; \backslash \; =\backslash \; \backslash int\; \_\{\backslash Gamma\; \}v\backslash ,\backslash nabla\; u\backslash cdot\; \{\backslash hat\; \{\backslash mathbf\; \{n\}\; \}\}\backslash ,d\backslash Gamma\; -\backslash int\; \_\{\backslash Omega\; \}v\backslash ,\backslash nabla\; ^\{2\}u\backslash ,d\backslash Omega.\}$

See also

• Integration by parts for the Lebesgue–Stieltjes integral
• Integration by parts for semimartingales, involving their quadratic covariation.
• Integration by substitution
• Legendre transformation

Notes

1. ^"Brook Taylor". History.MCS.St-Andrews.ac.uk. Retrieved May 25, 2018.
2. ^"Brook Taylor". Stetson.edu. Retrieved May 25, 2018.
3. ^"Integration by parts". Encyclopedia of Mathematics.
4. ^Kasube, Herbert E. (1983). "A Technique for Integration by Parts". The American Mathematical Monthly. 90(3): 210–211. doi :10.2307/2975556. JSTOR 2975556.
5. ^Thomas, G. B. ; Finney, R. L. (1988). Calculus and Analytic Geometry (7th ed.). Reading, MA: Addison-Wesley. ISBN 0-201-17069-8.
6. ^Horowitz, David (1990). "Tabular Integration by Parts" (PDF). The College Mathematics Journal. 21(4): 307–311. doi :10.2307/2686368. JSTOR 2686368.
7. ^Rogers, Robert C. (September 29, 2011). "The Calculus of Several Variables" (PDF).

Further reading

• Louis Brand (10 October 2013). Advanced Calculus: An Introduction to Classical Analysis. Courier Corporation. pp. 267–. ISBN 978-0-486-15799-3.
• Hoffmann, Laurence D.; Bradley, Gerald L. (2004). Calculus for Business, Economics, and the Social and Life Sciences (8th ed.). pp. 450–464. ISBN 0-07-242432-X.
• Willard, Stephen (1976). Calculus and its Applications. Boston: Prindle, Weber Schmidt. pp. 193–214. ISBN 0-87150-203-8.
• Washington, Allyn J. (1966). Technical Calculus with Analytic Geometry. Reading: Addison-Wesley. pp. 218–245. ISBN 0-8465-8603-7.

External links

The Wikibook Calculus has a page on the topic of: Integration by parts

• , Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Integration by parts—from MathWorld