Синус

тригонометрическая функция угла

Синус
Основные характеристики
Четность	нечетное
Домен	(- ∞, + ∞)
Кодомен	[−1, 1]
Период	2π
Конкретные значения
В нуле	0
Максимум	(2kπ + π / 2, 1)
Минимум	(2kπ - π / 2, −1)
Особенности
Корень	kπ
Критическая точка	kπ + π / 2
Перегиб точка	kπ
Фиксированная точка	0
Для вещественных чисел. Переменная k является целым числом.

В математике синус - это тригонометрическая функция угла угла. Синус острого угла определяется в контексте прямоугольного треугольника : для указанного угла это отношение длины стороны, противоположной этому углу, к длине самой длинной стороны. треугольника (гипотенуза ). Для угла $x\; \{\backslash \; displaystyle\; x\}$функция синуса обозначается просто как $sin\; \; x\; \{\backslash \; displaystyle\; \backslash \; sin\; x\}$.

В более общем смысле определение синуса ( и другие тригонометрические функции) могут быть расширены до любого действительного значения с точки зрения длины определенного линейного сегмента в единичной окружности . Более современные определения выражают синус как бесконечный ряд или как решение некоторых дифференциальных уравнений, что позволяет их расширить до произвольных положительных и отрицательных значений и даже до комплексных чисел.

Синусоидальная функция обычно используется для моделирования периодических явлений, таких как звук и световые волны, положение и скорость гармонических осцилляторов, интенсивность солнечного света и продолжительность светового дня, а также изменения средней температуры на всем протяжении год.

Функциональный синус можно проследить до функций jyā и koṭi-jyā, используемых в период Гупта Индийская астрономия (Aryabhatiya, Сурья Сиддханта ), путем перевода с санскрита на арабский, а затем с арабского на латинский. Слово «синус» (латинское «синус») произошло от латинского неправильного перевода Робертом Честерским арабского джиба, который является транслитерацией санскрита. слово для половины хорды, джья-ардха.

• 1 Определение прямоугольного треугольника
• 2 Определение единичного круга
• 3 Тождества
  • 3.1 Взаимное
  • 3.2 Обратное
  • 3.3 Исчисление
  • 3.4 Другие тригонометрические функции
  • 3.5 Функция квадрата синуса
• 4 Свойства, относящиеся к квадрантам
• 5 Определение ряда
  • 5.1 Непрерывная дробь
• 6 Фиксированная точка
• 7 Длина дуги
• 8 Закон синусов
• 9 Особые значения
• 10 Связь с комплексными числами
  • 10.1 Синус с комплексным аргументом
    • 10.1.1 Разложение комплексного синуса на частичную дробь и произведение
    • 10.1.2 Использование комплексного sine
  • 10.2 Сложные графы
• 11 История
  • 11.1 Этимология
• 12 Программные реализации
  • 12.1 Реализации на основе поворотов
• 13 См. также
• 14 Цитаты
• 15 Ссылки
• 16 Внешние ссылки

Для угла α функция синуса дает отношение длины противоположной стороны к длине гипотенузы.

Чтобы определить функцию синуса острого угла α, начните с прямоугольный треугольник, содержащий угол измерения α; на сопроводительном рисунке угол α в треугольнике ABC представляет собой интересующий угол. Три стороны треугольника названы следующим образом:

• Противоположная сторона - это сторона, противоположная интересующему углу, в данном случае сторона a.
• Гипотенуза - это сторона, противоположная прямому углу, в эта сторона дела h. Гипотенуза всегда является самой длинной стороной прямоугольного треугольника.
• Соседняя сторона - это оставшаяся сторона, в данном случае сторона b. Он образует сторону (и примыкает) как к интересующему углу (углу A), так и к прямому углу.

После выбора такого треугольника синус угла равен длине противоположной стороны, деленное на длину гипотенузы:

$sin\; \; (\alpha )\; =\; противоположная\; гипотенуза\; \{\backslash \; displaystyle\; \backslash \; sin\; (\backslash \; alpha)\; =\; \{\backslash \; frac\; \{\backslash \; textrm\; \{Against\}\}\; \{\backslash \; textrm\; \{hypotenuse\}\}\}\}$

Остальные тригонометрические функции угла можно определить аналогично; например, косинус угла - это отношение между соседней стороной и гипотенузой, а касательная дает отношение между противоположной и смежной сторонами.

Как указано, значение $sin\; \; (\alpha )\; \{\backslash \; displaystyle\; \backslash \; sin\; (\backslash \; alpha)\}$, по-видимому, зависит от выбора прямоугольного треугольника, содержащего угол измерения α. Однако это не так: все такие треугольники аналогичны, поэтому соотношение для каждого из них одинаково.

В тригонометрии, единичная окружность - это окружность радиуса 1 с центром в начале координат (0, 0) в Декартова система координат.

Единичная окружность: окружность с радиусом один

Пусть прямая, проходящая через начало координат, пересекает единичную окружность, составляя угол θ с положительной половиной оси x. Координаты x и y этой точки пересечения равны cos (θ) и sin (θ) соответственно. Это определение согласуется с определением синуса и косинуса в прямоугольном треугольнике, когда 0 ° < θ < 90°: because the length of the hypotenuse of the unit circle is always 1, $sin\; \; (\theta )\; =\; противоположная\; гипотенуза\; =\; противоположная\; точка\; 1\; =\; противоположная\; \{\backslash \; displaystyle\; \backslash \; sin\; (\backslash \; theta)\; =\; \{\backslash \; tfrac\; \{\backslash \; textrm\; \{напротив\}\}\; \{\backslash \; textrm\; \{гипотенуза\}\}\}\; =\; \{\backslash \; tfrac\; \{\backslash \; textrm\; \{напротив\}\}\; \{1\}\}\; =\; \{\backslash \; textrm\; \{напротив\}\}\}$. Длина противоположной стороны треугольника - это просто координата y. Аналогичный аргумент можно сделать для функции косинуса, чтобы показать, что $cos\; \; (\theta )\; =\; смежная\; гипотенуза\; \{\backslash \; displaystyle\; \backslash \; cos\; (\backslash \; theta)\; =\; \{\backslash \; tfrac\; \{\backslash \; textrm\; \{смежный\}\}\; \{\backslash \; textrm\; \{hypotenuse\}\; \}\}\}$когда 0 ° < θ < 90°, even under the new definition using the unit circle. tan(θ) is then defined as $грех\; \; (\theta )\; соз\; \; (\theta )\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{\backslash \; sin\; (\backslash \; theta)\}\; \{\backslash \; cos\; (\backslash \; theta)\}\}\}$, или, что то же самое, как наклон отрезка прямой.

Использование определения единичной окружности имеет то преимущество, что угол может быть расширен до любого действительного аргумента. Этого также можно добиться, потребовав определенные симметрии, и чтобы синус был периодической функцией.

• 

  Анимация, показывающая, как функция синуса (красным) $y\; =\; sin\; \; (\theta )\; \{\backslash \; displaystyle\; y\; =\; \backslash \; sin\; (\backslash \; theta)\}$строится по координате y (красная точка) точки на единичной окружности (зеленого цвета) под углом θ.

Точные идентификаторы (с использованием радиан ):

Они применяются для всех значений $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$.

$sin\; \; (\theta )\; знак\; равно\; соз\; \; (\pi \; 2\; -\; \theta )\; =\; 1\; csc\; \; (\theta )\; \{\backslash \; displaystyle\; \backslash \; sin\; (\backslash \; theta)\; =\; \backslash \; cos\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; -\; \backslash \; theta\; \backslash \; right)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; csc\; (\backslash \; theta)\}\}\}$

Взаимное

, обратное синуса - косеканс, т. е. обратное значение sin (A) это csc (A) или cosec (A). Косеканс дает отношение длины гипотенузы к длине противоположной стороны:

$csc\; \; (A)\; =\; 1\; sin\; \; (A)\; =\; гипотенуза\; напротив\; =\; h\; a.\; \{\backslash \; displaystyle\; \backslash \; csc\; (A)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sin\; (A)\}\}\; =\; \{\backslash \; frac\; \{\backslash \; textrm\; \{hypotenuse\}\}\; \{\backslash \; textrm\; \{напротив\}\}\}\; =\; \{\backslash \; frac\; \{h\}\; \{\; a\}\}.\}$

Обратный

Обычные главные значения функции arcsin (x), построенные на декартовой плоскости. Arcsin - это функция, обратная sin.

обратная функция синуса - это arcsine (arcsin или asin) или обратный синус (sin). Поскольку синус не является инъективным, это не точная обратная функция, а частичная обратная функция. Например, sin (0) = 0, но также sin (π) = 0, sin (2π) = 0 и т. Д. Отсюда следует, что функция арксинуса многозначна: arcsin (0) = 0, но также arcsin (0) = π, arcsin (0) = 2π и т. д. Когда требуется только одно значение, функция может быть ограничена ее главной ветвью. С этим ограничением для каждого x в домене выражение arcsin (x) будет оценивать только одно значение, называемое его главным значением.

$\theta \; =\; arcsin\; \; (противоположная\; гипотенуза)\; =\; sin\; -\; 1\; \; (ah).\; \{\backslash \; displaystyle\; \backslash \; theta\; =\; \backslash \; arcsin\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; text\; \{напротив\}\}\; \{\backslash \; text\; \{hypotenuse\}\}\}\; \backslash \; right)\; =\; \backslash \; sin\; ^\; \{-\; 1\}\; \backslash \; left\; (\{\backslash \; frac\; \{a\}\; \{\; h\}\}\; \backslash \; right).\}$

где (для некоторого целого числа k):

$sin\; \; (y)\; =\; x\; ⟺\; y\; =\; arcsin\; \; (x)\; +\; 2\; \pi \; k,\; или\; y\; =\; \pi \; -\; arcsin\; \; (\; Икс)\; +\; 2\; \pi \; К\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; sin\; (y)\; =\; x\; \backslash \; iff\; y\; =\; \backslash \; arcsin\; (x)\; +2\; \backslash \; pi\; k,\; \{\backslash \; text\; \{или\}\}\; \backslash \backslash \; y\; =\; \backslash \; pi\; -\; \backslash \; arcsin\; (x)\; +2\; \backslash \; pi\; k\; \backslash \; end\; \{align\}\}\}$

Или в одном уравнении:

$sin\; \; (y)\; =\; x\; ⟺\; y\; =\; (-\; 1)\; k\; arcsin\; \; (x)\; +\; \pi \; К\; \{\backslash \; displaystyle\; \backslash \; sin\; (y)\; =\; x\; \backslash \; iff\; y\; =\; (-\; 1)\; ^\; \{k\}\; \backslash \; arcsin\; (x)\; +\; \backslash \; pi\; k\}$

По определению, арксинус удовлетворяет уравнению:

$sin\; \; (arcsin\; \; (x))\; знак\; равно\; x\; \{\backslash \; displaystyle\; \backslash \; sin\; (\backslash \; arcsin\; (x))\; =\; x\; \backslash !\}$

и

$arcsin\; \; (sin\; \; (\theta ))\; =\; \theta \; для\; -\; \pi \; 2\; \le \; \theta \; \le \; \pi \; 2.\; \{\backslash \; displaystyle\; \backslash \; arcsin\; (\backslash \; sin\; (\backslash \; theta))\; =\; \backslash \; theta\; \backslash \; quad\; \{\backslash \; text\; \{for\}\}\; -\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; leq\; \backslash \; theta\; \backslash \; leq\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}.\}$

Исчисление

Для функции синуса:

$f\; (x)\; =\; sin\; \; (x)\; \{\backslash \; displaystyle\; f\; (x)\; =\; \backslash \; sin\; (x)\}$

Производная:

$f\; \text{'}(x)\; =\; cos\; \; (x)\; \{\backslash \; displaystyle\; f\text{'}\; (x)\; =\; \backslash \; cos\; (x)\}$

Первообразная:

$\int \; f\; (x)\; dx\; =\; -\; cos\; \; (x)\; +\; C\; \{\backslash \; displaystyle\; \backslash \; int\; f\; (x)\; \backslash ,\; dx\; =\; -\; \backslash \; cos\; (x)\; +\; C\}$

где C обозначает постоянную интегрирования.

Другие тригонометрические функции

Функции синуса и косинуса связаны множеством способов. Две функции сдвинуты по фазе на 90 °: $sin\; \; (\pi \; /\; 2\; -\; x)\; \{\backslash \; displaystyle\; \backslash \; sin\; (\backslash \; pi\; /\; 2-x)\}$= $cos\; \; (x)\; \{\backslash \; displaystyle\; \backslash \; cos\; (x)\}$для всех углов x. Кроме того, производной функции sin (x) является cos (x).

Любую тригонометрическую функцию можно выразить через любую другую (до знака плюс или минус или с помощью функции знака ).

В следующей таблице показано, как синус может быть выражен в терминах других общих тригонометрических функций :

	f θ	Использование плюса / минуса (±)					Использование функции знака (sgn)
		f θ =	± на квадрант				f θ =
			I	II	III	IV
соз	$грех\; \; (\theta )\; \{\backslash \; displaystyle\; \backslash \; sin\; (\backslash \; theta)\}$	$=\; \pm \; 1\; -\; cos\; 2\; \; (\theta )\; \{\backslash \; displaystyle\; =\; \backslash \; pm\; \{\backslash \; sqrt\; \{1-\; \backslash \; cos\; ^\; \{2\; \}\; (\backslash \; theta)\}\}\}$	+	+	−	−	$=\; sign\; \; (соз\; \; (\theta \; -\; \pi \; 2))\; 1\; -\; соз\; 2\; \; (\theta )\; \{\backslash \; displaystyle\; =\; \backslash \; operatorname\; \{sgn\}\; \backslash \; left\; (\backslash \; cos\; \backslash \; left\; (\backslash \; theta\; -\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; right)\; \backslash \; right)\; \{\backslash \; sqrt\; \{1-\; \backslash \; cos\; ^\; \{2\}\; (\backslash \; theta)\}\}\}$
	$cos\; \; (\theta )\; \{\backslash \; displaystyle\; \backslash \; соз\; (\backslash \; theta)\}$	$=\; \pm \; 1\; -\; грех\; 2\; \; (\theta )\; \{\backslash \; displaystyle\; =\; \backslash \; pm\; \{\backslash \; sqrt\; \{1-\; \backslash \; sin\; ^\; \{2\}\; (\backslash \; theta)\}\}\}$	+	−	−	+	$=\; sgn\; \; (грех\; \; (\theta \; +\; \pi \; 2))\; 1\; -\; грех\; 2\; \; (\theta )\; \{\backslash \; displaystyle\; =\; \backslash \; operatorname\; \{sgn\}\; \backslash \; left\; (\backslash \; sin\; \backslash \; left\; (\backslash \; theta\; +\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; вправо)\; \backslash \; вправо)\; \{\backslash \; sqrt\; \{1-\; \backslash \; sin\; ^\; \{2\}\; (\backslash \; theta)\}\}\}$
кроватка	$грех\; \; (\theta )\; \{\backslash \; displaystyle\; \backslash \; sin\; (\backslash \; theta)\}$	$=\; \pm \; 1\; 1\; +\; детская\; кроватка\; 2\; \; (\theta )\; \{\backslash \; displaysty\; le\; =\; \backslash \; pm\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1+\; \backslash \; cot\; ^\; \{2\}\; (\backslash \; theta)\}\}\}\}$	+	+	−	−	$=\; sgn\; \; (детская\; кроватка\; \; (\theta \; 2))\; 1\; 1\; +\; детская\; кроватка\; 2\; \; (\theta )\; \{\backslash \; displaystyle\; =\; \backslash \; operatorname\; \{sgn\}\; \backslash \; left\; (\backslash \; cot\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; theta\}\; \{2\}\}\; \backslash \; right)\; \backslash \; right)\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1+\; \backslash \; кроватка\; ^\; \{2\}\; (\backslash \; theta)\}\}\}\}$
	$детская\; кроватка\; \; (\theta )\; \{\backslash \; displaystyle\; \backslash \; cot\; (\backslash \; theta)\}$	$=\; \pm \; 1\; -\; sin\; 2\; \; (\theta )\; sin\; \; (\theta )\; \{\; \backslash \; displaystyle\; =\; \backslash \; pm\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{1-\; \backslash \; sin\; ^\; \{2\}\; (\backslash \; theta)\}\}\; \{\backslash \; sin\; (\backslash \; theta)\}\}\}$	+	−	−	+	$=\; sgn\; \; (sin\; \; (\theta \; +\; \pi \; 2))\; 1\; -\; грех\; 2\; \; (\theta )\; грех\; \; (\theta )\; \{\backslash \; displaystyle\; =\; \backslash \; operatorname\; \{sgn\}\; \backslash \; left\; (\backslash \; sin\; \backslash \; left\; (\backslash \; theta\; +\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; right)\; \backslash \; справа)\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{1-\; \backslash \; sin\; ^\; \{2\}\; (\backslash \; theta)\}\}\; \{\backslash \; sin\; (\backslash \; theta)\}\}\}$
tan	$грех\; \; (\theta )\; \{\backslash \; displaystyle\; \backslash \; sin\; (\backslash \; theta)\}$	$=\; \pm \; загар\; \; (\theta )\; 1\; +\; загар\; 2\; \; (\theta )\; \{\backslash \; displaystyle\; =\; \backslash \; pm\; \{\backslash \; frac\; \{\backslash \; tan\; (\backslash \; theta)\}\; \{\backslash \; sqrt\; \{1+\; \backslash \; tan\; ^\; \{\; 2\}\; (\backslash \; theta)\}\}\}\}$	+	−	−	+	$=\; sign\; \; (tan\; \; (2\; \theta \; +\; \pi \; 4))\; tan\; \; (\theta )\; 1\; +\; tan\; 2\; \; (\theta )\; \{\backslash \; displaystyle\; =\; \backslash \; operatorname\; \{sgn\}\; \backslash \; left\; (\backslash \; tan\; \backslash \; left\; (\{\backslash \; frac\; \{2\; \backslash \; theta\; +\; \backslash \; pi\}\; \{4\}\}\; \backslash \; right)\; \backslash \; right)\; \{\backslash \; frac\; \{\backslash \; tan\; (\backslash \; theta)\}\; \{\backslash \; sqrt\; \{1+\; \backslash \; tan\; ^\; \{2\; \}\; (\backslash \; theta)\}\}\}\}$
	$загар\; \; (\theta )\; \{\backslash \; Displaystyle\; \backslash \; загар\; (\backslash \; theta)\}$	$=\; \pm \; грех\; \; (\theta )\; 1\; -\; грех\; 2\; \; (\theta )\; \{\backslash \; displaystyle\; =\; \backslash \; pm\; \{\backslash \; frac\; \{\backslash \; sin\; (\backslash \; theta)\}\; \{\; \backslash \; sqrt\; \{1-\; \backslash \; sin\; ^\; \{2\}\; (\backslash \; theta)\}\}\}\}$	+	−	−	+	$=\; sgn\; \; (sin\; \; (\theta \; +\; \pi \; 2))\; sin\; \; (\theta )\; 1\; -\; sin\; 2\; \; (\theta )\; \{\backslash \; displaystyle\; =\; \backslash \; operatorname\; \{sgn\}\; \backslash \; left\; (\backslash \; sin\; \backslash \; left\; (\backslash \; theta\; +\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; right)\; \backslash \; right)\; \{\backslash \; frac\; \{\backslash \; sin\; (\backslash \; theta)\}\; \{\backslash \; sqrt\; \{\; 1-\; \backslash \; sin\; ^\; \{2\}\; (\backslash \; theta)\}\}\}\}$
сек	$грех\; \; (\theta )\; \{\backslash \; displaystyle\; \backslash \; sin\; (\backslash \; theta)\}$	$=\; \pm \; sec\; 2\; \; (\theta )\; -\; 1\; сек\; \; (\theta )\; \{\backslash \; displaystyle\; =\; \backslash \; pm\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{\backslash \; sec\; ^\; \{2\}\; (\backslash \; theta)\; -1\}\}\; \{\backslash \; sec\; (\backslash \; theta)\}\}\}$	+	−	+	−	$=\; sgn\; \; (\; сек\; \; (4\; \theta \; -\; \pi \; 2))\; сек\; 2\; \; (\theta )\; -\; 1\; сек\; \; (\theta )\; \{\backslash \; displaystyle\; =\; \backslash \; operatorname\; \{sgn\}\; \backslash \; left\; (\backslash \; sec\; \backslash \; left\; (\{\backslash \; frac\; \{4\; \backslash \; theta\; -\; \backslash \; pi\; \}\; \{2\}\}\; \backslash \; right)\; \backslash \; right)\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{\backslash \; sec\; ^\; \{2\}\; (\backslash \; theta)\; -1\}\}\; \{\backslash \; sec\; (\backslash \; theta)\}\}\}$
	$сек\; \; (\theta )\; \{\backslash \; displaystyle\; \backslash \; sec\; (\backslash \; theta)\}$	$=\; \pm \; 1\; 1\; -\; грех\; 2\; \; (\theta )\; \{\backslash \; displaystyle\; =\; \backslash \; pm\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1-\; \backslash \; sin\; ^\; \{2\}\; (\backslash \; тета)\}\}\}\}$	+	−	−	+	$=\; знак\; \; (грех\; \; (\theta \; +\; \pi \; 2))\; 1\; 1\; -\; грех\; 2\; \; (\theta )\; \{\backslash \; displaystyle\; =\; \backslash \; operatorname\; \{sgn\}\; \backslash \; left\; (\backslash \; sin\; \backslash \; left\; (\backslash \; th\; eta\; +\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; right)\; \backslash \; right)\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1-\; \backslash \; sin\; ^\; \{2\}\; (\backslash \; theta)\}\}\}\}$

Для всех уравнения, которые используют плюс / минус (±), результат будет положительным для углов в первом квадранте.

Основное соотношение между синусом и косинусом также может быть выражено как тригонометрическое тождество Пифагора :

$cos\; 2\; \; (\theta )\; +\; sin\; 2\; \; (\theta )\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; cos\; ^\; \{2\}\; (\backslash \; theta)\; +\; \backslash \; sin\; ^\; \{2\}\; (\backslash \; theta)\; =\; 1\; \backslash !\}$

где sin (x) означает (sin (x)).

Функция синус-квадрата

Синусоидальная функция синим цветом и функция синус-квадрата красным. Ось Y находится в радианах.

На графике показаны как функция синуса, так и функция в квадрате синуса, причем синус отображается синим цветом, а синус в квадрате - красным. Оба графика имеют одинаковую форму, но с разными диапазонами значений и разными периодами. Синус в квадрате имеет только положительные значения, но в два раза больше периодов.

Функция квадрата синуса может быть выражена как модифицированная синусоида из тождества Пифагора и уменьшения мощности - с помощью формулы двойного угла косинуса:

$sin\; 2\; \; (\theta )\; =\; 1\; -\; sin\; \; (2\; \theta \; +\; \pi \; 2)\; 2\; \{\backslash \; displaystyle\; \backslash \; sin\; ^\; \{2\}\; (\backslash \; theta)\; \backslash \; =\; \{\backslash \; frac\; \{1-\; \backslash \; sin\; (2\; \backslash \; theta\; +\; \{\backslash \; tfrac\; \{\backslash \; pi\}\; \{2\}\})\}\; \{2\}\; \}\; \backslash \}$

Четыре квадранта декартовой системы координат

В таблице ниже показаны многие ключевые свойства синусоидальной функции (знак, монотонность, выпуклость), упорядоченные по квадрантам аргумента. Для аргументов, не указанных в таблице, можно вычислить соответствующую информацию, используя периодичность $sin\; \; (\alpha \; +\; 360\; \circ )\; =\; sin\; \; (\alpha )\; \{\backslash \; displaystyle\; \backslash \; sin\; (\backslash \; alpha\; +360\; ^\; \{\backslash \; circ\})\; =\; \backslash \; sin\; (\backslash \; alpha)\}$синусоидальной функции.

Квадрант	Градусы	Радианы	Значение	Знак	Монотонность	Выпуклость
1-й квадрант				$+\; \{\backslash \; displaystyle\; +\}$	увеличение	вогнутый
2-й квадрант				$+\; \{\backslash \; displaystyle\; +\}$	уменьшение	вогнутый
3-й квадрант				$-\; \{\backslash \; displaystyle\; -\}$	уменьшение	выпуклый
4-й квадрант				$-\; \{\backslash \; displaystyle\; -\}$	увеличение	выпуклое

Квадранты единичной окружности и sin (x) с использованием декартовой системы координат

В следующей таблице приведены основная информация на границе квадрантов.

Градусы	Радианы	$грех\; \; (x)\; \{\backslash \; displaystyle\; \backslash \; sin\; (x)\}$	Тип точки
$0\; \circ \; \{\backslash \; displaystyle\; 0\; ^\; \{\backslash \; circ\}\}$	$0\; \{\; \backslash \; displaystyle\; 0\}$	$0\; \{\backslash \; displaystyle\; 0\}$	Корень, Inflection
$90\; \circ \; \{\backslash \; displaystyle\; 90\; ^\; \{\backslash \; circ\}\}$	$\pi \; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\}$	$1\; \{\backslash \; displaystyle\; 1\}$	Максимум
$180\; \circ \; \{\backslash \; displaystyle\; 180\; ^\; \{\backslash \; circ\}\}$	$\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$	$0\; \{\backslash \; displaystyle\; 0\}$	Корень, перегиб
$270\; \circ \; \{\backslash \; displaystyle\; 270\; ^\; \{\backslash \; circ\}\}$	$3\; \pi \; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{3\; \backslash \; pi\; \}\; \{2\}\}\}$	$-\; 1\; \{\backslash \; displaystyle\; -1\}$	Минимум

Синусоидальная функция (синий цвет) близко аппроксимируется своим многочленом Тейлора степени 7 (розовый) для полного цикла с центром в начале координат. Эта анимация показывает, как включение все большего и большего числа членов в частичную сумму своего ряда Тейлора приближается к синусоиде.

Использование только геометрии и свойств ограничивает, можно показать, что производная синуса является косинусом, и что де Производная косинуса является отрицательной величиной синуса.

Использование отражения из вычисленного геометрического вывода синуса с (4n + k) -й производной в точке 0:

$sin\; (4\; n\; +\; k)\; \; (0)\; =\; \{0\; когда\; k\; =\; 0\; 1,\; когда\; k\; =\; 1\; 0,\; когда\; k\; =\; 2\; -\; 1,\; когда\; k\; =\; 3\; \{\backslash \; displaystyle\; \backslash \; sin\; ^\; \{(4n\; +\; k)\}\; (0)\; =\; \{\backslash \; begin\; \{cases\}\; 0\; \{\backslash \; text\; \{when\}\; \}\; k\; =\; 0\; \backslash \backslash \; 1\; \{\backslash \; text\; \{when\}\}\; k\; =\; 1\; \backslash \backslash \; 0\; \{\backslash \; text\; \{when\}\}\; k\; =\; 2\; \backslash \backslash \; -\; 1\; \{\backslash \; text\; \{when\}\}\; k\; =\; 3\; \backslash \; end\; \{cases\}\}\; \}$

Это дает следующее разложение в ряд Тейлора при x = 0. Затем можно использовать теорию ряда Тейлора, чтобы показать, что следующие тождества выполняются для всех действительных чисел x ( где x - угол в радианах):

$sin\; \; (x)\; =\; x\; -\; x\; 3\; 3!\; +\; х\; 5\; 5!\; -\; х\; 7\; 7!\; +\; \cdots \; знак\; равно\; \sum \; N\; знак\; равно\; 0\; \infty \; (-\; 1)\; N\; (2\; N\; +\; 1)!\; Икс\; 2\; N\; +\; 1\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; sin\; (x)\; =\; x\; -\; \{\backslash \; frac\; \{x\; ^\; \{3\}\}\; \{3!\}\}\; +\; \{\backslash \; frac\; \{x\; ^\; \{5\}\}\; \{\; 5!\}\}\; -\; \{\backslash \; frac\; \{x\; ^\; \{7\}\}\; \{7!\}\}\; +\; \backslash \; Cdots\; \backslash \backslash \; [8pt]\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{n\}\}\; \{(2n\; +\; 1)!\}\}\; x\; ^\; \{2n\; +\; 1\}\; \backslash \backslash \; [8pt]\; \backslash \; end\; \{align\}\}\}$

Если бы x был выражен в градусах, тогда ряд содержал бы факторы, включающие степени π / 180: если x - количество градусов, количество радианов равно y = πx / 180, поэтому

$sin\; \; (xdeg)\; =\; sin\; \; (yrad)\; =\; \pi \; 180\; x\; -\; (\pi \; 180)\; 3\; х\; 3\; 3!\; +\; (\pi \; 180)\; 5\; х\; 5\; 5!\; -\; (\pi \; 180)\; 7\; х\; 7\; 7!\; +\; \cdots .\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; sin\; (x\; \_\; \{\backslash \; mathrm\; \{deg\}\})\; =\; \backslash \; sin\; (y\; \_\; \{\backslash \; mathrm\; \{rad\}\})\; \backslash \backslash \; =\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{180\}\}\; x-\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{180\}\}\; \backslash \; right)\; ^\; \{3\}\; \{\backslash \; frac\; \{x\; ^\; \{3\}\}\; \{3!\}\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{\; 180\}\}\; \backslash \; right)\; ^\; \{5\}\; \{\backslash \; frac\; \{x\; ^\; \{5\}\}\; \{5!\}\}\; -\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{180\}\}\; \backslash \; right)\; ^\; \{7\}\; \{\backslash \; frac\; \{x\; ^\; \{7\}\}\; \{7!\}\}\; +\; \backslash \; cdots.\; \backslash \; end\; \{align\}\}\}$

Формулы ряда для синуса и косинуса определяются однозначно, с точностью до выбора единицы для углов, согласно требованиям, что

$sin\; \; (0)\; =\; 0\; и\; sin\; \; (2\; x)\; =\; 2\; sin\; \; (x)\; cos\; \; (x)\; cos\; 2\; \; (x)\; +\; sin\; 2\; \; (x)\; =\; 1\; и\; соз\; \; (2\; Икс)\; знак\; равно\; соз\; 2\; \; (Икс)\; -\; грех\; 2\; \; (Икс)\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; sin\; (0)\; =\; 0\; \{\backslash \; text\; \{и\}\}\; \backslash \; sin\; (2x)\; =\; 2\; \backslash \; sin\; (x)\; \backslash \; cos\; (x)\; \backslash \backslash \backslash \; cos\; ^\; \{2\}\; (x)\; +\; \backslash \; sin\; ^\; \{2\}\; (x)\; =\; 1\; \{\backslash \; text\; \{and\}\}\; \backslash \; cos\; (2x)\; =\; \backslash \; cos\; ^\; \{2\}\; (x)\; -\; \backslash \; sin\; ^\; \{2\}\; (x)\; \backslash \backslash \backslash \; end\; \{align\}\}\}$

Радиан - это единица, которая приводит к разложению с ведущим коэффициентом 1 для синуса и определяется дополнительное требование:

$sin\; \; (x)\; \approx \; x,\; когда\; x\; \approx \; 0.\; \{\backslash \; displaystyle\; \backslash \; sin\; (x)\; \backslash \; приблизительно\; x\; \{\backslash \; text\; \{when\}\}\; x\; \backslash \; a\; pprox\; 0.\}$

Коэффициенты для серий синуса и косинуса, следовательно, могут быть получены путем подстановки их разложений в тождества пифагора и двойного угла, принимая ведущий коэффициент для синуса равным 1 и согласовывая остальные коэффициенты.

В общем, математически важные отношения между функциями синуса и косинуса и экспоненциальной функцией (см., Например, формулу Эйлера ) существенно упрощаются, когда углы выражаются в радианах, а не в градусах, градусах или других единицах. Поэтому в большинстве разделов математики, выходящих за рамки практической геометрии, считается, что углы выражаются в радианах.

Аналогичный ряд - это ряд Грегори для arctan, который получается путем опускания факториалов в знаменателе.

Непрерывная дробь

Функция синуса также может быть представлена ​​как обобщенная непрерывная дробь :

$sin\; \; (x)\; =\; x\; 1\; +\; x\; 2\; 2\; \cdot \; 3\; -\; x\; 2\; +\; 2\; \cdot \; 3\; x\; 2\; 4\; \cdot \; 5\; -\; x\; 2\; +\; 4\; \cdot \; 5\; x\; 2\; 6\; \cdot \; 7\; -\; x\; 2\; +\; \ddots .\; \{\backslash \; displaystyle\; \backslash \; sin\; (x)\; =\; \{\backslash \; cfrac\; \{x\}\; \{1\; +\; \{\backslash \; cfrac\; \{x\; ^\; \{2\}\}\; \{2\; \backslash \; cdot\; 3-x\; ^\; \{2\}\; +\; \{\backslash \; cfrac\; \{2\; \backslash \; cdot\; 3x\; ^\; \{\; 2\}\}\; \{4\; \backslash \; cdot\; 5-x\; ^\; \{2\}\; +\; \{\backslash \; cfrac\; \{4\; \backslash \; cdot\; 5x\; ^\; \{2\}\}\; \{6\; \backslash \; cdot\; 7-x\; ^\; \{2\}\; +\; \backslash \; ddots\}\}\}\}\}\}\}\}.\}$

Представление непрерывной дроби может быть получено из формулы непрерывной дроби Эйлера и выражает вещественное число, как рациональное, так и иррациональное синусоидальной функции.

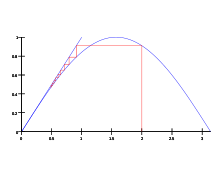
Итерация с фиксированной точкой x n + 1 = sin (x n) с начальным значением x 0 = 2 сходится к 0.

Ноль - единственная действительная фиксированная точка синусоидальной функции; другими словами, единственное пересечение синусоидальной функции и тождественной функции - это sin (0) = 0.

Длина дуги синусоидальной кривой между $a\; \{\backslash \; displaystyle\; a\}$и $b\; \{\backslash \; displaystyle\; b\}$равно $\int \; ab\; 1\; +\; cos\; 2\; \; (x)\; dx\; \{\backslash \; textstyle\; \backslash \; int\; \_\; \{\; a\}\; ^\; \{b\}\; \backslash !\; \{\backslash \; sqrt\; \{1+\; \backslash \; cos\; ^\; \{2\}\; (x)\}\}\; \backslash ,\; dx\}$. Этот интеграл является эллиптическим интегралом второго рода.

Длина дуги для полного периода равна $4\; 2\; \pi \; 3\; \Gamma \; (1/4)\; 2\; +\; \Gamma \; (1/4)\; 2\; 2\; \pi \; =\; 7.640395578\; \dots \; \{\backslash \; Textstyle\; \{\backslash \; frac\; \{4\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; ^\; \{3\}\}\}\}\; \{\backslash \; Gamma\; (1/4)\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; Gamma\; (1/4)\; ^\; \{2\}\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\}\}\}\; =\; 7.640395578\; \backslash \; ldots\}$, где $\Gamma \; \{\backslash \; displaystyle\; \backslash \; Gamma\}$- это гамма-функция.

Длина дуги синусоидальной кривой от 0 до x равна приведенному выше числу, деленному на $2\; \pi \; \{\backslash \; displaystyle\; 2\; \backslash \; pi\}$, умноженное на x, плюс поправка, которая периодически изменяется по x с периодом $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$. Ряд Фурье для этой поправки может быть записан в замкнутой форме с использованием специальных функций, но, возможно, более поучительно записать десятичные аппроксимации коэффициентов Фурье. Длина дуги синусоиды от 0 до x равна

$1,21600672\; x\; +\; 0,10317093\; sin\; \; (2\; x)\; -\; 0,00220445\; sin\; \; (4\; x)\; +\; 0,00012584\; sin\; \; (6\; x)\; -\; 0,00001011\; sin\; \; (8\; x)\; +\; \cdots \; \{\; \backslash \; displaystyle\; 1.21600672x\; +\; 0.10317093\; \backslash \; sin\; (2x)\; -0.00220445\; \backslash \; sin\; (4x)\; +0.00012584\; \backslash \; sin\; (6x)\; -0.00001011\; \backslash \; sin\; (8x)\; +\; \backslash \; cdots\}$

Главный член в приведенном выше уравнении и предел отношение длины дуги к расстоянию определяется следующим образом:

$\pi \; 2\; +\; 2\; \Gamma \; (3\; 4)\; 4\; 2\; \pi \; 3/2\; \Gamma \; (3\; 4)\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; pi\; ^\; \{2\}\; +2\; \backslash \; Гамма\; \backslash \; left\; (\{\backslash \; frac\; \{3\}\; \{4\}\}\; \backslash \; right)\; ^\; \{4\}\}\; \{\{\backslash \; sqrt\; \{2\}\}\; \backslash \; pi\; ^\; \{3/2\}\; \backslash \; Gamma\; \backslash \; left\; (\{\backslash \; frac\; \{3\}\; \{\; 4\}\}\; \backslash \; right)\; ^\; \{2\}\}\}\}$

Закон синусов гласит, что для произвольного треугольника со сторонами a, b и c и углы, противоположные этим сторонам A, B и C:

$sin\; \; A\; a\; =\; sin\; \; B\; b\; =\; sin\; \; C\; c.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; sin\; A\}\; \{a\}\}\; =\; \{\backslash \; frac\; \{\backslash \; sin\; B\}\; \{b\}\}\; =\; \{\backslash \; frac\; \{\backslash \; sin\; C\}\; \{c\}\}.\}$

Это эквивалентно равенство первых трех выражений ниже:

$a\; sin\; sin\; A\; =\; b\; sin\; \; B\; =\; c\; sin\; \; C\; =\; 2\; R,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{a\}\; \{\backslash \; sin\; A\}\}\; =\; \{\backslash \; frac\; \{\; b\}\; \{\backslash \; sin\; B\}\}\; =\; \{\backslash \; frac\; \{c\}\; \{\backslash \; sin\; C\}\}\; =\; 2R,\}$

где R - описанный радиус треугольника.

Это можно доказать, разделив треугольник на два правильные и используя приведенное выше определение синуса. Закон синусов полезен для вычисления длин неизвестных сторон треугольника, если известны два угла и одна сторона. Это обычная ситуация, возникающая в триангуляции, методе определения неизвестных расстояний путем измерения двух углов и доступного замкнутого расстояния.

Некоторые общие углы (θ) показаны на единичной окружности . Углы указаны в градусах и радианах вместе с соответствующей точкой пересечения на единичной окружности (cos (θ), sin (θ)).

Для некоторых целых чисел x градусов, значение sin (x) особенно просто. Таблица некоторых из этих значений приведена ниже.

x (угол)				sin (x)
Градусы	Радианы	Градианы	Повороты	Точное значение	Десятичное число
0°	0	0	0	0	0
180 °	π	200	1/2
15 °	1 / 12π	16+2/3	1/24	$6\; -\; 2\; 4\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\{\backslash \; sqrt\; \{6\}\}\; -\; \{\backslash \; sqrt\; \{2\}\}\}\; \{4\}\}\}$	0,258819045102521
165 °	11 / 12π	183 + 1/3	11/24
30 °	1 / 6π	33+1/3	1/12	1/2	0,5
150 °	5 / 6π	166+2/3	5/12
45 °	1 / 4π	50	1/8	$2\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{2\}\}\; \{2\}\}\}$	0,707106781186548
135 °	3 / 4π	150	3/8
60 °	1 / 3π	66 + 2/3	1/6	$3\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{3\}\}\; \{2\}\}\}$	0,866025403784439
120 °	2 / 3π	133+1/3	1/3
75 °	5 / 12π	83 + 1/3	5/24	$6\; +\; 2\; 4\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\{\backslash \; sqrt\; \{6\}\}\; +\; \{\backslash \; sqrt\; \{2\}\}\}\; \{4\}\}\}$	0,965925826289068
105 °	7 / 12π	116 + 2/3	7/24
90 °	1 / 2π	100	1/4	1	1

с шагом 90 градусов:

x в градусах	0°	90 °	180 °	270 °	360 °
x в радианах	0	π / 2	π	3π / 2	2π
x в углах	0	100	200	300	400
x по очереди	0	1/4	1/2	3/4	1
sin x	0	1	0	-1	0

Другие значения, не указанные выше:

$sin\; \; (\pi \; 60)\; знак\; равно\; грех\; \; (3\; \circ )\; знак\; равно\; (2–12)\; 5\; +\; 5\; +\; (10–2)\; (3\; +\; 1)\; 16\; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{60\}\}\; \backslash \; right)\; =\; \backslash \; sin\; (3\; ^\; \{\backslash \; circ\})\; =\; \{\backslash \; frac\; \{(2\; -\; \{\backslash \; sqrt\; \{12\}\})\; \{\backslash \; sqrt\; \{5\; +\; \{\backslash \; sqrt\; \{5\}\}\}\}\; +\; (\{\backslash \; sqrt\; \{10\}\; \}\; -\; \{\backslash \; sqrt\; \{2\}\})\; (\{\backslash \; sqrt\; \{3\}\}\; +\; 1)\}\; \{16\}\}\}$OEIS : A019812

$грех\; \; (\pi \; 30)\; =\; грех\; \; (6\; \circ )\; =\; 30\; -\; 180\; -\; 5\; -\; 1\; 8\; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{30\}\}\; \backslash \; right)\; =\; \backslash \; sin\; (6\; ^\; \{\backslash \; circ\})\; =\; \{\backslash \; frac\; \{\{\backslash \; sqrt\; \{30\; -\; \{\backslash \; sqrt\; \{180\}\}\}\}\; -\; \{\backslash \; sqrt\; \{5\}\}\; -\; 1\}\; \{8\}\}\}$OEIS : A019815

$грех\; \; (\pi \; 20)\; знак\; равно\; грех\; \; (9\; \circ )\; =\; 10\; +\; 2-20-80\; 8\; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{20\}\}\; \backslash \; right)\; =\; \backslash \; sin\; (9\; ^\; \{\backslash \; circ\})\; =\; \{\backslash \; frac\; \{\{\; \backslash \; sqrt\; \{10\}\}\; +\; \{\backslash \; sqrt\; \{2\}\}\; -\; \{\backslash \; sqrt\; \{20\; -\; \{\backslash \; sqrt\; \{80\}\}\}\}\}\; \{8\}\}\}$OEIS : A019818

$грех\; \; (\pi \; 15)\; =\; грех\; \; (12\; \circ )\; =\; 10\; +\; 20\; +\; 3-15\; 8\; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{15\}\}\; \backslash \; right)\; =\; \backslash \; sin\; (12\; ^\; \{\backslash \; circ\})\; =\; \{\backslash \; frac\; \{\{\backslash \; sqrt\; \{10\; +\; \{\backslash \; sqrt\; \{20\}\}\}\}\; +\; \{\backslash \; sqrt\; \{3\}\}\; -\; \{\backslash \; sqrt\; \{15\}\}\}\; \{8\}\}\}$OEIS : A019821

$грех\; \; (\pi \; 10)\; =\; грех\; \; (18\; \circ )\; =\; 5\; -\; 1\; 4\; =\; 1\; 2\; \phi \; -\; 1\; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{10\}\}\; \backslash \; right)\; =\; \backslash \; sin\; (18\; ^\; \{\backslash \; circ\})\; =\; \{\backslash \; frac\; \{\{\backslash \; sqrt\; \{5\}\}\; -\; 1\}\; \{4\}\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; \backslash \; varphi\; ^\; \{-\; 1\}\}$OEIS : A019827

$sin\; \; (7\; \pi \; 60)\; =\; sin\; \; (21\; \circ )\; =\; (2\; +\; 12)\; 5-5\; -\; (10\; +\; 2)\; (3-1)\; 16\; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; left\; (\{\backslash \; frac\; \{7\; \backslash \; pi\}\; \{60\}\}\; \backslash \; right)\; =\; \backslash \; sin\; (21\; ^\; \{\backslash \; circ\})\; =\; \{\backslash \; frac\; \{(2+\; \{\backslash \; sqrt\; \{12\}\})\; \{\backslash \; sqrt\; \{5\; -\; \{\backslash \; sqrt\; \{5\}\}\}\}\; -\; (\{\backslash \; sqrt\; \{10\}\}\; +\; \{\backslash \; sqrt\; \{2\}\})\; (\{\backslash \; sqrt\; \{3\}\}\; -\; 1)\}\; \{16\}\}\}$OEIS : A019830

$грех\; \; (\pi \; 8)\; =\; грех\; \; (22,5\; \circ )\; =\; 2–2\; 2\; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; left\; (\{\; \backslash \; frac\; \{\backslash \; pi\}\; \{8\}\}\; \backslash \; right)\; =\; \backslash \; sin\; (22,5\; ^\; \{\backslash \; circ\})\; =\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{2\; -\; \{\backslash \; sqrt\; \{2\}\}\}\}\; \{2\}\}\}$

$грех\; \; (2\; \pi \; 15)\; =\; грех\; \; (24\; \circ )\; =\; 3\; +\; 15\; -\; 10\; -\; 20\; 8\; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; left\; (\{\backslash \; frac\; \{2\; \backslash \; pi\}\; \{15\}\}\; \backslash \; right)\; =\; \backslash \; sin\; (24\; ^\; \{\backslash \; circ\})\; =\; \{\backslash \; frac\; \{\{\backslash \; sqrt\; \{\; 3\}\}\; +\; \{\backslash \; sqrt\; \{15\}\}\; -\; \{\backslash \; sqrt\; \{10\; -\; \{\backslash \; sqrt\; \{20\}\}\}\}\}\; \{8\}\}\}$OEIS : A019833

$грех\; \; (3\; \pi \; 20)\; знак\; равно\; грех\; \; (27\; \circ )\; =\; 20\; +\; 80-10\; +\; 2\; 8\; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; left\; (\{\backslash \; frac\; \{3\; \backslash \; pi\}\; \{20\}\}\; \backslash \; right)\; =\; \backslash \; sin\; (27\; ^\; \{\backslash \; circ\})\; =\; \{\backslash \; frac\; \{\{\backslash \; sqrt\; \{20\; +\; \{\backslash \; sqrt\; \{80\}\}\}\}\; -\; \{\backslash \; sqrt\; \{10\}\}\; +\; \{\backslash \; sqrt\; \{2\}\}\}\; \{8\}\}\}$OEIS : A019836

$грех\; \; (11\; \pi \; 60)\; =\; грех\; \; (33\; \circ )\; =\; (12–2)\; 5\; +\; 5\; +\; (10–2)\; (3\; +\; 1)\; 16\; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; left\; (\{\backslash \; frac\; \{11\; \backslash \; pi\}\; \{60\}\}\; \backslash \; right)\; =\; \backslash \; sin\; (33\; ^\; \{\backslash \; circ\})\; =\; \{\backslash \; frac\; \{(\{\backslash \; sqrt\; \{12\}\}\; -\; 2)\; \{\backslash \; sqrt\; \{5\; +\; \{\backslash \; sqrt\; \{5\}\}\}\}\; +\; (\{\backslash \; sqrt\; \{10\}\}\; -\; \{\backslash \; sqrt\; \{2\}\})\; (\{\backslash \; sqrt\; \{3\}\}\; +\; 1)\}\; \{16\}\}\}$OEIS : A019842

$грех\; \; (\pi \; 5)\; =\; грех\; \; (36\; \circ )\; =\; 10-20\; 4\; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{5\}\}\; \backslash \; справа)\; =\; \backslash \; sin\; (36\; ^\; \{\backslash \; circ\})\; =\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{10\; -\; \{\backslash \; sqrt\; \{20\}\}\}\}\; \{4\}\}\}$OEIS : A019845

$грех\; \; (13\; \pi \; 60)\; =\; грех\; \; (39\; \circ )\; =\; (2–12)\; 5–5\; +\; (10\; +\; 2)\; (3\; +\; 1)\; 16\; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; left\; (\{\backslash \; frac\; \{13\; \backslash число\; Пи\; \}\; \{60\}\}\; \backslash \; right)\; =\; \backslash \; sin\; (39\; ^\; \{\backslash \; circ\})\; =\; \{\backslash \; frac\; \{(2\; -\; \{\backslash \; sqrt\; \{12\}\})\; \{\backslash \; sqrt\; \{5\; -\; \{\backslash \; sqrt\; \{5\}\}\}\}\; +\; (\{\backslash \; sqrt\; \{10\}\}\; +\; \{\backslash \; sqrt\; \{2\}\})\; (\{\backslash \; sqrt\; \{3\}\}\; +\; 1)\}\; \{16\}\}\}$OEIS : A019848

$грех\; \; (7\; \pi \; 30)\; знак\; равно\; грех\; \; (42\; \circ )\; =\; 30\; +\; 180\; -\; 5\; +\; 1\; 8\; \{\backslash \; displaystyle\; \backslash \; sin\; \backslash \; left\; (\{\backslash \; frac\; \{7\; \backslash \; pi\}\; \{30\}\}\; \backslash \; right)\; =\; \backslash \; sin\; (\; 42\; ^\; \{\backslash \; circ\})\; =\; \{\backslash \; frac\; \{\{\backslash \; sqrt\; \{30\; +\; \{\backslash \; sqrt\; \{180\}\}\}\}\; -\; \{\backslash \; sqrt\; \{5\}\}\; +\; 1\}\; \{8\}\}\}$OEIS : A019851

Иллюстрация комплексной плоскости. мнимые числа расположены на вертикальной координатной оси.

Синус используется для определения мнимой части комплексного числа , заданного в полярных координатах. (г, φ):

$Z\; знак\; равно\; р\; (соз\; \; (\phi )\; +\; я\; грех\; \; (\phi ))\; \{\backslash \; Displaystyle\; Z\; =\; г\; (\backslash \; соз\; (\backslash \; varphi)\; +\; я\; \backslash \; грех\; (\backslash \; varphi))\}$

мнимая часть:

$Im\; \; (z)\; =\; r\; sin\; \; (\phi )\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Im\}\; (z)\; =\; r\; \backslash \; sin\; (\backslash \; varphi)\}$

r и φ представляют собой величину и угол комплексного числа соответственно. i - это мнимая единица. z - комплексное число ..

Несмотря на то, что мы имеем дело с комплексными числами, параметр синуса в этом случае по-прежнему является действительным числом. Синус также может принимать в качестве аргумента комплексное число.

Синус с комплексным аргументом

$sin\; \; (z)\; \{\backslash \; displaystyle\; \backslash \; sin\; (z)\}$.. Раскраска домена sin (z) в комплексной плоскости. Яркость указывает абсолютную величину, насыщенность представляет собой сложный аргумент. sin (z) как векторное поле $sin\; \; (\theta )\; \{\backslash \; displaystyle\; \backslash \; sin\; (\backslash \; theta)\}$- мнимая часть $ei\; \theta \; \{\backslash \; displaystyle\; e\; ^\; \{i\; \backslash \; theta\}\}$.

Определение синусоидальной функции для комплексных аргументов z:

$sin\; \; (z)\; =\; \sum \; n\; =\; 0\; \infty \; (-\; 1)\; n\; (\; 2\; п\; +\; 1)!\; z\; 2\; N\; +\; 1\; знак\; равно\; eiz\; -\; е\; -\; iz\; 2\; i\; =\; sinh\; \; (iz)\; i\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; sin\; (z)\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\; \backslash \; frac\; \{(-1)\; ^\; \{n\}\}\; \{(2n\; +\; 1)!\}\}\; z\; ^\; \{2n\; +\; 1\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{e\; ^\; \{iz\}\; -e\; ^\; \{-\; iz\}\}\; \{\; 2i\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{\backslash \; sinh\; \backslash \; left\; (iz\; \backslash \; right)\}\; \{i\}\}\; \backslash \; end\; \{align\}\}\}$

где i = −1, а sinh - гиперболический синус. Это целая функция. Кроме того, для чисто вещественного x

$sin\; \; (x)\; =\; Im\; \; (e\; i\; x).\; \{\backslash \; displaystyle\; \backslash \; sin\; (x)\; =\; \backslash \; operatorname\; \{Im\}\; (e\; ^\; \{ix\}).\}$

Для чисто мнимых чисел:

$sin\; \; (i\; y)\; =\; i\; sinh\; \; (y).\; \{\backslash \; displaystyle\; \backslash \; sin\; (iy)\; =\; i\; \backslash \; sinh\; (y).\}$

Также иногда полезно выразить сложную синусоидальную функцию в терминах действительной и мнимой частей ее аргумента:

$sin\; \; (x\; +\; iy)\; =\; sin\; \; (x)\; cos\; \; (iy)\; +\; cos\; \; (x)\; sin\; \; (iy)\; =\; sin\; \; (x)\; cosh\; \; (y)\; +\; i\; cos\; \; (x)\; sinh\; \; (y).\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; sin\; (x\; +\; iy)\; =\; \backslash \; sin\; (x)\; \backslash \; cos\; (iy)\; +\; \backslash \; cos\; (x)\; \backslash \; sin\; (iy)\; \backslash \backslash \; =\; \backslash \; sin\; (x)\; \backslash \; cosh\; (y)\; +\; i\; \backslash \; cos\; (x)\; \backslash \; sinh\; (y).\; \backslash \; end\; \{align\}\}\}$

Разложение на частичную дробь и произведение комплексного синуса

Использование техники разложения на частичную дробь в комплексный анализ, можно найти, что бесконечный ряд

$\sum \; n\; =\; -\; \infty \; \infty \; (-\; 1)\; nz\; -\; n\; =\; 1\; z\; -\; 2\; z\; \sum \; n\; =\; 1\; \infty \; (-\; 1)\; nn\; 2\; -\; z\; 2\; \{\; \backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; sum\; \_\; \{n\; =\; -\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{n\}\}\; \{zn\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{z\}\; \}\; -2z\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{n\}\}\; \{n\; ^\; \{2\}\; -z\; ^\; \{2\}\}\}\; \backslash \; end\; \{выровнено\}\}\}$

сходятся и равны $\pi \; sin\; \; (\pi \; z)\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{\backslash \; sin\; (\backslash \; pi\; z)\}\}\}$. Аналогично можно показать, что

$\pi \; 2\; sin\; 2\; \; (\pi \; z)\; =\; \sum \; n\; =\; -\; \infty \; \infty \; 1\; (z\; -\; n)\; 2.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; frac\; \{\backslash \; pi\; ^\; \{2\}\}\; \{\backslash \; sin\; ^\; \{2\}\; (\backslash \; pi\; z)\}\}\; =\; \backslash \; sum\; \_\; \{n\; =\; -\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{1\}\; \{(zn)\; ^\; \{2\}\}\}.\; \backslash \; end\; \{align\}\}\}$

Используя технику расширения произведения, можно вывести

$sin\; \; (\pi \; z)\; =\; \pi \; z\; \prod \; n\; =\; 1\; \infty \; (1\; -\; z\; 2\; n\; 2).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; sin\; (\backslash \; pi\; z)\; =\; \backslash \; pi\; z\; \backslash \; prod\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{z\; ^\; \{2\}\}\; \{n\; ^\{2\}\}\}\backslash right).\backslash end\{aligned\}\}\}$

Alternatively, the infinite product for the sine can be proved using complex Fourier series.

Proof of the infinite product for the sine

Using complex Fourier series, the function $cos\; \; (\; zx)\; \{\backslash displaystyle\; \backslash cos(zx)\}$can be decomposed as $cos\; \; (\; zx)\; =\; z\; sin\; \; (\; \pi \; z)\; \pi \; \sum \; n\; =\; -\; \infty \; \infty \; (\; -\; 1)\; neinxz\; 2\; -\; n\; 2,\; z\; \in \; C\; \setminus \; \{\; Z\; \},\; x\; \in \; [\; -\; \pi ,\; \pi \; ].\; \{\backslash displaystyle\; \backslash cos(zx)=\{\backslash frac\; \{z\backslash sin(\backslash pi\; z)\}\{\backslash pi\; \}\}\backslash displaystyle\; \backslash sum\; \_\{n=-\backslash infty\; \}^\{\backslash infty\; \}\{\backslash frac\; \{(-1)^\{n\}\backslash ,e^\{inx\}\}\{z^\{2\}-n^\{2\}\}\},\backslash ,z\backslash in\; \backslash mathbb\; \{C\}\; \backslash setminus\; \backslash \{\backslash mathbb\; \{Z\}\; \backslash \},\backslash ,x\backslash in\; [-\backslash pi,\backslash pi\; ].\}$ Setting $x\; =\; \pi \; \{\backslash displaystyle\; x=\backslash pi\; \}$yields $cos\; \; (\; \pi \; z)\; =\; z\; sin\; \; (\; \pi \; z)\; \pi \; \sum \; n\; =\; -\; \infty \; \infty \; 1\; z\; 2\; -\; n\; 2\; =\; z\; sin\; \; (\; \pi \; z)\; \pi \; (\; 1\; z\; 2\; +\; 2\; \sum \; n\; =\; 1\; \infty \; 1\; z\; 2\; -\; n\; 2).\; \{\backslash displaystyle\; \backslash cos(\backslash pi\; z)=\{\backslash frac\; \{z\backslash sin(\backslash pi\; z)\}\{\backslash pi\; \}\}\backslash displaystyle\; \backslash sum\; \_\{n=-\backslash infty\; \}^\{\backslash infty\; \}\{\backslash frac\; \{1\}\{z^\{2\}-n^\{2\}\}\}=\{\backslash frac\; \{z\backslash sin(\backslash pi\; z)\}\{\backslash pi\; \}\}\backslash left(\{\backslash frac\; \{1\}\{z^\{2\}\}\}+2\backslash displaystyle\; \backslash sum\; \_\{n=1\}^\{\backslash infty\; \}\{\backslash frac\; \{1\}\{z^\{2\}-n^\{2\}\}\}\backslash right).\}$ Therefore we get $\pi \; cot\; \; (\; \pi \; z)\; =\; 1\; z\; +\; 2\; \sum \; n\; =\; 1\; \infty \; z\; z\; 2\; -\; n\; 2.\; \{\backslash displaystyle\; \backslash pi\; \backslash cot(\backslash pi\; z)=\{\backslash frac\; \{1\}\{z\}\}+2\backslash displaystyle\; \backslash sum\; \_\{n=1\}^\{\backslash infty\; \}\{\backslash frac\; \{z\}\{z^\{2\}-n^\{2\}\}\}.\}$ The function $\pi \; cot\; \; (\; \pi \; z)\; \{\backslash displaystyle\; \backslash pi\; \backslash cot(\backslash pi\; z)\}$is the derivative of $ln\; \; (\; sin\; \; (\; \pi \; z))\; +\; C\; 0\; \{\backslash displaystyle\; \backslash ln(\backslash sin(\backslash pi\; z))+C\_\{0\}\}$. Furthermore, if $d\; f\; d\; z\; =\; z\; z\; 2\; -\; n\; 2\; \{\backslash textstyle\; \{\backslash frac\; \{df\}\{dz\}\}=\{\backslash frac\; \{z\}\{z^\{2\}-n^\{2\}\}\}\}$, then the function $f\; \{\backslash displaystyle\; f\}$such that the emerged series converges is $f\; =\; 1\; 2\; ln\; \; (\; 1\; -\; z\; 2\; /\; n\; 2)\; +\; C\; 1\; \{\backslash textstyle\; f=\{\backslash frac\; \{1\}\{2\}\}\backslash ln(1-z^\{2\}/n^\{2\})+C\_\{1\}\}$, which can be proved using the Weierstrass M-test. The interchange of the sum and derivative is justified by uniform convergence. It follows that $ln\; \; (\; sin\; \; (\; \pi \; z))\; =\; ln\; \; (\; z)\; +\; \sum \; n\; =\; 1\; \infty \; ln\; \; (\; 1\; -\; z\; 2\; n\; 2)\; +\; C.\; \{\backslash displaystyle\; \backslash ln(\backslash sin(\backslash pi\; z))=\backslash ln(z)+\backslash displaystyle\; \backslash sum\; \_\{n=1\}^\{\backslash infty\; \}\backslash ln\; \backslash left(1-\{\backslash frac\; \{z^\{2\}\}\{n^\{2\}\}\}\backslash right)+C.\}$ Exponentiating gives $sin\; \; (\; \pi \; z)\; =\; z\; e\; C\; \prod \; n\; =\; 1\; \infty \; (\; 1\; -\; z\; 2\; n\; 2).\; \{\backslash displaystyle\; \backslash sin(\backslash pi\; z)=ze^\{C\}\backslash displaystyle\; \backslash prod\; \_\{n=1\}^\{\backslash infty\; \}\backslash left(1-\{\backslash frac\; \{z^\{2\}\}\{n^\{2\}\}\}\backslash right).\}$ Since $lim\; z\; \to \; 0\; sin\; \; (\; \pi \; z)\; z\; =\; \pi \; \{\backslash textstyle\; \backslash lim\; \_\{z\backslash to\; 0\}\{\backslash frac\; \{\backslash sin(\backslash pi\; z)\}\{z\}\}=\backslash pi\; \}$and $lim\; z\; \to \; 0\; \prod \; n\; =\; 1\; \infty \; (\; 1\; -\; z\; 2\; n\; 2)\; =\; 1\; \{\backslash textstyle\; \backslash lim\; \_\{z\backslash to\; 0\}\backslash prod\; \_\{n=1\}^\{\backslash infty\; \}\backslash left(1-\{\backslash frac\; \{z^\{2\}\}\{n^\{2\}\}\}\backslash right)=1\}$, we have $e\; C\; =\; \pi \; \{\backslash displaystyle\; e^\{C\}=\backslash pi\; \}$. Hence $sin\; \; (\; \pi \; z)\; =\; \pi \; z\; \prod \; n\; =\; 1\; \infty \; (\; 1\; -\; z\; 2\; n\; 2)\; \{\backslash displaystyle\; \backslash sin(\backslash pi\; z)=\backslash pi\; z\backslash displaystyle\; \backslash prod\; \_\{n=1\}^\{\backslash infty\; \}\backslash left(1-\{\backslash frac\; \{z^\{2\}\}\{n^\{2\}\}\}\backslash right)\}$ for some open and connected subset of $C\; \{\backslash displaystyle\; \backslash mathbb\; \{C\}\; \}$. Let $a\; n\; (\; z)\; =\; -\; z\; 2\; n\; 2\; \{\backslash displaystyle\; \backslash textstyle\; \{a\_\{n\}(z)=-\{\backslash frac\; \{z^\{2\}\}\{n^\{2\}\}\}\}\}$. Since $\sum \; n\; =\; 1\; \infty \; |\; a\; n\; (\; z)\; |\; \{\backslash displaystyle\; \backslash textstyle\; \{\backslash sum\; \_\{n=1\}^\{\backslash infty\; \}|a\_\{n\}(z)|\}\}$converges uniformly on any closed disk, $\prod \; n\; =\; 1\; \infty \; (\; 1\; +\; a\; n\; (\; z))\; \{\backslash displaystyle\; \backslash textstyle\; \{\backslash prod\; \_\{n=1\}^\{\backslash infty\; \}(1+a\_\{n\}(z))\}\}$converges uniformly on any closed disk as well. It follows that the infinite product is holomorphic on $C\; \{\backslash displaystyle\; \backslash mathbb\; \{C\}\; \}$. By the identity theorem, the infinite product for the sine is valid for all $z\; \in \; C\; \{\backslash displaystyle\; z\backslash in\; \backslash mathbb\; \{C\}\; \}$, which completes the proof. $◼\; \{\backslash displaystyle\; \backslash blacksquare\; \}$

Usage of complex sine

sin(z) is found in the functional equation for the Gamma function,

$\Gamma \; (\; s)\; \Gamma \; (\; 1\; -\; s)\; =\; \pi \; sin\; \; (\; \pi \; s),\; \{\backslash displaystyle\; \backslash Gamma\; (s)\backslash Gamma\; (1-s)=\{\backslash pi\; \backslash over\; \backslash sin(\backslash pi\; s)\},\}$

which in turn is found in the functional equation for the Riemann zeta-function,

$\zeta \; (\; s)\; =\; 2\; (\; 2\; \pi )\; s\; -\; 1\; \Gamma \; (\; 1\; -\; s)\; sin\; \; (\; \pi \; s\; /\; 2)\; \zeta \; (\; 1\; -\; s).\; \{\backslash displaystyle\; \backslash zeta\; (s)=2(2\backslash pi)^\{s-1\}\backslash Gamma\; (1-s)\backslash sin(\backslash pi\; s/2)\backslash zeta\; (1-s).\}$

As a holomorphic function, sin z is a 2D solution of Laplace's equation :

$\Delta \; u\; (\; x\; 1,\; x\; 2)\; =\; 0.\; \{\backslash displaystyle\; \backslash Delta\; u(x\_\{1\},x\_\{2\})=0.\}$

The complex sine function is also related to the level curves of pendulums.

Complex graphs

Sine function in the complex plane

real component	imaginary component	magnitude

.

Arcsine function in the complex plane

real component	imaginary component	magnitude

While the early study of trigonometry can be traced to antiquity, the trigonometric functions as they are in use today were developed in the medieval period. The chord function was discovered by Hipparchus of Nicaea (180–125 BCE) and Ptolemy of Rom Египет (90–165 гг. н. э.).

Функцию синуса и версин (1 - косинус) можно проследить до функций jyā и koṭi-jyā, используемых в период Гупты (320–550 гг. Н. Э.) Индийская астрономия (Арьябхатия, Сурья Сиддханта ) посредством перевода с санскрита на арабский, а затем с арабского на латинский.

Все шесть используемых в настоящее время тригонометрических функций были известны в исламской математике к 9 веку, как и закон синусов, использовавшийся в решении треугольников. За исключением синуса (который был заимствован из индийской математики), арабскими математиками были открыты другие пять современных тригонометрических функций, включая косинус, тангенс, котангенс, секанс и косеканс. Аль-Хваризми (ок. 780–850) составил таблицы синусов, косинусов и тангенсов. Мухаммад ибн Джабир аль-Харрани аль-Баттани (853–929) открыл взаимные функции секанса и косеканса и создал первую таблицу косекансов. для каждой степени от 1 ° до 90 °.

Первое опубликованное использование сокращений sin, cos и tan принадлежит французскому математику 16 века Альбер Жирар ; в дальнейшем они были обнародованы Эйлером (см. ниже). Opus palatinum de triangulis Георга Иоахима Ретикуса, ученика Коперника, вероятно, был первым в Европе, который определил тригонометрические функции непосредственно в терминах прямоугольных треугольников, а не окружностей, с таблицами для все шесть тригонометрических функций; эта работа была закончена учеником Ретикуса Валентином Отоном в 1596 году.

В статье, опубликованной в 1682 году, Лейбниц доказал, что sin x не является алгебраической функцией x Роджер Котес вычислил производную синуса в своей Harmonia Mensurarum (1722). Введение Леонарда Эйлера в анализ бесконечности (1748) в основном отвечало за установление аналитического подхода к тригонометрическим функциям. в Европе, также определяя их как бесконечные серии и представляя «формулу Эйлера », а также почти современные сокращения sin., cos., tang., cot., sec. и cosec.

Этимология

Найдите sine в Wiktionary, бесплатном словаре.

Этимологически слово синус происходит от санскрита слово, обозначающее аккорд, jiva * (jya - его более популярный синоним). Это было транслитерировано на арабском как jiba جيب, что, однако, не имеет смысла на этом языке и сокращается как jb جب. Поскольку арабский язык написан без коротких гласных, «jb» интерпретировалось как слово jaib جيب, что означает «грудь». Когда в XII веке арабские тексты были переведены на латинский Герардом Кремонским, он использовал латинский эквивалент слова «лоно», sinus (что означает « лоно »или« гнедой »или« складкой »). Джерард, вероятно, был не первым ученым, использовавшим этот перевод; Роберт Честерский, кажется, предшествовал ему, и есть свидетельства более раннего использования. Английская форма синуса была введена в 1590-х годах.

Не существует стандартного алгоритма для вычисления синуса. IEEE 754-2008, наиболее широко используемый стандарт для вычислений с плавающей запятой, не касается вычисления тригонометрических функций, таких как синус. Алгоритмы вычисления синуса могут быть сбалансированы с учетом таких ограничений, как скорость, точность, переносимость или диапазон принимаемых входных значений. Это может привести к разным результатам для разных алгоритмов, особенно для особых обстоятельств, таких как очень большие входные данные, например sin (10).

Некогда распространенная оптимизация программирования, особенно используемая в трехмерной графике, заключалась в предварительном вычислении таблицы значений синуса, например, одно значение на градус. Это позволяло искать результаты в таблице, а не рассчитывать их в реальном времени. С современной архитектурой ЦП этот метод не может дать никаких преимуществ.

Алгоритм CORDIC обычно используется в научных калькуляторах.

Функция синуса, наряду с другими тригонометрическими функциями, широко доступна для разных языков и платформ программирования. В вычислениях это обычно сокращается до sin.

Некоторые архитектуры ЦП имеют встроенную инструкцию для синуса, включая FPU Intel x87 начиная с 80387.

В языках программирования sinобычно либо встроенная функция, либо находится в стандартной математической библиотеке языка.

Например, стандартная библиотека C определяет синусоидальные функции в пределах math.h : sin (double ), sinf (float )и sinl (long double ). Параметром каждого из них является значение с плавающей запятой, определяющее угол в радианах. Каждая функция возвращает тот же тип данных , который принимает.Множество других тригонометрических функций также определены в math.h, например, для косинуса, арксинуса и гиперболического синуса (sinh).

Аналогично, Python определяет math.sin (x)во встроенном модуле math. Сложные синусоидальные функции также доступны в Модуль cmath, например, cmath.sin (z). Математические функции CPython вызывают библиотеку C mathи используют Формат с плавающей запятой двойной точности.

.

Реализации на основе поворотов

Некоторые программные библиотеки предоставляют реализации синусоиды с использованием входного угла в половину- оборотов, где пол-оборота составляет угол 180 градусы или $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$радиан. Представление углов в поворотах или полуворотах в некоторых случаях дает преимущества в точности и эффективности.

Окружение	Название функции	Угловые единицы
MATLAB	sinpi	полуобороты
OpenCL	sinpi	полуобороты
R	sinpi	полуобороты
Julia	sinpi	полуобороты
CUDA	sinpi	полуобороты
ARM	sinpi	полуобороты

Преимущество точности проистекает из способности идеально представлять ключевые углы, такие как полный оборот, полуоборот и четверть оборота, без потерь в двоичной системе с плавающей запятой или с фиксированной запятой. Напротив, представляя $2\; \pi \; \{\backslash \; displaystyle\; 2\; \backslash \; pi\}$, $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$и $\pi \; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{\; 2\}\}\}$в двоичной плавающей запятой или двоичной масштабированной фиксированной запятой всегда влечет за собой потерю точности.

Повороты также имеют преимущество в точности и эффективности для вычисления по модулю до одного периода. Вычисление по модулю 1 оборот или по модулю 2 полуоборотов может выполняться без потерь и эффективно как с плавающей, так и с фиксированной точкой. Например, вычисление по модулю 1 или 2 для значения с фиксированной запятой, масштабированного по двоичной точке, требует только битового сдвига или операции побитового И. Напротив, вычисление по модулю $\pi \; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\}$включает неточности при представлении $\pi \; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\}$.

Для приложений, связанных с датчиками угла, датчик обычно обеспечивает угловые измерения в форме, напрямую совместимой с поворотами или полуоборотами. Например, датчик угла может отсчитывать от 0 до 4096 за один полный оборот. Если полуворота используются в качестве единицы измерения угла, тогда значение, предоставляемое датчиком, напрямую и без потерь отображается в тип данных с фиксированной точкой с 11 битами справа от двоичной точки. Напротив, если радианы используются в качестве единицы для хранения угла, то неточности и стоимость умножения необработанного целого числа датчика на приближение к $\pi \; 2048\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2048\}\}\}$будут понесены.

• таблицу синусов Рьябханы
• Формула аппроксимации синуса Бхаскары I
• Дискретное синусоидальное преобразование
• Формула Эйлера
• Обобщенная тригонометрия
• Гиперболическая функция
• Закон синусов
• Список периодических функций
• Список тригонометрических тождеств
• Серия Мадхав
• Таблица синусов Мадхавы
• Теорема оптического синуса
• Полярный синус - обобщение на углы вершин
• Доказательства тригонометрических тождества
• функция Sinc
• преобразования синуса и косинуса
• интеграл синуса
• квадрант синуса
• волна синуса
• уравнение синуса – Гордона
• синусоидальная модель
• тригонометрические функции
• тригонометрический интеграл

• Траупман, доктор философии, Джон К. (1966), Латинский и английский словарь Нью-колледжа, Торонто: Bantam, ISBN 0-553-27619-0
• Седьмой новый университетский словарь Вебстера, Спрингфилд: G. C. Merriam Company, 1969

• СМИ, связанные с функцией синуса на Wikimedia Commons

Найдите sine в Wiktionary, бесплатном словаре.