Синусоида

Математическая кривая, описывающая плавные повторяющиеся колебания; непрерывная волна Графики синусоиды (сплошной красный) и косинус (пунктирная синяя) являются синусоидами разных фаз

A синусоидой или синусоидой является математическая кривая, описывающая плавное периодическое колебание. Синусоидальная волна - это непрерывная волна. Он назван в честь функции синус, из которых это график. Это часто встречается как в чистой, так и в прикладной математике, а также в физике, инженерии, обработке сигналов и многих других областях. Его основная форма как функция времени (t):

$y\; (t)\; =\; A\; sin\; \; (2\; \pi \; ft\; +\; \phi )\; =\; A\; sin\; \; (\omega \; t\; +\; \phi )\; \{\backslash \; displaystyle\; y\; (t)\; =\; A\; \backslash \; sin\; (2\; \backslash \; pi\; ft\; +\; \backslash \; varphi)\; =\; A\; \backslash \; sin\; (\backslash \; omega\; t\; +\; \backslash \; varphi)\}$

где:

• A, амплитуда, пиковое отклонение функции от нуля.
• f, обычная частота, число колебаний (циклов), которые происходят каждую секунду.
• ω = 2πf, угловая частота, скорость изменения аргумента функции в единицах радиан в секунду
• $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$, phase, указывает (в радианах ), где в его цикле колебания находятся в точке t = 0. Когда $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$не равно нулю, вся форма волны кажется смещенной в время на величину $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$/ ω секунд. Отрицательное значение представляет задержку, а положительное значение - опережение.

	Синусоидальная волна 5 секунд синусоидальной волны 220 Гц
Проблемы с воспроизведением этого файла? См. .

Колебания незатухающей системы пружина-масса вокруг равновесия - это синусоидальная волна.

Синусоидальная волна важна в физике, потому что она сохраняет свою форму волны при добавлении к другой синусоиде та же частота и произвольная фаза и величина. Это единственный периодический сигнал, обладающий этим свойством. Это свойство обуславливает его важность в анализе Фурье и делает его уникальным в акустическом отношении.

Содержание

• 1 Общая форма
• 2 Вхождения
• 3 Ряд Фурье
• 4 Бегущие и стоячие волны
• 5 См. Также
• 6 Дополнительная литература

Общая форма

В общем, функция также может иметь:

• пространственную переменную x, которая представляет положение в измерении, в котором распространяется волна, и характеристический параметр k, называемый волновым числом (или угловым волновым числом), который представляет собой пропорциональность между угловой частотой ω и линейной скоростью (скорость распространения ) ν;
• ненулевой центральной амплитудой, D

, которая равна

$Y\; (Икс,\; T)\; знак\; равно\; A\; грех\; \; (Kx\; -\; \omega \; T\; +\; \phi )\; +\; D\; \{\backslash \; Displaystyle\; Y\; (x,\; t)\; =\; A\; \backslash \; sin\; (kx-\; \backslash \; omega\; t\; +\; \backslash \; varphi)\; +\; D\; \backslash ,\}$, если волна движется вправо

$y\; (x,\; t)\; =\; A\; sin\; \; (kx\; +\; \omega \; t\; +\; \phi )\; +\; D\; \{\backslash \; displaystyle\; y\; (x,\; t)\; =\; A\; \backslash \; sin\; (kx\; +\; \backslash \; omega\; t\; +\; \backslash \; varphi)\; +\; D\; \backslash ,\}$, если волна движется влево.

Волновое число связано с угловой частотой следующим образом: :.

$k\; =\; \omega \; v\; =\; 2\; \pi \; fv\; Знак\; равно\; 2\; \pi \; \lambda \; \{\backslash \; Displaystyle\; к\; =\; \{\backslash \; омега\; \backslash \; над\; v\}\; =\; \{2\; \backslash \; пи\; е\; \backslash \; over\; v\}\; =\; \{2\; \backslash \; pi\; \backslash \; over\; \backslash \; lambda\}\}$

где λ (лямбда) - длина волны , f - частота, а v - линейная скорость.

Это уравнение дает синусоидальную волну для одного измерения; таким образом, приведенное выше обобщенное уравнение дает смещение волны в точке x в момент времени t вдоль одной линии. Это можно было бы, например, считать величиной волны вдоль провода.

В двух или трех пространственных измерениях одно и то же уравнение описывает бегущую плоскую волну, если положение x и волновое число k интерпретируются как векторы, а их произведение как скалярное произведение. Для более сложных волн, таких как высота водной волны в пруду после падения камня, необходимы более сложные уравнения.

Появления

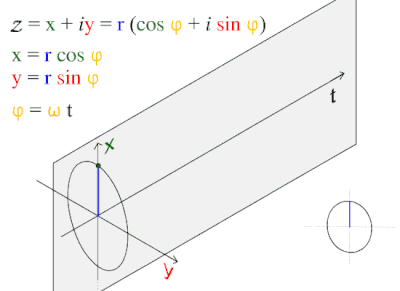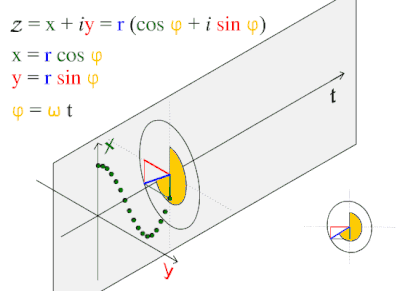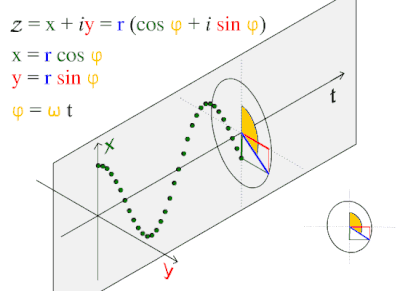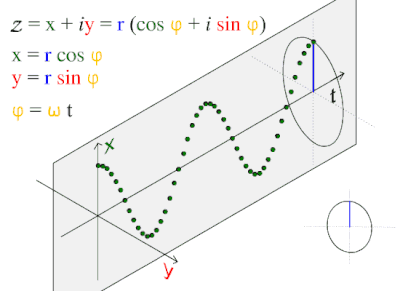Иллюстрация фундаментального отношения косинусоидальной волны к окружности.

Эта модель волны часто встречается в природе, включая ветровые волны, звуковые волны и световые волны.

A косинус волна называется синусоидальной, потому что $cos\; \; (x)\; =\; sin\; \; (x\; +\; \pi \; /\; 2),\; \{\backslash \; displaystyle\; \backslash \; cos\; (x)\; =\; \backslash \; sin\; (x\; +\; \backslash \; pi\; /\; 2),\}$, которая также является синусоидальной волной со сдвигом фазы π / 2 радиан. Из-за этого опережение часто говорят, что функция косинуса опережает функцию синуса или синус отстает от косинуса.

Человеческое ухо может распознавать одиночные синусоидальные волны как чистые, потому что синусоидальные волны представляют собой одну частоту без гармоник.

Для человека ухо, звук, состоящий из более чем одной синусоидальной волны, будет иметь заметные гармоники; добавление разных синусоидальных волн приводит к другой форме волны и, таким образом, изменяет тембр звука. Наличие высших гармоник в дополнение к основным причинам изменения тембра, по этой причине одна и та же музыкальная нота (одна и та же частота), воспроизводимая на разных инструментах, звучит по-разному. С другой стороны, если звук содержит апериодические волны наряду с синусоидальными волнами (которые являются периодическими), тогда звук будет восприниматься как зашумленный, поскольку шум характеризуется как апериодический или неповторяющийся. шаблон.

ряд Фурье

синус, квадрат, треугольник и пила формы сигналов

В 1822 году французский математик Жозеф Фурье обнаружил, что синусоидальные волны можно использовать в качестве простых строительных блоков для описания и аппроксимации любой периодической формы волны, включая прямоугольные волны. Фурье использовал его как аналитический инструмент при изучении волн и теплового потока. Он часто используется в обработке сигналов и статистическом анализе временных рядов.

бегущих и стоячих волн

Поскольку синусоидальные волны распространяются без изменения формы в распределенных линейных системах, они часто используется для анализа распространения волны. Синусоидальные волны, распространяющиеся в пространстве в двух направлениях, можно представить как

$u\; (t,\; x)\; =\; A\; sin\; \; (kx\; -\; \omega \; t\; +\; \phi )\; \{\backslash \; displaystyle\; u\; (t,\; x)\; =\; A\; \backslash \; sin\; (kx-\; \backslash \; omega\; t\; +\; \backslash \; varphi)\}$

Когда две волны, имеющие одинаковую амплитуду и частоту и распространяющиеся в противоположных направлениях, накладываются друг на друга, тогда создается образец стоячей волны. Обратите внимание, что на натянутой струне мешающие волны - это волны, отраженные от фиксированных конечных точек струны. Следовательно, стоячие волны возникают только на определенных частотах, которые называются резонансными частотами и состоят из основной частоты и ее высших гармоник. Резонансные частоты струны пропорциональны: длине между закрепленными концами; натяжение струны; и обратно пропорциональна массе на единицу длины струны.

См. Также

• Crest (физика)
• Затухающая синусоида
• преобразование Фурье
• Гармонический ряд (математика)
• Гармонический ряд (музыка)
• Уравнение Гельмгольца
• Мгновенная фаза
• Осциллограф
• Фазор
• Чистый тон
• Простое гармоническое движение
• Синусоидальная модель
• Волна (физика)
• Волновое уравнение
• ∿ символ синусоидальной волны (U + 223F)

Дополнительная литература

• «Синусоида». Энциклопедия математики. Springer. Получено 8 декабря 2013 г.