В электротехнике, электрический импеданс - это мера сопротивления, которое цепь цепи представляет току при приложении напряжения.
Количественно импеданс двухконтактного элемента схемы представляет собой отношение комплексного представления синусоидального напряжения между его выводами к комплексному представлению ток, текущий через него. В общем, это зависит от частоты синусоидального напряжения.
Импеданс расширяет понятие сопротивления до цепей переменного тока (AC) и имеет как величину, так и фазу, в отличие от сопротивления, которое имеет только величина. Когда цепь приводится в действие постоянным током (DC), нет различия между импедансом и сопротивлением; последнее можно рассматривать как импеданс с нулевым фазовым углом.
Импеданс - это комплексное число с теми же единицами измерения, что и сопротивление, для которого единица СИ является Ом (Ом). Его символ обычно Z, и он может быть представлен записью его величины и фазы в полярной форме | Z | ∠θ. Однако декартово представление комплексных чисел часто более эффективно для анализа схем.
Понятие импеданса полезно для выполнения анализа переменного тока электрических сетей, поскольку оно позволяет связывать синусоидальные напряжения и токи с помощью простого линейного закона. В сетях с несколькими портами двухполюсное определение импеданса неадекватно, но комплексные напряжения на портах и токи, протекающие через них, все еще линейно связаны импедансом . матрица.
обратная импеданса равна адмиттанс, единица SI которого равна siemens, ранее называвшаяся mho.
Приборы, используемые для измерения электрического импеданса, называются анализаторами импеданса.
Термин «импеданс» был придуман Оливером Хевисайдом в июле 1886 года. Артур Кеннелли был первым, кто представил импеданс комплексными числами в 1893 году.
Помимо сопротивления, наблюдаемого в цепях постоянного тока, импеданс в цепях переменного тока включает в себя эффекты индукции напряжений в проводниках магнитными полями (индуктивность ) и электростатическое накопление заряда, индуцированное напряжениями между проводниками (емкость ). Импеданс, вызванный этими двумя эффектами, вместе называется реактивным сопротивлением и образует мнимую часть комплексного импеданса, тогда как сопротивление составляет действительную часть.
Импеданс определяется как в частотной области отношение напряжения к току. Другими словами, это отношение напряжения к току для одной комплексной экспоненты на определенной частоте ω.
Для входного синусоидального тока или напряжения полярная форма комплексного импеданса связывает амплитуду и фазу напряжения и тока. В частности:
 Графическое представление плоскости комплексного импеданса
Графическое представление плоскости комплексного импеданса Импеданс двухполюсного элемента схемы представлен как комплексная величина 

где величина 




В декартовой форме импеданс определяется как

где действительная часть импеданса - это сопротивление 

В тех случаях, когда необходимо добавить или вычесть импедансы, декартова форма более удобна; но когда количества умножаются или делятся, расчет становится проще, если используется полярная форма. Расчет схемы, такой как определение полного импеданса двух параллельных импедансов, может потребовать преобразования между формами несколько раз во время расчета. Преобразование между формами следует обычным правилам преобразования комплексных чисел.
 Обобщенные импедансы в цепи могут быть обозначены тем же символом, что и резистор (US ANSI или DIN Euro) или помеченный прямоугольник.
Обобщенные импедансы в цепи могут быть обозначены тем же символом, что и резистор (US ANSI или DIN Euro) или помеченный прямоугольник. Для упрощения вычислений синусоидальные волны напряжения и тока обычно представляются как комплексные функции времени, обозначаемые как 


Импеданс биполярной цепи определяется как отношение этих величин:

Следовательно, обозначая 

Уравнение величины - это знакомый закон Ома, применяемый к амплитудам напряжения и тока, а второе уравнение определяет соотношение фаз.
Это представление с использованием комплексных экспонент может быть оправдано, отметив, что (по формуле Эйлера ):
![\ \ cos (\ omega t + \ phi) = {\frac {1}{2}}{\Big [}e^{j(\omega t+\phi)}+e^{-j(\omega t+\phi)}{\Big ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac6d2d678fbcb897277792546ef55f422d17c2dc)
Действительная синусоидальная функция, представляющая напряжение или ток, может быть нарушена на две комплексные функции. По принципу суперпозиции, мы можем анализировать поведение синусоиды в левой части, анализируя поведение двух сложных членов в правой части. Учитывая симметрию, нам нужно провести анализ только для одного правого члена. Результаты идентичны для другого. В конце любых вычислений мы можем вернуться к синусоидам с действительным знаком, отметив далее, что

 Источник переменного тока с напряжением
Источник переменного тока с напряжением  через load
через load  , управляя током
, управляя током 
Значение электрического импеданса можно понять, подставив его в закон Ома. Предполагая, что двухконтактный элемент схемы с полным сопротивлением 

Величина импеданса 




Подобно тому, как импеданс расширяет закон Ома на цепи переменного тока, другие результаты анализа цепей постоянного тока, такие как деление напряжения, деление тока, теорема Тевенина и Теорема Нортона также может быть распространена на цепи переменного тока путем замены сопротивления импедансом.
Векторы представлены постоянным комплексным числом, обычно выраженным в экспоненциальной форме, представляющим комплексную амплитуду (величину и фазу) синусоидальной функции времени. Фазоры используются инженерами-электриками для упрощения вычислений с использованием синусоид, где они часто могут свести проблему дифференциального уравнения к алгебраической.
Импеданс элемента схемы может быть определен как отношение векторного напряжения на элементе к векторному току через элемент, что определяется относительными амплитудами и фазами напряжения и тока. Это идентично определению из закона Ома, приведенного выше, с учетом того, что факторы 
 Фазовые углы в уравнениях для импеданса конденсаторов и катушек индуктивности показывают, что напряжение на конденсаторе отстает от проходящего через него тока на фазу
Фазовые углы в уравнениях для импеданса конденсаторов и катушек индуктивности показывают, что напряжение на конденсаторе отстает от проходящего через него тока на фазу  , а напряжение на катушке индуктивности опережает ток через нее на
, а напряжение на катушке индуктивности опережает ток через нее на  . Идентичные амплитуды напряжения и тока указывают на то, что величина импеданса равна единице.
. Идентичные амплитуды напряжения и тока указывают на то, что величина импеданса равна единице. Импеданс идеального резистора является чисто реальным и называется резистивным сопротивлением:

В этом случае формы сигналов напряжения и тока пропорциональны и синфазны.
Идеальные катушки индуктивности и конденсаторы имеют чисто мнимое реактивное сопротивление:
сопротивление катушек индуктивности увеличивается с увеличением частоты;

импеданс конденсаторов уменьшается с увеличением частоты;

В обоих случаях для приложенного синусоидального напряжения результирующий ток также синусоидальный, но в квадратуре, сдвинут по фазе на 90 градусов с напряжением. Однако фазы имеют противоположные знаки: в катушке индуктивности ток отстает; в конденсаторе ток является ведущим.
Обратите внимание на следующие тождества для мнимой единицы и обратной величины:

Таким образом, уравнения импеданса катушки индуктивности и конденсатора могут быть переписаны на полярная форма:

Величина показывает изменение амплитуды напряжения для данной амплитуды тока через импеданс, а экспоненциальные множители определяют фазовое соотношение.
Ниже приводится расчет импеданса для каждого из трех основных элементов цепи : резистора, конденсатора и катушки индуктивности.. Хотя эту идею можно расширить, чтобы определить взаимосвязь между напряжением и током любого произвольного сигнала , эти производные предполагают синусоидальные сигналы. Фактически, это применимо к любым произвольным периодическим сигналам, поскольку они могут быть аппроксимированы как сумма синусоид с помощью анализа Фурье.
Для резистора существует соотношение

что является законом Ома.
Учитывая, что сигнал напряжения равен

следует, что

Это означает, что отношение амплитуды переменного напряжения к переменному току ( Амплитуда переменного тока) на резисторе равна 
Этот результат обычно выражается как

Для конденсатора существует отношение:

Учитывая, что сигнал напряжения равен

следует, что

и, таким образом, как и ранее,

И наоборот, если ток в цепи предполагается синусоидальным, его комплексное представление будет

затем интегрирование дифференциального уравнения

приводит к

Член Const представляет собой фиксированное потенциальное смещение, наложенное на синусоидальный потенциал переменного тока, который не играет роли в анализе переменного тока. Для этой цели этот член можно принять равным 0, следовательно, снова полное сопротивление

Для катушки индуктивности у нас есть соотношение (из закона Фарадея ):

На этот раз, учитывая, что текущий сигнал равен:

следует, что:

Этот результат обычно выражается в полярной форме как

или, используя формулу Эйлера, как

Как и в случае с конденсаторами, эту формулу также можно вывести непосредственно из комплексного представления s напряжений и токов, или полагая синусоидальное напряжение между двумя полюсами индуктора. В этом более позднем случае интегрирование приведенного выше дифференциального уравнения приводит к постоянному члену для тока, который представляет фиксированное смещение постоянного тока, протекающее через катушку индуктивности. Это установлено на ноль, потому что анализ переменного тока с использованием импеданса в частотной области учитывает одну частоту за раз, а постоянный ток представляет в этом контексте отдельную частоту в ноль герц.
Импеданс, определенный в терминах jω, может строго применяться только к цепям, которые управляются установившимся сигналом переменного тока. Понятие импеданса может быть расширено до цепи, возбуждаемой любым произвольным сигналом, с использованием комплексной частоты вместо jω. Комплексная частота обозначается символом s и, как правило, является комплексным числом. Сигналы выражаются в терминах комплексной частоты путем принятия преобразования Лапласа выражения временной области сигнала. Импеданс основных элементов схемы в этом более общем обозначении выглядит следующим образом:
| Элемент | Выражение импеданса |
|---|---|
| Резистор |  |
| Индуктор |  |
| Конденсатор |  |
Для цепи постоянного тока это упрощается до s = 0. Для установившегося синусоидального сигнала переменного тока s = jω.
Сопротивление и реактивное сопротивление вместе определяют величину и фазу полного сопротивления посредством следующих соотношений:

Во многих приложениях относительная фаза напряжения и тока не критична, поэтому важна только величина импеданса.
Сопротивление 

Реактивность 


Чисто реактивный компонент отличается тем, что синусоидальное напряжение на компоненте находится в квадратуре с синусоидальным током, протекающим через компонент. Это означает, что компонент попеременно поглощает энергию из цепи, а затем возвращает энергию в цепь. Чистое реактивное сопротивление не рассеивает мощность.
Конденсатор имеет чисто реактивное сопротивление, которое обратно пропорционально сигналу частота. Конденсатор состоит из двух проводников, разделенных изолятором, также известным как диэлектрик.

Знак минус означает, что мнимая часть импеданс отрицательный.
На низких частотах конденсатор приближается к разомкнутой цепи, поэтому через него не течет ток.
Напряжение постоянного тока, приложенное к конденсатору, заставляет заряд накапливаться на одной стороне; электрическое поле из-за накопленного заряда является источником противодействия току. Когда потенциал, связанный с зарядом, точно уравновешивает приложенное напряжение, ток стремится к нулю.
Управляемый источником переменного тока, конденсатор накапливает только ограниченный заряд, прежде чем разность потенциалов изменит знак и заряд рассеется. Чем выше частота, тем меньше накапливается заряда и тем меньше сопротивление току.
Индуктивное реактивное сопротивление 



Катушка индуктивности состоит из спирального проводника. Закон Фарадея электромагнитной индукции дает обратное emf 


Для индуктора, состоящего из катушки с 

Обратная ЭДС является источником противодействия текущему потоку. Постоянный постоянный ток имеет нулевую скорость изменения и рассматривает индуктор как короткое замыкание (обычно он изготовлен из материала с низким удельным сопротивлением ). Переменный ток имеет усредненную по времени скорость изменения, которая пропорциональна частоте, это вызывает увеличение индуктивного сопротивления с частотой.
Полное реактивное сопротивление определяется как
 (обратите внимание, что
(обратите внимание, что  отрицательно)
отрицательно), так что общий импеданс равен

Общий импеданс многих простых сетей компонентов может быть вычислен с использованием правил объединения импедансов последовательно и параллельно. Правила идентичны правилам комбинирования сопротивлений, за исключением того, что числа, как правило, являются комплексными числами. В общем случае, однако, требуется эквивалентное преобразование импеданса в дополнение к последовательному и параллельному.
Для компонентов, соединенных последовательно, ток через каждый элемент схемы одинаков; полный импеданс - это сумма импедансов компонентов.
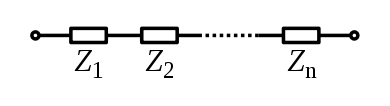

Или явно в действительном и мнимом выражении:

Для компонентов, соединенных параллельно, напряжение на каждом элементе схемы одинаково; отношение токов, протекающих через любые два элемента, является обратной величиной их импедансов.

Следовательно, обратный полный импеданс является суммой обратных величин импедансов компонентов:

или, если n = 2:


Эквивалентное сопротивление 



Измерение импеданса устройств и линий передачи это практическая проблема в радио технике и других областях. Измерения импеданса можно проводить на одной частоте, или может представлять интерес изменение импеданса устройства в диапазоне частот. Импеданс может быть измерен или отображен непосредственно в омах, или могут отображаться другие значения, связанные с импедансом; например, в радиоантенне коэффициент стоячей волны или коэффициент отражения могут быть более полезными, чем только импеданс. Измерение импеданса требует измерения величины напряжения и тока, а также разности фаз между ними. Импеданс часто измеряется «мостовыми» методами, аналогичными постоянному току мостом Уитстона ; калиброванный эталонный импеданс регулируется для компенсации влияния импеданса тестируемого устройства. Измерение импеданса в силовых электронных устройствах может потребовать одновременного измерения и подачи питания на работающее устройство.
Импеданс устройства можно вычислить сложным делением напряжения и тока. Импеданс устройства можно рассчитать, подав на устройство синусоидальное напряжение последовательно с резистором и измерив напряжение на резисторе и на устройстве. Выполнение этого измерения путем свипирования частот подаваемого сигнала позволяет определить фазу и величину импеданса.
Использование импульсной характеристики может использоваться в сочетании с быстрым преобразованием Фурье (БПФ) для быстро измерять электрическое сопротивление различных электрических устройств.
Измеритель LCR (индуктивность (L), емкость (C) и сопротивление (R)) - это устройство, обычно используемое для измерения индуктивность, сопротивление и емкость компонента; исходя из этих значений, можно рассчитать импеданс на любой частоте.
Рассмотрим контур LC резервуара. Комплексный импеданс цепи равен

Сразу видно, что значение 

Следовательно, угловая частота основного резонанса равна

Как правило, ни импеданс, ни проводимость не могут изменяться со временем, поскольку они определены для комплексных экспонент в котором -∞ < t < +∞. If the complex exponential voltage to current ratio changes over time or amplitude, the circuit element cannot be described using the frequency domain. However, many components and systems (e.g., варикапы, которые используются в радиотюнерах ), могут иметь нелинейные или изменяющиеся во времени отношения напряжения к току, которые кажутся линейными, не зависящими от времени (LTI) для слабых сигналов и в небольших окнах наблюдения, поэтому их можно грубо описать как если бы они имели изменяющийся во времени импеданс. Это описание является приблизительным: при больших колебаниях сигнала или широких окнах наблюдения зависимость напряжения от тока не будет LTI и не может быть описана импедансом.