Теория управления занимается управлением динамическими системами в инженерных процессах и машинах. Цель состоит в том, чтобы создать модель управления для управления такими системами с использованием управляющего воздействия оптимальным образом без задержек или перерегулирования и обеспечения управления стабильностью.
. Для этого контроллер необходимыми корректирующими поведением. Этот контроллер отслеживает регулируемую переменную процесса (PV) и сравнивает ее с опорным или заданным значением (SP). Различным фактическим и желаемым значением переменной процесса, называемым сигналом ошибки или ошибкой SP-PV, является в качестве обратной связи для генерации управляющего воздействия, чтобы привести переменную переменную процесса к тому же значению, что и заданное. Другие аспекты, которые также изучаются, - это управляемость и наблюдаемость. Это основа для передового типа автоматизации, который произвел революцию в производстве, авиастроении, связи и других отраслях. Это управление с обратной связью, которое включает в себя выполнение измерений с помощью датчика и выполнение расчетных регулировок для удержания измеряемой переменной в заданном диапазоне с помощью «конечного элемента управления», такого как регулирующий клапан.
Обычно широко используется стиль диаграммы, известный как блок-схема . В нем передаточная функция, также известная как системная функция или сетевая функция, представляет собой математическую модель отношений между входом и выходом, основанную на дифференциальных уравнениях, описывающих систему.
Теория управления восходит к 19 веку, когда теоретические основы работы регуляторов впервые были впечатления Джеймсом Клерком Максвеллом. Теория управления была развита Эдвардом Раутом в 1874 г., Чарльзом Штурмом и в 1895 г. Адольфом Гурвицем, которые все внесли свой вклад в установление критериев стабильности управления; а с 1922 г. - разработка теории ПИД-регулирования Николасом Минорским. Хотя прикладное применение математической теории управления находится в разработке систем управления, которая занимается проектированием систем управления процессами для промышленности, других приложений выходят далеко за рамки этого. Как общая теория систем с обратной связью, теория управления полезна везде, где возникает обратная связь - таким образом, теория управления также имеет приложения в биологических науках, компьютерной инженерии, социологии и исследованиях операций.
 Центробежный регулятор в двигателе Boulton Watt 1788 года
Центробежный регулятор в двигателе Boulton Watt 1788 года Хотя системы управления различными типами появились еще раньше В древности более формального анализа начался с анализа динамики центробежного регулятора, проведенного физиком Джеймсом Клерком Максвеллом в 1868 году под названием «О губернаторах». Центробежный регулятор уже использовался для регулирования скорости ветряных мельниц. Максвелл описал и проанализировал явление автоколебания, при задержке в системе может возникнуть чрезмерной компенсации и нестабильному поведению. Это вызвало волну интереса к теме, во время которой одноклассник Максвелла, Эдвард Джон Раус, абстрагировал Максвелла для общего класса линейных систем. Независимо, Адольф Гурвиц проанализировал устойчивость системы с помощью дифференциальных уравнений в 1877 году, что привело к тому, что теперь известно как теорема Рауса - Гурвица.
. Заметное применение динамического управления было в области пилотируемых полетов.. Братья Райт совершили свои первые успешные испытательные полеты 17 декабря 1903 года и отличались своей способностью контролировать свои полеты в течение многих периодов времени (больше, чем способность создавать подъемную силу от аэродинамического профиля, что известно). Для полетов продолжительностью более нескольких секунд требовалось постоянное и надежное управление самолетом.
К Вторая мировая война теория управления стала главной областью исследований. Ирмгард Флюгге-Лотц разработала теорию прерывистых систем автоматического управления и применила принцип к разработке оборудования автоматического управления полетом для самолетов. Другие области применения прерывистого контроля включаются системы управления огнем, системы наведения и электронику.
. Иногда для устойчивости систем используются механические методы. Например, стабилизаторы корабля - это киль, установленный ниже ватерлинии и выходящий сбоку. Чтобы противодействовать крену, вызываемому ветром или волнами, действующим на корабль кораблям, они способны противодействовать атакам.
Space Race также зависела от точного управления космическим кораблем, и теория управления также нашла все более широкое применение в таких областях, как экономика и искусственный интеллект. Здесь можно сказать, что цель - найти внутреннюю модель, которая подчиняется теореме о хорошем регуляторе. Так, например, в экономике, чем точнее модель торговли (акциями или товарами), тем легче она может контролировать этот рынок (и извлекать из «полезной работы» (прибыль)). В ИИ примером может быть чат-бот, моделирующий состояние дискурса людей: чем точнее он может моделировать состояние человека (например, на горячей линии телефонной голосовой поддержки), тем лучше он может манипулировать человеком (например, выполнять корректирующие действия). для решения проблемы, вызвавшей звонок в службу поддержки). Эти два используют узкую историческую теорию теории управления как набора различных, моделирующих и регулирующих кинетическое движение, и расширяют ее до обширного обобщения регулятора, взаимодействующего с используя.
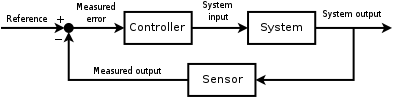 A отрицательной обратной связи системы управления с использованием контура обратной связи для управления процессом сравнения путем ее с желаемым Использование разницы в сигнале ошибки для генерации управляющего выхода для уменьшения или устранения ошибок.
A отрицательной обратной связи системы управления с использованием контура обратной связи для управления процессом сравнения путем ее с желаемым Использование разницы в сигнале ошибки для генерации управляющего выхода для уменьшения или устранения ошибок.  Пример одиночного промышленного контура управления; показывает непрерывно модулированное управление потоком процесса.
Пример одиночного промышленного контура управления; показывает непрерывно модулированное управление потоком процесса. По сути, существует два типа контуров управления: управление без обратной связи и управление с обратной связью.
При управлении без обратной связи управляющее действие контроллера не зависит от «выхода процесса» (или «регулируемой переменной процесса» - PV). Хорошим примером этого является котел отопления, управляемый только таймером, независимо от температуры в здании. Управляющее действие - это включение / выключение котла по времени.
При управлении обратным связью управляющее действие контроллера зависит от системы значений процесса (PV). В случае аналогии с котлом, замкнутый контур будет включен термостат для сравнения температуры здания (PV) с температурой, установленной на термостате (уставка - SP). Это генерирует выходной сигнал контроллера для поддержания заданной температуры в здании путем включения и выключения котла. Таким образом, контроллер с обратной связью имеет контроллер обратной связи, который гарантирует, что применяет управляющее действие, чтобы манипулировать переменным процессом, чтобы она была такая же, как «эталонный вход» или «уставка». По этой причине контроллеры с обратной связью также называют контроллерами с обратной связью.
Определение системы управления обратной связью в соответствии с Британским институтом стандартов - это «система управления, обладающая контрольной обратной связью, сигнал отклонения формируется в результате этой обратной связи используется для управления конечным элементом управления таким образом, уменьшить отклонение. до нуля ».
Аналогично; «Система управления с помощью одной системы контроля, поддерживает заданное отношение к другой системе сравнения функций контроля».
пример системы управления является автомобилем круиз-контроль, которое представляет собой устройство, предназначенное для поддержания скорости транспортных средств при желаемой или расчетной скорости, представленной водителем. Контроллер - это круиз-контроль, установка - это машина, а система - это машина и круиз-контроль. Выходные данные системы - это скорость автомобиля, а само управление - это положение дроссельной заслонки двигателя, которое определяет, какую мощность выдает двигатель.
Примитивный способ реализации круиз-контроля - просто заблокировать положение дроссельной заслонки, когда водитель включает круиз-контроль. Однако, если круиз-контроль включен на участке неровной дороги, автомобиль будет двигаться медленнее при подъеме и быстрее при спуске. Этот тип контроллера называется контроллером без обратной связи, потому что нет обратной связи ; никакие измерения выходной мощности системы (скорости автомобиля) не используются для изменения управления (положения дроссельной заслонки). В результате контроллер не может компенсировать изменения, воздействующие на автомобиль, например, изменение уклона дороги.
В системе управления с обратной связью данные датчика, отслеживающего скорость автомобиля (выходной сигнал системы), поступают в контроллер, который постоянно сравнивает представляющую скорость, с эталонной величиной, представляющую желаемую скорость. Разница, называемая ошибкой, положение дроссельной заслонки (контроль). Результатом является соответствие скорости автомобиля эталонной скорости (поддержание желаемой выходной мощности системы). Теперь, когда автомобиль едет в гору, разница между входным сигналом (измеренной скоростью) и заданным значением постоянно определяет положение дроссельной заслонки. Когда измеренная скорость падает ниже заданной, разница увеличивается, дроссельная заслонка открывается, и мощность двигателя увеличивается, ускоряя транспортное средство. Таким образом, контроллер динамически противодействует изменениям скорости автомобиля. Центральная идея этих систем управления - это контур обратной связи, контроллер влияет на выходной сигнал системы, который, в свою очередь, измеряется и передается обратно в контроллер.
Чтобы преодолеть ограничения контроллера с разомкнутым контуром, теория управления вводом обратную связь. Контроллер с обратной связью использует обратную связь для управления состояниями или выходами динамической системы. Его название происходит от информационного пути в системе: входные данные процесса (например, напряжение, приложенное к электродвигателю ) воздействуют на выходные данные процесса (например, скорость или крутящий момент мотор), который измеряется датчиками и обрабатывается контроллером; результат (управляющий сигнал) "возвращается" как вход в процесс, замыкая цикл.
Контроллеры с обратной связью имеют следующие преимущества перед контроллерами с обратной связью :
В некоторых системах управление с обратной связью и без обратной связи используется одновременно. В таких системах управление без обратной связи называется с связью и прямым для дальнейшего улучшения использования эталонного сигнала.
Распространенной архитектурой контроллера с обратной связью является ПИД-регулятор.
Выходной сигнал системы y (t) возвращается через датчик измерения. F для сравнения с эталонным значением r (t). Затем контроллер C принимает ошибку e (разность) между заданием и выходом, чтобы изменить вход в систему под управлением P. Это показано на рисунке. Этот тип контроллера представляет собой контроллер с обратной связью или контроллер с обратной связью.
Это называется системой управления с одним входом и одним выходом (SISO); Системы MIMO (т. Е. С использованием нескольких входов-множественных выходов) с более чем одним входом / выходом являются обычными. В таких случаях переменные представляются через тип вместо простых скалярных значений. Для некоторых систем с распределенными системами могут быть бесконечными - размерными (обычно функции).

Если мы предположим, что контроллер C, объект P и датчик F являются линейными и введенными во времени (т. Е. Элементы их передаточной функции (s), P (s) и F (s) не зависят от времени), с помощью вышеупомянутой системы можно анализировать с преобразования Лапласа чис. Это дает следующие отношения:



Решение относительно Y (s) через R (s) дает

Выражение 


 A блок-схема ПИД-регулятора в контуре обратной связи, r (t) - это желаемое значение процесса или «уставка», а y (t) - измеренный процесс
A блок-схема ПИД-регулятора в контуре обратной связи, r (t) - это желаемое значение процесса или «уставка», а y (t) - измеренный процесс Пропорционально-интегрально-производный регулятор (ПИД-регулятор) - это контур управления механизм обратной связи, широко используемый в системах управления.
ПИД-регулятор непрерывно вычисляет ошибки 
Теоретическое понимание и применение восходят к 1920-м годам, и они реализованы почти во всех аналоговых системах управления; использование в механических контроллерах, затем с использованием дискретной электроники, а затем в промышленных компьютерах. ПИД-регулятор, вероятно, является наиболее часто используемой конструкцией управления с обратной связью.
Если u (t) - это управляющий сигнал, отправленный в систему, y (t) - это измеренный выходной сигнал, а r (t) - это желаемый выходной сигнал, а 

Требуемая динамика замкнутого контура достигается путем настройки трех параметров 


Применение преобразования Лапласа приводит к преобразованному уравнению ПИД-регулятора


с передаточной функцией ПИД-регулятора

В качестве примера настройки ПИД-регулятор в замкнутой системе 

где 


где 




Вставка 





Однако применяемый чистый дифференциатор не является ни физически реализуемым, ни желательным из-за усиления шума и резонансных мод в системе. Поэтому вместо него используется подход типа фазового компенсатора или дифференциатор с спадом нижних частот.
Теория линейного управления может быть разделена на две части:
Математические методы анализа и проектирования систем управления делятся на две категории:
В отличие от анализа в частотной области классической теории управления, современная теория управления время -домен пространство состояний Представление, уравнение математической модели физической системы как набор входных, выходных и совместных состояний, связанных дифференциальных уравнений первого порядка. Чтобы абстрагироваться от количества входов, выходов и состояний, переменные выражаются в векторных видеов, а дифференциальные и алгебраические уравнения записываются в матричной форме (последнее возможно только в случае, если динамическая система является линейной). Представление в условиях временной области (также известное как «подход во временной области») обеспечивает удобный и компактный способ моделирования и систем с входами и выходами. Что касается входов и выходов, в противном случае пришлось бы записывать преобразование Лапласа для кодирования всей информации о системе. В отличие от подхода в частотной области, использование представления в пространстве состояний не ограничивается системами с линейными компонентами и нулевыми начальными условиями. «Пространство состояний» относится к пространству, оси которого являются переменными состояниями. Состояние системы можно представить в виде точки в этом визу.
Системы управления можно разделить на различные категории в зависимости от количества входов и выходов.
Устойчивость общей динамической системы без входа может быть описана с помощью критерия устойчивости по Ляпунову.
Для простоты следующего описания сосредоточены на непрерывном и дискретном времени линейных систем .
Математически это означает, что для причинно-следственной системы должны быть стабильны все полюса ее передаточной функции имеют отрицательные-действительные значения, т.е. действительная часть каждого полюса должна быть меньше нуля. Практически говоря, стабильность требует, чтобы комплексные полюса передаточной функции находились
Разница между двумя случаями просто из прикладных методов построения графика непрерывного и дискретного времени передаточных функций. Непрерывное преобразование Лапласа выполняется в декартовых координатах, где ось 

Когда удовлетворяются соответствующие условия, выше, система называется асимптотически устойчивой ; переменные асимптотически устойчивой системы управления всегда уменьшаются от своего начального значения и не испытывают постоянных колебаний. Постоянные колебания возникают, когда действующая часть полюса точно равна нулю (в случае непрерывного времени) или имеет модуль, равный единице (в случае дискретного времени). Если просто стабильный отклик системы не затухает и не растет с течением времени и не имеет колебаний, он незначительно стабилен ; в этом случае передаточная функция системы имеет неповторяющиеся полюса в начале комплексной плоскости (т.е. их действующая и комплексная составляющая равны нулю в случае непрерывного времени). Колебания присутствуют, когда у полюсов с действительной частью, равной нулю, мнимая часть не равна нулю.
Если рассматриваемая система импульсную характеристику имеетику
![\ x [n] = 0,5 ^ {n} u [n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3fe9bf89c5cffaf461081935fd41745dc768063)
тогда Z-преобразование (см. этот пример ), задается как

, имеющий полюс в 
Однако, если импульсная характеристика была
![\ x [n] = 1,5 ^ {n} u [n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b769b726a2a55b9fc5e5c8d800187d7715cf84cd)
, тогда Z-преобразование:

который имеет полюс в точке 
Существует множество инструментов для анализа полюсов системы. К ним относятся графические системы, такие как основной годограф, графики Боде или графики Найквиста.
. Механические изменения могут сделать оборудование (и системы управления) более стабильными. Моряки добавить балласт, чтобы улучшить остойчивость кораблей. Круизные лайнеры используют стабилизаторы поперечной устойчивости, которые выступают в поперечном направлении от борта судна примерно на 30 футов (10 м) и непрерывно вращаются вокруг осей для создания сил, противодействующих крену.
Управляемость и наблюдаемость - основные вопросы при анализе системы перед принятием решения о наилучшей стратегии управления, которая будет управлением, или о том, возможно ли контролировать или стабилизировать систему. Управляемость с помощью принуждения системы к определенному состоянию с соответствующим управляющим сигналом. Если состояние неуправляемо, то никакой сигнал никогда не сможет управлять состоянием. Если состояние неуправляемое, но его динамика стабильна, то состояние называется стабилизируемым. Вместо этого наблюдения за связями используйте наблюдения за состоянием системы выходных измерений. Если состояние ненаблюдаемое, контроллер не может определить поведение ненаблюдаемого состояния и, следовательно, не сможет использовать его для стабилизации системы. Однако, как и в случае с условием стабилизируемости, описанным выше, если состояние не может быть обнаружено, оно может быть обнаружено.
С геометрическим зрением, глядя на состояние каждого состояния системы, приводей, каждое "плохое" состояние этого состояния должно быть управляемым и наблюдаемым, хорошим хорошим поведением в замкнутом контуре. система. То есть, если одно из других значений системы не является одновременно управляемым и наблюдаемым, эта часть останется динамиками нетронутой в замкнутой системе. Если такое собственное значение нестабильно, динамика этого собственного значения будет присутствовать в замкнутой системе, которая, следовательно, будет нестабильной. Ненаблюдаемые полюсы не присутствуют в реализации передаточной функции представления в пространстве состояний, поэтому иногда последнее предпочтение отдается при анализе динамических систем.
Решение проблем, связанных с неуправляемой или ненаблюдаемой системой, включает добавление исполнительных механизмов и датчиков.
За последние годы было разработано несколько различных стратегий управления. Они варьируются от очень общих (ПИД-регулятор) до других, посвященных очень конкретным классам систем (особенно робототехника или круиз-контроль самолета).
Проблема управления может иметь несколько характеристик. Стабильность, конечно, присутствует всегда. Контроллер должен обеспечивать стабильность замкнутой системы независимо от стабильности разомкнутого контура. Неправильный выбор контроллера может даже ухудшить стабильность разомкнутой системы, чего обычно следует избегать. Иногда желательно получить определенную динамику в замкнутом контуре: например, чтобы полюса имели ![Re [\ lambda] <- { \ overline {\ lambda}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acd3c480f7bd6fa14fd42e56521994a3b4ad8e2d)

![Re [\ lambda] <0](https://wikimedia.org/api/rest_v1/media/math/render/svg/57bd3912e4d0e7aafac442e28a10f4748da7b90d)
Другая типичная спецификация - это отклонение ступенчатого возмущения; включение интегратора в цепь разомкнутого контура (т.е. непосредственно перед управляемой системой) легко позволяет добиться этого. Другие классы нарушений требуют включения других типов подсистем.
Другие «классические» спецификации теории управления касаются временной характеристики замкнутой системы. Эти включают время нарастания (время, необходимая система управления для достижения желаемого значения после возмущения), пиковое значение перерегулирование (максимальное значение, достигнутое реакцией до достижения желаемых значений) и другие (время установления, спад на четверть). Спецификации частотной области обычно связаны с устойчивостью (см. После).
Современные оценки используют некоторые вариации интегрированной ошибки (IAE, ISA, CQI).
Система управления всегда должна обладать некоторым своим потенциалом. Надежный контроллер таков, что его свойства не сильно меняются, если его применить к системе, немного отличной от математической, используемой для его синтеза. Это требование важно, поскольку ни одна реальная физическая система не ведет себя так, как серия математических систем, используемых для ее электрического представления. Обычно для упрощения расчетов выбирается более простая математическая модель, в случае чего реальная система может быть настолько сложной, что полная модель станет невозможной.
Процесс определения соотношений, управляющих динамикой модели, называется идентификацией системы. Это можно сделать в автономном режиме: например, выполнив серию измерений, на основе которых можно рассчитать приближающуюся математическую модель, обычно ее передаточную функцию или матрицу. Однако такая идентификация по выходным данным не может быть ненаблюдаемую динамику. Иногда модель строится непосредственно на основе общих физических соотношений, например, в случае системы масса-пружина-демпфер мы знаем, что 
Некоторые усовершенствованные методы управления включают в себя идентификацию «онлайн» (см. Ниже). Параметры рассчитываются («идентифицируются») во время работы самого контроллера. Таким образом, если происходит резкое изменение параметров, например, если рука робота освобождает груз, контроллер, соответственно, сам настраивает, чтобы обеспечить правильную работу.
Анализ надежности системы управления SISO (один вход - один выход) может быть в частотной области с учетом передаточной функции системы и с использованием диаграммы Найквиста и Боде. Темы включают усиление , запас по фазе и запас по амплитуде. Для MIMO (несколько входов и выходов) и в целом, более сложных систем управления необходимо выполнить теоретические результаты, использовать для каждого метода управления (см. Следующий раздел). То есть, если требуются особые качества устойчивости, инженер должен переключить свое внимание на метод управления, включить их свойства.
Особой проблемой является требование, чтобы система управления работала должным образом при наличии ограничений и состояний. В физическом мире каждый сигнал ограничен. Может случиться так, что контроллер будет посылать управляющие сигналы, которые не могут быть отслежены физической системой, например, попытка повернуть клапан с чрезмерной скоростью. Это может привести к нарушению поведения замкнутой системы или даже к поломке механизмов или других подсистем. Для решения этой проблемы доступны специальные методы управления: прогнозирующий контроль модели (см. Далее) и системы от заворота. Последний дополнительный блок управления, который гарантирует, что управляющий сигнал никогда не превышает заданный порог.
Для систем MIMO размещение полюсов может быть выполнено математически с использованием представления пространств разомкнутой системы и вычисление матрицы обратной связи, назначающая полюса в желаемых положениях. В комплексных системах это может потребовать компьютерных вычислений и не всегда может быть надежность. Кроме того, обычно наблюдаются не все состояния системы, поэтому в проекте размещения столбов должны быть включены наблюдатели.
Процессы в таких отраслях, как робототехника и аэрокосмическая промышленность, обычно имеют сильную нелинейную динамику. В теории управления иногда можно линеаризовать такие классы систем и применить линейные методы. Эти, например, линеаризация с обратной связью, обратный шаг, управление скользящим режимом, управление линеаризацией траектории, обычно используют, основанные на теории Ляпунова. Дифференциальная геометрия широко использовалась как инструмент для обобщения хорошо известных концепций линейного управления на нелинейный случай, а также для демонстрации тонкостей, которые делают эту проблему более. Теория управления также использовалась для расшифровки нейронного механизма, который управляет когнитивными состояниями.
Когда система управляется контроллерами, проблема заключается в децентрализованном управлении. Децентрализация полезна во многих отношениях, например, она помогает системам управления работать на большей географической территории. Агенты в децентрализованных системах управления могут взаимодействовать с помощью каналов связи и координировать свои действия.
Проблема стохастического управления - это проблема, в результате которой эволюция состояния подвергается случайным ударам извне системы. Задача детерминированного управления не подвержена внешним случайным шокам.
Каждая система управления должна в первую очередь устойчивость поведения замкнутого контура. Для линейных систем это может быть получено путем прямого размещения полюсов. в нелинейных системах управления используются специальные теории (обычно основанные на теории Александра Ляпунова ) для обеспечения устойчивости без учета внутренней динамики системы. Возможность выполнения различных спецификаций зависит от рассматриваемой модели и выбранной стратегии управления.
Многие активные и исторические личности внесли значительный в теорию управления, в том числе
| journal =()| В Викиучебнике есть книга по теме: Системы управления |
| На Викискладе есть материал ы, связанные с o Теория управления. |