Геометрическая алгебра

Алгебраическая структура, разработанная для геометрии

геометрическая алгебра (GA) вектора пространство - это алгебра над полем, известная своей операцией умножения, называемой геометрическим произведением на пространстве элементов, называемом многовектором, которое содержит как scalars $F\; \{\backslash \; displaystyle\; F\}$и векторное пространство $V\; \{\backslash \; displaystyle\; V\}$. Математически геометрическую алгебру можно определить как алгебру Клиффорда векторного пространства с квадратичной формой. Вклад Клиффорда заключался в определении нового продукта, геометрического продукта, который объединил алгебры Грассмана и Гамильтона в единую структуру. Добавление двойственного внешнего произведения Грассмана («встреча») позволяет использовать алгебру Грассмана – Кэли и конформную версию последней вместе с конформной алгеброй Клиффорда дает конформную геометрическую алгебру (CGA), обеспечивающую основу для классических геометрий. На практике эти и несколько производных операций допускают соответствие элементов, подпространств и операций алгебры геометрической интерпретации.

Скаляры и векторы имеют свою обычную интерпретацию и составляют отдельные подпространства ГА. Бивекторы обеспечивают более естественное представление псевдовекторных величин в векторной алгебре , таких как ориентированная площадь, ориентированный угол поворота, крутящий момент, угловой момент, электромагнитное поле и вектор Пойнтинга. Треугольник может представлять ориентированный объем и так далее. Элемент, называемый лезвием, может использоваться для представления подпространства $V\; \{\backslash \; displaystyle\; V\}$и ортогональных проекций на это подпространство. Вращения и отражения представлены как элементы. В отличие от векторной алгебры, ГА естественным образом вмещает любое количество измерений и любую квадратичную форму, такую ​​как относительность.

Примеры геометрических алгебр, применяемых в физике, включают алгебру пространства-времени (и менее распространенную алгебра физического пространства ) и конформная геометрическая алгебра. Геометрическое исчисление, расширение GA, которое включает дифференцирование и интегрирование, может использоваться для формулирования других теорий, таких как комплексный анализ и дифференциальная геометрия, например с помощью алгебры Клиффорда вместо дифференциальных форм. Геометрическая алгебра пропагандировалась, в первую очередь Дэвидом Хестенесом и Крисом Дораном, в качестве предпочтительной математической основы для физики. Сторонники утверждают, что он обеспечивает компактные и интуитивно понятные описания во многих областях, включая классическую и квантовую механику, электромагнитную теорию и относительность. GA также нашел применение в качестве вычислительного инструмента в компьютерной графике и робототехнике.

Геометрический продукт был впервые кратко упомянут Германом Грассманном, который был в основном заинтересован в разработке близкородственная внешняя алгебра. В 1878 г. Уильям Кингдон Клиффорд значительно расширил работу Грассмана, чтобы сформировать то, что сейчас обычно называют алгебрами Клиффорда в его честь (хотя сам Клиффорд решил называть их «геометрическими алгебрами»). В течение нескольких десятилетий геометрические алгебры несколько игнорировались, их сильно затмевали векторное исчисление, недавно разработанное для описания электромагнетизма. Термин «геометрическая алгебра» был популяризован в 1960-х годах Хестеном, который отстаивал его важность для релятивистской физики.

• 1 Определение и обозначения
  • 1.1 Геометрический продукт
  • 1.2 Лезвия, степени и канонический базис
  • 1.3 Проекция уклона
  • 1.4 Представление подпространств
  • 1.5 Единичные псевдоскаляры
  • 1.6 Двойной базис
  • 1.7 Расширения внутреннего и внешнего продуктов
  • 1.8 Линейные функции
• 2 Моделирование геометрии
  • 2.1 Модель векторного пространства
  • 2.2 Модель пространства-времени
  • 2.3 Однородная модель
  • 2.4 Конформная модель
  • 2.5 Модели для проективного преобразования
• 3 Геометрическая интерпретация
  • 3.1 Проекция и отклонение
  • 3.2 Отражение
  • 3.3 Вращения
  • 3.4 Versor
  • 3.5 Подгруппы Γ
• 4 Примеры и приложения
  • 4.1 Гиперобъем параллелотопа, натянутого на векторы
  • 4.2 Пересечение прямой и плоскость
  • 4.3 Системы вращения
• 5 Геометрическое исчисление
• 6 История
• 7 Программное обеспечение
  • 7.1 Активно разрабатываемые проекты с открытым исходным кодом
  • 7.2 Другие проекты
  • 7.3 Тестовый проект
• 8 См. Также
• 9 Примечания
• 10 Ссылки
• 11 Ссылки и дополнительная литература
• 12 Внешние ссылки

Есть несколько различных способов определить геометрическую алгебру. Первоначальный подход Хестена был аксиоматическим, «полным геометрического значения» и эквивалентен универсальной алгебре Клиффорда. Дано конечномерное квадратичное пространство $V\; \{\backslash \; displaystyle\; V\}$над полем $F\; \{\backslash \; displaystyle\; F\}$с симметричной билинейной формой (внутренний продукт, например, евклидова или лоренцева метрика ) $g:\; V\; \times \; V\; \to \; F\; \{\backslash \; displaystyle\; g:\; V\; \backslash \; times\; V\; \backslash \; rightarrow\; F\}$, геометрическая алгебра для этого квадратичного пространства - это алгебра Клиффорда $Cl\; \; (V,\; g)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Cl\}\; (V,\; g)\}$. Как обычно в этой области, в оставшейся части этой статьи будет использоваться только реальный случай, $F\; =\; R\; \{\backslash \; displaystyle\; F\; =\; \backslash \; mathbf\; \{R\}\}$считается. Обозначение $G\; (p,\; q)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (p,\; q)\}$(соответственно $G\; (p,\; q,\; r)\; \{\backslash \; displaystyle\; \{\; \backslash \; mathcal\; \{G\}\}\; (p,\; q,\; r)\}$) будет использоваться для обозначения геометрической алгебры, для которой билинейная форма $g\; \{\backslash \; displaystyle\; g\}$имеет подпись $(p,\; q)\; \{\backslash \; displaystyle\; (p,\; q)\}$(соответственно $(p,\; q,\; r)\; \{\backslash \; displaystyle\; (p,\; q),\; r)\}$).

Существенное произведение в алгебре называется геометрическим произведением, а произведение в содержащейся внешней алгебре называется внешним продуктом (часто называемым произведением клина и реже внешним произведением). Стандартно обозначать их, соответственно, сопоставлением (т. Е. Подавлением любого явного символа умножения) и символом $\wedge \; \{\backslash \; displaystyle\; \backslash \; wedge\}$. Приведенное выше определение геометрической алгебры является абстрактным, поэтому мы суммируем свойства геометрического продукта с помощью следующего набора аксиом. Геометрический продукт имеет следующие свойства для $A,\; B,\; C\; \in \; G\; (p,\; q)\; \{\backslash \; displaystyle\; A,\; B,\; C\; \backslash \; in\; \{\backslash \; mathcal\; \{G\}\}\; (p,\; q)\}$:

$AB\; \in \; G\; (p,\; q)\; \{\backslash \; displaystyle\; AB\; \backslash \; in\; \{\backslash \; mathcal\; \{G\}\}\; (p,\; q)\}$(закрытие )

$1\; A\; =\; A\; 1\; =\; A\; \{\backslash \; displaystyle\; 1A\; =\; A1\; =\; A\}$, где $1\; \{\backslash \; displaystyle\; 1\}$- элемент идентичности (наличие элемента идентичности )

$A\; (BC)\; =\; (AB)\; C\; \{\backslash \; displaystyle\; A\; (BC)\; =\; (AB)\; C\}$(ассоциативность )

$A\; (B\; +\; C)\; =\; AB\; +\; AC\; \{\backslash \; displaystyle\; A\; (B\; +\; C)\; =\; AB\; +\; AC\}$и $(B\; +\; C)\; A\; =\; BA\; +\; CA\; \{\backslash \; displaystyle\; (B\; +\; C)\; A\; =\; BA\; +\; CA\}$(дистрибутивность )

$a\; 2\; =\; g\; (a,\; a)\; 1\; \{\backslash \; displaystyle\; a\; ^\; \{2\; \}\; =\; g\; (a,\; a)\; 1\}$, где $a\; \{\backslash \; displaystyle\; a\}$- любой элемент подпространства $V\; \{\backslash \; displaystyle\; V\}$алгебры.

Внешний продукт имеет те же свойства, за исключением того, что последнее свойство выше заменено на $a\; \wedge \; a\; =\; 0\; \{\backslash \; displaystyle\; a\; \backslash \; wedge\; a\; =\; 0\}$для $a\; \in \; V\; \{\backslash \; displaystyle\; a\; \backslash \; in\; V\}$.

Обратите внимание, что in t Последнее свойство выше, действительное число $g\; (a,\; a)\; \{\backslash \; displaystyle\; g\; (a,\; a)\}$не обязательно должно быть неотрицательным, если $g\; \{\backslash \; displaystyle\; g\}$не является положительно-определенным. Важным свойством геометрического произведения является наличие элементов, имеющих мультипликативный обратный. Для вектора $a\; \{\backslash \; displaystyle\; a\}$, если $a\; 2\; \ne \; 0\; \{\backslash \; displaystyle\; a\; ^\; \{2\}\; \backslash \; neq\; 0\}$, то $a\; -\; 1\; \{\backslash \; displaystyle\; a\; ^\; \{-\; 1\}\}$существует и равен $g\; (a,\; a)\; -\; 1\; a\; \{\backslash \; displaystyle\; g\; (a,\; a)\; ^\; \{-\; 1\}\; a\; \}$. Ненулевой элемент алгебры не обязательно имеет мультипликативный обратный. Например, если $u\; \{\backslash \; displaystyle\; u\}$- вектор в $V\; \{\backslash \; displaystyle\; V\}$такой, что $u\; 2\; =\; 1\; \{\backslash \; displaystyle\; u\; ^\; \{2\}\; =\; 1\}$, элемент $1\; 2\; (1\; +\; u)\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (1\; +\; u)\}$является одновременно нетривиальным идемпотентным элементом и ненулевым делителем нуля и, следовательно, не имеет обратного.

Обычно идентифицируют $R\; \{\; \backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\}$и $V\; \{\backslash \; displaystyle\; V\}$с их изображениями под естественными вложениями $R\; \to \; G\; (\; p,\; q)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\; \backslash \; to\; \{\backslash \; mathcal\; \{G\}\}\; (p,\; q)\}$и $V\; \to \; G\; (p,\; q)\; \{\backslash \; displaystyle\; V\; \backslash \; в\; \{\backslash \; mathcal\; \{G\}\}\; (p,\; q)\}$. В этой статье предполагается такая идентификация. На всем протяжении термины скаляр и вектор относятся к элементам $R\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\}$и $V\; \{\backslash \; displaystyle\; V\}$соответственно (и их изображения при этом вложении).

Геометрическое произведение

Даны два вектора $a\; \{\backslash \; displaystyle\; a\}$и $b\; \{\backslash \; displaystyle\; b\}$, если геометрический продукт $ab\; \{\backslash \; displaystyle\; ab\}$является антикоммутативным; они перпендикулярны (вверху), потому что $a\; \cdot \; b\; =\; 0\; \{\backslash \; displaystyle\; a\; \backslash \; cdot\; b\; =\; 0\}$, если он коммутативен; они параллельны (внизу), потому что $a\; \wedge \; b\; =\; 0\; \{\backslash \; displaystyle\; a\; \backslash \; wedge\; b\; =\; 0\}$. Ориентация определяется упорядоченным набором векторов. Обратная ориентация соответствует отрицанию внешнего продукта. Геометрическая интерпретация элементов grade- $n\; \{\backslash \; displaystyle\; n\}$в реальной внешней алгебре для $n\; =\; 0\; \{\backslash \; displaystyle\; n\; =\; 0\}$(со знаком точка), $1\; \{\backslash \; displaystyle\; 1\}$(сегмент направленной линии или вектор), $2\; \{\backslash \; displaystyle\; 2\}$(элемент ориентированной плоскости), $3\; \{\backslash \; displaystyle\; 3\}$(ориентированный объем). Внешний продукт векторов $n\; \{\backslash \; displaystyle\; n\}$может быть визуализирован как любая $n\; \{\backslash \; displaystyle\; n\}$-мерная форма (например, $n\; \{\; \backslash \; displaystyle\; n\}$-параллелоэдр, $n\; \{\backslash \; displaystyle\; n\}$-эллипсоид ); с величиной (гиперобъем ) и ориентацией, определяемой его $(n\; -\; 1)\; \{\backslash \; displaystyle\; (n-1)\}$-размерным границы и с какой стороны находится внутренняя часть.

Для векторов $a\; \{\backslash \; displaystyle\; a\}$и $b\; \{\backslash \; displaystyle\; b\}$мы можем написать геометрическое произведение любых двух векторов $a\; \{\backslash \; displaystyle\; a\}$и $b\; \{\backslash \; displaystyle\; b\}$как суммы симметричного произведения и антисимметричного произведения:

$ab\; =\; 1\; 2\; (ab\; +\; ba)\; +\; 1\; 2\; (ab\; -\; ba)\; \{\backslash \; displaystyle\; ab\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (ab\; +\; ba)\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (ab-ba)\}$

Таким образом, мы можем определить внутреннее произведение векторов как

$a\; \cdot \; b:\; =\; g\; (a,\; b),\; \{\backslash \; displaystyle\; a\; \backslash \; cdot\; b:\; =\; g\; (a,\; b),\; \}$

так, чтобы симметричное произведение можно было записать как

$1\; 2\; (ab\; +\; ba)\; =\; 1\; 2\; ((a\; +\; b)\; 2\; -\; a\; 2\; -\; b\; 2)\; =\; a\; \cdot \; b\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (ab\; +\; ba)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; ((a\; +\; b)\; ^\; \{2\}\; -a\; ^\; \{2\}\; -b\; ^\; \{2\}\; \backslash \; right)\; =\; a\; \backslash \; cdot\; b\}$

И наоборот, $g\; \{\backslash \; displaystyle\; g\}$полностью определен нед по алгебре. Антисимметричная часть - это внешнее произведение двух векторов, произведение содержащейся внешней алгебры :

$a\; \wedge \; b:\; =\; 1\; 2\; (ab\; -\; ba)\; =\; -\; (b\; \wedge \; a)\; \{\backslash \; displaystyle\; a\; \backslash \; wedge\; b:\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (ab-ba)\; =\; -\; (b\; \backslash \; wedge\; a)\}$

Затем простым сложением:

$ab\; =\; a\; \cdot \; b\; +\; a\; \wedge \; b\; \{\backslash \; displaystyle\; ab\; =\; a\; \backslash \; cdot\; b\; +\; a\; \backslash \; wedge\; b\}$необобщенная или векторная форма геометрического произведения.

Внутренние и внешние произведения связаны со знакомыми понятиями из стандартной векторной алгебры. Геометрически, $a\; \{\backslash \; displaystyle\; a\}$и $b\; \{\backslash \; displaystyle\; b\}$являются параллельными, если их геометрическое произведение равно их внутреннему продукт, тогда как $a\; \{\backslash \; displaystyle\; a\}$и $b\; \{\backslash \; displaystyle\; b\}$являются перпендикулярными, если их геометрическое произведение равно их внешний продукт. В геометрической алгебре, для которой квадрат любого ненулевого вектора положителен, внутреннее произведение двух векторов может быть идентифицировано с помощью скалярного произведения стандартной векторной алгебры. Внешний продукт двух векторов может быть идентифицирован с помощью знаковой области, заключенной в параллелограмм , стороны которого являются векторами. векторное произведение двух векторов в измерениях $3\; \{\backslash \; displaystyle\; 3\}$с положительно определенной квадратичной формой тесно связано с их внешним произведением.

Большинство примеров интересующих геометрических алгебр имеют невырожденную квадратичную форму. Если квадратичная форма полностью вырождена, внутреннее произведение любых двух векторов всегда равно нулю, и тогда геометрическая алгебра является просто внешней алгеброй. Если не указано иное, в данной статье рассматриваются только невырожденные геометрические алгебры.

Внешний продукт естественным образом расширяется как ассоциативный билинейный бинарный оператор между любыми двумя элементами алгебры, удовлетворяющими тождествам

$1\; \wedge \; ai\; =\; ai\; \wedge \; 1\; =\; aia\; 1\; \wedge \; a\; 2\; \wedge \; \cdots \; \wedge \; ar\; =\; 1\; р!\; \sum \; \sigma \; \in \; S\; r\; sign\; \; (\sigma )\; a\; \sigma \; (1)\; a\; \sigma \; (2)\; \cdots \; a\; \sigma \; (r),\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; 1\; \backslash \; клин\; a\_\; \{i\}\; =\; a\_\; \{i\}\; \backslash \; клин\; 1\; =\; a\_\; \{i\}\; \backslash \backslash \; a\_\; \{1\}\; \backslash \; wedge\; a\_\; \{2\}\; \backslash \; wedge\; \backslash \; cdots\; \backslash \; wedge\; a\_\; \{r\}\; =\; \{\backslash \; frac\; \{1\}\; \{r!\}\}\; \backslash \; sum\; \_\; \{\backslash \; sigma\; \backslash \; in\; \{\backslash \; mathfrak\; \{S\}\}\; \_\; \{r\}\}\; \backslash \; operatorname\; \{sgn\}\; (\backslash \; sigma)\; a\; \_\; \{\backslash \; sigma\; (1)\}\; a\; \_\; \{\backslash \; sigma\; (2)\}\; \backslash \; cdots\; a\; \_\; \{\backslash \; sigma\; (r)\},\; \backslash \; end\; \{выравнивается\}\}\}$

, где сумма вычисляется по всем перестановкам индексов, причем $sgn\; \; (\sigma )\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{sgn\}\; (\backslash \; sigma)\}$знак перестановки и $ai\; \{\backslash \; displaystyle\; a\_\; \{i\}\}$являются векторами (а не общими элементами алгебры). Поскольку каждый элемент алгебры может быть выражен как сумма произведений этой формы, это определяет внешний продукт для каждой пары элементов алгебры. Из определения следует, что внешний продукт образует альтернативную алгебру.

Лезвия, степени и канонический базис

Мультивектор, который является внешним продуктом $r\; \{\backslash \; displaystyle\; r\}$линейно независимых векторов называется лопастью и, как говорят, имеет степень $r\; \{\backslash \; displaystyle\; r\}$. Мультивектор, являющийся суммой лопастей степени $r\; \{\backslash \; displaystyle\; r\}$, называется (однородным) многовектором степени $r\; \{\backslash \; displaystyle\; r\}$. Согласно аксиомам, с замыканием, каждый мультивектор геометрической алгебры представляет собой сумму лопастей.

Рассмотрим набор $r\; \{\backslash \; displaystyle\; r\}$линейно независимых векторов $\{a\; 1,\dots ,\; ar\}\; \{\backslash \; displaystyle\; \backslash \; \{a\_\; \{1\},\; \backslash \; ldots,\; a\_\; \{r\}\; \backslash \}\}$охватывающее $r\; \{\backslash \; displaystyle\; r\}$-мерное подпространство векторного пространства. С их помощью мы можем определить реальную симметричную матрицу (точно так же, как матрицу Грамиана )

$[A]\; ij\; =\; ai\; \cdot \; aj\; \{\backslash \; displaystyle\; [\backslash \; mathbf\; \{A\}]\; \_\; \{ij\}\; =\; a\_\; \{i\}\; \backslash \; cdot\; a\_\; \{j\}\}$

По спектральной теореме, $A\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{A\}\}$может быть диагонализована до диагональной матрицы $D\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{D\}\}$с помощью ортогональной матрицы $O\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{O\; \}\}$через

$\sum \; k,\; l\; [O]\; ik\; [A]\; kl\; [OT]\; lj\; =\; \sum \; k,\; l\; [O]\; ik\; [O]\; jl\; [A]\; kl\; =\; [D]\; ij\; »\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{k,\; l\}\; [\backslash \; mathbf\; \{O\}]\; \_\; \{ik\}\; [\backslash \; mathbf\; \{A\}]\; \_\; \{kl\}\; [\backslash \; mathbf\; \{O\}\; ^\; \{\backslash \; mathrm\; \{T\}\}]\; \_\; \{\; lj\}\; =\; \backslash \; sum\; \_\; \{k,\; l\}\; [\backslash \; mathbf\; \{O\}]\; \_\; \{ik\}\; [\backslash \; mathbf\; \{O\}]\; \_\; \{jl\}\; [\backslash \; mathbf\; \{A\}]\; \_\; \{kl\}\; =\; [\backslash \; mathbf\; \{D\; \}]\; \_\; \{ij\}\}$

Определите новый набор векторов $\{e\; 1,\dots ,\; er\}\; \{\backslash \; displaystyle\; \backslash \; \{e\_\; \{1\},\; \backslash \; ldots,\; e\_\; \{r\}\; \backslash \}\}$, известные как ортогональные базисные векторы, преобразованные ортогональной матрицей:

$ei\; =\; \sum \; j\; [O]\; ijaj\; \{\backslash \; displaystyle\; e\_\; \{i\}\; =\; \backslash \; sum\; \_\; \{j\}\; [\backslash \; mathbf\; \{O\}\; ]\; \_\; \{ij\}\; a\_\; \{j\}\}$

Поскольку ортогональные преобразования сохраняют внутренние продукты, отсюда следует, что $ei\; \cdot \; ej\; =\; [D]\; ij\; \{\backslash \; displaystyle\; e\_\; \{i\}\; \backslash \; cdot\; e\_\; \{j\}\; =\; [\backslash \; mathbf\; \{D\}]\; \_\; \{ij\}\}$и, следовательно, $\{e\; 1,\dots ,\; er\}\; \{\backslash \; displaystyle\; \backslash \; \{e\_\; \{1\},\; \backslash \; ldots,\; e\_\; \{r\}\; \backslash \}\}$перпендикулярны. Другими словами, геометрическое произведение двух различных векторов $ei\; \ne \; ej\; \{\backslash \; displaystyle\; e\_\; \{i\}\; \backslash \; neq\; e\_\; \{j\}\}$полностью определяется их внешним произведением или, в более общем смысле,

$e\; 1\; e\; 2\; \cdots \; er\; =\; e\; 1\; \wedge \; e\; 2\; \wedge \; \cdots \; \wedge \; er\; =\; (\sum \; j\; [O]\; 1\; jaj)\; \wedge \; (\sum \; j\; [O]\; 2\; jaj)\; \wedge \; \cdots \; \wedge \; (\sum \; j\; [O]\; rjaj)\; =\; (\; det\; O)\; a\; 1\; \wedge \; a\; 2\; \wedge \; \cdots \; \wedge \; ar\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{rl\}\; e\_\; \{1\}\; e\_\; \{2\}\; \backslash \; cdots\; e\_\; \{r\}\; =\; e\_\; \{1\}\; \backslash \; wedge\; e\_\; \{2\}\; \backslash \; wedge\; \backslash \; cdots\; \backslash \; wedge\; e\_\; \{r\}\; \backslash \backslash \; =\; \backslash \; left\; (\backslash \; sum\; \_\; \{j\}\; [\backslash \; mathbf\; \{O\}]\; \_\; \{1j\}\; a\_\; \{j\}\; \backslash \; right)\; \backslash \; wedge\; \backslash \; left\; (\backslash \; sum\; \_\; \{\; j\}\; [\backslash \; mathbf\; \{O\}]\; \_\; \{2j\}\; a\_\; \{j\}\; \backslash \; right)\; \backslash \; wedge\; \backslash \; cdots\; \backslash \; wedge\; \backslash \; left\; (\backslash \; sum\; \_\; \{j\}\; [\backslash \; mathbf\; \{O\}]\; \_\; \{rj\}\; a\_\; \{j\}\; \backslash \; right)\; \backslash \backslash \; =\; (\backslash \; det\; \backslash \; mathbf\; \{O\})\; a\_\; \{1\}\; \backslash \; wedge\; a\_\; \{2\}\; \backslash \; wedge\; \backslash \; cdots\; \backslash \; wedge\; a\_\; \{r\}\; \backslash \; end\; \{array\}\}\}$

Следовательно, каждое лезвие степени $r\; \{\backslash \; displaystyle\; r\}$можно записать как геометрическое произведение векторов $r\; \{\backslash \; displaystyle\; r\}$. В более общем смысле, если вырожденная геометрическая алгебра разрешена, то ортогональная матрица заменяется блочной матрицей , которая ортогональна в невырожденном блоке, а диагональная матрица имеет нулевые элементы по вырожденным измерениям. Если новые векторы невырожденного подпространства нормализованы согласно

$e\; ^\; i\; =\; 1\; |\; e\; i\; \cdot \; e\; i\; |\; ei,\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{e\}\}\; \_\; \{i\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{|\; e\_\; \{i\}\; \backslash \; cdot\; e\_\; \{i\}\; |\}\}\}\; e\_\; \{i\},\}$

, тогда эти нормализованные векторы должны возводиться в квадрат $+\; 1\; \{\backslash \; displaystyle\; +1\}$или $-\; 1\; \{\backslash \; displaystyle\; -1\}$. Согласно закону инерции Сильвестра, общее количество $+\; 1\; \{\backslash \; displaystyle\; +1\}$s и общее количество $-\; 1\; \{\backslash \; displaystyle\; -1\}$s вдоль диагональной матрицы инвариантно. Таким образом, общее количество $p\; \{\backslash \; displaystyle\; p\}$этих векторов, которые квадратов равны $+\; 1\; \{\backslash \; displaystyle\; +1\}$, а общее количество $q\; \{\backslash \; displaystyle\; q\}$этот квадрат в $-\; 1\; \{\backslash \; displaystyle\; -1\}$является неизменным. (Общее количество базисных векторов, которые возводятся в квадрат до нуля, также инвариантно и может быть ненулевым, если разрешен вырожденный случай.) Мы обозначаем эту алгебру $G\; (p,\; q)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (p,\; q)\}$. Например, $G\; (3,\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (3,0)\}$models $3\; \{\backslash \; displaystyle\; 3\}$-мерное евклидово пространство, $G\; (1,\; 3)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (1,3)\}$релятивистское пространство-время и $G\; (4,\; 1)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (4,1)\}$a конформная геометрическая алгебра из $3\; \{\backslash \; displaystyle\; 3\}$-мерноепространство.

Набор всех применений ортогональных базисных векторов $n\; \{\backslash \; displaystyle\; n\}$индексами в порядке возрастания, включая $1\; \{\backslash \; displaystyle\; 1\}$как пустой продукт образует основу геометрической алгебры (аналог теоремы PBW ). Например, используется следующее геометрической алгебры $G\; (3,\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (3,0)\}$:

$\{1,\; e\; 1,\; e\; 2,\; e\; 3,\; e\; 1\; e\; 2,\; e\; 1\; e\; 3,\; e\; 2\; e\; 3,\; e\; 1\; e\; 2\; e\; 3\}\; \{\backslash \; displaystyle\; \backslash \; \{1,\; e\_\; \{1\},\; e\_\; \{2\},\; e\_\; \{3\},\; e\_\; \{1\}\; e\_\; \{2\},\; e\_\; \{1\}\; e\_\; \{3\},\; e\_\; \{2\}\; e\_\; \{3\},\; e\_\; \{1\}\; e\_\; \{2\}\; e\_\; \{3\}\; \backslash \}\}$

Образованный таким образом базис называется канонический базис для геометрической алгебры и любой другой ортогональный базис для $V\; \{\backslash \; displaystyle\; V\}$создадут другой канонический базис. Каждый канонический базис состоит из элементов $2\; n\; \{\backslash \; displaystyle\; 2\; ^\; \{n\}\}$. Каждый мультивектор геометрической алгебры может быть выражен как линейная комбинация канонических базисных элементов. Если канонические базисные элементы равны $\{B\; i\; |\; я\; \in \; S\}\; \{\backslash \; Displaystyle\; \backslash \; \{B\_\; \{i\}\; |\; i\; \backslash \; in\; S\; \backslash \}\}$где $S\; \{\backslash \; displaystyle\; S\}$является набором индексов, тогда геометрическое произведение любых двух мультивекторов равно

$(\sum \; i\; \alpha \; i\; B\; i)\; (\sum \; j\; \beta \; j\; B\; j)\; =\; \sum \; i,\; j\; \alpha \; i\; \beta \; j\; B\; i\; B\; j.\; \{\backslash \; displaystyle\; \backslash \; left\; (\backslash \; sum\; \_\; \{i\}\; \backslash \; alpha\; \_\; \{i\}\; B\_\; \{i\}\; \backslash \; right)\; \backslash \; left\; (\backslash \; sum\; \_\; \{j\}\; \backslash \; beta\; \_\; \{j\}\; B\_\; \{j\}\; \backslash \; right)\; =\; \backslash \; sum\; \_\; \{i,\; j\}\; \backslash \; alpha\; \_\; \{i\}\; \backslash \; beta\; \_\; \{j\}\; B\_\; \{i\}\; B\_\; \{j\}.\}$

Терминология «$k\; \{\backslash \; displaystyle\; k\}$- вектор »Часто встречается для описания многовекторов, элементов только одного сорта. В области более высоких измерений некоторые такие многовекторы не являются лопастями (не могут быть учтены во внешнем произведении векторов $k\; \{\backslash \; displaystyle\; k\}$). Например, $e\; 1\; \wedge \; e\; 2\; +\; e\; 3\; \wedge \; e\; 4\; \{\backslash \; displaystyle\; e\_\; \{1\}\; \backslash \; wedge\; e\_\; \{2\}\; +\; e\_\; \{3\}\; \backslash \; wedge\; e\_\; \{4\}\}$в $G\; (4,\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (4,0)\}$не может быть разложен на множители; Однако обычно такие элементы алгебры не поддаются геометрической интерпретации как объекты. Только $0,\; 1,\; (n\; -\; 1)\; \{\backslash \; displaystyle\; 0,1,\; (n-1)\}$и $n\; \{\backslash \; displaystyle\; n\}$-векторы всегда являются лезвиями в $n\; \{\backslash \; displaystyle\; n\}$-пространстве.

Проекция уклона

Используя ортогональный базис, можно создать градиентного взаимодействия пространства. Элементы геометрической алгебры, которые являются скалярными кратными $1\; \{\backslash \; displaystyle\; 1\}$, относятся к классу- $0\; \{\backslash \; displaystyle\; 0\}$лезвиям и называются скалярами. Мультивекторы, которые находятся в диапазоне $\{e\; 1,\dots ,\; en\}\; \{\backslash \; displaystyle\; \backslash \; \{e\_\; \{1\},\; \backslash \; ldots,\; e\_\; \{n\}\; \backslash \}\}$, имеют степень- $1\; \{\backslash \; displaystyle\; 1\}$лезвия и являются обычными мирами. Мультивекторы в диапазоне являются лопастями степени- $2\; \{\backslash \; displaystyle\; 2\}$и являются бивекторами. Эта терминология продолжается до последней степени $n\; \{\backslash \; displaystyle\; n\}$-векторов. В качестве альтернативы, класс- $n\; \{\backslash \; displaystyle\; n\}$лезвия называют псевдоскалярами, класс- $(n\; -\; 1)\; \{\backslash \; displaystyle\; (n-1)\}$псевдовекторы лопастей и т. Д. Многие элементы алгебры не оцениваются по этой схеме, поскольку они представляют собой суммы элементов разной степени. Такие элементы считаются смешанными. Градация многовекторов не зависит от выбранной основы.

Это градуировка как векторное пространство, но не как алгебра. Время произведение $r\; \{\backslash \; displaystyle\; r\}$-blade и $s\; \{\backslash \; displaystyle\; s\}$-blade существует в диапазоне $От\; 0\; \{\backslash \; displaystyle\; 0\}$до $r\; +\; s\; \{\backslash \; displaystyle\; r\; +\; s\}$-bldes, геометрическая алгебра представляет собой фильтрованную алгебру.

мультивектор $A\; \{\backslash \; displaystyle\; A\; \}$можно разложить с помощью оператора проекции уровня $⟨A⟩\; r\; \{\backslash \; displaystyle\; \backslash \; langle\; A\; \backslash \; rangle\; \_\; \{r\}\}$, который выводит часть оценка- $r\; \{\backslash \; displaystyle\; r\}$из $A\; \{\backslash \; displaystyle\; A\}$. В результате:

$A\; =\; \sum \; r\; =\; 0\; n\; ⟨A⟩\; r\; \{\backslash \; displaystyle\; A\; =\; \backslash \; sum\; \_\; \{r\; =\; 0\}\; ^\; \{n\}\; \backslash \; langle\; A\; \backslash \; rangle\; \_\; \{r\}\}$

Например, геометрическое произведение двух векторов $ab\; =\; a\; \cdot \; b\; +\; a\; \wedge \; b\; =\; ⟨ab⟩\; 0\; +\; ⟨ab⟩\; 2\; \{\backslash \; displaystyle\; ab\; =\; a\; \backslash \; cdot\; b\; +\; a\; \backslash \; wedge\; b\; =\; \backslash \; langle\; ab\; \backslash \; rangle\; \_\; \{0\}\; +\; \backslash \; langle\; ab\; \backslash \; rangle\; \_\; \{2\}\}$, поскольку $⟨ab⟩\; 0\; =\; a\; \cdot \; b\; \{\backslash \; displaystyle\; \backslash \; langle\; ab\; \backslash \; rangle\; \_\; \{0\}\; =\; a\; \backslash \; cdot\; b\}$и $ab⟩\; 2\; =\; a\; \wedge \; b\; \{\backslash \; displaystyle\; \backslash \; langle\; ab\; \backslash \; rangle\; \_\; \{2\}\; =\; a\; \backslash \; wedge\; b\}$и $ab⟩\; я\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; langle\; ab\; \backslash \; rangle\; \_\; \{i\}\; =\; 0\}$, для $i\; \{\backslash \; displaystyle\; i\}$кроме $0\; \{\backslash \; displaystyle\; 0\}$и $2\; \{\backslash \; displaystyle\; 2\}$.

Разложение мультивектора $A\; \{\backslash \; displaystyle\; A\}$также может быть разделено на те компоненты, которые четные и нечетные:

$A\; +\; знак\; равно\; ⟨A⟩\; 0\; +\; ⟨A⟩\; 2\; +\; ⟨A⟩\; 4\; +\; \cdots \; \{\backslash \; displaystyle\; A\; ^\; \{+\}\; =\; \backslash \; langle\; A\; \backslash \; rangle\; \_\; \{0\}\; +\; \backslash \; langle\; A\; \backslash \; rangle\; \_\; \{2\}\; +\; \backslash \; langle\; \backslash \; Rangle\; \_\; \{4\}\; +\; \backslash \; cdot\; s\}$

$A\; -\; =\; ⟨A⟩\; 1\; +\; ⟨A⟩\; 3\; +\; ⟨A⟩\; 5\; +\; \cdots \; \{\backslash \; displaystyle\; A\; ^\; \{-\}\; =\; \backslash \; langle\; A\; \backslash \; rangle\; \_\; \{1\}\; +\; \backslash \; langle\; A\; \backslash \; rangle\; \_\; \{\; 3\}\; +\; \backslash \; langle\; A\; \backslash \; rangle\; \_\; \{5\}\; +\; \backslash \; cdots\}$

Это результат забывания структуры от $Z\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{Z\}\}$-градуированного пространства до $Z\; 2\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{Z\}\; \_\; \{2\}\}$-граду общественного пространства. Геометрический продукт соответствует этой более крупной градации. Таким образом, геометрическая алгебра не является только $Z\; 2\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{Z\}\; \_\; \{2\}\}$-градуированным векторным пространством, но является $Z\; 2\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{\; Z\}\; \_\; \{2\}\}$-градуированная алгебра или супералгебра.

Если ограничиться четной частью, произведение двух четных элементов также будет четным. Это означает, что четные многовекторы определяют четную подалгебру. Четная подалгебра $n\; \{\backslash \; displaystyle\; n\}$-мерной геометрической алгебры изоморфна (без сохранения фильтрации или градуировки) полной геометрической алгебре $(n\; -\; 1)\; \{\backslash \; displaystyle\; (\; n-1)\}$размеры. Примеры включают $G\; +\; (2,\; 0)\; \cong \; G\; (0,\; 1)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; ^\; \{+\}\; (2,0)\; \backslash \; cong\; \{\backslash \; mathcal\; \{G\}\}\; (0,\; 1)\}$и $G\; +\; (1,\; 3)\; \cong \; G\; (3,\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; ^\; \{+\}\; (1,3)\; \backslash \; cong\; \{\backslash \; mathcal\; \{G\}\}\; (3,0)\}$.

Представление подпространств

Геометрическая алгебра представляет подпространства $V\; \{\backslash \; displaystyle\; V\}$как лезвия, и поэтому они сосуществуют в той же алгебре с векторами из $V\; \{\backslash \; displaystyle\; V\}$. A $k\; \{\backslash \; displaystyle\; k\}$-мерное подпространство $W\; \{\backslash \; displaystyle\; W\}$из $V\; \{\backslash \; displaystyle\; V\}$представлен ортогональным базисом $\{b\; 1,\; b\; 2,\dots ,\; bk\}\; \{\backslash \; displaystyle\; \backslash \; \{b\_\; \{1\},\; b\_\; \{2\},\; \backslash \; ldots,\; b\_\; \{k\}\; \backslash \}\}$и используя геометрическое произведение для создания лезвия $D\; =\; b\; 1\; b\; 2\; \cdots \; bk\; \{\backslash \; displaystyle\; D\; =\; b\_\; \{1\}\; b\_\; \{2\}\; \backslash \; cdots\; b\_\; \{k\}\}$. Есть несколько лезвий, представляющих $W\; \{\backslash \; displaystyle\; W\}$; все представляющие $W\; \{\backslash \; displaystyle\; W\}$являются скалярными кратными $D\; \{\backslash \; displaystyle\; D\}$. Эти лезвия можно разделить на два набора: положительные кратные $D\; \{\backslash \; displaystyle\; D\}$и отрицательные кратные $D\; \{\backslash \; displaystyle\; D\}$. Положительные кратные $D\; \{\backslash \; displaystyle\; D\}$, как говорят, имеют ту же ориентацию, что и $D\; \{\backslash \; displaystyle\; D\}$, и отрицательная кратно противоположной ориентации.

Лезвия важны, поскольку геометрические операции, такие как проекции, вращение и отражение, зависят от факторизации через внешний продукт, который (ограниченный класс) $n\; \{\backslash \; displaystyle\; n\}$- лезвия обеспечьте, но этот (обобщенный класс) сорт- $n\; \{\backslash \; displaystyle\; n\}$мультивекторы не работают, когда $n\; \ge \; 4\; \{\backslash \; displaystyle\; n\; \backslash \; geq\; 4\}$.

единичные псевдоскаляры

Псевдоскаляры модулей - это лезвия, которые играют важную роль в GA. единичный псевдоскаляр для невырожденного подпространства $W\; \{\backslash \; displaystyle\; W\}$of $V\; \{\backslash \; displaystyle\; V\}$- это лезвие, которое является произведением членов ортонормированного базиса для $W\; \{\backslash \; displaystyle\; W\}$. Можно показать, что если $I\; \{\backslash \; displaystyle\; I\}$и $I\; \prime \; \{\backslash \; displaystyle\; I\; \text{'}\}$оба являются единичными псевдоскалярами для $W\; \{\backslash \; displaystyle\; W\}$, затем $I\; =\; \pm \; I\; \prime \; \{\backslash \; displaystyle\; I\; =\; \backslash \; pm\; I\; \text{'}\}$и $I\; 2\; =\; \pm \; 1\; \{\backslash \; displaystyle\; I\; ^\; \{2\; \}\; =\; \backslash \; pm\; 1\}$. Если не выбрать ортонормированный базис для $W\; \{\backslash \; displaystyle\; W\}$, тогда вложение Плюккера дает вектор во внешней алгебре, но только до масштабирования. Используя изоморфизм пространства между геометрической алгеброй и внешней алгеброй, это дает класс эквивалентности $\alpha \; I\; \{\backslash \; displaystyle\; \backslash \; alpha\; I\}$для всех $\alpha \; \ne \; 0\; \{\backslash \; displaystyle\; \backslash \; alpha\; \backslash \; neq\; 0\}$. Ортонормальность избавляет от этой двусмысленности, за исключением указанных выше знаков.

Предположим, что геометрическая алгебра $G\; (n,\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (n,\; 0)\}$со знакомым положительно определенным внутренним произведением на $R\; n\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\; ^\; \{n\}\}$сформировано. Учитывая плоскость ($2\; \{\backslash \; displaystyle\; 2\}$-мерное подпространство) $R\; n\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\; ^\; \{n\}\}$, один может найти ортонормированный базис $\{b\; 1,\; b\; 2\}\; \{\backslash \; displaystyle\; \backslash \; \{b\_\; \{1\},\; b\_\; \{2\}\; \backslash \}\}$, охватывающий плоскость, и, таким образом, найти единичный псевдоскаляр $I\; =\; b\; 1\; b\; 2\; \{\backslash \; displaystyle\; I\; =\; b\_\; \{1\}\; b\_\; \{2\}\}$, представляет эту плоскость. Геометрическое произведение двух векторов в диапазоне $b\; 1\; \{\backslash \; displaystyle\; b\_\; \{1\}\}$и $b\; 2\; \{\backslash \; displaystyle\; b\_\; \{2\}\}$лежит в $\{\alpha \; 0\; +\; \alpha \; 1\; я\; \mid \; \alpha \; я\; \in \; R\}\; \{\backslash \; displaystyle\; \backslash \; \{\backslash \; alpha\; \_\; \{0\}\; +\; \backslash \; alpha\; \_\; \{1\}\; I\; \backslash \; mid\; \backslash \; alpha\; \_\; \{i\}\; \backslash \; in\; \backslash \; mathbf\; \{R\}\; \backslash \}\; \}$, то есть это сумма $0\; \{\backslash \; displaystyle\; 0\}$-вектора и $2\; \{\backslash \; displaystyle\; 2\}$-вектор.

По свойствам геометрического продукта $I\; 2\; =\; b\; 1\; b\; 2\; b\; 1\; b\; 2\; =\; -\; b\; 1\; b\; 2\; b\; 2\; b\; 1\; =\; -\; 1\; \{\backslash \; displaystyle\; I\; ^\; \{2\}\; =\; b\_\; \{1\}\; b\_\; \{2\}\; b\_\; \{1\}\; b\_\; \{2\}\; =\; -\; b\_\; \{1\}\; b\_\; \{2\}\; b\_\; \{2\}\; b\_\; \{1\}\; =\; -\; 1\}$. Сходство с мнимой единицей не случайно: подпространство $\{\alpha \; 0\; +\; \alpha \; 1\; I\; \mid \; \alpha \; i\; \in \; R\}\; \{\backslash \; displaystyle\; \backslash \; \{\backslash \; alpha\; \_\; \{0\}\; +\; \backslash \; alpha\; \_\; \{1\}\; I\; \backslash \; mid\; \backslash \; alpha\; \_\; \{i\}\; \backslash \; in\; \backslash \; mathbf\; \{R\}\; \backslash \}\}$равно $R\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\}$-алгебра изоморфна в комплексные числа. Таким образом, копия комплексных чисел встраивается в геометрическую алгебру для каждого двумерного подпространства $V\; \{\backslash \; displaystyle\; V\}$, на котором квадратичная форма определена.

Иногда можно определить присутствующую единицу в физическом уравнении. Такие единицы представляют из одной из многих величин в реальной алгебре, которые в квадрате составляют $-\; 1\; \{\backslash \; displaystyle\; -1\}$, и они имеют геометрическое значение из-за свойств алгебры и взаимодействия его различных подпространств.

В $G\; (3,\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (3,0)\}$встречается еще один знакомый случай. Учитывая канонический базис, состоящий из ортонормированных векторов $ei\; \{\backslash \; displaystyle\; e\_\; \{i\}\}$из $V\; \{\backslash \; displaystyle\; V\}$, набор всех $2\; \{\; \backslash \; displaystyle\; 2\}$-векторы охватываются

$\{e\; 3\; e\; 2,\; e\; 1\; e\; 3,\; e\; 2\; e\; 1\}.\; \{\backslash \; displaystyle\; \backslash \; \{e\_\; \{3\}\; e\_\; \{2\},\; e\_\; \{1\}\; e\_\; \{3\},\; e\_\; \{2\}\; e\_\; \{1\}\; \backslash \}.\}$

Обозначение этих $i\; \{\backslash \; displaystyle\; i\}$, $j\; \{\backslash \; displaystyle\; j\}$и $k\; \{\backslash \; displaystyle\; k\}$(мгновенное отклонение от нашего соглашения о верхнем регистре), подпространство, генерируемое $0\; \{\; \backslash \; displaystyle\; 0\}$-векторы и $2\; \{\backslash \; displaystyle\; 2\}$-векторы точно $\{\alpha \; 0\; +\; i\; \alpha \; 1\; +\; j\; \alpha \; 2\; +\; k\; \alpha \; 3\; \mid \; \alpha \; я\; \in \; R\}\; \{\backslash \; Displaystyle\; \backslash \; \{\backslash \; alpha\; \_\; \{0\}\; +\; i\; \backslash \; alpha\; \_\; \{1\}\; +\; j\; \backslash \; alpha\; \_\; \{2\}\; +\; k\; \backslash \; alpha\; \_\; \{3\}\; \backslash \; mid\; \backslash \; alpha\; \_\; \{i\}\; \backslash \; in\; \backslash \; mathbf\; \{R\}\; \backslash \}\}$. Этот набор является четной подалгеброй в $G\; (3,\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (3,0)\}$, и, кроме того, изоморфен как $R\; \{\; \backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\}$-алгебра к кватернионам, еще одной важной алгебраической системе.

Двойная основа

Пусть $\{e\; 1,\dots ,\; en\}\; \{\backslash \; displaystyle\; \backslash \; \{e\_\; \{1\},\; \backslash \; ldots,\; e\_\; \{n\}\; \backslash \}\}$быть основой $V\; \{\backslash \; displaystyle\; V\}$, т.е. набором $n\; \{\backslash \; displaystyle\; n\}$линейно независимых векторов, которые охватывают $n\; \{\backslash \; displaystyle\; n\}$-мерное векторное пространство $V\; \{\backslash \; displaystyle\; V\}$. Базис, двойственный к $\{e\; 1,\dots ,\; en\}\; \{\backslash \; displaystyle\; \backslash \; \{e\_\; \{1\},\; \backslash \; ldots,\; e\_\; \{n\}\; \backslash \}\}$, представляет собой набор элементов двойное векторное пространство $V\; \ast \; \{\backslash \; displaystyle\; V\; ^\; \{*\}\}$, которое формирует биортогональную систему с этим базисом, таким образом являясь элементами, обозначенными $\{e\; 1,\dots ,\; en\}\; \{\backslash \; displaystyle\; \backslash \; \{e\; ^\; \{1\},\; \backslash \; ldots,\; e\; ^\; \{n\}\; \backslash \}\}$удовлетворяющий

$ei\; \cdot \; ej\; =\; \delta \; ij,\; \{\; \backslash \; displaystyle\; e\; ^\; \{i\}\; \backslash \; cdot\; e\_\; \{j\}\; =\; \backslash \; delta\; ^\; \{i\}\; \{\}\; \_\; \{j\},\}$

где $\delta \; \{\backslash \; displaystyle\; \backslash \; delta\}$- это Дельта Кронекера.

Данная невырожденная квадратичная форма на $V\; \{\backslash \; displaystyle\; V\}$, $V\; \ast \; \{\backslash \; displaystyle\; V\; ^\; \{*\}\}$естественно отождествляется с $V\; \{\backslash \; displaystyle\; V\}$, и двойная основа может рассматриваться как элементы $V\; \{\backslash \; displaystyle\; V\}$, но в целом они не совпадают с исходным набором. основание.

Для дальнейшего ГА $V\; \{\backslash \; displaystyle\; V\}$, пусть

$ϵ\; =\; e\; 1\; \wedge \; \cdots \; \wedge \; en\; \{\backslash \; displaystyle\; \backslash \; epsilon\; =\; e\_\; \{1\}\; \backslash \; wedge\; \backslash \; cdots\; \backslash \; wedge\; e\_\; \{n\}\}$

- псевдоскаляр (который не обязательно равен квадрату $\pm \; 1\; \{\backslash \; displaystyle\; \backslash \; pm\; 1\}$), сформированный из основы $\{\; е\; 1,\dots ,\; en\}\; \{\backslash \; displaystyle\; \backslash \; \{e\_\; \{1\},\; \backslash \; ldots,\; e\_\; \{n\}\; \backslash \}\}$. Двойственные базисные векторы могут быть построены как

$ei\; =\; (-\; 1)\; i\; -\; 1\; (e\; 1\; \wedge \; \cdots \; \wedge \; e\; ˇ\; i\; \wedge \; \cdots \; \wedge \; en)\; ϵ\; -\; 1,\; \{\backslash \; displaystyle\; e\; ^\; \{i\}\; =\; (-\; 1)\; ^\; \{i-1\}\; (e\_\; \{1\}\; \backslash \; wedge\; \backslash \; cdots\; \backslash \; wedge\; \{\backslash \; check\; \{e\}\}\; \_\; \{i\}\; \backslash \; wedge\; \backslash \; cdots\; \backslash \; wedge\; e\_\; \{n\})\; \backslash \; epsilon\; ^\; \{-\; 1\},\}$

, где $e\; ˇ\; i\; \{\backslash \; displaystyle\; \{\backslash \; check\; \{e\}\}\; \_\; \{i\}\}$означает, что $i\; \{\backslash \; displaystyle\; i\}$th базисный вектор не указывается в произведении.

Расширение внутреннего и внешнего продуктов

Обычной практикой является расширение внешнего произведения векторов на всю алгебру. Это можно сделать с помощью оператора проекции оценок:

$C\; \wedge \; D:\; =\; \sum \; r,\; s\; ⟨⟨C⟩\; r\; ⟨D⟩\; s⟩\; r\; +\; s\; \{\backslash \; displaystyle\; C\; \backslash \; wedge\; D:\; =\; \backslash \; sum\; \_\; \{r,\; s\}\; \backslash \; langle\; \backslash \; langle\; C\; \backslash \; rangle\; \_\; \{r\}\; \backslash \; langle\; D\; \backslash \; rangle\; \_\; \{s\}\; \backslash \; rangle\; \_\; \{r\; +\; s\}\}$(внешний продукт)

Это обобщение согласуется с приведенным выше определением антисимметризации. Другое обобщение, связанное с внешним продуктом, - это коммутаторное произведение:

$C\; \times \; D:\; =\; 1\; 2\; (CD\; -\; DC)\; \{\backslash \; displaystyle\; C\; \backslash \; times\; D:\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; (CD-DC)\}$(коммутаторный продукт)

Регрессивный продукт (обычно называемый «встречным») является двойным по отношению к внешнему продукту (или «соединению» в данном контексте). Двойная спецификация элементов допускает для лезвий $A\; \{\backslash \; displaystyle\; A\}$и $B\; \{\backslash \; displaystyle\; B\}$пересечение (или встречу), где двойственность следует брать относительно лезвия с наименьшим классом, содержащего как $A\; \{\backslash \; displaystyle\; A\}$, так и $B\; \{\backslash \; displaystyle\; B\}$(соединение).

$С\; \vee \; D:\; знак\; равно\; ((CI\; -\; 1)\; \wedge \; (DI\; -\; 1))\; I\; \{\backslash \; displaystyle\; C\; \backslash \; vee\; D:\; =\; ((CI\; ^\; \{-\; 1\})\; \backslash \; wedge\; (DI\; ^\; \{-\; 1\}))\; I\; \}$

с $I\; \{\backslash \; displaystyle\; I\}$единичный псевдоскаляр алгебры. Регрессивный продукт, как и внешний продукт, является ассоциативным.

Внутреннее произведение векторов также может быть обобщено, но более чем одним неэквивалентным способом. В статье (Dorst 2002) дается полное описание нескольких различных внутренних произведений, разработанных для геометрических алгебр, и их взаимосвязей, и обозначения взяты оттуда. Многие авторы используют тот же символ, что и для внутреннего произведения векторов для выбранного ими расширения (например, Hestenes и Perwass). Никаких последовательных обозначений не появилось.

Среди этих нескольких различных обобщений внутреннего произведения векторов:

$C\; \rfloor \; D:\; =\; \sum \; r,\; s\; ⟨⟨C⟩\; r\; ⟨D⟩\; s⟩\; s\; -\; r\; \{\backslash \; displaystyle\; C\; \backslash ;\; \backslash \; rfloor\; \backslash ;\; D:\; =\; \backslash \; sum\; \_\; \{r,\; s\}\; \backslash \; langle\; \backslash \; langle\; C\; \backslash \; rangle\; \_\; \{r\}\; \backslash \; langle\; D\; \backslash \; rangle\; \_\; \{s\}\; \backslash \; rangle\; \_\; \{sr\}\}$( левое сокращение)

$C\; \lfloor \; D:\; =\; \sum \; r,\; s\; ⟨⟨C⟩\; r\; ⟨D⟩\; s⟩\; r\; -\; s\; \{\backslash \; displaystyle\; C\; \backslash ;\; \backslash \; lfloor\; \backslash ;\; D:\; =\; \backslash \; sum\; \_\; \{r,\; s\}\; \backslash \; langle\; \backslash \; langle\; C\; \backslash \; rangle\; \_\; \{r\}\; \backslash \; langle\; D\; \backslash \; rangle\; \_\; \{s\}\; \backslash \; rangle\; \_\; \{rs\}\}$(правильное сокращение)

$C\; \ast \; D:\; =\; \sum \; r,\; s\; ⟨⟨\; C⟩\; р\; ⟨D⟩\; s⟩\; 0\; \{\backslash \; displaystyle\; C\; *\; D:\; =\; \backslash \; sum\; \_\; \{r,\; s\}\; \backslash \; langle\; \backslash \; langle\; C\; \backslash \; rangle\; \_\; \{r\}\; \backslash \; langle\; D\; \backslash \; rangle\; \_\; \{s\}\; \backslash \; rangle\; \_\; \{0\; \}\}$(скалярный продукт)

$C\; \bullet \; D:\; =\; \sum \; r,\; s\; ⟨⟨C⟩\; r\; ⟨D⟩\; s⟩\; |\; s\; -\; r\; |\; \{\backslash \; displaystyle\; C\; \backslash \; bullet\; D:\; =\; \backslash \; sum\; \_\; \{r,\; s\}\; \backslash \; langle\; \backslash \; langle\; C\; \backslash \; rangle\; \_\; \{r\}\; \backslash \; langle\; D\; \backslash \; rangle\; \_\; \{s\}\; \backslash \; rangle\; \_\; \{|\; sr\; |\}\}$(произведение «(жирных) точек»)

Дорст (2002) приводит аргумент в пользу использования сокращений в пользу внутреннего продукта Гестена; они алгебраически более регулярны и более чистую геометрическую интерпретацию. Ряд идентичностей, включающих сокращения, действительны без ограничения входных данных. Например,

$C\; \rfloor \; D\; знак\; равно\; (C\; \wedge \; (DI\; -\; 1))\; I\; \{\backslash \; displaystyle\; C\; \backslash ;\; \backslash \; rfloor\; \backslash ;\; D\; =\; (C\; \backslash \; клин\; (DI\; ^\; \{-\; 1\}))\; I\}$

$С\; \lfloor \; D\; знак\; равно\; я\; ((I\; -\; 1\; C)\; \wedge \; D)\; \{\backslash \; Displaystyle\; C\; \backslash ;\; \backslash \; lfloor\; \backslash ;\; D\; знак\; равно\; I\; ((I\; ^\; \{-\; 1\}\; C)\; \backslash \; клин\; D)\}$

$(A\; \wedge \; B)\; \ast \; C\; знак\; равно\; A\; \ast \; (B\; \rfloor \; C)\; \{\backslash \; Displaystyle\; (A\; \backslash \; клин\; B)\; *\; C\; =\; A\; *\; (В\; \backslash ;\; \backslash \; rfloor\; \backslash ;\; C)\}$

$C\; \ast \; (B\; \wedge \; A)\; =\; (C\; \lfloor \; В)\; \ast \; A\; \{\backslash \; Displaystyle\; C\; *\; (B\; \backslash \; клин\; A)\; =\; (C\; \backslash ;\; \backslash \; lfloor\; \backslash ;\; В)\; *\; A\}$

$A\; \rfloor \; (B\; \rfloor \; C)\; =\; (A\; \wedge \; B)\; \rfloor \; C\; \{\backslash \; displaystyle\; A\; \backslash ;\; \backslash \; rfloor\; \backslash ;\; (B\; \backslash ;\; \backslash \; rfloor\; \backslash ;\; C)\; =\; (A\; \backslash \; клин\; B)\; \backslash ;\; \backslash \; rfloor\; \backslash ;\; C\}$

$(A\; \rfloor \; B)\; \lfloor \; C\; =\; A\; \rfloor \; (B\; \lfloor \; C).\; \{\backslash \; Displaystyle\; (A\; \backslash ;\; \backslash \; rfloor\; \backslash ;\; B)\; \backslash ;\; \backslash \; lfloor\; \backslash ;\; С\; =\; А\; \backslash ;\; \backslash \; rfloor\; \backslash ;\; (B\; \backslash ;\; \backslash \; lfloor\; \backslash ;\; C).\}$

Преимущества использования левого сжатия в качестве расширения внутреннего продукта включает то, что тождество $ab\; =\; a\; \cdot \; b\; +\; a\; \wedge \; b\; \{\backslash \; displaystyle\; ab\; =\; a\; \backslash \; cdot\; b\; +\; a\; \backslash \; wedge\; b\}$расширяется до $a\; B\; =\; a\; \rfloor \; B\; +\; a\; \wedge \; B\; \{\backslash \; displaystyle\; aB\; =\; a\; \backslash ;\; \backslash \; rfloor\; \backslash ;\; B\; +\; a\; \backslash \; wedge\; B\}$для любого вектора $a\; \{\backslash \; displaystyle\; a\}$и мультивектор $B\; \{\backslash \; displaystyle\; B\}$, и что операция проекции $P\; b\; (a)\; =\; (a\; \cdot \; b\; -\; 1)\; b\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{P\}\}\; \_\; \{b\}\; (a)\; =\; (a\; \backslash \; cdot\; b\; ^\; \{-\; 1\})\; b\}$расширяется до $PB\; (A)\; =\; (A\; \rfloor \; В\; -\; 1)\; \rfloor \; В\; \{\backslash \; Displaystyle\; \{\backslash \; mathcal\; \{P\}\}\; \_\; \{B\}\; (A)\; =\; (A\; \backslash ;\; \backslash \; rfloor\; \backslash ;\; B\; ^\; \{-\; 1\})\; \backslash ;\; \backslash \; rfloor\; \backslash ;\; B\}$для любого лезвия $B\; \{\backslash \; displaystyle\; B\}$и любого мультивекторного $A\; \{\backslash \; displaystyle\; A\}$(с незначительной модификацией для размещения null $B\; \{\backslash \; displaystyle\; B\}$, если ниже).

Линейные функции

Хотя с версором легче работать, потому что он может быть представлен напрямую в алгебре как мультивектор, версоры представляют собой подгруппу линейных функций на мультивекторах., который можно использовать при необходимости. Геометрическая алгебра $n\; \{\backslash \; displaystyle\; n\}$-мерного пространства охватывается базисом $2\; n\; \{\backslash \; displaystyle\; 2\; ^\; \{n\}\}$элементы. Если многовектор представлен $2\; n\; \times \; 1\; \{\backslash \; displaystyle\; 2\; ^\; \{n\}\; \backslash \; times\; 1\}$вещественной матрицей столбцов коэффициентов базиса алгебры, тогда все линейные преобразования многовектора могут быть выражены как умножение матрицы на $2\; n\; \times \; 2\; n\; \{\backslash \; displaystyle\; 2\; ^\; \{n\}\; \backslash \; times\; 2\; ^\; \{n\}\}$вещественная матрица. Однако такое общее линейное преобразование допускает произвольный обмен между классами, такой как «поворот» скаляра в вектор, который не имеет очевидной геометрической интерпретации.

Представляет интерес общее линейное преобразование векторов в векторы. С естественным ограничением на сохранение индуцированной внешней алгебры внешний морфизм линейного преобразования является единственным расширением версора. Если $f\; \{\backslash \; displaystyle\; f\}$- линейная функция, которая отображает векторы в векторы, то ее внешний морфизм - это функция, которая подчиняется правилу

$f\; \_\; (a\; 1\; \wedge \; a\; 2\; \wedge \; \cdots \; \wedge \; ар)\; знак\; равно\; е\; (а\; 1)\; \wedge \; е\; (а\; 2)\; \wedge \; \cdots \; \wedge \; е\; (ар)\; \{\backslash \; Displaystyle\; \{\backslash \; underline\; \{\backslash \; mathsf\; \{f\}\}\}\; (а\_\; \{1\}\; \backslash \; клин\; а\_\; \{2\}\; \backslash \; клин\; \backslash \; cdots\; \backslash \; wedge\; a\_\; \{r\})\; =\; f\; (a\_\; \{1\})\; \backslash \; wedge\; f\; (a\_\; \{2\})\; \backslash \; wedge\; \backslash \; cdots\; \backslash \; wedge\; f\; (a\_\; \{r\})\}$

для лезвия, расширенного на всю алгебру за счет линейности.

Хотя много внимания было уделено CGA, следует отметить, что GA - это не просто одна алгебра, это одна из семейства алгебр с одинаковыми основными структура.

Модель векторного пространства

$G\; (3,\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (3,0)\}$может рассматриваться как расширение или завершение векторной алгебры. От векторов до геометрической алгебры охватывает базовую аналитическую геометрию и дает введение в стереографическую проекцию.

Четная подалгебра в $G\; (2,\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\; \}\}\; (2,0)\}$изоморфен комплексным числам, что можно увидеть, написав вектор $P\; \{\backslash \; displaystyle\; P\}$в терминах его компонентов в ортонормированном базисе и умножении слева на базисный вектор $e\; 1\; \{\backslash \; displaystyle\; e\_\; \{1\}\}$, что дает

$Z\; =\; e\; 1\; P\; =\; e\; 1\; (xe\; 1\; +\; ye\; 2)\; =\; x\; (1)\; +\; y\; (e\; 1\; e\; 2),\; \{\backslash \; displaystyle\; Z\; =\; e\_\; \{1\}\; P\; =\; e\_\; \{1\}\; (xe\_\; \{1\}\; +\; ye\_\; \{2\})\; =\; x\; (1)\; +\; y\; (e\_\; \{1\}\; e\_\; \{2\}),\}$

где мы идентифицируем $i\; \mapsto \; e\; 1\; e\; 2\; \{\backslash \; displaystyle\; i\; \backslash \; mapsto\; e\_\; \{1\}\; e\_\; \{2\}\}$поскольку

$(e\; 1\; e\; 2)\; 2\; =\; e\; 1\; e\; 2\; e\; 1\; e\; 2\; =\; -\; e\; 1\; e\; 1\; e\; 2\; e\; 2\; =\; -\; 1.\; \{\backslash \; displaystyle\; (\{e\_\; \{1\}\}\; \{e\_\; \{2\}\}))\; ^\; \{2\}\; =\; \{e\_\; \{1\}\}\; \{e\_\; \{2\}\}\; \{e\_\; \{1\}\}\; \{e\_\; \{2\}\}\; =\; -\; \{e\_\; \{1\}\}\; \{e\_\; \{1\}\}\; \{e\_\; \{2\}\}\; \{e\_\; \{2\}\}\; =\; -\; 1.\}$

Аналогично, четная подалгебра в $G\; (3,\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (3,0)\}$с основанием $\{1,\; e\; 2\; e\; 3,\; e\; 3\; e\; 1,\; e\; 1\; e\; 2\}\; \{\backslash \; displaystyle\; \backslash \; \{1,\; e\_\; \{2\}\; e\_\; \{3\},\; e\_\; \{3\}\; e\_\; \{1\},\; e\_\; \{1\}\; e\_\; \{2\}\; \backslash \; \}\}$изоморфен кватернионам , что можно увидеть, указав $i\; \mapsto \; -\; e\; 2\; e\; 3\; \{\backslash \; displaystyle\; i\; \backslash \; mapsto\; -e\_\; \{2\}\; e\_\; \{3\}\; \}$, $j\; \mapsto \; -\; e\; 3\; e\; 1\; \{\backslash \; displaystyle\; j\; \backslash \; mapsto\; -e\_\; \{3\}\; e\_\; \{1\}\}$и $k\; \mapsto \; -\; e\; 1\; e\; 2\; \{\backslash \; displaystyle\; k\; \backslash \; mapsto\; -e\_\; \{1\}\; e\_\; \{2\}\}$.

Каждая ассоциативная алгебра имеет матричное представление; замена трех декартовых базисных векторов на матрицы Паули дает представление $G\; (3,\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (3,0)\}$:

$e\; 1\; =\; \sigma \; 1\; =\; \sigma \; x\; =\; (0\; 1\; 1\; 0)\; e\; 2\; =\; \sigma \; 2\; =\; \sigma \; y\; =\; (0\; -\; ii\; 0)\; e\; 3\; =\; \sigma \; 3\; =\; \sigma \; z\; =\; (1\; 0\; 0\; -\; 1).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; e\_\; \{1\}\; =\; \backslash \; sigma\; \_\; \{1\}\; =\; \backslash \; sigma\; \_\; \{x\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 0\; 1\; \backslash \backslash \; 1\; 0\; \backslash \; end\; \{pmatrix\}\}\; \backslash \backslash \; e\_\; \{2\; \}\; =\; \backslash \; sigma\; \_\; \{2\}\; =\; \backslash \; sigma\; \_\; \{y\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 0\; -i\; \backslash \backslash \; i\; 0\; \backslash \; end\; \{pmatrix\}\}\; \backslash \backslash \; e\_\; \{3\}\; =\; \backslash \; sigma\; \_\; \{3\}\; =\; \backslash \; sigma\; \_\; \{z\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 1\; 0\; \backslash \backslash \; 0\; -1\; \backslash \; end\; \{pmatrix\}\}\; \backslash ,.\; \backslash \; end\; \{align\}\}\}$

Пунктирная линия "вектора Паули " (a диада ):

$\sigma \; =\; \sigma \; 1\; e\; 1\; +\; \sigma \; 2\; e\; 2\; +\; \sigma \; 3\; e\; 3\; \{\backslash \; displaystyle\; \backslash \; sigma\; =\; \backslash \; sigma\; \_\; \{1\}\; e\_\; \{1\}\; +\; \backslash \; sigma\; \_\; \{2\}\; e\_\; \{2\}\; +\; \backslash \; sigma\; \_\; \{3\}\; e\_\; \{3\}\}$с произвольными векторами $a\; \{\backslash \; displaystyle\; a\}$и $b\; \{\backslash \; displaystyle\; b\}$и умножение на него дает:

$(\sigma \; \cdot \; a)\; (\sigma \; \cdot \; b)\; =\; a\; \cdot \; b\; +\; a\; \wedge \; b\; \{\backslash \; displaystyle\; (\backslash \; sigma\; \backslash \; cdot\; a)\; (\backslash \; sigma\; \backslash \; cdot\; б)\; =\; a\; \backslash \; cdot\; b\; +\; a\; \backslash \; wedge\; b\}$(эквивалентно, при осмотре $a\; \cdot \; b\; +\; i\; \sigma \; \cdot \; \{\backslash \; displaystyle\; a\; \backslash \; cdot\; b\; +\; i\; \backslash \; sigma\; \backslash \; cdot\}$($a\; \{\backslash \; displaystyle\; a\}$× $b\; \{\backslash \; displaystyle\; b\}$))

Модель пространства-времени

В физике основными приложениями являются геометрическая алгебра пространства-времени Минковского 3 + 1, $G\; (1,\; 3)\; \{\backslash \; Displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (1,3)\}$, называемый алгеброй пространства-времени (STA), или, реже, $G\; (3,\; 0)\; \{\backslash \; displaystyle\; \{\; \backslash \; mathcal\; \{G\}\}\; (3,0)\}$, интерпретирует алгебру физического пространства (APS).

В то время как в STA точки пространства-времени представлены просто векторами, в APS точки $(3\; +\; 1)\; \{\backslash \; displaystyle\; (3\; +\; 1)\}$-мерного пространства-времени являются вместо этого представлены паравекторами : $3\; \{\backslash \; displaystyle\; 3\}$-мерный вектор (пространство) плюс $1\; \{\backslash \; displaystyle\; 1\}$-мерный скаляр (время).

В алгебре пространства-времени тензор электромагнитного поля имеет бивекторное представление $F\; =\; (E\; +\; ic\; B)\; \gamma \; 0\; \{\backslash \; displaystyle\; \{F\}\; =\; (\{E\}\; +\; ic\; \{B\})\; \backslash \; gamma\; \_\; \{0\}\}$. Здесь $i\; =\; \gamma \; 0\; \gamma \; 1\; \gamma \; 2\; \gamma \; 3\; \{\backslash \; displaystyle\; i\; =\; \backslash \; gamma\; \_\; \{0\}\; \backslash \; gamma\; \_\; \{1\}\; \backslash \; gamma\; \_\; \{2\}\; \backslash \; gamma\; \_\; \{3\}\}$- единичный псевдоскаляр (или элемент четырехмерного объема), $\gamma \; 0\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{0\}\}$- единичный вектор в направлении времени, а $E\; \{\; \backslash \; displaystyle\; E\}$и $B\; \{\backslash \; displaystyle\; B\}$- это классические векторы электрического и магнитного поля (с нулевой временной составляющей). Используя четверо-текущий $J\; \{\backslash \; displaystyle\; \{J\}\}$, уравнения Максвелла, затем переходите в

Формулировку	Однородные уравнения	Неоднородные уравнения
Поля	$DF\; =\; \mu \; 0\; J\; \{\backslash \; displaystyle\; DF\; =\; \backslash \; mu\; \_\; \{0\}\; J\}$
	$D\; \wedge \; F\; =\; 0\; \{\backslash \; displaystyle\; D\; \backslash \; wedge\; F\; =\; 0\}$	$D\; \rfloor \; F\; знак\; равно\; \mu \; 0\; J\; \{\backslash \; displaystyle\; D\; ~\; \backslash \; rfloor\; ~\; F\; =\; \backslash \; mu\; \_\; \{0\}\; J\}$
потенциалы (любой шкалы)	$F\; =\; D\; \wedge \; A\; \{\backslash \; displaystyle\; F\; =\; D\; \backslash \; клин\; A\; \}$	$D\; \rfloor \; (D\; \wedge \; A)\; =\; \mu \; 0\; J\; \{\backslash \; displaystyle\; D\; ~\; \backslash \; rfloor\; ~\; (D\; \backslash \; wedge\; A)\; =\; \backslash \; mu\; \_\; \{0\}\; J\}$
Потенциалы (калибровка Лоренца)	$F\; Знак\; равно\; DA\; \{\backslash \; displaystyle\; F\; =\; DA\}$ $D\; \rfloor \; A\; =\; 0\; \{\backslash \; displaystyle\; D\; ~\; \backslash \; rfloor\; ~\; A\; =\; 0\}$	$D\; 2\; A\; =\; \mu \; 0\; J\; \{\backslash \; displaystyle\; D\; ^\; \{2\}\; A\; =\; \backslash \; mu\; \_\; \{0\}\; J\}$

В геометрическом исчислении сопоставление векторов, например, в $DF\; \{\backslash \; displaystyle\; DF\}$, указывает на геометрическое произведение и может быть разложено на части как $DF\; Знак\; равно\; D\; \rfloor \; F\; +\; D\; \wedge \; F\; \{\backslash \; displaystyle\; DF\; =\; D\; ~\; \backslash \; rfloor\; ~\; F\; +\; D\; \backslash \; wedge\; F\}$. Здесь $D\; \{\backslash \; displaystyle\; D\}$является ковекторной производной в любом пространстве-времени и сокращается до $\nabla \; \{\backslash \; displaystyle\; \backslash \; nabla\}$в плоском пространстве-времени. Где $▽\; \{\backslash \; displaystyle\; \backslash \; bigtriangledown\}$играет роль в пространстве-времени Минковского $4\; \{\backslash \; displaystyle\; 4\}$, которое является синонимом роли $\nabla \; \{\backslash \; displaystyle\; \backslash \; nabla\}$в евклидовом $3\; \{\backslash \; displaystyle\; 3\}$-пространстве и связан с даламбертианом посредством $◻\; =\; ▽\; 2\; \{\backslash \; displaystyle\; \backslash \; Box\; =\; \backslash \; bigtriangledown\; ^\; \{2\}\}$. Действительно, для наблюдателя, представленного будущим указывающим времяподобным вектором $\gamma \; 0\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{0\}\}$, мы имеем

$\gamma \; 0\; \cdot \; ▽\; =\; 1\; c\; \partial \; \partial \; t\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{0\}\; \backslash \; cdot\; \backslash \; bigtriangledown\; =\; \{\backslash \; frac\; \{1\}\; \{c\}\}\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; t\}\}\}$

$\gamma \; 0\; \wedge \; ▽\; =\; \nabla \; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{0\}\; \backslash \; wedge\; \backslash \; bigtriangledown\; =\; \backslash \; nabla\}$

Повышение в этом лоренцевом метрическом пространстве имеет такое же выражение $e\; \beta \; \{\backslash \; displaystyle\; e\; ^\; \{\backslash \; beta\}\}$как вращение в евклидовом пространстве, где $\beta \; \{\backslash \; displaystyle\; \{\backslash \; beta\}\}$- это бивектор, порожденный задействованными направлениями времени и пространства, тогда как в евклидовом случае это бивектор, порожденный двумя космических направлений, усиливая «аналогию» почти до идентичности.

Матрицы Дирака представляют собой представление $G\; (1,\; 3)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (1,3)\}$, демонстрируя эквивалентность матричным представлениям, используемым физиками.

Однородная модель

Первая модель здесь - $G\; (4,\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (4,0)\}$, версия однородных координат GA, используемая в проективной геометрии. Здесь вектор представляет точку и внешнее произведение векторов ориентированной длины, но мы можем работать с алгеброй точно так же, как в $G\; (3,\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (3,\; 0)\}$. Однако полезный внутренний продукт не может быть определен в пространстве, и поэтому не существует геометрического продукта, оставляя только внешний продукт и неметрические применения двойственности, такие как встреча и соединение.

Тем не менее, были исследованы 4-мерные альтернативы полной 5-мерной CGA для ограниченной геометрии, такой как движения твердого тела. Некоторые из них можно найти в Части IV Руководства по геометрической алгебре на практике. Обратите внимание, что алгебра $G\; (3,\; 0,\; 1)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (3,0,1)\}$появляется как подалгебра CGA при выборе только одного нуля базисный вектор и отбрасывая другой, и далее, что «моторная алгебра» (изоморфная двойственным кватернионам) является четной подалгеброй в $G\; (3,\; 0,\; 1)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (3,0,\; 1)\}$.

Конформная модель

Краткое описание текущего состояния техники предоставлено Bayro-Corrochano Scheuermann (2010), которое также включает дополнительные ссылки, в в частности Dorst, Fontijne Mann (2007). Другие полезные ссылки: Li (2008) и Bayro-Corrochano (2010).

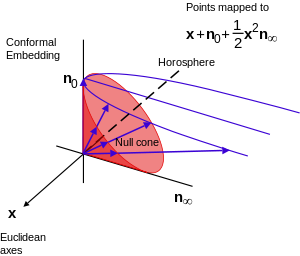
Работа в GA, евклидово пространство $E\; 3\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{E\}\}\; ^\; \{\; 3\}\}$(вместе с бесконечно удаленной конформной точкой) проективно вложен в CGA $G\; (4,\; 1)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (4,1)\}$через идентификацию евклидовых точек с подпространствами $1\; \{\backslash \; displaystyle\; 1\}$-d в $4\; \{\backslash \; displaystyle\; 4\}$-d null конус векторного подпространства CGA $5\; \{\backslash \; displaystyle\; 5\}$-d. Это позволяет выполнять все конформные преобразования как вращения и отражения и является ковариантным, распространяя отношения инцидентности проективной геометрии на окружности и сферы.

В частности, мы добавляем ортогональные базисные векторы $e\; +\; \{\backslash \; displaystyle\; e\; \_\; \{+\}\}$и $e\; -\; \{\backslash \; displaystyle\; e\; \_\; \{-\}\}$такое, что $e\; +\; 2\; =\; +\; 1\; \{\backslash \; displaystyle\; \{e\; \_\; \{+\}\}\; ^\; \{2\}\; =\; +\; 1\}$и $e\; -\; 2\; =\; -\; 1\; \{\backslash \; displaystyle\; \{\; e\; \_\; \{-\}\}\; ^\; \{2\}\; =\; -\; 1\}$к основе векторного пространства, которое порождает $G\; (3,\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (3,\; 0)\}$и определить нулевые векторы

$n\; \infty \; =\; e\; -\; +\; e\; +\; \{\backslash \; displaystyle\; n\; \_\; \{\backslash \; infty\}\; =\; e\; \_\; \{-\}\; +\; e\; \_\; \{+\}\}$как конформная точка на бесконечности (см. Компактификация ) и

$no\; =\; 1\; 2\; (e\; -\; -\; e\; +)\; \{\backslash \; displaystyle\; n\; \_\; \{\backslash \; text\; \{o\}\}\; =\; \{\backslash \; tfrac\; \{1\; \}\; \{2\}\}\; (e\; \_\; \{-\}\; -\; e\; \_\; \{+\})\}$в качестве точки в начале координат, что дает

$n\; \infty \; \cdot \; no\; =\; -\; 1\; \{\backslash \; displaystyle\; n\; \_\; \{\backslash \; infty\}\; \backslash \; cdot\; n\; \_\; \{\backslash \; text\; \{o\}\}\; =\; -\; 1\}$.

Эта процедура имеет некоторые сходства с процедурой работы с однородными координатами в проективной геометрии и в этом случае позволяет моделировать евклидову преобразования из $R\; 3\; \{\backslash \; displaystyle\; \backslash \; math\; bf\; \{R\}\; ^\; \{3\}\}$как ортогональные преобразования подмножества $R\; 4,\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\; ^\; \{4,1\}\}$.

Быстро меняющаяся и изменчивая область GA, CGA, также исследуется для приложений к релятивистской физике.

Модели проективного преобразования

Два потенциальных кандидата в настоящее время исследуются в качестве основы для аффинной и проективной геометрии в 3-х измерениях $R\; (3,\; 3)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{R\}\}\; (3,3)\}$и $R\; (4,\; 4)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{R\}\}\; (4,4)\}$, который включает представления для сдвигов и неравномерного масштабирования, а также квадратичных поверхностей и конических сечений.

Новая исследовательская модель, квадратичная конформная геометрическая алгебра (QCGA) $R\; (9,\; 6)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{R\}\}\; (9,6)\}$расширение CGA, посвященное квадратичным поверхностям. Идея состоит в том, чтобы представить объекты в подпространствах малой размерности алгебры. QCGA может строить квадратичные поверхности с использованием контрольных точек или неявных уравнений. Кроме того, QCGA может вычислять пересечение квадратичных поверхностей, а также касательные к поверхности и векторы нормали в точке, лежащей в квадратичной поверхности.

Проекция и отклонение

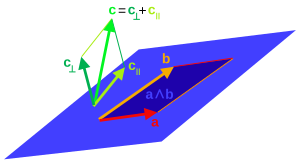
В трехмерном пространстве бивектор $a\; \wedge \; b\; \{\backslash \; displaystyle\; a\; \backslash \; land\; b\}$определяет подпространство 2-мерной плоскости (светло-голубой, бесконечно простирается в указанных направлениях). Любой вектор $c\; \{\backslash \; displaystyle\; c\}$в трехмерном пространстве можно разложить на его проекцию $c\; \Vert \; \{\backslash \; displaystyle\; c\; \_\; \{\backslash \; |\}\}$на плоскость и ее отклонение $c\; \perp \; \{\backslash \; displaystyle\; c\; \_\; \{\backslash \; perp\}\}$от этой плоскости.

Для любого вектора $a\; \{\backslash \; displaystyle\; a\}$и любой обратимый вектор $m\; \{\backslash \; displaystyle\; m\}$,

$a\; =\; amm\; -\; 1\; =\; (a\; \cdot \; m\; +\; a\; \wedge \; m)\; m\; -\; 1\; =\; a\; \Vert \; m\; +\; a\; \perp \; m,\; \{\backslash \; displaystyle\; a\; =\; amm\; ^\; \{\; -1\}\; =\; (a\; \backslash \; cdot\; m\; +\; a\; \backslash \; wedge\; m)\; m\; ^\; \{-\; 1\}\; =\; a\; \_\; \{\backslash \; |\; m\}\; +\; a\; \_\; \{\backslash \; perp\; m\},\}$

где проекция $a\; \{\backslash \; displaystyle\; a\}$на $m\; \{\backslash \; displaystyle\; m\}$(или параллельная часть) равно

$a\; \Vert \; m\; =\; (a\; \cdot \; m)\; m\; -\; 1\; \{\backslash \; displaystyle\; a\; \_\; \{\backslash \; |\; m\}\; =\; (a\; \backslash \; cdot\; m)\; m\; ^\; \{-\; 1\}\}$

и отклонение из $a\; \{\backslash \; displaystyle\; a\}$из $m\; \{\backslash \; displaystyle\; m\}$(или ортогональная часть) равно

$a\; \perp \; m\; =\; a\; -\; a\; \Vert \; m\; =\; (a\; \wedge \; m)\; m\; -\; 1.\; \{\backslash \; displaystyle\; a\; \_\; \{\backslash \; perp\; m\}\; =\; a-a\; \_\; \{\backslash \; |\; m\}\; =\; (a\; \backslash \; wedge\; m)\; m\; ^\; \{-\; 1\}.\}$

Использование концепции a $k\; \{\backslash \; displaystyle\; k\}$-blade $B\; \{\backslash \; displaystyle\; B\}$как представляющее подпространство $V\; \{\backslash \; displaystyle\; V\}$, и каждый мультивектор в конечном итоге выражается в в терминах векторов, это обобщается на проекцию общего многовектора на любой обратимый $k\; \{\backslash \; displaystyle\; k\}$-blade $B\; \{\backslash \; displaystyle\; B\}$as

$PB\; (A)\; =\; (\; А\; \rfloor \; В\; -\; 1)\; \rfloor \; В,\; \{\backslash \; Displaystyle\; \{\backslash \; mathcal\; \{P\}\}\; \_\; \{B\}\; (A)\; =\; (A\; \backslash ;\; \backslash \; rfloor\; \backslash ;\; B\; ^\; \{-\; 1\})\; \backslash ;\; \backslash \; rfloor\; \backslash ;\; B,\; \}$

с отклонением, определяемым как

$PB\; \perp \; (A)\; =\; A\; -\; PB\; (A).\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{P\}\}\; \_\; \{B\}\; ^\; \{\backslash \; perp\}\; (A)\; =\; A\; -\; \{\backslash \; mathcal\; \{P\}\}\; \_\; \{B\}\; (A).\}$

Проекция и отклонение обобщаются на нулевые лезвия $B\; \{\backslash \; displaystyle\; B\}$путем замены обратного $B\; -\; 1\; \{\backslash \; displaystyle\; B\; ^\; \{-\; 1\}\}$псевдообратным $B\; +\; \{\backslash \; displaystyle\; B\; ^\; \{+\}\}$в отношении контрактного продукта. Результат проекции совпадает в обоих случаях для ненулевых лопастей. Для нулевых лопастей $B\; \{\backslash \; displaystyle\; B\}$следует использовать определение проекции, приведенное здесь с первым сокращением, а не вторым, на псевдообратное, поскольку только тогда результат обязательно будет в подпространство, представленное $B\; \{\backslash \; displaystyle\; B\}$. Проекция обобщается через линейность на общие мультивекторы $A\; \{\backslash \; displaystyle\; A\}$. Проекция не является линейной в $B\; \{\backslash \; displaystyle\; B\}$и не распространяется на объекты $B\; \{\backslash \; displaystyle\; B\}$, которые не являются лезвиями.

Отражение

Простые отражения в гиперплоскости легко выражаются в алгебре через сопряжение с одним вектором. Они служат для генерации группы общих вращательных отражений и вращений.

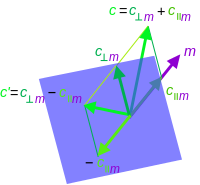
Отражение вектора $c\; \{\backslash \; displaystyle\; c\}$вдоль вектора $m\; \{\backslash \; displaystyle\; m\}$. Инвертируется только компонент $c\; \{\backslash \; displaystyle\; c\}$, параллельный $m\; \{\backslash \; displaystyle\; m\}$.

Отражение $c\; \prime \; \{\; \backslash \; displaystyle\; c\; \text{'}\}$вектора $c\; \{\backslash \; displaystyle\; c\}$вдоль вектора $m\; \{\backslash \; displaystyle\; m\}$, или эквивалентно в гиперплоскости, ортогональной $m\; \{\backslash \; displaystyle\; m\}$, это то же самое, что отрицание компонента вектора, параллельного $m\; \{\backslash \; displaystyle\; m\}$. Результатом отражения будет

$c\; \prime \; =\; -\; c\; \Vert \; m\; +\; c\; \perp \; m\; =\; -\; (c\; \cdot \; m)\; m\; -\; 1\; +\; (c\; \wedge \; m)\; m\; -\; 1\; =\; (-\; m\; \cdot \; c\; -\; m\; \wedge \; c)\; m\; -\; 1\; =\; -\; mcm\; -\; 1\; \{\backslash \; displaystyle\; c\; \text{'}=\; \{-\; c\; \_\; \{\backslash \; |\; m\}\; +\; c\; \_\; \{\backslash \; perp\; m\}\}\; =\; \{-\; (c\; \backslash \; cdot\; m)\; m\; ^\; \{-\; 1\}\; +\; (c\; \backslash \; клин\; m)\; m\; ^\; \{-\; 1\}\}\; =\; \{(-\; m\; \backslash \; cdot\; cm\; \backslash \; wedge\; c)\; m\; ^\; \{-\; 1\}\}\; =\; -\; mcm\; ^\; \{-\; 1\}\}$

Это не самая общая операция, которая может считаться отражением, если размер $n\; \ge \; 4\; \{\backslash \; displaystyle\; n\; \backslash \; geq\; 4\}$. Общее отражение может быть выражено как совокупность любого нечетного числа одноосных отражений. Таким образом, общее отражение $a\; \prime \; \{\backslash \; displaystyle\; a\; \text{'}\}$вектора $a\; \{\backslash \; displaystyle\; a\}$может быть записано

$a\; \mapsto \; a\; \prime \; =\; -\; M\; a\; M\; -\; 1,\; \{\backslash \; displaystyle\; a\; \backslash \; mapsto\; a\; \text{'}=\; -\; MaM\; ^\; \{-\; 1\},\}$

где

$M\; =\; pq\; \cdots \; r\; \{\backslash \; displaystyle\; M\; =\; pq\; \backslash \; cdots\; r\}$и $M\; -\; 1\; =\; (pq\; \cdots \; r)\; -\; 1\; =\; r\; -\; 1\; \cdots \; q\; -\; 1\; p\; -\; 1.\; \{\backslash \; displaystyle\; M\; ^\; \{-\; 1\}\; =\; (pq\; \backslash \; cdots\; r)\; ^\; \{-\; 1\}\; =\; r\; ^\; \{-\; 1\}\; \backslash \; cdots\; q\; ^\; \{-\; 1\}\; p\; ^\; \{-\; 1\}.\}$

Если мы определим отражение вдоль ненулевого вектора $m\; \{\backslash \; displaystyle\; m\}$произведения векторов как отражение каждого вектора в произведении вдоль того же вектора, мы получаем для любого произведения нечетного количество векторов, которые, например,

$(abc)\; \prime \; =\; a\; \prime \; b\; \prime \; c\; \prime \; =\; (-\; mam\; -\; 1)\; (-\; mbm\; -\; 1)\; (-\; mcm\; -\; 1)\; =\; -\; ma\; (m\; -\; 1\; m)\; b\; (m\; -\; 1\; m)\; cm\; -\; 1\; =\; -\; mabcm\; -\; 1\; \{\backslash \; displaystyle\; (abc)\; \text{'}=\; a\text{'}b\text{'}c\text{'}\; =\; (-\; mam\; ^\; \{-\; 1\})\; (-\; mbm\; ^\; \{-\; 1\})\; (-mcm\; ^\; \{-\; 1\})\; =\; -\; ma\; (m\; ^\; \{-\; 1\}\; m)\; b\; (m\; ^\; \{-\; 1\}\; m)\; cm\; ^\; \{-\; 1\}\; =\; -\; mabcm\; ^\; \{-\; 1\}\; \backslash ,\}$

и для произведения четного числа векторов

$(abcd)\; \prime \; =\; a\; \prime \; b\; \prime \; c\; \prime \; d\; \prime \; =\; (-\; mam\; -\; 1)\; (-\; mbm\; -\; 1)\; (-\; mcm\; -\; 1)\; (-\; mdm\; -\; 1)\; =\; mabcdm\; -\; 1.\; \{\backslash \; displaystyle\; (abcd)\; \text{'}=\; a\text{'}b\text{'}c\text{'}d\text{'}\; =\; (-\; mam\; ^\; \{-\; 1\})\; (-\; mbm\; ^\; \{-\; 1\})\; (-\; mcm\; ^\; \{-\; 1\})\; (-\; mdm\; ^\; \{-\; 1\})\; =\; mabcdm\; ^\; \{-\; 1\}.\}$

Используя концепцию каждого многовектора, в конечном счете выражаемого в терминах векторов, отражение общего многовектора $A\; \{\backslash \; displaystyle\; A\}$используя любой вариант отражения $M\; \{\backslash \; displaystyle\; M\}$можно записать

$A\; \mapsto \; M\; \alpha \; (A)\; M\; -\; 1,\; \{\backslash \; displaystyle\; A\; \backslash \; mapsto\; M\; \backslash \; alpha\; (A)\; M\; ^\; \{-1\},\}$

где $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$- это автоморфизм отражения через начало координат векторного пространства. ($v\; \mapsto \; -\; v\; \{\backslash \; displaystyle\; v\; \backslash \; mapsto\; -v\}$) расширен через линейность на всю алгебру.

Вращения

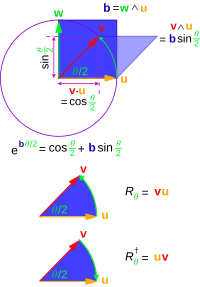
Ротор, который вращает векторы в плоскости, вращает векторы на угол $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$, то есть $x\; \mapsto \; R\; \theta \; x\; R\; \theta \; †\; \{\backslash \; displaystyle\; x\; \backslash \; mapsto\; R\; \_\; \{\backslash \; theta\}\; xR\; \_\; \{\backslash \; theta\}\; ^\; \{\backslash \; dagger\}\}$- поворот на $x\; \{\backslash \; displaystyle\; x\}$через угол $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$. Угол между $u\; \{\backslash \; displaystyle\; u\}$и $v\; \{\backslash \; displaystyle\; v\}$равен $\theta \; /\; 2\; \{\backslash \; displaystyle\; \backslash \; theta\; /\; 2\}$. Подобные интерпретации действительны для общего многовектора $X\; \{\backslash \; displaystyle\; X\}$вместо вектора $x\; \{\backslash \; displaystyle\; x\}$.

Если у нас есть произведение векторов $R\; =\; a\; 1\; a\; 2\; \cdots \; ar\; \{\backslash \; displaystyle\; R\; =\; a\_\; \{1\}\; a\_\; \{2\}\; \backslash \; cdots\; a\_\; \{r\}\}$, то мы обозначим обратное как

$R\; †\; =\; (a\; 1\; a\; 2\; \cdots \; ar)\; †\; =\; ar\; \cdots \; a\; 2\; a\; 1.\; \{\backslash \; displaystyle\; R\; ^\; \{\backslash \; dagger\}\; =\; (a\_\; \{1\}\; a\_\; \{2\}\; \backslash \; cdots\; a\_\; \{r\})\; ^\; \{\backslash \; dagger\}\; =\; a\_\; \{r\}\; \backslash \; cdots\; a\_\; \{2\}\; a\_\; \{1\}.\}$

В качестве примера предположим, что $R\; =\; ab\; \{\backslash \; displaystyle\; R\; =\; ab\}$мы получаем

$RR\; †\; =\; abba\; =\; ab\; 2\; a\; =\; a\; 2\; b\; 2\; =\; ba\; 2\; b\; =\; baab\; =\; R\; †\; R.\; \{\backslash \; Displaystyle\; RR\; ^\; \{\backslash \; dagger\}\; =\; abba\; =\; ab\; ^\; \{2\}\; a\; =\; a\; ^\; \{2\}\; b\; ^\; \{2\}\; =\; ba\; ^\; \{2\}\; b\; =\; baab\; =\; R\; ^\; \{\backslash \; dagger\}\; R.\}$

Масштабирование $R\; \{\backslash \; displaystyl\; e\; R\}$так, чтобы $RR\; †\; =\; 1\; \{\backslash \; displaystyle\; RR\; ^\; \{\backslash \; dagger\}\; =\; 1\}$

$(R\; v\; R\; †)\; 2\; знака\; равно\; р\; v\; 2\; R\; †\; знак\; равно\; v\; 2\; RR\; †\; =\; v\; 2\; \{\backslash \; displaystyle\; (RvR\; ^\; \{\backslash \; dagger\})\; ^\; \{2\}\; =\; Rv\; ^\; \{2\}\; R\; ^\; \{\backslash \; dagger\}\; =\; v\; ^\; \{2\}\; RR\; ^\; \{\backslash \; dagger\}\; =\; v\; ^\; \{2\}\}$

, поэтому $R\; v\; R\; †\; \{\backslash \; displaystyle\; RvR\; ^\; \{\backslash \; dagger\}\}$сохраняет длину $v\; \{\backslash \; displaystyle\; v\}$без изменений. Мы также можем показать, что

$(R\; v\; 1\; R\; †)\; \cdot \; (R\; v\; 2\; R\; †)\; =\; v\; 1\; \cdot \; v\; 2\; \{\backslash \; displaystyle\; (Rv\_\; \{1\}\; R\; ^\; \{\backslash \; dagger\})\; \backslash \; cdot\; (Rv\_\; \{\; 2\}\; R\; ^\; \{\backslash \; dagger\})\; =\; v\_\; \{1\}\; \backslash \; cdot\; v\_\; \{2\}\}$

, поэтому преобразование $R\; v\; R\; †\; \{\backslash \; displaystyle\; RvR\; ^\; \{\backslash \; dagger\}\}$сохраняет как по длине, так и по бокам. Следовательно, это можно определить как вращение или вращательное отражение; $R\; \{\backslash \; displaystyle\; R\}$называется ротором, если это правильное вращение (как если бы оно могло быть выражено как произведение четное число векторов) и является примером того, что в GA называется версором.

Существует общий метод поворота вектора, включающий формирование многовектора вида $R\; =\; e\; -\; B\; \theta \; /\; 2\; \{\backslash \; displaystyle\; R\; =\; e\; ^\; \{-\; B\; \backslash \; theta\; /\; 2\}\}$, который производит вращение $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$в плоскости и с ориентацией, определенной $2\; \{\backslash \; displaystyle\; 2\}$-blade $B\; \{\backslash \; displaystyle\; B\}$.

Роторы - это обобщение кватернионов на $n\; \{\backslash \; displaystyle\; n\}$-мерные пространства.

Versor

A $k\; \{\backslash \; displaystyle\; k\}$-versor - многовектор, который может быть выражен как геометрическое произведение $k\; \{\backslash \; displaystyle\; k\}$Обратимые преподав. Единичные кватернионы (установленные названные Гамильтоном версорами) могут быть отождествлены с роторами в трехмерном пространстве почти так же, как реальные двухмерные роторы включают комплексные числа; подробности см. в Дорст.

Некоторые используют термин «продукт Versor» для обозначения часто встречающегося случая, когда операнд «зажат» между операторами. Описание вращений и отражений, включая их внешние морфизмы, являются примерами такого сэндвича. Эти внешние морфизмы имеют особенно простую алгебраическую форму. В частности, отображение векторов вида

$V\; \to \; V:\; a\; \mapsto \; R\; a\; R\; -\; 1\; \{\backslash \; displaystyle\; V\; \backslash \; to\; V:\; a\; \backslash \; mapsto\; RaR\; ^\; \{-\; 1\}\}$распространяется на Внешний морфизм $G\; (V)\; \to \; G\; (V):\; A\; \mapsto \; RAR\; -\; 1.\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (V)\; \backslash \; to\; \{\backslash \; mathcal\; \{G\}\}\; (V):\; A\; \backslash \; mapsto\; RAR\; ^\; \{-\; 1\}.\}$

и операнды, действующие в режиме реального времени, используются варианты использования альтернативных вариантов, таких как вращение ротора или отражение спинора, всегда при условии, что такие операции могут быть придано какое-то геометрическое или физическое.

Согласно теореме Картана - Дьедонне мы имеем, что любая изометрия может быть задана как отражение в гиперплоскостях, поскольку составные отражения обеспечивают вращения, то ортогональные преобразования являются версорами.

В групповых терминах для действительного невырожденного $G\; (p,\; q)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; (p,\; q)\}$, имеющего идентифицировал группу $G\; \times \; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\; ^\; \{\backslash \; times\}\}$как группа всех обратимых элементов $G\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{G\}\}\}$, Лундхольм приводит доказательство того, что «группа версоров» $\{v\; 1\; v\; 2\; \cdots \; vk\; \in \; G:\; vi\; \in \; V\; \times \}\; \{\backslash \; displaystyle\; \backslash \; \{v\_\; \{1\}\; v\_\; \{2\}\; \backslash \; cdots\; v\_\; \{k\}\; \backslash \; in\; G:\; v\_\; \{i\}\; \backslash \; in\; V\; ^\; \{\backslash \; times\}\; \backslash \}\}$(множество обратимых версоров) совпадает с липшицевой группой $\Gamma \; \{\backslash \; displaystyle\; \backslash \; Gamma\}$(иначе группа Клиффорда, хотя Лундхольм осуждает это использование).

Подгруппы Γ

Лундхольм определяет $контакт\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Pin\}\}$, $Spin\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Spin\}\}$и $Spin\; +\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Spin\}\; ^\; \{+\}\}$подгруппы, генерируется единичными векторами, а в случае $Spin\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Spin\}\}$и $Spin\; +\; \{\backslash \; dis\; playstyle\; \backslash \; operatorname\; \{Spin\}\; ^\; \{+\}\}$, может присутствовать только четное число таких векторных факторов.

Подгруппа	Определение	Описание
$Пин\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Pin\}\}$	$X\; \in \; \Gamma :\; XX\; †\; =\; \pm \; 1\; \{\backslash \; displaystyle\; X\; \backslash \; in\; \backslash \; Гамма:\; XX\; ^\; \{\backslash \; dagger\}\; =\; \backslash \; pm\; 1\}$	версоры
$Spin\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Spin\}\}$	$Pin\; \cap \; G\; +\; \{\backslash \; displaystyle\; \{\backslash \; operatorname\; \{Pin\}\}\; \backslash \; cap\; \{\backslash \; mathcal\; \{G\}\}\; ^\; \{+\}\}$	четные версии единиц
$Spin\; +\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Spin\}\; ^\; \{+\}\}$	$X\; \in \; Spin:\; XX\; †\; =\; 1\; \{\backslash \; displaystyle\; X\; \backslash \; in\; \backslash \; operatorname\; \{Spin\}:\; XX\; ^\; \{\backslash \; dagger\}\; =\; 1\}$	роторы

Спиноры опасностей как элементы четной подалгебры реального ГА; анализ подхода ГА к спинорам дан Фрэнсисом и Косовски.

Гипер объем параллелотопа, натянутого на землю

Для векторов $a\; \{\backslash \; displaystyle\; a\}$>$b\; \{\; \backslash \; displaystyle\; b\}$, охватывающую параллелограмм, мы имеем

$a\; \wedge \; b\; =\; ((a\; \wedge \; b)\; b\; -\; 1)\; b\; =\; a\; \perp \; bb\; \{\backslash \; displaystyle\; a\; \backslash \; wedge\; b\; =\; ((a\; \backslash \; клин\; b)\; b\; ^\; \{-\; 1\})\; b\; =\; a\; \_\; \{\backslash \; perp\; b\}\; b\}$

, в результате $a\; \wedge \; b\; \{\backslash \; displaystyle\; a\; \backslash \; wedge\; b\}$является линейным по произведению "высоты" и "основания" параллелограмма, то есть его площади.

Аналогичные интерпретации верны для любого числа векторов, охватывающих $n\; \{\backslash \; displaystyle\; n\}$-мерный параллелоэдр ; внешнее произведение векторов $a\; 1,\; a\; 2,\dots ,\; an\; \{\backslash \; displaystyle\; a\_\; \{1\},\; a\_\; \{2\},\; \backslash \; ldots,\; a\_\; \{n\}\}$, то есть $\bigwedge \; я\; =\; 1\; nai\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \backslash \; bigwedge\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; a\_\; \{i\}\}$, имеет значение, равное объему $n\; \{\backslash \; displaystyle\; n\}$-параллелоэдр. $n\; \{\backslash \; displaystyle\; n\}$-вектор не обязательно имеет форму параллелотопа - это удобная визуализация. Это может быть любая форма, хотя по объему она равна параллелотопу.

Пересечение прямой и плоскостью

Линия L, определяемая точками T и P (которые мы ищем), плоскость, определяемая бивектором B, содержащим точки P и Q.

Мы можем определить линию параметрически: $п\; =\; T\; +\; \alpha \; v\; \{\backslash \; displaystyle\; p\; =\; t\; +\; \backslash \; alpha\; \backslash \; v\}$, где $p\; \{\backslash \; displaystyle\; p\}$и $t\; \{\backslash \; displaystyle\; t\}$- гибкое положение для точек P и T, а $v\; \{\backslash \; displaystyle\; v\}$- вектор направления для линии.

Тогда

$B\; \wedge \; (p\; -\; q)\; =\; 0\; \{\backslash \; displaystyle\; B\; \backslash \; wedge\; (pq)\; =\; 0\}$и $B\; \wedge \; (t\; +\; \alpha \; v\; -\; q)\; Знак\; равно\; 0\; \{\backslash \; Displaystyle\; B\; \backslash \; клин\; (t\; +\; \backslash \; alpha\; vq)\; =\; 0\}$

, поэтому

$\alpha \; =\; B\; \wedge \; (q\; -\; t)\; B\; \wedge \; v\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; \{\backslash \; frac\; \{\; B\; \backslash \; wedge\; (qt)\}\; \{B\; \backslash \; wedge\; v\}\}\}$

и

$p\; =\; t\; +\; (B\; \wedge \; (q\; -\; t)\; B\; \wedge \; v)\; v.\; \{\backslash \; Displaystyle\; p\; =\; t\; +\; \backslash \; left\; (\; \{\backslash \; frac\; \{B\; \backslash \; wedge\; (qt)\}\; \{\backslash \; wedge\; v\}\}\; \backslash \; right)\; v.\}$

Вращающиеся системы

Математическое описание вращательных сил таких как крутящий момент и угловой момент часто использовать произведение из исчисления в трех измерениях с условием ориентации (ручная).

Перекрестное произведение по отношению к внешнему продукту. Красным цветом обозначены единичный вектор нормали и «параллельный» единичный бивектор.

Перекрестное рассмотрение можно рассматривать с точки зрения внешнего вида, что позволяет более естественную геометрическую интерпретацию системы как бивектора с использованием двойного элемента отношение

$a\; \times \; b\; =\; -\; I\; (a\; \wedge \; b).\; \{\backslash \; displaystyle\; a\; \backslash \; times\; b\; =\; -I\; (a\; \backslash \; wedge\; b).\}$

Обычно крутящий момент определяется как величина перпендикулярной составляющей силы, умноженная на расстояние, или работа на единицу угла.

Предположим, что круговой путь в произвольной плоскости, произведенный ортонормированные стандарты $u\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{u\}\}\}$и $v\; ^\; \{\backslash \; displaystyle\; \{\; \backslash \; \backslash \; hat\; \{v\}\}\}$параметризуется углом.

$р\; знак\; равно\; г\; (и\; ^\; соз\; \; \theta \; +\; v\; ^\; грех\; \; \theta )\; =\; ru\; ^\; (соз\; \; \theta \; +\; и\; ^\; v\; ^\; грех\; \; \theta )\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{г\}\; =\; г\; (\{\backslash \; шляпа\; \{u\}\}\; \backslash \; cos\; \backslash \; theta\; +\; \{\backslash \; hat\; \{v\}\}\; \backslash \; sin\; \backslash \; theta)\; =\; r\; \{\backslash \; hat\; \{u\}\}\; (\backslash \; cos\; \backslash \; theta\; +\; \{\backslash \; hat\; \{u\}\}\; \{\backslash \; hat\; \{v\}\}\; \backslash \; sin\; \backslash \; theta)\}$

Обозначив единичный бивектор этой плоскости мнимым числом.

$я\; =\; u\; ^\; v\; ^\; =\; u\; ^\; \wedge \; v\; ^\; \{\backslash \; displaystyle\; \{i\}\; =\; \{\backslash \; hat\; \{u\}\}\; \{\backslash \; hat\; \{v\}\}\; =\; \{\backslash \; hat\; \{u\}\}\; \backslash \; wedge\; \{\backslash \; hat\; \{\; v\}\}\}$

$i\; 2\; =\; -\; 1\; \{\backslash \; displaystyle\; i\; ^\; \{2\}\; =\; -\; 1\}$

этот вектор пути удобно записать в комплексной экспоненциальной форме

$r\; =\; ru\; ^\; ei\; \theta \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{r\}\; =\; r\; \{\backslash \; hat\; \{u\}\}\; e\; ^\; \{i\; \backslash \; theta\}\}$

и производной по части составляет

$drd\; \theta \; =\; ru\; ^\; iei\; \theta \; =\; ri.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{r\}\}\; \{d\; \backslash \; theta\}\}\; =\; r\; \{\backslash \; hat\; \{u\}\}\; т.е.\; ^\; \{i\; \backslash \; theta\}\; =\; \backslash \; mathbf\; \{r\}\; i.\}$

Итак, крутящий момент, скорость изменения работы $W\; \{\backslash \; displaystyle\; W\}$из-за силы $F\; \{\; \backslash \; displaystyle\; F\}$, составляет

$\tau \; =\; d\; W\; d\; \theta \; =\; F\; \cdot \; drd\; \theta \; =\; F\; \cdot \; (ri).\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; \{\backslash \; frac\; \{dW\}\; \{d\; \backslash \; theta\}\}\; =\; F\; \backslash \; cdot\; \{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; theta\}\}\; =\; F\; \backslash \; cdot\; (\backslash \; mathbf\; \{r\}\; i).\}$

В отличие от описания перекрестного произведения крутящего момента, $\tau \; =\; r\; \times \; F\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; \backslash \; mathbf\; \{r\}\; \backslash \; times\; F\}$, описание геометрической алгебры не вводит вектор в нормальное направление; вектор, который не существует в двух измерениях и не уникален в более чем трех измерениях. Единичный бивектор описывает плоскость и ориентацию вращения, а направление вращения определяется углом между векторами $u\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{u\}\}\}$и $v\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{v\}\}\}$.

Геометрическое исчисление расширяет формализм, включая дифференцирование и интегрирование, включая дифференциальную геометрию и дифференциальные формы.

По существу, производная вектора определяется так, чтобы версия теоремы Грина была верна,

$\int \; A\; d\; A\; \nabla \; f\; =\; \oint \; \partial \; A\; dxf\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{A\}\; dA\; \backslash ,\; \backslash \; набла\; f\; =\; \backslash \; oint\; \_\; \{\backslash \; partial\; A\}\; dx\; \backslash ,\; f\}$

, а затем можно написать

$\nabla \; f\; =\; \nabla \; \cdot \; f\; +\; \nabla \; \wedge \; f\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\; =\; \backslash \; nabla\; \backslash \; cdot\; f\; +\; \backslash \; nabla\; \backslash \; wedge\; f\}$

как геометрическое произведение, эффективно обобщающее теорему Стокса (включая ее версию в дифференциальной форме).

В $1\; D\; \{\backslash \; displaystyle\; 1D\}$, когда $A\; \{\backslash \; displaystyle\; A\}$- это кривая с конечными точками $a\; \{\backslash \; displaystyle\; a\}$и $b\; \{\backslash \; displaystyle\; b\}$, затем

$\int \; A\; d\; A\; \nabla \; f\; =\; \oint \; \partial \; A\; dxf\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{A\}\; dA\; \backslash ,\; \backslash \; nabla\; f\; =\; \backslash \; oint\; \_\; \{\backslash \; partial\; A\}\; dx\; \backslash ,\; f\}$

сводится к

$\int \; abdx\; \nabla \; f\; =\; \int \; abdx\; \cdot \; \nabla \; f\; =\; \int \; abdf\; =\; f\; (b)\; -\; f\; (a)\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; dx\; \backslash ,\; \backslash \; nabla\; f\; =\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; dx\; \backslash \; cdot\; \backslash \; nabla\; f\; =\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; df\; =\; f\; (b)\; -f\; (a)\}$

или основная теорема интегрального исчисления.

Также развиты концепция векторного многообразия и геометрическая теория интегрирования (которая обобщает дифференциальные формы).

До 20 века

Хотя связь геометрии с алгеброй восходит, по крайней мере, к Евклиду Элементам в третьем век до нашей эры (см. греческая геометрическая алгебра ), GA в том смысле, в каком она используется в этой статье, не была разработана до 1844 года, когда она использовалась систематически для описания геометрических свойств и преобразований пространства. В том году Герман Грассман представил идею геометрической алгебры в полной общности как некоего исчисления (аналогичного исчислению высказываний ), которое закодировало всю геометрическую информацию о пространстве. Алгебраическая система Грассмана могла быть применена к множеству различных видов пространств, главным из которых является евклидово пространство, аффинное пространство и проективное пространство. Вслед за Грассманом в 1878 г. Уильям Кингдон Клиффорд исследовал алгебраическую систему Грассмана вместе с кватернионами из Уильям Роуэн Гамильтон в (Клиффорд 1878) harv error : нет цели: CITEREFClifford1878 (справка ). С его точки зрения, кватернионы описывали определенные преобразования (которые он назвал роторами), тогда как алгебра Грассмана описывала определенные свойства (или Strecken, такие как длина, площадь и объем). Его вклад состоял в том, чтобы определить новый продукт - геометрический продукт - на существующей алгебре Грассмана, в которой кватернионы были реализованы как живущие в этой алгебре. Впоследствии Рудольф Липшиц в 1886 г. обобщил интерпретацию Клиффорда кватернионов и применил их к геометрии вращения в измерениях $n\; \{\backslash \; displaystyle\; n\}$. Позже эти разработки привели других математиков 20-го века к формализации и исследованию свойств алгебры Клиффорда.

Тем не менее, другое революционное развитие 19-го века полностью затмило геометрические алгебры: метод векторного анализа, независимо разработанный Джозайей Уиллардом Гиббсом и Оливер Хевисайд. Векторный анализ был мотивирован исследованиями Джеймса Клерка Максвелла по электромагнетизму и, в частности, необходимостью удобно выражать и манипулировать некоторыми дифференциальными уравнениями. Векторный анализ имел некоторую интуитивную привлекательность по сравнению со строгостью новых алгебр. И физики, и математики с готовностью приняли его в качестве своего предпочтительного геометрического инструментария, особенно после выхода влиятельного учебника 1901 года Векторный анализ автора Эдвина Бидвелла Уилсона после лекций Гиббса.

Более подробно, было три подхода к геометрической алгебре: кватернионный анализ, инициированный Гамильтоном в 1843 году и геометризованный как роторы Клиффордом в 1878 году; геометрическая алгебра, начатая Грассманом в 1844 году; и шаблонов, основанных на кватернионном анализе в конце 19 века Гиббсом и Хевисайдом. Наследие кватернионного анализа в векторном анализе можно увидеть в использовании $i\; \{\backslash \; displaystyle\; i\}$, $j\; \{\backslash \; displaystyle\; j\}$, $k\; \{\backslash \; displaystyle\; k\}$для обозначения базисных видов $R\; 3\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\; ^\; \{3\}\}$: они исследуются как чисто мнимые кватернионы. С точки зрения геометрической алгебры, четная подалгебра алгебры пространства-времени изоморфна GA трехмерного евклидова пространства, а кватернионы изоморфны четной подалгебре трехмерного евклидова пространства GA, что объединяет три подхода.

XX век и настоящее время

Прогресс в изучении алгебр Клиффорда в двадцатом веке незаметно продвинулся вперед, хотя в степени благодаря работе абстрактных алгебраистов, таких как Герман Вейль и Клод Шевалле. Геометрический подход к геометрическим алгебрам пережил ряд возрождений в 20-м веке. В математике в «Геометрической алгебре» Эмиля Артина обсуждается алгебра, рассматриваемая с каждой из связок геометрии, включая аффинную геометрию, проективную геометрию, симплектическую геометрию и ортогональная геометрия. В физике геометрические алгебры были созданы «новые» методы изучения классической механики и электромагнетизма вместе с более продвинутыми темами, такими как квантовая механика и калибровочная теория. Дэ Хестенес переосмыслил Паули и матрицы Дирака как конструкция в обычном пространстве и пространстве-времени, соответственно и были современными методами использования геометрической алгебры.

В компьютерной графике и робототехнике геометрические алгебры были возрождены, чтобы эффективно отображать вращения и другие преобразования. По вопросам применения ГА в робототехнике (теория винта, кинематика и динамика с использованием версоров), компьютерном зрении, управлении и нейронных вычислениях (геометрическое обучение) см. Байро (2010).

GA - это очень прикладная тема. С этим довольно крутая начальная кривая обучения, но ее можно несколько облегчить, используя соответствующее программное обеспечение. Ниже приведен список свободно доступного программного обеспечения, которое не требует владения коммерческими продуктами или каких-либо коммерческих продуктов для этой цели:

Активно разработаны проекты с открытым исходным кодом

• clifford - Модуль числовой геометрической алгебры для Python.
• galgebra - Модуль символьной геометрической алгебры для Python от Алана Бромборски (использует sympy).
• GATL - Библиотека шаблонов C ++, использующая стратегию ленивого вычисления для автоматически выполнять низкоуровневые алгебраические операции во время компиляции для создания более эффективных программ.
• ganja.js - Геометрическая алгебра для Javascript (с перегрузкой операторов и алгебраическими литералами)
• klein - Производство-ориентированная SSE-оптимизированная библиотека C ++, специализирующаяся на трехмерной проективной геометрической алгебре ($P\; (R\; 3,\; 0,\; 1\; \ast )\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{P\}\; (\backslash \; mathbb\; \{R\}\; \_\; \{3,0,1\}\; ^\; \{*\})\}$)
• Versor, облегченная шаблонная библиотека C ++ с интерфейсом OpenGL для эффективной программы геометрической алгебры поиск в произвольных метриках, включая конформный
• Grassmann.jl - алгебра конформного геометрического произведения на основе статических двойных мультивекторов с градуированной алгебры (написано на языке Julia)

Другие проекты

• GA Viewer Fontijne, Dorst, Bouma Mann
• GAwxM GitHub - GA с использованием wxMaxima, программного обеспечения с открытым исходным кодом, использующего бесплатную систему компьютерной алгебры, включает файлы readme для мотивации и настройки.
• CLUViz Perwass

Программное обеспечение, позволяющее создавать сценарии, включая образцы визуализаций, руководство и введение в GA.

• Gaigen Fontijne

Для программистов это генератор кода с поддержкой C, C ++, C # и Java.

• Cinderella Visualizations Hitzer и Dorst.
• Gaalop [1] Автономное приложение с графическим интерфейсом пользователя, использующее программное обеспечение компьютерной алгебры с открытым исходным кодом Maxima для разбиения кода CLUViz на код C / C ++ или Java.
• Прекомпилятор Gaalop [2] Прекомпилятор на основе Gaalop, интегрированный с CMake.
• Gaalet, Библиотека шаблонов выражений C ++ Сейболд.
• Алгебра Клиффорда с Mathematica clifford.m
• Алгебра Клиффорда со встроенными классами GiNaC

Тестовый проект

• ga-benchmark - Тест для библиотек геометрической алгебры C / C ++ и генераторов библиотек. Последние результаты ga-benchmark можно найти здесь.

• Сравнение векторной алгебры и геометрической алгебры
• Алгебра Клиффорда
• Алгебра Грассмана - Кэли
• Алгебра пространства-времени
• Spinor
• Quaternion
• Алгебра физического пространства
• Универсальная геометрическая алгебра

В хронологическом порядке

• Grassmann, Hermann (1844), Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik : dargestellt und durch Anwendungen auf die übrigen Zweige der Mathematik, wie auch auf die Statik, Mechanik, die Lehre vom Magnetonomtomus 69, Лейпциг: О. Виганд, OCLC 20521674
• Артин, Эмиль (1988) [1957], Геометрическая алгебра, Wiley Classics Library, Wiley, doi : 10.1002 / 9781118164518, ISBN 978-0-471-60839-4, MR 1009557
• Гестен, Дэвид (1966), Пространственно-временная алгебра, Гордон и Брич, ISBN 978-0-677-01390-9, OCLC 996371
• Уиллер, Дж. А.; Миснер, К.; Торн, К. С. (1973), Гравитация, W.H. Фриман, ISBN 978-0-7167-0344-0
• Бурбаки, Николас (1980), "Глава 9" Альжебр-де-Клиффорд "", Eléments de Mathématique. Альгебре, Германн, ISBN 9782225655166
• Гестенес, Дэвид ; Собчик, Гаррет (1984), От алгебры Клиффорда до геометрического исчисления, унифицированного языка математики и физики, Springer, Нидерланды, ISBN 9789027716736
• Hestenes, David (1986), J.S.R. Чисхолм; А.К. Коммонс (ред.), «Унифицированный язык математики и физики», Алгебры Клиффорда и их приложения в математической физике, Серия ASI НАТО (серия C), Springer, 183 : 1–23, doi : 10.1007 / 978-94-009-4728-3_1, ISBN 978-94-009-4728-3
• Доран, Крис JL (1994), Геометрическая алгебра и ее применение в математической физике (докторская диссертация), Кембриджский университет, doi : 10.17863 / CAM.16148, hdl : 1810/251691, OCLC 53604228
• Бейлис, WE, изд. (2011) [1996], Клиффордская (геометрическая) алгебра с приложениями к физике, математике и инженерии, Биркхойзер, ISBN 9781461241058
• Арагон, Г.; Арагон, J.L.; Родригес, Массачусетс (1997), «Алгебры Клиффорда и геометрическая алгебра», Успехи в прикладных алгебрах Клиффорда, 7 (2): 91–102, doi : 10.1007 / BF03041220, S2CID 120860757
• Hestenes, David (1999), Новые основы классической механики (2-е изд.), Springer Verlag, ISBN 978-0-7923-5302-7
• Ласенби, Джоан; Ласенби, Энтони Н.; Доран, Крис Дж. Л. (2000), «Единый математический язык для физики и инженерии в 21 веке» (PDF), Философские труды Королевского общества A, 358 (1765): 21–39, Bibcode : 2000RSPTA.358... 21L, doi : 10.1098 / rsta.2000.0517, S2CID 91884543
• Baylis, WE (2002), Electrodynamics: A Modern Geometric Approach (2nd ed.), Birkhäuser, ISBN 978 -0-8176-4025-5
• Дорст, Лео (2002), «Внутренние произведения геометрической алгебры», в Дорст, Л.; Доран, К.; Lasenby, J. (eds.), Applications of Geometric Algebra in Computer Science and Engineering, Birkhäuser, pp. 35–46, doi : 10.1007 / 978-1- 4612-0089-5_2, ISBN 978-1-4612-0089-5
• Доран, Крис Дж. Л. ; Ласенби, Энтони Н. (2003), Геометрическая алгебра для физиков (PDF), Cambridge University Press, ISBN 978-0-521-71595-9
• Hestenes, Дэвид (2003), «Лекция, посвященная медали Эрстеда, 2002 год: реформа математического языка физики» (PDF), Am. J. Phys., 71 (2): 104–121, Bibcode : 2003AmJPh..71..104H, CiteSeerX 10.1.1.649.7506, doi : 10.1119 / 1.1522700
• Хильденбранд, Дитмар; Фонтийне, Даниэль; Первасс, Кристиан; Дорст, Лео (2004), «Геометрическая алгебра и ее применение в компьютерной графике» (PDF), Proceedings of Eurographics 2004, doi : 10.2312 / egt.20041032
• Бейн, Дж. (2006), «Структура пространства-времени: §5 Многообразия против геометрической алгебры», в Деннис Дикс (редактор), Онтология пространства-времени, Elsevier, стр.. 54 и далее, ISBN 978-0-444-52768-4
• Дорст, Лео; Фонтийне, Даниэль; Манн, Стивен (2007), Геометрическая алгебра для информатики: объектно-ориентированный подход к геометрии, Elsevier, ISBN 978-0-12-369465-2, OCLC 132691969
• Пенроуз, Роджер (2007), Дорога к реальности, Винтажные книги, ISBN 978-0 -679-77631-4
• Фрэнсис, Мэтью Р.; Косовский, Артур (2008), «Построение спиноров в геометрической алгебре», Annals of Physics, 317 (2): 383–409, arXiv : math-ph / 0403040v2, Bibcode : 2005AnPhy.317..383F, doi : 10.1016 / j.aop. 2004.11.008, S2CID 119632876
• Ли, Хунбо (2008), Инвариантные алгебры и геометрическое мышление, World Scientific, ISBN 9789812770110. Глава 1 в формате PDF
• Винс, Джон А. (2008), Геометрическая алгебра для компьютерной графики, Springer, ISBN 978-1-84628-996-5
• Лундхольм, Дуглас; Свенссон, Ларс (2009), «Алгебра Клиффорда, геометрическая алгебра и приложения», arXiv : 0907.5356v1 [math-ph ]
• Perwass, Christian (2009), Геометрическая алгебра с приложениями в инженерии, геометрии и вычислении, 4, Springer Science Business Media, Bibcode : 2009gaae.book..... P, doi : 10.1007 / 978-3-540-89068-3, ISBN 978-3-540-89068-3
• Байро-Коррочано, Эдуардо (2010), Геометрические вычисления для вейвлет-преобразований, зрение, обучение, управление и действие, Springer Verlag, ISBN 9781848829299
• Байро-Коррочано, Э.; Scheuermann, Gerik, ред. (2010), Вычисления геометрической алгебры в технике и информатике, Springer, ISBN 9781849961080 Извлечение онлайн по адресу http: //geocalc.clas.asu.edu / html / UAFCG.html # 5 Новые инструменты для вычислительной геометрии и обновления теории винта
• Рон Гольдман (2010), Переосмысление кватернионов: теория и вычисления, Морган и Клейпул, часть III. Переосмысление кватернионов и алгебр Клиффорда, ISBN 978-1-60845-420-4
• Дорст, Лео.; Ласенби, Джоан (2011), Практическое руководство по геометрической алгебре, Springer, ISBN 9780857298119
• Макдональд, Алан (2011), линейная и геометрическая алгебра, CreateSpace, ISBN 9781453854938, OCLC 704377582
• Снигг, Джон (2011), Новый подход к дифференциальной геометрии с использованием геометрической алгебры Клиффорда, Спрингер, ISBN 978-0-8176-8282-8
• Хильденбранд, Дитмар (2013), Основы вычислений геометрической алгебры, Материалы конференции AIP, 1479, стр. 27–30, Bibcode : 2012AIPC.1479... 27H, CiteSeerX 10.1.1.364.9400, doi : 10.1063 / 1.4756054, ISBN 978-3-642-31793-4
• Бромборский, Алан (2014), Введение в геометрическую алгебру и (PDF)
• Клавиттер, Дэниел (2014), Алгебры Клиффорда: геометрическое моделирование и цепная геометрия с применением в кинематике, Springer, ISBN 9783658076184
• Канатани, Кеничи ( 20 15), Понимание геометрической алгебры: Гамильтон, Грассманн и Клиффорд для компьютерного зрения и графики, CRC Press, ISBN 9781482259513
• Ли, Хунбо; Хуанг, Лэй; Шао, Чанпэн; Донг, Лэй (2015), «Трехмерная проективная геометрия с геометрической алгеброй», arXiv : 1507.06634v1 [math.MG ]
• Hestenes, David (11 апреля 2016). «Генезис геометрической алгебры: личная ретроспектива». Успехи в прикладной алгебре Клиффорда. 27 (1): 351–379. DOI : 10.1007 / s00006-016-0664-z. S2CID 124014198. CS1 maint: ref = harv (ссылка )
• Дорст, Лео (2016), 3D-ориентированная проективная геометрия через версию $R\; 3,\; 3\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\; ^\; \{3,\; 3\}\}$, Springer, ISBN 9783658076184
• Vaz, Jayme; da Rocha, Roldão (2016), Введение в алгебры Клиффорда и спиноры, ISBN 978-0-19-878292-6
• Рамирес, Серхио Рамос; Гонсалес, Хосе Альфонсо Хуарес; Собчик, Гаррет (2018), «От векторов к геометрической алгебре», arXiv : 1802.08153v1 [math.GM ]
• Байро-Коррочано, Эдуардо (2018). Компьютерное зрение, Графика и нейрокомпьютеры. Приложения геометрической алгебры. I . Springer. ISBN 978-3-319-74830-6.
• Lavor, Carlile; Xambó-Descamps, Sebastià; Zaplana, Isiah (2018). Приглашение геометрической алгебры к изучению физики пространства-времени, робототехники и молекулярной геометрии. Springer. Стр. 1–. ISBN 978-3-319-90665-2.

Вики учебники книга на тему: Физика на языке геометрической алгебры. Подход с помощью алгебры физического пространства

Викиверситет имеет учебные ресурсы по изучению геометрической геометрической алгебры

• Обзор геометрической алгебры и геометрическому исчислению Алан Макдональд, Лютер Колледж, Айова.
• Мнимые числа не реальности - геометрическая алгебра пространства-времени. Введение (Кембриджская группа GA).
• Геометрическая алгебра 2015, магистерский курс по научным вычислениям, от доктора Криса Дорана (Кембридж).
• Математика для программистов (игр): 5 - Мультивекторные методы. Всестороннее введение и справочные материалы для программистов из Иэна Белла.
• Летняя школа IMPA 2010 Введение и слайды Фернандеса Оливейры.
• Университет Фукуи E.S.M. Публикации Hitzer и Japan GA.
• Группа Google для GA
• Учебник по геометрической алгебре Введение в GA, Яап Сутер.
• Ресурсы по геометрической алгебре кураторская вики, Пабло Блейер.
• Прикладные геометрические алгебры in Computer Science and Engineering 2018 Early Proceedings

• GAME2020 Geometric Algebra Mini Event

Английские переводы ранних книг и статей

• G. Комбебиак, «Исчисление три-кватернионов» (докторская диссертация)
• М. Маркич, «Трансформанты: новый математический аппарат. Синтез трикватернионов Комбебиака и геометрической системы Грассмана. Исчисление квадрикватернионов »
• К. Бурали-Форти, «Метод Грассмана в проективной геометрии» Сборник из трех заметок по внешней алгебры к проективной геометрии
• C. Бурали-Форти, «Введение в дифференциальную геометрию по методу Х. Грассмана » Ранняя книга по применению алгебры Грассмана
• Х. Грассманн, «Механика в соответствии с принципами теории расширений» Одна из его статей о приложениях внешней алгебры.

Исследовательские группы

• Geometric Calculus International. Ссылки на исследовательские группы, программное обеспечение и конференции по всему миру.
• Кембриджская группа геометрической алгебры. Полнотекстовые онлайн-публикации и другие материалы.
• Группа Амстердамского университета
• Исследования и разработки по геометрическому исчислению (Университет штата Аризона).
• блог GA-Net и архив информационных бюллетеней. Геометрическая алгебра Новости развития алгебры Клиффорда.
• Геометрическая алгебра для системного восприятия и действия. Группа геометрической кибернетики (CINVESTAV, Campus Guadalajara, Мексика).