A вейвлет представляет собой волну -подобное колебание с амплитудой , который начинается с нуля, увеличивается, а затем снова уменьшается до нуля. Обычно это можно визуализировать как «кратковременное колебание», подобное тому, которое регистрируется сейсмографом или кардиомонитором. Как правило, вейвлеты намеренно создаются с особыми свойствами, которые делают их полезными для обработки сигналов. Используя свертку, вейвлеты можно комбинировать с известными частями поврежденного сигнала для извлечения информации из неизвестных частей.
 Сейсмический вейвлет
Сейсмический вейвлет Например, вейвлет может быть создан с частотой Средний C и короткой продолжительностью примерно 32-я нота. Если бы этот вейвлет был свернут с сигналом, созданным из записи песни, то полученный сигнал был бы полезен для определения того, когда в песне игралась средняя нота C. Математически вейвлет будет коррелировать с сигналом, если неизвестный сигнал содержит информацию аналогичной частоты. Эта концепция корреляции лежит в основе многих практических приложений теории всплесков.
В качестве математического инструмента вейвлеты могут использоваться для извлечения информации из многих различных типов данных, включая, помимо прочего, аудиосигналы и изображения. Наборы вейвлетов обычно необходимы для полного анализа данных. Набор «дополнительных» вейвлетов будет разлагать данные без пропусков или перекрытий, так что процесс разложения будет математически обратимым. Таким образом, наборы дополнительных вейвлетов полезны в алгоритмах сжатия / декомпрессии на основе вейвлетов , где желательно восстановить исходную информацию с минимальными потерями.
Формально это представление является вейвлет-серией представлением интегрируемой с квадратом функции относительно любой полной, ортонормированный набор базисных функций, или сверхполный набор или фрейм векторного пространства для гильбертова пространства квадратично интегрируемые функции. Это достигается с помощью когерентных состояний.
Слово вейвлет использовалось десятилетиями в области цифровой обработки сигналов и разведочной геофизики. Эквивалентное французское слово ondelette, означающее «маленькая волна», использовалось Морле и Гроссманном в начале 1980-х годов.
Теория вейвлетов применима к нескольким предметам. Все вейвлет-преобразования могут рассматриваться как формы частотно-временного представления для непрерывного времени (аналоговых) сигналов и, таким образом, связаны с гармоническим анализом. Дискретное вейвлет-преобразование (непрерывное во времени) сигнала с дискретным временем (дискретизированное) с использованием discrete-time наборов фильтров диадической (октавной полосы) конфигурации является вейвлет-приближение к этому сигналу. Коэффициенты такого банка фильтров называются вейвлет-коэффициентами и масштабными коэффициентами в номенклатуре вейвлетов. Эти наборы фильтров могут содержать либо фильтры с конечной импульсной характеристикой (FIR), либо фильтры с бесконечной импульсной характеристикой (IIR). Вейвлеты, образующие непрерывное вейвлет-преобразование (CWT), подчиняются принципу неопределенности соответствующей теории выборки анализа Фурье: учитывая сигнал с некоторым событием в нем, нельзя одновременно назначить точное шкала времени и частоты отклика на это событие. Произведение неопределенностей шкалы времени и частотной характеристики имеет нижнюю границу. Таким образом, на шкале шкалы непрерывного вейвлет-преобразования этого сигнала такое событие отмечает всю область на плоскости шкалы времени, а не только одну точку. Кроме того, дискретные вейвлет-основы можно рассматривать в контексте других форм принципа неопределенности.
Вейвлет-преобразования в целом делятся на три класса: непрерывные, дискретные и основанные на множественном разрешении.
В непрерывных вейвлет-преобразованиях заданный сигнал конечной энергии проецируется на непрерывное семейство полос частот (или аналогичные подпространства функционального пространства L L(R)). Например, сигнал может быть представлен на каждой полосе частот в виде [f, 2f] для всех положительных частот f>0. Затем исходный сигнал может быть восстановлен путем подходящего интегрирования по всем результирующим частотным компонентам.
Полосы частот или подпространства (подполосы) являются масштабированными версиями подпространства в масштабе 1. Это подпространство, в свою очередь, в большинстве ситуаций генерируется сдвигами одной производящей функции ψ в L (R ), материнский вейвлет. Для примера масштабирования одной полосы частот [1, 2] эта функция равна

с (нормализованной) функцией sinc. Это, Мейер и два других примера материнских вейвлетов:
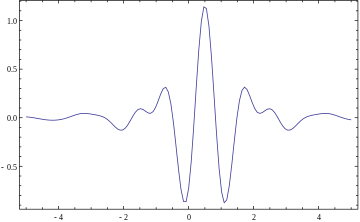 Мейер Мейер |
 Морле Морле |
 Мексиканская шляпа Мексиканская шляпа |
Подпространство шкалы a или полосы частот [1 / a, 2 / a] генерируется функции (иногда называемые дочерними вейвлетами)

где a положительно и определяет масштаб, а b - любое действительное число и определяет сдвиг. Пара (a, b) определяет точку в правой полуплоскости R+× R.
Тогда проекция функции x на подпространство масштаба a имеет вид

с вейвлет-коэффициентами

Для анализа сигнала x можно собрать вейвлет-коэффициенты в скейлограмму сигнала.
См. Список некоторых Непрерывных вейвлетов.
Вычислительно невозможно проанализировать сигнал с использованием всех вейвлетов. коэффициентов, так что можно задаться вопросом, достаточно ли выбрать дискретное подмножество верхней полуплоскости, чтобы иметь возможность восстановить сигнал из соответствующих вейвлет-коэффициентов. Одной из таких систем является аффинная система для некоторых реальных параметров a>1, b>0. Соответствующее дискретное подмножество полуплоскости состоит из всех точек (a, nab) с m, n в Z . Соответствующие дочерние вейвлеты теперь задаются как

Достаточное условие для восстановления любого сигнала x конечной энергии по формуле

заключается в том, что функции 
 Вейвлет D4
Вейвлет D4 В любом дискретизированном вейвлет-преобразовании существует только конечное число вейвлет-коэффициентов для каждой ограниченной прямоугольной области в верхней полуплоскости. Тем не менее, каждый коэффициент требует вычисления интеграла. В особых ситуациях этой числовой сложности можно избежать, если масштабированные и сдвинутые вейвлеты образуют анализ с множественным разрешением. Это означает, что должна существовать вспомогательная функция, отцовский вейвлет φ в L (R ), и что a является целым числом. Типичный выбор - a = 2 и b = 1. Самая известная пара вейвлетов отца и матери - это вейвлет Добеши с 4 отводами. Обратите внимание, что не каждый ортонормированный дискретный вейвлет-базис может быть связан с анализом с множественным разрешением; например, вейвлет Журна не допускает анализа с кратным разрешением.
Из вейвлетов от матери и отца строятся подпространства


Отцовский вейвлет 

Из них требуется, чтобы последовательность

формирует анализ с множественным разрешением L и что подпространства 

По аналогии с теоремой выборки можно сделать вывод, что пространство V m с расстоянием дискретизации 2 более или менее покрывает полосу частот модулирующих сигналов от 0 до 2. В качестве ортогонального дополнения W m примерно покрывает полосу частот [2, 2].
Из этих включений и соотношений ортогональности, особенно 


 так, чтобы
так, чтобы  и
и так, что
так, что 
Вторая идентичность первая пара - это уточняющее уравнение для отцовского вейвлета φ. Обе пары тождеств составляют основу алгоритма быстрого вейвлет-преобразования ..
Из анализа с множественным разрешением выводит ортогональное разложение пространства L как

Для любого сигнала или функции 

, где коэффициенты равны
 и
и .
.Для практических приложений и повышения эффективности r Поэтому в качестве материнского (прототипа) вейвлета (функций) предпочитают непрерывно дифференцируемые функции с компактной опорой. Однако для удовлетворения аналитических требований (в непрерывном WT) и в целом по теоретическим причинам вейвлет-функции выбираются из подпространства пространства 
 и
и 
Пребывание в этом пространстве гарантирует, что можно сформулировать условия нулевого среднего и квадратичной нормы один:
 - условие для нулевого среднего, а
- условие для нулевого среднего, а - условие для квадратичной нормы, равной единице.
- условие для квадратичной нормы, равной единице.Для того чтобы ψ было вейвлетом для непрерывного вейвлет-преобразования (см. Там для точного утверждения), материнский вейвлет должен удовлетворять критерию допустимости (грубо говоря, своего рода полудифференцируемости), чтобы чтобы получить стабильно обратимое преобразование.
Для дискретного вейвлет-преобразования необходимо, по крайней мере, условие, что серия вейвлетов является представлением идентичности в пространстве L(R). Большинство построений дискретного WT используют анализ с множественным разрешением, который определяет вейвлет с помощью функции масштабирования. Эта функция масштабирования сама по себе является решением функционального уравнения.
В большинстве ситуаций полезно ограничить ψ как непрерывную функцию с большим числом M исчезающих моментов, т.е. для всех целых m < M

Материнский вейвлет масштабируется (или расширяется) с коэффициентом из a и сдвинут (или сдвинут) в b раз, чтобы получить (согласно исходной формулировке Морле):

Для непрерывного WT, пара (a, b) изменяется во всей полуплоскости R+× R; для дискретного WT эта пара меняется на его дискретном подмножестве, которое также называется аффинной группой.
Эти функции часто ошибочно называют базовыми функциями (непрерывного) преобразования. Фактически, как и в случае непрерывного преобразования Фурье, в непрерывном вейвлет-преобразовании нет основы. Частотно-временная интерпретация использует несколько иную формулировку (по Дельпрату).
Ограничение :
(1) 
(2) 
Вейвлет-преобразование часто сравнивается с преобразованием Фурье, в котором сигналы представлены как сумма синусоид. Фактически, преобразование Фурье можно рассматривать как частный случай непрерывного вейвлет-преобразования с выбором материнского вейвлета 
В частности, предполагая прямоугольную область окна, можно думать о STFT как о преобразовании с немного другим ядром

где 



Отсюда квадрат временной опоры окна смещение по времени u определяется как

и квадрат спектральной опоры окна, действующего на частоте

Умножение с прямоугольным окном во временной области соответствует свертке с 


произведение времени и ширины ячейки с заданным разрешением не может быть превышено с помощью STFT. Все базовые элементы STFT поддерживают равномерную спектральную и временную поддержку всех временных сдвигов или смещений, тем самым достигая одинакового разрешения во времени для низких и высоких частот. Разрешение определяется исключительно шириной выборки.
Напротив, свойства множественного разрешения вейвлет-преобразования обеспечивают большую временную поддержку для более низких частот при сохранении короткой временной ширины для более высоких частот за счет свойств масштабирования вейвлет-преобразования. Это свойство расширяет традиционный частотно-временной анализ на анализ временной шкалы.
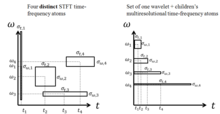 Атомы временной шкалы STFT (слева) и атомы временной шкалы DWT (справа). Атомы время-частота - это четыре различные базисные функции, используемые для STFT (т. Е., требуются четыре отдельных преобразования Фурье ). Атомы временной шкалы DWT достигают небольшой временной ширины для высоких частот и хорошей временной ширины для низких частот с базисным набором одиночного преобразования.
Атомы временной шкалы STFT (слева) и атомы временной шкалы DWT (справа). Атомы время-частота - это четыре различные базисные функции, используемые для STFT (т. Е., требуются четыре отдельных преобразования Фурье ). Атомы временной шкалы DWT достигают небольшой временной ширины для высоких частот и хорошей временной ширины для низких частот с базисным набором одиночного преобразования. Дискретное вейвлет-преобразование менее вычислительно сложное, что занимает O (N) время по сравнению с O (N log N) для быстрого преобразования Фурье. Это вычислительное преимущество не присуще преобразованию, но отражает выбор логарифмического деления частоты, в отличие от равномерного частотного деления БПФ (быстрое преобразование Фурье), которое использует те же базисные функции, что и ДПФ (дискретное преобразование Фурье).. Также важно отметить, что эта сложность применима только тогда, когда размер фильтра не имеет отношения к размеру сигнала. Вейвлет без компактной опоры, такой как вейвлет Шеннона, потребует O (N). (Например, логарифмическое преобразование Фурье также существует со сложностью O (N), но исходный сигнал должен быть дискретизирован логарифмически по времени, что полезно только для определенных типов сигналов.)
Существует несколько способов определения вейвлета (или семейства вейвлетов).
Ортогональный вейвлет полностью определяется масштабирующим фильтром - фильтром нижних частот с конечной импульсной характеристикой (FIR) длиной 2N и суммой 1. В биортогональные вейвлеты, отдельные фильтры разложения и восстановления.
Для анализа с ортогональными вейвлетами фильтр верхних частот вычисляется как квадратурный зеркальный фильтр нижних частот, а фильтры восстановления являются обратными по времени фильтрами разложения.
Вейвлеты Добеши и Симлета могут быть определены с помощью масштабирующего фильтра.
Вейвлеты определяются функцией вейвлета ψ (t) (т. Е. Материнским вейвлетом) и функцией масштабирования φ (t) (также называемой «исходным вейвлетом») во временной области.
Вейвлет-функция, по сути, является полосовым фильтром, масштабирование которого для каждого уровня уменьшает его полосу вдвое. Это создает проблему, заключающуюся в том, что для покрытия всего спектра потребуется бесконечное количество уровней. Функция масштабирования фильтрует самый низкий уровень преобразования и обеспечивает охват всего спектра. См. Подробное объяснение.
Для вейвлета с компактной опорой φ (t) может считаться конечной по длине и эквивалентен масштабному фильтру g.
Вейвлеты Мейера могут быть определены функциями масштабирования
Вейвлет имеет представление только во временной области как вейвлет-функция ψ (t).
Например, вейвлеты мексиканской шляпы могут быть определены с помощью вейвлет-функции. См. Список из нескольких непрерывных вейвлетов.
Развитие вейвлетов может быть связано с несколькими отдельными направлениями мысли, начиная с Хаара работы в начале 20 века. Более поздняя работа Денниса Габора дала атомы Габора (1946), которые построены аналогично вейвлетам и применяются для аналогичных целей.
Вейвлет-сжатие, форма кодирования с преобразованием, которая использует вейвлет-преобразования в сжатие данных, началось после разработки дискретного косинусное преобразование (DCT), блочный алгоритм сжатия данных, впервые предложенный Насиром Ахмедом в начале 1970-х годов. Введение DCT привело к развитию вейвлет-кодирования, варианта DCT-кодирования, в котором используются вейвлеты вместо блочного алгоритма DCT.
С тех пор значительный вклад в теорию вейвлетов можно отнести к Цвейгу Открытие непрерывного вейвлет-преобразования (CWT) в 1975 году (первоначально называвшееся кохлеарным преобразованием и обнаруженное при изучении реакции уха на звук), Пьер Гупийо, Гроссманн и формулировка Морле того, что сейчас известно как CWT (1982), ранняя работа Ян-Олова Стрёмберга по дискретным вейвлетам (1983), LeGall-Tabatabai (LGT) 5/3 вейвлет, разработанный Дидье Ле Галлом и Али Дж. Табатабаи (1988), Ингрид Добеши 'ортогональные вейвлеты с компактной опорой (1988), мультиразрешающая структура Маллата (1989), Биномиальный QMF Али Акансу (1990), частотно-временная интерпретация CWT Натали Дельпрат (1991), гармоническое вейвлет-преобразование Ньюленда (1993) и установить разделение в иерархических деревьях (SPIHT), разработанное Амиром Саидом и Уильямом А. Перлманом в 1996 году.
Стандарт JPEG 2000 был разработан с 1997 по 2000 год комитетом Joint Photographic Experts Group (JPEG) под председательством Тураджа Эбрахими (впоследствии президента JPEG). В отличие от алгоритма DCT, используемого в исходном формате JPEG, JPEG 2000 вместо этого использует алгоритмы дискретного вейвлет-преобразования (DWT). Он использует вейвлет-преобразование CDF 9/7 (разработанное Ингрид Добешис в 1992 г.) для своего алгоритма сжатия с потерями и вейвлет-преобразование ЛеГалла-Табатабаи (LGT) 5/3 (разработанное Дидье Ле Галл и Али Дж. Табатабаи в 1988 г.) за алгоритм сжатия без потерь. Была выбрана технология JPEG 2000, которая включает расширение Motion JPEG 2000 как стандарт кодирования видео для цифрового кино в 2004 году.
Вейвлет - это математическая функция, используемая для разделения заданной функции или сигнала непрерывного времени на различные компоненты масштаба. Обычно каждому компоненту шкалы можно присвоить частотный диапазон. Затем можно изучить каждый компонент шкалы с разрешением, которое соответствует его масштабу. Вейвлет-преобразование - это представление функции вейвлетами. Вейвлеты представляют собой масштабированные и преобразованные копии (известные как «дочерние вейвлеты») конечной длины или быстро затухающие осциллирующие волны (известные как «материнские вейвлеты»). Вейвлет-преобразования имеют преимущества по сравнению с традиционными преобразованиями Фурье для представления функций, которые имеют разрывы и острые пики, а также для точного деконструирования и восстановления конечных, не периодических и / или не- стационарных сигналы.
Вейвлет-преобразования подразделяются на дискретные вейвлет-преобразования (DWT) и непрерывные вейвлет-преобразования (CWT). Обратите внимание, что и DWT, и CWT - это непрерывные (аналоговые) преобразования. Их можно использовать для представления (аналоговых) сигналов с непрерывным временем. CWT работают со всеми возможными масштабами и перемещениями, тогда как DWT используют определенное подмножество значений масштаба и перемещения или сетку представления.
Существует большое количество вейвлет-преобразований, каждое из которых подходит для различных приложений. Полный список см. В списке преобразований, связанных с вейвлетами, но наиболее распространенные из них перечислены ниже:
Существует ряд обобщенных преобразований, из которых вейвлет-преобразование является особым кейс. Например, Йосеф Джозеф Сегман ввел масштаб в группу Гейзенберга, создав пространство непрерывного преобразования, которое является функцией времени, масштаба и частоты. CWT - это двухмерный срез полученного трехмерного объема в масштабе времени и частоте.
Другим примером обобщенного преобразования является преобразование chirplet, в котором CWT также является двумерным срезом через преобразование chirplet.
Важной областью применения обобщенных преобразований являются системы, в которых решающее значение имеет высокое разрешение по частоте. Например, темное поле электронно-оптические преобразования, промежуточные между прямым и обратным пространством, широко использовались в гармоническом анализе кластеризации атомов, т. Е. В исследовании кристаллы и дефекты кристаллов. Теперь, когда просвечивающие электронные микроскопы способны предоставлять цифровые изображения с пикометрической информацией об атомной периодичности в наноструктуре всех видов, в диапазоне распознавания образов и деформация / метрология приложений для промежуточных преобразований с высоким частотным разрешением (например, кистей и риджлетов) быстро растет.
Дробное вейвлет-преобразование (FRWT) - это обобщение классического вейвлет-преобразования в областях дробного преобразования Фурье. Это преобразование способно одновременно предоставлять информацию во временной и дробной областях и представлять сигналы в плоскости дробно-временной области.
Как правило, приближение к DWT является используется для сжатия данных, если сигнал уже дискретизирован, и CWT для анализа сигнала. Таким образом, приближение DWT обычно используется в инженерии и информатике, а CWT - в научных исследованиях.
Подобно некоторым другим преобразованиям, вейвлет-преобразования могут использоваться для преобразования данных, а затем кодирования преобразованных данных, что приводит к эффективному сжатию. Например, JPEG 2000 - это стандарт сжатия изображений, в котором используются биортогональные вейвлеты. Это означает, что, хотя кадр переполнен, это плотный кадр (см. Типы кадров векторного пространства ), и те же функции кадра (за исключением сопряжения в случае сложных вейвлетов) используются для как анализ, так и синтез, т. е. как в прямом, так и в обратном преобразовании. Подробнее см. вейвлет-сжатие.
Связанное использование - сглаживание / уменьшение шума данных на основе порогового значения вейвлет-коэффициента, также называемого вейвлет-сжатием. Путем адаптивного определения порога вейвлет-коэффициентов, которые соответствуют нежелательным частотным компонентам, могут выполняться операции сглаживания и / или удаления шума.
Вейвлет-преобразования также начинают использоваться для коммуникационных приложений. Вейвлет OFDM - это основная схема модуляции, используемая в HD-PLC (технология связи по линиям электропередач, разработанная Panasonic ), и в одном из дополнительных режимов, включенных в стандарт IEEE 1901. Вейвлет OFDM может достигать более глубоких отметок, чем традиционный FFT OFDM, а вейвлетный OFDM не требует защитного интервала (который обычно представляет собой значительные накладные расходы в системах FFT OFDM).
Часто сигналы могут быть хорошо представлены в виде суммы синусоид. Однако рассмотрите прерывистый сигнал с резким разрывом; этот сигнал все еще может быть представлен в виде суммы синусоид, но требует бесконечного числа, что является наблюдением, известным как феномен Гиббса. Таким образом, для этого требуется бесконечное количество коэффициентов Фурье, что непрактично для многих приложений, таких как сжатие. Вейвлеты более полезны для описания этих сигналов с разрывами из-за их локализованного во времени поведения (и преобразования Фурье, и вейвлет-преобразования локализованы по частоте, но вейвлеты обладают дополнительным свойством локализации во времени). Из-за этого на практике многие типы сигналов могут быть не разреженными в области Фурье, но очень разреженными в области вейвлетов. Это особенно полезно при восстановлении сигнала, особенно в недавно популярной области сжатого считывания. (Обратите внимание, что кратковременное преобразование Фурье (STFT) также локализовано по времени и частоте, но часто возникают проблемы с компромиссом частотно-временного разрешения. Вейвлеты лучше представляют сигнал из-за анализ с множественным разрешением.)
Это мотивирует то, почему вейвлет-преобразования теперь применяются для огромного числа приложений, часто заменяя обычное преобразование Фурье. Этот сдвиг парадигмы произошел во многих областях физики, включая молекулярную динамику, теорию хаоса, ab initio вычисления, астрофизику, гравитационная волна анализ переходных процессов, матрица плотности локализация, сейсмология, оптика, турбулентность и квантовая механика. Это изменение также произошло в обработке изображений, ЭЭГ, ЭМГ, анализах ЭКГ, ритмах мозга, ДНК анализ, анализ белков, климатология, анализ сексуальной реакции человека, общая обработка сигналов, распознавание речи, акустика, вибрационные сигналы, компьютерная графика, мультифрактальный анализ и разреженное кодирование. В компьютерном зрении и обработке изображений понятие представления масштабного пространства и операторов производной Гаусса рассматривается как каноническое многомасштабное представление.
Предположим, мы измеряем зашумленный сигнал 
Итак, 
Большинство элементов в p равны 0 или близки к 0, и
Поскольку W ортогонален, проблема оценки сводится к восстановлению сигнала в iid гауссовском шуме. Поскольку p является разреженным, одним из методов является применение модели смеси Гаусса для p.
Предположим априорную 


Тогда 



Маленькие коэффициенты в основном представляют собой шумы, а большие коэффициенты содержат фактический сигнал.
Наконец, примените обратное вейвлет-преобразование, чтобы получить
| Найдите wavelet в Викисловаре, бесплатном словаре. |
| Викискладе есть материалы, связанные с Wavelet. |