Юля набор

Набор Джулии Воспроизвести медиа Трехмерные срезы (четырехмерного) множества Джулиа функции на кватернионах

В контексте сложной динамики, в теме математики, то множество Жюлиа и множество Фату два взаимодополняющие набор (Julia «шнурки» и Фата «дусты»), определенные из функции. Неформально набор Фату функции состоит из значений со свойством, что все близлежащие значения ведут себя одинаково при повторной итерации функции, а набор Жюлиа состоит из таких значений, что сколь угодно малое возмущение может вызвать радикальные изменения в последовательности повторяемой функции. ценности. Таким образом, поведение функции на множестве Фату "регулярное", а на множестве Жюлиа - " хаотическое ".

Множество Жюлиа функции f обычно обозначается, а множество Фату обозначают. Эти множества названы в честь французских математиков Гастона Жюлиа и Пьера Фату, чьи работы положили начало изучению сложной динамики в начале 20 века. ${\ Displaystyle \; \ OperatorName {J} (е) \ ;,}$${\ Displaystyle \; \ OperatorName {F} (е) \ ;.}$

• 1 Формальное определение
• 2 Эквивалентные описания множества Джулия
• 3 Свойства множества Жюлиа и множества Фату
• 4 Примеры
• 5 Квадратичные многочлены
• 6 Обобщения
• 7 Псевдокод
  • 7.1 Псевдокод для нормальных множеств Жюлиа
  • 7.2 Псевдокод для множеств Жюлиа
• 8 Потенциальная функция и реальный номер итерации
• 9 Полевые линии
• 10 Построение множества Джулии
  • 10.1 Использование обратной (инверсной) итерации (IIM)
  • 10.2 Использование DEM / J
• 11 См. Также
• 12 Примечания
• 13 Ссылки
• 14 Библиография
• 15 Внешние ссылки

Пусть - непостоянная голоморфная функция из сферы Римана на себя. Такие функции - это в точности непостоянные комплексные рациональные функции, то есть где и являются комплексными многочленами. Предположим, что p и q не имеют общих корней и хотя бы одно из них имеет степень больше 1. Тогда существует конечное число открытых множеств, которые остаются инвариантными в силу и таковы, что: ${\ displaystyle f (z)}$ ${\ displaystyle f (z)}$ ${\ Displaystyle е (г) = п (г) / д (г)}$${\ displaystyle p (z)}$${\ Displaystyle д (г)}$ ${\ displaystyle F_ {1},..., F_ {r}}$${\ displaystyle f (z)}$

1. Объединение множеств плотно на плоскости и${\ displaystyle F_ {i}}$
2. ${\ displaystyle f (z)}$ведет себя равномерно и одинаково на каждом из наборов.${\ displaystyle F_ {i}}$

Последнее утверждение означает, что концы последовательностей итераций, порожденных точками, являются либо в точности одним и тем же множеством, которое в таком случае является конечным циклом, либо они являются конечными циклами множеств круговой или кольцевой формы, лежащих концентрически. В первом случае цикл притягивающий, во втором - нейтральный. ${\ displaystyle F_ {i}}$

Эти наборы являются доменами Фаты о, и их объединение Фата набор из. Каждая из областей Фату содержит, по меньшей мере, одну критическую точку из, то есть (конечная) точка г, удовлетворяющая, или если степень числителя по меньшей мере, два больше, чем степень знаменателя, или если по какой - то с и а рациональная функция, удовлетворяющая этому условию. ${\ displaystyle F_ {i}}$${\ displaystyle f (z)}$${\ displaystyle \ operatorname {F} (f)}$${\ displaystyle f (z)}$ ${\ displaystyle f (z)}$${\ displaystyle f '(z) = 0}$${\ Displaystyle е (г) = \ infty}$${\ displaystyle p (z)}$${\ Displaystyle д (г)}$${\ Displaystyle е (г) = 1 / г (г) + с}$${\ displaystyle g (z)}$

Дополнением является множество Жюлиа из. Если все критические точки предпериодические, то есть они не периодические, но в конечном итоге попадают в периодический цикл, то это вся сфера. В противном случае это нигде не плотное множество (без внутренних точек) и несчетное множество (той же мощности, что и действительные числа). Как, остается инвариантным, и на этом наборе итерация отталкивается, что означает, что для всех w в окрестности z (внутри). Это означает, что на множестве Жюлиа ведет себя хаотично. Хотя в множестве Жюлиа есть точки, последовательность итераций которых конечна, их только счетное число (и они составляют бесконечно малую часть множества Жюлиа). Последовательности, генерируемые точками вне этого набора, ведут себя хаотично - явление, называемое детерминированным хаосом. ${\ displaystyle \ operatorname {F} (f)}$${\ displaystyle \ operatorname {J} (f)}$${\ displaystyle f (z)}$${\ displaystyle \ operatorname {J} (f)}$${\ displaystyle \ operatorname {J} (f)}$ ${\ displaystyle \ operatorname {F} (f)}$${\ displaystyle \ operatorname {J} (f)}$${\ displaystyle f (z)}$${\ Displaystyle | е (г) -f (ш) |gt; | zw |}$${\ displaystyle \ operatorname {J} (f)}$${\ displaystyle f (z)}$

Были проведены обширные исследования множеств Фату и Джулиа повторяющихся рациональных функций, известных как рациональные отображения. Например, известно, что множество Фату рационального отображения имеет либо 0, 1, 2, либо бесконечно много компонентов. Каждый компонент множества Фату рациональной карты может быть отнесен к одному из четырех различных классов.

• ${\ Displaystyle \; \ OperatorName {J} (е) \;}$- наименьшее замкнутое множество, содержащее не менее трех точек, полностью инвариантное относительно f.
• ${\ Displaystyle \; \ OperatorName {J} (е) \;}$является замыканием множества отталкивающих периодических точек.
• Для всех точек, кроме двух, множество Джулиа является набором предельных точек полной обратной орбиты (это предлагает простой алгоритм построения множеств Джулиа, см. Ниже).${\ Displaystyle \; г \ в Х \ ;,}$${\ Displaystyle \ bigcup _ {п} е ^ {- п} (г) \ ;.}$
• Если f - целая функция, то это граница множества точек, сходящихся к бесконечности при итерации.${\ Displaystyle \; \ OperatorName {J} (е) \;}$
• Если f - многочлен, то граница заполненного множества Жюлиа ; то есть те точки, орбиты которых при итерациях f остаются ограниченными.${\ Displaystyle \; \ OperatorName {J} (е) \;}$

Множество Жюлиа и множество Фата из F является вполне инвариантны при итерациях голоморфных функций F:

${\ displaystyle f ^ {- 1} (\ operatorname {J} (f)) = f (\ operatorname {J} (f)) = \ operatorname {J} (f) ~,}$

${\ displaystyle f ^ {- 1} (\ operatorname {F} (f)) = f (\ operatorname {F} (f)) = \ operatorname {F} (f) ~.}$

Поскольку множество Жюлиа - это единичный круг, и на нем итерация задается удвоением углов (операция, которая хаотична в точках, аргумент которых не является рациональной долей). Есть две области Фату: внутренняя и внешняя части круга с итерацией к 0 и ∞ соответственно. ${\ Displaystyle \; е (г) = г ^ {2} \;}$${\ displaystyle 2 \ pi}$

Для множества Жюлиа это отрезок прямой между -2 и 2. Есть одна область Фату : точки, не лежащие на отрезке, повторяются в направлении ∞. (Помимо сдвига и масштабирования области, эта итерация эквивалентна единичному интервалу, который обычно используется в качестве примера хаотической системы.) ${\ Displaystyle \; г (г) = г ^ {2} -2 \;}$ ${\ Displaystyle \; х \ до 4 (х - {\ tfrac {\, 1 \,} {2}}) ^ {2} \;}$

Функции f и g имеют вид, где c - комплексное число. Для такой итерации множество Жюлиа, как правило, не простая кривая, а фрактал, и для некоторых значений c он может принимать удивительные формы. См. Картинки ниже. ${\ Displaystyle \; z ^ {2} + с \;}$

Множество Жюлиа (выделено белым) для рациональной функции, связанной с методом Ньютона для f  : z → z ³ −1. Окраска Фату задается в красный, зеленый и синий тона согласно трем аттракторам (трем корням f).

Для некоторых функций f ( z) можно заранее сказать, что множество Жюлиа является фракталом, а не простой кривой. Это из-за следующего результата на итерациях рациональной функции:

Теорема. Каждая из областей Фату имеет одну и ту же границу, которая, следовательно, является множеством Жюлиа.

Это означает, что каждая точка множества Жюлиа является точкой накопления для каждого из доменов Фату. Следовательно, если существует более двух областей Фату, каждая точка множества Жюлиа должна иметь точки более чем двух различных открытых множеств, бесконечно близких, и это означает, что множество Жюлиа не может быть простой кривой. Это явление происходит, например, когда f ( z) - итерация Ньютона для решения уравнения: ${\ Displaystyle \; P (z): = z ^ {n} -1 = 0 ~: ~ ngt; 2 \;}$

${\ displaystyle f (z) = z - {\ frac {P (z)} {P '(z)}} = {\ frac {\; 1+ (n-1) z ^ {n} \;} { nz ^ {n-1}}} ~.}$

На изображении справа показан случай n = 3.

Очень популярная сложная динамическая система дается семейством комплексных квадратичных многочленов, частным случаем рациональных отображений. Такие квадратичные многочлены могут быть выражены как

${\ displaystyle f_ {c} (z) = z ^ {2} + c ~,}$

где c - комплексный параметр. Зафиксируем некоторые достаточно большие, чтобы (например, если c находится в множестве Мандельброта, тогда мы можем просто разрешить) Тогда заполненное множество Жюлиа для этой системы является подмножеством комплексной плоскости, заданной формулой ${\ displaystyle Rgt; 0}$${\ Displaystyle R ^ {2} -R \ geq | c |.}$ ${\ displaystyle | c | \ leq 2,}$${\ Displaystyle R = 2 ~.}$

${\ Displaystyle К (f_ {c}) = \ left \ {z \ in \ mathbb {C}: \ forall n \ in \ mathbb {N}, | f_ {c} ^ {n} (z) | \ leq R \ right \} ~,}$

где есть п - й итерации из Жюлиа этой функции является границей. ${\ displaystyle f_ {c} ^ {n} (z)}$ ${\ displaystyle f_ {c} (z).}$${\ Displaystyle J (е_ {с})}$${\ Displaystyle К (е_ {с})}$

• 

  Жюлиа для где а находится в диапазоне от 0 до${\ displaystyle z ^ {2} +0.7885 \, e ^ {ia},}$${\ displaystyle 2 \ pi}$

• Воспроизвести медиа

  Видео с наборами Джулии, как осталось

• 

  Заполненный набор Джулии для f c, c = 1 - φ, где φ - золотое сечение

• 

  Множество Жюлиа для f c, c = ( φ - 2) + ( φ - 1) i = −0.4 + 0.6 i

• 

  Множество Жюли для f c, c = 0,285 + 0 i

• 

  Набор Джулии для f c, c = 0,285 + 0,01 i

• 

  Набор Джулии для f c, c = 0,45 + 0,1428 i

• 

  Множество Жюлиа для f c, c = −0,70176 - 0,3842 i

• 

  Множество Жюлиа для f c, c = −0,835 - 0,2321 i

• 

  Множество Жюлиа для f c, c = −0,8 + 0,156 i

• 

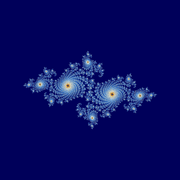
  Множество Жюлиа для f c, v c = −0,7269 + 0,1889 i

• 

  Множество Жюлиа для f c, c = −0,8 i

• 

  Коллекция наборов Julia размещена в сетке 100 × 100, так что центр каждого изображения соответствует той же позиции в комплексной плоскости, что и значение набора. При таком расположении изображение в целом напоминает фотографическую мозаику, изображающую набор Мандельброта.

Плоскость параметров квадратичных многочленов, то есть плоскость возможных значений c, дает начало знаменитому множеству Мандельброта. Действительно, множество Мандельброта определяется как множество всех с таким, что будет подключен. Для параметров вне множества Мандельброта множество Жюлиа является канторовым пространством : в этом случае его иногда называют пылью Фату. ${\ Displaystyle J (е_ {с})}$

Во многих случаях множество Жюлиа точки c выглядит как множество Мандельброта в достаточно малых окрестностях точки c. Это верно, в частности, для так называемых параметров Мисиуревича, т.е. параметров c, для которых критическая точка является предпериодической. Например:

• При c = i, более коротком переднем пальце передней части стопы, набор Julia выглядит как разветвленная молния.
• При c = −2, кончике длинного остроконечного хвоста, множество Джулиа представляет собой отрезок прямой линии.

Другими словами, множества Жюлиа локально подобны вокруг точек Мисюревича. ${\ Displaystyle J (е_ {с})}$

Определение множеств Жюлиа и Фату легко переносится на случай некоторых карт, изображение которых содержит их область определения; особенно трансцендентные мероморфные функции и карты конечного типа Адама Эпштейна.

Множества Жюлиа также обычно определяются при изучении динамики нескольких комплексных переменных.

Приведенные ниже реализации псевдокода жестко кодируют функции для каждого фрактала. Рассмотрите возможность реализации сложных числовых операций, чтобы обеспечить более динамичный и повторно используемый код.

Псевдокод для нормальных множеств Жюлиа

${\ Displaystyle е (г) = г ^ {2} + с}$

R = escape radius # choose R gt; 0 such that R**2 - R gt;= sqrt(cx**2 + cy**2) for each pixel (x, y) on the screen, do: { zx = scaled x coordinate of pixel # (scale to be between -R and R) # zx represents the real part of z. zy = scaled y coordinate of pixel # (scale to be between -R and R) # zy represents the imaginary part of z. iteration = 0 max_iteration = 1000 while (zx * zx + zy * zy lt; R**2 AND iteration lt; max_iteration) { xtemp = zx * zx - zy * zy zy = 2 * zx * zy + cy zx = xtemp + cx iteration = iteration + 1 } if (iteration == max_iteration) return black; else return iteration; }

Псевдокод для множеств Джулиа

${\ Displaystyle е (г) = г ^ {п} + с}$

R = escape radius # choose R gt; 0 such that R**n - R gt;= sqrt(cx**2 + cy**2) for each pixel (x, y) on the screen, do: { zx = scaled x coordinate of pixel # (scale to be between -R and R) zy = scaled y coordinate of pixel # (scale to be between -R and R) iteration = 0 max_iteration = 1000 while (zx * zx + zy * zy lt; R**2 AND iteration lt; max_iteration) { xtmp = (zx * zx + zy * zy) ^ (n / 2) * cos(n * atan2(zy, zx)) + cx; zy = (zx * zx + zy * zy) ^ (n / 2) * sin(n * atan2(zy, zx)) + cy; zx = xtmp; iteration = iteration + 1 } if (iteration == max_iteration) return black; else return iteration; }

Множество Жюлиа для представляет собой единичную окружность, а во внешней области Фату потенциальная функция φ ( z) определяется формулой φ ( z) = log | z |, Эквипотенциальные линии для этой функции представляют собой концентрические окружности. Как у нас ${\ Displaystyle е (г) = г ^ {2}}$ ${\ Displaystyle | е (г) | = | г | ^ {2}}$

${\ displaystyle \ varphi (z) = \ lim _ {k \ to \ infty} {\ frac {\ log | z_ {k} |} {2 ^ {k}}},}$

где - последовательность итераций, порожденная z. Для более общей итерации было доказано, что если множество Жюлиа связно (то есть, если c принадлежит (обычному) множеству Мандельброта), то существует биголоморфное отображение ψ между внешней областью Фату и внешней областью единичный круг такой, что. Это означает, что потенциальная функция на внешней области Фату, определяемая этим соответствием, задается следующим образом: ${\ displaystyle z_ {k}}$${\ Displaystyle е (г) = г ^ {2} + с}$ ${\ Displaystyle | \ psi (е (z)) | = | \ psi (z) | ^ {2}}$

${\ displaystyle \ varphi (z) = \ lim _ {k \ to \ infty} {\ frac {\ log | z_ {k} |} {2 ^ {k}}}.}$

Эта формула имеет смысл также, если множество Жюлиа не связано, так что мы для всех c можем определить потенциальную функцию в области Фату, содержащей ∞, по этой формуле. Для общей рациональной функции f ( z) такой, что ∞ является критической точкой и неподвижной точкой, то есть такой, что степень m числителя как минимум на два больше, чем степень n знаменателя, мы определяем потенциальную функцию в области Фату, содержащей ∞:

${\ displaystyle \ varphi (z) = \ lim _ {k \ to \ infty} {\ frac {\ log | z_ {k} |} {d ^ {k}}},}$

где d = m - n - степень рациональной функции.

Если N - очень большое число (например, 10 ¹⁰⁰), и если k - это номер первой итерации, такой, что мы имеем, что ${\ displaystyle | z_ {k} |gt; N}$

${\ displaystyle {\ frac {\ log | z_ {k} |} {d ^ {k}}} = {\ frac {\ log (N)} {d ^ {\ nu (z)}}},}$

для некоторого действительного числа, которое следует рассматривать как реальный номер итерации, и мы имеем это: ${\ Displaystyle \ ню (г)}$

${\ displaystyle \ nu (z) = k - {\ frac {\ log (\ log | z_ {k} | / \ log (N))} {\ log (d)}},}$

где последнее число находится в интервале [0, 1).

Для итерации в направлении конечного цикла притяжения порядка r мы имеем, что если - точка цикла, то ( r- кратная композиция) и число ${\ displaystyle z ^ {*}}$${\ Displaystyle е (е (... е (z ^ {*}))) = z ^ {*}}$

${\ Displaystyle \ альфа = {\ гидроразрыва {1} {\ left | (d (f (f (\ cdots f (z)))) / dz) _ {z = z ^ {*}} \ right |}} \ qquad (gt; 1)}$

является привлечение цикла. Если вес является точкой очень близко и ш 'является ш итерированными г раз, мы получаем, что ${\ displaystyle z ^ {*}}$

${\ displaystyle \ alpha = \ lim _ {k \ to \ infty} {\ frac {| wz ^ {*} |} {| w'-z ^ {*} |}}.}$

Следовательно, число почти не зависит от k. Определим потенциальную функцию в области Фату следующим образом: ${\ displaystyle | z_ {kr} -z ^ {*} | \ alpha ^ {k}}$

${\ displaystyle \ varphi (z) = \ lim _ {k \ to \ infty} {\ frac {1} {(| z_ {kr} -z ^ {*} | \ alpha ^ {k})}}.}$

Если ε - очень малое число, а k - номер первой итерации, такой, что мы имеем, что ${\ displaystyle | z_ {k} -z ^ {*} | lt;\ epsilon}$

${\ displaystyle \ varphi (z) = {\ frac {1} {(\ varepsilon \ alpha ^ {\ nu (z)})}}}$

для некоторого действительного числа, которое следует рассматривать как реальный номер итерации, и мы имеем это: ${\ Displaystyle \ ню (г)}$

${\ displaystyle \ nu (z) = k - {\ frac {\ log (\ varepsilon / | z_ {k} -z ^ {*} |)} {\ log (\ alpha)}}.}$

Если притяжение равно ∞, что означает, что цикл является сверхпритягивающим, что опять же означает, что одна из точек цикла является критической точкой, мы должны заменить α на

${\ displaystyle \ alpha = \ lim _ {k \ to \ infty} {\ frac {\ log | w'-z ^ {*} |} {\ log | wz ^ {*} |}},}$

где ш 'является ш итеративных г времен и формулы для ф ( г) с помощью:

${\ displaystyle \ varphi (z) = \ lim _ {k \ to \ infty} {\ frac {\ log (1 / | z_ {kr} -z ^ {*} |)} {\ alpha ^ {k}} }.}$

А теперь реальный номер итерации равен:

${\ displaystyle \ nu (z) = k - {\ frac {\ log (\ log | z_ {k} -z ^ {*} | / \ log (\ varepsilon))} {\ log (\ alpha)}}.}$

Для раскраски у нас должна быть циклическая шкала цветов (построенная математически, например) и содержащая H цветов, пронумерованных от 0 до H −1 (например, H = 500). Мы многократно реальное число фиксированного вещественного числа, определяющее плотность цвета в изображении, и взять на себя неотъемлемую часть этого числа по модулю H. ${\ Displaystyle \ ню (г)}$

Определение потенциальной функции и наш способ раскраски предполагают, что цикл является притягивающим, то есть не нейтральным. Если цикл нейтральный, мы не можем раскрасить домен Фату естественным образом. Поскольку конечной точкой итерации является вращающееся движение, мы можем, например, раскрасить по минимальному расстоянию от цикла, оставшемуся фиксированным на итерации.

Эквипотенциальные линии для итерации к бесконечности Строки поля для итерации формы ${\ displaystyle {\ frac {(1-z ^ {3} / 6)} {(zz ^ {2} / 2) ^ {2}}} + c}$

В каждой области Фату (которая не является нейтральной) есть две системы линий, ортогональных друг другу: эквипотенциальные линии (для потенциальной функции или действительного числа итераций) и силовые линии.

Если мы раскрашиваем область Fatou в соответствии с номером итерации (а не реальным номером итерации, как определено в предыдущем разделе), полосы итерации показывают ход эквипотенциальных линий. Если итерация стремится к ∞ (как в случае с внешней областью Фату для обычной итерации), мы можем легко показать ход линий поля, а именно, изменив цвет в соответствии с тем, как последняя точка в последовательности итераций находится выше или ниже оси x (первое изображение), но в этом случае (точнее: когда область Фату является сверхпритягивающей) мы не можем провести линии поля когерентно - по крайней мере, не с помощью метода, который мы описываем здесь. В этом случае силовая линия также называется внешним лучом. ${\ Displaystyle \ ню (г)}$${\ displaystyle z ^ {2} + c}$

Пусть z - точка в притягивающей области Фату. Если мы итерация Z большого числа раз, то конец последовательности итерации является конечным циклом С, а область Фата (по определению) множество точек последовательности итераций сходятся по отношению к которой C. Линии поля выдавать из точек С и из (бесконечного числа) указывает, что итерации в точке С. И они заканчиваются на множестве Жюлиа точками, которые не хаотичны (т. Е. Образуют конечный цикл). Пусть г есть порядок цикла C (его количество точек) и пусть быть точкой в C. У нас есть (r-кратная композиция), и мы определяем комплексное число α как ${\ displaystyle z ^ {*}}$${\ Displaystyle е (е (\ точки е (z ^ {*}))) = z ^ {*}}$

${\ Displaystyle \ альфа = (d (е (е (\ точки f (z)))) / dz) _ {z = z ^ {*}}.}$

Если точки C такие, α - произведение r чисел. Действительное число 1 / | α | является притяжением цикла, и наше предположение, что цикл не является ни нейтральным, ни сверхпритягивающим, означает, что 1 lt;${\ displaystyle z_ {i}, i = 1, \ dots, r (z_ {1} = z ^ {*})}$${\ displaystyle f '(z_ {i})}$ 1/| α |lt;∞. Точка является фиксированной точкой для, и около этой точки карта имеет (в связи с линиями поля) характер вращения с аргументом β от α (то есть). ${\ displaystyle z ^ {*}}$${\ Displaystyle е (е (\ точки f (z)))}$${\ Displaystyle е (е (\ точки f (z)))}$${\ Displaystyle \ альфа = | \ альфа | е ^ {\ бета я}}$

Чтобы раскрасить область Фату, мы выбрали небольшое число ε и установили последовательность итераций, чтобы они останавливались, когда, и мы раскрашиваем точку z в соответствии с числом k (или реальным номером итерации, если мы предпочитаем плавную раскраску). Если мы выберем направление из заданного углом θ, силовая линия, исходящая из этого направления, будет состоять из точек z, таких, что аргумент ψ числа удовлетворяет условию, что ${\ Displaystyle z_ {к} (к = 0,1,2, \ точки, z_ {0} = z)}$${\ displaystyle | z_ {k} -z ^ {*} | lt;\ epsilon}$${\ displaystyle z ^ {*}}$${\ displaystyle z ^ {*}}$${\ displaystyle z_ {k} -z ^ {*}}$

${\ Displaystyle \ psi -k \ beta = \ theta \ mod \ pi. \,}$

Поскольку, если мы проходим полосу итераций в направлении силовых линий (и от цикла), номер итерации k увеличивается на 1, а число ψ увеличивается на β, поэтому число остается постоянным вдоль силовой линии. ${\ displaystyle \ psi -k \ beta \ mod \ pi}$

Картинки в строках поля для итерации формы ${\ displaystyle z ^ {2} + c}$

Раскраска линий поля области Фату означает, что мы раскрашиваем промежутки между парами линий поля: мы выбираем ряд правильно расположенных направлений, исходящих из, и в каждом из этих направлений мы выбираем два направления вокруг этого направления. Поскольку может случиться так, что две линии поля пары не заканчиваются в одной и той же точке множества Жюлиа, наши цветные линии поля могут разветвляться (бесконечно) на своем пути к множеству Жюлиа. Мы можем раскрашивать, исходя из расстояния до центральной линии поля, и мы можем смешивать эту раскраску с обычной раскраской. Такие картины могут быть очень декоративными (второй рисунок). ${\ displaystyle z ^ {*}}$

Цветная линия поля (область между двумя линиями поля) разделена полосами итераций, и такая часть может быть поставлена ​​во взаимно однозначное соответствие с единичным квадратом: одна координата (вычисляется из) расстояния от одной из ограничивающих линий поля, другая - это (рассчитывается из) расстояния от внутренней из ограничивающих полос итераций (это число является нецелой частью реального номера итерации). Поэтому мы можем помещать картинки в линии поля (третье изображение).

Воспроизвести медиа Бинарное разложение интерьера в случае внутреннего угла 0

Методы:

• Метод оценки расстояния для множества Джулии (DEM / J)
• Обратный итерационный метод (IIM)

Использование обратной (обратной) итерации (IIM)

Сюжет множества Джулии, созданный с использованием случайных IIM График множества Джулии, созданный с помощью MIIM

Как упоминалось выше, множество Жюлиа можно найти как множество предельных точек множества прообразов (по существу) любой данной точки. Итак, мы можем попытаться построить набор Джулии данной функции следующим образом. Начните с любой точкой г мы знаем, что в множестве Жюлиа, такие как отталкивающая периодической точка, и вычислить все прообразы г при некоторой высокой итерации по е. ${\ displaystyle f ^ {n}}$

К сожалению, поскольку количество повторных предварительных изображений растет экспоненциально, это невозможно с вычислительной точки зрения. Однако мы можем настроить этот метод аналогично методу «случайной игры» для систем с повторяющимися функциями. То есть на каждом шаге мы случайным образом выбираем одно из прообразов f.

Например, для квадратичного многочлена f c обратная итерация описывается следующим образом:

${\ displaystyle z_ {n-1} = {\ sqrt {z_ {n} -c}}.}$

На каждом шаге случайным образом выбирается один из двух квадратных корней.

Обратите внимание, что к некоторым частям набора Джулии довольно сложно получить доступ с помощью обратного алгоритма Джулии. По этой причине необходимо модифицировать IIM / J (он называется MIIM / J) или использовать другие методы для получения более качественных изображений.

Использование DEM / J

• Образы Юлии наборы для ${\ displaystyle f_ {c} (z) = z ^ {2} + c}$
• 

  ${\ displaystyle c = -0.74543 + 0.11301 * i}$

• 

  ${\ displaystyle c = -0,75 + 0,11 * i}$

• 

  ${\ displaystyle c = -0,1 + 0,651 * i}$

• 

  Множество Джулии нарисовано путем оценки расстояния, итерация имеет вид ${\ displaystyle 1-z ^ {2} + z ^ {5} / (2 + 4z) + c}$

• 

  Трехмерный рендеринг набора Джулии с использованием оценки расстояния

Поскольку множество Джулии бесконечно тонкое, мы не можем эффективно нарисовать его путем обратной итерации от пикселей. Он будет казаться фрагментированным из-за непрактичности изучения бесконечного количества начальных точек. Поскольку счетчик итераций сильно меняется около набора Джулии, частичное решение состоит в том, чтобы подразумевать контур набора из ближайших цветовых контуров, но набор будет иметь тенденцию выглядеть мутным.

Лучший способ нарисовать набор Джулии в черно-белом цвете - это оценить расстояние пикселей (ЦМР) от набора и раскрасить каждый пиксель, центр которого находится близко к набору. Формула для оценки расстояния выводится из формулы для потенциальной функции φ ( z). Когда эквипотенциальные линии для φ ( z) расположены близко, их число велико, и наоборот, поэтому эквипотенциальные линии для функции должны лежать приблизительно регулярно. Было доказано, что значение, найденное по этой формуле (с точностью до постоянного множителя), сходится к истинному расстоянию для z, сходящегося к множеству Жюлиа. ${\ Displaystyle | \ varphi '(г) |}$${\ displaystyle \ delta (z) = \ varphi (z) / | \ varphi '(z) |}$

Мы предполагаем, что f ( z) рациональна, то есть где p ( z) и q ( z) - комплексные многочлены степеней m и n соответственно, и нам нужно найти производную приведенных выше выражений для φ ( z). И, как это только что меняется, мы должны вычислить производную от по отношению к г. Но as ( k- кратная композиция) является произведением чисел, и эту последовательность можно вычислить рекурсивно, начиная с ( до вычисления следующей итерации). ${\ Displaystyle е (г) = п (г) / д (г)}$${\ displaystyle z_ {k}}$${\ displaystyle z '_ {k}}$${\ displaystyle z_ {k}}$${\ Displaystyle Z_ {к} = е (е (\ cdots f (z)))}$${\ displaystyle z '_ {k}}$${\ displaystyle f '(z_ {k})}$${\ displaystyle z '_ {k + 1} = f' (z_ {k}) z '_ {k}}$${\ displaystyle z '_ {0} = 1}$${\ displaystyle z_ {k + 1} = f (z_ {k})}$

Для итерации в сторону ∞ (точнее, когда m ≥ n + 2, так что ∞ является суперпритягивающей неподвижной точкой), мы имеем

${\ displaystyle | \ varphi '(z) | = \ lim _ {k \ to \ infty} {\ frac {| z' _ {k} |} {| z_ {k} | d ^ {k}}}, }$

( d = m - n) и, следовательно:

${\ displaystyle \ delta (z) = \ varphi (z) / | \ varphi '(z) | = \ lim _ {k \ to \ infty} \ log | z_ {k} || z_ {k} | / | z '_ {k} |. \,}$

Для итерации в направлении конечного цикла притяжения (который не является суперпритягивающим), содержащего точку и имеющего порядок r, мы имеем ${\ displaystyle z ^ {*}}$

${\ displaystyle | \ varphi '(z) | = \ lim _ {k \ to \ infty} | z' _ {kr} | / (| z_ {kr} -z ^ {*} | ^ {2} \ alpha ^ {к}), \,}$

и следовательно:

${\ displaystyle \ delta (z) = \ varphi (z) / | \ varphi '(z) | = \ lim _ {k \ to \ infty} | z_ {kr} -z ^ {*} | / | z' _ {kr} |. \,}$

Формула суперпритягивающего цикла:

${\ displaystyle \ delta (z) = \ lim _ {k \ to \ infty} \ log | z_ {kr} -z ^ {*} | ^ {2} / | z '_ {kr} |. \,}$

Мы вычисляем это число, когда итерация останавливается. Обратите внимание, что оценка расстояния не зависит от привлекательности цикла. Это означает, что он имеет значение для трансцендентных функций «бесконечной степени» (например, sin ( z) и tan ( z)).

Помимо рисования границы, функция расстояния может быть представлена ​​как 3-е измерение для создания твердого фрактального ландшафта.

• Кролик дуади
• Предел установлен
• Стабильные и нестабильные наборы
• Теорема об отсутствии блуждающей области
• Теория хаоса

• Карлесон, Леннарт ; Гамелен, Теодор В. (1993). Сложная динамика. Springer.
• Дуади, Адриан; Хаббард, Джон Х. (1984). "Динамический этюд комплексов полиномов". Prepublications mathémathiques d'Orsay. 2 ;   "[ op.cit. ]". 4. 1985 г. Цитировать журнал требует |journal=( помощь )
• Милнор, JW (2006) [1990]. Динамика в одной комплексной переменной. Анналы математических исследований. 160 (Третье изд.). Издательство Принстонского университета; Впервые появился как «Препринт Stony Brook IMS». доступно как «arXiV: math.DS / 9201272».
• Богомольный Александр. «Множество Мандельброта и индексация множеств Жюлиа». разрубить узел. Учебная программа по алгебре.
• Демидов, Евгений (2003). «Анатомия множеств Мандельброта и Жюлиа».
• Бирдон, Алан Ф. (1991). Итерация рациональных функций. Springer. ISBN   0-387-95151-2.

• «Набор Джулии», Энциклопедия математики, EMS Press, 2001 [1994]
• Вайсштейн, Эрик В. «Джулия Сет». MathWorld.
• Бурк, Поль. «Юля установила фрактал (2D)» (персональный сайт).
• Сойер, Джейми. «Юля Наборы» (блог).
• Макгудвин, Майкл. «Драгоценности Джулии: Исследование наборов Джулии» (персональный сайт).
• Прингл, Люси. «Круги на полях Юлия Сет» (персональный сайт).
• Грейг, Джош. «Интерактивный апплет Julia Set». Архивировано из оригинала на 2012-03-26.
• Джойс, Дэвид Э. «Исследователь множеств Джулии и Мандельбротов» (личный сайт академика). Университет Кларка.
• «Простая программа для генерации множеств Жюлиа». liazardie.com. Архивировано из оригинала на 2011-03-17. - Windows, 370 кБ
• «Сборник программок». SourceForge. - один из апплетов может отображать наборы Джулии с помощью систем итерационных функций.
• «Юлия знакомится с HTML5». Google Labs. Архивировано из оригинала на 2011-02-18. Генератор фракталов HTML5 для вашего браузера
• «Юля». r-project.org. Пакет GNU R. сгенерировать набор Джулии или Мандельброта в заданной области и разрешении
• «Юля устанавливает». - Наглядное объяснение Джулии Сетс.
• «ФракталТС». github.io. - Мандельброт, Горящий корабль и соответствующий генератор наборов Джулии.
• «Юля набор изображений, онлайн-рендеринг». finengin.net.