| 24 ячейки | |
|---|---|
 Диаграмма Шлегеля. (вершины и ребра) Диаграмма Шлегеля. (вершины и ребра) | |
| Тип | Выпуклый правильный 4-многогранник |
| символ Шлефли | {3,4,3}. r {3,3,4} =  . {3} = . {3} =  |
| диаграмма Кокстера | |
| Cells | 24 {3, 4} |
| Грани | 96 {3} |
| Ребра | 96 |
| Вершины | 24 |
| Вершина | Куб |
| многоугольник Петри | двенадцатигранник |
| группа Кокстера | F4, [3, 4,3], порядок 1152. B4, [4,3,3], порядок 384. D4, [3], порядок 192 |
| Двойной | Самодвойственный |
| Свойства | выпуклый, изогональный, изотоксальный, изоэдральный |
| равномерный индекс | 22 |
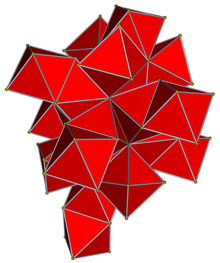 Net
Net в четырехмерной геометрии, 24-ячейка - это выпукл ый правильный 4-многогранник с символом Шлефли {3,4,3}. Его также называют C24, или икоситетрахорон, октаплекс (сокращение от «октаэдрический комплекс»), икосатетраэдроид,октакуб, гипералмаз или полиоктаэдр, состоящий из октаэдрических ячеек.
Граница 24-ячеек состоит из 24 октаэдрических ячеек, шесть из которых пересекаются на каждой вершине и по три на каждой вершине в каждом ребре. Вместе они имеют 96 треугольных граней, 96 ребер и 24 вершины. Вершинная фигура - это куб. 24 ячейки - это самодвойственный. Он и тессеракт - единственные выпуклые правильные 4-многогранники, в которых длина ребра равна радиусу.
24-ячейка не имеет регулярного аналога в 3-х измерениях. Это единственный из шести выпуклых правильных 4-многогранников, который не является четырехмерным аналогом из пяти правильных Платоновых тел. Однако его можно рассматривать как аналог пары нерегулярных тел: кубооктаэдр и его двойник ромбический додекаэдр.
Сдвинутые копии 24-ячеечного тела могут размещать мозаику в четырехмерном пространстве. к поверхности, образуя 24-элементную соту. Как может мозаично перемещаться, 24-ячейка является примером параллелоэдра, простейшего из них, который является также зонотопом.
24 ячейки - это симметричное объединение геометрий каждого выпуклого правильного многогранника в первых четырех измеренийх, кроме тех, у которых в символе Шлефли стоит 5 или больше. Особенно полезно исследовать 24-ячейку, потому что можно увидеть все геометрические отношения между всеми этими многогранниками в одной 24-ячейке или ее сотах.
24-ячейка - четвертая в последовательность 6 выпуклых правильных 4-многогранников (в порядке размера и сложности). Его можно деконструировать на 3 перекрывающихся экземпляра своего предшественника тессеракт (8-элементный), так как 8-элементный может быть разделен на 2 перекрывающихся экземпляра его предшественника 16-элементного. Самостоятельная процедура для создания одного из экземпляров своего предшественника.
24-ячейка - это выпуклая оболочка его вершин, которую можно описать как 24 координатные перестановки :
 .
.Эти координаты могут быть построены как ![]()
![]()
![]()
![]()
![]()
![]()
![]() , исправление 16-ячейка,
, исправление 16-ячейка, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , с 8 перестановками вершин (± 2,0,0,0). Вершина 16-ячеечная - это октаэдр ; таким образом, разрезание вершин 16-ячеек посередине его дополнительных ребер дает 8 октаэдрических ячеек. Этот процесс также выпрямляет тетраэдрические ячейки 16-ячеек, которые становятся 16 октаэдрами, давая 24-ячеечными 24-ячеечными ячейками.
, с 8 перестановками вершин (± 2,0,0,0). Вершина 16-ячеечная - это октаэдр ; таким образом, разрезание вершин 16-ячеек посередине его дополнительных ребер дает 8 октаэдрических ячеек. Этот процесс также выпрямляет тетраэдрические ячейки 16-ячеек, которые становятся 16 октаэдрами, давая 24-ячеечными 24-ячеечными ячейками.
В этой форме 24-ячейка имеет ребра длиной √2 и вписана в 3-сферу радиуса √2. Примечательно, что длина ребра равна радиусу описанной окружности, как в шестиугольнике или кубооктаэдре. Такие многогранники радиально равносторонние.
24 вершины можно рассматривать как вершины 6 ортогональных экваториальных квадратов, которые пересекаются только в их общем центре.
 24 кватернионных элемента бинарной тетраэдрической группы соответствуют вершинам 24-ячеек. В проекции 4-кратной симметрии:. * 1 порядок-1: 1. * 1 порядок-2: -1. * 6 порядок-4: ± i, ± j, ± k. * 8 порядок-6: (+ 1 ± i ± j ± k) / 2. * 8 порядок-3: (-1 ± i ± j ± k) / 2.
24 кватернионных элемента бинарной тетраэдрической группы соответствуют вершинам 24-ячеек. В проекции 4-кратной симметрии:. * 1 порядок-1: 1. * 1 порядок-2: -1. * 6 порядок-4: ± i, ± j, ± k. * 8 порядок-6: (+ 1 ± i ± j ± k) / 2. * 8 порядок-3: (-1 ± i ± j ± k) / 2. 24 ячейки - это самодвойственный, имеющий такое же количество вершин (24), что и ячеек, и такое же количество ребер (96), как граней.
Если взять двойную из 24-х ячеек с длиной ребра √2, совершая возвратно-поступательные движения вокруг вписанной сферы, то будет найдена еще одна 24-ячейка с длиной ребра и радиусом 1 описанной окружности, и ее координаты обнаруживают большую структуру. В этом виде вершины 24-ячейки могут быть заданы следующим образом:
8 вершин, получивших перестановкой целочис координат:
и 16 вершин с полуцелыми координатами вида :
, все 24 из которых лежат на расстоянии 1 от начала координат.
Рассматриваемые как кватернионы, это единичные кватернионы Гурвица.
24-ячейка имеет единичный радиус и единичную размерки в этой системе координат. Мы называем систему координатами единого радиуса, чтобы отличить ее от других, например, координаты √2 радиуса, использованные выше.
. 24 вершины можно рассматривать как вершины 4 ортогональных экваториальных шестиугольников, которые пересекаются только в их центр общих.
24 вершины можно рассматривать как вершины 8 равносторонних треугольников, лежащих в 4 ортогональных экваториальных плоскостях, которые пересекаются только в их общем центре.
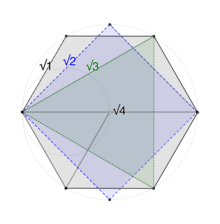 Геометрия вершин радиально равносторонней 24 ячейки, показывающая 3 многоугольника большого круга и 4 длины хорды от вершины к вершине.
Геометрия вершин радиально равносторонней 24 ячейки, показывающая 3 многоугольника большого круга и 4 длины хорды от вершины к вершине. 24 вершины, занимающие 24 ячейки, распределены на четырех различных отрезках хорды друг от друга: √1, √2, √3 и √4.
Каждая вершина соединена с 8 другими ребром длиной 1, охватывающим 60 ° = π / 3 дуги. Следующими ближайшими являются 6 вершин, расположенных на расстоянии 90 ° = π / 2, вдоль внутренних хорды длиной √2. Еще 8 вершин лежат на расстоянии 120 ° = 2π / 3 по внутренней хорде длиной √3. Противоположная вершина находится на расстоянии 180 ° = π по диаметру длиной 2. Наконец, поскольку 24-ячейка радиально равносторонняя, ее центр можно рассматривать как 25-ю каноническую вершину вершины, что составляет 1 длину ребра. подальше от всех остальных.
Чтобы наглядно представить себе, как внутренние многогранники 24-элементного типа, подходящие друг к другу (как описано ниже ), имейте в виду, что четыре длины хорды (√1, √2, √ 3, √ 4) - длинные диаметры гиперкубов размерностей с 1 по 4: длинный диаметр квадрата равен √2; длинный диаметр куба √3; а длинный диаметр тессеракта равен √4. Более того, длинный диаметр октаэдра равен √2, как квадрат; а длинный диаметр самой 24-числа равен √4, как у тессеракта.
Хорды вершин 24-ячеек расположены в геодезических больших окружностях, которые лежат в наборах ортогональных еты. геодезическое расстояние между двумя 24-угольными вершинами вдоль пути из √1 ребер всегда равно 1, 2 или 3, и оно равно 3 только для противоположных вершин.
√1 ребра встречаются в 16 шестиугольных больших кругах (4 набора по 4 ортогональных плоскости), 4 из которых пересекаются в каждой вершине. 96 различных ребер √1 делят поверхность на 96 треугольных граней и 24 октаэдрических ячейки: 24 ячейки.
Хорды √2 образуют 18 больших квадратных кругов (3 набора по 6 ортогональных плоскостей), 3 из которых пересекаются в каждой вершине. 72 различных хорды √2 не проходят в тех же плоскостях, что и большие шестиугольные круги; они не следуют за гранями 24-ячеек, они проходят через центры ее ячеек под одним из ее средних краев.
хорды √3 встречаются в 32 треугольных больших окружностях в 16 плоскостях (4 набора 4 ортогональных плоскости), 4 из пересекаются в каждой вершине. 96 различных хорд √3 проходят от вершины к каждой другой вершине в тех же плоскостях, что и гексагональные большие окружности.
Хорды √4 образуют 12 диаметров от вершины к вершине (3 по 4 ортогональные оси), 24 радиуса вокруг 25-й центральной вершины.
Ребра √1 образуют 48 параллельных пар, разделенных √3. Хорды √2 образуют 36 параллельных пар, разделенных √2. Хорды √3 образуют 48 параллельных пар, отстоящих друг от друга на √1.
Каждая плоскость большого круга пересекается с каждой из других плоскостей большого круга или плоскостью граней, к которой она ортогональна только в центральной точке, и с каждой плоскостью. других, которому он не ортогонален ни на одном из краев. В каждом случае это ребро является одной из хорд вершин 24 ячейки.
Треугольники и квадраты уникальным образом объединяются в 24-ячейке, чтобы генерировать в качестве внутренних элементов все элементы правильные выпуклые многогранники с треугольными и квадратными гранями в первых четырех измерениях (с оговорками для 5-ячеечной и 600-ячеечной ). Следовательно, существует множество способов сконструировать или разобрать 24 клетки.
8 целочисленных вершин (± 1, 0, 0, 0) являются вершинами правильного 16-ячеечного, а 16 полуцелых вершин ( ± 1/2, ± 1/2, ± 1/2, ± 1/2) являются вершинами его двойственного, тессеракта (8-элементный). Тессеракт дает конструкцию Госсета из 24 ячеек, эквивалентную разрезанию тессеракта на 8 кубических пирамид, а затем прикреплению их к граням второго тессеракта. Аналогичная конструкция в 3-м пространстве дает ромбический додекаэдр, который, однако, является неправильным. 16-ячеечная конструкция дает конструкцию, обратную 24-элементную конструкцию Чезаро, эквивалентную исправлению 16-ячеечной конструкции (усечение ее углов по средним краям, как описано в выше ). Аналогичная конструкция в 3-м пространстве дает кубооктаэдр (двойной ромбический додекаэдру), который, однако, не является правильным. Тессеракт и 16-ячейка - единственные правильные 4-многогранники в 24-ячейке.
Далее мы можем разделить последние 16 вершин на две группы: те, координаты которых содержат четное число минус (-) знаки и с нечетным номером. Каждая из этих групп из 8 вершин также определяет обычную 16-клетку. Это показывает, что вершины с 24 ячейками могут быть сгруппированы в три непересекающихся набора из восьми, каждое из которых определяет обычную 16-ячейку, а дополнение определяет двойной тессеракт. Это также показывает, что симметрии 16-сегментов образуют подгруппу индекса 3 группы симметрии 24-сегментов.
Мы можем усечь 24-ячейку, разрезая внутренние ячейки, ограниченные хордами вершин, чтобы удалить вершины, обнажая фасеты внутренние 4-многогранники вписаны в 24-ячейку. Можно разрезать 24 ячейки на две части через любой плоский шестиугольник с 6 вершинами, любой прямоугольник с 4 вершинами или любой треугольник с 3 вершинами. Плоскости большого круга (выше) - лишь некоторые из этих плоскостей. Здесь мы покажем некоторые из других: плоскости граней внутренних многогранников, которые делят 24-ячейку на две неравные части.
Начиная с 24-элементного целого, удалите 8 ортогональных вершин (4 противоположные пары на 4 перпендикных осях) и 8 ребулярных, расходящихся от каждой, разрезав 8 кубических ячеек, ограниченных √ 1 ребрами, чтобы удалить 8 кубических пирамид, чьи вершины - удаляемые вершины. Это удаляет 4 ребра из шестиугольного большого круга (сохраняя только одну противоположную пару ребер), поэтому не остается непрерывных шестиугольных больших кругов. Теперь встречаются 3 перпендикулярных ребра и образуют угол куба в каждой из 16 оставшихся вершин, а 32 оставшихся ребра делят поверхность на 24 квадратных грани и 8 кубических ячеек: тессеракт . Есть три метода сделать это (выбрать набор из 8 ортогональных вершин из 24), так что в 24-ячейку вписано три таких тессеракта. Они перекрываются друг с другом, но их наборов элементов не пересекаются: они имеют общее количество вершин, но не имеют ребра, площади грани или объемные ячейки. Они разделяют 4-элементное содержимое, их общее ядро.
Начало с полных 24-ячеек, удалите 16 вершин тессеракта (сохранив 8 вершин, которые вы удалили выше), разрезая 16 тетраэдрических ячеек, ограниченных √2 хордами, чтобы удалить 16 тетраэдрических пирамид, вершины которые являются удаляемыми вершинами. Это удаляет 12 квадратных больших кругов (сохраняя только один ортогональный набор) и все ребра √1, открывая √2 хорды как новые ребра. Теперь оставшиеся 6 квадратных больших кругов пересекаются перпендикулярно, по 3 в каждой из 8 оставшихся вершин, и их 24 ребра делят поверхность на 32 треугольные грани и 16 тетраэдрических ячеек: a 16-ячейка. Есть три способа сделать это (удалить 1 из 3 наборов вершин тессеракта), так что в 24-ячейку вписано три таких 16-ячеек. Они перекрываются друг с другом, но большинство их наборов элементов не пересекаются: у них нет общего количества вершин, длины ребер или площади грани, но они имеют общий объем ячеек. У них также есть 4-элементное общее ядро.
24-ячейка может быть построена радиально из 96 равносторонних треугольников с длиной ребра √1, которые встречаются в центре многогранника, каждый из которых дает два радиуса и кромку. Они образуют 96 √1 тетраэдров, имеющую общую 25-ю центральную вершину. Они образуют 24 октаэдрических пирамиды (полу-16 ячеек) с вершинами в центре.
24 ячейки могут быть построены из 96 равносторонних треугольников длиной ребра √2, где три вершины каждого треугольника расположены на расстоянии 90 ° = π / 2 друг от друга. Они образуют 48 √2 тетраэдров (ячейки трех 16-ячеек ) с центром на 24 средних радиусах 24 ячейки.
24-ячейка, три тессеракта и три 16-ячеечной ячейки глубоко переплетены вокруг своего общего центра и пересекаются в общем ядре. Тессеракты вписаны в 24-ячейку таким образом, что их вершины и ребра лежат на поверхности 24-ячеек (они являются элементами 24-ячеечной ячейки), но их квадратные грани и кубические ячейки лежат внутри 24-ячеечной ячейки (они не являются элементами 24-ячеечной). 16-ячеек вписаны в 24-ячейку так, что только их вершины лежат на поверхности: их ребра, треугольные грани и тетраэдрические ячейки лежат внутри 24-ячейки. Внутренние ребра из 16 ячеек имеют длину √2.
 Рисунок Кеплера тетраэдров, вписанных в куб.
Рисунок Кеплера тетраэдров, вписанных в куб. 16-ячеечные ребра также вписаны в тессеракты: их √2 ребра являются диагоналями граней тессеракта, и их 8 вершин занимают все остальные вершины тессеракта. В каждом тессеракт вписано по 16-ячеек (занимающих две противоположные вершины и диагонали граней), так что каждая 16-ячейка вписана в две из трех 8-ячеек. Это напоминает способ, которым в трех измерениях можно вписать два тетраэдра в куб, открытый Кеплером. Фактически это точная размерная аналогия (демигиперкубов ), и 48 тетраэдрических ячеек вписаны в 24 кубических ячейки именно таким образом.
24-ячейка окружает три тессеракта. внутри оболочки из октаэдрических граней, оставляя в некоторых местах 4-мерное пространство между оболочкой и оболочкой каждого тессеракта. Каждый тессеракт включает в себя две из трех 16-ячеек, оставляя в некоторых местах 4-мерное пространство между его оболочкой и каждой 16-элементной оболочкой тетраэдров. Таким образом, между конвертами из 24, 8 и 16 ячеек есть измеримые четырехмерные промежутки. Формы, заполняющие эти промежутки, предоставьте собой 4-пирамиды, упомянутые выше.
Несмотря на четырехмерные промежутки между 24-ячеечными, 8-ячеечными и 16-ячеечными оболочками, трехмерные объемы перекрываются. Различные конверты в одних местах разделены, а в других - соприкасаются (где между ними нет четырех пирамид). Там, где они соприкасаются, они сливаются и разделяют объем: в этих местах они выделяют одну и ту же 3-мембрану, а не два отдельных, а несколько смежных слоев. Поскольку всего существует 7 конвертов, есть места, где несколько конвертов объединяются и объединяются в объем, а также места, где конверты пересекаются (пересекаются изнутри наружу).
Некоторые внутренние элементы лежат внутри (внешней) граничной оболочки самой 24-элементной ячейки: каждая октаэдрическая ячейка делится пополам на три перпендикулярных квадрата (по одному от каждого из тессерактов), и диагонали этих квадратов (которые пересекаются друг с другом перпендикулярно в центре октаэдра) - ребра с 16 ячейками (по одному от каждой 16 ячеек). Каждый квадрат делит октаэдр пополам на две квадратные пирамиды, а также связывает две смежные кубические ячейки тессеракта вместе как их общую грань.
Как мы видели выше, тетраэдрические ячейки √2 с 16 ячейками вписаны в кубические ячейки тессеракта √1 и имеют один и тот же объем. 24-ячеечные √1 октаэдрические ячейки перекрывают свой объем √1 кубическими ячейками: квадратной гранью они делятся пополам на две квадратные пирамиды, вершины которых также лежат в вершине куба. Октаэдры имеют общий объем не только с кубами, но и с вписанными в них тетраэдрами; таким образом, 24 ячейки, тессеракты и 16 ячеек разделяют некоторый граничный объем.
Эта матрица конфигурации представляет 24-ячейку. Строки и столбцы соответствуют вершинам, ребрам, граням и ячейкам. Диагональные числа говорят, сколько элементов каждого элемента встречается во всех 24 ячейках. Недиагональные числа говорят, сколько элементов столбца встречается в элементе строки или рядом с ним.
Поскольку 24-ячейка самодуальна, ее матрица идентична ее повороту на 180 градусов.
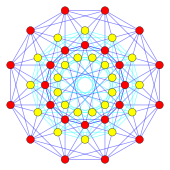 24 вершины 24-ячейки (красные узлы) и ее двойных (желтые узлы) представляют 48 корневых векторов группы F4, как показано на этой проекции F 4 плоскости Кокстера
24 вершины 24-ячейки (красные узлы) и ее двойных (желтые узлы) представляют 48 корневых векторов группы F4, как показано на этой проекции F 4 плоскости Кокстера 24 корневых вектора D4корневой системы простые группы Ли SO (8) образуют вершины 24-ячеек. Вершины можно увидеть в 3 гиперплоскостях, с 6 вершинами ячеек октаэдра на каждой из внешних гиперплоскостей и 12 вершинами кубооктаэдра на центральной гиперплоскости. Эти вершины, объединенные с 8 вершинами 16-ячеек, представляют 32 корневых простых простых групп Ли B 4 и C 4.
48 вершин (или, строго говоря, их радиус-образ) объединение 24-ячеечной и двойной к ней, образуют образ корневую систему типа F4. 24 вершины исходной системы 24-ячейки образуют корневую систему типа D 4 ; его размер имеет соотношение √2: 1. То же верно и для 24 вершин двойника. Полная группа симметрии 24-ячейки - это группа Вейля F 4, которая генерируется отражениями через ортогональные гиперплоскости. к корням F 4. Это разрешимая группа порядка 1152. Группа вращательной симметрии 24-ячеек имеет порядок 576.
При интерпретации как кватернионы, решетка корней F 4 (которая является целым промежутком вершин 24-ячейкой) замкнута при умножении и является таким кольцом . Это кольцо интегральных кватернионов Гурвица. Вершины 24-ячейки образуют группу элементов (то есть группу обратимых элементов) в кольце кватернионов Гурвица (эта группа также известна как бинарная тетраэдрическая группа ). Вершины с 24 ячейками - это в точности 24 кватерниона Гурвица с квадратом нормы 1, а вершины двойной квадратом нормы 2. Решетка корней D 4 - это дуальный из F 4 и задается подкольцом кватернионов Гурвица с четным квадратом нормы.
Вершины других выпуклых правильных 4-многогранников также образуют мультипликативные группы кватернионов, но некоторые из них образуют корневую решетку.
Ячейки Вороного основная решетки D4 выделите собой обычные 24 ячейки. Соответствующая тесселяция Вороного дает тесселяцию 4-мерного евклидова пространства регулярными 24 ячейками, 24-ячеечную соту. 24 ячейки центрированы в точках решетки D 4 (кватернионы Гурвица с квадратом четной нормы), тогда как вершины находятся в точках решетки F 4 с квадратом нечетной нормы. Каждая 24-ячеечная мозаика имеет 24 соседа. С каждым из них он имеет общий октаэдр. У него также есть 24 других соседа, с которым он разделяет только одну вершину. Восемь 24-ячеек встречаются в любой заданной вершине этой мозаики. Символ Шлефли для этой мозаики равен {3,4,3,3}. Это одна из трех обычных мозаик R.
. Единичные шары, вписанные в 24 ячейки этой мозаики, дают начало самой плотной из известных решетчатой упаковки из гиперсфер в 4-х измерениях. Также было показано, что вершинная конфигурация 24-ячеечной соты дает максимально возможное число поцелуев в 4-х измерениях.
Двойная мозаика 24-ячеечной соты {3,4, 3,3} - это сотовая структура с 16 ячейками {3,3,4,3}. Третья регулярная мозаика четырехмерного пространства - это тессерактические соты {4,3,3,4}, вершины которых могут быть 4-целыми декартовыми координатами. Конгруэнтные отношения между этими тремя мозаиками могут быть полезны при визуализации 24-ячеек, в частности радиальной равносторонней симметрии, которую он разделяет с тессерактом.
Сота из 24 ячеек с единичной длиной ребра может быть наложена. на соте тессерактов с единичной длиной ребра, так что каждая вершина тессеракта (каждая 4-целая координата) также является вершиной 24-ячеечного (и ребра тессеракта также являются 24-ячеечными ребрами), и каждая центр 24-элементная ячейка также является центром тессеракта. 24 ячейки вдвое больше тессерактов по 4-мерному содержанию (гиперобъем), так что в целом за каждые 24-ячеек приходится два тессеракта, только половина из которых вписана в 24-ячеечную. Если эти тессеракты окрашены в черный цвет, имеют соседние с ними тессеракты (с общей общей кубической грань) окрашены в красный цвет, получается четырехмерная шахматная доска. Из 24 радиусов от центра к вершине каждой 24 ячейки 16 имеют радиусами тессеракта, вписанного в 24 ячейки. Остальные 8 радиусов выходят за пределы черного тессеракта (через центры его кубических граней) к центрам 8 смежных красных тессерактов. Таким образом, соты из 24 ячеек и соты тессерактики совпадают особым образом: 8 из 24 вершин каждой 24 ячейки не встречаются в вершине тессеракта (вместо этого они находятся в центре тессеракта). Каждый черный тессеракт вырезается из 24-ячеек путем его усечения в этих 8 вершинах, отсекая 8 кубических пирамид (как при обращении конструкции Госсета, но вместо удаления пирамиды просто окрашиваются в красный цвет и оставляются на месте). Восемь 24-ячеек встречаются в центре каждого красного тессеракта: каждая встречает свою противоположность в этой общей вершине, а шесть других - в общей октаэдрической ячейке.
Красные мозаики предоставляют собой заполненные ячейки (они содержат центральную вершину и радиусы); черные тессеракты - это пустые ячейки. Множество вершин этого объединения двух сот включает вершины всех 24-ячеек и тессерактов, а также центров красных тессерактов. Добавление центров с 24 ячейками (которые также являются центрами черного тессеракта) к соте дает соту с этими 16 ячейками, набор вершин которой включает все вершины и центры всех 24 ячеек и тессерактов. Ранее пустые центры противоположных 24 ячеек противоположными вершинами 16-ячеек с единичной длиной ребра. 24 полу-16-ячеек (октаэдрические пирамиды) встречаются в каждом ранее пустом, чтобы заполнить каждую 24-ячейку, а их октаэдрические основания - это 6-вершинные октаэдрические грани 24-ячеечной (вместе с соседней 24-ячейкой).
Существуют три различных ориентации тессерактических сот, которые можно сделать так, чтобы они совпадали с 24-ячеечными сотами таким образом, в зависимости от того, какой из трех непересекающихся наборов 24-ячеек. его выравнивания было выбрано 8 ортогональных вершин (набор из 4 перпендикулярных осей), точно так же, как три тессеракта могут быть вписаны в 24 ячейки, повернутую относительно друг друга. Расстояние от одной из этих ориентаций до другого составляет изоклиническое вращение на 45 градусов (двойное вращение на 45 градусов в каждой из двух ортогональных плоскостей осей вокруг одной фиксированной точки).
 Конверты проекции 24-ячеечной. (Каждая ячейка нарисована гранями разного цвета, перевернутые ячейки не нарисованы)
Конверты проекции 24-ячеечной. (Каждая ячейка нарисована гранями разного цвета, перевернутые ячейки не нарисованы) Параллельная проекция с 24 ячейками с первой вершиной в трехмерном пространстве ромбический додекаэдр огибающую. Двенадцать из 24 октаэдрических ячеек попарно проектируются на шесть квадратных дипирамид, которые встречаются в ромбическом додекаэдра. Остальные 12 октаэдрических ячеек проецируются на 12 ромбических граней ромбического додекаэдра.
Параллельная проекция 24-элементной ячейки в трехмерном пространстве имеет кубооктаэдрическую огибающую. Две октаэдрические ячейки, ближайшие и удаленные от наблюдателя вдоль оси w, проецируются на октаэдр, вершины которого лежат в центре квадратных граней кубооктаэдра. Этот центральный октаэдр окружают выступы 16 других ячеек, имеющих 8 пар, которые служат в одном из 8 центральных, лежащих между треугольной гранью октаэдра и ближайшей треугольной гранью кубооктаэдра. Остальные 6 ячеек выступают на квадратные грани кубооктаэдра. Это соответствует разложению куба правильных октаэдр и 8 неправильных, но равных октаэдров, каждый из которых имеет форму выпуклой оболочки куба с удаленными двумя противоположными вершинами.
Параллельная проекция, обращенная сначала ребром, имеет удлиненную гексагональную дипирамидальную огибающую, параллельную проекцию, обращенную сначала лицом, имеет неоднородную гексагональную би- антипризматическую огибающую.
Перспективная проекция вершины 24-емкостные в 3-мерное пространство имеет четырехгранную шестигранную огибающую. Расположение ячеек на этом изображении похоже на изображение при параллельной проекции.
Следующая последовательность изображений показывает трехмерную перспективную проекции 24-ячеек. Точка обзора 4D размещена на расстоянии в пять раз превышающем радиус центра вершины 24 ячейки.
| Перспективная проекция первой ячейки | ||
|---|---|---|
 . На этой ближайшей ячейке отображается красным цветом, а остальные - контурами края. Для ясности отбракованы направлено в противоположную сторону от точки обзора 4D. . На этой ближайшей ячейке отображается красным цветом, а остальные - контурами края. Для ясности отбракованы направлено в противоположную сторону от точки обзора 4D. | 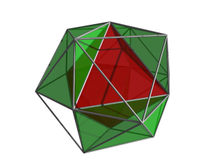 . На этом изображении из 8 ячеек, окружающих ближайшую ячейку, изображено зеленым. Четвертая ячейка находится за центральной ячейкой с этой точки зрения (слегка различима, поскольку красная ячейка полупрозрачна). . На этом изображении из 8 ячеек, окружающих ближайшую ячейку, изображено зеленым. Четвертая ячейка находится за центральной ячейкой с этой точки зрения (слегка различима, поскольку красная ячейка полупрозрачна). |  . Наконец, все 8 ячеек, окружающих ближайшую ячейку, последние четыре пурпурным цветом. . Наконец, все 8 ячеек, окружающих ближайшую ячейку, последние четыре пурпурным цветом. |
| Обратите внимание, что эти изображения не содержат отсеков, которые обращены в сторону от точки обзора 4D. Следовательно, здесь показано только 9 ячеек. На дальней стороне 24-элементной ячейки находятся еще 9 ячеек в идентичном расположении. Остальные 6 ячеек лежат на «экваторе» 24 ячеек и соединяют два набора ячеек. | ||
 . Стереографическая проекция . Стереографическая проекция |  . Трехмерная проекция 24-ячеек, выполняющая простое вращение. . Трехмерная проекция 24-ячеек, выполняющая простое вращение. | |
 . Анимированное поперечное сечение 24-ячеек . Анимированное поперечное сечение 24-ячеек | ||
 . A стереоскопическая 3D-проекция икоситетрахорона (24-ячеечная). . A стереоскопическая 3D-проекция икоситетрахорона (24-ячеечная). | ||
 Воспроизвести медиа. Изометрическая ортогональная проекция: 8 ячеек (Тессеракт) + 16 ячеек = 24 ячейки Воспроизвести медиа. Изометрическая ортогональная проекция: 8 ячеек (Тессеракт) + 16 ячеек = 24 ячейки | ||
| Плоскость Кокстера | F4 | |
|---|---|---|
| График |  | |
| Двугранная симметрия | [12] | |
| Плоскость Кокстера | B3/ A 2 (a) | B3/ A 2 (b) |
| График | 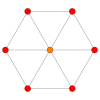 |  |
| Двугранная симметрия | [6] | [6] |
| Плоскость Кокстера | B4 | B2/ A 3 |
| График |  | 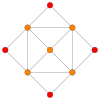 |
| Двугранная симметрия | [8] | [ 4] |
24 ячейки ограничены 24 октаэдрическими ячейками. Для целей визуализации удобно, что октаэдр имеет противоположные параллельные грани (черта, которую он разделяет с ячейками тессеракта и 120-элементного ). Октаэдры можно сложить лицом по прямому, изогнутой в 4-м направлении, в большой круг с окружностью из 6 ячеек. Расположение ячеек поддается описанию гиперсферическим. Выберите произвольную ячейку и назовите ее «Северный полюс ». Восемь меридианов большого круга (длиной в две ячейки) расходятся в измерениях трехх, сходясь в третьей ячейке «Южный полюс ». Этот скелет составляет 18 из 24 ячеек (2 + 8 × 2). См. Таблицу ниже.
Есть еще один связанный большой круг в 24-ячейке, двойной по отношению к предыдущему. Путь, который пересекает 6 вершин только по ребрам, находится в двойном многограннике, который является самодвойственным, поскольку самодвойственен. Это шестиугольные геодезические , описанные выше. Этот путь легко проследить при визуализации поперечного сечения экваториального кубооктаэдра .
Начало с Северного полюса, мы можем построить 24-ячейку в 5 широтных слоях. За исключением полюсов, каждый слой представляет собой отдельную 2-сферу, а экватор - большую 2-сферу. Ячейки, помеченные экваториальными в следующей таблице, являются промежуточными по отношению к ячейкам большого круга меридиана. Промежуточные «экваториальные» ячейки касаются гранями ячеек меридиана. Они касаются друг друга и полюсных ячеек в их вершинах. Это последнее подмножество восьми немеридиональных и полюсных ячеек имеет такое же относительное положение друг относительно друга, что и ячейки в тессеракте (8-ячейка), хотя они касаются вершин, а не граней.
| Уровень № | Количество ячеек | Описание | Colatitude | Область |
|---|---|---|---|---|
| 1 | 1 ячейка | Северный полюс | 0 ° | Северное полушарие |
| 2 | 8 ячеек | Первый слой ячеек меридиана | 60 ° | |
| 3 | 6 ячеек | Не -меридиан / промежуточный | 90 ° | Экватор |
| 4 | 8 ячеек | Второй слой ячеек меридиана | 120 ° | Южный Полушарие |
| 5 | 1 ячейка | Южный полюс | 180 ° | |
| Всего | 24 ячейки | |||
 Перспективная проекция края-центра, показывающая одно из четырех колец 6 октаэдров вокруг экватора
Перспективная проекция края-центра, показывающая одно из четырех колец 6 октаэдров вокруг экватора 24-ячейка может быть разделена на непересекающиеся наборы из четырех из этих 6-элементных колец большого круга, образуя дискретное расслоение Хопфа из четырех взаимосвязанных колец. Одно кольцо является «вертикальным» и включает в себя полюсные ячейки и четыре меридиональных ячейки. Каждое из трех других колец охватывает две экваториальные ячейки и четыре меридиональных ячейки, две из северного полушария и два из южного.
Обратите внимание, что этот путь большого круга шестиугольника подразумевает, что внутренний / двугранный угол между соседними ячейками составляет 180 - 360/6 = 120 градусов. Это говорит о том, что вы можете расположить ровно три 24 ячейки рядом друг с другом в плоскости и сформировать четырехмерную соту из 24 ячеек, как описано ранее.
Можно также пройти по маршруту большого круга через противоположные вершины октаэдров, длина которого составляет четыре ячейки. Это квадрат геодезических вдоль четырех √2 хорд , описанных выше. Этот путь соответствует переходу по диагонали через квадраты в поперечном сечении кубооктаэдра. 24-элементный многогранник - единственный правильный многогранник более чем в двух измерениях, где вы можете пересечь большой круг только через противоположные вершины (и внутреннюю часть) каждой ячейки. Этот большой круг самодвойственен. Этот путь был затронут выше относительно набора из 8 немеридиональных (экваториальных) и полюсных ячеек. 24 ячейки могут быть равнораспределены на три подмножества по 8 ячеек, каждое из которых имеет структуру тессеракта. Каждый из этих подмножеств может быть далее равнораспределен на две взаимосвязанные цепочки больших кругов длиной четыре ячейки. Вместе эти три подмножества теперь образуют другое, шестикольцевое дискретное расслоение Хопфа.
Существуют две формы более низкой симметрии 24-элементного элемента, полученные как выпрямленный 16-элементный, с B 4 или [3,3,4] симметрия, нарисованная двухцветным образом с 8 и 16 октаэдрическими ячейками. Наконец, его можно построить на основе симметрии D 4 или [3] и нарисовать трехцветным с 8 октаэдрами в каждом.
| Три сети из 24 ячеек с ячейками, раскрашенными D 4, B 4 и F 4 симметрией | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Исправленный demitesseract | Исправленный 16-элементный | Обычный 24-элементный | |||||||||
| D4, [3], порядок 192 | B4, [3,3,4], порядок 384 | F4, [3,4, 3], заказ 1152 | |||||||||
 | |||||||||||
| Три набора из 8 выпрямленных тетраэдрических ячеек | Один набор из 16 выпрямленных тетраэдрических ячеек и один набор из 8 октаэдрических ячеек. | Один набор из 24 октаэдрических ячеек | |||||||||
| Вершинная фигура. (каждое ребро соответствует одной треугольной грани, раскрашенной симметрично) | |||||||||||
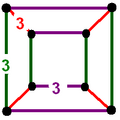 |  |  | |||||||||
правильный комплексный многоугольник 4{3} 4, ![]()
![]()
![]() или
или ![]()
![]()
![]() содержит 24 вершины из 24 ячеек и 24 4-ребра, которые соответствуют центральным квадратам 24 из 48 октаэдрических ячеек. Его симметрия: 4 [3] 4, порядок 96.
содержит 24 вершины из 24 ячеек и 24 4-ребра, которые соответствуют центральным квадратам 24 из 48 октаэдрических ячеек. Его симметрия: 4 [3] 4, порядок 96.
Правильный комплексный многогранник 3 {4} 3, ![]()
![]()
![]() или
или ![]()
![]()
![]() в
в 
| Имя | {3,4,3}, | 4{3} 4, | 3{4} 3, |
|---|---|---|---|
| Симметрия | [3,4,3], | 4[3] 4, | 3[4] 3, |
| Вершины | 24 | 24 | 24 |
| Кромки | 96 2-кромочные | 24 4-кромочные | 24 3 -кромочные |
| Изображение |  . 24 ячейки в плоскости Кокстера F4 с 24 вершинами в двух кольцах по 12 и 96 ребрами. . 24 ячейки в плоскости Кокстера F4 с 24 вершинами в двух кольцах по 12 и 96 ребрами. | 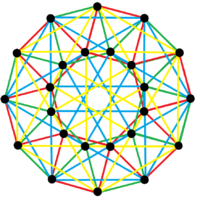 . 4{3} 4, . 4{3} 4, | 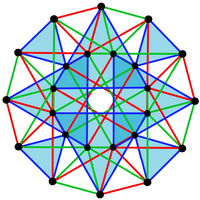 . 3{4} 3 или . 3{4} 3 или |
Несколько однородных 4-многогранников могут быть получены из 24-ячеек посредством усечения :
96 ребер 24-ячеечной ячейки могут быть разделены на золотое сечение для получения 96 вершин курноса 24 ячейки. Это делается путем размещения векторов по краям 24-ячеек таким образом, чтобы каждая двумерная грань была ограничена циклом, аналогичным образом разбивая каждое ребро на золотое сечение в его направлении. Аналогичная модификация октаэдра дает икосаэдр, или «курносый октаэдр».
24-ячейка - это уникальный выпуклый самодвойственный правильный евклидов многогранник, который не является ни многоугольником, ни симплексом. Ослабление условий выпуклости допускает еще две фигуры: большой 120-элементный и большой звездчатый 120-элементный. Сам с собой он может образовывать составной многогранник : the.
| D4однородные полихоры | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  | ||||
| {3,3}. h {4,3,3} | 2r {3,3}. h3{4, 3,3} | t {3,3}. div class="ht"{4,3,3} | 2t {3,3}. div class="ht",3 {4,3,3} | r {3,3}. {3} = {3,4,3} | rr{3,3}. r {3} = r {3,4, 3} | tr{3,3}. t {3} = t {3,4,3} | sr{3,3}. s {3} = s {3,4,3} | ||||
| 24-элементные семейные многогранники | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Имя | 24-ячеечное | усеченное 24-элементное | курносое 24-элементное | выпрямленное 24-элементное | усеченные 24 ячейки | усеченные биты 24 ячейки | кантитусеченные 24 ячейки | ранцинированные 24 ячейки | бегусеченные 24 ячейки | омнитусеченные 24 ячейки | |
| символ Шлефли. | {3,4, 3} | t0,1{3,4,3}. t {3,4,3} | s {3,4, 3} | t1{3,4,3}. r {3,4,3} | t0,2{3,4,3}. rr {3,4, 3} | t1,2 {3,4,3}. 2t {3,4,3} | t0,1,2{3, 4,3}. tr {3,4,3} | t0,3{3,4,3} | t0, 1,3 {3, 4,3} | t0,1,2,3{3,4,3} | |
| Диаграмма Кокстера. | |||||||||||
| Диаграмма Шлегеля. |  |  |  |  |  |  |  |  |  |  | |
| F4 |  |  |  |  |  |  |  |  |  |  | |
| B4 |  |  |  |  |  |  |  |  |  |  | |
| B3(a) |  |  |  |  |  |  |  |  |  |  | |
| B3(b) |  |  |  |  |  |  | |||||
| B2 |  |  |  |  |  |  |  |  |  |  | |
Т 24-элементный также может быть получен как выпрямленный 16-элементный:
| многогранник симметрии B4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Имя | тессеракт | выпрямленный. тессеракт | усеченный. тессеракт | канеллированный. tesseract | runcinated. tesseract | bitruncated. tesseract | cantitruncated. tessecitruncated | run. тессеракт | всенаправленный. тессеракт | ||
| Coxeter диаграмма | |||||||||||
| Шлефли. символ | {4,3,3} | t1{4,3,3}. r { 4,3,3} | t0,1 {4,3,3}. t {4,3,3} | t0,2{4, 3,3}. rr {4,3,3} | t0,3{4,3,3} | t1,2{4, 3,3}. 2t {4,3,3} | t0,1,2 {4,3,3}. tr {4,3,3} | t0,1,3 {4,3, 3} | t0,1,2,3{4,3,3} | ||
| диаграмма Шлегеля. |  |  |  |  |  |  |  |  |  | ||
| B4 |  |  |  |  |  |  |  |  |  | ||
| Имя | 16-ячеечная | исправленная. 16-ячеечная | усеченна я. 16-ячеечная | скошенная. 16-ячеечная | ранцинированная. 16-ячеечная | усеченная по битам. 16-ячеечная | не обрезанная. 16 ячеек | runcitruncated. 16-cell | omnitruncated. 16-cell | ||
| Coxeter. d iagram | |||||||||||
| Schläfli. symbol | {3,3,4} | t1{3,3,4}. r {3,3,4} | t0,1 {3,3,4}. t {3,3,4} | t0,2{3,3,4}. rr {3,3,4} | t0,3{3,3,4} | t1,2{3,3,4}. 2t {3,3,4} | t0,1,2 {3,3,4}. tr {3,3,4} | t0,1,3{3,3, 4} | t0,1,2,3{3,3,4} | ||
| диаграмма Шлегеля. |  |  |  |  |  |  |  |  |  | ||
| B4 |  |  |  |  |  |  |  |  |  | ||
| {3, p, 3} многогранники | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Пространство | S | H | |||||||||
| Форма | Конечная | Компактная | Паракомпактная | Некомпактная | |||||||
| {3, p, 3} | {3,3,3} | {3,4,3} | {3,5,3} | {3,6,3} | {3,7,3} | {3,8,3} | ... {3, ∞, 3} | ||||
| Изображение |  |  |  |  |  |  |  | ||||
| Ячейки |  . {3,3} . {3,3} |  . {3,4} . {3,4} |  . {3,5} . {3,5} |  . {3,6} . {3,6} |  . {3,7} . {3,7} |  . {3,8} . {3,8} |  . {3, ∞} . {3, ∞} | ||||
| Vertex. рисунок |  . {3,3} . {3,3} |  . { 4,3} . { 4,3} |  . {5,3} . {5,3} |  . {6,3} . {6,3} |  . {7,3} . {7,3} |  . {8,3} . {8,3} |  . {∞, 3} . {∞, 3} | ||||
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | ||||||||
| Треугольник | Квадрат | p-угольник | Шестиугольник | Пентагон | ||||||||
| Тетраэдр | Октаэдр • Куб | Демикуб | Додекаэдр • Икосаэдр | |||||||||
| 5-элементный | 16-элементный • Тессеракт | Димитессеракт | 24-элементный | 120-элементный • 600 -ячейка | ||||||||
| 5-симплекс | 5-ортоплекс • 5-куб | 5-полукуб | ||||||||||
| 6-симплекс | 6-ортоплекс • 6 -куб | 6-полукуб | 122 • 221 | |||||||||
| 7-симплекс | 7-ортоплекс • 7-куб | 7-полукуб | 132 • 231 • 321 | |||||||||
| 8-симплекс | 8-ортоплекс • 8-куб | 8-полукуб | 142 • 241 • 421 | |||||||||
| 9-симплекс | 9-ортоплекс • 9-куб | 9-полукуб | ||||||||||
| 10-симплекс | 10-ортоплекс • 10-куб | 10-полукуб | ||||||||||
| n-симплекс | n-ортоплекс • n- куб | n-полукуб | 1k2 • 2k1 • k21 | n-пятиугольный многогранник | ||||||||
| Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений | ||||||||||||