 . Усеченный квадрат представляет собой правильный восьмиугольник:. t {4} = {8}. . Усеченный квадрат представляет собой правильный восьмиугольник:. t {4} = {8}. | 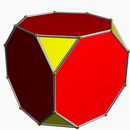 . Усеченный куб. t {4,3} или . Усеченный куб. t {4,3} или |  . Усеченные кубические соты. t {4,3,4} или . Усеченные кубические соты. t {4,3,4} или |
В геометрии усечение - это операция в любом измерении, которая разрезает вершины многогранника , создавая новый фасет вместо каждой вершины. Термин происходит от названий Кеплера для архимедовых тел.
В общем, любой многогранник (или многогранник) также может быть усечен с определенной степенью свободы относительно глубины разреза, как показано в операции усечения нотации многогранника Конвея.
Особый вид усечения, обычно подразумеваемый, - это равномерное усечение, оператор усечения, применяемый к правильному многограннику (или правильному многограннику ), который создает результирующий однородный многогранник (однородный многогранник ) с равными длинами ребер. Нет степеней свободы, и он представляет собой фиксированную геометрическую форму, как и правильные многогранники.
В общем, все однородные одинарные кольцевые многогранники имеют равномерное усечение. Например, икосододекаэдр, представленный как символы Шлефли r {5,3} или 
![]()
![]()
![]()
![]()
![]() или
или ![]()
![]()
![]() имеет равномерное усечение, усеченный икосододекаэдр, представленный как tr {5,3 } или
имеет равномерное усечение, усеченный икосододекаэдр, представленный как tr {5,3 } или 
![]()
![]()
![]() . В диаграмме Кокстера-Дынкина эффект усечения состоит в том, чтобы прозвонить все узлы, смежные с кольцевым узлом.
. В диаграмме Кокстера-Дынкина эффект усечения состоит в том, чтобы прозвонить все узлы, смежные с кольцевым узлом.
Равномерное усечение, выполняемое для правильного треугольного мозаичного изображения {3,6}, приводит к правильному шестиугольному мозаичному покрытию {6,3}.
Усеченный n-сторонний многоугольник будет иметь 2n сторон (ребер). Правильный многоугольник, равномерно усеченный, станет другим правильным многоугольником: t {n} равно {2n}. Полное усечение (или исправление ), r {3}, является другим правильным многоугольником в его двойной позиции.
Правильный многоугольник также может быть представлен его диаграммой Кокстера-Дынкина, ![]()
![]()
![]() , его равномерным усечением
, его равномерным усечением ![]()
![]()
![]() и его полным усечением
и его полным усечением ![]()
![]()
![]() . График
. График ![]()
![]()
![]() представляет группу Кокстера I2(n), где каждый узел представляет зеркало, а край представляет угол π / n между зеркалами, а вокруг одного или обоих зеркал приводится круг, чтобы показать какие из них активны.
представляет группу Кокстера I2(n), где каждый узел представляет зеркало, а край представляет угол π / n между зеркалами, а вокруг одного или обоих зеркал приводится круг, чтобы показать какие из них активны.
 . {3}. . {3}. |  |  . t {3} = {6}. . t {3} = {6}. |  |  . r {3} = {3}. . r {3} = {3}. |
Многоугольники звезды также могут быть усечены. Усеченная пентаграмма {5/2} будет выглядеть как пятиугольник, но на самом деле это двухугольник (вырожденный) декагон ({10/2}) с двумя наборами перекрывающихся вершин и ребер. Усеченная большая гептаграмма {7/3} дает тетрадекаграмму {14/3}.
 Усечение куба без исправления
Усечение куба без исправления Когда «усечение» применяется к платоновым телам или правильным мозаикам, обычно подразумевается «равномерное усечение», что означает усечение до тех пор, пока исходные грани не станут правильными многоугольниками с вдвое большим количеством сторон, чем исходная форма.

Эта последовательность показывает пример усечения куба с использованием четырех этапов непрерывного процесса усечения между полным кубом и исправленным кубом. Последний многогранник - это кубооктаэдр. Среднее изображение - унифицированный усеченный куб ; он представлен символом Шлефли t{p, q,...}.
A bitruncation - более глубокое усечение, удаляющее все исходные края, но оставляющее внутреннюю часть исходных граней. Пример: усеченный октаэдр - это усеченный битом куб: t {3,4} = 2t {4,3}.
Полное усечение битов, называемое биректификацией, уменьшает исходные грани до точек. Для многогранников это становится двойным многогранником. Пример: октаэдр - это двунаправленная диаграмма куба : {3,4} = 2r {4,3}.
Другой тип усечения, cantellation, обрезает ребра и вершины, удаляя исходные ребра, заменяя их прямоугольниками, удаляя исходные вершины и заменяя их гранями двойных оригинальные правильные многогранники или мозаики.
Многогранники более высокой размерности имеют более высокие усечения. Runcination вырезает грани, ребра и вершины. В пяти измерениях стерилизация разрезает клетки, грани и края.


 Усечение ребер куба, создание куба со скошенной кромкой
Усечение ребер куба, создание куба со скошенной кромкой Усечение ребер - это скос или фаска для многогранников, похож на cantellation, но с сохранением исходных вершин и заменой ребер шестиугольниками. В 4-многогранниках при усечении ребер ребра заменяются на ячейки удлиненной бипирамиды.


 Равномерное чередование усеченного кубооктаэдра дает неоднородный курносый куб.
Равномерное чередование усеченного кубооктаэдра дает неоднородный курносый куб.Чередование или частичное усечение удаляет только некоторые из исходных вершин.
В частичном усечении или альтернации половина вершин и соединяющиеся ребра полностью удаляются. Операция применима только к многогранникам с четными гранями. Количество граней уменьшается вдвое, а квадратные грани превращаются в ребра. Например, тетраэдр является чередующимся кубом h {4,3}.
Уменьшение - это более общий термин, используемый в отношении тел Джонсона для удаления одной или нескольких вершин, ребер или граней многогранника без нарушения других вершин. Например, трехуменьшенный икосаэдр начинается с обычного икосаэдра с удаленными 3 вершинами.
Другие частичные усечения основаны на симметрии; например, тетраэдрически уменьшенный додекаэдр.
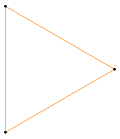
 Типы усечений, показанные на ребре , изолированном от большего многоугольника или многогранника с красными и синими вершинами. Ребро меняет направление после полного усечения.
Типы усечений, показанные на ребре , изолированном от большего многоугольника или многогранника с красными и синими вершинами. Ребро меняет направление после полного усечения. Процесс линейного усечения можно обобщить, допустив параметрические усечения, которые являются отрицательными или выходящими за пределы средней точки ребер, вызывая самопересекающиеся звездчатые многогранники и могут параметрически относиться к некоторым из правильные звездчатые многоугольники и однородные звездчатые многогранники.
 . Типы усечения на квадрате, {4}, показывая красные исходные края и новые усеченные края в голубой. Равномерно усеченный квадрат - это правильный восьмиугольник, t {4} = {8}. Полный усеченный квадрат становится новым квадратом с диагональной ориентацией. Вершины располагаются в порядке против часовой стрелки, 1-4, с усеченными парами вершин как a и b. . Типы усечения на квадрате, {4}, показывая красные исходные края и новые усеченные края в голубой. Равномерно усеченный квадрат - это правильный восьмиугольник, t {4} = {8}. Полный усеченный квадрат становится новым квадратом с диагональной ориентацией. Вершины располагаются в порядке против часовой стрелки, 1-4, с усеченными парами вершин как a и b. |
 . ⇨taC . ⇨taC |  . Куб. {4,3} C . Куб. {4,3} C |  . ⇨tC . ⇨tC |  . Усечение. t {4,3} tC . Усечение. t {4,3} tC |  . ⇨tC . ⇨tC |  . Полное усечение. r {4,3} aC . Полное усечение. r {4,3} aC |  . ⇩thC . ⇩thC |
 . Антитрубка taC . Антитрубка taC |  . Гипертусечение thC . Гипертусечение thC | |||||
 . ⇧taC . ⇧taC |  . Полное квазиусечение. aqC . Полное квазиусечение. aqC |  . ⇦ . ⇦ |  . Квазиусечение. t {4 / 3,3} tqC . Квазиусечение. t {4 / 3,3} tqC |  . ⇦tqC . ⇦tqC |  . Полное гипертканание ahC . Полное гипертканание ahC |  . ⇦thC . ⇦thC |
| 1 =()| Seed | Truncation | Rectification | Bitruncation | Dual | Expansion | Omnitruncation | Alternations | ||
|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  | |||||
| t0{p,q}. {p, q } | t01{p,q}. t {p, q} | t1{p,q}. r {p, q} | t12{p, q}. 2t {p, q} | t2{p,q}. 2r {p, q} | t02{p,q}. rr {p, q } | t012{p,q}. tr {p, q} | ht0{p,q}. h {q, p} | ht12{p, q}. s {q, p} | ht012{p,q}. sr {p, q} |