символ Шлефли

редактировать

додекаэдр - это правильный многогранник с символом Шлефли {5,3}, имеющий 3 пятиугольника вокруг каждой вершины .

В геометрии символ Шлефли представляет собой обозначение формы {p, q, r,...}, которое определяет правильные многогранники и мозаики.

Символ Шлефли назван в честь швейцарского математика 19 века Людвига Шлефли, который обобщил евклидову геометрию на более чем три измерения и открыл все их выпуклые правильные многогранники, в том числе шесть, встречающиеся в четырех измерениях.

Содержание

1 Определение
2 Свойства
3 История и варианты
4 Случаи
- 4.1 Группы симметрии
- 4.2 Правильные многоугольники (плоскость)
- 4.3 Правильные многогранники (3 измерения)
- 4.4 Правильные 4-многогранники (4 измерения)
- 4.5 Правильные n-многогранники (высшие измерения)
- 4.6 Двойные многогранники
- 4.7 Призматические многогранники
5 Продолжение символов Шлефли
- 5.1 Полигоны и круговые мозаики
- 5.2 Многогранники и мозаики
  - 5.2.1 Чередования, четверти и курносые
  - 5.2.2 Измененные и голостильные
- 5.3 Полихора и соты
  - 5.3.1 Чередования, четверти и курносые
  - 5.3.2 Бифуркационные семейства
6 Тесселяции
7 Ссылки
8 Источники
9 Внешние ссылки

Определение

Символ Шлефли - это рекурсивное описание, начиная с {p} для p-стороннего правильного многоугольника, который является выпуклым. Например, {3} - это равносторонний треугольник, {4} - это квадрат, {5} выпуклый правильный пятиугольник и так далее.

Правильные звездообразные многоугольники не являются выпуклыми, а их символы Шлефли {/ q } содержат неприводимые дроби /q, где p - количество вершин, а q - их число поворота. Эквивалентно, {/ q } создается из вершин {p}, соединенных через каждые q. Например, {⁄ 2 } - это пентаграмма ; {⁄ 1 } - это пятиугольник.

A правильный многогранник, который имеет q правильных p-сторонних многоугольников вокруг каждой вершины. представлен {p, q}. Например, куб имеет 3 квадрата вокруг каждой вершины и представлен как {4,3}.

Правильный 4-мерный многогранник с r {p, q} правильными многогранными ячейками вокруг каждого края представлен как {p, q, r}. Например, тессеракт , {4,3,3}, имеет 3 куба, {4,3} по краю.

В общем, правильный многогранник {p, q, r,..., y, z} имеет z {p, q, r,..., y} грани вокруг каждой вершины, где вершина - это вершина в многограннике, ребро в 4-многограннике, грань в 5 -полигранник, ячейка в 6-многограннике и (n-3) -граница в n-многограннике.

Свойства

Правильный многогранник имеет правильную фигуру вершины . Вершинная фигура правильного многогранника {p, q, r,..., y, z} - это {q, r,..., y, z}.

Правильные многогранники могут иметь элементы звездообразного многоугольника, такие как пентаграмма, с символом {⁄ 2 }, представленным вершинами пятиугольник, но соединены попеременно.

Символ Шлефли может представлять конечный выпуклый многогранник, бесконечную мозаику евклидова пространства или бесконечную мозаику гиперболического пробел, в зависимости от углового дефекта конструкции. Дефект с положительным углом позволяет фигуре вершины сворачиваться в более высокое измерение и возвращается в себя как многогранник. Дефект с нулевым углом разбивает пространство мозаикой того же размера, что и фасеты. Дефект с отрицательным углом не может существовать в обычном пространстве, но может быть построен в гиперболическом пространстве.

Обычно фасет или фигура вершины считается конечным многогранником, но иногда сама может рассматриваться как тесселяция.

Правильный многогранник также имеет двойственный многогранник, представленный элементами символа Шлефли в обратном порядке. Автодуальный регулярный многогранник будет иметь симметричный символ Шлефли.

Помимо описания евклидовых многогранников, символы Шлефли могут использоваться для описания сферических многогранников или сферических сот.

История и вариации

Работы Шлефли при его жизни были почти неизвестны, и его система обозначений для описания многогранников была переоткрыта независимо несколькими другими авторами. В частности, Торольд Госсет заново открыл символ Шлефли, который он написал как | p | q | г |... | z | вместо скобок и запятых, как это делал Шлефли.

Форма Госсета имеет большую симметрию, поэтому количество измерений равно количеству вертикальных полос, а символ точно включает подсимволы для фигуры фасета и вершины. Госсет считает | p как оператор, который можно применить к | q |... | z | создать многогранник с p-угольными гранями, фигура вершины которого равна | q |... | z |,

Случаи

Группы симметрии

символы Шлефли тесно связаны с (конечными) группами симметрии симметрии, которые точно соответствуют конечные группы Кокстера и задаются теми же индексами, но квадратными скобками вместо [p, q, r,...]. Такие группы часто называют правильными многогранниками, которые они порождают. Например, [3,3] - это группа Кокстера для отражающей тетраэдрической симметрии, [3,4] - это отражательная октаэдрическая симметрия, а [3,5] - отражающая икосаэдральная симметрия.

Правильные многоугольники (плоскость)

Правильные выпуклые и звездчатые многоугольники с 3–12 вершинами, помеченные символами Шлефли

Символ Шлефли (выпуклого) правильного многоугольника с p ребрами это {p}. Например, правильный пятиугольник представлен {5}.

Для (невыпуклых) звездообразных многоугольников используется конструктивное обозначение {⁄ q }, где p - количество вершин, а q - 1 - число вершин, пропущенных при рисовании каждого ребра звезды. Например, {⁄ 2 } представляет пентаграмму.

Правильные многогранники (3 измерения)

Символ Шлефли правильного многогранника равен { p, q}, если его грани являются p-угольниками, и каждая вершина окружена q гранями (фигура вершины является q-угольником).

Например, {5,3} - это правильный додекаэдр. Он имеет пятиугольные (5 ребер) грани и по 3 пятиугольника вокруг каждой вершины.

См. 5 выпуклых Платоновых тел, 4 невыпуклых многогранника Кеплера-Пуансо.

Топологически правильную двумерную мозаику можно рассматривать как подобен (3-мерному) многограннику, но такой, что угловой дефект равен нулю. Таким образом, символы Шлефли могут также быть определены для регулярных мозаик евклидова или гиперболического пространства аналогично многогранникам. Аналогия верна и для более высоких измерений.

Например, шестиугольная мозаика представлена {6,3}.

Правильные 4-многогранники (4 измерения)

Символ Шлефли правильного 4-многогранника имеет форму {p, q, r}. Его (двумерные) грани - правильные p-угольники ({p}), клетки - правильные многогранники типа {p, q}, фигуры вершин - правильные многогранники типа {q, r}, а фигуры ребер - правильные r-угольники (тип {r}).

См. Шесть выпуклых правильных и 10 правильных звездных 4-многогранников.

Например, 120-элементный представлен как {5,3, 3}. Он состоит из додекаэдра ячеек {5,3} и имеет по 3 ячейки по каждому краю.

Существует одна регулярная мозаика евклидова 3-пространства: кубические соты с символом Шлефли {4,3,4}, состоящие из кубических ячеек и 4 кубов по каждому краю..

Есть также 4 обычных компактных гиперболических мозаики, включая {5,3,4}, гиперболические маленькие додекаэдрические соты, которые заполняют пространство ячейками додекаэдра.

Правильные n-многогранники (более высокие измерения)

Для многомерных регулярных многогранников символ Шлефли рекурсивно определяется как {p 1, p 2,..., p n - 1 }, если фасеты имеют символ Шлефли {p 1,p2,..., p n - 2 } и фигуры вершин имеют символ Шлефли {p 2,p3,..., p n - 1 }.

Вершинная фигура фасетки многогранника и фасет вершинной фигуры одного и того же многогранника одинаковы: {p 2,p3,..., p n - 2 }.

Есть только 3 правильных многогранника в 5 измерениях и выше: симплекс, {3,3,3,..., 3}; кросс-многогранник, {3,3,..., 3,4}; и гиперкуб, {4,3,3,..., 3}. Не существует невыпуклых правильных многогранников выше четырех измерений.

Двойные многогранники

Если многогранник размерности n ≥ 2 имеет символ Шлефли {p 1,p2,..., p n - 1 }, то его dual имеет символ Шлефли {p n - 1,..., p 2,p1}.

Если последовательность палиндромная, т. Е. Одинаковая вперед и назад, многогранник самодвойственный. Каждый двумерный правильный многогранник (многоугольник) самодвойственен.

Призматические многогранники

Равномерные призматические многогранники могут быть определены и названы как декартово произведение (с оператором "×") регулярных многогранников меньшей размерности.

В 0D точка представлена (). Его диаграмма Кокстера пуста. Его нотация Кокстера симметрична] [.
В 1D отрезок линии представлен {}. Его диаграмма Кокстера равна . Его симметрия равна [].
В 2D прямоугольник представлен как {} × {}. Его диаграмма Кокстера равна . Его симметрия равна [2].
В 3D p-угольная призма представлена как {} × {p}. Его диаграмма Кокстера . Его симметрия равна [2, p].
В 4D однородная {p, q} -эдральная призма представлена как {} × {p, q}. Его диаграмма Кокстера - . Его симметрия равна [2, p, q].
В 4D однородная p-q дуопризма представлена как {p} × {q}. Его диаграмма Кокстера . Его симметрия равна [p, 2, q].

Призматические двойники или бипирамиды могут быть представлены как составные символы, но с оператором сложения «+».

В 2D, ромб представлен как {} + {}. Его диаграмма Кокстера . Его симметрия равна [2].
В 3D p-угольная бипирамида представлена как {} + {p}. Его диаграмма Кокстера - . Его симметрия равна [2, p].
В 4D {p, q} -эдральная бипирамида представлена как {} + {p, q}. Его диаграмма Кокстера - . Его симметрия - [p, q].
В 4D дуопирамида p-q представлена как {p} + {q}. Его диаграмма Кокстера - . Его симметрия равна [p, 2, q].

Пирамидальные многогранники, содержащие вершины, смещенные ортогонально, могут быть представлены с помощью оператора соединения "∨". Каждая пара вершин между соединенными фигурами соединена ребрами.

В 2D равнобедренный треугольник может быть представлен как () ∨ {} = () ∨ [() ∨ ()].

В 3D:

A бигональный дисфеноид можно представить как {} ∨ {} = [() ∨ ()] ∨ [() ∨ ()].
A p-угольная пирамида представлен как () ∨ {p}.

В 4D:

A pq-эдральная пирамида представлена как () ∨ {p, q}.
A 5-элементная представлена как () ∨ [() ∨ {3}] или [() ∨ ()] ∨ {3} = {} ∨ {3}.
Квадратная пирамидальная пирамида представлена как () ∨ [() ∨ {4}] или [() ∨ ()] ∨ {4} = {} ∨ {4}.

При смешивании операторов порядок операций от высшего к низшему ×, +, ∨.

Осевые многогранники, содержащие вершины на параллельных смещенных гиперплоскостях, могут быть представлены символом || оператор. Однородная призма - это {n} || {n}, а антипризма {n} || r {n}.

Расширение символов Шлефли

Многоугольники и мозаики окружностей

Усеченный правильный многоугольник удваивается по сторонам. Правильный многоугольник с четными сторонами можно разделить пополам. Измененный четный правильный 2n-угольник образует соединение звезды, 2 {n}.

Форма	символ Шлефли	Симметрия	Диаграмма Кокстера
Обычная	{p}	[p]		Шестиугольник
Усеченный	t {p} = {2p}	[[p]] = [2p]	=	Усеченный шестиугольник. (Додекагон)	=
Изменен и. Holosnubbed	a {2p} = β {p}	[2p]	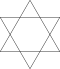=	Измененный шестиугольник. (Гексаграмма)	=
Половина и. Сглаженный	h {2p} = s {p} = {p}	[1,2p] = [p]	= =	Половина шестиугольника. (Треугольник)	= =

Многогранники и мозаики

Коксетер расширил использование символа Шлефли до квазирегулярных многогранников, добавив к символу вертикальное измерение. Это была отправная точка к более общей диаграмме Кокстера. Норман Джонсон упростил обозначение вертикальных символов с префиксом r. T-нотация является наиболее общей и напрямую соответствует кольцам диаграммы Кокстера. Символы имеют соответствующее чередование , заменяющее кольца отверстиями на диаграмме Кокстера и префикс h, обозначающий половину, конструкция ограничена требованием, что соседние ветви должны иметь четный порядок, и сокращает порядок симметрии вдвое. Связанный оператор, a для измененного, показан с двумя вложенными отверстиями, представляет собой составные многогранники с обеими чередующимися половинами, сохраняющими исходную полную симметрию. Курсор - это половина формы усечения, а голоскуб - это обе половины попеременного усечения.

Форма	символы Шлефли			Симметрия
Обычная	${p, q} {\ displaystyle {\ begin { Bmatrix} p, q \ end {Bmatrix}}}$ ${\ begin {Bmatrix} p, q \ end {Bmatrix}}$	{p, q}	t0{p, q}	[p, q]. или. [(p, q, 2)]	Куб
Усеченный	$t {p, q} {\ displaystyle t {\ begin {Bmatrix} p, q \ end {Bmatrix}}}$ $т { \ begin {Bmatrix} p, q \ end {Bmatrix}}$	t {p, q }	t0,1 {p, q}		Усеченный куб
Bitruncation. (Усеченное двойное)	$t {q, p} {\ displaystyle t {\ begin {Bmatrix} q, p \ end {Bmatrix}}}$ $t {\ begin {Bmatrix} q, p \ end {Bmatrix}}$	2t {p, q}	t1,2 {p, q}		Усеченный октаэдр
Выпрямленный. (Квазирегулярный )	${pq} {\ displaystyle {\ begin {Bmatrix} p \\ q \ end {Bmatrix}}}$ ${ \ begin {Bmatrix} p \\ q \ end {Bmatrix}}$	r {p, q}	t1{p, q}		Кубооктаэдр
Биректификация. (Обычное двойственное)	${q, p} {\ displaystyle {\ begin {Bmatrix} q, p \ end {Bmatrix}}}$ ${\ begin {Bmatrix} q, p \ end {Bmatrix}}$	2r {p, q}	t2{p, q }		Октаэдр
Cantellated. (Ректифицированный ректифицированный )	$r {pq} {\ displaystyle r {\ begin {Bmatrix} p \\ q \ end {Bmatrix}}}$ $r {\ begin {Bmatrix} p \\ q \ end {Bmatrix}}$	rr {p, q }	t0,2 {p, q}		Ромбокубооктаэдр
Cantitruncate d. (усеченное выпрямленное)	$t {pq} {\ displaystyle t {\ begin {Bmatrix} p \\ q \ end {Bmatrix}}}$ $t { \ begin {Bmatrix} p \\ q \ end {Bmatrix}}$	tr {p, q}	t0,1,2 {p, q}		Усеченный кубооктаэдр

Чередования, четверти и курносые

Чередования имеют половину симметрии групп Кокстера и представлены незаполненными кольцами. Возможны два варианта выбора половины вершин, но символ не указывает, какая именно. Формы четверти показаны здесь со знаком + внутри полого кольца, что означает, что они представляют собой два независимых чередования.

Чередования
Форма	символы Шлефли			Симметрия	Диаграмма Кокстера
Чередование (половинное) регулярное	$h {2 p, q} {\ displaystyle h {\ begin {Bmatrix} 2p, q \ end {Bmatrix}}}$ $h {\ begin {Bmatrix} 2p, q \ end {Bmatrix}}$	h{2p,q}	ht0{2p,q}	[1,2p, q]	=	Demicube. (Tetrahedron )
Snub regular	$s {p, 2 q} {\ displaystyle s {\ begin {Bmatrix} p, 2q \ end {Bmatrix}}}$ $s {\ begin {Bmatrix} p, 2q \ end {Bmatrix}}$	s{p,2q}	ht0,1{p,2q}	[p, 2q]
Плоский сдвоенный обычный	$s {q, 2 p} {\ displaystyle s {\ begin {Bmatrix} q, 2p \ end {Bmatrix}}}$ $s{\begin{Bmatrix}q,2p\end{Bmatrix}}$	s{q,2p}	ht1,2{2p,q}	[ 2p, q]		Плоский октаэдр. (Икосаэдр )
Переменный выпрямленный. (p и q четные)	$h {pq} {\ displaystyle h {\ begin {Bmatrix} p \\ q \ end {Bmatrix}}}$ $h{\begin{Bmatrix}p\\q\end{Bmatrix}}$	hr{p,q}	ht1{p,q}	[p, 1, q]
Чередование выпрямленного ректификата. ( p и q четны)	$hr {pq} {\ displaystyle hr {\ begin {Bmatrix} p \\ q \ end {Bmatrix}}}$ $hr {\ begin { Bmatrix} p \\ q \ end {Bmatrix}}$	hrr {p, q}	ht0,2 {p, q}	[(p, q, 2)]
Разделенный на четыре части. (p и q четные)	$q { pq} {\ displaystyle q {\ begin {Bmatrix} p \\ q \ end {Bmatrix}}}$ $q {\ begin {Bmatrix} p \\ q \ end {Bmatrix}}$	q{p,q}	ht0ht2{p,q}	[1, p, q, 1]
Snub rectified. Snub quasiregular	$s {pq} {\ displaystyle s {\ begin {Bmatrix} p \\ q \ end {Bmatrix}}}$ $s {\ begin {Bmatrix} p \\ q \ end {Bmatrix}}$	sr {p, q}	ht0,1,2 {p, q}	[p, q]		Курносый кубооктаэдр. (Курносый куб)

Измененный и голонубусный

Измененные и голонубчатые формы обладают полной симметрией группы Кокстера и представлены двойными незаполненными кольцами, но могут быть представлены как соединения.

Измененная и голографическая
Форма	символы Шлефли			Симметрия	Диаграмма Кокстера		Пример, {4,3}
Измененная регулярная	$a {p, q } {\ displaystyle a {\ begin {Bmatrix} p, q \ end {Bmatrix}}}$ $a {\ begin {Bmatrix} p, q \ end {Bmatrix}}$	a{p,q}	at0{p,q}	[p, q]	= ∪			Звездчатый октаэдр
Двойной правильный Голоснуб	ß {q, p}	ß {q, p}	at0,1 {q, p}	[p, q]				Соединение двух икосаэдров

ß, похожее на греческую букву beta (β), это буква немецкого алфавита eszett.

Polychora и соты

Линейные семейства
Форма	символ Шлефли
Обычный	${p, q, r} {\ displaystyle {\ begin {Bmatrix} p, q, r \ end {Bmatrix}}}$ ${\ begin {Bmatrix} p, q, r \ end {Bmatrix}}$	{p, q, r}	t0{p, q, r}	Тессеракт
Усеченный	$t {p, q, r} {\ displaystyle t {\ begin {Bmatrix} p, q, r \ end {Bmatrix}}}$ $t {\ begin { Bmatrix} p, q, r \ end {Bmatrix}}$	t {p, q, r}	t0,1 {p, q, r}	Усеченный тессеракт
Исправленный	${pq, r} {\ displaystyle \ left \ {{\ begin {array} {l} p \\ q, r \ end {массив}} \ right \}}$ $\ left \ {{\ begin {array} {l} p \\ q, r \ end {array}} \ right \}$	r {p, q, r}	t1{p, q, r}	Исправленный тессеракт	=
Усеченный бит		2t {p, q, r}	t1, 2 {p, q, r}	Bitruncated tesseract
Birectified. (Rectified dual)	${q, pr} {\ displaystyle \ left \ {{\ begin {array} { l} q, p \\ r \ end {array}} \ right \}}$ $\ left \ {{\ begin {array} {l} q, p \\ r \ end {array}} \ right \}$	2r {p, q, r} = r {r, q, p}	t2{p, q, r}	Исправленный 16-элементный	=
Tritruncated. (Усеченный двойственный)	$t {r, q, p} {\ displaystyle t {\ begin {Bmatrix} r, q, p \ end {Bmatrix}}}$ $t {\ begin {Bmatrix} r, q, p \ end {Bmatrix}}$	3t {p, q, r} = t {r, q, p}	t2,3 {p, q, r}	Обрезанный тессеракт
Trirectified. (Dual)	${r, q, p} {\ displaystyle {\ begin {Bmatrix} r, q, p \ end {Bmatrix}}}$ ${\ begin {Bmatrix} r, q, p \ end {Bmatrix}}$	3r {p, q, r} = {r, q, p }	t3{p, q, r} = {r, q, p}	16-элементный
Cantellated	$r {pq, r} {\ displaystyle r \ left \ {{\ begin { array} {l} p \\ q, r \ end {array}} \ right \}}$ $r \ left \ {{\ begin {array} {l} p \\ q, r \ end {array}} \ right \}$	rr {p, q, r}	t0,2 {p, q, r}	Кантеллированный тессеракт	=
усеченный	$t {pq, r} {\ displaystyle t \ left \ {{\ begin {array} {l} p \\ q, r \ end {array}} \ right \} }$ $t \ left \ {{\ begin {array} {l} p \\ q, r \ end {array}} \ right \}$	tr {p, q, r}	t0,1,2 {p, q, r}	Cantit runcated tesseract	=
Runcinated. (Expanded )	$e 3 {p, q, r} {\ displaystyle e_ {3} {\ begin {Bmatrix} p, q, r \ end {Bmatrix}} }$ $e_ {3} {\ begin {Bmatrix} p, q, r \ end {Bmatrix}}$	e3{p, q, r}	t0,3 {p, q, r}	Запущенный тессеракт
Runcitruncated			t0,1,3 {p, q, r}	Выполнить усеченный тессеракт
Усеченный тессеракт			t0,1,2,3 {p, q, r}	Усеченный тессеракт

Чередование, четверти и пренебрежение

Чередование
Форма	символ Шлефли
Чередования
Половина. p четный	$h {p, q, r} {\ displaystyle h {\ begin {Bmatrix} p, q, r \ end {Bmatrix}}}$ $h {\ begin {Bmatrix} p, q, r \ end {Bmatrix}}$	h {p, q, r}	ht0{p, q, r}	16 -cell
Четверть. p и r четное	$q {p, q, r} {\ displaystyle q {\ begin {Bmatrix} p, q, r \ end {Bmatrix}}}$ $q {\ begin {Bmatrix} p, q, r \ end {Bmatrix}}$	q {p, q, r}	ht0ht3{p, q, r}
Snub. q even	$s {p, q, r} {\ displaystyle s {\ begin {Bmatrix} p, q, r \ end {Bmatrix}}}$ $s {\ begin {Bmatrix} p, q, r \ end {Bmatrix}}$	s {p, q, r}	ht0,1 {p, q, r}	Snub 24-элементный
Snub исправленный. r даже	$s {pq, r} {\ displaystyle s \ left \ {{\ begin {array} {l} p \\ q, r \ end {array}} \ right \}}$ $s\left\{{\begin{array}{l}p\\q,r\end{array}}\right\}$	sr {p, q, r}	ht0,1,2 {p, q, r}	Курносый 24-элементный	=
Чередующаяся дуопризма		s {p} s {q}	ht0,1,2,3 {p, 2, q}	Большая дуоантипризма

Разветвляющиеся семьи

Разветвляющиеся семейства
Форма	Расширенный символ Шлефли
Квазирегулярная	${p, qq} {\ displaystyle \ left \ {p, {q \ atop q} \ right \}}$ $\ left \ {p, {q \ atop q} \ right \}$	{p, q}	t0{p, q}	16-элементный
Усеченный	$t {p, qq} {\ displaystyle t \ left \ {p, {q \ atop q} \ right \}}$ $t \ left \ {p, {q \ atop q} \ right \}$	t {p, q}	t0,1 {p, q}	Усеченный 16-элементный
Исправленный	${pqq } {\ displaystyle \ left \ {{\ begin {array} {l} p \\ q \\ q \ end {array}} \ right \}}$ $\ left \ {{\ begin {array} {l} p \\ q \\ q \ end {array}} \ right \}$	r {p, q}	t1{p, q}	24 ячейки
Cantellated	$r {pqq} {\ displaystyle r \ left \ {{\ begin {array} {l} p \\ q \\ q \ end {array}} \ вправо \}}$ $r \ left \ {{\ begin {array} {l} p \\ q \\ q \ end {array}} \ right \}$	rr {p, q}	t0,2,3 {p, q}	Кантеллированный, 16 ячеек
Cantitruncated	$t {pqq} {\ displaystyle t \ left \ {{\ begin {array} {l} p \\ q \\ q \ end {array}} \ right \}}$ $t \ left \ {{\ begin {array} {l } p \\ q \\ q \ end {array}} \ right \}$	tr {p, q}	t0,1,2, 3 {p, q}	C усеченный из 16 ячеек
Snub rectified	$s {pqq} {\ displaystyle s \ left \ {{\ begin {array} {l} p \\ q \\ q \ end {array}} \ right \} }$ $s \ left \ {{\ begin {array} {l} p \\ q \\ q \ end {array}} \ right \}$	sr {p, q}	ht0,1,2,3 {p, q}	Snub 24-cell
Quasiregular	${r, pq} {\ displaystyle \ left \ {r, {p \ atop q} \ right \}}$ $\ left \ {r, {p \ atop q} \ right \}$	{r, / q \, p}	t0{r, / q \, p}
Усеченный	$t { р, pq} {\ displaystyle t \ left \ {r, {p \ atop q} \ right \}}$ $t \ left \ {r, {p \ atop q} \ right \}$	t {r, / q \, p}	t0,1 {r, / q \, p}
Исправлено	${rpq} {\ displaystyle \ left \ {{\ begin {array} {l} r \\ p \\ q \ end {array}} \ right \}}$ $\ left \ {{\ begin {array} {l} r \ \ p \\ q \ end {array}} \ right \}$	r {r, / q \, p}	t1{r, / q \, p}
Cantellated	$r {rpq} {\ displaystyle r \ left \ {{\ begin {array} {l} r \\ p \\ q \ end {array}} \ right \}}$ $r \ left \ {{\ begin {array} {l} r \\ p \\ q \ end {array}} \ right \}$	rr {r, / q \, p}	t0,2,3 {r, / q \, p}
Cantitruncated	$t {rpq} {\ displaystyle t \ left \ {{\ begin {array} {l} r \\ p \\ q \ end {array}} \ right \}}$ $t \ left \ {{\ begin {array} {l} r \\ p \\ q \ end {array}} \ right \}$	tr {r, / q \, p}	t0,1,2,3 {r, / q \, p}
Курносый, исправленный	$s {pqr} {\ displaystyle s \ left \ {{\ begin {array} {l} p \\ q \\ r \ end {array}} \ right \}}$ $s \ left \ {{\ begin {array } {l} p \\ q \\ r \ end {array}} \ right \}$	sr {p, / q, \ r}	ht0, 1,2,3 {p, / q \, r}

Мозаика

Сферическая

Обычная

Полурегулярный

Гиперболический

Ссылки

Источники

Кокстер, Гарольд Скотт Макдональд (1973) [1948]. Правильные многогранники (3-е изд.). Dover Publications. стр. 14, 69, 149. ISBN 0-486-61480-8. OCLC 798003. Правильные многогранники.
Шерк, Ф. Артур; Макмаллен, Питер; Томпсон, Энтони С.; Вайс, Азия Ивич, ред. (1995). Калейдоскопы: Избранные произведения Х.С.М. Кокстер. Вайли. ISBN 978-0-471-01003-6.
- (Документ 22) стр. 251–278 Кокстер, H.S.M. (1940). «Правильные и полурегулярные многогранники I». Математика. Zeit. 46 : 380–407. doi : 10.1007 / BF01181449. Zbl 0022.38305.MR 2,10
- (Paper 23) стр. 279–312 - (1985). «Правильные и полурегулярные многогранники II». Математика. Zeit. 188 (4): 559–591. doi : 10.1007 / BF01161657. Zbl 0547.52005.
- (Документ 24) стр. 313–358 - (1988). «Правильные и полурегулярные многогранники III». Математика. Zeit. 200 (1): 3–45. doi : 10.1007 / BF01161745. Zbl 0633.52006.

Внешние ссылки

Вайсштейн, Эрик У. «Символ Шлефли». MathWorld. Получено 28 декабря 2019 г.
Старк, Морис (13 апреля 2012 г.). "Многогранные имена и обозначения". Поездка по миру многогранников. Получено 28 декабря 2019 г.