5-симплексный - 5-simplex

редактировать

5-симплексный. Hexateron (hix)
Тип	однородный 5-многогранник
символ Шлефли	{3}
Диаграмма Кокстера
4-грань	6	6 {3,3,3}
Ячейки	15	15 {3,3}
Лица	20	20 {3}
Ребра	15
Вершины	6
Фигура вершины	. 5-ячеечная
Группа Кокстера	A5, [3], порядок 720
Двойной	самодвойственный
Базовая точка	(0,0,0,0,0,1)
Окружной радиус	0,645497
Свойства	выпуклый, изогональный обычный, самодвойственный

В пятимерной геометрии, 5- симплекс - самодвойственный регулярный 5-многогранник. Он имеет шесть вершин, 15 ребер, 20 треугольников граней, 15 четырехгранных ячеек и 6 5-ячеек фасеты. Он имеет двугранный угол cos (1/5), или приблизительно 78,46 °.

5-симплекс - это решение проблемы: составьте 20 равносторонних треугольников, используя 15 спичек, где каждая сторона каждого треугольника представляет собой ровно одну спичку.

Содержание

1 Альтернативные имена
2 Как конфигурация
3 Обычные декартовы координаты в гексатероне
4 Проецируемые изображения
5 Формы более низкой симметрии
6 Составные
7 Соответствующая униформа 5 -polytopes
8 Примечания
9 Ссылки
10 Внешние ссылки

Альтернативные имена

Его также можно назвать hexateron или hexa-5 -топ как 6- фасетный многогранник в 5-мерном пространстве. Имя гексатерон происходит от гекса- для наличия шести фасетов и терон (при этом терон является искажением тетра- ) для имеющий четырехмерные грани.

Джонатаном Бауэрсом, гексатерону дается аббревиатура hix .

Как конфигурация

Эта матрица конфигурации представляет 5-симплекс. Строки и столбцы соответствуют вершинам, ребрам, граням, ячейкам и 4-граням. Диагональные числа говорят, сколько элементов каждого элемента встречается во всем 5-симплексе. Недиагональные числа говорят, сколько элементов столбца встречается в элементе строки или рядом с ним. Матрица этого самодвойственного симплекса идентична его повороту на 180 градусов.

$[6 5 10 10 5 2 15 4 6 4 3 3 20 3 3 4 6 4 15 2 5 10 10 5 6] {\ displaystyle {\ begin {bmatrix} {\ begin {matrix} 6 5 10 10 5 \\ 2 15 4 6 4 \\ 3 3 20 3 3 \\ 4 6 4 15 2 \\ 5 10 10 5 6 \ end {matrix}} \ end {bmatrix}}}$ ${\ displaystyle {\ begin {bmatrix} {\ begin {matrix} 6 5 10 10 5 \\ 2 1 5 4 6 4 \\ 3 3 20 3 3 \\ 4 6 4 15 2 \\ 5 10 10 5 6 \ end {matrix}} \ end {bmatrix}}}$

Правильные гексатероны

декартовы координаты

может быть построен из 5-ячейки путем добавления 6-й вершины так, чтобы она была равноудалена от всех остальных вершин 5-ячейки.

Декартовы координаты для вершин правильного гексатерона с центром в начале координат и длиной ребра 2:

(1 15, 1 10, 1 6, 1 3, ± 1) (1 15, 1 10, 1 6, - 2 3, 0) (1 15, 1 10, - 3 2, 0, 0) (1 15, - 2 2 5, 0, 0, 0) (- 5 3, 0, 0, 0, 0) {\ displaystyle {\ begin {align} \ left ({\ tfrac {1} {\ sqrt {15}}}, \ {\ tfrac {1} {\ sqrt {10}) }}, \ {\ tfrac {1} {\ sqrt {6}}}, \ {\ tfrac {1} {\ sqrt {3}}}, \ \ pm 1 \ right) \\ [5pt] \ left ({\ tfrac {1} {\ sqrt {15}}}, \ {\ tfrac {1} {\ sqrt {10}}}, \ {\ tfrac {1} {\ sqrt {6}}}, \ - {\ tfrac {2} {\ sqrt {3}}}, \ 0 \ right) \\ [5pt] \ left ({\ tfrac {1} {\ sqrt {15}}}, \ {\ tfrac {1 } {\ sqrt {10}}}, \ - {\ tfrac {\ sqrt {3}} {\ sqrt {2}}}, \ 0, \ 0 \ right) \\ [5pt] \ left ({\ tfrac {1} {\ sqrt {15}}}, \ - {\ tfrac {2 {\ sqrt {2}}} {\ sqrt {5}}}, \ 0, \ 0, \ 0 \ right) \\ [5pt] \ left (- {\ tfrac {\ sqrt {5}} {\ sqrt {3}}}, \ 0, \ 0, \ 0, \ 0 \ right) \ end {align}}}

{\ displaystyle {\ begin {align} \ left ({\ tfrac {1} {\ sq rt {15}}}, \ {\ tfrac {1} {\ sqrt {10}}}, \ {\ tfrac {1} {\ sqrt {6}}}, \ {\ tfrac {1} {\ sqrt { 3}}}, \ \ pm 1 \ right) \\ [5pt] \ left ({\ tfrac {1} {\ sqrt {15}}}, \ {\ tfrac {1} {\ sqrt {10}} }, \ {\ tfrac {1} {\ sqrt {6}}}, \ - {\ tfrac {2} {\ sqrt {3}}}, \ 0 \ right) \\ [5pt] \ left ({ \ tfrac {1} {\ sqrt {15}}}, \ {\ tfrac {1} {\ sqrt {10}}}, \ - {\ tfrac {\ sqrt {3}} {\ sqrt {2}}}, \ 0, \ 0 \ right) \\ [5pt] \ left ({\ tfrac {1} {\ sqrt {15}}}, \ - {\ tfrac {2 {\ sqrt {2}}} {\ sqrt {5}}}, \ 0, \ 0, \ 0 \ right) \\ [5pt] \ left (- {\ tfrac {\ sqrt {5}} {\ sqrt {3}}}, \ 0, \ 0, \ 0, \ 0 \ right) \ end {align}}}

Вершины 5-симплекса проще разместить на гиперплоскости в 6-пространстве как перестановки (0,0,0,0,0, 1) или (0,1,1,1,1,1). Эти конструкции можно рассматривать как грани 6-ортоплекса или выпрямленного 6-куба соответственно.

Проецируемые изображения

ортогональные проекции
Ak. плоскость Кокстера	A5	A4
График
Двугранная симметрия	[6]	[5]
Ak. плоскость Кокстера	A3	A2
График
Двугранная симметрия	[4]	[3]

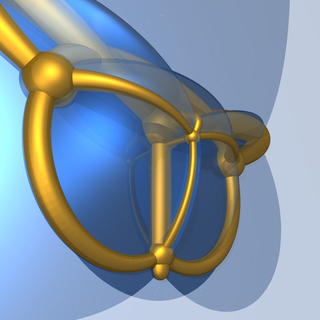. Стереографическая проекция 4D в 3D Диаграмма Шлегеля 5D в 4D гексатерона.

Формы более низкой симметрии

Формы более низкой симметрии - это 5-элементная пирамида () v {3,3,3} с [3,3,3] порядком симметрии 120, построенная как 5-элементное основание в 4-пространственной гиперплоскости и точка вершина над гиперплоскостью. Пять сторон пирамиды состоят из 5-ти ячеек. Они выглядят как фигуры вершин усеченных правильных 6-многогранников, как усеченный 6-куб.

Другой формой является {} v {3,3}, с [2,3,3] порядок симметрии 48, соединение ортогонального двуугольника и тетраэдра, смещение ортогонально, со всеми парами вершин, соединенными между собой. Другая форма - {3} v {3} с [3,2,3] порядком симметрии 36 и расширенной симметрией [[3,2,3]], порядком 72. Она представляет собой соединение двух ортогональных треугольников, ортогонально смещенных, со всеми парами вершин, соединенными между собой.

Они видны на фигурах вершин усеченных битами и усеченных трех регулярных 6-многогранников, таких как усеченный битами 6-куб и усеченный 6-симплексный. Метки кромок здесь представляют типы граней в этом направлении и, следовательно, представляют различную длину кромок.

Фигуры вершин для усеченных 6-симплексов
() v {3,3,3}		{} v {3,3}		{3} v {3}

усеченный 6-симплекс.	усеченный 6-куб.	усеченный бит 6-симплекс.	усеченный бит 6-куб.	усеченный 6-симплекс.

Соединение

Составное Два 5-симплекса в двойных конфигурациях можно увидеть в этой проекции A6 плоскости Кокстера с красными и синими 5-симплексными вершинами и ребрами. Это соединение имеет симметрию [[3,3,3,3]], порядок 1440. Пересечение этих двух 5-симплексов представляет собой однородный двунаправленный 5-симплекс. = ∩ .

Связанные однородные 5-многогранники

Он является первым в ряду размерностей однородных многогранников и сот, выраженных Кокстером как 1 3k рядов. Вырожденный 4-мерный случай существует как 3-сферическая мозаика, тетраэдрический диэдр.

13kразмерные фигуры
Пространство	Конечное				Евклидово	Гиперболическое
n	4	5	6	7	8	9
Группа Кокстера. группа	A3A1	A5	D6	E7	$E ~ 7 {\ displaystyle {\ tilde {E}} _ {7}}$ ${\ tilde {E}} _ {7}$ =E7	$T ¯ 8 {\ displaystyle {\ bar {T}} _ {8}}$ ${\ bar {T}} _ {8}$ =E7
Диаграмма Кокстера.
Симметрия	[3]	[3]	[3]	[3]	[[3]]	[3]
Порядок	48	720	23,040	2,903,040	∞
График					-	-
Имя	13, -1	130	131	132	133

Это первое в размерном ряду однородных многогранников и сот, выраженных Кокстером как 3 k1 серий. Вырожденный 4-мерный случай существует как 3-сферическая мозаика, тетраэдрический осоэдр.

3k1размерные фигуры
Пространство	Конечное				Евклидово	Гиперболическое
n	4	5	6	7	8	9
Группа Кокстера. группа	A3A1	A5	D6	E7	$E ~ 7 {\ displaystyle {\ tilde {E}} _ {7}}$ ${\ tilde {E}} _ {7}$ =E7	$T ¯ 8 {\ displaystyle {\ bar {T}} _ {8}}$ ${\ bar {T}} _ {8}$ =E7
диаграмма Кокстера.
Симметрия	[3]	[3]	[[3]]. = [4,3,3,3, 3]	[3]	[3]	[3]
Порядок	48	720	46,080	2,903,040	∞
График					-	-
Имя	31, -1	310	311	321	331

5-симплекс, поскольку 2 20 многогранник является первым в размерной серии 2 2k.

22kфигуры n измерений
Пространство	Конечное			Евклидово	Гиперболическое
n	4	5	6	7	8
группа Кокстера.	A2A2	A5	E6	$E ~ 6 {\ displaystyle {\ tilde { E}} _ {6}}$ ${\ tilde {E}} _ {6}$ =E6	E6
Диаграмма Кокстера.
График				∞	∞
Имя	22, -1	220	221	222

Обычный 5-симплекс является одним из 19 однородных политеров на основе [3,3,3,3] группы Кокстера, все показано здесь в орфографическом проекте A 5плоскости Кокстера ионы. (Вершины окрашены в соответствии с порядком перекрытия проекций: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый, число вершин постепенно увеличивается)

Многогранники A5
. t0	. t1	. t2	. t0,1	. t0,2	. t1,2	. t0,3
. t1,3	. t0,4	. t0,1,2	. t0,1,3	. t0,2,3	. t1,2,3	. t0,1,4
. t0,2,4	. t0,1,2,3	. t0,1,2,4	. t0,1,3,4	. t0, 1,2,3,4

Примечания

Ссылки

Gosset, T. (1900). «О правильных и полурегулярных фигурах в пространстве n измерений». Посланник математики. Макмиллан. С. 43–.
Coxeter, H.S.M. :
- - (1973). «Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерном пространстве (n≥5)». Правильные многогранники (3-е изд.). Дувр. Стр. 296. ISBN 0-486-61480-8.
- Шерк, Ф. Артур; Макмаллен, Питер; Томпсон, Энтони С.; Вайс, Азия Ивич, ред. (1995). Калейдоскопы: Избранные произведения Х.С.М. Кокстер. Вайли. ISBN 978-0-471-01003-6.
  - (Документ 22) - (1940). "Правильные и полурегулярные многогранники I". Математика. Zeit. 46 : 380–407. doi : 10.1007 / BF01181449. S2CID 186237114.
  - (Документ 23) - (1985). «Правильные и полурегулярные многогранники II». Математика. Zeit. 188 (4): 559–591. doi : 10.1007 / BF01161657. S2CID 120429557.
  - (Документ 24) - (1988). "Правильные и полурегулярные многогранники III". Математика. Zeit. 200 : 3–45. doi : 10.1007 / BF01161745. S2CID 186237142.
Конвей, Джон Х. ; Берджел, Хайди; Гудман-Штрасс, Хаим (2008). «26. Hemicubes: 1 n1 ». Симметрии вещей. п. 409. ISBN 978-1-56881-220-5.
Джонсон, Норман (1991). "Uniform Polytopes" (Manuscript). Для цитирования журнала требуется | journal =()
- Johnson, NW (1966). Теория однородных многогранников и сот (Доктор философии). Университет Торонто.

Внешние ссылки

Ольшевский, Джордж. "Simplex". Глоссарий по гиперпространству. Архивировано из оригинала 4 февраля 2007 года. Cite имеет пустой неизвестный параметр: | 1 =()
Многогранники различных измерений, Джонатан Бауэрс
Многомерный глоссарий

v t Фундаментальная выпуклость правильный и однородные многогранники в измерениях 2–10
An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Треугольник	Квадрат	p-угольник	Шестиугольник	Пентагон
Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
5-элементный	16-элементный • Тессеракт	Demitesseract	24-элементный	120-элементный • 600-элементный
5-симплексный	5-ортоплексный • 5-кубовый	5-полукуб
6-симплекс	6-ортоплекс • 6-куб	6-полукуб	122 • 221
7-простой ex	7-ортоплекс • 7-куб	7-полукуб	132 • 231 • 321
8-симплекс	8-ортоплекс • 8-куб	8- demicube	142 • 241 • 421
9-симплекс	9-ортоплекс • 9-куб	9-demicube
10-симплекс	10-ортоплекс • 10- куб	10-полукуб
n-симплекс	n-ортоплекс • n- куб	n-полукуб	1k2 • 2k1 • k21	n-пятиугольный многогранник
Темы: Семейства политопов • Правильный многогранник • Список правильных многогранников и соединений