В геометрии форма 5-многогранник - это пятимерный однородный многогранник. По определению, равномерный 5-многогранник является вершинно-транзитивным и построен из равномерного 4-многогранника фасетов.
Полный набор выпуклых равномерных 5-многогранников не был определен, но многие из них могут быть сделаны как конструкции Wythoff из небольшого набора групп симметрии. Эти операции представлены перестановками колец диаграмм Кокстера.
Правильные 5-многогранники могут быть представлены символом Шлефли {p, q, r, s}, с s {p, q, r} 4-многогранником фасетами вокруг каждой грани. Таких правильных многогранников ровно три, все выпуклые:
Не существует невыпуклых правильных многогранников в 5,6,7,8,9,10,11 и 12 измеренийх.
| Нерешенная задача в математике :. Что такое полный набор равномерных 5-многогранников? (больше нерешенных задач в математике) |
Известно 104 выпуклых однородных 5-многогранников, а также множество бесконечных семейств призм дуопризмы и дуопризм многоугольника и многогранника. Все, кроме большой антипризмы, основаны на конструкциях Витхоффа, симметрии отражения, созданной с помощью групп Кокстера.
5 - simplex - это обычная форма в семействе A 5. 5-куб и 5-ортоплекс регулярными формами в семействе B 5. Бифуркационный граф семейства D 5 содержит 5-ортоплекс, а также 5-полукуб, который является чередующимся 5-куб.
Каждый отражающий однородный 5-многогранник может быть построен в одной или нескольких отражающих точек в 5 измерениях с помощью конструкции Wythoff, представленной кольцами вокруг перестановок узлов в Диаграмма Кокстера. Зеркальные гиперплоскости могут быть сгруппированы по цветным узлам, разделенными четными ветвями. Группы симметрии вида [a, b, b, a] имеют расширенную симметрию [[a, b, b, a]], как и [3,3,3,3], удваивая порядок симметрии. Равномерные многогранники в этой группе с симметричными кольцами содержат эту расширенную симметрию.
Если все зеркала данного цвета не связаны (неактивны) в данном однородном многограннике, он будет иметь конструкцию с более низкой симметрией за счет удаления всех неактивных зеркал. Если все узлы данного цвета обведены (активны), операция чередования может сгенерировать новый 5-многогранник с хиральной симметрией, показанный как «пустые» обведенные узлы », но геометрия обычно не регулируется для создания единообразных решений.
 Соответствует диаграмм Кокстера между семействами и более высокая симметрия внутри диаграмм. Узлы одного цвета в каждой строке указывает идентичные зеркала. Черные узлы не активны в соответствиях.
Соответствует диаграмм Кокстера между семействами и более высокая симметрия внутри диаграмм. Узлы одного цвета в каждой строке указывает идентичные зеркала. Черные узлы не активны в соответствиях. | Группа. символ | Порядок | График Кокстера. | Кронштейн. обозначение | Коммутатор. подгруппа | Номер Кокстера.. (h) | Отражения. m = 5/2 h | ||
|---|---|---|---|---|---|---|---|---|
| A5 | 720 | [3,3,3,3] | [3,3, 3,3] | 6 | 15 | |||
| D5 | 1920 | [3,3,3] | [3,3,3] | 8 | 20 | |||
| B5 | 3840 | [4, 3,3,3] | 10 | 5 | 20 | |||
Существует 5 конечных категориальных однородных призматических семейств многогранников, основанных на непризматических однородных 4-многогранниках. Существует одно бесконечное семейство из 5 -полигопы на основе призмных однородных дуопризм {p} × {q} × {}.
| Группа Кокстера. | Порядок | Схема Кокстера. | Обозначение Кокстера. | Коммутатор. подгруппа | Отражения | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A4A1 | 120 | [3, 3,3,2] = [3,3,3] × [] | [3,3,3] | 10 | 1 | ||||||
| D4A1 | 384 | [3,2] = [3] × [] | [3] | 12 | 1 | ||||||
| B4A1 | 768 | [4,3,3,2] = [4,3,3] × [] | 4 | 12 | 1 | ||||||
| F4A1 | 2304 | [3,4,3,2] = [3,4,3] × [] | [3,4,3] | 12 | 12 | 1 | |||||
| H4A1 | 28800 | [5,3,3,2] = [3,4,3] × [] | [5,3,3] | 60 | 1 | ||||||
| Двупризматический (використовуйте 2p и 2q для эвенов.) | |||||||||||
| I2(p) I 2 (q) A 1 | 8pq | [p, 2, q, 2] = [p] × [q] × [] | [p, 2, q] | p | q | 1 | |||||
| I2(2p) I 2 (q) A 1 | 16pq | [2p, 2, q, 2] = [2p] × [ q] × [] | p | p | q | 1 | |||||
| I2(2p) I 2 (2q) A 1 | 32pq | [2p, 2,2q, 2] = [2p] × [2q] × [] | p | p | q | q | 1 | ||||
Существуют 3 категориальных однородных дуопризматических семейства многогранников, основанных на декартовых произведений однородных многогранников ников ников ников и правильные многоугольники : {q, r} × {p}.
| Группа Кокстера. | Порядок | Схема Кокстера. | Обозначение Кокстера. | Коммутатор. подгруппа | Отражения | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Призматические группы (використовуйте 2p для четных) | |||||||||||
| A3I2(p) | 48p | [3,3,2, p] = [3,3] × [p] | [(3,3), 2, p] | 6 | p | ||||||
| A3I2(2p) | 96p | [3,3,2,2p] = [3,3] × [2p] | 6 | p | p | ||||||
| B3I2(p) | 96p | [4,3,2, p] = [4,3] × [p] | 3 | 6 | p | ||||||
| B3I2(2p) | 192p | [4,3,2,2p] = [ 4,3] × [2p] | 3 | 6 | p | p | |||||
| H3I2(p) | 240p | [5,3,2, p] = [5,3] × [p] | [ (5,3), 2, p] | 15 | p | ||||||
| H3I2(2p) | 480p | [5,3,2,2p] = [5,3] × [2p] | 15 | p | p | ||||||
В результате получается: 19 + 31 + 8 + 45 + 1 = 104
Кроме того, существует:
Существует 19 форм, основанных на всех перестановках диаграмм Кокстера с одним или больше колец. (16 + 4-1 случаев)
Они названы Норманом Джонсоном из операций построения Wythoff на регулярном 5-симплексе (гексатерон).
Семейство A5 имеет симметрию порядка 720 (6 факториал ). 7 из 19 рисунков с симметрично окольцованными диаграммами Кокстера имеют удвоенную симметрию, порядок 1440.
Координаты однородных 5 -огранников с 5-симплексной симметрией могут быть сгенерированы как перестановки простых целых чисел в 6-мерном пространстве, все в гиперплоскости с вектором нормали (1,1,1,1,1,1).
| # | Базовая точка | Джонсон система имен. Имя Бауэрса и (акроним). Диаграмма Кокстера | количество элементов k-грани | Вершина. рисунок | Подсчет фасетов по местоположению: [3,3,3,3] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | |||||||||
| 1 | (0, 0,0,0,0,1) или (0,1,1,1,1,1) | 5-симплекс. гексатерон (hix). | 6 | 15 | 20 | 15 | 6 | 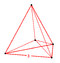 . {3,3,3} . {3,3,3} | (5).  . {3,3,3} . {3,3,3} | - | - | - | - |
| 2 | (0,0,0,0,1,1) или (0,0,1,1,1,1) | Ректифицированный 5-симплекс. ректификованный гексатерон (rix). | 12 | 45 | 80 | 60 | 15 | 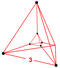 . t {3,3} × {} . t {3,3} × {} | (4).  . r {3,3,3} . r {3,3,3} | - | - | - | (2).  . {3,3,3} . {3,3,3} |
| 3 | (0,0,0,0,1,2) или (0,1,2,2,2,2) | Усеченный 5-симплекс. усеченный гексатерон (tix). | 12 | 45 | 80 | 75 | 30 |  . Тетрах.пир . Тетрах.пир | (4).  . t {3,3,3} . t {3,3,3} | - | - | - | (1).  . {3,3,3} . {3,3,3} |
| 4 | (0,0,0,1,1,2) или (0,1, 1,2,2,2) | Кантеллированный 5-симплекс. малый ромбовидный гексатерон (sarx). | 27 | 135 | 290 | 240 | 60 | (3).  . rr {3,3,3} . rr {3,3,3} | - | - | (1). | (1).  . r {3,3,3} . r {3,3,3} | |
| 5 | (0,0, 0,1,2,2) или (0,0,1,2,2, 2) | Bitruncated 5-simplex. bitruncated hexateron (bittix). | 12 | 60 | 140 | 150 | 60 |  | (3).  . 2t {3,3,3} . 2t {3,3,3} | - | - | - | (2).  . t {3,3,3} . t {3,3,3} |
| 6 | (0,0,0,1,2, 3) или (0,1,2,3,3,3) | Усеченный 5-симплекс. большой ромбовидный гексатерон (гаркс). | 27 | 135 | 290 | 300 | 120 | 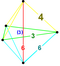 |  . tr {3,3,3} . tr {3,3,3} | - | - |  . t {3,3,3 } . t {3,3,3 } | |
| 7 | (0,0,1,1,1,2) или (0,1,1,1,2,2) | 5-симплексный раструб. гексатерон с малой призмой. | 47 | 255 | 420 | 270 | 60 |  | (2).  . t0,3 {3,3, 3} . t0,3 {3,3, 3} | - | (3).  . {3} × {3} . {3} × {3} | (3). | (1).  . r {3, 3,3} . r {3, 3,3} |
| 8 | (0,0,1,1,2,3) или (0,1,2,2, 3,3) | Выполнить усеченный 5-симплексный. призматоусеченный гексатерон (pattix). | 47 | 315 | 720 | 630 | 180 | 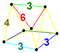 |  . t0,1,3 {3,3, 3} . t0,1,3 {3,3, 3} | - |  . rr {3,3,3} . rr {3,3,3} | ||
| 9 | (0,0, 1,2,2, 3) или (0,1,1,2,3,3) | Ранциантеллированный 5-симплексный. призматический гексатерон (пиркс). | 47 | 255 | 570 | 540 | 180 | 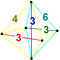 |  . t0,1,3 {3,3,3} . t0,1,3 {3,3,3} | - |  . {3} × {3} . {3} × {3} |  . 2t {3,3,3} . 2t {3,3,3} | |
| 10 | (0,0,1,2,3,4) или (0, 1,2,3, 4,4) | Бегунусеченное усеченное 5-симплексное. большой призматический гексатерон (гиппикс). | 47 | 315 | 810 | 900 | 360 |  . Irr. 5-элементный . Irr. 5-элементный |  . t0,1,2,3 {3,3,3} . t0,1,2,3 {3,3,3} | - |  . rr {3,3,3} . rr {3,3,3} | ||
| 11 | (0,1,1,1,2,3) или (0,1,2,2,2,3) | Стери усеченный 5-симплекс. клеточно-призматический гексатерон (каппикс). | 62 | 330 | 570 | 420 | 120 |  |  . t {3,3,3} . t {3,3,3} |  . t0,3 {3,3,3} . t0,3 {3,3,3} | |||
| 12 | (0,1,1,2,3,4) или (0,1,2,3,3,4) | Стериканитусеченное 5-симплексное. целое гексатерон (cograx). | 62 | 480 | 1140 | 1080 | 360 |  . tr {3,3,3} . tr {3,3,3} |  . t0,1,3 {3,3,3} . t0,1,3 {3,3,3} | ||||
| # | Базовая точка | Джонсон система имен. Имя и (акроним) Бауэрса. диаграмма Кокстера | количество элементов k-грани | Вершина. рисунок | Подсчет фасетов по местоположению: [3,3,3,3] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | |||||||||
| 13 | (0,0,0,1,1,1) | Двунаправленный 5- симплексный. додекатерон (точка). | 12 | 60 | 120 | 90 | 20 |  . {3} × {3} . {3} × {3} | (3).  . r {3,3,3} . r {3,3,3} | - | - | - | (3).  . r {3,3,3} . r {3,3,3} |
| 14 | (0, 0,1,1,2,2) | Бикантеллированный 5-симплекс. маленький биомбированный додекатерон (sibrid). | 32 | 180 | 420 | 360 | 90 |  | (2).  . rr {3,3,3} . rr {3,3,3} | - | (8).  . {3} × {3} . {3} × {3} | - | (2).  . rr {3,3,3} . rr {3,3,3} |
| 15 | (0,0,1, 2,3,3) | Бикантитуксус d 5-симплекс. большой биомбированный додекатерон (гибрид). | 32 | 180 | 420 | 450 | 180 | 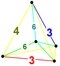 |  . tr {3,3,3} . tr {3,3,3} | - |  . {3} × {3} . {3} × {3} | - |  . tr {3,3,3} . tr {3,3,3} |
| 16 | (0,1,1,1,1, 2) | стерилизованный 5-симплексный. додекатерон с малыми ячейками (scad). | 62 | 180 | 210 | 120 | 30 |  . Irr. 16-элементный . Irr. 16-элементный | (1).  . {3,3,3} . {3,3,3} | (4). | (6).  . {3 } × {3} . {3 } × {3} | (4). | (1).  . {3,3,3} . {3,3,3} |
| 17 | (0, 1,1,2,2,3) | Просттеллированный 5-симплексный. малый клеточный додекатерон (карта). | 62 | 420 | 900 | 720 | 180 |  |  . rr {3,3,3} . rr {3,3,3} |  . {3} × {3} . {3} × {3} |  . rr {3,3,3} . rr {3,3,3} | ||
| 18 | (0,1,2,2,3,4) | Стериро-усеченный 5-симплекс. клеткапризматоусеченный додекатерон (каптид). | 62 | 450 | 1110 | 1080 | 360 |  . t0,1, 3 {3,3,3} . t0,1, 3 {3,3,3} |  . {6} × {6} . {6} × {6} |  . t0, 1, 3 {3, 3,3} . t0, 1, 3 {3, 3,3} | |||
| 19 | (0,1,2,3,4,5) | Омноусеченный 5-симплекс. большой клетчатый додекатерон (гокад). | 62 | 540 | 1560 | 1800 | 720 |  . Irr. {3,3,3} . Irr. {3,3,3} | (1).  . t0,1,2,3 {3,3,3} . t0,1,2,3 {3,3,3} | (1). | (1).  . {6} × {6} . {6} × {6} | (1). | (1).  . t0,1,2, 3 {3,3,3} . t0,1,2, 3 {3,3,3} |
Семейство B5 имеет симметрию порядка 3840 (5! × 2).
Это семейство 2-1 = 31 однородный имеет многогранник Витоффа, сгенерированный путем маркировки одного или нескольких узлов диаграмм Кокстера.
Для простоты оно разделено на две подгруппы, каждая с 12 формами и 7 «средние» формы, которые в равной степени принадлежат обеим.
Семейство 5-кубов из 5-многогранников задается выпуклыми оболочками базовых точек, перечисленных в следующей таблице, с учетом всех перестановок координат и знаков. Каждая базовая точка порождает отдельный однородный 5-многогранник. Все координаты соответствуют однородным 5-многогранникам с длиной ребра 2.
| # | Базовая точка | Имя. Диаграмма Кокстера | Количество элементов | Вершина. фигура | Фасет подсчитывается по местоположению: [4,3,3,3] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | |||||||||
| 20 | (0,0,0,0,1) √2 | 5-ортоплекс (tac). | 32 | 80 | 80 | 40 | 10 |  . {3,3,4} . {3,3,4} |  . {3,3, 3 } . {3,3, 3 } | - | - | - | - |
| 21 | (0,0,0,1,1) √2 | Выпрямленный 5-ортоплекс (крыса). | 42 | 240 | 400 | 240 | 40 |  . {} × {3,4} . {} × {3,4} |  .. {3,3,4} .. {3,3,4} | - | - | - |  . r {3,3,3} . r {3,3,3} |
| 22 | (0,0,0,1,2) √2 | Усеченный 5-ортоплекс (tot). | 42 | 240 | 400 | 280 | 80 |  . (Octah.pyr) . (Octah.pyr) |  . t {3,3,3} . t {3,3,3} |  . {3,3,3} . {3,3,3} | - | - | - |
| 23 | (0,0, 1, 1,1) √2 | Двунаправленный 5-куб (нит). (Двунаправленный 5-ортоплекс). | 42 | 280 | 640 | 480 | 80 |  . {4} × {3} . {4} × {3} |  . r {3,3,4} . r {3,3,4} | - | - | - |  . r {3,3,3} . r {3,3,3} |
| 24 | (0, 0,1,1,2) √2 | Сквозной 5 - ортоплекс (sart). | 82 | 640 | 1520 | 1200 | 240 |  . Призматический клин . Призматический клин | r {3,3, 4} | {} × {3,4} | - | - |  . rr {3,3,3} . rr {3,3,3} |
| 25 | (0,0,1,2,2) √ 2 | 5-ортоплекс с усеченным битом (бит). | 42 | 280 | 720 | 720 | 240 |  | т {3,3, 4} | - | - | - |  . 2t {3,3, 3} . 2t {3,3, 3} |
| 26 | (0,0,1,2,3) √2 | Кантоусеченный 5-ортоплекс (гарт). | 82 | 640 | 1520 | 1440 | 480 | 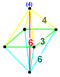 | rr{3,3,4} | {} × r {3,4} |  . {6} × {4} . {6} × {4} | - |  . t0,1,3 {3,3,3} . t0,1,3 {3,3,3} |
| 27 | (0,1,1,1,1) √ 2 | Выпрямленный 5-куб (рин). | 42 | 200 | 400 | 320 | 80 |  . {3,3} × {} . {3,3} × {} |  . r {4,3,3} . r {4,3,3} | - | - | - |  . {3,3,3} . {3,3,3} |
| 28 | (0,1,1,1,2) √2 | Ранцинированный 5- ортоплекс (спат). | 162 | 1200 | 2160 | 1440 | 320 |  | r {4,3,3} | - |  . {3} × {4} . {3} × {4} |  . t0,3 {3,3, 3} . t0,3 {3,3, 3} | |
| 29 | (0,1,1,2,2) √2 | Бикантеллированный 5-куб (сибрант). (двухканальный 5-ортоплекс). | 122 | 840 | 2160 | 1920 | 480 |  |  . rr {4,3, 3} . rr {4,3, 3} | - |  . {4} × {3} . {4} × {3} | - |  . rr {3, 3,3} . rr {3, 3,3} |
| 30 | (0,1,1,2,3) √2 | Выполнить усеченный 5-ортоплекс (pattit). | 162 | 1440 | 3680 | 3360 | 960 | 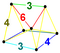 | rr{3,3,4} | {} × r {3,4} |  . {6} × {4} . {6} × {4} | - |  . t0,1,3 {3,3,3} . t0,1,3 {3,3,3} |
| 31 | (0,1,2, 2, 2) √ 2 | Обрезанный битами 5-куб (tan). | 42 | 280 | 720 | 800 | 320 |  |  . 2т {4, 3,3} . 2т {4, 3,3} | - | - | - |  . t {3,3,3} . t {3,3,3} |
| 32 | (0,1,2,2,3) √2 | Ранкантеллированный 5-ортоплекс (пирт). | 162 | 1200 | 2960 | 2880 | 960 |  | {} × t {3,4} | 2t {3,3,4} |  . {3} × {4} . {3} × {4} | - |  . t0,1,3 {3,3,3} . t0,1,3 {3,3,3} |
| 33 | (0, 1,2, 3,3) √2 | Двухкоординатно-усеченный 5-куб (гигрант). (Двухкоординатный 5-ортоплекс). | 122 | 840 | 2160 | 2400 | 960 |  |  . rr {4,3,3} . rr {4,3,3} | - |  . {4} × {3} . {4} × {3} | - |  . rr {3,3,3} . rr {3,3,3} |
| 34 | (0,1,2,3,4) √2 | Ранкоусеченный 5-ортоплекс (гиппит). | 162 | 1440 | 4160 | 4800 | 1920 |  | tr{3,3,4} | {} × t {3,4} |  . {6} × {4} . {6} × {4} | - |  . t0,1,2,3 {3,3,3} . t0,1,2,3 {3,3,3} |
| 35 | ( 1,1, 1,1,1) | 5-куб (отложено). | 10 | 40 | 80 | 80 | 32 |  . {3,3,3} . {3,3,3} |  . {4,3,3} . {4,3,3} | - | - | - | - |
| 36 | (1, 1,1,1,1). + (0,0,0,0,1) √2 | стерилизованный 5-кубический (скудный). (стерилизованный 5 -ортоплекс). | 242 | 800 | 1040 | 640 | 160 | 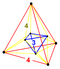 . Tetr.antiprm . Tetr.antiprm |  . {4, 3,3} . {4, 3,3} |  . {4, 3} × {} . {4, 3} × {} |  . {4} × {3} . {4} × {3} |  . {} × {3,3} . {} × {3,3} |  . {3,3,3} . {3,3,3} |
| 37 | (1, 1,1,1,1). + (0,0,0,1,1) √2 | Бегущий 5-кубик (диапазон). | 202 | 1240 | 2160 | 1440 | 320 | 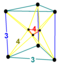 |  . t0,3 {4,3,3} . t0,3 {4,3,3} | - |  . {4 } × {3} . {4 } × {3} |  . {} × r {3,3} . {} × r {3,3} |  . {3,3,3} . {3,3,3} |
| 38 | (1,1,1,1,1). + (0,0,0,1,2) √2 | Стеритоусеченный 5 -ортоплекс (каппин). | 242 | 1520 | 2880 | 2240 | 640 | 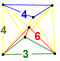 | t0,3 {3,3,4} | {} × {4,3} | - | - |  . t {3,3, 3} . t {3,3, 3} |
| 39 | (1,1,1,1, 1). + (0,0, 1,1,1) √2 | Сквозной 5-куб (сирн). | 122 | 680 | 1520 | 1280 | 320 |  . rr {4,3,3} . rr {4,3,3} | - | - |  . {} × {3,3} . {} × {3,3} |  . r {3,3,3} . r {3,3,3} | |
| 40 | (1, 1,1,1,1). + (0,0,1,1,2) √2 | Стерикантеллированный 5-куб (карнит). (Стерикантеллированный 5- ортоплекс). | 242 | 2080 | 4720 | 3840 | 960 |  |  . рр {4,3,3} . рр {4,3,3} |  . рр { 4,3} × {} . рр { 4,3} × {} |  . {4} × {3} . {4} × {3} |  . {} × rr {3,3} . {} × rr {3,3} |  . rr {3,3,3} . rr {3,3,3} |
| 41 | (1,1, 1,1,1). + (0, 0,1,2,2) √2 | Ранцителлированный 5-куб (принт). | 202 | 1240 | 2960 | 2880 | 960 |  |  . t0,1,3 {4,3,3} . t0,1,3 {4,3,3} | - |  . {4} × {3 } . {4} × {3 } |  . {} × t {3,3} . {} × t {3,3} |  . 2t {3, 3,3} . 2t {3, 3,3} |
| 42 | (1,1, 1,1,1). + (0,0,1,2,3) √2 | Стериканто-усеченный 5-ортоплекс (когарт). | 242 | 2320 | 5920 | 5760 | 1920 |  . {} × rr {3, 4} . {} × rr {3, 4} |  . t0, 1,3 {3, 3,4} . t0, 1,3 {3, 3,4} |  . {6} × {4} . {6} × {4} |  . {} × t {3,3} . {} × t {3,3} |  . tr {3, 3,3} . tr {3, 3,3} | |
| 43 | (1, 1,1, 1,1). + (0,1,1,1,1) √2 | Усеченный 5-куб (tan). | 42 | 200 | 400 | 400 | 160 |  . Tetrah.pyr . Tetrah.pyr |  . t {4,3,3} . t {4,3,3} | - | - | - |  . {3,3,3} . {3,3,3} |
| 44 | (1,1, 1,1,1). + (0,1,1,1,2) √2 | стерилизованное усеченное 5-куб (capt). | 242 | 1600 | 2960 | 2240 | 640 | 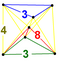 |  . t {4,3, 3} . t {4,3, 3} |  . t {4,3} × {} . t {4,3} × {} |  . {8} × {3} . {8} × {3} |  . {} × {3,3} . {} × {3,3} |  . t0,3 {3,3,3 } . t0,3 {3,3,3 } |
| 45 | (1,1,1,1,1). + (0,1,1,2,2) √2 | Выполнить усеченный 5-куб (паттин). | 202 | 1560 | 3760 | 3360 | 960 |  |  . t0,1,3 {4,3, 3} . t0,1,3 {4,3, 3} | {} × t {4,3} |  . {6} × {8} . {6} × {8} | {} × t {3,3} | t0,1,3 {3,3, 3}]] |
| 46 | (1,1, 1,1,1). + (0,1,1,2,3) √2 | Стериро-усеченный 5-куб (каптинт). (стерически усеченный 5-ортоплекс). | 242 | 2160 | 5760 | 5760 | 1920 |  . t0, 1,3 {4,3,3} . t0, 1,3 {4,3,3} |  . т {4, 3} × {} . т {4, 3} × {} |  . {8} × {6} . {8} × {6} |  . {} × t {3,3} . {} × t {3,3} |  . t0,1,3 {3,3,3} . t0,1,3 {3,3,3} | |
| 47 | (1,1,1,1,1). + (0,1,2, 2, 2) √2 | Кантоусеченный 5-куб (гирн). | 122 | 680 | 1520 | 1600 | 640 |  |  . tr {4,3,3} . tr {4,3,3} | - | - |  . {} × {3,3} . {} × {3,3} |  . t {3,3,3} . t {3,3,3} |
| 48 | (1,1, 1,1, 1). + (0,1,2,2,3) √2 | Стерико-усеченный 5-куб (когрин). | 242 | 2400 | 6000 | 5760 | 1920 |  . tr {4,3,3} . tr {4,3,3} |  . tr {4,3} × {} . tr {4,3} × {} |  . {8} × {3} . {8} × {3} |  . {} × t 0,2 {3,3} . {} × t 0,2 {3,3} |  . t0,1,3 {3,3, 3} . t0,1,3 {3,3, 3} | |
| 49 | (1,1,1,1,1). + (0,1,2, 3,3) √2 | Рунцикантитусеченный 5-куб (гиппин). | 202 | 1560 | 4240 | 4800 | 1920 |  |  . t0,1,2,3 {4,3, 3} . t0,1,2,3 {4,3, 3} | - |  . {8} × {3} . {8} × {3} |  . {} × t {3,3} . {} × t {3,3} |  . tr {3, 3,3} . tr {3, 3,3} |
| 50 | (1,1, 1,1,1). + (0,1,2,3,4) √2 | Усеченный 5-куб (гакнет). (5-ортоплекс без усечения). | 242 | 2640 | 8160 | 9600 | 3840 |  . Irr. {3,3,3} . Irr. {3,3,3} |  . tr {4,3} × {} . tr {4,3} × {} |  . tr {4,3} × {} . tr {4,3} × {} |  . {8} × {6} . {8} × {6} |  . {} × tr {3, 3} . {} × tr {3, 3} |  . t0,1,2,3 {3,3,3} . t0,1,2,3 {3,3,3} |
Семья D5 имеет симметрию порядка 1920 (5! х 2).
В этом семействе 23 однородных многогранника Витоффа из 3x8-1 перестановок D 5диаграмма Кокстера с одним или одним кольцами. 15 (2x8-1) повторяются из семейства B 5, а 8 являются уникальными для этого семейства.
| # | Диаграмма Кокстера. символ Шлефли символы. имена Джонсон и Бауэрс | Количество элементов | Вершина. рисунок | Фасеты по местоположению: | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | ||||||||
| 51 | 26 | 120 | 160 | 80 | 16 |  . t1{3,3,3} . t1{3,3,3} | {3,3,3} | t0(111) | - | - | - | |
| 52 | 42 | 280 | 640 | 560 | 160 |  | ||||||
| 53 | 42 | 360 | 880 | 720 | 160 | |||||||
| 54 | 82 | 480 | 720 | 400 | 80 | |||||||
| 55 | 42 | 360 | 1040 | 1200 | 480 | |||||||
| 56 | 82 | 720 | 1840 | 1680 | 480 | |||||||
| 57 | 82 | 560 | 1280 | 1120 | 320 | |||||||
| 58 | 82 | 720 | 2080 | 2400 | 960 | |||||||
Есть 5 конечных категорий однородных призматических семейств многогранников на основе непризматических однородных 4-многогранников :
Это призматическое семейство Имеется е т 9 форм :
Семейство A1x A 4 имеет симметрию порядка 240 (2 * 5!).
| # | Диаграмма Кокстера. и Шляфли. символы. Имя | Количество элементов | ||||
|---|---|---|---|---|---|---|
| Лицевые стороны | Ячейки | Грани | Ребра | Вершины | ||
| 59 | 7 | 20 | 30 | 25 | 10 | |
| 60 | 12 | 50 | 90 | 70 | 20 | |
| 61 | 12 | 50 | 100 | 100 | 40 | |
| 62 | 22 | 120 | 250 | 210 | 60 | |
| 63 | 32 | 130 | 200 | 140 | 40 | |
| 64 | 12 | 60 | 140 | 150 | 60 | |
| 65 | 22 | 120 | 280 | 300 | 120 | |
| 66 | 32 | 180 | 390 | 360 | 120 | |
| 67 | 32 | 210 | 540 | 600 | 240 | |
Это призматическое семейство имеет 16 форм. (Три являются общими с семейством [3,4,3] × [])
Семейство A1×B4 имеет симметрию порядка 768 (24!).
| # | Диаграмма Кокстера. и Шляфли. символы. Имя | Количество элементов | ||||
|---|---|---|---|---|---|---|
| Лицевые стороны | Ячейки | Грани | Ребра | Вершины | ||
| [16] | 10 | 40 | 80 | 80 | 32 | |
| 68 | 26 | 136 | 272 | 224 | 64 | |
| 69 | 26 | 136 | 304 | 320 | 128 | |
| 70 | 58 | 360 | 784 | 672 | 192 | |
| 71 | 82 | 368 | 608 | 448 | 128 | |
| 72 | 26 | 168 | 432 | 480 | 192 | |
| 73 | 58 | 360 | 880 | 960 | 384 | |
| 74 | 82 | 528 | 1216 | 1152 | 384 | |
| 75 | 82 | 624 | 1696 | 1920 | 768 | |
| 76 | 18 | 64 | 88 | 56 | 16 | |
| 77 | 26 | 144 | 288 | 216 | 48 | |
| 78 | 26 | 144 | 312 | 288 | 96 | |
| 79 | 50 | 336 | 768 | 672 | 192 | |
| 80 | 50 | 336 | 864 | 960 | 384 | |
| 81 | 82 | 528 | 1216 | 1152 | 384 | |
| 82 | 146 | 768 | 1392 | 960 | 192 | |
Это призматическое семейство имеет 10 форм.
Семейство A1x F 4 имеет симметрию порядка 2304 (2 * 1152). Три многогранника 85, 86 и 89 (зеленый фон) имеют двойную симметрию [[3,4,3], 2], порядок 4608. Последний, плоскодонная 24-элементная призма (синий фон) имеет [3,4,3, 2] симметрия, порядок 1152.
| # | диаграмма Кокстера. и Шлефли. символы. Имя | Количество элементов | ||||
|---|---|---|---|---|---|---|
| Фасеты | Ячейки | Лица | Ребра | Вершины | ||
| [77] | 26 | 144 | 288 | 216 | 48 | |
| [79] | 50 | 336 | 768 | 672 | 192 | |
| [80] | 50 | 336 | 864 | 960 | 384 | |
| 83 | 146 | 1008 | 2304 | 2016 | 576 | |
| 84 | 242 | 1152 | 1920 | 1296 | 288 | |
| 85 | 50 | 432 | 1248 | 1440 | 576 | |
| 86 | 146 | 1008 | 2592 | 2880 | 1152 | |
| 87 | 242 | 1584 | 3648 | 3456 | 1152 | |
| 88 | 242 | 1872 | 5088 | 5760 | 2304 | |
| [82] | 146 | 768 | 1392 | 960 | 192 | |
Это призматическое семейство имеет 15 форм :
Семейство A1x H 4 имеет симметрию порядка 28800 (2 * 14400).
| # | Диаграмма Кокстера. и Шляфли. символы. Имя | Количество элементов | ||||
|---|---|---|---|---|---|---|
| Лицевые стороны | Ячейки | Грани | Ребра | Вершины | ||
| 89 | 122 | 960 | 2640 | 3000 | 1200 | |
| 90 | 722 | 4560 | 9840 | 8400 | 2400 | |
| 91 | 722 | 4560 | 11040 | 12000 | 4800 | |
| 92 | 1922 | 12960 | 29040 | 25200 | 7200 | |
| 93 | 2642 | 12720 | 22080 | 16800 | 4800 | |
| 94 | 722 | 5760 | 15840 | 18000 | 7200 | |
| 95 | 1922 | 12960 | 32640 | 36000 | 14400 | |
| 96 | 2642 | 18720 | 44880 | 43200 | 14400 | |
| 97 | 2642 | 22320 | 62880 | 72000 | 28800 | |
| 98 | 602 | 2400 | 3120 | 1560 | 240 | |
| 99 | 722 | 5040 | 10800 | 7920 | 1440 | |
| 100 | 722 | 5040 | 11520 | 10080 | 2880 | |
| 101 | 1442 | 11520 | 28080 | 25200 | 7200 | |
| 102 | 1442 | 11520 | 31680 | 36000 | 14400 | |
| 103 | 2642 | 18720 | 44880 | 43200 | 14400 | |
Большая антипризменная призма - единственная известная выпуклая неуитхоффовская униформа 5 -полигон. Он имеет 200 вершин, 1100 ребер, 1940 граней (40 пятиугольников, 500 квадратов, 1400 треугольников), 1360 ячеек (600 тетраэдров, 40 пятиугольных антипризм, 700 треугольных призм, 20 пятиугольных призм ) и 322 гиперячейки (2 большие антипризмы  , 20 пятиугольные антипризмы призмы
, 20 пятиугольные антипризмы призмы  и 300 тетраэдрические призмы
и 300 тетраэдрические призмы  ).
).
| # | Имя | Количество элементов | ||||
|---|---|---|---|---|---|---|
| Грани | Ячейки | Лица | Ребра | Вершины | ||
| 104 | . Gappip | 322 | 1360 | 1940 | 1100 | 200 |
Построение отражающих 5-мерных однородных многогранников выполняется с помощью процесса конструирования Wythoff и представляется с помощью диаграммы Кокстера, где каждый узел представляет собой зеркало. Узлы обведены кружком, чтобы обозначить, какие зеркала активны. Сгенерированный полный набор однородных многогранников основан на уникальных перестановках кольцевых узлов. Равномерные 5-многогранники названы в соответствии с правильными многогранниками в каждом семействе. У некоторых семейств есть два обычных конструктора, поэтому их можно назвать двумя способами.
Вот основные операторы, доступные для построения и именования однородных 5-многогранников.
Последняя операция, пренебрежение и, в более общем смысле, чередование - это операция, которая может создавать неотражающие формы. Они нарисованы «полыми кольцами» в узлах.
Призматические формы и бифуркационные графы могут использовать ту же нотацию индексации усечения, но для ясности требуют явной системы нумерации узлов.
| Операция | Расширенный. символ Шлефли | диаграмма Кокстера | Описание | |
|---|---|---|---|---|
| Родитель | t0{p, q, r, s} | {p, q, r, s} | Любой правильный 5-многогранник | |
| Ректифицированный | t1{p,q,r,s} | r {p, q, r, s} | Края полностью обрезаны до отдельных точек. 5-многогранник теперь имеет комбинированные грани родительского и двойственного. | |
| Birectified | t2{p,q,r,s} | 2r {p, q, r, s} | Биректификация сокращает лица до точек, ячейки - до их duals. | |
| Trirectified | t3{p,q,r,s} | 3r {p, q, r, s} | Триректификация сокращает ячейки до точек. (Двойное исправление) | |
| Квадриректификация | t4{p,q,r,s} | 4r {p, q, r, s} | Квадриректификация превращает 4-грани в точки. (Двойной) | |
| Урезанный | t0,1{p,q,r,s} | t {p, q, r, s} | Каждый оригинал vertex is cut off, with a new face filling the разрыв. У усечения есть степень свободы, которая имеет одно решение, которое создает единый усеченный 5-многогранник. 5-многогранник имеет свои исходные грани, удвоенные по сторонам, и содержит грани двойственного..  | |
| Cantellated | t0,2 {p, q, r, s} | rr { p, q, r, s} | В дополнение к усечению вершин, каждое исходное ребро скашивается, и на их месте появляются новые прямоугольные грани..  | |
| Runcinated | t0,3 {p, q, r, s} | Runcination уменьшает ячейки и создает новые ячейки в вершинах и краях. | ||
| Стерифицированный | t0,4{p,q,r,s} | 2r2r {p, q, r, s} | Стерилизация уменьшает фасеты и создает новые фасеты (гиперячейки) в вершинах и ребрах в зазорах. (То же, что и операция расширения для 5-многогранников.) | |
| Омноусеченный | t0,1,2,3,4 {p, q, r, s} | Все четыре применяются операторы, усечение, кантелляция, ранцинирование и стерилизация. | ||
| Половина | h {2p, 3, q, r} | Чередование, то же самое, что | ||
| Cantic | div class="ht"{2p, 3, q, r} | То же как | ||
| Runcic | h3{2p, 3, q, r} | То же, что и | ||
| Runcicantic | div class="ht",3 {2p, 3, q, r} | То же, что и | ||
| Стерический | h4{2p, 3, q, r} | То же, что | ||
| Рунцистерический | h3,4 {2p, 3, q, r} | То же, что | ||
| Stericantic | div class="ht",4 {2p, 3, q, r} | То же, что и | ||
| Steriruncicantic | div class="ht",3,4 {2p, 3, q, r} | То же, что и | ||
| Snub | s {p, 2q, r, s} | Альтернативное усечение | ||
| Snub rectified | sr {p, q, 2r, s} | Чередование усеченного исправления | ||
| ht0,1,2,3 {p, q, r, s} | Чередование циклического усечения | |||
| Полное курносое | ht0,1,2,3,4 {p, q, r, s} | Чередование всестороннего усечения | ||
 Соответствия диаграмм Кокстера между семействами и более высокая симметрия внутри диаграмм. Узлы одного цвета в каждом ряду одинаковые одинаковые зеркала. Черные узлы не активны в корреспонденции.
Соответствия диаграмм Кокстера между семействами и более высокая симметрия внутри диаграмм. Узлы одного цвета в каждом ряду одинаковые одинаковые зеркала. Черные узлы не активны в корреспонденции. Существует пять фундаментальных аффинных групп Кокстера и 13 призматических групп, которые генерируют регулярные и однородные мозаики в евклидовом 4-пространстве.
| # | Группа Кокстера | Диаграмма Кокстера | Формы | ||
|---|---|---|---|---|---|
| 1 |  | [3pting | [(3, 3,3,3)] | 7 | |
| 2 |  | [4,3,3,4] | 19 | ||
| 3 |  | [4,3,3 impression | [4,3,3,4,1] | 23 (8 новых) | |
| 4 |  | [3 visible | [1,4,3,3,4,1] | 9 (0 новых) | |
| 5 |  | [3,4,3,3] | 31 (21 новых) | ||
Есть три правильных сот евклидова 4-мерного пространства:
Другие семейства, образующие однородные соты:
 ,
,  : [3]
: [3] не -Wythoffian однородные мозаики в четырехмерном пространстве также существуют за счет удлинения (вставки слоев) и вращения (вращения слоев) этих отражающих форм.
| # | Группа Кокстера | Диаграмма Кокстера | |
|---|---|---|---|
| 1 |  × × | [4,3,4,2, ∞] | |
| 2 |  × × | [4,3,2, ∞] | |
| 3 |  × × | [3,2, ∞] | |
| 4 |  × × x x | [4, 4,2, ∞, 2, ∞] | |
| 5 |  × × x x | [6,3,2, ∞, 2, ∞] | |
| 6 |  × × x x | [3,2, ∞, 2, ∞] | |
| 7 |  × × x x x x | [∞, 2, ∞, 2, ∞, 2, ∞] | |
| 8 |  x x | [3,2,3] | |
| 9 |  × × | [3,2,4,4] | |
| 10 |  × × | [3,2,6,3] | |
| 11 |  × × | [4,4,2,4,4] | |
| 12 |  × × | [4,4,2,6, 3] | |
| 13 |  × × | [6, 3,2,6,3 ] | |
В пространстве H существует пять видов выпуклых регулярных сот типа и четыре звездчатых сот:
| Имя соты | Schläfli. Символ. {p, q, r, s} | Диаграмма Кокстера | Фасет. тип. {p, q, r} | Ячейка. тип. {p, q} | Грань. тип. {p} | Грань. рисунок. {s} | Край. рисунок. {r, s} | Vertex. figure. {q, r, s} | Двойной |
|---|---|---|---|---|---|---|---|---|---|
| 5-элементный порядок 5 | {3,3,3,5} | {3,3,3} | {3, 3} | {3} | {5} | {3,5} | {3,3,5} | {5,3,3,3} | |
| Заказ-3, 120 ячеек | {5,3,3,3} | {5,3,3} | {5, 3} | {5} | {3} | {3,3} | {3,3,3} | {3,3,3,5} | |
| Тессерактика порядка 5 | {4,3,3,5} | {4, 3,3} | {4,3} | {4} | {5} | {3,5} | {3,3,5} | {5,3, 3,4} | |
| Заказ-4, 120 ячеек | {5,3,3,4} | {5,3, 3} | {5,3} | {5} | {4} | {3,4} | {3,3,4} | {4,3, 3,5} | |
| З аказ-5, 120 ячеек | {5,3,3,5} | {5,3, 3} | {5,3} | {5} | {5} | {3,5} | {3, 3,5} | Самодвойственный |
В пространстве H четыре обычные звезды-соты:
| Имя соты | Schläfli. Символ. {p, q, r, s} | Кокс диаграмма этера | Facet. тип. {p, q, r} | Ячейка. тип. {p, q} | Лицо. тип. {p} | Грань. фигура. {s} | Край. фигура. {r, s} | Вершина. фигура. {q, r, s} | Двойной |
|---|---|---|---|---|---|---|---|---|---|
| Малый звездчатый 120-элементный порядок 3 | {5 / 2,5,3,3} | {5/2, 5,3} | {5 / 2,5} | {5} | {5} | {3,3} | {5,3,3} | {3,3, 5,5 / 2} | |
| Заказ-5/2, 600 ячеек | {3,3,5,5 / 2} | {3,3,5} | {3, 3} | {3} | {5/2} | {5, 5/2} | {3,5,5 / 2 } | {5 / 2,5,3,3} | |
| Икосаэдр порядка 5, 120 ячеек | {3,5,5 / 2,5} | {3,5,5 / 2} | {3,5} | {3} | {5} | {5 / 2,5} | {5,5 / 2,5} | {5,5 / 2,5,3} | |
| Большой 120-элементный заказ-3 | {5,5 / 2,5,3} | {5,5 / 2,5} | {5,5 / 2} | {5} | {3} | {5,3} | {5/2, 5,3} | {3,5, 5 / 2,5} |
Имеется 5 компактных гиперболических групп Кокстера ранга 5, каждую из порождает однородные соты в гиперболическом 4-м изображении как перестановки колец диаграмм Кокстера. Также 9 паракомпактных гиперболических групп Кокстера ранга 5, каждая из которых существует порождает однородные соты в 4-пространства как перестановки колец диаграмм Кокстера. Паракомпактные группы образуют соты с бесконечными фасетами или фигурами вершин.
|
|  = [3,3,3,5]: = [3,3,3,5]:
|
|
|
|
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | ||||||||
| Треугольник | Квадрат | п-угольник | Шестиугольник | Пентагон | ||||||||
| Тетраэдр | Октаэдр • Куб | Демикуб | Додекаэдр • Икосаэдр | |||||||||
| 5 ячеек | 16 ячеек • Tesseract | Demitesseract | 24 ячейки | 120 ячеек • 600 ячеек | ||||||||
| 5 симплекс | 5-ортоплекс • 5-куб | 5-полукуб | ||||||||||
| 6-симплекс | 6-ортоплекс • 6-куб | 6-полукуб | 122 • 221 | |||||||||
| 7-симплекс | 7-ортоплекс • 7-куб | 7-полукуб | 132 • 231 • 321 | |||||||||
| 8-симплекс | 8-ортоплекс • 8-куб | 8-полукуб | 142 • 241 • 421 | |||||||||
| 9-симплекс | 9-ортоплекс • 9-куб | 9-полукуб | ||||||||||
| 10-симплекс | 10-ортоплекс • 10-куб | 10-полукуб | ||||||||||
| n-симплекс | n-ортоплекс • n- куб | n-демикуб | 1k2 • 2k1 • k21 | n-пятиугольный многогранник | ||||||||
| Темы: Семейства многогранников • Правильный многогранник • Список правильных многоугольников вершины и соединения | ||||||||||||
| ||||||
|---|---|---|---|---|---|---|
 |  |  |  |  / /  / /  | ||
| {3} | δ3 | hδ3 | qδ3 | Гексагональный | ||
| {3} | δ4 | hδ4 | qδ4 | |||
| {3} | δ5 | hδ5 | qδ5 | 24-элементный сотовый | ||
| {3} | δ6 | hδ6 | qδ6 | |||
| {3} | δ7 | hδ7 | qδ7 | 222 | ||
| {3} | δ8 | hδ8 | qδ8 | 133 • 331 | ||
| {3} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 | ||
| {3} | δ10 | hδ10 | qδ10 | |||
| {3} | δ n | hδ n | qδ n | 1 k2 • 2 k1 • k21 | ||