| Выпрямленная 5-ячеечная | ||
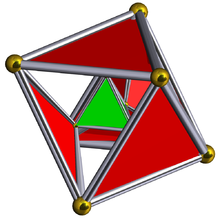 . диаграмма Шлегеля с показанными 5 тетраэдрическими ячейками. . диаграмма Шлегеля с показанными 5 тетраэдрическими ячейками. | ||
| Тип | Равномерный 4-многогранник | |
| символ Шлефли | t1{3,3,3} или r {3,3,3}. {3} =  | |
| Диаграмма Кокстера-Дынкина | ||
| Ячейки | 10 | 5 {3,3} |
| Грани | 30 {3} | |
| Ребра | 30 | |
| Вершины | 10 | |
| Вершинная фигура | 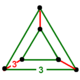 . Треугольная призма . Треугольная призма | |
| Группа симметрии | A4, [3,3,3], порядок 120 | |
| Многоугольник Петри | Пентагон | |
| Свойства | выпуклый, изогональный, изотоксальный | |
| Равномерный индекс | 1 2 3 | |
В четырехмерной геометрии, выпрямленный 5-элементный - это равномерный 4-многогранник, состоящий из 5 правильных тетраэдрических и 5 правильных октаэдрических ячеек. Каждое ребро имеет один тетраэдр и два октаэдра. Каждая вершина состоит из двух тетраэдров и трех октаэдров. Всего у него 30 треугольных граней, 30 ребер и 10 вершин. Каждая вершина окружена 3 октаэдрами и 2 тетраэдрами; вершинная фигура представляет собой треугольную призму.
Топологически, при ее высшей симметрии [3,3,3], существует только одна геометрическая форма, содержащая 5 правильных тетраэдров и 5 выпрямленных тетраэдров ( геометрически такой же, как правильный октаэдр). Он также топологически идентичен сегментохорону тетраэдр-октаэдр.
фигура вершины выпрямленной 5-ячейки представляет собой однородную треугольную призму, образованную тремя октаэдры по сторонам и два тетраэдра на противоположных концах.
Несмотря на то, что они имеют такое же количество вершин, что и ячейки (10), и такое же количество ребер, что и грани ( 30), выпрямленная 5-ячейка не является самодуальной, поскольку вершинная фигура (однородная треугольная призма) не является двойственной ячейкам полихорона.
В матрице конфигурации показаны все числа инцидентов между элементами. Числа диагонального f-вектора выводятся с помощью конструкции Wythoff, разделяющей полный порядок групп в порядке подгрупп, удаляя по одному зеркалу за раз.
| A4 | k-face | fk | f0 | f1 | f2 | f3 | k-цифра | Примечания | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A2A1 | () | f0 | 10 | 6 | 3 | 6 | 3 | 2 | {3} x {} | A4/A2A1= 5! / 3! / 2 = 10 | |
| A1A1 | {} | f1 | 2 | 30 | 1 | 2 | 2 | 1 | {} v () | A4/A1A1= 5! / 2/2 = 30 | |
| A2A1 | {3} | f2 | 3 | 3 | 10 | * | 2 | 0 | {} | A4/A2A1= 5! / 3! / 2 = 10 | |
| A2 | 3 | 3 | * | 20 | 1 | 1 | A4/A2= 5! / 3! = 20 | ||||
| A3 | r {3,3} | f3 | 6 | 12 | 4 | 4 | 5 | * | () | A4/A3= 5! / 4! = 5 | |
| A3 | {3,3} | 4 | 6 | 0 | 4 | * | 5 | ||||
Вместе с симплексом и 24-ячейкой, эта фигура и ее двойственный (многогранник с десять вершин и десять треугольных бипирамид фасет) был одним из первых известных 2-простых 2-симплициальных 4-многогранников. Это означает, что все его двумерные грани и все двумерные грани двойственного объекта являются треугольниками. В 1997 году Том Брэйден нашел еще одну двойную пару примеров, склеив два выпрямленных 5-элементных элемента вместе; с тех пор было построено бесконечно много 2-простых 2-симплициальных многогранников.
Это один из трех полуправильных 4-многогранников, состоящих из двух или более клетки, которые являются Платоновыми телами, обнаруженными Торольдом Госсетом в его статье 1900 года. Он назвал его тетроктаэдром, потому что он состоит из клеток тетраэдра и октаэдра.
E. Л. Элте определил его в 1912 году как полуправильный многогранник, обозначив его как tC 5.
| Ak. плоскость Кокстера | A4 | A3 | A2 |
|---|---|---|---|
| График |  |  | 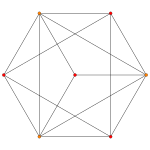 |
| Двугранная симметрия | [5] | [4] | [3] |
 . стереографическая проекция. (с центром на октаэдре ) . стереографическая проекция. (с центром на октаэдре ) | 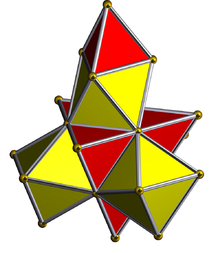 . Сеть (многогранник) . Сеть (многогранник) |
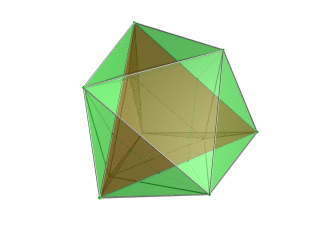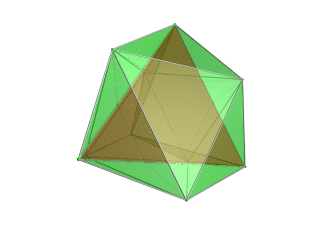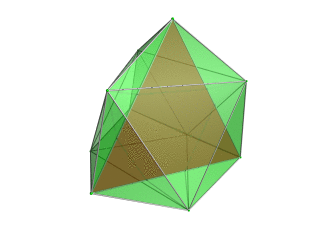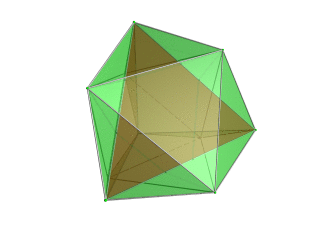 | Тетраэдр -центрированная перспективная проекция в трехмерное пространство, при этом ближайший тетраэдр к четырехмерной точке обзора отображается красным цветом, а 4 окружающих его октаэдра - зеленым.Клетки, лежащие на дальней стороне многогранника, отбракованы для ясности (хотя их можно различить по контуры края). Поворот выполняется только для трехмерного проекционного изображения, чтобы показать его структуру, а не для поворота в четырехмерном пространстве. |
Декартовы координаты вершин выпрямленной 5-ячейки с центром в начале координат и длиной ребра 2:
| Координаты | |
|---|---|
Проще говоря, вершины выпрямленной 5-ячейки могут быть расположены на гиперплоскости в 5- пространство как перестановки (0,0,0,1,1) или (0,0,1,1,1). Эти конструкции можно рассматривать как положительные или грани выпрямленного пентакросса или двунаправленного пентеракта соответственно.
Выпуклая оболочка выпрямленной 5-ячеечной и двойственной ей (при условии, что они конгруэнтны) представляет собой неоднородный полихорон, состоящий из 30 ячеек: 10 тетраэдров, 20 октаэдров (как треугольные антипризмы) и 20 вершин. Его вершинная фигура - треугольный двустворчатый.
Этот многогранник является вершинной фигурой 5-полукуба, а фигура края однородного многогранника 221.
Это также один из 9 равномерных 4-многогранников, построенных из [3,3,3] группы Кокстера.
| Название | 5-элементный | усеченный 5-элементный | выпрямленный 5-элементный | сквошенный 5-элементный | усеченный 5-элементный | усеченный 5-элементный | ранцинированный 5-элементный | runcitruncated 5-cell | omnitruncated 5-cell |
|---|---|---|---|---|---|---|---|---|---|
| Schläfli. symbol | {3,3,3}. 3r {3,3,3} | t {3,3,3}. 2t {3,3,3} | r {3,3,3}. 2r {3,3,3} | rr {3,3,3}. r2r {3,3,3} | 2t {3,3,3} | tr {3,3,3}. t2r {3,3,3} | t0,3 {3,3,3} | t0,1,3 {3,3,3}. t 0, 2,3 {3,3,3} | t0,1,2,3 {3,3,3} |
| Диаграмма Кокстера. | |||||||||
| Диаграмма Шлегеля. |  |  |  |  |  |  |  |  |  |
| A4. Плоскость Кокстера. График |  |  |  |  |  |  |  |  |  |
| A3Плоскость Кокстера. График |  |  |  |  |  |  |  |  |  |
| A2Плоскость Кокстера. График |  |  |  |  |  |  |  |  |  |
Выпрямленная 5-ячейка является второй в размерной серии полуправильных многогранников. Каждый прогрессивный однородный многогранник строится как фигура вершины предыдущего многогранника. Торольд Госсет идентифицировал эту серию в 1900 году как содержащую все фасеты правильного многогранника, содержащие все симплексы и ортоплексы (тетраэдры и октаэдры в случае выпрямленного 5-ячеечного). символ Кокстера для выпрямленных 5-ячеек - это 0 21.
| k21цифр в n-мерном | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| пространстве | Конечном | евклидовом | Гиперболическая | ||||||||
| En | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| группа Кокстера. | E3=A2A1 | E4=A4 | E5=D5 | E6 | E7 | E8 | E9=  = E 8 = E 8 | E10=  = E 8 = E 8 | |||
| Диаграмма Кокстера. | |||||||||||
| Симметрия | [3] | [3] | [3] | [3] | [3] | [3] | [3] | [3] | |||
| Заказ | 12 | 120 | 1,920 | 51,840 | 2,903,040 | 696,729,600 | ∞ | ||||
| График |  |  |  |  |  |  | - | - | |||
| Название | −121 | 021 | 121 | 221 | 321 | 421 | 521 | 621 | |||
| Разм. | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| Имя. Кокстер | Шестиугольник. | Октаэдр.  | Decachoron. | Додекатерон.  | Тетрадекапетон. | Гексадекапетон.  | Octadecazetton. |
| Изображения |  |   |   |   |   |   |   |
| Фигура вершины | () v () |  . {} × {} . {} × {} |  . {} v { } . {} v { } |  . {3} × {3} . {3} × {3} |  . {3} v {3} . {3} v {3} | {3,3} x {3,3} |  . {3,3} v {3,3} . {3,3} v {3,3} |
| Фасеты | {3} | t {3,3} | r {3,3,3} | 2t {3,3,3,3} | 2r {3,3, 3,3,3} | 3t {3,3,3,3,3} | |
| As. пересекающиеся. двойные. симплексы |  . . |  . . |   . . |
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | ||||||||
| Треугольник | Квадрат | p-угольник | Шестиугольник | Пентагон | ||||||||
| Тетраэдр | Октаэдр • Куб | Демикуб | Додекаэдр • Икосаэдр | |||||||||
| 5-элементный | 16-элементный • Тессеракт | Demitesseract | 24-элементный | 120-элементный • 600-элементный | ||||||||
| 5-симплекс | 5-ортоплекс • 5-куб | 5-полукуб | ||||||||||
| 6-симплекс | 6-ортоплекс • 6-куб | 6-полусуплекс | 122 • 221 | |||||||||
| 7-симплекс | 7-ортоплекс • 7-куб | 7-полукуб | 132 • 231 • 321 | |||||||||
| 8-симплекс | 8-ортоплекс • 8-куб | 8-полукуб | 142 • 241 • 421 | |||||||||
| 9-симплекс | 9-ортоплекс • 9-куб | 9-полукуб | ||||||||||
| 10-симплекс | 10-ортоплекс • 10-куб | 10-полукуб | ||||||||||
| n-симплекс | n-ортоплекс • n- куб | n-полукуб | 1k2 • 2k1 • k21 | n-пятиугольный многогранник | ||||||||
| Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений | ||||||||||||