| Курчавая 24-ячейка | ||
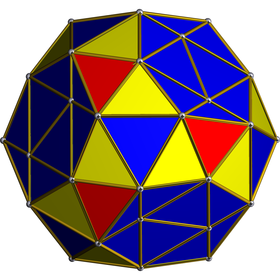 . Ортогональная проекция. Центрирована на гиперплоскости одного икосаэдра. . Ортогональная проекция. Центрирована на гиперплоскости одного икосаэдра. | ||
| Тип | Равномерный 4-многогранник | |
| символ Шлефли | s {3,4,3}. sr {3,3,4}. s {3} | |
| Coxeter- Диаграммы Дынкина. |
| |
| Ячейки | 144 | 96 3.3.3 (наклонная) |
| Грани | 480 {3} | |
| Ребра | 432 | |
| Вершины | 96 | |
| Вершинная фигура | 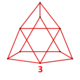 . (Треугольный икосаэдр ) . (Треугольный икосаэдр ) | |
| Группы симметрии | [3,4,3], ½F 4, порядок 576 [(3, 3), 4], ½B 4, порядок 192. [3], ½D 4, порядок 96 | |
| Свойства | выпуклый | |
| Равномерный индекс | 30 31 32 | |
 Вершинная фигура : Трехмерный икосаэдр. 8 граней:.
Вершинная фигура : Трехмерный икосаэдр. 8 граней:. 
 . 5 3.3.3 и 3 3.3.3.3.3
. 5 3.3.3 и 3 3.3.3.3.3 В геометрии курносый 24-ячейка или курносый дисикозитетрахорон представляет собой выпуклый равномерный 4-многогранник, составленный из 120 правильных тетраэдрических и 24 икосаэдрических ячеек. В каждой вершине встречаются пять тетраэдров и три икосаэдра. Всего у него 480 треугольных граней, 432 ребра и 96 вершин. Его можно построить из 600 ячеек, уменьшив избранное подмножество икосаэдрических пирамид и оставив только их икосаэдрические основания, тем самым удалив 480 тетраэдров и заменив их 24 икосаэдрами.
Топологически, при высшей симметрии [3,4,3], как чередование усеченных 24-ячеечных, он содержит 24 пиритоэдра (икосаэдр с T h симметрия), 24 правильных тетраэдра и 96 треугольных пирамид.
Это один из трех полурегулярные 4-многогранники, состоящие из двух или более ячеек, которые являются Платоновыми телами, обнаруженными Торольдом Госсетом в его статье 1900 года. Он назвал его тетрикосаэдром, потому что он состоит из клеток тетраэдра и икосаэдра. (Два других - это выпрямленный 5-элементный и выпрямленный 600-элементный.)
Курточная 24-ячейка связана с усеченными 24-ячейками операцией чередования. Половина вершин удаляется, 24 усеченный октаэдр ячейки становятся 24 ячейками икосаэдра, 24 куба становятся 24 ячейками тетраэдра, а 96 удаленных пустот вершин создают 96 новых ячеек тетраэдра.
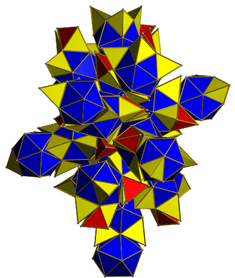 . A net курносой 24-ячейки с синими икосаэдрами, а также красных и желтых тетраэдров. . A net курносой 24-ячейки с синими икосаэдрами, а также красных и желтых тетраэдров. |
Курчавая 24-ячейка также может быть построена путем конкретного уменьшения 600-ячейки : путем удаления 24 вершин из 600-ячеек, соответствующих ячейкам записанного 24-ячеечного, а затем взяв выпуклая оболочка остальных вершин. Это эквивалентно удалению 24 икосаэдрических пирамид из 600 ячеек.
| Курточная 24-ячейка | 600-ячейка |
|---|---|
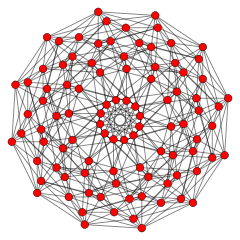 |  |
Вершины курносой 24-ячейки с центром в начале 4-мерного пространства и ребрами длины 2, получаются путем взятия четных перестановок из
(где φ = (1 + √5) / 2 - золотое сечение ).
Эти 96 вершин можно найти, разделив каждое из 96 ребер 24-ячеечной на золотое сечение последовательным образом, почти так же, как 12 вершин икосаэдр или «курносый октаэдр» можно получить, разделив 12 ребер октаэдра в золотом сечении. Это делается путем размещения векторов по краям 24-ячеек таким образом, чтобы каждая двумерная грань была ограничена циклом, а затем аналогичным образом разбивая каждое ребро на золотое сечение в направлении его вектора. 96 вершин курносой 24-ячеек вместе с 24 вершинами 24-ячеек образуют 120 вершин 600-ячеечной.
Каждая ячейка икосаэдра соединена с 8 другие икосаэдрические ячейки на 8 треугольных гранях в положениях, соответствующих вписывающему октаэдру. Остальные треугольные грани соединены с тетраэдрическими ячейками, которые образуются парами, имеющими общий край на икосаэдрической ячейке.
Тетраэдрические ячейки можно разделить на две группы, по 96 ячеек и 24 ячейки соответственно. Каждая тетраэдрическая ячейка в первой группе соединяется своими треугольными гранями с 3 икосаэдрическими ячейками и одной тетраэдрической ячейкой во второй группе, в то время как каждая тетраэдрическая ячейка во второй группе присоединяется к 4 тетраэдрам в первой группе.
Курносая 24-ячейка имеет три вершинно-транзитивных раскраски на основе конструкции Wythoff на группе Кокстера, из которого чередуется : F 4 определяет 24 взаимозаменяемых икосаэдра, тогда как группа B 4 определяет две группы икосаэдров с отсчетом 8:16, и наконец, группа D 4 имеет 3 группы икосаэдров со счетами 8: 8: 8.
| Симметрия. (порядок) | Конструктивное имя | Диаграмма Кокстера-Дынкина. Расширенная символ Шлефли | Вершинная фигура. (Треугольный икосаэдр ) | Ячейки. (окрашены в виде граней на фигурах вершин) |
|---|---|---|---|---|
| ½F4. [3,4,3]. (576) | Курносая, 24 ячейки | 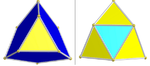 | Один набор из 24 икосаэдров (синий). Два набора тетраэдров: 96 (желтый) и 24 (голубой) | |
| ½B4. [(3,3), 4]. (192) | Snub-ректифицированный 16-элементный | 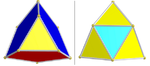 | Два набора икосаэдров: 8, по 16 (красный и синий). Два набора тетраэдров: 96 (желтый) и 24 (голубой) | |
| ½D4. [3]. (96) | Omnisnub demitesseract | 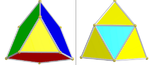 | Три набора по 8 икосаэдров (красный, зеленый и синий). Два набора тетраэдров: 96 (желтый) и 24 (голубой)) |
И наоборот, 600-элементная ячейка может быть сконструирована из курносой 24-элементной ячейки путем добавления к ней 24 икосаэдрических пирамид.
| Плоскость Кокстера | F4 | B4 |
|---|---|---|
| График |  | 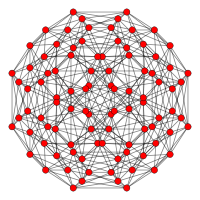 |
| Двугранная симметрия | [12] | [8/2 ] |
| Плоскость Кокстера | D4/ B 3 / A 2 | B2/ A 3 |
| График | 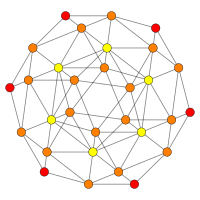 |  |
| Двугранная симметрия | [6 ] | [ 4] |
| Перспективные проекции | |
|---|---|
 . Перспективные проекции с центром в икосаэдрической ячейке с четырехмерной точкой обзора, расположенной на расстоянии, в 5 раз превышающем радиус центра вершины. Ближайшая ячейка икосаэдра отображается сплошным цветом, а остальные ячейки - краями. Клетки, обращенные от точки обзора 4D, отбраковываются, чтобы уменьшить визуальный беспорядок. . Перспективные проекции с центром в икосаэдрической ячейке с четырехмерной точкой обзора, расположенной на расстоянии, в 5 раз превышающем радиус центра вершины. Ближайшая ячейка икосаэдра отображается сплошным цветом, а остальные ячейки - краями. Клетки, обращенные от точки обзора 4D, отбраковываются, чтобы уменьшить визуальный беспорядок. | 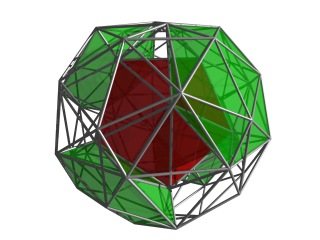 . Та же самая проекция, теперь 4 из 8 ячеек икосаэдра, окружающих центральную ячейку, показаны зеленым. . Та же самая проекция, теперь 4 из 8 ячеек икосаэдра, окружающих центральную ячейку, показаны зеленым. |
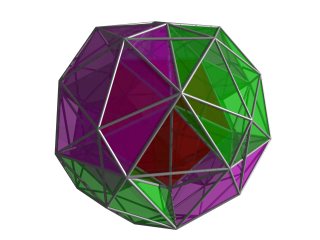 . Та же проекция, что и выше, теперь с другими четырьмя икосаэдрическими ячейками, окружающими центральную ячейку, показаны пурпурным цветом. Анимированная версия этого изображения дает хорошее представление о расположении этих ячеек. . Та же проекция, что и выше, теперь с другими четырьмя икосаэдрическими ячейками, окружающими центральную ячейку, показаны пурпурным цветом. Анимированная версия этого изображения дает хорошее представление о расположении этих ячеек. С этой конкретной точки зрения можно увидеть одну из щелей, содержащих тетраэдрические ячейки. Каждый из этих промежутков заполнен 5 тетраэдрическими ячейками, здесь не показаны. |  . Та же проекция, что и выше, теперь с заполненной центральной тетраэдрической ячейкой в зазоре. Эта тетраэдрическая ячейка соединена с 4 другими тетраэдрическими ячейками, две из которых заполняют два зазора, видимые на этом изображении. Два других находятся между зеленой тетраэдрической ячейкой, пурпурной ячейкой и центральной ячейкой, слева и справа от желтой тетраэдрической ячейки. . Та же проекция, что и выше, теперь с заполненной центральной тетраэдрической ячейкой в зазоре. Эта тетраэдрическая ячейка соединена с 4 другими тетраэдрическими ячейками, две из которых заполняют два зазора, видимые на этом изображении. Два других находятся между зеленой тетраэдрической ячейкой, пурпурной ячейкой и центральной ячейкой, слева и справа от желтой тетраэдрической ячейки. Обратите внимание, что на этих изображениях клетки, обращенные от точки обзора 4D, отбракованы; следовательно, здесь учтено всего 1 + 8 + 6 + 24 = 39 ячеек. Остальные ячейки лежат с другой стороны от курносой 24 ячейки. Здесь можно различить часть контура края одной из них - икосаэдрическую ячейку, лежащую над желтым тетраэдром. |
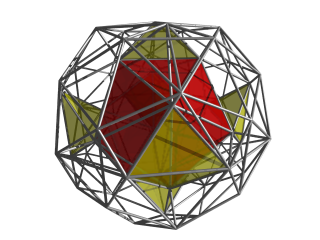 . На этом изображении показаны только ближайшая икосаэдрическая ячейка и 6 желтых тетраэдрических ячеек с предыдущего изображения. . На этом изображении показаны только ближайшая икосаэдрическая ячейка и 6 желтых тетраэдрических ячеек с предыдущего изображения. |  . Теперь показаны 12 тетраэдрических ячеек, соединенных с центральной икосаэдрической ячейкой, и показаны 6 желтых тетраэдрических ячеек. Каждая из этих ячеек окружена центральным икосаэдром и двумя другими икосаэдрическими ячейками, показанными ранее. . Теперь показаны 12 тетраэдрических ячеек, соединенных с центральной икосаэдрической ячейкой, и показаны 6 желтых тетраэдрических ячеек. Каждая из этих ячеек окружена центральным икосаэдром и двумя другими икосаэдрическими ячейками, показанными ранее. |
 . Наконец, здесь показаны другие 12 тетраэдрических ячеек, соединенных с 6 желтыми тетраэдрическими ячейками. Эти ячейки вместе с 8 показанными ранее икосаэдрическими ячейками включают все ячейки, которые имеют как минимум 1 вершину с центральной ячейкой. . Наконец, здесь показаны другие 12 тетраэдрических ячеек, соединенных с 6 желтыми тетраэдрическими ячейками. Эти ячейки вместе с 8 показанными ранее икосаэдрическими ячейками включают все ячейки, которые имеют как минимум 1 вершину с центральной ячейкой. | |
Курносая 24-ячейка может быть получена как уменьшение 600-ячейки в 24 ее вершинах, фактически вершин вписанной 24 -ячейка. Также существует такое двойное уменьшение, когда также уменьшаются вершины второй вписанной вершины 24-ячейки. Соответственно, этот известен как bi-24-уменьшенная 600-клеточная.
| D4однородная полихора | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  | ||||
| {3,3}. h {4,3,3} | 2r {3,3}. h3{4,3,3} | t {3,3}. div class="ht"{4,3,3} | 2t {3,3}. div class="ht",3 {4,3,3} | r{3,3}. {3} = {3,4,3} | rr{3,3}. r {3} = r {3,4,3} | tr{3,3}. t {3} = t {3,4,3} | sr {3,3}. s {3} = s {3,4,3} | ||||
Курносый 24-элементный также называется полу-курносым 24-элементным, потому что он не является истинным второстепенным (чередование полностью усеченных 24-ячеек). 24-элементный полный курносый элемент также может быть построен, хотя он не является однородным и состоит из неправильных тетраэдров на чередующихся вершинах.
Курносые 24-ячеечные соты являются самой большой гранью 4-х мерных сот, курносые 24-ячеечные соты.
Курчавые 24-ячеечные соты являются частью F 4 семейство симметрий однородных 4-многогранников.
| Семейные многогранники с 24 ячейками | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Имя | 24 ячейки | усеченные 24 ячейки | курносые 24 ячейки | выпрямленные 24 ячейки | скошенные 24 ячейки | усеченные биты 24-элементный | усеченный 24-элементный | ранцинированный 24-элементный | усеченный 24-элементный | полностью усеченный 24-элементный | |
| символ Шлефли. | {3,4,3} | t0,1 {3,4,3}. t {3,4,3} | s {3,4,3} | t1{3,4, 3}. r {3,4,3} | t0,2{3,4,3}. rr {3,4,3} | t1,2 {3,4,3}. 2t {3,4,3} | t0,1,2{3,4,3}. tr { 3,4,3} | t0,3{3,4,3} | t0,1,3{3,4,3} | t0, 1,2,3 {3,4,3} | |
| диаграмма Кокстера. | |||||||||||
| диаграмма Шлегеля. |  |  |  |  |  |  |  |  |  |  | |
| F4 |  |  |  |  |  |  |  |  |  |  | |
| B4 |  |  |  |  |  |  |  |  |  |  | |
| B3(a) |  |  |  |  |  |  |  |  |  |  | |
| B3(b) |  |  |  |  |  |  | |||||
| B2 |  |  |  |  |  |  |  |  |  |  | |
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | ||||||||
| Треугольник | Квадрат | p-угольник | Шестиугольник | Пентагон | ||||||||
| Тетраэдр | Октаэдр • Куб | Демикуб | Додекаэдр • Икосаэдр | |||||||||
| 5-элементный | 16-элементный • Тессеракт | Демитессеракт | 24-элементный | 120- ячейка • 600 ячеек | ||||||||
| 5-симплекс | 5-ортоплекс • 5-куб | 5-полукуб | ||||||||||
| 6-симплекс | 6- ортоплекс • 6-куб | 6-полукуб | 122 • 221 | |||||||||
| 7-симплекс | 7-ортоплекс • 7-куб | 7-полукуб | 132 • 231 • 321 | |||||||||
| 8- симплекс | 8-ортоплекс • 8-куб | 8-полукруг | 142 • 241 • 421 | |||||||||
| 9-симплекс | 9-ортоплекс • 9-куб | 9- demicube | ||||||||||
| 10-симплекс | 10-ортоплекс • 10-куб | 10-demicube | ||||||||||
| n-симплекс | n-ортоплекс • n- куб | n-demicube | 1k2 • 2k1 • k21 | n-пятиугольный многогранник | ||||||||
| Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и составных частей | ||||||||||||