Строительство Wythoff

Витоффовские конструкции из 3-х зеркал, образующих прямоугольный треугольник.

В геометрии, построение визофф, названный в честь математика Виллем Абрахама Уайтофф, является способом построения однородного многогранник или плоской плитки. Его часто называют калейдоскопической конструкцией Витхоффа.

• 1 Процесс строительства
• 2 Невитхоффовские конструкции
• 3 См. Также
• 4 ссылки
• 5 Внешние ссылки

Метод основан на идее черепицы в сфере, с сферическими треугольниками - см Schwarz треугольников. Эта конструкция размещает три зеркала по сторонам треугольника, как в калейдоскопе. Однако в отличие от калейдоскопа зеркала не параллельны, а пересекаются в одной точке. Поэтому они заключают сферический треугольник на поверхность любой сферы с центром в этой точке, и повторяющиеся отражения создают множество копий треугольника. Если углы сферического треугольника выбраны надлежащим образом, треугольники будут замощать сферу один или несколько раз.

Если поместить вершину в подходящую точку внутри сферического треугольника, окруженного зеркалами, можно гарантировать, что отражения этой точки образуют однородный многогранник. Для сферического треугольника ABC у нас есть четыре возможности, которые позволят создать однородный многогранник:

1. В точке A помещается вершина. Это дает многогранник с символом Витоффа a | b   c, где a равно π, деленному на угол треугольника в A, и аналогично для b и c.
2. Вершина помещается в точку на прямой AB так, чтобы она делила угол при C пополам. Это дает многогранник с символом Витоффа a   b | c.
3. Вершина помещается так, что она находится на вписанной в АВС. Это дает многогранник с символом Витоффа a   b   c |.
4. Вершина находится в такой точке, что, когда она вращается вокруг любого из углов треугольника на удвоенный угол в этой точке, она смещается на такое же расстояние для каждого угла. Используются только четные отражения исходной вершины. Многогранник имеет символ Витхоффа | а   б   в.

Этот процесс в целом также применим к многомерным правильным многогранникам, включая 4-мерные однородные 4-многогранники.

Примеры

Гексагональной призмы строится из обоих (6 2 2) и (3) 2 2 семей.

Усечен квадратный паркет строится в двух различных положениях симметрии в семье (4 4 2).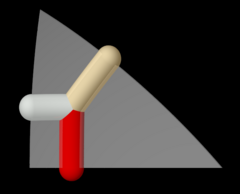

Узор Wythoff pq2 | = 432 |. Орбита вышеприведенного паттерна Wythoff под действием полной октаэдрической группы.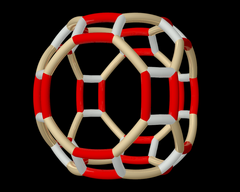

Равномерные многогранники, которые не могут быть созданы с помощью конструкции зеркала Wythoff, называются non-Wythoffian. Как правило, они могут быть получены из Wythoffian форм либо путем чередования (удаления альтернативных вершин), либо путем вставки чередующихся слоев частичных фигур. Оба этих типа фигур будут содержать вращательную симметрию. Иногда курносые формы считаются Wythoffian, хотя они могут быть построены только путем чередования полностью усеченных форм.

Примеры

Гексагональной антипризма строится чередованием в двенадцатиугольными призмы.

Удлиненный треугольные плиточные построена по наслаивания квадратной плитки и треугольных облицовочных рядов.

Большой dirhombicosidodecahedron является единственным не-Wythoffian равномерной многогранник.

• Символ Wythoff - символ построения Wythoff равномерных многогранников и равномерных мозаик.
• Диаграмма Кокстера – Дынкина - обобщенный символ построения Витхоффа однородных многогранников и сот.

• Регулярные многогранники Кокстера, Третье издание, (1973), Дуврское издание, ISBN   0-486-61480-8 (Глава V: Калейдоскоп, Раздел: 5.7 Построение Витхоффа)
• Coxeter The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN   0-486-40919-8 (Глава 3: Конструкция Витоффа для однородных многогранников)
• Хар'Эль З. Однородное решение для однородных многогранников., Geometriae Dedicata 47, 57-110, 1993. [1] (Раздел 4: Калейдоскоп)
• WA Wythoff, Связь между многогранниками семейства C600, Koninklijke Akademie van Wetenschappen te Amsterdam, Proceedings of the Section of Sciences, 20 (1918) 966–970.

• Апплет Грега Игана для отображения однородных многогранников с использованием метода построения Wythoff
• Рендеринг метода построения Wythoff методом Shadertoy

• Jenn, программа, которая генерирует виды (сферических) многогранников и полихор по группам симметрии