| Большой диромбикосододекаэдр | |
|---|---|
 | |
| Тип | Равномерный звездчатый многогранник |
| Элементы | F = 124, E = 240. V = 60 (χ = −56) |
| Грани по сторонам | 40 {3} +60 {4} +24 {5/2} |
| Символ Wythoff | | 3/2 5/3 3 5/2 |
| Группа симметрии | Ih, [5,3], * 532 |
| Ссылки на указатель | U 75, C 92, W 119 |
| Двойной многогранник | Большой диромбикосидодекакрон |
| Вершина рисунок |  . 4.5 / 3.4.3.4.5 / 2.4.3 / 2 . 4.5 / 3.4.3.4.5 / 2.4.3 / 2 |
| Акроним Бауэрса | Gidrid |
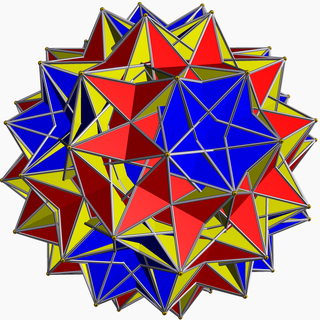
 3D-модель большого диромбикосододекаэдра.
3D-модель большого диромбикосододекаэдра. В геометрии, большой диромбикосододекаэдр (или большой курносый дисикозидисдодекаэдр ) является невыпуклым однородным многогранником, последним индексированным как U 75. У него 124 грани (40 треугольников, 60 квадратов и 24 пентаграммы ), 240 ребер и 60 вершин.
Это только невырожденный однородный многогранник с более чем шестью гранями, пересекающимися в вершине. Каждая вершина состоит из 4 квадратов, которые проходят через центральную ось вершины (и, следовательно, через центр фигуры), чередующиеся с двумя треугольниками и двумя пентаграммами. Еще одна необычная особенность заключается в том, что все грани образуют компланарные пары.
Это также единственный однородный многогранник, который не может быть образован с помощью конструкции Витхоффа из сферического треугольника. Он имеет специальный символ Wythoff | 3/2 5/3 3 5/2 относит его к сферическому четырехугольнику. Этот символ предполагает, что это своего рода курносый многогранник, за исключением того, что не курносые грани окружены курносыми треугольниками, как в большинстве курносых многогранников, они окружены курносыми квадратами.
Он получил прозвище «чудовище Миллера» (в честь JCP Miller, который с помощью HSM Coxeter и MS Longuet-Higgins перечислил однородные многогранники в 1954 г.).
Если определение однородного многогранника ослабляется, чтобы разрешить любое четное число граней, смежных с ребром, то это определение дает начало еще одному многограннику: большому диргомбидодекаэдру, который имеет те же вершины и ребра, но с другим расположением треугольных граней.
Вершины и ребра также являются общими для однородных соединений 20 октаэдров или 20 тетрагемигексаэдров. 180 из 240 ребер совпадают с большим курносым додецикосододекаэдром.
 . Выпуклой оболочкой . Выпуклой оболочкой |  . Большим курносым додецикосододекаэдром . Большим курносым додецикосододекаэдром |  . Большим диргомбикосододекаэдром . Большим диргомбикосододекаэдром |
 . Большим диснуб-диромбидододекаэдром . Большим диснуб-диромбидододекаэдром |  . Соединением двадцати174 октаэдров тетрагемигексаэдры . Соединением двадцати174 октаэдров тетрагемигексаэдры |
.
декартовы координаты для вершин большого диргомбикосододекаэдра - это все четные перестановки


где τ = (1 + √5) / 2 - золотой отношение (иногда пишется φ). Эти вершины дают длину ребра 2√2.
.
 . Традиционное наполнение . Традиционное наполнение |  . Заполнение по модулю 2 . Заполнение по модулю 2 |  . Внутренний вид, заполнение по модулю 2 . Внутренний вид, заполнение по модулю 2 |