Обозначение орбифолда

редактировать

Обозначение для двумерных сферических, евклидовых и гиперболических групп симметрии

В геометрии, орбифолд нотация (или орбифолд сигнатура ) - это система, изобретенная математиком Джоном Конвеем для представления типов групп симметрии в виде двух размерные пространства постоянной кривизны. Преимущество обозначения состоит в том, что оно описывает эти группы таким образом, который указывает на многие свойства групп: в частности, он следует за Уильямом Терстоном в описании орбифолда, полученного путем взятия частное евклидова пространства по рассматриваемой группе.

Группы, представленные в этой нотации, включают точечные группы на сфере ( $S 2 {\ displaystyle S ^ {2}}$ $S ^ {2}$ ), группы фризов и группы обоев евклидовой плоскости ( $E 2 {\ displaystyle E ^ {2}}$ $E ^ {2}$ ), и их аналоги на гиперболической плоскости ( $H 2 {\ displaystyle H ^ {2}}$ $H ^ {2}$ ).

Содержание

1 Определение обозначения
- 1.1 Хорошие орбифолды
2 Хиральность и ахиральность
3 Эйлерова характеристика и порядок
4 Равные группы
5 Двумерные группы
6 Таблицы соответствий
- 6.1 Сферическая
- 6.2 Евклидова плоскость
  - 6.2.1 Фризные группы
  - 6.2.2 Группы обоев
- 6.3 Гиперболическая плоскость
7 См. Также
8 Ссылки
9 Внешние ссылки

Определение нотации

В группе, описываемой орбифолдной нотацией, могут встречаться следующие типы евклидова преобразования:

отражение через линию (или плоскость)
перемещение вектора
вращение конечного порядка вокруг точки
бесконечное вращение вокруг линии в 3-м пространстве
скольжение-отражение, то есть отражение с последующим перемещением.

Предполагается, что все происходящие трансляции образуют дискретную подгруппу описываемых групповых симметрий.

Каждая группа обозначается в орбифолдной нотации конечной строкой, состоящей из следующих символов:

положительные целые $1, 2, 3,… {\ displaystyle 1, 2,3, \ dots}$ $1,2,3, \ dots$
символ бесконечности, $∞ {\ displaystyle \ infty}$ $\ infty$
звездочка , *
символ o (сплошной круг в старых документах), который называют чудом, а также ручкой, потому что он топологически представляет собой замкнутую поверхность тора (1-ручка). Шаблоны повторяются с двумя переводами.
символ $× {\ displaystyle \ times}$ $\ times$ (белый кружок в старых документах), который называется чудом и представляет собой топологический crosscap, где узор повторяется в зеркальном отображении, не пересекая зеркальную линию.

Строка, выделенная жирным шрифтом, представляет группу симметрий евклидова 3-мерного пространства. Строка, не выделенная жирным шрифтом, представляет собой группу симметрий евклидовой плоскости, которая, как предполагается, содержит два независимых перевода.

Каждый символ соответствует отдельному преобразованию:

целое число n слева от звездочки указывает на поворот порядка n вокруг точки вращения
целое число n справа от звездочки указывает на преобразование порядка 2n, которое вращается вокруг калейдоскопической точки и отражается через линию (или плоскость)
an $× {\ displaystyle \ times}$ $\ times$ указывает на скользящее отражение
символ $∞ {\ displaystyle \ infty}$ $\ infty$ указывает на бесконечную симметрию вращения вокруг линии; это может произойти только для групп, выделенных жирным шрифтом. Злоупотребляя языком, мы можем сказать, что такая группа является подгруппой симметрий евклидовой плоскости только с одним независимым переводом. группы фризов возникают таким образом.
исключительный символ o указывает на то, что существует ровно два линейно независимых перевода.

Хорошие орбифолды

Символ орбифолда называется хорошо, если это не одно из следующих: p, pq, * p, * pq, для p, q≥2 и p ≠ q.

Хиральность и ахиральность

Объект является хиральным, если его группа симметрии не содержит отражений; в противном случае он называется ахиральным . Соответствующий орбифолд ориентируемый в киральном случае и неориентируемый в противном случае.

Эйлерова характеристика и порядок

Эйлерова характеристика для орбифолда может быть прочитана по его символу Конвея следующим образом. У каждой функции есть значение:

n без звездочки или до нее считается как $n - 1 n {\ displaystyle {\ frac {n-1} {n}}}$ ${\ frac {n-1} {n}}$
n после звездочки считается как $n - 1 2 n {\ displaystyle {\ frac {n-1} {2n}}}$ ${\ frac {n-1} {2n}}$
звездочка и $× {\ displaystyle \ times}$ $\ times$ считаются как 1
o считается как 2.

Вычитание суммы этих значений из 2 дает эйлерову характеристику.

Если сумма значений характеристик равна 2, порядок бесконечен, т. Е. Обозначение представляет группу обоев или группу фризов. Действительно, «Магическая теорема» Конвея указывает, что 17 групп обоев - это именно те, у которых сумма значений признаков равна 2. В противном случае порядок равен 2, деленному на характеристику Эйлера.

Равные группы

Следующие группы изоморфны:

1 * и * 11
22 и 221
* 22 и * 221
2 * и 2 * 1.

Это потому, что 1-кратное вращение является «пустым» вращением.

Двумерные группы

. Идеальная снежинка будет иметь * 6 • симметрию,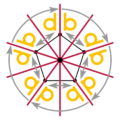

. пятиугольник имеет симметрию * 5 •, все изображение с стрелки 5 •.

. Флаг Гонконга имеет 5-кратную симметрию вращения, 5 •.

Симметрия объекта 2D без трансляционной симметрии может быть описана типом трехмерной симметрии путем добавления третьего измерения к объекту, которое не добавляет или не портит симметрию. Например, для 2D-изображения мы можем рассматривать кусок картонной коробки с этим изображением, отображаемым на одной стороне; форма коробки должна быть такой, чтобы она не нарушала симметрию, иначе ее можно представить себе бесконечной. Таким образом, мы имеем n • и * n •. Маркер (•) добавлен к одно- и двумерным группам, чтобы указать на существование фиксированной точки. (В трех измерениях эти группы существуют в n-кратном двуугольном орбифолде и представлены как nn и * nn.)

Аналогичным образом можно нарисовать 1D изображение горизонтально на картонной коробке, чтобы избежать дополнительной симметрии относительно линии изображения, например нарисовав горизонтальную полосу под изображением. Таким образом, дискретные группы симметрии в одном измерении - это * •, * 1 •, ∞ • и * ∞ •.

Другой способ построения трехмерного объекта из одномерного или двухмерного объекта для описания симметрии - это взятие декартова произведения объекта и асимметричного двухмерного или одномерного объекта соответственно.

Таблицы соответствия

Сферические

Фундаментальные области групп отражающих 3D-точек
(* 11), C 1v=Cs	(* 22), C 2v	(* 33), C 3v	(* 44), C 4v	(* 55), C 5v	(* 66), C 6v
. Заказ 2	. Заказ 4	. Заказ 6	. Заказ 8	. Порядок 10	. Порядок 12
(* 221), D 1h=C2v	(* 222), D 2h	(* 223), D 3h	(* 224), D 4h	(* 225), D 5h	(* 226), D 6h
. Заказ 4	. Заказ 8	. Заказ 12	. Заказ 16	. Заказ 20	. Заказ 24
(* 332), T d		(* 432), O h		(* 532), I h
. Порядок 24		. Порядок 48		. Порядок 120

Группы сферической симметрии
Орбифолд. Подпись	Coxeter	Schönflies	Hermann – Mauguin	Порядок
Полиэдральные группы
*532	[3,5 ]	Ih	53m	120
532	[3,5]	I	532	60
*432	[3,4]	Oh	м3 · м	48
432	[3,4 ]	O	432	24
*332	[3,3]	Td	43м	24
3*2	[3,4]	Th	m3	24
332	[3,3]	T	23	12
Двугранный и циклические группы: n = 3,4,5...
* 22n	[2, n]	Dnh	н / ммм или 2нм2	4n
2*n	[2,2n]	Dnd	2n2m или нм	4n
22n	[2, n]	Dn	n2	2n
*nn	[n]	Cnv	nm	2n
n*	[n, 2]	Cnh	n / m или 2n	2n
n×	[2,2n]	S2n	2n или n	2n
nn	[n]	Cn	n	n
Особые случаи
* 222	[2,2]	D2h	2 / ммм или 22м2	8
2 * 2	[2,4]	D2d	222м или 2м	8
222	[2,2]	D2	22	4
* 22	[2]	C2v	2m	4
2*	[2,2]	C2h	2 / м или 22	4
2×	[2,4]	S4	22 или 2	4
22	[2 ]	C2	2	2
*22	[1,2]	D1h=C2v	1 / ммм или 21м2	4
2*	[2,2]	D1d=C2h	212м или 1м	4
22	[1, 2]	D1=C2	12	2
*1	[]	C1v=Cs	1m	2
1*	[2,1]	C1h=Cs	1 / m или 21	2
1×	[2,2]	S2=Ci	21 или 1	2
1	[]	C1	1	1

Евклидова плоскость

Frieze группы

Frieze группы
IUC	Cox	Schön. Struct.	Диаграмма. Orbifold	Примеры. и Conway ник	Описание
p1	[∞].	C∞. Z∞	. ∞∞	FFFFFFFF . . . переход	(T) Только переводы:. Эта группа создается отдельно, путем перевода наименьшее расстояние, на котором шаблон является периодическим.
p11g	[∞, 2].	S∞. Z∞	. ∞×	F ᖶ F ᖶ F ᖶ F ᖶ . . . step	(TG) Скользящие отражения и переводы:. Эта группа генерируется по отдельности за счет скользящего отражения, а переводы получаются путем объединения двух скользящих отражений.
p1m1	[∞].	C∞v. Dih ∞	. * ∞∞	Λ Λ Λ Λ Λ Λ Λ Λ . . . бочок	(TV) Вертикальные линии отражения и переводы:. Группа такая же, как нетривиальная группа в одномерном случае; он создается перемещением и отражением по вертикальной оси.
p2	[∞, 2].	D∞. Dih ∞	. 22∞	SSSSSSSS . . . вращающийся прыжок	(TR) Сдвиги и вращения на 180 °:. Группа создается перевод и поворот на 180 °.
p2mg	[∞, 2].	D∞d. Dih ∞	. 2 * ∞	V Λ V Λ V Λ V Λ . . . спиннинг	(TRVG) Вертикальные линии отражения, скользящие отражения, смещения и вращения на 180 °:. Переводы здесь возникают из-за скользящих отражений, поэтому эта группа генерируется скользящим отражением и либо вращением, либо вертикальным отражением.
p11m	[∞, 2].	C∞h. Z∞× Dih 1	. ∞*	BBBBBBBB . . . jump	(THG) Переводы, горизонтальные отражения, отражения скольжения:. Эта группа создается перемещением и отражением по горизонтальной оси. Скользящее отражение здесь возникает как композиция переноса и горизонтального отражения
p2mm	[∞, 2].	D∞h. Dih ∞ × Dih 1	. * 22∞	HHHHHHHH . . . прыжок с вращением	(TRHVG) Горизонтальные и вертикальные линии отражения, смещения и поворота на 180 °:. Для этой группы требуются три генератора, с одной генераторной установкой, состоящей из смещения, отражение по горизонтали ось и отражение по вертикальной оси.

Обозначение точечной группы Шенфлиса расширено здесь как бесконечные случаи эквивалентных симметрий двугранных точек

На диаграмме показана одна фундаментальная область желтым цветом, с линиями отражения синим цветом, скользящими линиями отражения в пунктирная зеленая линия, нормали сдвига - красным, а точки двойного вращения - в виде маленьких зеленых квадратов.

Группы обоев

Фундаментальные области евклидовых отражающих групп
(* 442), p4m	(4 * 2), p4g

(* 333), p3m	(632), p6

17 группы обоев
Orbifold. Подпись	Coxeter	Hermann -. Mauguin	Speiser. Ниггли	Polya. Guggenhein	Fejes Toth. Cadwell
*632	[6,3]	p6m	C6v	D6	W6
632	[6,3]	p6	C6	C6	W6
* 442	[4,4]	p4m	C4	D4	W4
4 * 2	[4,4 impression	p4g	C4v	D4	W4
442	[4,4 impression	p4	C4	C4	W4
*333	[3]	p3m1	C3v	D3	W3
3*3	[3,6 ]	p31m	C3v	D3	W3
333	[3]	p3	C3	C3	W3
* 2222	[∞, 2, ∞]	pmm	C2v	D2kkkk	W2
2 * 22	[∞, 2, ∞]	см	C2v	D2кг кг	W2
22 *	[(∞, 2), ∞]	pmg	C2v	D2кгг	W2
22 ×	[ ∞, 2, ∞]	pgg	C2v	D2gggg	W2
2222	[∞, 2, ∞]	p2	C2	C2	W2
**	[∞, 2, ∞]	pm	Cs	D1kk	W1
*×	[∞, 2, ∞]	cm	Cs	D1kg	W1
××	[∞, (2, ∞)]	pg	C2	D1gg	W1
o	[∞, 2, ∞]	p1	C1	C1	W1

гиперболическая плоскость

модель диска Пуанкаре фундаментальной области треугольников
Пример прямоугольных треугольников (* 2pq)
. * 237	. * 238	. * 239	. * 23∞
. * 245	. * 246	. * 247	. * 248	. * ∞42
. * 255	. * 256	. * 257	. * 266	. * 2∞∞
Пример общих треугольников (* pqr)
. * 334	. * 335	. * 336	. * 337	. * 33∞
. * 344	. * 366	. * 3∞∞	. *6	. *∞
Пример высших многоугольников (* pqrs...)
. * 2223	. * (23)	. * (24)	. *3	. *4
. *2	. *2	. *2	. *2
. * 222∞	. * (2∞)	. *∞	. *2	. *∞

Первые несколько гиперболических групп, упорядоченных по их эйлеровой характеристике:

Гиперболические Группы симметрии
-1 / χ	Орбифолды	Коксетер
84	*237	[7,3]
48	*238	[8, 3]
42	237	[7,3 impression
40	*245	[5,4]
36 - 26,4	* 239, * 2 3 10	[9,3], [10,3]
26.4	* 2 3 11	[11,3]
24	* 2 3 12, * 246, * 334, 3 * 4, 238	[12,3], [6,4], [(4,3,3)], [3,8 ], [8,3]
22,3 - 21	* 2 3 13, * 2 3 14	[13,3], [14,3]
20	* 2 3 15, * 255, 5 * 2, 245	[15,3], [5,5], [5,4], [5,4]
19,2	* 2 3 16	[16,3]
18+2/3	*247	[7,4]
18	* 2 3 18, 239	[18,3], [9,3]
17,5 - 16,2	* 2 3 19, * 2 3 20, * 2 3 21, * 2 3 22, * 2 3 23	[19,3], [20,3], [20,3], [21,3], [22,3], [23,3]
16	* 2 3 24, * 248	[24,3], [8,4]
15	* 2 3 30, * 256, * 335, 3 * 5, 2 3 10	[ 30,3], [6,5], [(5,3,3)], [3,10], [10,3]
14 + 2/5 - 13 + 1/3	* 2 3 36... * 2 3 70, * 249, * 2 4 10	[36,3]... [60,3], [9,4], [10, 4]
13+1/5	* 2 3 66, 2 3 11	[66,3], [11,3]
12 + 8/11	* 2 3 105, * 257	[105,3], [7,5]
12+4/7	* 2 3 132, * 2 4 11...	[132,3], [11,4],...
12	* 23∞, * 2 4 12, * 266, 6 * 2, * 336, 3 * 6, * 344, 4 * 3, * 2223, 2 * 23, 2 3 12, 246, 334	[∞, 3] [12,4], [6, 6], [6,4], [(6,3,3)], [3,12], [(4,4,3)], [4,6], [∞, 3, ∞], [ 12,3], [6,4] [(4,3,3)]
...

См. Также

Мутация орбифолдов
Нотация фибрифолда - расширение нотации орбифолда для трехмерных пространственных групп

Ссылки

Джон Х. Конвей, Олаф Дельгадо Фридрихс, Дэниел Х. Хьюсон и Уильям П. Терстон. О трехмерных орбифолдах и пространственных группах. Вклад в алгебру и геометрию, 42 (2): 475-507, 2001.
J. Х. Конвей, Д. Х. Хьюсон. Обозначения орбифолда для двумерных групп. Structural Chemistry, 13 (3-4): 247–257, август 2002.
J. Х. Конвей (1992). «Орбифолдная запись для поверхностных групп». В: М. В. Либек и Дж. Саксл (ред.), Группы, комбинаторика и геометрия, Труды L.M.S. Даремский симпозиум, 5–15 июля, Дарем, Великобритания, 1990 г.; Лондонская математика. Soc. Конспект лекций 165 . Издательство Кембриджского университета, Кембридж. стр. 438–447
Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1- 56881-220-5
Хьюз, Сэм (2019), Когомологии фуксовых групп и неевклидовых кристаллографических групп, arXiv : 1910.00519, Bibcode : 2019arXiv191000519H

Внешние ссылки

Полевое руководство по орбифолдам (Заметки из класса по «Геометрия и воображение» в Миннеаполисе, с Джоном Конвеем, Питером Дойлом, Джейн Гилман и Билл Терстон, 17–28 июня 1991 г. См. также PDF, 2006 )
2DTiler Программное обеспечение для визуализации двумерных мозаик плоскости и редактирования их групп симметрии в орбифолдной нотации