Космическая группа

редактировать

Пространственная группа шестиугольника H 2 O ice равна P6 3 / mmc. Первый m указывает плоскость зеркала, перпендикулярную ось c (a), второй m указывает плоскость зеркала, параллельные оси c (b), а c указывает плоскости скольжения (b) и (c). Черные ящики очерчивают элементарную ячейку.

В математике, физике и химии, пространственная группа - это группа симметрии конфигурации в пространстве, обычно в трех измеренийх. В трех измерениях существует 219 различных типов 230, если хиральные номера имеют отдельный. Пространственные группы также изучаются в измерениях, отличных от 3, где они иногда называются группой Бибербаха, и представляют собой дискретные компактные группы изометрий ориентированное евклидово пространство.

В кристаллографии пространственные группы также называются кристаллографическими или федоровскими группами и описанием симметрии кристалла. Конечным элементом касающимся трехмерных пространственных групп, являются Международные таблицы кристаллографии (Hahn (2002)).

Содержание

1 История
2 элемента
- 2.1 Элементы, фиксирующие точку
- 2.2 Переводы
- 2.3 Переводы
- 2.3 Скачки скольжения
- 2.4 Винтовые оси
- 2.5 Общая формула Плоский
3 Обозначения
4 Системы классификации
5 В других измерений
- 5.1 Теоремы Бибербаха
- 5.2 Классификация в малых измерениях
- 5.3 Магнитные группы и обращение времени
6 Таблица пространственных групп в двух измерениях (группы обоев)
7 Таблица пространственных групп в 3 измерениях
8 Производный класс кристалла из пространственной группы
9 Ссылки
10 Внешние ссылки

История

Пространственные группы в 2 размерах - 17 групп обоев, которые были известны в течение нескольких столетий, хотя доказательство того, что список был полным, было дано только в 1891 году, после того, как в основном завершена намного более сложная классификация космических групп. В 1879 году немецкий математик Леонард Зонке перечислил 65 пространственных групп (так называемых групп Сонке), элементы сохраняют киральность. Точнее, он перечислил 66 групп, но и русский математик и кристаллограф Евграф Федоров и немецкий математик Артур Мориц Шенфлис заметили, что две из них действительно совпадают. Первый раз в списке в 1891 году Федоровым (в чьем списке было два пропусков (I43d и Fdd2) и одно дублирование (Fmm2)), вскоре после этого в 1891 году были независимо Шенфлис (в чьем списке было четыре пропусков) (I43d, Pc, Cc,?) И одна дупликация (P42 1 m)). Правильный список из 230 пространственных групп был найден к 1892 году во время переписки между Федоровым и Шенфлисом. Барлоу (1894) позже перечислил группы четырьмя другими методами, но пропустил группы (Fdd2, I42d, P42 1 d и P42 1 c) даже при том, что у него уже был правильный список из 230 групп от Федорова и Шенфлиса; распространенное утверждение, что Барлоу не знал об их работе, неверно. Буркхардт (1967) подробно описывают историю открытия космических групп.

Элементы

Пространственные группы в трех измерениях состоят из комбинаций 32 кристаллографических точечных групп с 14 решетками Браве, каждая из последних относится к одной из 7 решетчатых систем. Это означает, что поведение любого элемента данной пространственной группы может быть выражено как поведение элемента точечной группы, за которым может следовать перевод. Таким образом, пространственная группа представляет собой некоторую комбинацию трансляционной симметрии элементарной ячейки (включая центрирование решетки), операции симметрии точечной группы отражения, вращения и неправильное вращение (также называемое ротоинверсией), а также операции симметрии оси винта и плоскости скольжения. Комбинация всех этих операций симметрии дает в общей сложности 230 различных пространственных групп, описывающих все возможные симметрии кристаллов.

Элементы, фиксирующие точку

Элементами пространственной группы, фиксирующими точки пространства, являются элементами идентичности, отражения, вращения и неправильные вращения.

Переводы

Переводы образуют нормальную абелеву подгруппу ранга 3, называемую решеткой Браве. Существует 14 типов решетки Браве. Фактор пространственной группы по решетке - это конечная группа, которая является одной из 32 преступников точечных групп.

Плоскости скольжения

A плоскость скольжения является отражением в плоскости с последующим переводом этой следующей переводом. плоскости. На это указывает $a {\ displaystyle a}$ $a$ , $b {\ displaystyle b}$ $b$ или $c {\ displaystyle c}$ $c$ , в зависимости от того, на какой скольжение продолжается. Также есть $n {\ displaystyle n}$ $n$ glide, которое представляет собой скольжение по половине диагонали лица, и $d {\ displaystyle d}$ $d$ скольжение, что составляет четверть пути вдоль грани или пространственной диагонали элементарной ячейки. Последний называется плоскостью скольжения алмаза, поскольку он присутствует в структуре алмаза. В 17 космических группах из-за центрирования ячейки скольжения происходят одновременно в двух перпендикулярных направлениях, т.е. одна и та же плоскость скольжения может называться b или c, a или b, a или c. Например, группа Abm2 также может называться Acm2, группа Ccca может называться Cccb. В 1992 году для таких самолетов было предложено использовать символ e. Изменены символы для пяти групп пробелов:

Номер группы пробелов	39	41	64	67	68
Новый символ	Aem2	Aea2	Cmce	Cmme	Ccce
Старый символ	Abm2	Aba2	Cmca	Cmma	Ccca

Оси винта

A ось винта - это вращение вокруг оси с последующим перемещением в направлении оси. Они отмечаются числами для обозначения вращения, где число показывает, сколько операций должно быть выполнено для полного поворота (например, 3 будет означать поворот на одну третье пути вокруг оси каждый раз). Затем степень смещения перемещается в виде индекса, показывающего, как часть вектора параллельной решетки. Итак, 2 1 - это двойной поворот, за которым следует перенос 1/2 события решетки.

Общая формула

Общая формула действия элемента пространственной группы:

y = Mx + D

, где M - его матрица, D - его вектор, и где элемент преобразует точку x в точку у. В общем, D = D (решетка ) + D (M), где D (M) - уникальная функция M, которая равна нулю, если M является тождеством. Матрицы M образуют точечную группу. решетка должна быть симметричной относительно этой точечной группы, но сама кристаллическая структура не может быть симметричной относительно этой точечной группы применительно к какой-либо конкретной точке (то есть без трансляции). Например, структура алмазного куба не имеет точки, в которой применяется кубическая точечная группа.

Размер решетки может быть меньше общего размера, что приводит к "субпериодической" пространственной группе. Для общего размера, размера решетки):

(1,1): Одномерные группы линий
(2,1): Двумерные группы линий : группы фризов
(2,2): группы обоев
(3,1): трехмерные группы линий ; трехмерными кристаллографическими точечными группами, группы стержней
(3,2): Группы слоев
(3,3): пространственные группы, обсуждаемые в этой статье

Обозначение

Существует не менее десяти способов присвоения пространственным группам. Некоторые из этих методов используют одну и ту же пространственную группу нескольких разных имен, поэтому в целом существует много тысяч разных имен.

Номер: Международный союз кристаллографии публикует таблицы всех типов пространственных групп и присваивает каждую из них уникальной системой от 1 до 230. Нумерация произвольная, за исключением групп с одинаковой общей системой или точе группой даны последовательные числа.

Обозначение нового символа

Обозначение Германа - Могена

Обозначение Германа - Могена обозначение решетку и некоторые образующие группы. Он имеет сокращенную форму, называемую международным коротким символом, который наиболее часто используется в кристаллографии и обычно состоит из набора из четырех символов. Первый уровень центрирования решетки Браве (P, A, C, I, R или F). Следующие три описывают наиболее заметную операцию симметрии, видимую при проецировании одного из участков высокой симметрии кристалла. Эти символы такие же, как используемые в точечных групп, с добавлением плоскостей скольжения и оси винта, описанных выше. В качестве пространственной группы кварца равна P3 1 21, форма, что он демонстрирует примитивное центрирование мотива (то есть, один раз элемент на элементарную ячейку), с осью винта тройного направления. и ось двойного вращения. Обратите внимание, что он явно не содержит кристаллическую систему , хотя она уникальна для каждой пространственной группы (в случае P3 1 21 она тригональная). В международном коротком символе первый символ (3 1 в этом примере) обозначает симметрию вдоль большой оси (ось c в тригональных случаях), второй (в данном случае 2) вдоль осей вторичных важ ( а и б) и третий символ симметрии в другом направлении. В тригональном случае также пространственная группа P3 1 12. В этой космической группе оси второго порядка расположены не вдоль осей a и b, а в направлении, повернутом на 30 °. Международные символы и короткие короткие символы для некоторых космических групп были немного между 1935 и 2002 годами, используемыми в космических группах 4 международных символа.

Направления обзора 7 кристаллических систем показались ниже.

Положение в символе	Triclinic	Monoclinic	Орторомбический	Тетрагональный	Тригональный	Гексагональный	Кубический
1	—	b	a	c	c	c	a
2	—		b	a	a	a	[111]
3	—		c	[110]	[210]	[210]	[110]

Нотация Холла: Обозначение пространственной группы с явным происхождением. Символы вращения, перемещения и оси четко разделены, центры инверсии явно определены. Конструкция и формат записи делают ее особенно подходящей для компьютерной генерации информации о симметрии. Например, группа номер 3 имеет три символа Холла: P 2y (P 1 2 1), P 2 (P 1 1 2), P 2x (P 2 1 1).
Обозначение Шенфлиса: Пространственные группы с заданными группами точек нумеруются цифрами 1, 2, 3,… (в том же порядке, что и их международный номер), и этот номер добавляется в качестве верхнего элемента к символу Schönflies для группы точек. Например, группы с номерами от 3 до 5 с точечной группой C 2 имеют символы Шенфлиса C. 2, C. 2, C. 2.

Федоров обозначение

символ Шубникова

Обозначение Strukturbericht

Соответствующее обозначение для кристаллических структур с буквой и индексом: A Элементы (одноатомные), B для соединений AB, C для AB 2 соединения, D для соединений A m Bn, (E, F,..., K Более сложные соединения), L Сплавы, O Органические соединения, S Силикаты. Некоторые структурные обозначения имеют одни и те же пространственные группы. Например, пространственная группа 225 - это A 1, B 1 и C 1. Пространственная группа 221 - это A h и B 2. Кристаллографы не будут использовать нотацию Strukturbericht для описания пространственной группы, скорее она будет описывать конфигурационную структуру группы (пространственная группа + расположение элементов (мотив)).

Нотация орбифолда (2D)

Обозначение фибрифолда (3D)

Как следует из названия, нотация орбифолда, это орбифолд, обязательный фактор евклидова пространства по пространственной группе, а не образующими пространственной группы. Он был введен Конвеем и Терстоном и практически не используется вне математики. С некоторыми из пространственных групп связано несколько различных фиброобразностей, поэтому они имеют несколько разных символов фиброобразия.

Обозначение Кокстера: Пространственные и точечные группы симметрии, представленные как модификации чисто отражающих групп Кокстера.
: A геометрических обозначение алгебры.

Системы классификации

Существует (по крайней мере) 10 различных способов классификации групп в классы. Отношения между некоторыми из них в следующей таблице. Каждая классификационная система является усовершенствованием нижеследующих.

(Кристаллографические) типы пространственных групп (230 в трех измерениях)
Две пространственные группы, рассматриваемые как подгруппы группы аффинные преобразователи пространства, имеют один и тот же тип пространственной группы, если они сопряжены с помощью с помощью аффинного преобразования, сохраняющего киральность. В трех измерениях для 11 групп аффинного пространства не существует сохраняющего киральность отображения группы на ее зеркальное отображение, поэтому, если каждая из них разделится на два случая (например, как P4 1 и P4 3). Итак, существует 54 + 11 = 65 типов пространственных групп, которые сохраняют киральность (группы Зонке).
Типы аффинных пространственных групп (219 в трех измерениях)
Две пространственные группы, рассматриваемые как подгруппы группы аффинных преобразований пространства, имеют один и тот же тип аффинных пространственных групп, если они сопряжены при аффинном преобразовании. Тип аффинной пространственной группы абстрактной пространственной группы. В трех измеренийх существует 54 типа аффинных пространственных групп, сохраняющих киральность.
Арифметические классы кристаллов (73 в трех измерениях)
Иногда их называют Z-классами. Они опасной точечной группой вместе с точечной группой на подгруппу переводов. Другими словами, арифметические кристаллические классы соответствуют классам сопряженности конечной подгруппы общей линейной группы GL n(Z) над целыми числами. Пространственная группа называется симморфной (или расщепленной ), если существует точка, в которой все симметрии являются продуктом симметрии, фиксирующей эту точку, и сдвига. Эквивалентно, пространственная группа симморфна, если она является полупрямым произведением своей точечной группы с ее подгруппой трансляции. Существует 73 симморфных пространственных группы, по одному в каждом арифметическом кристаллическом классе. Также существует 157 несимморфных пространственных типов с различными числами в классах арифметических структур. Арифметические классы кристаллов могут интерпретироваться как разные ориентации точечных групп в решетке, при этом матричные компоненты групповых элементов ограничиваются наличием целочисленных коэффициентов в пространстве решетки. Это довольно легко изобразить в двухмерном корпусе группы обоев. У некоторых точечных групп есть отражение, и линии отражения могут проходить вдоль направления решетки, на полпути между ними или в обоих направлениях. Нет: C 1 : p1; C 2 : p2; C 3 : p3; C 4 : p4; C 6 : p6 Вдоль: D 1 : pm, pg; D 2 : pmm, pmg, pgg; D 3 : p31m Между: D 1 : см; D 2 : см; D 3 : p3m1 Оба: D 4 : p4m, p4g; D 6 : p6m
(геометрический) Классы кристаллов (32 в трех измерениях)	Стаи Браве (14 в трех измерениях)
Иногда называют Q -классы. Кристаллический класс пространственной группы ее точечной группой: фактор-группа по подгруппе трансляций, действующая на решетке. Две пространственные группы находятся в одном и том же кристаллическом классе, когда их точечные группы, которые являются подгруппами GL n(Z), сопряжены в большей группе GL n(Q).	Они базовым типом решетки Браве. Они соответствуют классам сопряженности точечных групп решетки в GL n(Z), где точечная группа решетки - это группа симметрий основной решетки, которая фиксирует точку решетки и содержит точечную группу.
Кристаллические системы (7 в трех измерениях)	Решетчатые системы (7 в трех измерениях)
Кристаллические системы представляют собой специальную модификацию решетчатых систем, чтобы сделать их согласованными с классификацией в соответствии с для точечных групп. Они отличаются от семейств кристаллов тем, что семейство гексагональных кристаллов разделено на два подмножества, называемых тригональными и гексагональными кристаллическими системами. Тригональная кристаллическая система больше, чем система ромбоэдрическая решетки, гексагональная кристаллическая система меньше, чем система гексагональной решетки, а остальные кристаллические системы и системы решеток такие же.	Решеточная система пространственной группы определяется сопряженности точечной группы решетки (подгруппа GL n(Z)) в большей группе GL n(Q). В трех измерениях точечная группа решетки может иметь один из 7 различных порядков 2, 4, 8, 12, 16, 24 или 48. Семейство гексагональных кристаллов разделено на два подмножества, называемых системами ромбоэдрической и гексагональной решеток.
Семейства кристаллов (6 в трех измерениях)
Точечная группа пространственной группы не совсем определяет ее решеточную систему, потому что иногда две пространственные группы с одной и той же точечной группой могут находиться в разных решетчатых системах. Семейства кристаллов образуются из систем решеток путем слияния двух систем решеток всякий раз, когда это происходит, так что кристаллическое семейство пространственной группы определяется либо ее системой решеток, либо ее точечной группой. В трехмерном пространстве единственные два семейства решеток, которые объединяются таким образом, - это гексагональная и ромбоэдрическая системы решеток, которые объединены в гексагональное кристаллическое семейство. Шесть семейств кристаллов в трех измерениях называются триклинными, моноклинными, ромбическими, тетрагональными, гексагональными и кубическими. Семейства кристаллов обычно используются в популярных книгах по кристаллам, где их иногда называют кристаллическими системами.

Конвей, Дельгадо Фридрихс, Хусон и др. (2001) дал другую классификацию пространственных групп, названную нотацией фибрифолда, в соответствии со структурами фибрифолда на соответствующем орбифолде. Они разделили 219 аффинных пространственных групп на приводимые и неприводимые группы. Приводимые группы делятся на 17 классов, соответствующих 17 группам обоев, а оставшиеся 35 неприводимых групп аналогичны кубическим группам и классифицируются отдельно.

В других измерениях

Теоремы Бибербаха

В n измерениях аффинная пространственная группа, или группа Бибербаха, представляет собой дискретную подгруппу изометрий n-мерного евклидова пространства с компактная фундаментальная область. Бибербах (1911, 1912) доказал, что подгруппа трансляций любой такой группы содержит n линейно независимых трансляций и является свободной абелевой подгруппой конечного индекса, а также является единственной максимальной нормальной абелевой подгруппой. Он также показал, что в любой размерности n существует только конечное число возможностей для класса изоморфизма основной группы пространственной группы, и, более того, действие группы наевклидовом сопроводительно уникально с помощью аффинных преобразований. Это частично отвечает на восемнадцатую проблему Гильберта. Цассенхаус (1948) показал, что, наоборот, любая группа, которая является расширением Z с помощью конечной группы, действующей точно, группа является аффинного пространства. Объединение этих результатов показывает, что классификация пространственных в nх измерения с помощью групп сопряжения с помощью аффинных преобразований по существу же самое, что классификация классов изоморфизма для групп, которые являются расширениями Z конечной группой, действующей точно.

В теоремах Бибербаха важно предположить, что группа действует как изометрии; теоремы не обобщаются на дискретные кокомпактные группы аффинных преобразований евклидова пространства. Контрпримером является 3-мерная группа Гейзенберга целых чисел, действующая посредством переводов на группу Гейзенберга вещественных чисел, отождествленную с 3-мерным евклидовым пространством. Это дискретная кокомпактная группа аффинных преобразований пространства, но не содержит подгруппы Z.

Классификация малых размеровх

В этой таблице указано количество типов пространственных групп в малых измерениях, включая количество различных классов космической группы. В скобках указаны номера энантиоморфных пар.

Размеры	Семейства кристаллов (последовательность A004032 в OEIS )	Кристаллические системы (последовательность A004031 в OEIS )	Решетки Бравэ (последовательность A256413 в OEIS )	абстрактных кристаллографических точечных групп (последовательность A006226 в OEIS )	геометрические классы кристаллов, Q-классы, группы кристаллографических точек ( последовательность A004028 в OEIS )	Арифметические классы кристаллов, Z-классы (последовательность A004027 в OEIS )	Типы аффинных пространственных групп (последовательность A004029 в OEIS )	Типы кристаллографических пространственных групп (последовательных A006227 в OEIS )
0	1	1	1	1	1	1	1	1
1	1	1	1	2	2	2	2	2
2	4	4	5	9	10	13	17	17
3	6	7	14	18	32	73	219 (+11)	230
4	23 (+6)	33 (+7)	64 (+10)	118	227 (+44)	710 (+70)	4783 (+111)	4894
5	32	59	189	239	955	6079	222018 (+79)	222097
6	91	251	841	1594	7103	85308 (+?)	28927915 (+?)	?

Магнитные группы и обращение времени

Помимо кристаллографических пространственных объектов есть групп еще магнитное пространство группы (также называемые двухцветными (черно-белыми) кристаллографическими группами или группами Шубникова). Эти симметрии содержат элемент, известный как обращение. Они рассматривают как дополнительное измерение, и элементы группы включают обращение времени как отражение в нем. Они важны в магнитных структур, которые содержат упорядоченные неспаренные спины, т.е. ферро-, ферри- или антиферромагнитные структуры, как исследовал нейтронография. Элемент обращения времени переворачивает магнитное вращение, оставляя всю остальную неизменную неизменную, и его можно комбинировать с рядом других элементов симметрии. Включая обращение времени, имеется 1651 магнитная пространственная группа в 3D (Kim 1999, стр.428). Также было возможно сконструировать магнитные версии для других габаритных размеров и размеров решетки (статьи Дэниела Литвина, (Литвин 2008), (Литвин 2005)). Группы Frieze представляют собой группы магнитных одномерных линий, группы слоев - это группы магнитных обоев, а группы осевых трехмерных точек - это группы магнитных 2D-точек. Количество исходных и магнитных групп по (общему, решетчатому) размеру :( Palistrant 2012) (Souvignier 2006)

Общий. размер	Решетка. размер	Обычные группы			Магнитные группы
Общий. размер	Решетка. размер	Имя	Символ	Счетчик	Символ	Счетчик
0	0	Группа нульмерной симметрии	$G 0 {\ displaystyle G_ {0}}$ $G_ {0}$	1	$G 0 1 {\ displaystyle G_ {0} ^ {1}}$ ${\ displaystyle G_ {0} ^ {1}}$	2
1	0	Одномерные точечные группы	$G 10 {\ displaystyle G_ {10 }}$ $G _ {{10}}$	2	$G 10 1 {\ displaystyle G_ {10} ^ {1}}$ ${\ displaystyle G_ {10} ^ {1}}$	5
1	1	Одномерные дискретные группы симметрии	$G 1 {\ displaystyle G_ {1}}$ $G_ { 1}$	2	$G 1 1 {\ displaystyle G_ {1} ^ {1}}$ ${\ displaystyle G_ {1} ^ {1}}$	7
2	0	Двумерные группы точек	$G 20 {\ displaystyle G_ {20}}$ ${ \ displaystyle G_ {20}}$	10	$G 20 1 {\ displaystyle G_ {20} ^ {1}}$ ${\ displaystyle G_ {20} ^ {1}}$	31
	1	Группы Frieze	$G 21 {\ displaystyle G_ {21}}$ ${\ displaystyle G_ {21}}$	7	$G 21 1 {\ displaystyle G_ {21} ^ {1}}$ ${\ displaystyle G_ {21} ^ {1}}$	31
	2	Группы обоев	$G 2 {\ displaystyle G_ {2}}$ $G_ {2}$	17	$G 2 1 {\ displaystyle G_ {2} ^ {1}}$ ${\ displaystyle G_ {2} ^ {1}}$	80
3	0	Три -мерные то чечные группы	$G 30 {\ displaystyle G_ {30}}$ ${\ displaystyle G_ {30}}$	32	$G 30 1 {\ displaystyle G_ {30} ^ {1}}$ ${\ displaystyle G_ {30} ^ {1}}$	122
	1	Группы стержней	$G 31 {\ displaystyle G_ {31}}$ ${\ displaystyle G_ {31}}$	75	$G 31 1 {\ displaystyle G_ {31} ^ {1}}$ ${\ displaystyle G_ {31} ^ {1}}$	394
	2	Группы слоев	$G 32 {\ displaystyle G_ { 32}}$ ${\ displaystyle G_ {32}}$	80	$G 32 1 {\ displaystyle G_ {32} ^ {1}}$ ${\ displaystyle G_ {32} ^ {1}}$	528
	3	Трехмерные пространственные группы	$G 3 {\ displaystyle G_ {3}}$ ${\ displaystyle G_ {3}}$	230	$G 3 1 {\ displaystyle G_ {3} ^ {1}}$ ${\ displaystyle G_ { 3} ^ {1}}$	1651
4	0	Четырехмерные группы точек	$G 40 {\ displaystyle G_ {40}}$ ${\ displaystyle G_ {40}}$	271	$G 40 1 {\ displaystyle G_ {40} ^ {1}}$ ${\ displaystyle G_ {40} ^ {1 }}$	1202
	1		$G 41 {\ displaystyle G_ {41}}$ ${\ displaystyle G_ {41 }}$	343
	2		$G 42 {\ displaystyle G_ {42}}$ ${\ displaystyle G_ {42}}$	1091
	3		$G 43 {\ displaystyle G_ {43}}$ ${\ displaystyle G_ {43}}$	1594
	4	Четырехмерные дискретные группы симметрии	$G 4 {\ displaystyle G_ {4}}$ $G_ {4}$	4894	$G 4 1 {\ displaystyle G_ {4} ^ {1}}$ ${\ displaystyle G_ {4} ^ {1}}$	62227

Таблица пространственных групп в 2 измерениях (группы обоев)

Таблица групп обоев с использованием классификации трехмерные пространственные группы:

Кристаллическая система. (Решетка Браве)	Геометрический класс. Группа точек				Арифметика. класс	Группы обоев. (диаграмма ячеек)
Кристаллическая система. (Решетка Браве)	Шен.	Орбифолд	Кокс.	Порядок.	Арифметика. класс	Группы обоев. (диаграмма ячеек)
Наклон.	C1	(1)	[]	1	Нет	p1. (1)
Наклон.	C2	(22)	[2]	2	Нет	p2. (2222)
Прямоугольник. (Центрированный ромбический).	D1	(*)	[]	2	Вдоль	pm. (**)	pg. (××)
Прямоугольник. (Центрированный ромбический).	D2	( * 22)	[2]	4	Вдоль	pmm. (* 2222)	pmg. (22 *)
Ромбический. (прямоугольный по центру).	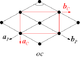D1	(*)	[]	2	Между	cm. (* ×)
Ромбический. (прямоугольный по центру).	D2	(* 22)	[2]	4	Между	см. (2 * 22)	pgg. (22x)
Квадрат.	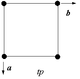C4	(44)	[4]	4	Нет	p4. ( 442)
Квадрат.	D4	(* 44)	[4]	8	Оба	p4m. (* 442)	p4g. (4 * 2)
Гексагональный.	C3	(33)	[3]	3	Нет	p3. (333)
	D3	(* 33)	[3]	6	Между	p3m1. (*333)	p31m. (3*3)
	C6	(66)	[6]	6	Нет	p6. (632)
	D6	(* 66)	[6pting	12	Оба	p6m. (* 632)

Для каждой геометрии ric возможные арифметические классы:

Нет: нет линий отражения
Вдоль: линии отраже вдоль направления решетки
Между: линии отражения на полпути между направлениями решетки
Оба: линии отражения вдоль и между направлениями решетки

Таблица пространственных групп в 3 измерениях

#	Кристаллическая система. (количество). Решетка Браве	Точечная группа					Пространственные группы (международный короткий символ)
#	Кристаллическая система. (количество). Решетка Браве	Int'l	Schön.	Orbifold	Cox.	Поряд.	Пространственные группы (международный короткий символ)
1	Triclinic. (2).	1	C1	11	[]	1	P1
2	Triclinic. (2).	1	Ci	1×	[2,2]	2	P1
3–5	Моноклиника. (13).	2	C2	22	[2]	2	P2, P2 1. C2
6–9		m	Cs	*11	[]	2	Pm, Pc. Cm, Cc
10–15		2 / m	C2h	2*	[2, 2]	4	P2 / м, P2 1/m. C2 / m, P2 / c, P2 1/c. C2 / c
16–24	Орторомбический. (59). .	222	D2	222	[2,2]	4	P222, P222 1, P2 1212, P2 12121, C222 1, C222, F222, I222, I2 12121
25–46		мм2	C2v	* 22	[2]	4	Pmm2, Pmc2 1, Pcc2, Pma2, Pca2 1, Pnc2, Pmn2 1, Pba2, Pna2 1, Pnn2. Cmm2, Cmc2 1, Ccc2, Amm2, Aem2, Ama2, Aea2. Fmm2, Fdd2. Imm2, Iba2, Ima2
47–74		mmm	D2h	*222	[2,2]	8	Pmmm, Pnnn, Pccm, Pban, Pmma, Pnna, Pmna, Pcca, Pbam, Pccn, Pbcm, Pnnm, Pmmn, Pbcn, Pbca, Pnma. Cmcm, Cmce, Cmmm, Cccm, Cmme, Ccce. Fmmm, Fmmm. Иммм, Ибам, Ибка, Имма
75–80	Тетрагональный. (68). .	4	C4	44	[4]	4	P4, P4 1, P4 2, P4 3, I4, I4 1
81–82		4	S4	2×	[2,4]	4	P4, I4
83–88		4 / м	C4h	4*	[2,4]	8	P4 / m, P4 2 / m, P4 / n, P4 2/n. I4 / m, I4 1 / a
89–98		422	D4	224	[2,4]	8	P422, P42 1 2, P4 1 22, P4 1212, P4 2 22, P4 2212, P4 3 22, P4 3212. I422, I4 1 22
99–110		4мм	C4v	* 44	[4]	8	P4mm, P4bm, P4 2 см, P4 2 нм, P4cc, P4nc, P4 2 mc, P4 2bc. I4mm, I4cm, I4 1 м d, I4 1 cd
111–122		42 мес.	D2d	2*2	[2,4]	8	P42m, P42c, P42 1 m, P42 1 c, P4m2, P4c2, P4b2, P4n2. I4m2, I4c2, I42m, I42d
123–142		4/mmm	D4h	*224	[2,4]	16	P4 / ммм, P4 / mcc, P4 / nbm, P4 / nnc, P4 / mbm, P4 / mnc, P4 / nmm, P4 / ncc, P4 2 / mmc, P4 2 / мкм, P4 2 / nbc, P4 2 / нмм, P4 2 / mbc, P4 2 / ммм, P4 2 / nmc, P4 2 / ncm. I4 / mmm, I4 / mcm, I4 1 / amd, I4 1 / acd
143–146	Тригональный. (25).	3	C3	33	[3]	3	P3, P3 1, P3 2. R3
147–148		3	S6	3×	[2,6]	6	P3, R3
149–155		32	D3	223	[2,3]	6	P312, P321, P3 1 12, P3 1 21, P3 2 12, P3 221. R32
156–161		3m	C3v	*33	[3]	6	P3m1, P31m, P3c1, P31c. R3m, R3c
162–167		3m	D3d	2*3	[2,6]	12	P31m, P31c, P3m1, P3c1. R3m, R3c
168–173	Гексагональный. ( 27).	6	C6	66	[6]	6	P6, P6 1, P6 5, P6 2, P6 4, P6 3
17 4		6	C3h	3*	[2,3]	6	P6
175–176		6 / м	C6h	6*	[2,6]	12	P6 / м, P6 3 / м
177–182		622	D6	226	[2,6]	12	P622, P6 1 22, P6 5 22, P6 2 22, P6 4 22, P6 3 22
183–186		6мм	C6v	*66	[6 совершение	12	P6mm, P6cc, P6 3 см, P6 3 mc
187–190		6m2	D3h	*223	[2,3 ]	12	P6m2, P6c2, P62m, P62c
191–194		6/mmm	D6h	*226	[2, 6]	24	P6 / mmm, P6 / mcc, P6 3 / mcm, P6 3 / mmc
195–199	Кубический. (36). . .	23	T	332	[3,3]	12	P23, F23, I23. P213, I2 13
200–206		m3	Th	3*2	[3,4]	24	Pm3, Pn3, Fm3, Fd3, Im3, Pa3, Ia3
207–214		432	O	432	[3,4 оттиска	24	P432, P4 232. F432, F4 132. I432. P4332, P4 1 32, I4 1 32
215–220		43m	Td	*332	[3,3]	24	P43m, F43m, I43m. P43n, F43c, I43d
221–230		m3m	Oh	*432	[3, 4]	48	Pm3m, Pn3n, Pm3n, Pn3m. Fm3m, Fm3c, Fd3m, Fd3c. Im3m, Ia3d

Примечание. Плоскость e - это двойное скольжение. самолет, у которого есть скольжение в двух разных направлениях. Они находятся в семи ромбических, пяти тетрагональных и пяти кубических пространственных группах, все с центрированной решеткой. Использование символов e стало официальным с Hahn (2002).

Решетчатую систему можно найти следующим образом. Если кристаллическая система не тригональная, то и решеточная система однотипна. Эта кристаллическая система является тригональной, то система является гексагональной, пространственная группа не является одной из семи в ромбоэдрической решеточной системой, состоящей из 7 тригональных пространственных групп в приведенной выше таблице, имя начинается с R. Термин ромбоэдрическая система также иногда используется как альтернативное название для всей тригональной системы.) Система гексагональной решетки больше, чем гексагональная кристаллическая система, и состоит из гексагональной кристаллической системы вместе с 18 группами тригональная кристаллическая система, отличная от семи, чьи имена начинаются с R.

Решетка Браве пространственной группы определяется системой решеток вместе с начальной буквой ее названия, которая для не ромбоэдрические группы - это P, I, F, A или C, обозначающие основные решетки, центрированные по телу, центрированные по граням, центрированные по A-грани или C-центрированные решетки.

Производный класс кристалла от пространственной группы

Оставьте тип Браве
Преобразуйте все элементы симметрии с трансляционными компонентами в их соответствующие элементы симметрии без трансляционной симметрии (плоскости скольжения преобразуются в простые зеркальные плоскости; винтовые оси преобразуются в простые оси вращения)
Оси вращения, оси вращения и зеркальные плоскости остаются неизменными.

Ссылки

Barlow, W (1894), " Über die geometrischen Eigenschaften starrer Strukturen und ihre Anwendung auf Kristalle " [О геометрических свойствах твердых структур и их применении в кристаллах], Zeitschrift für Kristallographie, 23 : 1–63, doi : 10.1524 / zkri.1894.23.1.1
Бибербах, Людвиг (1911), «Über die Bewegungsgruppen der Euklidischen Räume» [О группах жестких преобразований в евклидовых пространствах], Mathematische Annalen, 70(3): 297–336, doi : 10.1007 / BF01564500, ISSN 0025-5831
Бибербах, Людвиг (1912), «Über die Bewegungsgruppen der Euklidischen Räume (Zweite Abhandlung.) Die Gruppen mit einem endlichen Fundamentalbereich» 486 [О группах жесткие преобразования в евклидовых пространствах (второе эссе). Группы с конечной фундаментальной областью], Mathematische Annalen, 72(3): 400–412, doi : 10.1007 / BF01456724, ISSN 0025-5831
Браун, Гарольд; Бюлов, Рольф; Нойбюзер, Иоахим; Вондрачек, Ганс; Zassenhaus, Hans (1978), Кристаллографические группы четырехмерного пространства, Нью-Йорк: Wiley-Interscience [John Wiley Sons], ISBN 978-0-471-03095- 9, MR 0484179
Буркхардт, Иоганн Якоб (1947), Die Bewegungsgruppen der Kristallographie [Группы жестких преобразований в кристаллографии], Lehrbücher und Monographien aus demchafenisser. из области точных наук), 13, Verlag Birkhäuser, Basel, MR 0020553
Буркхардт, Иоганн Якоб (1967), «Zur Geschichte der Entdeckung der 230 Raumgruppen» [Об истории открытия 230 пространственных групп ], Архив истории точных наук, 4(3): 235–246, doi : 10.1007 / BF00412962, ISSN 0003- 9519, MR 0220837
Конвей, Джон Хортон ; Дельгадо Фридрихс, Олаф; Хьюсон, Дэниел Х.; Терстон, Уильям П. (2001), «О трехмерных пространственных данных», Beiträge zur Algebra und Geometrie, 42 (2): 475–507, ISSN 0138-4821, MR 1865535
Федоров Е.С. (1891), «Симметрия правильных системъ фигуръ» [Симметрия правильных систем фигур, Симметрия регулярных систем фигур], Записки Императорского С.-Петербургского Минералогического общества (Записки Императорского Санкт-Петербургскова Минералогического общества, Известия Императорского Санкт-Петербургского минералогического общества), 2-я серия, 28 (2): 1– 146
Федоров Е.С. (1971), Симметрия кристаллов, Монография ACA, 7, Американская кристаллографическая ассоциация
Hahn, Th. (2002), Хан, Тео (ред.), Международные таблицы для кристаллографии, Том A: Симметрия космической группы, Международные таблицы для кристаллографии, A (5-е изд.), Берлин, Нью-Йорк: Springer-Verlag, doi : 10.1107 / 97809553602060000100, ISBN 978-0-7923- 6590-7
Холл, SR (1981), «Обозначение пространственных с группным явным происхождением», Acta Crystallographica A, 37 (4): 517–525, Bibcode : 1981AcCrA..37..517H, doi : 10. 1107 / s0567739481001228
Янссен, Т. ; Бирман, Дж. Л.; Денойе, Ф.; Копцик В.А.; Verger-Gaugry, J.L.; Вайгель, Д.; Ямамото, А.; Abrahams, S.C.; Копский В. (2002), «Отчет подкомитета по номенклатуре n-мерной кристаллографии. II. Символы для арифметических классов кристаллов, классов Браве и пространственных групп », Acta Crystallographica A, 58 (Pt 6): 605–621, doi : 10.1107 / S010876730201379X
Ким, Шун К. (1999), Теоретико-групповые методы и приложения к молекулам и кристаллам, Cambridge University Press, doi : 10.1017 / CBO9780511534867, ISBN 978-0-521-64062-6, MR 1713786
Литвин ДБ (Май 2008 г.), «Таблицы кристаллографических свойств магнитных пространственных групп», Acta Crystallographica A, 64 (Pt 3): 419–24, Bibcode : 2008AcCrA.. 64..419L, doi : 10.1107 / S010876730800768X, PMID 18421131
Литвин, ДБ (Май 2005 г.), «Таблицы свойств магнитных субпериодических групп» (PDF), Acta Crystallographica A, 61 (Pt 3): 382–5, Bibcode : 2005AcCrA..61..382L, doi : 10.1107 / S010876730500406X, PMID 15846043
Нойбюзер, Дж.; Souvignier, B.; Вондрачек, Х. (2002), «Поправки к кристаллографическим группам четырехмерного пространства, Браун и др. (1978) [Нью-Йорк: Уайли и сыновья] », Acta Crystallographica A, 58 (Pt 3): 301, doi : 10.1107 / S0108767302001368, PMID 11961294
Опгенорт, Дж; Плескен, Вт; Шульц, Т. (1998), «Кристаллографические алгоритмы и таблицы», Acta Crystallographica A, 54 (Pt 5): 517–531, doi : 10.1107 / S010876739701547X
Палистрант, AF (2012), «Полная схема четырехмерных кристаллографических групп симметрии», Crystallography Reports, 57 (4): 471–477, Bibcode : 2012CryRp..57..471P, doi : 10.1134 / S1063774512040104
Плескен, Вильгельм; Hanrath, W (1984), «Решетки шестимерного пространства», Math., 43 (168): 573–587, doi : 10,1090 / s0025-5718-1984-0758205-5
Плескен, Вильгельм; Шульц, Тилман (2000), «Подсчет кристаллографических групп малых размеровх», Экспериментальная математика, 9 (3): 407–411, doi : 10.1080 / 10586458.2000.10504417, ISSN 1058-6458, MR 1795312
Шёнфлис, Артур Мориц (1923), «Теория кристаллической структуры» [Теория кристаллической структуры], Гебрюдер Борнтрегер, Берлин.
Souvignier, Bernd (2006), "Четырехмерная магнитная точка и пространственные группы", Zeitschrift für Kristallographie, 221 : 77–82, Bibcode : 2006ZK.... 221... 77S, doi : 10.1524 / zkri.2006.221.1.77
Винберг, Э. (2001) [1994], Энциклопедия математики, EMS Press
Zassenhaus, Hans (1948), «Über einen Algorithmus zur Bestimmung der Raumgruppen» [ Об алгоритме определения пространственных групп], Commentarii Mathematici Helvetici, 21 : 117–141, doi : 10.1007 / BF02568029, ISSN 0010 -2571, MR 0024424
Сувинье, Б. ernd (2003), «Энантиоморфизм кристаллографических групп в более высоких измерений с результатами в размерах до 6», Acta Crystallographica A, 59 (3): 210–220, doi : 10.1107 / S0108767303004161

Внешние ссылки

На Викискладе есть материалы, связанные с Космическими группами.