Пятиугольный шестигранник

редактировать

Пятиугольный шестиугольник
. (Нажмите здесь, чтобы посмотреть модель вращения)
Тип	Каталонское твердое тело
Диаграмма Кокстера
Обозначение Конвея	gD
Тип лица	V3.3.3.3.5 . неправильный пятиугольник
Лица	60
Ребра	150
Вершины	92
Вершины по типу	12 {5}. 20 + 60 {3}
Группа симметрии	I, 1 / 2H 3, [5,3], (532)
Группа вращения	I, [5,3], (532)
Двугранный угол	153 ° 10′43 ″
Свойства	выпуклый, гранно-транзитивный хиральный
. Плоский додекаэдр. (двойной многогранник )	. Сеть

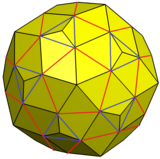
3D модель пятиугольного гексеконтаэдра

В геометрии, пятиугольный гексеконтаэдр представляет собой каталонское твердое тело, двойственное к курносому додекаэдру. Он имеет две различные формы, которые являются зеркальными отображениями (или «энантиоморфами ») друг друга. У него 92 вершины, охватывающие 60 пятиугольных граней. Это каталонское тело с наибольшим количеством вершин. Среди каталонских и архимедовых тел у него второе по величине число вершин после усеченного икосододекаэдра, которое имеет 120 вершин.

Содержание

1 Конструкция
2 Геометрия
- 2.1 Варианты
3 Ортогональные проекции
4 Связанные многогранники и мозаики
5 См. Также
6 Ссылки
7 Внешние ссылки

Конструкция

Пентагональный гексеконтаэдр может быть построен из курносого додекаэдра без двойного. Пятиугольные пирамиды добавляются к 12 пятиугольным граням курносого додекаэдра, а треугольные пирамиды добавляются к 20 треугольным граням, которые не имеют общего ребра с пятиугольником. Высота пирамиды регулируется, чтобы сделать их копланарными с другими 60 треугольными гранями курносого додекаэдра. В результате получается пятиугольный шестиугольник.

Геометрия

Грани представляют собой неправильные пятиугольники с двумя длинными краями и тремя короткими краями. Пусть $ξ ≈ 0,943 151 259 24 {\ displaystyle \ xi \ приблизительно 0,943 \, 151 \, 259 \, 24}$ ${\ displaystyle \ xi \ приблизительно 0.943 \, 151 \, 259 \, 24}$ будет действительным нулем многочлена $x 3 + 2 x 2. - ϕ 2 {\ displaystyle x ^ {3} + 2x ^ {2} - \ phi ^ {2}}$ ${\ displaystyle x ^ {3} + 2x ^ {2 } - \ phi ^ {2}}$ , где $ϕ = 1 + 5 2 {\ displaystyle \ phi = {\ frac {1 + {\ sqrt {5}}} {2}}}$ $\ phi = {\ frac {1 + {\ sqrt {5}}} {2}}$ - это золотое сечение. Тогда отношение длин ребер $l {\ displaystyle l}$ $l$ определяется как:

l = 1 + ξ 2 - ξ 2 ≈ 1,749 852 566 74 {\ displaystyle l = {\ frac {1+ \ xi} {2- \ xi ^ {2}}} \ приблизительно 1,749 \, 852 \, 566 \, 74}

{\ displaystyle l = {\ frac {1+ \ xi} {2- \ xi ^ {2}}} \ приблизительно 1,749 \, 852 \, 566 \, 74}

Грани имеют четыре одинаковых тупых угла и один острый угол (между двумя длинными края). Тупые углы равны $arccos ⁡ (- ξ / 2) ≈ 118,136 622 758 62 ∘ {\ displaystyle \ arccos (- \ xi / 2) \ приблизительно 118,136 \, 622 \, 758 \, 62 ^ {\ circ}. }$ ${\ displaystyle \ arccos (- \ xi / 2) \ приблизительно 118.136 \, 622 \, 758 \, 62 ^ {\ circ}}$ , а острый равен $arccos ⁡ (- ϕ 2 ξ / 2 + ϕ) ≈ 67,453 508 965 51 ∘ {\ displaystyle \ arccos (- \ phi ^ {2} \ xi / 2+ \ phi) \ приблизительно 67,453 \, 508 \, 965 \, 51 ^ {\ circ}}$ ${\ displaystyle \ arccos (- \ phi ^ { 2} \ xi / 2 + \ phi) \ приблизительно 67.453 \, 508 \, 965 \, 51 ^ {\ circ}}$ . Двугранный угол равен $arccos ⁡ (- ξ / (2 - ξ)) ≈ 153,178 732 558 45 ∘ {\ displaystyle \ arccos (- \ xi / (2- \ xi)) \ приблизительно 153,178 \, 732 \, 558 \, 45 ^ {\ circ}}$ ${ \ Displaystyle \ arccos (- \ xi / (2- \ xi)) \ приблизительно 153,178 \, 732 \, 558 \, 45 ^ {\ circ}}$ . Обратите внимание, что центры граней курносого додекаэдра не могут служить непосредственно вершинами пятиугольного гексеконтаэдра: четыре центра треугольника лежат в одной плоскости, а центр пятиугольника - нет; его нужно вытолкнуть радиально, чтобы сделать его копланарным с центрами треугольников. Следовательно, не все вершины пятиугольного гексаконтаэдра лежат на одной сфере, и по определению это не зоноэдр.

. Чтобы найти объем и площадь поверхности пятиугольного гексеконтаэдра, обозначьте длинную сторону одного из пятиугольные грани как $b {\ displaystyle b}$ $b$ и установить константу t $t = 44 + 12 ϕ (9 + 81 ϕ - 15) 3 + 44 + 12 ϕ (9 - 81 ϕ - 15) 3–4 12 ≈ 0,471 575 629 622 {\ displaystyle t = {\ frac {{\ sqrt [{3}] {44 + 12 \ phi (9 + {\ sqrt {81 \ phi -15}) })}} + {\ sqrt [{3}] {44 + 12 \ phi (9 - {\ sqrt {81 \ phi -15}})}} - 4} {12}} \ приблизительно 0,471 \, 575 \, 629 \, 622}$ ${\ displaystyle t = {\ frac {{\ sqrt [{3}] {44 + 12 \ phi (9 + {\ sqrt {81 \ phi -15}})}} + {\ sqrt [{3}] {44 + 12 \ phi (9 - {\ sqrt {81 \ phi -15}})}} - 4} {12}} \ приблизительно 0,471 \, 575 \, 629 \, 622}$ .

Тогда площадь поверхности (A) равна:

$A = 30 b 2 ⋅ (2 + 3 t) ⋅ 1 - t 2 1-2 t 2 ≈ 162,698 964 198 b 2 { \ Displaystyle A = {\ frac {30b ^ {2} \ cdot (2 + 3t) \ cdot {\ sqrt {1-t ^ {2}}}} {1-2t ^ {2}}} \ приблизительно 162,698 \, 964 \, 198b ^ {2}}$ ${\ displaystyle A = {\ frac {30b ^ {2} \ cdot (2 + 3t) \ cdot {\ sqrt {1-t ^ {2}}}} {1-2t ^ { 2}}} \ приблизительно 162.698 \, 964 \, 198b ^ {2}}$ .

И объем (V) равен:

$V = 5 b 3 (1 + t) (2 + 3 t) (1-2 t 2) ⋅ 1 - 2 t ≈ 189,789 852 067 b 3 {\ displaystyle V = {\ frac {5b ^ {3} (1 + t) (2 + 3t)} {(1-2t ^ {2}) \ cdot {\ sqrt {1 -2t}}}} \ около 189.789 \, 852 \, 067b ^ {3}}$ ${\ displaystyle V = {\ frac {5b ^ {3} (1 + t) (2 + 3t)} {(1-2t ^ {2}) \ cdot {\ sqrt {1-2t}}}} \ приблизительно 189.789 \, 852 \, 067b ^ {3}}$ .

Варианты

Изогранные варианты могут быть построены с пятиугольными гранями с 3 длинами ребер.

Этот показанный вариант может быть построен путем добавления пирамид к 12 пятиугольным граням и 20 треугольным граням курносого додекаэдра таким образом, чтобы новые треугольные грани были параллельны другим треугольникам и могли быть объединены в лица пятиугольника.

. Плоский додекаэдр с увеличенными пирамидами и объединенными гранями

. Вариант примера

. Сеть

Ортогональные проекции

Пентагональный гексеконтаэдр имеет три положения симметрии, два на вершинах и одно среднее - край.

Ортогональные проекции
Проективная. симметрия	[3]	[5 ]	[2]
Изображение
Двойное. image

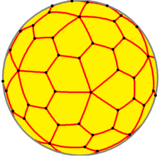Связанные многогранники и мозаики

Сферический пятиугольный шестигранник

Семейство однородных икосаэдрических многогранников
Симметрия : [5,3], (* 532)							[5,3], (532)


{5,3}	t {5,3}	r {5,3}	t {3,5}	{3,5}	rr {5,3}	tr {5,3}	sr {5,3}
Двойник к однородным многогранникам

V5.5.5	V3. 10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Этот многогранник топологически связана как часть последовательности многогранников и мозаик пятиугольников с конфигурациями граней (V3.3.3.3.n). (Последовательность переходит в разбиение гиперболической плоскости на любое n.) Эти грани-транзитивные фигуры имеют (n32) вращательную симметрию.

n32 мутаций симметрии плоскостных плиток: 3.3.3.3.n v
Симметрия. n32	Сферическая				Евклидова	Компактная гиперболическая		Паракомп.
Симметрия. n32	232	332	432	532	632	732	832	∞32
Snub. цифры
Конфиг.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Гироскоп. цифры
Конфиг.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3. 3.3.3.8	V3.3.3.3.∞

См. Также

Ссылки

Роберт Уильямс (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X.(Раздел 3-9)
Веннингер, Магнус (1983), Двойные модели, Cambridge University Press, doi : 10.1017 / CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 (Тринадцать полуправильных выпуклых многогранников и их двойники, стр.29, пятиугольный гексеконтаэдр)
Симметрии вещей 2008, Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штраус, ISBN 978-1-56881-220-5 [1] (Глава 21, Именование архимедовых и каталонских многогранников и мозаик, стр. 287, пятиугольный шестиугольник)

Внешние ссылки

Эрик В. Вайсштейн, Пятиугольный гексеконтаэдр (Каталонское твердое тело ) в MathWorld.
Пятиугольный гексеконтраэдр - Модель интерактивного многогранника