Равносторонний многоугольник

В геометрия, три или более трех прямых линий (или сегментов линии) составляют многоугольник, а равносторонний многоугольник - это многоугольник, который имеет все стороны такая же длина. За исключением случая треугольник, он не обязательно должен быть равноугольным (не обязательно, чтобы все углы были равны), но если это так, то это обычный многоугольник. Если количество сторон не менее пяти, равносторонний многоугольник не обязательно должен быть выпуклым многоугольником : он может быть вогнутым или даже самопересекающимся.

• 1 Примеры
• 2 Triambi
• 3 Ссылки
• 4 Внешние ссылки

Все правильные многоугольники и изотоксальные многоугольники равносторонние.

равносторонний треугольник - это правильный треугольник с 60 ° внутренними углами.

Равносторонний четырехугольник называется ромб, изотоксальный многоугольник, описываемый углом α. В качестве особого случая он включает квадрат.

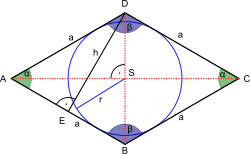
Выпуклый равносторонний пятиугольник можно описать двумя углами α и β, которые вместе определяют другие углы. Существуют вогнутые равносторонние пятиугольники, а также вогнутые равносторонние многоугольники с любым большим количеством сторон.

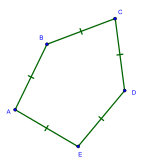
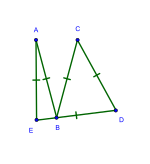
Равносторонний многоугольник, который является циклическим (его вершины находятся на окружности), является правильным многоугольником (многоугольник, который одновременно является равносторонним и равноугольным ).

A касательный многоугольник (имеющий вписанную окружность, касательную ко всем своим сторонам) является равносторонним тогда и только тогда, когда альтернативные углы равны (то есть углы 1, 3, 5,... равны и углы 2, 4,... равны). Таким образом, если количество сторон n нечетное, касательный многоугольник является равносторонним тогда и только тогда, когда он правильный.

Теорема Вивиани обобщается на равносторонние многоугольники: сумма перпендикулярных расстояний от внутренней точки до сторон равносторонний многоугольник не зависит от расположения внутренней точки.

Каждая из главных диагоналей шестиугольника делит шестиугольник на четырехугольники. В любом выпуклом равностороннем шестиугольнике с общей стороной a существует главная диагональ d 1 такая, что

$d\; 1\; a\; \le \; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\_\; \{1\}\}\; \{a\}\}\; \backslash \; leq\; 2\}$

и главная диагональ d 2 такие, что

$d\; 2\; a>3.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\_\; \{2\}\}\; \{a\}\}>\{\backslash \; sqrt\; \{3\}\}.\}$

Триамбий равносторонние шестиугольники с тригональная симметрия:

• 

  вогнутая

• 

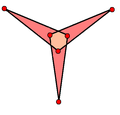
  самопересекающаяся

• СМИ, связанные с Равносторонними многоугольниками на Wikimedia Commons
• Равносторонний треугольник С интерактивной анимацией
• Свойство равносторонних многоугольников: что это такое? обсуждение теоремы Вивиани на Cut-the-knot.