 Несколько простых многоугольников.
Несколько простых многоугольников. В геометрии, простой многоугольник - это многоугольник, который не пересекает сам и не имеет отверстий. То есть это плоская форма, состоящая из прямых непересекающихся отрезков линий или «сторон», которые соединяются попарно для образования единого замкнутого пути. Если стороны пересекаются, то многоугольник не простой. Квалификатор "простой" часто опускается, и тогда понимается, что приведенное выше определение определяет многоугольник в целом.
Приведенное выше определение обеспечивает следующие свойства:
Два ребра, встречающиеся в углу, обычно требуются для образования угла, который не является прямым (180 °); в противном случае отрезки коллинеарной линии будут считаться частями одной стороны.
Математики обычно используют «многоугольник» для обозначения только формы, образованной линейными сегментами, а не замкнутой области, однако некоторые могут использовать «многоугольник» для обозначения плоскости рисунок, который ограничен замкнутым путем, состоящим из конечной последовательности отрезков прямых линий (т. е. замкнутой многоугольной цепью ). Согласно используемому определению, эта граница может быть или не быть частью самого многоугольника.
Простые многоугольники также называются многоугольниками Жордана, поскольку теорема о кривой Жордана может использоваться, чтобы доказать, что такой многоугольник делит плоскость на две области: область внутри нее и область за ее пределами. Многоугольник на плоскости является простым тогда и только тогда, когда он топологически эквивалентен окружности. Его внутренняя часть топологически эквивалентна диску.
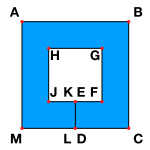
Если совокупность непересекающихся отрезков прямых образует границу области плоскости, топологически эквивалентной диску, тогда эта граница называется слабо простым многоугольником . На изображении слева ABCDEFGHJKLM - это слабо простой многоугольник в соответствии с этим определением, с синим цветом, отмеченным областью, для которой он является границей. Этот тип слабо простого многоугольника может возникнуть в компьютерной графике и CAD как компьютерное представление многоугольных областей с отверстиями: для каждого отверстия создается «вырез», чтобы соединить его с внешней границей. Ссылаясь на изображение выше, ABCM - это внешняя граница плоской области с отверстием FGHJ. Разрез ED соединяет отверстие с внешней стороной и дважды пересекается в результирующем слабо простом многоугольном представлении.
В альтернативном и более общем определении слабо простых многоугольников они представляют собой пределы последовательностей простых многоугольников одного комбинаторного типа со сходимостью при расстоянии Фреше. Это формализует представление о том, что такой многоугольник позволяет сегментам касаться, но не пересекаться. Однако этот тип слабо простого многоугольника не обязательно должен формировать границу области, так как его «внутренность» может быть пустой. Например, обращаясь к изображению выше, многоугольная цепочка ABCBA является слабо простым многоугольником в соответствии с этим определением: ее можно рассматривать как предел «сжатия» многоугольника ABCFGHA.
В вычислительной геометрии несколько важных вычислительных задач включают входные данные в форме простого многоугольника; в каждой из этих задач различие между внутренним и внешним является решающим при определении проблемы.