Список плоских групп симметрии

В этой статье собраны классы дискретных группы симметрии евклидовой плоскости. Группы симметрии названы здесь тремя схемами именования: Международная нотация, Орбифолдная нотация и Нотация Кокстера. Существует три типа групп симметрии плоскости:

• 2 семейства групп розеток - 2D точечные группы
• 7 группы фризов - 2D группы линий
• 17 группы обоев - 2D пространственные группы.

Содержание

• 1 группы розеток
• 2 группы Frieze
• 3 группы обоев
• 4 отношения подгрупп обоев
• 5 См. также
• 6 Примечания
• 7 Ссылки
• 8 Внешние ссылки

Группы розеток

Есть два семейства дискретных двумерных групп точек, и они задаются параметром n, который порядок группы вращений в группе.

Семейство	Intl. (орбифолд )	Schön.	Geo. Coxeter	Order	Примеры
Циклическая симметрия	n. (n •)	Cn	n. [n].	n	. C1, [] (•)	. C2, [2] (2 •)	. C3, [3] (3 •)	. C4, [4] (4 •)	. C5, [5] (5 •)	. C6, [6] (6 •)
Двугранная симметрия	nm. (* n •)	Dn	n. [n].	2n	. D1, [] (* •)	. D2, [2] (* 2 •)	. D3, [3] (* 3 •)	. D4, [4] (* 4 •)	. D5, [5] (* 5 •)	. D6, [6] (* 6 •)

Группы фриза

7 групп фризов, двумерные группы линий, с направления периодичности даны с пятью условными обозначениями. Обозначение Шенфлиса дано как бесконечные пределы 7 диэдральных групп. Желтые области представляют собой бесконечную фундаментальную область в каждой.

[1, ∞], IUC. (орбифолд ) Geo Schönflies Coxeter Фундаментальный. домен Пример p1. (∞ •) p1 C∞ [1, ∞]. . скачок p1m1. (* ∞ •) p1 C∞v [1, ∞]. . sidle [2, ∞], IUC. (orbifold) Geo Schönflies Coxeter Фундаментальный. домен Пример p11g. (∞ ×) p.g1 S2∞ [2, ∞]. . шаг p11m. (∞*) стр. 1 C∞h [2, ∞]. . прыжок

[2, ∞], IUC. (орбифолд) Geo Schönflies Кокстер Фундаментальный. домен Пример p2. (22∞) p2 D∞ [2, ∞]. . спиннинг-прыжок p2mg. (2 * ∞) p2g D∞d [2, ∞]. . вращающийся сайдл p2mm. (* 22∞) p2 D∞h [2, ∞]. . прыжок с вращением

Группы обоев

17 групп обоев с конечными фундаментальными доменами заданы международной нотацией, орбифолдной нотацией и нотацией Кокстера, классифицированной 5 решетками Браве на плоскости: квадрат, наклонный (параллелограммный), гексагональный (равносторонний треугольник), прямоугольный (центрированный ромбический) и ромбический (центрированный прямоугольник).

Группы p1 и p2 без отражательной симметрии повторяются во всех классах. Связанная чисто отражательная группа Кокстера дана со всеми классами, кроме наклонной.

Квадрат. [4,4], IUC. (Сфера ). Гео Коксетер Фундаментальный. домен p1. (°). p1 p2. (2222). p2 [4,1,4]. . [1,4,4,1]. pgg. (22 ×). pg2g [4,4]. 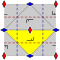pmm. (* 2222). p2 [4,1,4]. . [1,4,4,1]. cmm. (2 * 22). c2 [(4, 4,2)]. p4. (442). p4 [4,4]. p4g. (4 * 2). pg4 [4,4]. p4m. (* 442). p4 [4,4].

Прямоугольный. [∞h, 2, ∞ v ], IUC. (Орб.). Гео Кокстер Основная. область p1. (°). p1 [∞, 2, ∞]. p2. (2222). p2 [∞, 2, ∞]. 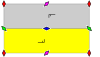pg (h). (× ··· ×). pg1. h: [∞, (2, ∞)]. pg (v). (× ··· ×). pg1 v: [(∞, 2), ∞]. 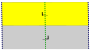pgm. (22 *). pg2 h: [(∞, 2), ∞]. pmg. (22 *). pg2 v: [∞, (2, ∞)]. 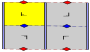pm (h). (**). p1 h: [∞, 2, ∞]. pm (v). (**). p1 v: [∞, 2, ∞ ]. pmm. (* 2222). p2 [∞, 2, ∞].

Ромбический. [∞h, 2, ∞ v ], IUC. ( Orb.). Geo Coxeter Фундаментальный. домен p1. (°). p1 [∞, 2, ∞]. p2. (2222). p2 [∞, 2, ∞]. см (в). (* ×). c1 в: [∞, 2, ∞]. см (в). (* ×). c1 v: [∞, 2, ∞]. 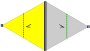pgg. (22 ×). pg2g [((∞, 2))]. 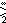cmm. (2 * 22). c2 [∞, 2, ∞]. Параллелограмматический (наклонный ) p1. (°). p1 p2. (2222). p2

Гексагональный / треугольный. [6,3], / [3], p1. (°). p1 p2. (2222). p2 [6,3] см. (2 * 22). c2 [6,3] p3. (333). p3 [1,6,3]. . [3]. 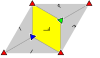p3m1. (* 333). p3 [1,6,3]. . [3]. p31m. (3 * 3). h3 [6,3]. p6. (632). p6 [6,3]. p6m. (* 632). p6 [6,3].

Отношения подгруппы обоев

См. Также

• Список групп сферической симметрии
• Обозначение орбифолда # Гиперболическая плоскость - группы гиперболической симметрии

Примечания

Ссылки

• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Орбифолдная нотация для многогранников, Евклидовы и гиперболические мозаики)
• On Quaternions and Octonions, 2003, Джон Хортон Конвей и Дерек А. Смит ISBN 978-1-56881-134-5
• Калейдоскопы: Избранные труды HSM Кокстер, под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони С. Томпсона, Асии Ивич Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0 -471-01003-6 [2]
  • (Бумага 22) HSM Кокстер, Правильные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
  • (Документ 23) H.S.M. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559–591]
  • (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3–45]
• Кокстер, Х. С. М. и Мозер, У. О. Дж. (1980). Генераторы и отношения для дискретных групп. Нью-Йорк: Springer-Verlag. ISBN 0-387-09212-9.
• N.W. Джонсон : Геометрии и преобразования, (2018) ISBN 978-1-107-10340-5 Глава 12: Евклидовы группы симметрии

Внешние ссылки

• «Рукопись Конвея» в нотации Орбифолд (Нотация изменена с этого оригинала, x теперь используется вместо открытой точки, а o используется вместо закрытой точки)
• 17 групп обоев