Кривая Безье

Кривая, используемая в компьютерной графике и связанных областях Кубическая кривая Безье с четырьмя контрольными точками Базовые функции в диапазоне t в [0,1] для кубических кривых Безье: синий: y = (1 - t), зеленый: y = 3 (1 - t) t, красный: y = 3 (1 - t) t и голубой: y = t.

A кривая Безье () - параметрическая кривая используется в компьютерной графике и связанные области. Кривая, связанная с полиномом Бернштейна, названа в честь Пьера Безье, который использовал ее в 1960-х годах для построения кривых кузова автомобилей Renault.. Другие применения включают программу компьютерных шрифтов и анимации. Кривые Безье можно комбинировать для формирования сплайна Безье или обобщить на более высокие измерения для формирования поверхности Безье. Треугольник Безье - частный случай последнего.

В векторной графике кривые Безье используются для моделирования сглаженных кривых, которые можно масштабировать бесконечно. «Пути», как их обычно используют в программах обработки изображений, соответствующих комбинациям кривых Безье. Пути не ограничены пределами растровых изображений и интуитивно понятны для изменений.

Кривые Безье также используются во временной области, в частности, в анимации, дизайне пользовательского интерфейса и сглаживании траектории курсора в интерфейсах, управляемых взглядом. Например, кривую Безье можно использовать для определения скорости движения объекта, такого значок, с течением времени из точки A в точку B, вместо того, чтобы просто перемещаться с фиксированным числом за шаг. Когда аниматоры или дизайн интерфейса говорят о «физике» или «ощущении» операции, они могут иметь в виду конкретную кривую Безье, используемую для управления скоростью во времени рассматриваемого движения.

Это также относится к робототехнике, где, например, движение сварочного рычага должно быть плавным, чтобы избежать ненужного износа.

• 1 Изобретение
• 2 Конкретные случаи
  • 2.1 Линейные кривые Безье
  • 2.2 Квадратичные кривые Безье
  • 2.3 Кубические кривые Безье
• 3 Общее определение
  • 3.1 Рекурсивное определение
  • 3.2 Явное определение
  • 3.3 Терминология
  • 3.4 Полиномиальная форма
  • 3.5 Свойства
  • 3.6 Кривая второго порядка - параболический сегмент
  • 3.7 Производная
• 4 Построение кривых Безье
  • 4.1 Линейные кривые
  • 4.2 Квадратичные кривые
  • 4.3 Кривые более высокого порядка
  • 4.4 Повреждение (также называемые штриховкой) кривых Безье
• 5 Наклон в градусах
  • 5.1 Повторное повышение в градусах
• 6 Рациональные кривые Безье
• 7 Приложения
  • 7.1 Компьютерная графика
  • 7.2 Анимация
  • 7.3 Шрифты
• 8 См. Также
• 9 Примечания
• 10 Ссылки
  • 10.1 Цитаты
  • 10.2 Источники
• 11 Дополнительная литература
• 12 Внешние ссылки

Математическая основа для кривых Безье - полиномы Бернштейна - была создана в 1912 году, но полиномы не применялись к графику примерно через 50 лет. Когда математик Поль де Кастельжау в 1959 году разработал алгоритм де Кастельжау, численно устойчивый метод оценки кривых, и стал первым, кто применил его к компьютерум. Системы автоматизированного проектирования на французском автопроизводителе Citroën. Многочлены были широко известны в 1960-х годах французским инженером Пьером Безье, который использовал их для конструирования автомобильных кузовов в Renault.

Кривая Безье определяется набором контрольных точек с P0по Pn, где n называется ее порядком (n = 1 для линейной, 2 для квадратичной и т. Д.). Первая и последняя контрольные точки всегда являются конечными точками кривой; однако промежуточные контрольные точки (если есть) обычно не лежат на кривой. Суммы в следующих разделах следует понимать как аффинные комбинации, сумма коэффициентов равна 1.

Линейные кривые Безье

Для различных точек P0и P1, линейная кривая Безье - это просто прямая между этими точками. Кривая задается следующим образом:

$B\; (t)\; =\; P\; 0\; +\; t\; (P\; 1\; -\; P\; 0)\; =\; (1\; -\; t)\; P\; 0\; +\; t\; P\; 1,\; 0\; \le \; t\; \le \; 1\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; (t)\; =\; \backslash \; mathbf\; \{P\}\; \_\; \{0\}\; +\; t\; (\backslash \; mathbf\; \{P\}\; \_\; \{1\}\; -\; \backslash \; mathbf\; \{P\}\; \_\; \{0\})\; =\; (1-t)\; \backslash \; mathbf\; \{P\}\; \_\; \{0\; \}\; +\; t\; \backslash \; mathbf\; \{P\}\; \_\; \{1\}\; \{\backslash \; t\_dv\; \{,\}\}\; 0\; \backslash \; leq\; t\; \backslash \; leq\; 1\}$

и эквивалент линейной интерполяции.

Квадратичные кривые Безье

Квадратичные кривые Безье в строковой графике : Конечные точки (• ) и контрольная точка (× ) определяют квадратичную кривую Безье (⋯).

Квадратичная кривая Безье - это путь отслеживается функция B (t), заданными точками P0, P1, и P2,

$B\; (t)\; =\; (1\; -\; t)\; [(1\; -\; t)\; P\; 0\; +\; t\; P\; 1]\; +\; t\; [(1\; -\; t)\; п\; 1\; +\; T\; п\; 2],\; 0\; \le \; T\; \le \; 1\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{B\}\; (т)\; =\; (1-т)\; [(1-т)\; \backslash \; mathbf\; \{P\}\; \_\; \{0\}\; +\; т\; \backslash \; mathbf\; \{\; P\}\; \_\; \{1\}]\; +\; t\; [(1-t)\; \backslash \; mathbf\; \{P\}\; \_\; \{1\}\; +\; t\; \backslash \; mathbf\; \{P\}\; \_\; \{2\}]\; \{\backslash \; t\_dv\; \{,\}\}\; 0\; \backslash \; leq\; t\; \backslash \; leq\; 1\; \}$,

, который можно интерпретировать как линейный интерполянт соответствующих точек на линейных кривых Бе зье от P0до P1и от P1до P2соответственно. Уравнение g дает:

$B\; (t)\; =\; (1\; -\; t)\; 2\; P\; 0\; +\; 2\; (1\; -\; t)\; t\; P\; 1\; +\; t\; 2\; P\; 2,\; 0\; \le \; t\; \le \; 1.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; (t)\; =\; (1-t)\; ^\; \{2\}\; \backslash \; mathbf\; \{P\}\; \_\; \{0\}\; +2\; (1-t)\; t\; \backslash \; mathbf\; \{P\}\; \_\; \{1\}\; +\; t\; ^\; \{2\}\; \backslash \; mathbf\; \{P\}\; \_\; \{2\}\; \{\backslash \; t\_dv\; \{,\}\}\; 0\; \backslash \; leq\; t\; \backslash \; leq\; 1.\}$

Это можно записать таким образом, чтобы подчеркнуть симметрию относительно P1:

$B\; (t)\; =\; P\; 1\; +\; (1\; -\; t)\; 2\; (П\; 0\; -\; п\; 1)\; +\; t\; 2\; (п\; 2\; -\; п\; 1),\; 0\; \le \; t\; \le \; 1.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; (t)\; =\; \backslash \; mathbf\; \{P\}\; \_\; \{1\}\; +\; (1-t)\; ^\; \{2\}\; (\backslash \; mathbf\; \{P\}\; \_\; \{0\}\; -\; \backslash \; mathbf\; \{P\}\; \_\; \{1\})\; +\; t\; ^\; \{2\}\; (\backslash \; mathbf\; \{P\}\; \_\; \{2\}\; -\; \backslash \; mathbf\; \{P\}\; \_\; \{\; 1\})\; \{\backslash \; t\_dv\; \{,\}\}\; 0\; \backslash \; leq\; t\; \backslash \; leq\; 1.\}$

Что сразу дает производную кривую Безье по t:

$B\; \prime \; (t)\; =\; 2\; (1\; -\; t)\; (P\; 1\; -\; П\; 0)\; +\; 2\; т\; (П\; 2\; -\; П\; 1).\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; \text{'}(t)\; =\; 2\; (1-t)\; (\backslash \; mathbf\; \{P\}\; \_\; \{1\}\; -\; \backslash \; mathbf\; \{P\}\; \_\; \{0\})\; +\; 2t\; (\backslash \; mathbf\; \{P\}\; \_\; \{\; 2\}\; -\; \backslash \; mathbf\; \{P\}\; \_\; \{1\})\; \backslash ,.\}$

из которого можно сделать вывод, что касательные к кривой в точках P0и P2пересекаются в точках P1. При увеличении от 0 до 1 кривая отклоняется от P0в направлении P1, затем изгибается, чтобы достичь P2от направления P1.

. Вторая производная кривая Безье по t равна

$B\; ″\; (t)\; =\; 2\; (P\; 2\; -\; 2\; P\; 1\; +\; P\; 0).\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{B\}\; \text{'}\text{'}\; (т)\; =\; 2\; (\backslash \; mathbf\; \{P\}\; \_\; \{2\}\; -2\; \backslash \; mathbf\; \{P\}\; \_\; \{1\}\; +\; \backslash \; mathbf\; \{P\}\; \_\; \{0\})\; \backslash ,.\; \}$

Кубические кривые Безье

Четыре точки P0, P1, P2и P3на плоскости или в многомерном пространстве определяют кубическую кривую Безье. Кривая начинается от P0по направлению к P1и начинается P3в направлении от P2. Обычно он не проходит через P1или P2; эти точки только для получения информации о направлении. Расстояние между P1и P2определяет «насколько» и «насколько быстро» кривая перемещается в сторону P1до поворота в сторону P2.

. Запись BPi,Pj,Pk(t) для квадратичной кривой Безье, точными точками Pi, Pjи Pkкубическая кривая Безье может быть определена как аффинная комбинация двух квадратичных кривых Безье:

$B\; (t)\; =\; (1\; -\; t)\; BP\; 0,\; П\; 1,\; п\; 2\; (t)\; +\; t\; ВР\; 1,\; п\; 2,\; п\; 3\; (t),\; 0\; \le \; t\; \le \; 1.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; (t)\; =\; (1-t)\; \backslash \; mathbf\; \{B\; \}\; \_\; \{\backslash \; mathbf\; \{P\}\; \_\; \{0\},\; \backslash \; mathbf\; \{P\}\; \_\; \{1\},\; \backslash \; mathbf\; \{P\}\; \_\; \{2\}\}\; (t)\; +\; t\; \backslash \; mathbf\; \{B\}\; \_\; \{\backslash \; mathbf\; \{P\}\; \_\; \{1\},\; \backslash \; mathbf\; \{P\}\; \_\; \{2\},\; \backslash \; mathbf\; \{P\}\; \_\; \{3\}\}\; (t)\; \{\backslash \; t\_dv\; \{,\}\}\; 0\; \backslash \; leq\; t\; \backslash \; leq\; 1.\}$

Явный вид кривой :

$B\; (t)\; Знак\; равно\; (1\; -\; t)\; 3\; п\; 0\; +\; 3\; (1\; -\; t)\; 2\; t\; п\; 1\; +\; 3\; (1\; -\; t)\; t\; 2\; P\; 2\; +\; t\; 3\; P\; 3,\; 0\; \le \; t\; \le \; 1.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; (t)\; =\; (1-t)\; ^\; \{3\}\; \backslash \; mathbf\; \{P\}\; \_\; \{0\}\; +3\; (1-t)\; ^\; \{2\}\; t\; \backslash \; mathbf\; \{P\}\; \_\; \{1\}\; +3\; (1-\; t)\; t\; ^\; \{2\}\; \backslash \; mathbf\; \{P\}\; \_\; \{2\}\; +\; t\; ^\; \{3\}\; \backslash \; mathbf\; \{P\}\; \_\; \{3\}\; \{\backslash \; t\_dv\; \{,\}\}\; 0\; \backslash \; leq\; t\; \backslash \; leq\; 1.\}$

Для некоторых вариантов P1и P2кривая может пересекаться сама с собой или содержать острие .

Любая серия из 4 различных точек может быть преобразована в кубическом ую кривую Безье, которая проходит через все 4 точки по порядку. Учитывая начальную и конечную точку некоторой кубической кривой Безье и точки вдоль кривой, соответствующие t = 1/3 и t = 2/3, можно восстановить контрольные точки для исходной кривой Безье.

Производная кубической кривой Безье по t равна

$B\; \prime \; (t)\; =\; 3\; (1\; -\; t)\; 2\; (P\; 1\; -\; P\; 0)\; +\; 6\; (1\; -\; t)\; t\; (P\; 2\; -\; P\; 1).\; +\; 3\; т\; 2\; (П\; 3\; -\; П\; 2).\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; \text{'}(t)\; =\; 3\; (1-t)\; ^\; \{2\}\; (\backslash \; mathbf\; \{P\}\; \_\; \{1\}\; -\; \backslash \; mathbf\; \{P\}\; \_\; \{0\})\; +\; 6\; (1-t)\; t\; (\backslash \; mathbf\; \{P\}\; \_\; \{2\}\; -\; \backslash \; mathbf\; \{P\}\; \_\; \{1\})\; +\; 3t\; ^\; \{2\}\; (\backslash \; mathbf\; \{P\}\; \_\; \{3\}\; -\; \backslash \; mathbf\; \{P\}\; \_\; \{2\})\; \backslash ,.\}$

Вторая производная кривая Безье по t равна

$B\; ″\; (t)\; =\; 6\; (1\; -\; t)\; (P\; 2\; -\; 2\; P\; 1\; +\; P\; 0)\; +\; 6\; t\; (P\; 3\; -\; 2\; П\; 2\; +\; П\; 1).\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; \text{'}\text{'}\; (t)\; =\; 6\; (1-t)\; (\backslash \; mathbf\; \{P\}\; \_\; \{2\}\; -2\; \backslash \; mathbf\; \{P\}\; \_\; \{1\}\; +\; \backslash \; mathbf\; \{P\}\; \_\; \{0\; \})\; +\; 6t\; (\backslash \; mathbf\; \{P\}\; \_\; \{3\}\; -2\; \backslash \; mathbf\; \{P\}\; \_\; \{2\}\; +\; \backslash \; mathbf\; \{P\}\; \_\; \{1\})\; \backslash ,.\}$

Кривые Безье могут быть оценены для любой степени n.

Рекурсивное определение

Рекурсивное определение Безье степени n выражает ее как двухточечную линейную комбинацию (линейная интерполяция ) пары точек соответствующих точек на двух кривых Безье степени n - 1.

Пусть $BP\; 0\; P\; 1\dots \; P\; n\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; \_\; \{\backslash \; mathbf\; \{P\}\; \_\; \{0\}\; \backslash \; mathbf\; \{P\}\; \_\; \{1\}\; \backslash \; ldots\; \backslash \; mathbf\; \{P\}\; \_\; \{n\}\}\}$обозначает кривую Безье, определяемую любым выбором точек P0, P1,..., Pn. Затем для начала

$BP\; 0\; (t)\; =\; P\; 0\; и\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; \_\; \{\backslash \; mathbf\; \{P\}\; \_\; \{0\}\}\; (t)\; =\; \backslash \; mathbf\; \{P\}\; \_\; \{0\}\; \{\backslash \; текст\; \{,\; и\}\}\}$

$B\; (t)\; =\; BP\; 0\; P\; 1\dots \; P\; n\; (t)\; =\; (1\; -\; t)\; BP\; 0\; P\; 1\dots \; P\; n\; -\; 1\; (t)\; +\; t\; BP\; 1\; P\; 2\dots \; п\; N\; (т)\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{B\}\; (t)\; =\; \backslash \; mathbf\; \{B\}\; \_\; \{\backslash \; mathbf\; \{P\}\; \_\; \{0\}\; \backslash \; mathbf\; \{P\}\; \_\; \{1\}\; \backslash \; ldots\; \backslash \; mathbf\; \{P\}\; \_\; \{n\}\}\; (t)\; =\; (1-t)\; \backslash \; mathbf\; \{B\}\; \_\; \{\backslash \; mathbf\; \{P\}\; \_\; \{0\}\; \backslash \; mathbf\; \{P\}\; \_\; \{1\}\; \backslash \; ldots\; \backslash \; mathbf\; \{P\}\; \_\; \{n\; -1\; \}\}\; (t)\; +\; t\; \backslash \; mathbf\; \{B\}\; \_\; \{\backslash \; mathbf\; \{P\}\; \_\; \{1\}\; \backslash \; mathbf\; \{P\}\; \_\; \{2\}\; \backslash \; ldots\; \backslash \; mathbf\; \{P\}\; \_\; \{n\}\}\; (t)\}$

Эта рекурсия поясняется в анимации ниже.

Явное определение

Формула может быть явно выражена следующим образом:

$B\; (t)\; =\; \sum \; i\; =\; 0\; n\; (ni)\; (1\; -\; t)\; n\; -\; iti\; P\; i\; =\; (\; 1\; -\; t)\; n\; P\; 0\; +\; (n\; 1)\; (1\; -\; t)\; n\; -\; 1\; t\; P\; 1\; +\; \cdots \; +\; (nn\; -\; 1)\; (1\; -\; t)\; tn\; -\; 1\; P\; n\; -\; 1\; +\; tn\; P\; n\; 0\; ⩽\; t\; ⩽\; 1\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; mathbf\; \{B\}\; (t)\; =\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{n\}\; \{n\; \backslash \; select\; i\}\; (1-t)\; ^\; \{ni\}\; t\; ^\; \{i\}\; \backslash \; mathbf\; \{P\}\; \_\; \{i\}\; \backslash \backslash \; =\; (1-t)\; ^\; \{n\}\; \backslash \; mathbf\; \{P\}\; \_\; \{0\}\; +\; \{n\; \backslash \; choose\; 1\}\; (1-t)\; ^\; \{n\; -\; 1\}\; t\; \backslash \; mathbf\; \{P\}\; \_\; \{1\}\; +\; \backslash \; cdots\; +\; \{n\; \backslash \; choose\; n-1\}\; (1-t)\; t\; ^\; \{n-1\}\; \backslash \; mathbf\; \{P\}\; \_\; \{n-1\}\; +\; t\; ^\; \{n\}\; \backslash \; mathbf\; \{P\}\; \_\; \{n\}\; 0\; \backslash \; leqslant\; t\; \backslash \; leqslant\; 1\; \backslash \; end\; \{align\}\}\}$

где $(ni)\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{n\; \backslash \; choose\; i\}\}$- это биномиальные коэффициенты.

, для n = 5:

$B\; (t)\; =\; (1\; -\; t)\; 5\; P\; 0\; +\; 5\; t\; (1\; -\; t)\; 4\; P\; 1\; +\; 10\; t\; 2\; (1\; -\; t)\; 3\; P\; 2\; +\; 10\; t\; 3\; (1\; -\; t)\; 2\; P\; 3\; +\; 5\; t\; 4\; (1\; -\; t)\; P\; 4\; +\; t\; 5\; P\; 5\; 0\; ⩽\; t\; ⩽\; 1\; \{\backslash \; displaystyle\; \{\backslash \; начало\; \{выровнено\}\; \backslash \; mathbf\; \{B\}\; (t)\; =\; (1-t)\; ^\; \{5\}\; \backslash \; mathbf\; \{P\}\; \_\; \{0\}\; +\; 5t\; (1-t)\; ^\; \{4\}\; \backslash \; mathbf\; \{P\}\; \_\; \{1\; \}\; +\; 10t\; ^\; \{2\}\; (1-t)\; ^\; \{3\}\; \backslash \; mathbf\; \{P\}\; \_\; \{2\}\; +\; 10t\; ^\; \{3\}\; (1-t)\; ^\; \{2\}\; \backslash \; math\; bf\; \{P\}\; \_\; \{3\}\; +\; 5t\; ^\; \{4\}\; (1-t)\; \backslash \; mathbf\; \{P\}\; \_\; \{4\}\; +\; t\; ^\; \{5\}\; \backslash \; mathbf\; \{P\}\; \_\; \{5\}\; 0\; \backslash \; leqslant\; t\; \backslash \; leqslant\; 1\; \backslash \; end\; \{align\}\}\}$

Терминология

С этими параметрическими кривыми связями некоторая терминология. У нас есть

$B\; (t)\; =\; \sum \; я\; знак\; равно\; 0\; nbi,\; n\; (t)\; P\; i,\; 0\; \le \; t\; \le \; 1\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; (t)\; =\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{n\}\; b\_\; \{i,\; n\}\; (t)\; \backslash \; mathbf\; \{P\}\; \_\; \{i\},\; \backslash \; quad\; 0\; \backslash \; leq\; t\; \backslash \; leq\; 1\}$

где многочлены

$bi,\; n\; (t)\; =\; (ni)\; ti\; (1\; -\; t)\; n\; -\; i,\; i\; =\; 0,\dots ,\; n\; \{\backslash \; displaystyle\; b\_\; \{i,\; n\}\; (t)\; =\; \{n\; \backslash \; select\; i\}\; t\; ^\; \{i\}\; (1-t)\; ^\; \{ni\; \},\; \backslash \; quad\; i\; =\; 0,\; \backslash \; ldots,\; n\}$

известные как базисные полиномы Бернштейна степень n.

Обратите внимание, что t = 1, (1 - t) = 1 и что биномиальный коэффициент, $(ni)\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{n\; \backslash \; choose\; i\}\}$, это:

$(ni)\; =\; n!\; я!\; (п\; -\; я)!\; \{\backslash \; displaystyle\; \{n\; \backslash \; choose\; i\}\; =\; \{\backslash \; frac\; \{n!\}\; \{i!\; (n-i)!\}\}\}$

Точки Piназываются контрольными точками кривой Безье. Многоугольник , образованный соединением точек Безье с линиями, начиная с P0и заканчивая Pn, называется многоугольником Безье (или контрольным многоугольником). Выпуклая оболочка многоугольника Безье содержит кривую Безье.

Полиномиальная форма

Иногда желательно выразить кривую Безье в виде полинома вместо суммы менее простых полиномов Бернштейна. Применение биномиальной теоремы к определению кривой с последовательной перегруппировкой даст:

$B\; (t)\; =\; \sum \; j\; =\; 0\; ntj\; C\; j\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; (t)\; =\; \backslash \; sum\; \_\; \{j\; =\; 0\}\; ^\; \{n\}\; \{t\; ^\; \{j\}\; \backslash \; mathbf\; \{C\}\; \_\; \{j\}\}\}$

где

$C\; j\; =\; n!\; (n\; -\; j)!\; \sum \; я\; знак\; равно\; 0\; J\; (-\; 1)\; я\; +\; J\; P\; я\; я!\; (j\; -\; i)!\; Знак\; равно\; \prod \; м\; знак\; равно\; 0\; J\; -\; 1\; (N\; -\; т)\; \sum \; я\; знак\; равно\; 0\; J\; (-\; 1)\; я\; +\; J\; P\; я\; я!\; (j\; -\; i)!.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{C\}\; \_\; \{j\}\; =\; \{\backslash \; frac\; \{n!\}\; \{(nj)!\}\}\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{j\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{i\; +\; j\}\; \backslash \; mathbf\; \{P\}\; \_\; \{i\}\}\; \{я!\; (ji)!\}\}\; =\; \backslash \; prod\; \_\; \{m\; =\; 0\}\; ^\; \{j-1\}\; (nm)\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{j\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{i\; +\; j\}\; \backslash \; mathbf\; \{P\}\; \_\; \{i\}\}\; \{я!\; (ji)!\}\}.\}$

Это может быть практично, если $C\; j\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{C\}\; \_\; \{j\}\}$можно вычислить до многих вычислений $B\; (т)\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{B\}\; (т)\}$; однако следует проявлять осторожность, поскольку кривым высокого порядка может не хватать числовой стабильности (в этом случае следует использовать алгоритм де Кастельжау ). Обратите внимание, что пустой продукт равен 1.

Свойства

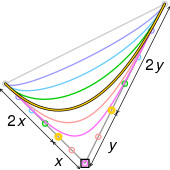Кубическую кривую Безье (желтая) можно сделать идентичной кривой (черной) на 1. Копирование конечных точек и 2. Размещение двух средних контрольных точек (желтые кружки) на 2/3 вдоль отрезков линии от конечных точек до средней контрольной точки квадратичной кривой (черный прямоугольник)

• Кривая начинается в P0и заканчивается в Pn; это так называемое свойство интерполяции конечной точки.
• Кривая является прямой линией тогда и только тогда, когда все контрольные точки коллинеарны.
• Начало и конец кривой имеют касательную к первому и последнему участку многоугольника Безье, соответственно.
• Кривая может быть разделена в любой точке на две подкривые или на произвольное количество подкривых, из каждой также кривой Безье.
• Некоторые кривые, которые кажутся простыми, такие как круг, не могут быть точно стимулы ни с помощью Безье, ни с помощью кусочно кривой Безье; кубическая кривая Без одной части из четырех частей может аппроксимировать круг (см. составная кривая Без ) с максимальной радиальной погрешностью менее одной части из тысячи, когда каждая внутренняя контрольная точка (или автономная точка) расстояние $4\; (2\; -1)\; 3\; \{\backslash \; displaystyle\; \backslash \; textst\; yle\; \{\backslash \; frac\; \{4\; \backslash \; left\; (\{\backslash \; sqrt\; \{2\}\}\; -\; 1\; \backslash \; right)\}\; \{3\}\}\}$по горизонтали или вертикально от внешней контрольной точки на единичной окружности. В более общем смысле, кубическая кривая Безье из n частей может аппроксимировать круг, когда каждая внутренняя контрольная точка находится на расстоянии $4\; 3\; tan\; \; (t\; /\; 4)\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \{\backslash \; frac\; \{4\}\; \{3\}\}\; \backslash \; tan\; (t\; /\; 4)\}$от внешней контрольной точки на единичной окружности, где t равно 360 / n градусов, а n>2.
• Каждая квадратичная кривая Безье также является кубической кривая Безье, и в более общем плане каждая степень кривая Безье также является кривой степени m для любого m>n. Более подробно, кривая степень n с контрольными точками P0,..., Pnэквивалентна (включая параметры) кривой степени n + 1 с контрольными точками P'0,..., P'n + 1, где $P\; k\; \text{'}=\; kn\; +\; 1\; P\; k\; -\; 1\; +\; (1\; -\; kn\; +\; 1)\; P\; k\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{P\}\text{'}\; \_\; \{k\}\; =\; \{\backslash \; tfrac\; \{k\}\; \{n\; +\; 1\; \}\}\; \backslash \; mathbf\; \{P\}\; \_\; \{k-1\}\; +\; \backslash \; left\; (1\; -\; \{\backslash \; tfrac\; \{k\}\; \{n\; +\; 1\}\}\; \backslash \; right)\; \backslash \; mathbf\; \{P\}\; \_\; \{k\}\}$.
• Кривые Безье имеют свойство уменьшение вариации. Интуитивно это означает, что кривая Безье не «волнообразна» больше, чем многоугольник ее контрольных точек, и может «волнообразно» меньше, чем это.
• Нет кривых Без изменения степени n - Это означает, что любое изменение контрольной точки требует пересчета и таким образом, влияет на аспект всей кривой, «хотя чем дальше от контрольной точки, которая была изменена, тем меньше изменение кривой».
• Кривая Безье более высокого порядка, чем два, может пересекаться сама с собой или иметь точку возврата для некоторых выбранных контрольных точек.

Кривая второго порядка - это параболический сегмент

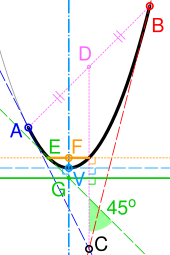Эквивалентность квадратичной кривой Безье и параболического сегмента

Квадратичная кривая Безье также является отрезком параболы . Некоторые источники называют квадратичную кривую Безье «коническими дугами», поэтому парабола - это коническое сечение. Со ссылкой на рисунок справа, важные характеристики параболы могут быть получены следующим образом:

1. Касательные к параболе в конечных точках кривой (A и B) пересекаются в ее контрольной точке (C).
2. Если D - середина AB, касательная к кривой, перпендикулярной CD (пунктирная голубая линия), укажите ее вершину (V). Его ось симметрии (голубой штрих-пунктир) проходит через V и перпендикулярна касательной.
3. E - любая точка на кривой с касательной под углом 45 ° к CD (пунктирная зеленая линия). Если G является пересечением этой касательной и оси, прямая, проходящая через G и перпендикулярная CD, является директрисой (сплошной зеленый).
4. Фокус (F) находится на пересечении оси и линии проходящий через E и перпендикулярный CD (желтая пунктирная линия). Прямая кишка - это отрезок прямой внутри кривой (сплошной желтый).

Производная

Производная для обработки порядка n соответствует

$B\; \prime \; (t)\; =\; n\; \sum \; i\; =\; 0\; n\; -\; 1\; би,\; п\; -\; 1\; (т)\; (п\; я\; +\; 1\; -\; п\; я)\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{B\}\; \text{'}(т)\; =\; п\; \backslash \; сумма\; \_\; \{я\; =\; 0\}\; ^\; \{п-1\}\; b\_\; \{я,\; n-1\}\; (t)\; (\backslash \; mathbf\; \{P\}\; \_\; \{я\; +\; 1\; \}\; -\; \backslash \; mathbf\; \{P\}\; \_\; \{i\})\}$

Линейные кривые

Значение t в функции для линейной кривой Безье можно рассматривать как описание того, как далеко B (t) находится от P0до P1. Например, когда t = 0,25, B (t) составляет одну четверть пути от точки P0до P1. Время t изменяется от 0 до 1, B (t) изображает прямую линию от P0до P1.

Анимация линейной кривой Безье, t в [0,1]

Квадратичные кривые

Для квадратичных кривых Безье можно построить промежуточные точки Q0и Q1так, что при изменении t от 0 до 1:

• Точка Q0(t) изменяется от P0до P1и имеющую линейную кривую Безье.
• Точка Q1(t) изменяется от P1до P2и приведную линейную кривую Безье.
• Точка B (t) интерполируется линейно между Q0(t) и Q1(t) и имеет квадратичную кривую Безье.

Построение квадратичной кривой Безье		Анимация квадратичной кривой Безье, t в [0, 1]

Кривые более высокого порядка

Для кривых более высокого порядка требуется соответственно больше промежуточных точек. Для кубических кривых можно построить промежуточные точки Q0, Q1и Q2, описывающие линейные кривые Безье, и точки R0R1, описывающие квадратичные кривые Безье:

Построение кубической кривой Безье		Анимация кубической кривой Безье кривая, t в [ 0,1]

Для кривых четвертого порядка можно построить промежуточные точки Q0, Q1, Q2Q3, описывающие линейные кривые Безье, точки R0, R1R2, описывающие квадратичные кривые Безье, и точки S0S1, описывающие кубическую кривую Безье. кривые:

Построение кривой Безье четвертой степени		Анимация кривой Безье четвертой степени, t в [0,1]

Для кривых пятого порядка можно построить аналогичные промежуточные точки.

Анимация кривой Безье пятого порядка, t в [0,1] красный. Также показаны кривые Безье для каждого из нижнихathbf {P} _{1}\ldots \mathbf {P} _{n-1}}(t)+t\mathbf {B} _{\mathbf {P} _{1}\mathbf {P} _{2}\ldots \mathbf {P} _{n}}(t)<34><35>\textstyle {\frac {4}{3}}\tan(t/4)<35><36>\mathbf {P<36><37>i<37><38>{\displaystyle {\begin{cases}{n+1 \choose i}(1-t)\mathbf {b} _{i,n}={n \choose i}\mathbf {b} _{i,n+1}\\{n+1 \choose i+1}t\mathbf {b} _{i,n}={n \choose i}\mathbf {b} _{i+1,n+1}\end{cases}}\quad \Rightarrow \quad {\begin{cases}(1-t)\mathbf {b} _{i,n}={\frac {n+1-i}{n+1}}\mathbf {b} _{i,n+1}\\t\mathbf {b} _{i,n}={\frac {i+1}{n+1}}\mathbf {b} _{i+1,n+1}\end{cases}}}<38><39>t<39><40>\mathbf {B} (t)={\frac {\sum _{i=0}^{n}{n \choose i}t^{i}(1-t)^{n-i}\mathbf {P} _{i}w_{i}}{\sum _{i=0}^{n}{n \choose i}t^{i}(1-t)^{n-i}w_{i}}}.<40><41>Animation of a quartic Bézier curve, t in [0,1]<41><42>\mathbf {B} (t)=(1-t)[(1-t)\mathbf {P} _{0}+t\mathbf {P} _{1}]+t[(1-t)\mathbf {P} _{1}+t\mathbf {P} _{2}]{\t_dv{, }}0\leq t\leq 1<42><43>\mathbf {P} _{i,r}=\sum _{j=0}^{n}\mathbf {P} _{j}{\tbinom {n}{j}}{\frac {\tbinom {r}{i-j}}{\tbinom {n+r}{i}}}<43><44>Construction of a quadratic Bézier curve<44><45>Animation of the construction of a fifth-order Bézier curve<45><46>{\displaystyle y=\pm x}<46><47>Construction of a quartic Bézier curve<47><48>{\displaystyle {\begin{aligned}\mathbf {B} (t)=\sum _{i=0}^{n}{n \choose i}(1-t)^{n-i}t^{i}\mathbf {P} _{i}\\=(1-t)^{n}\mathbf {P} _{0}+{n \choose 1}(1-t)^{n-1}t\mathbf {P} _{1}+\cdots +{n \choose n-1}(1-t)t^{n-1}\mathbf {P} _{n-1}+t^{n}\mathbf {P} _{n}0\leqslant t\leqslant 1\end{aligned}}}<48><49>{\displaystyle {\begin{aligned}\mathbf {B} (t)=(1-t)^{5}\mathbf {P} _{0}+5t(1-t)^{4}\mathbf {P} _{1}+10t^{2}(1-t)^{3}\mathbf {P} _{2}+10t^{3}(1-t)^{2}\mathbf {P} _{3}+5t^{4}(1-t)\mathbf {P} _{4}+t^{5}\mathbf {P} _{5}0\leqslant t\leqslant 1\end{aligned}}}<49>html Последняя правка сделана 2021-05-13 07:49:05 Содержание доступно по лицензии CC BY-SA 3.0 (если не указано иное). Обратная связь: support@alphapedia.ru Соглашение О проекте