Коническое сечение

Кривая, полученная путем пересечения конуса и плоскости

Типы конических сечений:. 1. Парабола. 2. Круг и эллипс. 3. Гипербола Таблица коник, Циклопедия, 1728

В математике, коническое сечение (или просто коническое ) представляет собой кривую , полученную как пересечение поверхности конуса конуса с плоскостью . Три типа конического сечения: гипербола, парабола и эллипс ; круг - частный случай эллипса, хотя исторически его иногда называли четвертым типом. Древнегреческие математики изучали конические сечения, достигнув кульминации около 200 г. до н.э. с систематической работой Аполлония Пергского над их свойствами.

Конические сечения в евклидовой плоскости обладают различными отличительными свойствами, многие из которых могут использоваться в качестве альтернативных определений. Одно такое свойство определяет некруглую конику как набор тех точек, расстояние от которых до некоторой конкретной точки, называемой focus, и некоторой конкретной линии, называемой директрисой, находятся в фиксированном соотношении, называемом эксцентриситет. Тип конуса определяется величиной эксцентриситета. В аналитической геометрии коника может быть определена как плоская алгебраическая кривая степени 2; то есть как набор точек, координаты которых удовлетворяют квадратному уравнению с двумя переменными. Это уравнение может быть записано в матричной форме, а некоторые геометрические свойства могут быть изучены как алгебраические условия.

На евклидовой плоскости три типа конических сечений выглядят совершенно разными, но имеют много общих свойств. Расширяя евклидову плоскость, чтобы включить линию на бесконечности, получая проективную плоскость, очевидное различие исчезает: ветви гиперболы пересекаются в двух бесконечно удаленных точках, образуя единую замкнутую кривую; и два конца параболы встречаются, образуя замкнутую кривую, касающуюся линии на бесконечности. Дальнейшее расширение путем расширения вещественных координат до допуска комплексных координат, предоставляет средства для алгебраического анализа этого объединения.

• 1 Евклидова геометрия
  • 1.1 Определение
  • 1.2 Эксцентриситет, фокус и направляющая
  • 1.3 Конические параметры
  • 1.4 Стандартные формы в декартовых координатах
  • 1.5 Общая декартова форма
    • 1.5.1 Матричная запись
    • 1.5.2 Дискриминант
    • 1.5.3 Инварианты
    • 1.5.4 Эксцентриситет в терминах коэффициентов
    • 1.5.5 Преобразование в каноническую форму
  • 1.6 Полярные координаты
  • 1.7 Свойства
• 2 История
  • 2.1 Менехм и ранние произведения
  • 2.2 Аполлоний Пергский
  • 2.3 Аль-Кухи
  • 2.4 Омар Хайям
  • 2.5 Европа
• 3 Приложения
• 4 В реальном проективная плоскость
  • 4.1 Пересечение на бесконечности
  • 4.2 Однородные координаты
  • 4.3 Проективное определение окружности
  • 4.4 Проективное определение коники Штейнера
  • 4.5 Прямые коники
  • 4.6 Определение фон Штаудта
  • 4.7 Построения
• 5 В комплексной проективной плоскости
• 6 Вырожденные случаи
• 7 Карандаш коник
• 8 Пересечение двух коник
• 9 Обобщения
• 10 В других областях математики
• 11 См. также
• 12 Примечания
• 13 Ссылки
• 14 Внешние ссылки

Конические сечения изучались в течение тысяч лет и дали богатый источник интересных и красивых результатов в Евклидова геометрия.

Определение

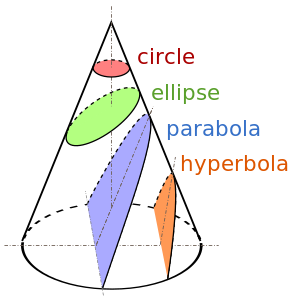Черные границы цветных областей представляют собой конические участки. Не показана другая половина гиперболы, которая находится на не показанной другой половине двойного конуса.

A коническая - кривая, полученная как пересечение плоскости плоскости, называемой секущей плоскостью., с поверхностью двойного конуса (конуса с двумя выступами). Обычно для упрощения описания предполагается, что конус является правильным круговым конусом, но это не требуется; любой двойной конус с круглым поперечным сечением будет достаточно. Плоскости, которые проходят через вершину конуса, будут пересекать конус в точке, линии или паре пересекающихся линий. Они называются вырожденными кониками, и некоторые авторы вообще не считают их кониками. Если не указано иное, «коника» в этой статье будет относиться к невырожденной конике.

Существует три типа коник: эллипс, парабола и гипербола. Круг - это особый вид эллипса, хотя исторически Аполлоний считался четвертым типом. Эллипсы возникают, когда пересечение конуса и плоскости является замкнутой кривой. Окружность получается, когда секущая плоскость параллельна плоскости образующей окружности конуса; для правого конуса это означает, что секущая плоскость перпендикулярна оси. Если секущая плоскость параллельна ровно одной образующей конуса, то коника не ограничена и называется параболой. В последнем случае фигура представляет собой гиперболу: плоскость пересекает обе половины конуса, образуя две отдельные неограниченные кривые.

Эксцентриситет, фокус и направляющая

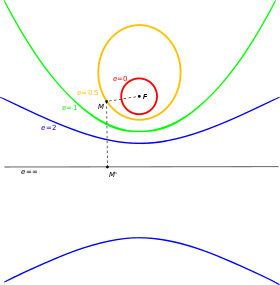Круг (e = 0), эллипс (e = 1/2), парабола (e = 1) и гипербола (e = 2) с фиксированным фокусом F и направляющей ( e = ∞).

В качестве альтернативы можно определить коническое сечение исключительно в терминах геометрии плоскости: это геометрическое место всех точек P, расстояние до которых до фиксированной точки F (называемое focus ) является постоянным кратным (называемым eccentricity e) расстояния от P до фиксированной линии L (называемой директрисой ). Для 0 < e < 1 we obtain an ellipse, for e = 1 a parabola, and for e>1 гипербола.

Круг является предельным случаем и не определяется фокусом и направляющей в евклидовой плоскости. Эксцентриситет круга равен нулю, а его фокус - это центр круга, но его направляющую можно принять только как линию на бесконечности в проективной плоскости.

Эксцентриситет эллипса может быть равен рассматривается как мера того, насколько эллипс отклоняется от круга.

Если угол между поверхностью конуса и его осью равен $\beta \; \{\backslash \; displaystyle\; \backslash \; beta\}$и угол между секущей плоскостью и осью равен $\alpha ,\; \{\backslash \; displaystyle\; \backslash \; alpha,\}$эксцентриситет $cos\; \; \alpha \; cos\; \; \beta .\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; cos\; \backslash \; alpha\}\; \{\backslash \; cos\; \backslash \; beta\}\}.\}$

Доказательство того, что приведенные выше кривые, определенные свойством focus-directrix, совпадают с кривыми, полученными плоскостей, пересекающих конус, упрощается за счет использования сфер Данделина.

Конических параметров

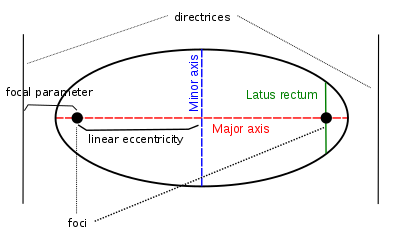Конических параметров в случае эллипса

В дополнение к эксцентриситету (e), фокусам и директрисам, различные геометрические характеристики и длины связаны с коническим сечением.

Основная ось - это линия, соединяющая фокусы эллипса или гиперболы, а ее средняя точка - это центр кривой. У параболы нет центра.

линейный эксцентриситет (c) - это расстояние между центром и фокусом.

прямая кишка - это хорда, параллельная директрисе и проходящая через фокус; его полудлина - это прямая полу-латусная мышца (ℓ).

Параметр фокуса (p) - это расстояние от фокуса до соответствующей директрисы.

Основная ось - это хорда между двумя вершинами: самая длинная хорда эллипса, самая короткая хорда между ветвями гиперболы. Его полудлина равна большой полуоси (a). Когда эллипс или гипербола находятся в стандартном положении, как в приведенных ниже уравнениях, с фокусами на оси x и центром в начале координат, вершины коники имеют координаты (−a, 0) и (a, 0), причем неотрицательный.

Малая ось - это самый короткий диаметр эллипса, а его полудлина - это малая полуось (b), то же значение b, что и в стандартном уравнении ниже. По аналогии, для гиперболы мы также называем параметр b в стандартном уравнении малой полуосью.

Имеют место следующие отношения:

• $\ell \; =\; pe\; \{\backslash \; displaystyle\; \backslash \; \backslash \; ell\; =\; pe\}$
• $c\; =\; ae\; \{\backslash \; displaystyle\; \backslash \; c\; =\; ae\}$
• $p\; +\; c\; =\; ae\; \{\backslash \; displaystyle\; \backslash \; p\; +\; c\; =\; \{\backslash \; frac\; \{a\}\; \{e\}\}\}$

Для коников в стандартном положении эти параметры имеют следующие значения: $a,\; b>0\; \{\backslash \; displaystyle\; a,\; b>0\; \}$.

коническое сечение	уравнение	эксцентриситет (e)	линейный эксцентриситет (c)	полу-широчайшая прямая кишка (ℓ)	фокусный параметр (p)
круг	$x\; 2\; +\; y\; 2\; =\; a\; 2\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; =\; a\; ^\; \{2\}\; \backslash ,\}$	$0\; \{\backslash \; displaystyle\; 0\; \backslash ,\}$	$0\; \{\backslash \; displaystyle\; 0\; \backslash ,\}$	$a\; \{\backslash \; displaystyle\; a\; \backslash ,\}$	$\infty \; \{\backslash \; displaystyle\; \backslash \; infty\}$
эллипс	$x\; 2\; a\; 2\; +\; Y\; 2\; b\; 2\; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{y\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\}\}\; =\; 1\}$	$1\; -\; b\; 2\; a\; 2\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{b\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\}\}\}$	$a\; 2\; -\; b\; 2\; \{\backslash \; displaystyle\; \{\backslash \; sqr\; t\; \{a\; ^\; \{2\}\; -b\; ^\; \{2\}\}\}\}$	$b\; 2\; a\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{b\; ^\; \{2\}\}\; \{a\}\}\}$	$b\; 2\; a\; 2\; -\; b\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{b\; ^\; \{2\}\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; -b\; ^\; \{2\}\}\}\}\}$
парабола	$y\; 2\; =\; 4\; ax\; \{\backslash \; displaystyle\; y\; ^\; \{\; 2\}\; =\; 4ax\; \backslash ,\}$	$1\; \{\backslash \; displaystyle\; 1\; \backslash ,\}$	N / A	$2\; a\; \{\backslash \; displaystyle\; 2a\; \backslash ,\}$	$2\; a\; \{\backslash \; displaystyle\; 2a\; \backslash ,\}$
гипербола	$x\; 2\; a\; 2\; -\; y\; 2\; b\; 2\; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{y\; ^\; \{2\}\}\; \{b\; ^\; \{2\}\}\}\; =\; 1\}$	$1\; +\; b\; 2\; a\; 2\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{1\; +\; \{\backslash \; frac\; \{b\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\}\}\}$	$a\; 2\; +\; b\; 2\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}$	$b\; 2\; a\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{b\; ^\; \{2\}\}\; \{a\}\}\; \}$	$b\; 2\; a\; 2\; +\; b\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{b\; ^\; \{2\}\}\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; b\; ^\; \{2\}\}\}\}\}$

Стандартные формы в декартовой системе координат координаты

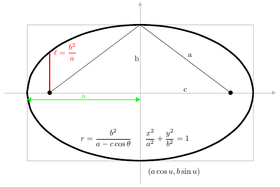Стандартные формы эллипса 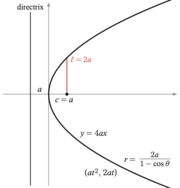Стандартные формы параболы 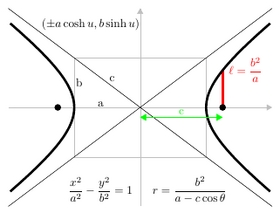Стандартные формы гиперболы

После введения декартовых координат свойство focus-directrix может использоваться для получения уравнения, которым удовлетворяют точки конического сечения. Посредством изменения координат (вращение и перемещение осей ) эти уравнения могут быть приведены в стандартные формы. Для эллипсов и гипербол стандартная форма имеет ось x в качестве главной оси и начало координат (0,0) в качестве центра. Вершины - это (± a, 0) и фокусы (± c, 0). Определим b уравнениями c = a - b для эллипса и c = a + b для гиперболы. Для круга c = 0, поэтому a = b. Для параболы стандартная форма имеет фокус на оси x в точке (a, 0), а направляющую - на прямой с уравнением x = −a. В стандартной форме парабола всегда проходит через начало координат.

Для прямоугольной или равностороннейгиперболы, асимптоты которой перпендикулярны, существует альтернативная стандартная форма, в которой асимптоты являются координатами оси, а прямая x = y - главная ось. Тогда фокусы имеют координаты (c, c) и (−c, −c).

• Круг: x + y = a
• Эллипс: x / a + y / b = 1
• Парабола: y = 4ax с a>0
• Гипербола: x / a - y / b = 1
• Прямоугольная гипербола: xy = c / 2

Первые четыре из них формы симметричны как относительно оси x, так и относительно оси y (для окружности, эллипса и гиперболы) или только относительно оси x (для параболы). Однако прямоугольная гипербола симметрична относительно прямых y = x и y = −x.

Эти стандартные формы могут быть записаны параметрически как,

• Circle : (cos θ, a sin θ),
• Ellipse : (a cos θ, b sin θ),
• Парабола : (at, 2at),
• Гипербола : (a sec θ, b tan θ) или (± a ch u, b sinh u),
• Прямоугольная гипербола : $(dt,\; dt)\; \{\backslash \; displaystyle\; (dt,\; \{\backslash \; frac\; \{d\}\; \{t\}\})\}$где $d\; =\; c\; 2.\; \{\backslash \; displaystyle\; d\; =\; \{\backslash \; frac\; \{c\}\; \{\backslash \; sqrt\; \{2\}\}\}.\}$

Общая декартова форма

В декартовой системе координат график квадратного уравнения с двумя переменными всегда является коническим сечением (хотя оно может быть вырожденным), и все конические сечения возникают таким образом. Наиболее общее уравнение имеет вид

$A\; x\; 2\; +\; B\; xy\; +\; C\; y\; 2\; +\; D\; x\; +\; E\; y\; +\; F\; =\; 0,\; \{\backslash \; displaystyle\; Ax\; ^\; \{2\}\; +\; Bxy\; +\; Cy\; ^\; \{2\}\; +\; Dx\; +\; Ey\; +\; F\; =\; 0,\}$

со всеми коэффициентами действительными числами и A, B, C не всеми нулями.

Матричная запись

Вышеприведенное уравнение может быть записано в матричной записи как

$(xy)\; (AB\; /\; 2\; B\; /\; 2\; C)\; (xy)\; +\; (DE)\; (xy)\; +\; F\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; begin\; \{matrix\}\; x\; y\; \backslash \; end\; \{matrix\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; begin\; \{matrix\}\; A\; B\; /\; 2\; \backslash \backslash \; B\; /\; 2\; C\; \backslash \; end\; \{matrix\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; begin\; \{matrix\}\; x\; \backslash \backslash \; y\; \backslash \; end\; \{matrix\}\}\; \backslash \; right)\; +\; \backslash \; left\; (\{\backslash \; begin\; \{matrix\}\; DE\; \backslash \; end\; \{matrix\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; begin\; \{matrix\}\; x\; \backslash \backslash \; y\; \backslash \; end\; \{matrix\}\}\; \backslash \; right)\; +\; F\; =\; 0.\}$

Общее уравнение также можно записать как

$(xy\; 1)\; (AB\; /\; 2\; D\; /\; 2\; B\; /\; 2\; CE\; /\; 2\; D\; /\; 2\; E\; /\; 2\; F)\; (ху\; 1)\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; begin\; \{matrix\}\; x\; y\; 1\; \backslash \; end\; \{matrix\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; begin\; \{matrix\}\; AB\; /\; 2\; D\; /\; 2\; \backslash \backslash \; B\; /\; 2\; C\; E\; /\; 2\; \backslash \backslash \; D\; /\; 2\; E\; /\; 2\; F\; \backslash \; end\; \{matrix\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; begin\; \{matrix\}\; x\; \backslash \backslash \; y\; \backslash \backslash \; 1\; \backslash \; end\; \{matrix\}\}\; \backslash \; справа)\; =\; 0.\}$

Эта форма является специализацией однородной формы, используемой в более общих условиях проективной геометрии (см. ниже).

Discriminant

Конические участки, описываемые этим уравнением, можно классифицировать по значению $B\; 2–4\; AC\; \{\backslash \; displaystyle\; B\; ^\; \{2\}\; -4AC\}$, называемый дискриминантом уравнения. Таким образом, дискриминант равен - 4Δ, где Δ - определитель матрицы $|\; A\; B\; /\; 2\; B\; /\; 2\; C\; |.\; \{\backslash \; displaystyle\; \backslash \; left\; |\; \{\backslash \; begin\; \{matrix\}\; A\; B\; /\; 2\; \backslash \backslash \; B\; /\; 2\; C\; \backslash \; end\; \{matrix\}\}\; \backslash \; right\; |.\}$

Если коника невырожденная, то:

• если B - 4AC < 0, the equation represents an эллипс ;
  • , если A = C и B = 0, уравнение представляет собой круг, который является частным случаем эллипса;
• если B - 4AC = 0, уравнение представляет собой параболу ;
• , если B - 4AC>0, уравнение представляет собой гиперболу ;
  • , если A + C = 0, уравнение представляет прямоугольную гиперболу.

В используемых здесь обозначениях A и B являются полиномиальными коэффициентами, в отличие от некоторых источников, которые обозначают большую и малую полуоси как A и B.

Инварианты

Дискриминант B - 4AC квадратного уравнения конического сечения (или, что то же самое, определителя AC - B / 4 матрицы 2 × 2) и величины A + C (след матрицы 2 × 2) инвариантны относительно произвольных поворотов и перемещений осей координат, как и определитель матрицы 3 × 3 выше. Постоянный член F и сумма D + E инвариантны только относительно вращения.

Эксцентриситет в терминах коэффициентов

Когда коническое сечение алгебраически записывается как

$A\; x\; 2\; +\; B\; xy\; +\; C\; y\; 2\; +\; D\; x\; +\; E\; y\; +\; F\; =\; 0,\; \{\backslash \; displaystyle\; Ax\; ^\; \{2\}\; +\; Bxy\; +\; Cy\; ^\; \{2\}\; +\; Dx\; +\; Ey\; +\; F\; =\; 0,\; \backslash ,\}$

эксцентриситет может быть записывается как функция коэффициентов квадратного уравнения. Если 4AC = B, коника является параболой и ее эксцентриситет равен 1 (при условии, что она невырожденная). В противном случае, если предположить, что уравнение представляет собой невырожденную гиперболу или эллипс, эксцентриситет определяется как

$e\; =\; 2\; (A\; -\; C)\; 2\; +\; B\; 2\; \eta \; (A\; +\; C)\; +\; (A\; -\; C)\; 2\; +\; B\; 2,\; \{\backslash \; displaystyle\; e\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{2\; \{\backslash \; sqrt\; \{(AC)\; ^\; \{2\}\; +\; B\; ^\; \{2\}\}\}\}\; \{\backslash \; eta\; (A\; +\; C)\; +\; \{\backslash \; sqrt\; \{(AC)\; ^\; \{2\}\; +\; B\; ^\; \{2\}\}\}\}\}\},\}$

где η = 1, если определитель матрицы 3 × 3 выше отрицателен, и η = −1, если это определитель положительный.

Также можно показать, что эксцентриситет является положительным решением уравнения

$\Delta \; e\; 4\; +\; [(A\; +\; C)\; 2\; -\; 4\; \Delta ]\; e\; 2\; -\; [(A\; +\; C)\; 2\; -\; 4\; \Delta ]\; знак\; равно\; 0,\; \{\backslash \; Displaystyle\; \backslash \; Delta\; e\; ^\; \{4\}\; +\; [(A\; +\; C)\; ^\; \{2\}\; -4\; \backslash \; Delta]\; e\; ^\; \{2\}\; -\; [(A\; +\; C)\; ^\; \{2\}\; -4\; \backslash \; Delta]\; =\; 0,\}$

где снова $\Delta \; =\; AC\; -\; B\; 2\; 4.\; \{\backslash \; displaystyle\; \backslash \; Delta\; =\; AC\; -\; \{\backslash \; frac\; \{B\; ^\; \{2\}\}\; \{4\}\}.\}$У этого есть ровно одно положительное решение - эксцентриситет - в случае параболы или эллипса, тогда как в случае гиперболы она имеет два положительных решения, одно из которых - эксцентриситет.

Преобразование в каноническую форму

В случае эллипса или гиперболы уравнение

$A\; x\; 2\; +\; B\; xy\; +\; C\; y\; 2\; +\; D\; x\; +\; E\; y\; +\; F\; =\; 0\; \{\backslash \; displaystyle\; Ax\; ^\; \{2\}\; +\; Bxy\; +\; Cy\; ^\; \{2\}\; +\; Dx\; +\; Ey\; +\; F\; =\; 0\; \backslash ,\}$

можно преобразовать в каноническую форму в преобразованных переменных $x\; \prime ,\; y\; \prime \; \{\backslash \; displaystyle\; x\; \text{'},\; y\text{'}\}$as

$x\; \prime \; 2\; -\; S\; /\; (\lambda \; 1\; 2\; \lambda \; 2)\; +\; y\; \prime \; 2\; -\; S\; /\; (\lambda \; 1\; \lambda \; 2\; 2)\; =\; 1,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\; \text{'}^\; \{\; 2\}\}\; \{-\; S\; /\; (\backslash \; lambda\; \_\; \{1\}\; ^\; \{2\}\; \backslash \; lambda\; \_\; \{2\})\}\}\; +\; \{\backslash \; frac\; \{y\; \text{'}^\; \{2\}\}\; \{-\; S\; /\; (\backslash \; lambda\; \_\; \{1\}\; \backslash \; lambda\; \_\; \{2\}\; ^\; \{2\})\}\}\; =\; 1,\}$

или эквивалентно

$x\; \prime \; 2\; -\; S\; /\; (\lambda \; 1\; \Delta )\; +\; y\; \prime \; 2\; -\; S\; /\; (\lambda \; 2\; \Delta )\; =\; 1,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\; \text{'}^\; \{2\}\}\; \{-\; S\; /\; (\backslash \; lambda\; \_\; \{1\}\; \backslash \; Delta)\}\}\; +\; \{\backslash \; frac\; \{y\text{'}\; ^\; \{2\}\}\; \{-\; S\; /\; (\backslash \; lambda\; \_\; \{2\}\; \backslash \; Delta)\}\}\; =\; 1,\}$

где $\lambda \; 1\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{1\}\}$и $\lambda \; 2\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{2\}\}$- это собственные значения матрицы $(AB\; /\; 2\; B\; /\; 2\; C)\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; begin\; \{matrix\}\; A\; B\; /\; 2\; \backslash \; \backslash \; B\; /\; 2\; C\; \backslash \; end\; \{matrix\}\}\; \backslash \; right)\}$- то есть решения уравнения

$\lambda \; 2\; -\; (A\; +\; C)\; \lambda \; +\; (AC\; -\; (B\; /\; 2)\; 2)\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; lambda\; ^\; \{2\}\; -\; (A\; +\; C)\; \backslash \; lambda\; +\; (AC-\; (B\; /\; 2)\; ^\; \{2\})\; =\; 0\}$

- и $S\; \{\backslash \; displaystyle\; S\}$- определитель матрицы 3 × 3 выше, а $\Delta \; =\; \lambda \; 1\; \lambda \; 2\; \{\backslash \; displaystyle\; \backslash \; Delta\; =\; \backslash \; lambda\; \_\; \{\; 1\}\; \backslash \; lambda\; \_\; \{2\}\}$снова является определителем матрицы 2 × 2. В случае эллипса квадраты двух полуосей задаются знаменателями в канонической форме.

Полярные координаты

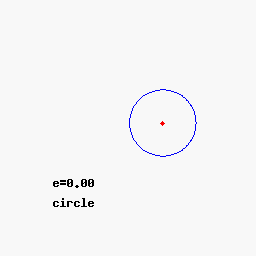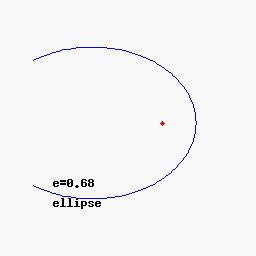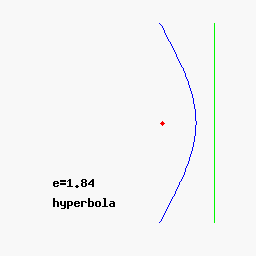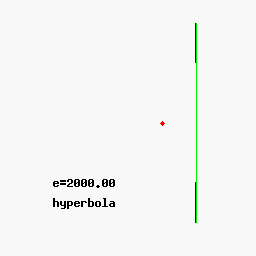Развитие конического сечения при увеличении эксцентриситета e

В полярных координатах коническое сечение с одним фокусом в начале координат и, если есть, другим при отрицательном значении (для эллипса) или положительном значении (для гиперболы) по оси x, задается уравнением

$r\; =\; l\; 1\; +\; e\; cos\; \; \theta ,\; \{\backslash \; displaystyle\; r\; =\; \{\backslash \; frac\; \{l\}\; \{1\; +\; e\; \backslash \; cos\; \backslash \; theta\}\},\}$

где e - эксцентриситет, а l - прямая полушария прямой кишки.

Как и выше, для e = 0 график представляет собой круг, для 0 < e < 1the graph is an ellipse, for e = 1 a parabola, and for e>1 - гиперболу.

Полярная форма уравнения коники часто используется в динамике ; например, определение орбит объектов, вращающихся вокруг Солнца.

Свойства

Так же, как две (отдельные) точки определяют линию, пять точек определяют конус. Формально, учитывая любые пять точек на плоскости в общем линейном положении, что означает отсутствие трех коллинеарных, через них проходит уникальная коника, которая будет невырожденной; это верно как для евклидовой плоскости, так и для ее продолжения, реальной проективной плоскости. Действительно, для любых пяти точек через них проходит коника, но если три точки лежат на одной прямой, то коника будет вырожденной (приводимой, поскольку она содержит прямую) и может не быть единственной; см. дальнейшее обсуждение.

Четыре точки на плоскости в общем линейном положении определяют уникальную конику, проходящую через первые три точки и имеющую четвертую точку в качестве своего центра. Таким образом, знание центра эквивалентно знанию двух точек на конике с целью определения кривой.

Кроме того, коника определяется любой комбинацией k точек в общем положении, через которые она проходит, и 5 - k касательные к нему линии для 0≤k≤5.

Любая точка на плоскости находится либо на нуле, либо на одной или двух касательных прямых коники. Точка только на одной касательной находится на конике. Точка без касательной называется внутренней точкой (или внутренней точкой ) коники, а точка на двух касательных линиях является внешней точкой <235.>(или внешняя точка ).

Все конические секции обладают общим свойством отражения, которое можно сформулировать следующим образом: все зеркала в форме невырожденной конической секции отражают свет, идущий от одного фокуса или идущий к одному фокусу, к другому фокусу или от него. В случае параболы второй фокус нужно рассматривать как бесконечно удаленный, чтобы световые лучи, идущие к второму фокусу или исходящие от него, были параллельны.

Теорема Паскаля касается коллинеарности трех точек построенные из шести точек на любой невырожденной конике. Теорема также верна для вырожденных коник, состоящих из двух прямых, но в этом случае она известна как теорема Паппа.

Невырожденные конические сечения всегда «гладкие ». Это важно для многих приложений, таких как аэродинамика, где требуется гладкая поверхность для обеспечения ламинарного потока и предотвращения турбулентности.

Менахм и ранние работы

Считается, что первое определение конического сечения было дано Менахмом (умер в 320 г. до н.э.) как часть его решения проблемы Делиана (Дублирование куба ). Его работы не сохранились, даже имена, которые он использовал для этих кривых, и известны только из вторичных источников. Определение, используемое в то время, отличается от того, что обычно используется сегодня. Конусы были построены путем вращения прямоугольного треугольника вокруг одного из его катетов, так что гипотенуза образует поверхность конуса (такая линия называется образующей ). Три типа конусов определялись по углам их вершин (измеренным как удвоенный угол, образованный гипотенузой и катетом, вращающимся вокруг прямоугольного треугольника). Затем определялось коническое сечение путем пересечения одного из этих конусов плоскостью, перпендикулярной образующей. Тип конуса определяется типом конуса, то есть углом, образованным в вершине конуса: если угол острый, то коника является эллипсом; если угол прямой, то коника - парабола; а если угол тупой, то коника - это гипербола (но только одна ветвь кривой).

Евклид (эт. 300 г. до н. э.), как говорят, написал четыре книги по коникам, но и они были утеряны.. Архимед (умер около 212 г. до н. Э.), Как известно, изучал коники, определив площадь, ограниченную параболой и хордой в квадратуре параболы. Его основной интерес был с точки зрения измерения площадей и объемов фигур, относящихся к коникам, и часть этой работы сохранилась в его книге о телах вращения коников «О коноидах и сфероидах».

Аполлоний Пергский

Схема из Коник Аполлония, в арабском переводе IX века

Наибольший прогресс в изучении коник древними греками был достигнут благодаря Аполлонию Пергскому (умер около 190 г. до н. Э.), Чей Восьмитомный Conic Sections или Conics обобщил и значительно расширил существующие знания. Изучение Аполлонием свойств этих кривых позволило показать, что любая плоскость, пересекающая фиксированный двойной конус (две вершины), независимо от ее угла, будет давать конус в соответствии с более ранним определением, что привело к определению, обычно используемому сегодня. Круги, которые нельзя построить более ранним методом, также можно получить этим способом. Это может объяснить, почему Аполлоний считал окружности четвертым типом конического сечения, но это различие больше не проводится. Аполлоний использовал имена эллипс, парабола и гипербола для этих кривых, заимствуя терминологию из более ранних работ Пифагора о площадях.

Паппу Александрийскому (умер около 350 г. н.э.) приписывают разъяснение важности концепции фокус коники и подробное описание связанной концепции директрисы, включая случай параболы (которая отсутствует в известных работах Аполлония).

Аль-Кухи

Инструмент для рисования конических сечений был впервые описан в 1000 г. н.э. исламским математиком Аль-Кухи.

Омар Хайям

Работа Аполлония была переведена на арабский язык, и большая часть его работ сохранилась только на арабском языке. версия. Персы нашли применение теории, в первую очередь персидский математик и поэт Омар Хайям, который нашел геометрический метод решения кубических уравнений с использованием конических сечений.

Европа

Иоганн Кеплер расширил теорию коник с помощью «принципа непрерывности », предшественника концепции пределов. Кеплер впервые использовал термин фокусы в 1604 году.

Жирар Дезарг и Блез Паскаль разработали теорию коник, используя раннюю форму проективной геометрии, и это помогло придать импульс для изучения этой новой области. В частности, Паскаль открыл теорему, известную как hexagrammum mysticum, из которой можно вывести многие другие свойства коник.

Рене Декарт и Пьер Ферма оба применили свою недавно открытую аналитическую геометрию к изучению коник. В результате геометрические проблемы коник были сведены к задачам алгебры. Однако именно Джон Уоллис в своем трактате 1655 года Tractatus de sectionibus conicis первым определил конические сечения как примеры уравнений второй степени. Написанная ранее, но опубликованная позже, Яна де Витта Elementa Curvarum Linearum начинается с кинематической конструкции коник Кеплера, а затем развиваются алгебраические уравнения. Эта работа, в которой используется методология Ферма и нотация Декарта, была названа первым учебником по этому вопросу. Де Витт изобрел термин директриса.

Форма параболоида формы археоциат создает конические сечения на скалах

Конические сечения важны в астрономия : орбиты двух массивных объектов, которые взаимодействуют согласно закону всемирного тяготения, представляют собой конические сечения, если учесть их общий центр масс быть в покое. Если они связаны вместе, они оба начертят эллипсы; если они расходятся, они оба будут следовать параболам или гиперболам. См. задача двух тел..

Отражающие свойства конических секций используются в конструкции прожекторов, радиотелескопов и некоторых оптических телескопов. В прожекторах в качестве отражателя используется параболическое зеркало с лампочкой в ​​фокусе; и аналогичная конструкция используется для параболического микрофона . В оптическом телескопе Herschel размером 4,2 метра на Ла-Пальме, на Канарских островах, используется первичное параболическое зеркало, чтобы отражать свет во вторичное гиперболическое зеркало, которое снова отражает его в фокус за первым зеркалом.

Конические сечения обладают некоторыми очень похожими свойствами в евклидовой плоскости, и причины этого становятся более ясными, если рассматривать коники с точки зрения более крупной геометрии. Евклидова плоскость может быть вложена в реальную проективную плоскость , а коники могут рассматриваться как объекты в этой проективной геометрии. Один из способов сделать это - ввести однородные координаты и определить конику как набор точек, координаты которых удовлетворяют неприводимому квадратному уравнению с тремя переменными (или, что то же самое, нули неприводимой квадратичной формы ). Более технически, множество точек, которые являются нулями квадратичной формы (при любом количестве переменных), называется квадрикой, а неприводимые квадрики в двумерном проективном пространстве (то есть с тремя переменными) традиционно называются кониками.

Евклидова плоскость R вложена в действительную проективную плоскость путем присоединения к линии на бесконечности (и соответствующей ей точки на бесконечности ), так что все прямые параллельные классы встречаются на этой линии. С другой стороны, начиная с реальной проективной плоскости, евклидова плоскость получается путем выделения некоторой прямой как линии на бесконечности и удаления ее и всех ее точек.

Пересечение на бесконечности

В проективном пространстве над любым телом, но, в частности, над вещественными или комплексными числами, все невырожденные коники эквивалентны, и таким образом, в проективной геометрии просто говорят о «конике» без указания типа. То есть существует проективное преобразование, которое отобразит любую невырожденную конику в любую другую невырожденную конику.

Три типа конических сечений снова появятся в аффинной плоскости, полученной выбором прямой проективной коники. пространство, чтобы быть линией на бесконечности. Затем эти три типа определяются по тому, как эта бесконечно удаленная линия пересекает конику в проективном пространстве. В соответствующем аффинном пространстве получается эллипс, если коника не пересекает линию на бесконечности, парабола, если коника пересекает прямую на бесконечности в одной двойной точке, соответствующей оси, и гипербола, если коника пересекает линию на бесконечности в двух точках, соответствующих асимптотам.

Однородные координаты

В однородных координатах коническое сечение может быть представлено как:

$A\; Икс\; 2\; +\; В\; ху\; +\; С\; Y\; 2\; +\; D\; xz\; +\; E\; yz\; +\; F\; z\; 2\; =\; 0.\; \{\backslash \; displaystyle\; Ax\; ^\; \{2\}\; +\; Bxy\; +\; Cy\; ^\; \{2\}\; +\; Dxz\; +\; Eyz\; +\; Fz\; ^\; \{2\}\; =\; 0.\}$

Или в матричной записи

$(xyz)\; (AB\; /\; 2\; D\; /\; 2\; B\; /\; 2\; CE\; /\; 2\; D\; /\; 2\; E\; /\; 2\; F)\; (xyz)\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; begin\; \{matrix\}\; x\; y\; z\; \backslash \; end\; \{matrix\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; begin\; \{matrix\}\; A\; B\; /\; 2\; D\; /\; 2\; \backslash \backslash \; B\; /\; 2\; C\; E\; /\; 2\; \backslash \backslash \; D\; /\; 2\; E\; /\; 2\; F\; \backslash \; end\; \{matrix\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; begin\; \{matrix\}\; x\; \backslash \backslash \; y\; \backslash \backslash \; z\; \backslash \; end\; \{matrix\}\}\; \backslash \; right)\; =\; 0.\}$

Матрица 3 × 3 выше называется матрицей коническое сечение.

Некоторые авторы предпочитают записывать общее однородное уравнение в виде

$A\; x\; 2\; +\; 2\; B\; xy\; +\; C\; y\; 2\; +\; 2\; D\; xz\; +\; 2\; E\; yz\; +\; F\; z\; 2\; =\; 0,\; \{\backslash \; displaystyle\; Ax\; ^\; \{2\}\; +\; 2Bxy\; +\; Cy\; ^\; \{2\}\; +\; 2Dxz\; +\; 2Eyz\; +\; Fz\; ^\; \{2\}\; =\; 0,\}$

(или его вариант), так что матрица конического сечения имеет более простой вид,

$M\; =\; (ABDBCEDEF),\; \{\backslash \; displaystyle\; M\; =\; \backslash \; left\; (\{\backslash \; begin\; \{matrix\}\; A\; B\; D\; \backslash \backslash \; B\; C\; E\; \backslash \backslash \; D\; E\; F\; \backslash \; end\; \{matrix\}\}\; \backslash \; right),\}$

но это обозначение не используется в этом article.

Если определитель матрицы конического участка равен нулю, конический участок будет вырожденным.

Поскольку умножение всех шести коэффициентов на один и тот же ненулевой скаляр дает уравнение с тем же множество нулей, можно рассматривать коники, представленные (A, B, C, D, E, F), как точки в пятимерном проективном пространстве $P\; 5.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{P\}\; ^\; \{5\}.\}$

Проективное определение круга

Метрические концепции евклидовой геометрии (концепции, связанные с измерением длины и углов) не могут быть немедленно распространены на реальные проективная плоскость. Они должны быть переопределены (и обобщены) в этой новой геометрии. Это можно сделать для произвольных проективных плоскостей, но чтобы получить реальную проективную плоскость в качестве расширенной евклидовой плоскости, необходимо сделать определенный выбор.

Зафиксируйте произвольную прямую на проективной плоскости это будет обозначаться как абсолютная линия . Выберите две различные точки на абсолютной линии и назовите их абсолютными точками . Со ссылкой на эти варианты можно определить несколько метрических концепций. Например, для прямой, содержащей точки A и B, средняя точка отрезка AB определяется как точка C, которая является проективным гармоническим сопряженным точки пересечения AB. и абсолютная линия относительно A и B.

Коника на проективной плоскости, которая содержит две абсолютные точки, называется окружностью . Поскольку пять точек определяют конику, окружность (которая может быть вырожденной) определяется тремя точками. Чтобы получить расширенную евклидову плоскость, абсолютная линия выбирается как бесконечно удаленная от евклидовой плоскости, а абсолютные точки - это две особые точки на этой прямой, называемые круговыми точками на бесконечности. Линии, содержащие две точки с действительными координатами, не проходят через круговые точки на бесконечности, поэтому в евклидовой плоскости круг, согласно этому определению, определяется тремя точками, которые не коллинеарны.

Было упомянуто, что круги в евклидовой плоскости не может быть определено свойством фокус-директрисы. Однако, если рассматривать линию на бесконечности как направляющую, тогда, если принять эксцентриситет равным e = 0, круг будет обладать свойством фокус-направляющей, но по-прежнему не определяется этим свойством. В этой ситуации нужно быть осторожным, чтобы правильно использовать определение эксцентриситета как отношение расстояния от точки на окружности до фокуса (длина радиуса) к расстоянию от этой точки до направляющей (это расстояние бесконечно). что дает нулевое предельное значение.

Проективное коническое сечение Штейнера

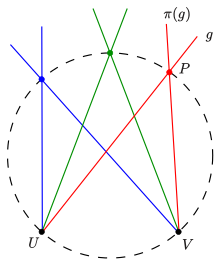Определение конического сечения Штейнера

A синтетический (безкоординатный) подход к определению конических сечений на проективной плоскости было дано Якоб Штайнер в 1867 году.

• Даны два карандаша $B\; (U),\; B\; (V)\; \{\backslash \; displaystyle\; B\; (U),\; B\; (V)\}$линий в двух точках. $U,\; V\; \{\backslash \; displaystyle\; U,\; V\}$(все строки, содержащие $U\; \{\backslash \; displaystyle\; U\}$и $V\; \{\backslash \; displaystyle\; V\}$соответственно) и проективное, но не перспективное отображение $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$из $B\; (U)\; \{\backslash \; displaystyle\; B\; (U)\}$на $B\; (V)\; \{\backslash \; displaystyle\; B\; (V)\}$. Тогда точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение.

Отображение перспективы $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$карандаша $B\; (U)\; \{\backslash \; displaystyle\; B\; (U)\}$на карандаш $B\; (V)\; \{\backslash \; displaystyle\; B\; (V)\}$- это биекция (соответствие 1-1) такая, что соответствующие линии пересекаются на фиксированной прямой $a\; \{\backslash \; displaystyle\; a\}$, которая называется осью перспективы $\pi \; \{\backslash \; displaystyle\; \backslash \; pi\}$.

Проективное отображение конечная последовательность перспективных отображений.

Поскольку проективное отображение в проективной плоскости над полем (папповская плоскость ) однозначно определяется заданием изображений трех прямых, для генерации конического сечения Штейнера, помимо двух точек $U,\; V\; \{\backslash \; displaystyle\; U,\; V\}$должны быть указаны только изображения трех строк. Эти 5 элементов (2 точки, 3 линии) однозначно определяют коническое сечение.

Линейные коники

Согласно Принципу двойственности в проективной плоскости двойственная точка каждой точки является линией, а двойственная точка геометрического места точек (набор точек, удовлетворяющих некоторому условию) называется огибающей прямых. Используя определение Штейнера коники (это множество точек теперь будем называть точечной коникой) как пересечения соответствующих лучей двух связанных пучков, легко дуализировать и получить соответствующую оболочку, состоящую из стыков соответствующих точек два связанных диапазона (точки на линии) на разных основаниях (линии, на которых находятся точки). Такая огибающая называется линейной конической (или двойной конической ).

В реальной проективной плоскости точечная коника обладает тем свойством, что каждая прямая пересекает ее в двух точках (которые могут совпадать или могут быть сложными), и любой набор точек с этим свойством является точечной коникой. Отсюда вдвойне следует, что у прямой коники есть две прямые, проходящие через каждую точку, и любая огибающая прямых с этим свойством является прямой конической. В каждой точке точечной коники есть уникальная касательная линия, и, вдвойне, на каждой прямой конической прямой есть единственная точка, называемая точкой контакта. Важная теорема утверждает, что касательные линии точечной коники образуют прямую конику, а точки соприкосновения прямой коники образуют точечную конику.

Определение фон Штаудта

Карл Георг Кристиан фон Штаудт определил коническую как точка, заданная всеми абсолютными точками полярности, которая имеет абсолютные точки. Фон Штаудт ввел это определение в Geometrie der Lage (1847) как часть своей попытки удалить все метрические концепции из проективной геометрии.

A полярность, π, проективной плоскости P, является инволютивным (т. Е. Второго порядка) биекцией между точками и линиями P, которая сохраняет отношение инцидентности. Таким образом, полярность связывает точку Q с линией q, и, следуя Жергонну, q называется полярным Q, а Q полюсом q. Абсолютная точка (линия ) полярности - это точка, падающая на ее полюс (полюс).

Коника фон Штаудта в реальной проективной плоскости эквивалентна на конику Штейнера.

Конструкции

Невозможно построить непрерывную дугу коники с помощью линейки и циркуля. Однако существует несколько построений линейки и циркуля для любого количества отдельных точек на дуге.

Одна из них основана на обратной теореме Паскаля, а именно, если точки пересечения противоположных сторон шестиугольника лежат на одной прямой, то шесть вершин лежат на конике. В частности, из пяти точек A, B, C, D, E и прямой, проходящей через E, скажем EG, \ можно построить точку F, которая лежит на этой прямой и находится на конике, определяемой этими пятью точками. Пусть AB пересекает DE в L, BC пересекает EG в M и пусть CD пересекает LM в N. Тогда AN пересекает EG в требуемой точке F. Изменяя прямую, проходящую через E, можно построить столько дополнительных точек на конике, сколько нужно.

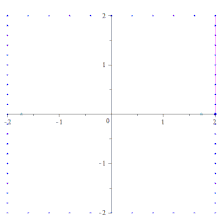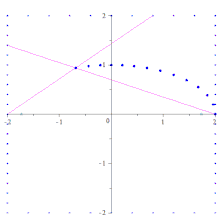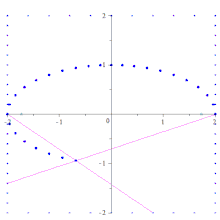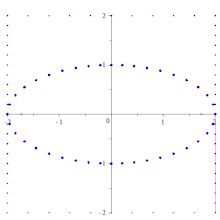Метод параллелограмма для построения эллипса

Другой метод, основанный на конструкции Штейнера и полезный в инженерных приложениях, - это метод параллелограмма, в котором конус строится точка за точкой посредством соединения определенные равномерно расположенные точки на горизонтальной и вертикальной линиях. В частности, чтобы построить эллипс с уравнением x / a + y / b = 1, сначала постройте прямоугольник ABCD с вершинами A (a, 0), B (a, 2b), C (−a, 2b) и D (- а, 0). Разделите сторону BC на n равных отрезков и используйте параллельную проекцию относительно диагонали AC, чтобы сформировать равные отрезки на стороне AB (длины этих отрезков будут в b / a раз больше длины отрезков на BC). На стороне BC обозначьте левые конечные точки сегментов от A 1 до A n, начиная с B и идя к C. На стороне AB отметьте верхние конечные точки D 1 в D n, начиная с A и идя в сторону B. Точки пересечения, AA i ∩ DD i для 1 ≤ i ≤ n будут точками эллипса между A и P (0, b). Маркировка связывает линии карандаша через точку A с линиями карандаша через точку D проективно, но не в перспективе. Искомая коника получается с помощью этой конструкции, поскольку три точки A, D и P и две касательные (вертикальные прямые в точках A и D) однозначно определяют конику. Если другой диаметр (и сопряженный с ним диаметр) используется вместо большой и малой осей эллипса, в конструкции используется параллелограмм, который не является прямоугольником, давая имя методу. Объединение линий карандашей может быть расширено, чтобы получить другие точки на эллипсе. Конструкции гипербол и парабол аналогичны.

Еще один общий метод использует свойство полярности для построения касательной огибающей коники (прямой коники).

В комплексной плоскости C, эллипсы и гиперболы неотличимы: можно рассматривать гиперболу как эллипс с мнимой длиной оси. Например, эллипс $x\; 2\; +\; y\; 2\; =\; 1\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; =\; 1\}$становится гиперболой при замене $y\; =\; iw,\; \{\backslash \; displaystyle\; y\; =\; iw,\}$геометрически сложное вращение, дающее $x\; 2\; -\; w\; 2\; =\; 1\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; -w\; ^\; \{2\}\; =\; 1\}$. Таким образом, существует двухсторонняя классификация: эллипс / гипербола и парабола. Продолжение кривых до комплексной проективной плоскости, это соответствует пересечению линии на бесконечности либо в 2 различных точках (соответствующих двум асимптотам), либо в 1 двойной точке (соответствующей оси параболы); таким образом, реальная гипербола является более убедительным реальным изображением для сложного эллипса / гиперболы, так как она также имеет 2 (реальных) пересечения с линией на бесконечности.

Дальнейшее объединение происходит в комплексной проективной плоскости CP: невырожденные коники нельзя отличить друг от друга, поскольку любая может быть переведена в любую другую с помощью линейного проективного преобразования 777>Можно доказать, что в CP два конических участка имеют четыре общих точки (если учитывать кратность ), поэтому имеется от 1 до 4 пересечений баллов. Возможны следующие варианты пересечения: четыре различные точки, две особые точки и одна двойная точка, две двойные точки, одна особая точка и одна с кратностью 3, одна точка с кратностью 4. Если любая точка пересечения имеет кратность>1, две кривые называются быть касательной. Если имеется точка пересечения с кратностью не менее 3, две кривые называются соприкасающимися. Если имеется только одна точка пересечения, которая имеет кратность 4, две кривые называются супероскуляцией.

Кроме того, каждая прямая дважды пересекает каждый конический участок. Если точка пересечения двойная, линия является касательной . Каждая коническая секция, пересекающаяся с линией на бесконечности, имеет две бесконечно удаленные точки. Если эти точки действительны, кривая представляет собой гиперболу ; если они мнимые сопряженные, это эллипс ; если есть только одна двойная точка, это парабола . Если бесконечно удаленные точки являются циклическими точками (1, i, 0) и (1, –i, 0), коническое сечение представляет собой окружность. Если коэффициенты конического сечения действительны, бесконечно удаленные точки либо действительны, либо комплексно сопряжены.

Что следует рассматривать как вырожденный случай коническая форма зависит от используемого определения и геометрических параметров конического сечения. Некоторые авторы определяют конику как двумерную невырожденную квадрику. В этой терминологии нет вырожденных коник (только вырожденные квадрики), но мы будем использовать более традиционную терминологию и избегать этого определения.

В евклидовой плоскости, используя геометрическое определение, возникает вырожденный случай, когда секущая плоскость проходит через вершину конуса. Вырожденная коника - это либо: точка точка, когда плоскость пересекает конус только на вершине; прямая, когда плоскость касается конуса (она содержит ровно одну образующую конуса); или пара пересекающихся прямых (две образующие конуса). Они соответствуют соответственно предельным формам эллипса, параболы и гиперболы.

Если коника в евклидовой плоскости определяется нулями квадратного уравнения (то есть как квадрика), то вырожденными кониками являются: пустое множество, точка, или пара прямых, которые могут быть параллельны, пересекаться в точке или совпадать. Случай пустого набора может соответствовать либо паре комплексно сопряженных параллельных прямых, например, с уравнением $x\; 2\; +\; 1\; =\; 0,\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; 1\; =\; 0,\}$или в воображаемый эллипс, например, с уравнением $x\; 2\; +\; y\; 2\; +\; 1\; =\; 0.\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; 1\; =\; 0.\}$Мнимый эллипс не удовлетворяет общему определению вырожденности и поэтому обычно не считается вырожденным. Случай двух линий возникает, когда квадратичное выражение делится на два линейных множителя, нули каждого из которых дают линию. В случае, когда коэффициенты одинаковы, соответствующие линии совпадают, и мы называем эту линию двойной линией (линия с кратностью 2), и это предыдущий случай касательной плоскости сечения.

В реальной проективной плоскости, поскольку параллельные прямые пересекаются в точке на бесконечности, случай параллельной прямой евклидовой плоскости можно рассматривать как пересекающиеся прямые. Однако, поскольку точка пересечения является вершиной конуса, сам конус вырождается в цилиндр , то есть с вершиной, находящейся на бесконечности. Остальные секции в этом случае называются цилиндрическими секциями. Невырожденные цилиндрические участки представляют собой эллипсы (или окружности).

Если смотреть с точки зрения комплексной проективной плоскости, вырожденные случаи действительной квадрики (т. Е. Квадратное уравнение имеет действительные коэффициенты) можно рассматривать как пару линий, возможно, совпадающих. Пустым набором может быть бесконечно удаленная линия, рассматриваемая как двойная линия, (действительная) точка - это пересечение двух комплексно сопряженных линий и других случаев, как упоминалось ранее.

Чтобы отличить вырожденные случаи от невырожденных случаев (включая пустое множество с последним), используя матричную запись, пусть β будет определителем матрицы 3 × 3 конического сечения, то есть β = (AC - B / 4) F + КРОВАТЬ - CD - AE / 4; и пусть дискриминант α = B - 4AC. Тогда коническое сечение невырожденное тогда и только тогда, когда β ≠ 0. Если β = 0, мы имеем точку, когда α < 0, two parallel lines (possibly coinciding) when α = 0, or two intersecting lines when α>0.

A (невырожденная) коника полностью определяется пять точек в общем положении (нет трех коллинеарных ) на плоскости, а система коник, которые проходят через фиксированный набор из четырех точек (опять же в плоскости, а не трех коллинеарных), называется пучок коник . Четыре общие точки называются базовыми точками карандаша. Через любую точку, кроме базовой, проходит единственный конус карандаша. Эта концепция обобщает пучок окружностей.

Решения системы двух уравнений второй степени с двумя переменными можно рассматривать как координаты точек пересечения двух конических коник общего вида. разделы. В частности, две коники могут не иметь ни одной, двух или четырех возможно совпадающих точек пересечения. Эффективный метод определения местоположения этих решений использует однородное матричное представление конических сечений, то есть симметричную матрицу 3x3 , которая зависит от шести параметров.

Процедура определения точек пересечения включает следующие шаги, где коники представлены матрицами:

• с учетом двух коник $C\; 1\; \{\backslash \; displaystyle\; C\_\; \{1\}\}$и $C\; 2\; \{\backslash \; displaystyle\; C\_\; \{2\}\}$, рассмотрим пучок коник, заданный их линейной комбинацией $\lambda \; C\; 1\; +\; \mu \; C\; 2.\; \{\backslash \; displaystyle\; \backslash \; lambda\; C\_\; \{1\}\; +\; \backslash \; mu\; C\_\; \{2\}.\}$
• идентифицируют однородные параметры $(\lambda ,\; \mu )\; \{\backslash \; displaystyle\; (\backslash \; lambda,\; \backslash \; mu)\}$которые соответствуют вырожденной конике пучка. Это можно сделать, наложив условие, что $det\; (\lambda \; C\; 1\; +\; \mu \; C\; 2)\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; det\; (\backslash \; lambda\; C\_\; \{1\}\; +\; \backslash \; mu\; C\_\; \{2\})\; =\; 0\}$и решение для $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$и $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$. Они оказываются решениями уравнения третьей степени.
• с учетом вырожденной коники $C\; 0\; \{\backslash \; displaystyle\; C\_\; \{0\}\}$, идентифицируйте два, возможно совпадающих, линии, составляющие его.
• пересекают каждую идентифицированную линию с любой из двух исходных коник; этот шаг можно эффективно выполнить, используя двойное коническое представление $C\; 0\; \{\backslash \; displaystyle\; C\_\; \{0\}\}$
• , точки пересечения будут представлять решения исходной системы уравнений.

Обобщения

Коники могут быть определены поверх других полей (то есть в других папповых геометриях ). Однако следует проявлять осторожность, когда поле имеет характеристику 2, поскольку некоторые формулы использовать нельзя. Например, матричные представления, используемые выше, требуют деления на 2.

Обобщением невырожденной коники на проективной плоскости является овал. Овал - это набор точек, обладающий следующими свойствами, присущими коникам: 1) любая прямая пересекает овал ни в одной, ни в одной или двух точках, 2) в любой точке овала существует единственная касательная линия.

Обобщение свойств фокуса коник на случай, когда имеется более двух фокусов, дает наборы, называемые обобщенные коники.

Классификация на эллиптические, параболические, а гиперболика широко распространена в математике и часто разделяет поле на четко определенные подполя. Классификация в основном возникает из-за наличия квадратичной формы (в двух переменных это соответствует ассоциированному дискриминанту ), но также может соответствовать эксцентриситету.

Классификация квадратичных форм:

Квадратичные формы

Квадратичные формы над вещественными числами классифицируются по закону инерции Сильвестра, а именно по их положительному, нулевому и отрицательному индексам: квадратичная форма от n переменных может быть преобразована в диагональную форму, как $x\; 1\; 2\; +\; x\; 2\; 2\; +\; \cdots \; +\; xk\; 2\; -\; xk\; +\; 1\; 2\; -\; \cdots \; -\; xk\; +\; \ell \; 2,\; \{\; \backslash \; Displaystyle\; x\_\; \{1\}\; ^\; \{2\}\; +\; x\_\; \{2\}\; ^\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{k\}\; ^\; \{2\}\; -x\_\; \{k\; +\; 1\}\; ^\; \{2\}\; -\; \backslash \; cdots\; -x\_\; \{k\; +\; \backslash \; ell\}\; ^\; \{2\},\}$где количество коэффициентов +1, k, является положительным индексом, количество коэффициентов −1,, является отрицательным индексом, а остальные переменные равны нулю индекс m, поэтому $k\; +\; \ell \; +\; m\; =\; n.\; \{\backslash \; displaystyle\; k\; +\; \backslash \; ell\; +\; m\; =\; n.\}$В двух переменных ненулевые квадратичные формы классифицируются как:

• $x\; 2\; +\; y\; 2\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\}$- положительно-определенный (отрицательный тоже включен), соответствующий эллипсам,
• $x\; 2\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\}$- вырожденный, соответствующий в параболы, и
• $x\; 2\; -\; y\; 2\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; -y\; ^\; \{2\}\}$- неопределенный, соответствующий гиперболам.

По двум переменным классифицируются квадратичные формы по дискриминанту, аналогично коникам, но в более высоких измерениях более полезная классификация: определенная (все положительные или все отрицательные), вырожденная (некоторые нули) или неопределенная (смесь положительных и отрицательных, но без нулей). Эта классификация лежит в основе многих последующих.

Кривизна

Гауссова кривизна поверхности описывает бесконечно малую геометрию, и в каждой точке может быть либо положительная - эллиптическая геометрия, нулевая - евклидова геометрия (плоская, парабола) или отрицательная - гиперболическая геометрия ; бесконечно малым образом, до второго порядка поверхность выглядит как график $x\; 2\; +\; y\; 2,\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\},\}$$x\; 2\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; \}$(или 0), или $x\; 2\; -\; y\; 2\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; -y\; ^\; \{2\}\}$. Действительно, по теореме униформизации каждая поверхность может считаться глобально (в каждой точке) положительно изогнутой, плоской или отрицательно изогнутой. В более высоких измерениях тензор кривизны Римана представляет собой более сложный объект, но многообразия с постоянной секционной кривизной являются интересными объектами исследования и обладают совершенно разными свойствами, как обсуждалось на секционной кривизне. кривизна.

УЧП второго порядка

Уравнения с частными производными (УЧП) второго порядка классифицируются в каждой точке как эллиптические, параболические или гиперболические, соответственно, поскольку их члены второго порядка соответствуют эллиптическая, параболическая или гиперболическая квадратичная форма. Поведение и теория этих различных типов УЧП разительно различаются - характерным примером является то, что уравнение Пуассона является эллиптическим, уравнение теплопроводности является параболическим, а волновым уравнением является гиперболическим.

Классификация эксцентриситета включает:

преобразования Мёбиуса

Реальные преобразования Мёбиуса (элементы PSL 2(R) или его 2-кратного покрытия, SL2(R) ): классифицируются как как эллиптические, параболические или гиперболические соответственно, поскольку их полуследа $|\; tr\; \; |\; /\; 2\; =\; 1,\; \{\backslash \; displaystyle\; |\; \backslash \; Operatorname\; \{tr\}\; |\; /\; 2\; =\; 1,\}$или $|\; tr\; \; |\; /\; 2>1,\; \{\backslash \; displaystyle\; |\; \backslash \; operatorname\; \{tr\}\; |\; /\; 2>1,\}$отражение классификации по эксцентриситету.

Отношение дисперсии к среднему

Отношение дисперсии к среднему классифицирует несколько важных семейств дискретные распределения вероятностей : постоянное распределение как круговое (эксцентриситет 0), биномиальное распределение как эллиптическое, распределение Пуассона как параболическое и отрицательное биномиальное распределение как гиперболическое. Это разработано в кумулянтах некоторых дискретных распределений вероятностей.

В этом интерактивном SVG перемещайте влево и вправо по изображению SVG, чтобы повернуть двойной конус

• Окружные и неконусные
• Восстание конических секций, протесты студентов Йельского университета
• Директорский круг
• Эллиптическая система координат
• Эквидистантный набор
• Девятиточечная коническая
• Параболические координаты
• Квадратичная функция

• Акопян, А.В.; Заславский, А.А. (2007). Геометрия коник. Американское математическое общество. ISBN 978-0-8218-4323-9.
• Artzy, Rafael (2008) [1965], Linear Geometry, Dover, ISBN 978-0-486-46627-9
• Boyer, Carl B. (2004) [1956], History of Analytic Geometry, Dover, ISBN 978-0-486-43832-0
• Браннан, Дэвид А.; Эсплен, Мэтью Ф.; Грей, Джереми Дж. (1999), Геометрия, Cambridge University Press, ISBN 978-0-521-59787-6
• Coxeter, HSM ( 1964), Projective Geometry, Blaisdell, ISBN 9780387406237
• Coxeter, HSM (1993), Реальная проективная плоскость, Springer Science Business Media
• Downs, J.W. (2003) [1993], Практические конические сечения: геометрические свойства эллипсов, парабол и гипербол, Dover, ISBN 0-486-42876-1
• Eves, Howard (1963), A Survey of Geometry (Volume One), Boston: Allyn and Bacon
• Хартманн, Эрих, Геометрия плоского круга, введение в плоскости Мебиуса, Лагерра и Минковского (PDF), получено 20 сентября 2014 г. (PDF; 891 кБ).
• Виктор Дж. Кац (1998), История математики / Введение (2-е изд.), Аддисон Уэсли Лонгман, ISBN 978-0-321-01618-8
• Кендиг, Кит (2005), Коникс, Математическая ассоциация Америки, ISBN 978-0-88385-335-1
• Фолкнер, Т.Э. (1952), Проективная геометрия (2-е изд.), Эдинбург: Оливер и Бойд
• Мерсерв, Брюс Э. (1983) [1959], Фундаментальные концепции геометрии, Довер, ISBN 0-486-63415-9
• Проттер, Мюррей H.; Морри, младший, Чарльз Б. (1970), Колледж по исчислению с аналитической геометрией (2-е изд.), Чтение: Аддисон-Уэсли, LCCN 76087042
• Рихтер -Геберт, Юрген (2011). Перспективы проективной геометрии: экскурсия по реальной и сложной геометрии. Springer. ISBN 9783642172854.
• Сэмюэл, Пьер (1988), Проективная геометрия, Тексты для студентов по математике (Чтения по математике), New Йорк: Springer-Verlag, ISBN 0-387-96752-4
• Thomas, George B.; Финни, Росс Л. (1979), Исчисление и аналитическая геометрия (пятое изд.), Addison-Wesley, p. 434, ISBN 0-201-07540-7
• Wilson, W.A.; Трейси, Дж. (1925), Analytic Geometry (Revised ed.), DC Heath and Company

На Викискладе есть средства массовой информации, связанные с коническими разделами.

Викиучебники имеют книгу по темам: Конические секции

Wikisource содержат текст Британской энциклопедии 1911 года статьи Коническое сечение.

• Коническое сечение (Геометрия) на Британская энциклопедия
• Можете ли вы действительно получить конические формулы из конуса? архив 2007-07-15 (Пенсильванский университет штата Индиана
• Конические разделы в Специальные плоские кривые.
• Вайсштейн, Эрик У. «Коническое сечение». MathWorld.
• Возникновение конусов. Коники в природе и в других местах.
• См. Конические сечения в разрубают узел для точного доказательства того, что любое конечное коническое сечение является эллипсом, и Xah Lee для аналогичной обработки других коник.
• Восьмиточка конической формы в Эскизы динамической геометрии
• Локус неявных уравнений второго порядка Интеракт. Живой Java-графический редактор коник; использует общее неявное уравнение второго порядка.