Плавность

редактировать

Свойство, измеряющее, сколько раз функция может быть дифференцирована

A функция рельефа - это плавная функция с компактной поддержкой.

В математическом анализе гладкость функции - это свойство, измеряемое количеством непрерывных производных у него есть какой-то домен. Как минимум, функция может считаться «гладкой», если она всюду дифференцируема (следовательно, непрерывна). С другой стороны, он может также обладать производными всех порядков в своей области, и в этом случае он называется бесконечно дифференцируемым и упоминается как Функция C-бесконечность (или $C ∞ {\ displaystyle C ^ {\ infty}}$ $C ^ {{\ infty}}$ функция).

Содержание

1 Классы дифференцируемости
- 1.1 Примеры
- 1.2 Классы многомерной дифференцируемости
- 1.3 Пространство C-функций
2 Параметрическая непрерывность
- 2.1 Определение
- 2.2 Порядок непрерывности
3 Геометрическая непрерывность
- 3.1 Гладкость кривых и поверхностей
- 3.2 Гладкость кусочно заданных кривых и поверхностей
4 Другие концепции
- 4.1 Связь с аналитичностью
- 4.2 Гладкие разбиения единицы
- 4.3 Гладкие функции на многообразиях и между ними
- 4.4 Гладкие функции между подмножествами многообразий
5 См. Также
6 Ссылки

Классы дифференцируемости

Класс дифференцируемости - это классификация функций в соответствии со свойствами их производных. Это мера производной высшего порядка, которая существует для функции.

Рассмотрим открытый набор на действительной строке и функцию f, определенную на этом наборе с действительными значениями. Пусть k будет неотрицательным целым числом. Функция f называется (дифференцируемой) классом C, если производные f ′, f ″,..., f существуют и непрерывны (непрерывность подразумевается дифференцируемостью для все производные, кроме f). Функция f называется бесконечно дифференцируемой, гладкой или класса C, если она имеет производные всех порядков. Говорят, что функция f принадлежит классу C или аналитическому, если f гладкая и если ее разложение в ряд Тейлора вокруг любого точка в своей области определения сходится к функции в некоторой окрестности точки. Таким образом, C строго содержится в C. Функции выдавливания являются примерами функций в C, но не в C.

Другими словами, класс C состоит из всех непрерывных функций. Класс C состоит из всех дифференцируемых функций, производная которых непрерывна; такие функции называются непрерывно дифференцируемыми . Таким образом, функция C - это в точности функция, производная которой существует и относится к классу C. В общем, классы C могут быть определены рекурсивно, объявив C как набор всех непрерывных функций и объявив C для любое натуральное число k должно быть набором всех дифференцируемых функций, производная которых находится в C. В частности, C содержится в C для любого k>0, и есть примеры, показывающие, что это включение является строгим (C ⊊ C). Класс C бесконечно дифференцируемых функций является пересечением классов C при изменении k над неотрицательными целыми числами.

Примеры

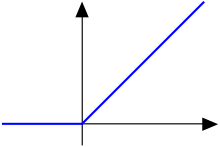C-функция f (x) = x для x ≥ 0 и 0. в противном случае.

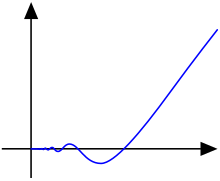Функция g (x) = x sin (1 / x) для x>0.

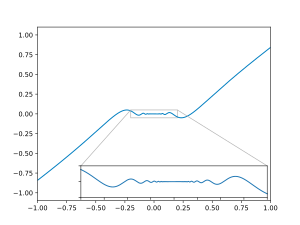Функция

f: R → R {\ displaystyle f: \ mathbb {R} \ to \ mathbb {R}}

f : \ mathbb {R} \ to \ mathbb {R}

f (x) = x 2 sin ⁡ ( 1 x) {\ displaystyle f (x) = x ^ {2} \ sin \ left ({\ tfrac {1} {x}} \ right)}

{\ displaystyle f (x) = x ^ {2} \ sin \ left ({\ tfrac {1} {x}} \ right)}

для

x ≠ 0 {\ displaystyle x \ neq 0}

х \ neq 0

f (0) = 0 {\ displaystyle f (0) = 0}

f (0) = 0

дифференцируемый. Однако эта функция не является непрерывно дифференцируемой.

Гладкая функция, которая не является аналитической.

Функция

f (x) = {x, если x ≥ 0, 0, если x < 0 {\displaystyle f(x)={\begin{cases}x{\t_dv{if }}x\geq 0,\\0{\text{if }}x<0\end{cases}}}

{\ displaystyle f (x) = {\ begin {cases} x {\ t_dv {if}} x \ geq 0, \\ 0 {\ текст {if}} x <0 \ end {cases}}}

, непрерывна, но не дифференцируема в точке x = 0, поэтому она относится к классу C, но не к классу C.

Функция

g (x) = {x 2 sin ⁡ (1 x), если x ≠ 0, 0, если x = 0 {\ displaystyle g (x) = {\ begin {cases} x ^ {2} \ sin {({\ tfrac {1} {x}})} {\ text {if}} x \ neq 0, \\ 0 {\ text {if}} x = 0 \ end {cases}}}

{\ displaystyle g (x) = {\ begin {cases} x ^ {2} \ sin {({\ tfrac {1}) {x}})} {\ text {if}} x \ neq 0, \\ 0 {\ text {if}} x = 0 \ end {cases}}}

дифференцируемо с производной

g ′ (x) = {- cos ⁡ (1 x) + 2 x sin ⁡ (1 x), если x ≠ 0, 0, если x = 0. {\ displaystyle g '(x) = {\ begin {cases} - {\ mathord {\ cos ({\ tfrac {1} {x}) })}} + 2x \ sin ({\ tfrac {1} {x}}) {\ text {if}} x \ neq 0, \\ 0 {\ text {if}} x = 0. \ End { case}}}

g'(x)={\begin{cases}-{\mathord {\cos({\tfrac {1}{x}})}}+2x\sin({\tfrac {1}{x}}){\text{if }}x\neq 0,\\0{\text{if }}x=0.\end{cases}}

Поскольку $cos ⁡ (1 / x) {\ displaystyle \ cos (1 / x)}$ ${\ displaystyle \ cos (1 / x)}$ колеблется при x → 0, $g ′ (x) { \ displaystyle g '(x)}$ $g'(x)$ не является непрерывным в нуле. Следовательно, $g (x) {\ displaystyle g (x)}$ $г (Икс)$ дифференцируемо, но не принадлежит к классу C. Более того, если взять $g (x) = x 4/3 sin ⁡ (1 / x) {\ displaystyle g (x) = x ^ {4/3} \ sin (1 / x)}$ ${\ displaystyle g (x) = x ^ {4/3} \ sin (1 / x)}$ (x ≠ 0) в этом примере можно использовать, чтобы показать, что производная функция дифференцируемой функции может быть неограниченной на компакте и, следовательно, дифференцируемая функция на компакте может не быть локально липшицевой.

Функции

f (x) = | х | k + 1 {\ displaystyle f (x) = | x | ^ {k + 1}}

f(x)=|x|^{k+1}

где k четно, непрерывны и k раз дифференцируемы при всех x. Но при x = 0 они не дифференцируемы (k + 1) раз, поэтому они относятся к классу C, но не к классу C, где j>k.

экспоненциальная функция является аналитической и, следовательно, попадает в класс C. тригонометрические функции также являются аналитическими, где бы они ни были определены.

Функция выдавливания

f (x) = {e - 1 1 - x 2, если | х | < 1, 0 otherwise {\displaystyle f(x)={\begin{cases}e^{-{\frac {1}{1-x^{2}}}}{\text{ if }}|x|<1,\\0{\text{ otherwise }}\end{cases}}}

{\ displaystyle f (x) = {\ begin {cases} e ^ {- {\ frac {1} {1-x ^ {2}}}} {\ text {if}} | x | <1, \\ 0 {\ text {else}} \ end {cases}}}

является гладким, поэтому относится к классу C, но не является аналитическим при x = ± 1 и, следовательно, не относится к классу C. Функция f является примером гладкой функции с компактной опорой.

Многомерная классы дифференцируемости

Функция $f: U ⊂ R n → R {\ displaystyle f: U \ subset \ mathbb {R} ^ {n} \ to \ mathbb {R}}$ ${\ displaystyle f: U \ subset \ mathbb {R} ^ {n} \ to \ mathbb {R}}$ , определенный на открытом наборе $U {\ displaystyle U}$ $U$ из $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ , как говорят быть из класса $C k {\ displaystyle C ^ {k}}$ $C ^ {k}$ на $U {\ displaystyle U}$ $U$ , для положительного целого числа $k {\ displaystyle k}$ $к$ , если все частные производные

∂ α f ∂ x 1 α 1 ∂ x 2 α 2 ⋯ ∂ xn α n (y 1, y 2,…, yn) { \ Displaystyle {\ frac {\ partial ^ {\ alpha} f} {\ partial x_ {1} ^ {\ alpha _ {1}} \, \ partial x_ {2} ^ {\ alpha _ {2}} \, \ cdots \, \ partial x_ {n} ^ {\ alpha _ {n}}}} (y_ {1}, y_ {2}, \ ldots, y_ {n})}

{\ displaystyle {\ frac {\ partial ^ {\ alpha} f} {\ partial x_ {1} ^ {\ alpha _ {1}} \, \ partial x_ {2} ^ {\ alpha _ {2}} \, \ cdots \, \ partial x_ {n} ^ {\ alpha _ {n}}}} (y_ {1}, y_ {2}, \ ldots, y_ {n})}

существуют и являются непрерывными, для каждые $α 1, α 2,…, α n {\ displaystyle \ alpha _ {1}, \ alpha _ {2}, \ ldots, \ alpha _ {n}}$ ${\ displaystyle \ alpha _ {1}, \ alpha _ {2}, \ ldots, \ alpha _ {n}}$ неотрицательные целые числа, такие, что $α = α 1 + α 2 + ⋯ + α n ≤ k {\ displaystyle \ alpha = \ alpha _ {1} + \ alpha _ {2} + \ cdots + \ alpha _ {n} \ leq k}$ ${\ displaystyle \ alpha = \ alpha _ {1} + \ alpha _ {2} + \ cdots + \ alpha _ {n} \ leq k}$ , и каждый $(y 1, y 2,…, yn) ∈ U {\ displaystyle (y_ {1}, y_ {2}, \ ldots, y_ {n}) \ in U}$ ${\ displaystyle (y_ {1}, y_ {2}, \ ldots, y_ {n}) \ in U}$ . Считается, что функция $f {\ displaystyle f}$ $f$ относится к классу $C {\ displaystyle C}$ $C$ или $C 0 {\ displaystyle C ^ { 0}}$ $C ^ 0$ , если он непрерывен на $U {\ displaystyle U}$ $U$ .

A function $f: U ⊂ R n → R m {\ displaystyle f: U \ subset \ mathbb {R} ^ {n} \ to \ mathbb {R} ^ {m}}$ ${\ displaystyle f: U \ subset \ mathbb {R} ^ {n} \ to \ mathbb {R} ^ {m}}$ , определенный на открытом наборе $U {\ displaystyle U}$ $U$ из $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ {n}$ , относится к классу $C k {\ displaystyle C ^ {k}}$ $C ^ {k}$ на $U {\ displaystyle U}$ $U$ , для положительного целого числа $k {\ displaystyle k}$ $к$ , если все его компоненты

fi (x 1, x 2,…, Xn) = (π i ∘ f) (x 1, x 2,…, xn) = π i (f (x 1, x 2,…, xn)) для i = 1, 2, 3,…, m {\ displaystyle f_ {i} (x_ {1}, x_ {2}, \ ldots, x_ {n}) = (\ pi _ {i} \ circ f) (x_ {1}, x_ {2}, \ ldots, x_ {n}) = \ pi _ {i} (f (x_ {1}, x_ {2}, \ ldots, x_ {n})) {\ text {for}} i = 1,2, 3, \ ldots, m}

{\ displaystyle f_ {i} (x_ {1}, x_ {2}, \ ldots, x_ {n}) = (\ pi _ {i} \ circ f) (x_ {1}, x_ {2}, \ ldots, x_ {n}) = \ pi _ {i} (f (x_ {1}, x_ {2}, \ ldots, x_ {n})) { \ text {for}} i = 1,2,3, \ ldots, m}

относятся к классу $C k {\ displaystyle C ^ {k}}$ $C ^ {k}$ , где $π i {\ displaysty le \ pi _ {i}}$ $\ pi _ {i}$ - это естественные проекции $π i: R m → R {\ displaystyle \ pi _ {i}: \ mathbb {R} ^ {m} \ to \ mathbb {R}}$ ${\ displaystyle \ pi _ {i}: \ mathbb {R} ^ {m} \ to \ mathbb {R}}$ определяется как $π i (x 1, x 2,…, xm) = xi {\ displaystyle \ pi _ {i} (x_ {1 }, x_ {2}, \ ldots, x_ {m}) = x_ {i}}$ ${\ displaystyle \ pi _ {i} (x_ {1}, x_ {2}, \ ldots, x_ {m}) = x_ {i}}$ . Говорят, что он принадлежит к классу $C {\ displaystyle C}$ $C$ или $C 0 {\ displaystyle C ^ {0}}$ $C ^ 0$ , если он непрерывный, или эквивалентно, если все компоненты $fi {\ displaystyle f_ {i}}$ $f_ {i}$ являются непрерывными, на $U {\ displaystyle U}$ $U$ .

пространство функций C

Пусть D - открытое подмножество реальной линии. Множество всех C вещественнозначных функций, определенных на D, является векторным пространством Фреше со счетным семейством полунорм

p K, m = sup x ∈ K | f (m) (x) | {\ displaystyle p_ {K, m} = \ sup _ {x \ in K} \ left | f ^ {(m)} (x) \ right |}

p_ {K, m} = \ sup_ {x \ in K} \ слева | е ^ {(м)} (х) \ справа |

где K изменяется в возрастающей последовательности компактные множества, у которых union есть D, и m = 0, 1,..., k.

Набор функций C над D также образует пространство Фреше. Один использует те же полунормы, что и выше, за исключением того, что m разрешено пробегать все неотрицательные целые числа.

Вышеупомянутые пробелы естественным образом встречаются в приложениях, где необходимы функции, имеющие производные определенного порядка; однако, особенно при изучении дифференциальных уравнений в частных производных, иногда может быть более плодотворным работать с пространствами Соболева.

Параметрическая непрерывность

Термины параметрическая непрерывность и геометрическая Непрерывность (G) была введена Брайаном Барски, чтобы показать, что плавность кривой может быть измерена путем снятия ограничений на скорость, с которой параметр отслеживает кривую.

Параметрическая непрерывность - это концепция, применяемая к параметрическим кривым, которая описывает плавность значения параметра с расстоянием вдоль кривой.

Определение

(параметрическая) кривая $s: [0, 1] → R n {\ displaystyle s: [0,1] \ to \ mathbb {R} ^ { n}}$ ${\ displaystyle s: [0,1] \ to \ mathbb {R} ^ {n}}$ относится к классу C, если $dksdtk {\ displaystyle \ textstyle {\ frac {d ^ {k} s} {dt ^ {k}}}}$ ${\ displaystyle \ textstyle {\ frac {d ^ {k} s} {dt ^ {k}}}}$ существует и является непрерывным на $[0, 1] {\ displaystyle [0,1]}$ $[0,1]$ , где производные в конечных точках $0, 1 ∈ [0, 1 ] {\ displaystyle 0,1 \ in [0,1]}$ ${\ displaystyle 0,1 \ in [0,1]}$ принимаются как односторонние производные (т. е. при $0 {\ displaystyle 0}$ ${\ displaystyle 0}$ справа и в $1 {\ displaystyle 1}$ $1$ слева).

В качестве практического применения этой концепции кривая, описывающая движение объекта с параметром времени, должна иметь непрерывность C - чтобы объект имел конечное ускорение. Для более плавного движения, например движения камеры при съемке пленки, требуются более высокие порядки параметрической непрерывности.

Порядок непрерывности

Два присоединенных сегмента кривой Безье, которые являются только непрерывными C

Два сегмента кривой Безье, прикрепленных таким образом, что они являются непрерывными C

Различные порядок параметрической непрерывности можно описать следующим образом:

C: кривые непрерывны
C: первые производные непрерывны
C: первая и вторая производные непрерывны
C: Производные с первой по n-ю являются непрерывными

Геометрическая непрерывность

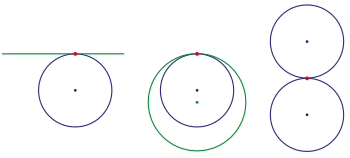Кривые с G-контактом (кружки, линия)

(1 - ε 2) x 2 - 2 px + y 2 = 0, p>0, ε ≥ 0 {\ Displaystyle (1- \ varepsilon ^ {2}) x ^ {2} -2px + y ^ {2} = 0, \ p>0 \, \ varepsilon \ geq 0}

(1-\varepsilon^2) x^2 -2px+y^2=0, \ p>0 \, \ varepsilon \ ge 0

карандаш конических сечений с G-контактом: p fix,

ε {\ displaystyle \ varepsilon}

\ varepsilon

переменная. (

ε = 0 {\ displaystyle \ varepsilon = 0}

\ varepsilon = 0

: круг,

ε = 0,8 {\ displaystyle \ varepsilon = 0,8}

\ vareps ilon = 0,8

: эллипс,

ε = 1 {\ displaystyle \ varepsilon = 1}

\ varepsilon = 1

: парабола,

ε = 1.2 {\ displaystyle \ varepsilon = 1.2}

\ varepsilon = 1.2

: гипербола)

Концепция геометрической или геометрической непрерывности в первую очередь применялась к коническим сечениям (и родственные формы) математиков, таких как Лейбниц, Кеплер и Понселе. Эта концепция была ранней попыткой описания посредством геометрии, а не алгебры, концепции непрерывности, выраженной через параметрическую функцию.

Основная идея геометрической непрерывности заключалась в том, что пять конических сечений действительно были пять разных версий одной и той же формы. Эллипс стремится к окружности, когда эксцентриситет приближается к нулю, или к параболе, когда приближается к единице; и гипербола стремится к параболе при уменьшении эксцентриситета к единице; он также может иметь тенденцию к пересечению линий. Таким образом, между коническими сечениями сохранялась непрерывность. Эти идеи привели к другим концепциям непрерывности. Например, если бы круг и прямая линия были двумя выражениями одной и той же формы, возможно, линию можно было бы рассматривать как круг бесконечного радиуса. Для этого нужно сделать линию замкнутой, допустив, чтобы точка $x = ∞ {\ displaystyle x = \ infty}$ ${\ displaystyle x = \ infty}$ была точкой на окружности, а для $x = + ∞ {\ displaystyle x = + \ infty}$ ${\ displaystyle x = + \ infty}$ и $x = ¬ ∞ {\ displaystyle x = \ neg \ infty}$ ${\ displaystyle x = \ neg \ infty}$ , чтобы быть идентичными. Такие идеи были полезны при разработке современной, алгебраически определенной, идеи о непрерывности функции и $∞ {\ displaystyle \ infty}$ $\ infty$ (см. проективно расширенный действительная линия для более подробной информации).

Гладкость кривых и поверхностей

A кривая или поверхность может быть описана как имеющая непрерывность G, где n является возрастающей мерой гладкость. Рассмотрим сегменты по обе стороны от точки на кривой:

G: Кривые соприкасаются в точке соединения.
G: Кривые также имеют общее направление касательной в точке соединения точка.
G: Кривые также имеют общий центр кривизны в точке соединения.

В общем, G-непрерывность существует, если кривые могут быть изменены для получения C (параметрической) непрерывности. Повторная параметризация кривой геометрически идентична исходной; затрагивается только параметр.

Эквивалентно две векторные функции f (t) и g (t) имеют G-непрерывность, если f (t) ≠ 0 и f (t) ≡ kg (t), для скаляра k>0 (т. Е. если направление, но не обязательно величина, двух векторов одинаковы).

Хотя может быть очевидно, что кривая потребует, чтобы непрерывность G выглядела гладкой, для хорошей эстетики, например, тех, к которым стремятся в архитектуре и спорте В конструкции автомобиля требуются более высокие уровни геометрической непрерывности. Например, отражения в кузове автомобиля не будут выглядеть гладкими, если тело не имеет непрерывности G.

Прямоугольник со скругленными углами (с дугами окружности девяноста градусов в четырех углах) имеет непрерывность G, но не имеет непрерывности G. То же самое верно и для круглого куба с октантами сферы по углам и четвертьцилиндрами по краям. Если требуется редактируемая кривая с непрерывностью G, то обычно выбираются кубические шлицы ; эти кривые часто используются в промышленном дизайне.

Гладкость кусочно определенных кривых и поверхностей

Другие концепции

Отношение к аналитичности

Хотя все аналитические функции являются «гладкими» (т. е. имеют непрерывные производные) на множестве, на котором они являются аналитическими, такие примеры, как функции рельефа (упомянутые выше), показывают, что обратное неверно для функций на вещественные числа: существуют гладкие вещественные функции, которые не являются аналитическими. Простые примеры функций, которые являются гладкими, но не аналитическими в любой точке, могут быть построены с помощью ряда Фурье ; другой пример - функция Фабиуса. Хотя может показаться, что такие функции являются скорее исключением, чем правилом, оказывается, что аналитические функции очень тонко разбросаны среди гладких; более строго, аналитические функции образуют скудное подмножество гладких функций. Более того, для каждого открытого подмножества A вещественной прямой существуют гладкие функции, аналитические на A и нигде больше.

Полезно сравнить ситуацию с повсеместным распространением трансцендентных чисел на действительной строке. Как на вещественной прямой, так и на множестве гладких функций, примеры, которые мы придумываем на первый взгляд (алгебраические / рациональные числа и аналитические функции), ведут себя гораздо лучше, чем в большинстве случаев: трансцендентные числа и нигде не аналитические функции имеют полную меру. (их дополнения скудны).

Описанная таким образом ситуация резко отличается от сложных дифференцируемых функций. Если комплексная функция дифференцируема только один раз на открытом множестве, она будет бесконечно дифференцируемой и аналитической на этом множестве.

Гладкие разбиения единицы

Гладкие функции с заданной замкнутой поддержкой используются при построении гладких разбиений единицы (см. разбиение единства и глоссарий топологии ); они необходимы при изучении гладких многообразий, например, чтобы показать, что римановы метрики могут быть определены глобально, исходя из их локального существования. Простым случаем является случай функции выдавливания на действительной прямой, то есть гладкой функции f, которая принимает значение 0 вне интервала [a, b] и такая, что

f (x)>0 для < x < b. {\displaystyle f(x)>0 \ quad {\ text {for}} \ quad a

f(x)>0 \ quad \ text {for} \ quad a < x < b.\,

Учитывая количество перекрывающихся интервалов на На каждой из них и на полубесконечных интервалах (−∞, c] и [d, + ∞) могут быть построены функции выпуклости, покрывающие всю прямую, так что сумма функций всегда равна 1.

Из того, что только что было сказано, разбиение единицы не применяется к голоморфным функциям ; их различное поведение по отношению к существованию и аналитическое продолжение является одним из корней теории пучков. Напротив, пучки гладких функций обычно не несут много топологической информации.

Гладкие функции на коллекторах и между ними

Для гладкого коллектора $M {\ displaystyle M}$ $M$ , размер m, с атласом $U = {(U α, ϕ α)} α {\ displaystyle {\ mathfrak {U}} = \ {(U _ {\ alpha}, \ phi _ {\ alpha}) \} _ {\ alpha}}$ ${\ displaystyle {\ mathfrak { U}} = \ {(U _ {\ alpha}, \ phi _ {\ alpha}) \} _ {\ alpha}}$ , тогда карта $f: M → R {\ displaystyle f: M \ to \ mathbb {R}}$ ${\ displaystyle f: M \ to \ mathbb {R}}$ будет гладкой на M, если для все $p ∈ M {\ displaystyle p \ in M}$ $p \ in M $ существует диаграмма $∃ (U, ϕ) ∈ U: p ∈ U {\ displaystyle \ exists (U, \ phi) \ in {\ mathfrak {U}}: p \ in U}$ ${\ displaystyle \ exists (U, \ phi) \ in {\ mathfrak {U}}: p \ in U}$ , так что откат $f {\ displaystyle f}$ $f$ на $ϕ - 1 {\ displaystyle \ phi ^ {- 1}}$ $\ phi ^ {- 1}$ , обозначается $(ϕ - 1) ∗ f = f ∘ ϕ - 1: ϕ (U) → R {\ displaystyle (\ phi ^ { -1}) ^ {*} f = f \ circ \ phi ^ {- 1}: \ phi (U) \ to \ mathbb {R}}$ ${\ displaystyle (\ phi ^ {- 1}) ^ {*} f = f \ circ \ phi ^ {- 1}: \ phi (U) \ to \ mathbb {R}}$ гладко как функция от $R от m {\ displaystyle \ mathbb {R} ^ {m}}$ $\ mathbb {R} ^ {m}$ до $R {\ displaystyle \ mathbb {R}}$ $\ mathbb {R}$ в окрестности $ϕ (p) {\ displaystyle \ phi (p)}$ $\ phi (p)$ (а все частные производные до заданного порядка непрерывны). Обратите внимание, что гладкость может быть проверена относительно любой предпочтительной диаграммы около p в атласе, так как требования гладкости для функций перехода между диаграммами гарантируют, что если $f {\ displaystyle f}$ $f$ гладко около p на одной диаграмме, оно будет плавным около p на любой другой карте атласа. Если вместо этого $F: M → N {\ displaystyle F: M \ to N}$ $F: M \ to N$ - это карта из $M {\ displaystyle M}$ $M$ в n-мерное многообразие $N {\ displaystyle N}$ $N$ , тогда F гладко, если для каждого p ∈ M существует диаграмма $(U, ϕ) {\ displaystyle (U, \ phi) }$ $(U, \ phi)$ о р в $M {\ displaystyle M}$ $M$ и диаграмме $(V, ψ) {\ displaystyle (V, \ psi)}$ ${\ displaystyle (V, \ psi)}$ около $F (p) {\ displaystyle F (p)}$ $F (p)$ in $N {\ displaystyle N}$ $N$ с $F (U) ⊂ V {\ displaystyle F (U) \ subset V}$ ${\ displaystyle F (U) \ subset V}$ , такое, что $ψ ∘ F ∘ ϕ - 1: ϕ (U) → ψ (V) {\ displaystyle \ psi \ circ F \ circ \ phi ^ {- 1}: \ phi (U) \ to \ psi (V)}$ ${\ Displaystyle \ psi \ circ F \ circ \ phi ^ {- 1}: \ phi (U) \ to \ psi (V)}$ является гладкой функцией от R до R.

. Гладкие отображения между многообразиями индуцируют линейные карты между касательными пространствами : для $F: M → N {\ displaystyle F: M \ to N}$ $F: M \ to N$ , в каждой точке переход вперед ( или дифференциал) отображает касательные векторы в точке p в касательные векторы в точке F (p): $F ∗, p: T p M → TF (p) N {\ displaystyle F _ {*, p}: T_ {p} M \ to T_ {F (p)} N}$ ${\ displaystyle F _ {*, p}: T_ {p} M \ to T_ {F (p)} N}$ , а на уровне касательной связки, прямой является гомоморфизмом векторного расслоения : $F ∗: TM → TN {\ displaystyle F _ {*}: TM \ to TN}$ ${\ displaystyle F _ {*}: TM \ to TN}$ . Двойной к прямому движению является откат, который «тянет» ковекторы на $N {\ displaystyle N}$ $N$ обратно к ковекторам на $M {\ displaystyle M}$ $M$ , а из k-форм в k-формы: $F ∗: Ω k (N) → Ω k (M) {\ displaystyle F ^ {*}: \ Omega ^ {k} (N) \ to \ Omega ^ {k} (M)}$ ${\ displaystyle F ^ {*}: \ Omega ^ {k} (N) \ to \ Omega ^ {k} (M)}$ . Таким образом, гладкие функции между многообразиями могут переносить локальные данные, такие как векторные поля и дифференциальные формы, от одного многообразия к другому или вниз в евклидово пространство, где выполняются вычисления. как интеграция хорошо понятны.

Прообразы и прогнозы по гладким функциям, как правило, не являются многообразиями без дополнительных предположений. Прообразы регулярных точек (т. Е. Если дифференциал не обращается в нуль на прообразе) являются многообразиями; это теорема о прообразе. Аналогичным образом, прямолинейные движения вдоль вложений - это многообразия.

Гладкие функции между подмножествами многообразий

Существует соответствующее понятие гладкого отображения для произвольных подмножеств многообразий. Если f: X → Y - функция , область и диапазон которой являются подмножествами многообразий X ⊂ M и Y ⊂ N соответственно. f называется гладким, если для всех x ∈ X существует открытое множество U ⊂ M с x ∈ U и гладкая функция F: U → N такие, что F (p) = f (p) для всех p ∈ U ∩ X.

Плавность

Содержание

Классы дифференцируемости

Примеры

Многомерная классы дифференцируемости

пространство функций C

Параметрическая непрерывность

Определение

Порядок непрерывности

Геометрическая непрерывность

Гладкость кривых и поверхностей

Гладкость кусочно определенных кривых и поверхностей

Другие концепции

Отношение к аналитичности

Гладкие разбиения единицы

Гладкие функции на коллекторах и между ними

Гладкие функции между подмножествами многообразий

См. также

Ссылки