Механическое преимущество - это мера увеличения силы, достигаемая с помощью инструмента, механического устройства или системы станка. Устройство противопоставляет входные силы движению, чтобы получить желаемое увеличение выходной силы. Модель для этого - закон рычага. Компоненты машин, предназначенные для управления силами и движением таким образом, называются механизмами. Идеальный механизм передает мощность, не прибавляя и не убавляя ее. Это означает, что идеальный механизм не включает в себя источник энергии, не имеет трения и состоит из твердых тел, которые не деформируются и не изнашиваются. Производительность реальной системы относительно этого идеала выражается в показателях эффективности, которые учитывают отклонения от идеала.
Рычаг представляет собой подвижный стержень, который поворачивается на оси, прикрепленной к фиксированной точке или расположенной на ней или поперек нее. Рычаг действует, прикладывая силы на разном расстоянии от точки опоры. Расположение точки опоры определяет класс рычага. Когда рычаг вращается непрерывно, он действует как поворотный рычаг 2-го класса. Движение конечной точки рычага описывает фиксированную орбиту, по которой может происходить обмен механической энергией. (см. например, ручную рукоятку.)
В наше время этот вид поворотных рычагов широко используется; см. (поворотный) рычаг 2-го класса; см. шестерни, шкивы или фрикционный привод, используемые в механической схеме передачи энергии. Обычно механическим преимуществом манипулируют в «свернутой» форме за счет использования более чем одной шестерни (зубчатой передачи). В такой зубчатой передаче используются шестерни с меньшим радиусом и меньшими механическими преимуществами. Чтобы использовать механическое преимущество отсутствия складывания, необходимо использовать поворотный рычаг «истинной длины». См. Также включение механических преимуществ в конструкцию некоторых типов электродвигателей; один дизайн - «опережающий».
Когда рычаг поворачивается на опоре, точки, расположенные дальше от этой оси, перемещаются быстрее, чем точки, расположенные ближе к ней. Мощности в и из рычага то же самое, так что должно выйти так же, когда расчеты ведутся. Сила - это произведение силы и скорости, поэтому силы, приложенные к точкам, находящимся дальше от оси поворота, должны быть меньше, чем когда они применяются к точкам ближе.
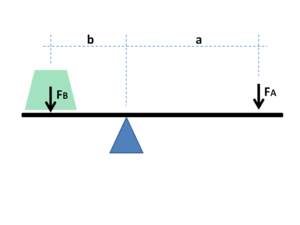
Если и б являются расстояние от точки опоры до точек A и B, а если силы Р примененного к A является входным сила и F B, оказываемым на B является выходным сигналом, отношение скоростей точек A и B даются а / b, поэтому отношение выходной силы к входящей или механическое преимущество определяется выражением
Это закон рычага, доказанный Архимедом с помощью геометрических рассуждений. Он показывает, что если расстояние a от точки опоры до места приложения входной силы (точка A) больше, чем расстояние b от точки опоры до места приложения выходной силы (точка B), то рычаг усиливает входную силу. Если расстояние от точки опоры до входной силы меньше, чем от точки опоры до выходной силы, то рычаг уменьшает входную силу. Признавая глубокие последствия и практическую ценность закона рычага, Архимеду была приписана известная цитата: «Дайте мне место, чтобы встать, и с помощью рычага я переверну весь мир».
Использование скорости в статическом анализе рычага - это применение принципа виртуальной работы.
Требование входной мощности к идеальному механизму для равной выходной мощности обеспечивает простой способ вычисления механического преимущества на основе соотношения скоростей входа-выхода системы.
Входной мощности к зубчатой передаче с крутящим моментом T A применяется к шкиву привода, который вращается с угловой скоростью amp; omega A является P = T A со |.
Поскольку поток мощности постоянен, крутящий момент T B и угловая скорость ω B выходной шестерни должны удовлетворять соотношению
что дает
Это показывает, что для идеального механизма соотношение скоростей на входе и выходе равно механическому преимуществу системы. Это относится ко всем механическим системам, от роботов до рычажных механизмов.
Зубья шестерни сконструированы таким образом, чтобы количество зубьев на шестерне было пропорционально радиусу его делительной окружности, и чтобы делительные окружности зацепляющихся шестерен катились друг по другу без проскальзывания. Передаточное число для пары зацепляющихся шестерен можно вычислить из соотношения радиусов делительной окружности и отношения числа зубьев на каждой шестерне, ее передаточного числа.
 Две зацепляющиеся шестерни передают вращательное движение.
Две зацепляющиеся шестерни передают вращательное движение. Скорость v точки контакта на делительной окружности одинакова на обеих шестернях и определяется выражением
где входная шестерня A имеет радиус r A и входит в зацепление с выходной шестерней B радиуса r B, следовательно,
где N A - количество зубьев входной шестерни, а N B - количество зубьев выходной шестерни.
Механическое преимущество пары зубчатых колес, у которых входная шестерня имеет N A зубьев, а выходная шестерня имеет N B зубьев, определяется выражением
Это показывает, что если выходная шестерня G B имеет больше зубьев, чем входная шестерня G A, то зубчатая передача усиливает входной крутящий момент. И, если выходная шестерня имеет меньше зубьев, чем входная шестерня, то зубчатая передача снижает входной крутящий момент.
Если выходная шестерня зубчатой передачи вращается медленнее, чем входная, то зубчатая передача называется редуктором скорости (множителем силы). В этом случае, поскольку выходная шестерня должна иметь больше зубьев, чем входная шестерня, редуктор будет усиливать входной крутящий момент.
Механизмы, состоящие из двух звездочек, соединенных цепью, или двух шкивов, соединенных ремнем, предназначены для обеспечения определенного механического преимущества в системах передачи энергии.
Скорость v цепи или ремня одинакова при контакте с двумя звездочками или шкивами:
где ведущая звездочка или шкив A зацепляется с цепью или ремнем по продольному радиусу r A, а выходная звездочка или шкив B зацепляется с этой цепью или ремнем по продольному радиусу r B,
следовательно
где N A - количество зубьев на входной звездочке, а N B - количество зубьев на выходной звездочке. Для зубчато-ременной передачи можно использовать количество зубьев на звездочке. Для приводов с фрикционным ремнем необходимо использовать радиус деления входного и выходного шкивов.
Механическое преимущество пары цепной или зубчато-ременной передачи с ведущей звездочкой с N A зубьев и выходной звездочкой с N B зубьями определяется выражением
Механическое преимущество фрикционных ременных приводов обеспечивается:
Цепи и ремни рассеивают мощность за счет трения, растяжения и износа, что означает, что выходная мощность на самом деле меньше потребляемой мощности, а это означает, что механическое преимущество реальной системы будет меньше, чем рассчитанное для идеального механизма. Цепной или ременной привод может терять до 5% мощности через систему из-за тепла трения, деформации и износа, и в этом случае КПД привода составляет 95%.
 Механическое преимущество на разных передачах велосипеда. Показаны типичные силы, прикладываемые к педали велосипеда и к земле, а также соответствующие расстояния, на которые педаль перемещается и вращается колесом. Обратите внимание, что даже на низкой передаче MA велосипеда меньше 1.
Механическое преимущество на разных передачах велосипеда. Показаны типичные силы, прикладываемые к педали велосипеда и к земле, а также соответствующие расстояния, на которые педаль перемещается и вращается колесом. Обратите внимание, что даже на низкой передаче MA велосипеда меньше 1. Рассмотрим 18-скоростной велосипед с шатунами 7 дюймов (радиус) и колесами диаметром 26 дюймов. Если звездочки на кривошипе и на заднем ведущем колесе имеют одинаковый размер, то отношение выходного усилия на шину к входному усилию на педали можно рассчитать по закону рычага:
Теперь предположим, что передние звездочки имеют выбор между 28 и 52 зубьями, а задние звездочки - с 16 и 32 зубьями. Используя различные комбинации, мы можем вычислить следующие соотношения скоростей между передними и задними звездочками:
| ввод (малый) | вход (большой) | выход (малый) | вывод (большой) | передаточное отношение | передаточное число кривошипа | общая MA | |
|---|---|---|---|---|---|---|---|
| низкая скорость | 28 год | - | - | 32 | 1.14 | 0,54 | 0,62 |
| середина 1 | - | 52 | - | 32 | 0,62 | 0,54 | 0,33 |
| середина 2 | 28 год | - | 16 | - | 0,57 | 0,54 | 0,31 |
| высокоскоростной | - | 52 | 16 | - | 0,30 | 0,54 | 0,16 |
Отношение силы, приводящей велосипед к усилию на педали, которое является общим механическим преимуществом велосипеда, является произведением передаточного отношения (или отношения зубьев выходной звездочки / входной звездочки) и передаточного отношения рычага кривошипа..
Обратите внимание, что в каждом случае сила на педалях больше, чем сила, движущая велосипедом вперед (на рисунке выше указана соответствующая обратная сила реакции на землю). Это небольшое механическое преимущество удерживает скорость кривошипа педали на низком уровне по сравнению со скоростью ведущего колеса даже на низких передачах.
Блок и решение представляет собой сборку из веревок и шкивов, которые используются для подъема грузов. Несколько шкивов собраны вместе, чтобы сформировать блоки, один фиксированный, а другой перемещающийся вместе с грузом. Канат продет через шкивы, чтобы обеспечить механическое преимущество, которое усиливает силу, прилагаемую к канату.
Чтобы определить механическое преимущество системы блокировки и захвата, рассмотрим простой случай ружейной снасти, которая имеет один установленный или фиксированный шкив и один подвижный шкив. Трос обвивается вокруг неподвижного блока и падает на подвижный блок, где он обвивается вокруг шкива и поднимается вверх, чтобы завязать узел на неподвижном блоке.
 Механическое преимущество блока и снасти равняется количеству секций каната, на которых держится подвижный блок; здесь показано 2, 3, 4, 5 и 6 соответственно.
Механическое преимущество блока и снасти равняется количеству секций каната, на которых держится подвижный блок; здесь показано 2, 3, 4, 5 и 6 соответственно. Пусть S будет расстоянием от оси неподвижного блока до конца каната, который равен A, где приложена входная сила. Пусть R будет расстоянием от оси неподвижного блока до оси подвижного блока, то есть B, где приложена нагрузка.
Общую длину веревки L можно записать как
где K - постоянная длина каната, которая проходит по шкивам и не изменяется при перемещении блока и снасти.
Скорости V A и V B точек A и B связаны постоянной длиной веревки, то есть
или
Отрицательный знак показывает, что скорость груза противоположна скорости приложенной силы, что означает, что когда мы тянем веревку вниз, груз движется вверх.
Пусть V A положительно вниз, а V B положительно вверх, так что это соотношение может быть записано как отношение скоростей
где 2 - количество секций каната, поддерживающих подвижный блок.
Пусть F A будет входной силой, приложенной к концу веревки A, и пусть F B будет силой в точке B движущегося блока. Как и скорости, F A направлен вниз, а F B направлен вверх.
Для идеальной системы блокировки и захвата нет трения в шкивах и прогиба или износа каната, что означает, что мощность, подводимая приложенной силой F A V A, должна равняться выходной мощности, действующей на нагрузку F B V B, это
Отношение выходной силы к входящей - это механическое преимущество идеальной системы захвата ружья.
Этот анализ обобщается на идеальный блок и захват с подвижным блоком, поддерживаемым n секциями каната,
Это показывает, что сила, прилагаемая идеальным блоком и снастью, в n раз превышает входную силу, где n - количество секций каната, поддерживающих движущийся блок.
Механическое преимущество, которое вычисляется с использованием предположения, что мощность не теряется из-за прогиба, трения и износа машины, является максимальной производительностью, которую можно достичь. По этой причине его часто называют идеальным механическим преимуществом (ИМА). В процессе эксплуатации прогиб, трение и износ уменьшают механическое преимущество. Величина этого снижения от идеального до фактического механического преимущества (AMA) определяется фактором, называемым эффективностью, величиной, которая определяется экспериментальным путем.
Например, используя блок и снасть с шестью секциями каната иНагрузка 600 фунтов, оператор идеальной системы должен был бы тянуть веревку на шесть футов и прикладывать100 фунтов силы F для подъема груза на одну ногу. Оба отношения F out / F in и V in / V out показывают, что IMA равно шести. Для первого отношения100 фунтов F силовые входные результаты в600 фунтов F из вытеснять. В реальной системе из-за трения в шкивах выходное усилие будет меньше 600 фунтов. Второе соотношение также дает МА, равное 6 в идеальном случае, но меньшее значение в практическом сценарии; он не учитывает должным образом потери энергии, такие как растяжение каната. Вычитание этих потерь из IMA или использование первого коэффициента дает AMA.
Идеально подходят механическое преимущество (ИМА), или теоретическое механическое преимущество, это механическое преимущество устройства с предположением, что его компоненты не изгибаться, нет трения, и нет никакого износа. Он рассчитывается с использованием физических размеров устройства и определяет максимальную производительность, которую может достичь устройство.
Допущения об идеальной машине эквивалентны требованию, чтобы машина не накапливала и не рассеивала энергию; Таким образом, мощность, подаваемая в машину, равна выходной мощности. Следовательно, мощность P постоянна через машину, и сила, умноженная на скорость в машине, равна силе, умноженной на скорость на выходе, то есть
Идеальное механическое преимущество - это отношение силы, исходящей из машины (нагрузки), к силе, действующей в машине (усилие), или
Применение отношения постоянной мощности дает формулу для этого идеального механического преимущества с точки зрения передаточного числа:
Передаточное число машины можно рассчитать, исходя из ее физических размеров. Таким образом, допущение постоянной мощности позволяет использовать передаточное число для определения максимального значения механического преимущества.
Фактическое механическое преимущество (АМА) является механическое преимущество определяется путем физического измерения входных и выходных сил. Фактическое механическое преимущество учитывает потерю энергии из-за прогиба, трения и износа.
AMA машины рассчитывается как отношение измеренной выходной силы к измеренной входной силе,
где входные и выходные силы определены экспериментально.
Отношение экспериментально определенного механического преимущества к идеальному механическому преимуществу составляет механический КПД η машины,