Соединение (механическое)

Двигатель с регулируемым ходом (Autocar Handbook, Девятое издание)

A Механическое соединение представляет собой совокупность кузовов, соединенных с управлять силами и движением. Движение тела или звена изучается с помощью геометрии, поэтому звено считается жестким. Связи между звеньями моделируются как обеспечивающие идеальное движение, например, чистое вращение или скольжение, и называются соединениями. Связь, смоделированная как сеть жестких звеньев и идеальных соединений, называется кинематической цепью.

Связи могут быть построены из открытых цепей, замкнутых цепей или комбинации открытых и замкнутых цепей. Каждое звено в цепи соединено стыком с одним или несколькими другими звеньями. Таким образом, кинематическая цепь может быть смоделирована как граф, в котором звенья являются путями, а суставы - вершинами, что называется графом связей.

Развертываемая зеркальная связь состоит из серии ромбических или ножничных связей. Расширенный ножничный подъемник

Движение идеального сустава обычно ассоциируется с подгруппой группы евклидовых смещений. Количество параметров в подгруппе называется степенями свободы (DOF) сустава. Механические связи обычно предназначены для преобразования заданной входной силы и движения в желаемую выходную силу и движение. Отношение выходной силы к входной силе известно как механическое преимущество рычажного механизма, тогда как отношение входной скорости к выходной скорости известно как передаточное отношение. Передаточное число и механическое преимущество определены таким образом, что они дают одинаковое число в идеальном рычаге.

Кинематическая цепь, в которой одно звено фиксировано или неподвижно, называется механизмом, а звено, предназначенное для того, чтобы быть неподвижным, называется структурой .

• 1 Использует
• 2 История
• 3 Подвижность
  • 3.1 Плоское и сферическое движение
• 4 Суставы
• 5 Анализ и синтез связей
• 6 Плоские связи с одной степенью свободы
• 7 Другие интересные связи
  • 7.1 Механизмы прямых линий
  • 7.2 Биологические связи
• 8 Галерея изображений
• 9 См. Также
• 10 Ссылки
• 11 Дополнительная литература
• 12 Внешние ссылки

пространственное 3 Привязка глубины резкости для приложений с джойстиком.

Возможно, самым простым соединением является рычаг , который представляет собой звено, которое вращается вокруг точки, прикрепленной к земле, или фиксированной точки. Когда сила вращает рычаг, точки, далекие от точки опоры, имеют большую скорость, чем точки вблизи точки опоры. Поскольку мощность, приложенная к рычагу, равна выходной мощности, небольшая сила, приложенная в точке, удаленной от точки опоры (с большей скоростью), равна большей силе, приложенной к точке рядом с точкой опоры (с меньшей скоростью). Величина усиления силы называется механическим преимуществом. Это закон рычага.

Два рычага, соединенных стержнем, так что сила, приложенная к одному, передается второму, известна как четырехзвенная связь. Рычаги называются кривошипами, а точки опоры называются шарнирами. Шатун еще называют муфтой. Четвертый стержень в этом узле - это земля или рама, на которой установлены кривошипы.

Связи - важные компоненты машин и инструментов. Примеры варьируются от четырехзвенного рычага, используемого для усиления усилия в болторезе или для обеспечения независимой подвески в автомобиле, до сложных систем рычагов в роботизированных манипуляторах и шагающие машины. В двигателе внутреннего сгорания используется четырехзвенный рычажный механизм ползункового кривошипа, образованный его поршнем, шатуном и коленчатым валом для преобразования мощности. от расширения горящих газов во вращательную силу. Относительно простые связи часто используются для выполнения сложных задач.

Интересные примеры связей включают стеклоочиститель, подвеску велосипеда, ножной механизм в шагающей машине и гидравлические приводы. для тяжелого оборудования. В этих примерах компоненты рычажного механизма перемещаются в параллельных плоскостях и называются плоскими рычагами. Связь с хотя бы одной связью, которая перемещается в трехмерном пространстве, называется пространственной связью. Каркасы робототехнических систем являются примерами пространственных связей. Геометрический дизайн этих систем основан на современном программном обеспечении автоматизированного проектирования.

Архимед применил геометрию для исследования рычага. В 1500-е годы работы Архимеда и Героя Александрии были основными источниками теории машин. Леонардо да Винчи внес изобретательскую энергию в машины и механизмы.

В середине 1700-х годов паровая машина приобрела все большее значение, и Джеймс Уатт понял, что эффективность может быть увеличена за счет использования различных цилиндров для расширения и конденсации пара. Это побудило его искать рычаг, который мог бы преобразовать вращение кривошипа в линейное скольжение, и в результате он обнаружил то, что называется рычажным механизмом Ватта. Это привело к изучению связей, которые могут образовывать прямые линии, пусть даже приблизительно; и вдохновил математика Дж. Дж. Сильвестр, читавший лекцию о рычажном механизме Поселье, который образует точную прямую линию от вращающегося кривошипа.

Работа Сильвестра вдохновила А. Б. Кемпе, который показал, что связи для сложения и умножения можно собрать в систему, которая прослеживает заданную алгебраическую кривую. Методика проектирования Кемпе вдохновила на исследования на стыке геометрии и информатики.

В конце 1800-х годов Ф. Рило, А.Б.У.Кеннеди и Л. Burmester формализовал анализ и синтез систем связи, используя описательную геометрию и P. Л. Чебышев представил аналитические методы исследования и изобретения связей.

В середине 1900-х Ф. Фройденштейн и Г. Н. Сандор использовали недавно разработанный цифровой компьютер для решения петлевых уравнений связи и определения ее размеров для желаемой функции, начав компьютерное проектирование связей. В течение двух десятилетий эти компьютерные методы стали неотъемлемой частью анализа сложных систем машин и управления роботами-манипуляторами.

Р. Э. Кауфман объединил способность компьютера быстро вычислять корни полиномиальных уравнений с графическим пользовательским интерфейсом, чтобы объединить методы Фройденштейна с геометрическими методами Рёло и Burmester и сформировать KINSYN, интерактивный система компьютерной графики для проектирования рычагов

Современные исследования взаимосвязей включают анализ и проектирование шарнирных систем, которые используются в роботах, станках, системах с тросовым приводом и тенсегрити. Эти методы также применяются к биологическим системам и даже к изучению белков.

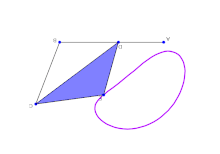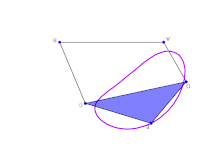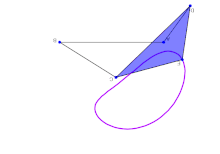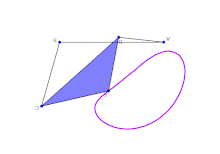Простые связи способны производить сложное движение.

Конфигурация системы жестких звеньев, соединенных идеальными шарнирами, определяется набором параметров конфигурации, таких как углы вокруг вращения соединение и салазки вдоль призматических соединений, измеренных между соседними звеньями. Геометрические ограничения связи позволяют рассчитать все параметры конфигурации в терминах минимального набора, которые являются входными параметрами. Количество входных параметров называется подвижностью или степенью свободы системы связи.

Система из n твердых тел, движущихся в пространстве, имеет 6n степеней свободы, измеренных относительно неподвижного каркаса. Включите эту рамку в подсчет тел, чтобы мобильность не зависела от выбора фиксированной рамки, тогда мы имеем M = 6 (N - 1), где N = n + 1 - количество движущихся тел плюс неподвижное тело..

Соединения, соединяющие тела в этой системе, устраняют степени свободы и уменьшают подвижность. В частности, петли и ползунки накладывают пять ограничений и, следовательно, устраняют пять степеней свободы. Удобно определить количество ограничений c, которые налагает сустав, в терминах свободы сустава f, где c = 6 - f. В случае шарнира или ползуна, которые представляют собой шарниры с одной степенью свободы, мы имеем f = 1 и, следовательно, c = 6 - 1 = 5.

Таким образом, подвижность системы рычагов, образованной из n перемещений звеньев и j соединений, каждое с f i, i = 1,..., j, степени свободы можно вычислить как,

$M\; =\; 6\; n\; -\; \sum \; i\; =\; 1\; j\; (6\; -\; fi)\; =\; 6\; (N\; -\; 1\; -\; J)\; +\; \sum \; я\; =\; 1\; jfi,\; \{\backslash \; displaystyle\; M\; =\; 6n-\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{j\}\; (6-f\_\; \{i\})\; =\; 6\; (N-1\; -j)\; +\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{j\}\; \backslash \; f\_\; \{i\},\}$

где N включает фиксированную ссылку. Это известно как уравнение Куцбаха – Грюблера

. Есть два важных частных случая: (i) простая открытая цепь и (ii) простая замкнутая цепь. Простая открытая цепь состоит из n подвижных звеньев, соединенных встык j стыков, причем один конец соединен с заземляющим звеном. Таким образом, в этом случае N = j + 1 и подвижность цепи

$M\; =\; \sum \; i\; =\; 1\; j\; f\; i.\; \{\backslash \; displaystyle\; M\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{j\}\; \backslash \; f\_\; \{i\}.\}$

Для простой замкнутой цепи n подвижных звеньев соединены встык с помощью n + 1 сочленения, так что два конца соединены с заземлением, образуя петлю. В этом случае мы имеем N = j, а подвижность цепи равна

$M\; =\; \sum \; i\; =\; 1\; jfi\; -\; 6.\; \{\backslash \; displaystyle\; M\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{j\}\; \backslash \; f\_\; \{i\; \}\; -6.\}$

Пример простой открытой цепи - серийный робот-манипулятор. Эти робототехнические системы состоят из серии звеньев, соединенных шестью поворотными или призматическими соединениями с одной степенью свободы, поэтому система имеет шесть степеней свободы.

Примером простой замкнутой цепи является пространственная четырехзвенная связь RSSR. Сумма свободы этих сочленений равна восьми, поэтому подвижность рычажного механизма равна двум, где одна из степеней свободы - это вращение муфты вокруг линии, соединяющей два S-сочленения.

Плоское и сферическое перемещение

Подвижность рычажного механизма 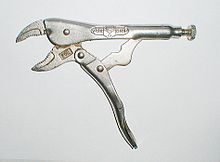Блокирующий плоскогубцы служат примером механического сцепления с четырьмя стержнями, одной степенью свободы. Регулируемый базовый шарнир делает эту связь с двумя степенями свободы пятизвенной связью.

Обычной практикой является проектирование системы рычагов таким образом, чтобы движение всех тел ограничивалось параллельными плоскостями, чтобы образуют так называемое плоское соединение. Также возможно сконструировать систему сцепления так, чтобы все тела двигались по концентрическим сферам, образуя сферическую связь. В обоих случаях степень свободы звена теперь равна трем, а не шести, а ограничения, накладываемые суставами, теперь равны c = 3 - f.

В этом случае формула мобильности имеет вид

$M\; =\; 3\; (N\; -\; 1\; -\; j)\; +\; \sum \; i\; =\; 1\; jfi,\; \{\backslash \; displaystyle\; M\; =\; 3\; (N-1-j)\; +\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{j\}\; \backslash \; f\_\; \{i\},\}$

и у нас есть особые случаи,

• плоская или сферическая простая открытая цепь,

$M\; =\; \sum \; i\; =\; 1\; jfi,\; \{\backslash \; displaystyle\; M\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{j\}\; \backslash \; f\_\; \{i\},\}$

• плоская или сферическая простая замкнутая цепь,

$M\; =\; \sum \; i\; =\; 1\; jfi\; -\; 3.\; \{\backslash \; displaystyle\; M\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{j\}\; \backslash \; f\_\; \{i\}\; -3.\}$

Примером плоской простой замкнутой цепи является плоская четырехзвенная связь, которая представляет собой четырехзвенную петлю с четыре шарнира с одной степенью свободы и, следовательно, имеют подвижность M = 1.

Самыми известными шарнирами для систем рычажных механизмов являются поворотный или шарнирный шарнир обозначается буквой R, а призматическое, или скользящее соединение, обозначается буквой P. Большинство других соединений, используемых для пространственных связей, моделируются как комбинации поворотных и призматических соединений. Например,

• цилиндрический шарнир состоит из последовательной цепи RP или PR, сконструированной таким образом, что оси шарнира вращения и призматического шарнира параллельны,
• универсальный шарнир состоит из RR последовательная цепь, сконструированная таким образом, что оси шарнирных соединений пересекаются под углом 90 °;
• сферическое соединение состоит из последовательной цепи RRR, для которой каждая из осей шарнирного соединения пересекается в в той же точке;
• плоский стык может быть сконструирован как плоская последовательная цепь RRR, RPR и PPR, имеющая три степени свободы.

Основной математический инструмент для анализа связи известен как кинематические уравнения системы. Это последовательность преобразования твердого тела вдоль последовательной цепи внутри рычажного механизма, который устанавливает плавающее звено относительно наземной рамы. Каждая последовательная цепь в звене, соединяющем это плавающее звено с землей, предоставляет набор уравнений, которым должны удовлетворять параметры конфигурации системы. Результатом является набор нелинейных уравнений, которые определяют параметры конфигурации системы для набора значений входных параметров.

Фройденштейн представил метод использования этих уравнений для проектирования плоской четырехзвенной связи для достижения заданного отношения между входными параметрами и конфигурацией связи. Другой подход к проектированию планарной четырехзвенной связи был предложен Л. Burmester и называется Теория Burmester.

Формула подвижности позволяет определить количество звеньев и шарниров в плоской связке, которая дает связь с одной степенью свободы. Если мы требуем, чтобы подвижность плоского рычага была M = 1 и f i = 1, результат будет

$M\; =\; 3\; (N\; -\; 1\; -\; j)\; +\; j\; =\; 1,\; \{\backslash \; displaystyle\; M\; =\; 3\; (N-1-j)\; +\; j\; =\; 1,\; \backslash !\}$

или

$j\; =\; 3\; 2\; N\; -\; 2.\; \{\backslash \; displaystyle\; j\; =\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; N-\; 2.\; \backslash !\}$

Эта формула показывает, что соединение должно иметь четное количество звеньев, поэтому мы имеем

• N = 2, j = 1: это двухстоечный рычаг, известный как рычаг . ;
• N = 4, j = 4: это четырехрычажная связь ;
• N = 6, j = 7: это шестиконечная связь [имеет две связи которые имеют три соединения, называемых тройными связями, и существуют две топологии этой связи в зависимости от того, как эти связи связаны. В топологии Watt две тройные связи соединены стыком. В топологии Стефенсона две тройные связи соединены двоичными связями;
• N = 8, j = 10: восьмизвенная связь имеет 16 различных топологий;
• N = 10, j = 13: 10-стержневой рычажный механизм имеет 230 различных топологий,
• N = 12, j = 16: 12-стержневой рычажный механизм имеет 6856 топологий.

См. Количество 14- и 16- в Сункари и Шмидт. стержневые топологии, а также количество связей, имеющих две, три и четыре степени свободы.

Плоское соединение с четырьмя стержнями, вероятно, является самым простым и наиболее распространенным соединением. Это система с одной степенью свободы, которая преобразует входное вращение кривошипа или смещение ползуна в выходное вращение или ползунок.

Примерами четырехзвенных рычагов являются:

• кривошипно-рычажный механизм, в котором входной кривошип полностью вращается, а выходное звено качается вперед и назад;
• ползунок-кривошип в где входной кривошип вращается, а выходной ползун перемещается вперед и назад;
• механизмы тяги, в которых входной кривошип полностью вращается и перетаскивает выходной кривошип в полностью вращательное движение.

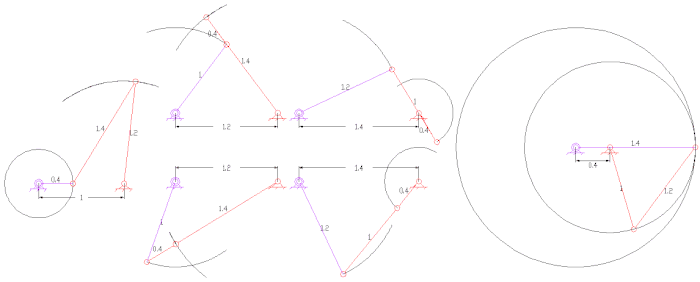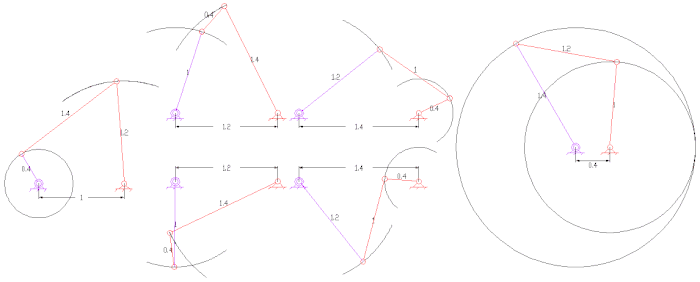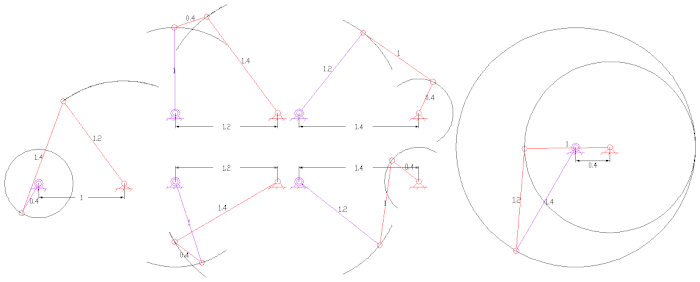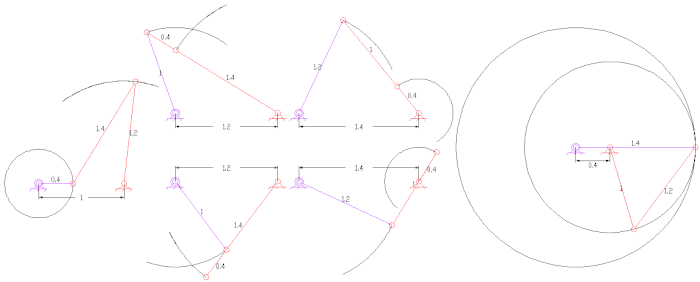Типы четырех- стержневые связи с длинами звеньев, назначенными каждому звену - обратите внимание на самое короткое звено S и самое длинное звено L каждого из этих механизмов. 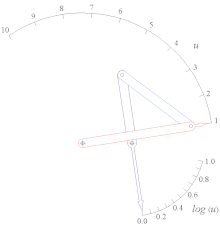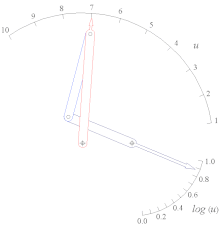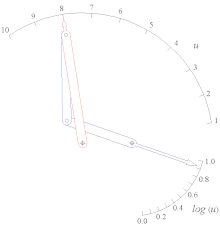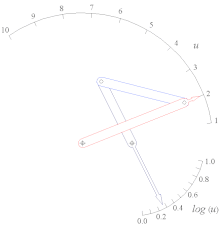Четыре стержня генератор функций функции Log (u) для 1 < u < 10.

• Пантограф (четыре стержня, две степени резкости)
• Пятизвенные связи часто имеют зацепляющие шестерни для двух звеньев, создавая связь с одной степенью резкости. Они могут обеспечить большую передачу энергии с большей гибкостью конструкции, чем четырехзвенные рычаги.
• Рычажный механизм Янсена представляет собой восьмизвенный ножной механизм, изобретенный кинетическим скульптором Тео Янсеном.
• Рычажный механизм Кланна - это рычажный механизм с шестью стержнями, который образует ножной механизм. ;
• Механизмы переключения - это рычаги с четырьмя стержнями, размеры которых позволяют складывать и фиксировать их. Положения переключателя определяются коллинеарностью двух движущихся звеньев. Размер рычага рассчитан таким образом, чтобы рычаг достигал положения переключения непосредственно перед складыванием. Высокое механическое преимущество позволяет входной рукоятке деформировать рычажный механизм ровно настолько, чтобы вытолкнуть его за пределы положения переключения. Это блокирует ввод на месте. Механизмы переключения используются в качестве зажимов.

Механизмы прямой линии

• параллельное движение Джеймса Ватта и связь Ватта
• связь Поселье – Липкина, первая плоская связь для создания идеальный прямой вывод от поворотного входа; восемь стержней, одна степень свободы.
• A Тяга Скотта Рассела, которая преобразует линейное движение в (почти) линейное движение по линии, перпендикулярной входу.
• Чебышевская тяга, которая обеспечивает почти прямое движение точки с четырехзвенной связью.
• рычажный механизм Хукенса, который обеспечивает почти прямолинейное перемещение точки с помощью четырехзвенного рычага.
• рычажный механизм Сарруса, который обеспечивает движение одной поверхности в направление, перпендикулярное другому.
• инвертор Харта, который обеспечивает идеальное прямолинейное движение без скользящих направляющих.

Биологические связи

Системы сцепления широко распространены у животных. Наиболее полный обзор различных типов связей у животных был предоставлен Мисом Мюллером, который также разработал новую систему классификации, которая особенно хорошо подходит для биологических систем. Хорошо известный пример - крестообразные связки колена.

Важное различие между биологическими и инженерными связями состоит в том, что вращающиеся стержни редко встречаются в биологии и что обычно возможен лишь небольшой диапазон теоретически возможного из-за дополнительных механических ограничений (особенно необходимости доставки крови). Биологические связи часто соответствуют . Часто одна или несколько перемычек образованы связками, и часто связи являются трехмерными. Известны сопряженные системы рычагов, а также пяти-, шести- и даже семи-стержневые связи. Четырех стержневые связи являются наиболее распространенными.

Связи могут быть обнаружены в суставах, таких как колено четвероногих, скакательный сустав овцы и черепной механизм птицы и рептилии. Последний отвечает за движение верхнего клюва вверх у многих птиц.

Механизмы сцепления особенно часты и разнообразны в голове костистых рыб, таких как губаны, у которых развилось много специализированных механизмы подачи. Особенно развиты рычажные механизмы выступа челюсти. Для всасывающего кормления система связанных четырех стержней отвечает за скоординированное открытие рта и трехмерное расширение ротовой полости. Другие связи отвечают за выступ предчелюстной кости.

. Связи также присутствуют в качестве фиксирующих механизмов, например, в колене лошади, что позволяет животному спать стоя, без активного сокращения мышц.. В круглом питании, используемом некоторыми костными рыбами, четырехзвенная связь сначала фиксирует голову в изогнутом вентральном положении за счет совмещения двух планок. Освобождение запирающего механизма подбрасывает голову вверх и перемещает рот к жертве за 5–10 мс.

• 

  Генератор качающегося движка функции Log (u) для 1 < u < 10.

• 

  Генератор ползункового переключателя функции Tan (u) для 0 < u < 45°.

• 

  Фиксированные и движущиеся центроды четырехзвенный рычажный механизм

• 

  реечный четырехзвенный рычажный механизм

• 

  механизм RTRTR

• 

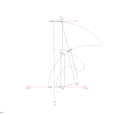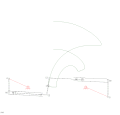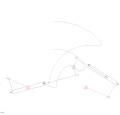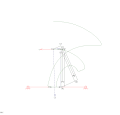
  механизм RTRTR

• 

  шестеренчатые механизмы с пятью рычагами

• 

  трехмерный кривошипно-ползунковый механизм

• 

  Анимированный персонаж Пиночио

• 
• 

  Crawford

• 

  Раскладывающийся наружу механизм

• 

  Раскладывающийся внутрь механизм

• Группы Ассура
• Развертываемая конструкция
• Механизм остановки
• Инженерная механика
• Четырехзвенная связь
• Механический генератор функций
• Кинематика
• Кинематическая связь
• Кинематическая пара
• Кинематический синтез
• Кинематические модели в Mathcad
• Механизм ножки
• Рычаг
• Станок
• Краткое описание станков
• Перегрузка механизма
• Параллельное движение
• Возвратно-поступательное движение
• Ползун-кривошипно-рычажный механизм
• Трехточечная навеска

Викискладе есть медиафайлы, связанные с Linkage (Mechanical).

• Kinematic Models for Design Digital Library (KMODDL) - основной веб-ресурс по кинематике. Фильмы и фотографии сотен работающих моделей механических систем из коллекции механизмов и машин Рило в Корнельском университете, а также 5 других крупных коллекций. Включает библиотеку электронных книг с десятками классических текстов по машиностроению и проектированию. Включает модели CAD и стереолитографические файлы для выбранных механизмов.
• Библиотека цифровых механизмов и зубчатых колес (DMG-Lib) (на немецком языке: Digitale Mechanismen- und Getriebebibliothek) - онлайн-библиотека о связях и кулачках (в основном на немецком языке)
• Вычисления связей
• Вводная лекция по связям
• Виртуальные механизмы, анимированные с помощью Java
• Устройство для рисования на основе связей Роберта Хоусэра
• (ASOM) Анализ, синтез и оптимизация многополюсных связей
• Анимация связей в механическом дизайне101. com включают плоские и сферические связи с четырьмя и шестью стержнями.
• Анимация плоских и сферических связей с четырьмя стержнями.
• Анимация связи Беннета.
• Пример генератора функций с шестью стержнями, который вычисляет высоту угол для заданного диапазона.
• Анимация шестиконечной навески для подвески велосипеда.
• Разнообразные конструкции шестиконечной навески.
• Введение в связи
• Моделирование механизма планарной связи с открытым исходным кодом и механическое система синтеза.

.