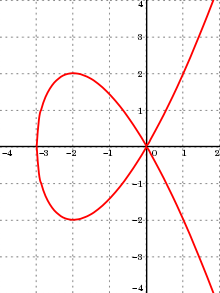Алгебраическая кривая

Кривая, определяемая как нули многочленов Кубика Чирнхаузена - это алгебраическая кривая третьей степени. 601>В математике, аффинная алгебраическая плоская кривая - это нулевой набор полинома от двух переменных. проективная алгебраическая плоская кривая - это нулевой набор в проективной плоскости однородного многочлена от трех переменных. Аффинная алгебраическая плоская кривая может быть завершена в проективной алгебраической плоской кривой посредством гомогенизации ее определяющего полинома. И наоборот, проективная алгебраическая плоская кривая однородного уравнения h (x, y, t) = 0 может быть ограничена аффинной алгебраической плоской кривой уравнения h (x, y, 1) = 0. Каждая из этих двух операций обратный к другому; поэтому фраза алгебраическая плоская кривая часто используется без явного указания того, является ли рассматриваемый случай аффинным или проективным.

В более общем смысле, алгебраическая кривая является алгебраической разновидностью с размерностью один. Эквивалентно, алгебраическая кривая - это алгебраическое многообразие, которое бирационально эквивалентно алгебраической плоской кривой. Если кривая содержится в аффинном пространстве или в проективном пространстве, для такой бирациональной эквивалентности можно взять проекцию.

Эти бирациональные эквивалентности сводят большую часть изучения алгебраических кривых к изучению алгебраических плоских кривых. Однако некоторые свойства не соблюдаются при бирациональной эквивалентности и должны изучаться на неплоских кривых. Это, в частности, имеет место для степени и гладкости. Например, существуют гладкие кривые рода 0 и степени больше двух, но любая плоская проекция таких кривых имеет особые точки (см. формула род – степень ).

Неплоская кривая часто называется пространственной кривой или кривой наклона.

• 1 В евклидовой геометрии
• 2 Плоские проективные кривые
• 3 Замечательные точки плоская кривая
  • 3.1 Пересечение с прямой
  • 3.2 Касательная в точке
  • 3.3 Асимптоты
  • 3.4 Особые точки
• 4 Аналитическая структура
• 5 Неплоские алгебраические кривые
• 6 Алгебраическая функция поля
• 7 Комплексные кривые и вещественные поверхности
  • 7.1 Компактные римановы поверхности
• 8 Особенности
  • 8.1 Классификация особенностей
• 9 Примеры кривых
  • 9.1 Рациональные кривые
  • 9.2 Рациональные плоские кривые
  • 9.3 Эллиптические кривые
  • 9.4 Кривые рода больше одного
    • 9.4.1 Кривые на проекционной плоскости
    • 9.4.2 Кривые в произведении проективных прямых
• 10 См. Также
  • 10.1 Классическая алгебраическая геометрия
  • 10.2 Современная алгебраическая геометрия
  • 10.3 Геометрия римановых поверхностей
• 11 Примечания
• 12 Ссылки

Алгебраическая кривая в евклидовой плоскости набор точки, координаты являются решениями двумерного полиномиального уравнения p (x, y) = 0. Это уравнение часто называют неявным уравнением кривой, в отличие от кривых, которые являются графиком функции, явно определяющей y как функцию от x.

Для кривой, заданной таким неявным уравнением, первая задача состоит в том, чтобы определить форму кривой и нарисовать ее. Эти проблемы не так легко решить, как в случае графика функции, для которого y можно легко вычислить для различных значений x. Тот факт, что определяющее уравнение является полиномом, означает, что кривая обладает некоторыми структурными свойствами, которые могут помочь в решении этих проблем.

Каждую алгебраическую кривую можно однозначно разложить на конечное число гладких монотонных дуг (также называемых ветвями), иногда соединенных некоторыми точками, иногда называемыми «замечательными точками», и, возможно, конечным числом изолированные точки называются узлами. Гладкая монотонная дуга - это график гладкой функции, которая определена и монотонна на открытом интервале оси x. В каждом направлении дуга либо неограничена (обычно называемая бесконечной дугой), либо имеет конечную точку, которая является либо особой точкой (это будет определено ниже), либо точкой с касательной, параллельной одной из осей координат.

Например, для кубики Чирнхаузена есть две бесконечные дуги, имеющие начало (0,0) в качестве конечной точки. Эта точка является единственной особой точкой кривой. Есть также две дуги, имеющие эту особую точку в качестве одной конечной точки и имеющие вторую конечную точку с горизонтальной касательной. Наконец, есть две другие дуги, каждая из которых имеет одну из этих точек с горизонтальной касательной в качестве первой конечной точки и уникальную точку с вертикальной касательной в качестве второй конечной точки. Напротив, синусоида определенно не является алгебраической кривой, имеющей бесконечное количество монотонных дуг.

Чтобы нарисовать алгебраическую кривую, важно знать замечательные точки и их касательные, бесконечные ветви и их асимптоты (если есть), а также то, как дуги соединяют их. Также полезно рассматривать точки перегиба как замечательные точки. Когда вся эта информация нанесена на лист бумаги, форма кривой обычно видна довольно четко. Если нет, достаточно добавить несколько других точек и их касательные, чтобы получить хорошее описание кривой.

Методы вычисления замечательных точек и их касательных описаны ниже, после раздела Проективные кривые.

Часто желательно рассматривать кривые в проективное пространство. Алгебраическая кривая в проективной плоскости или плоской проективной кривой - это набор точек на проективной плоскости, проективные координаты которых равны нулю. однородного многочлена от трех переменных P (x, y, z).

Каждая аффинная алгебраическая кривая уравнения p (x, y) = 0 может быть завершена в проективную кривую уравнения $hp\; (x,\; y,\; z)\; =\; 0,\; \{\backslash \; displaystyle\; ^\; \{h\}\; p\; (x,\; y,\; z)\; =\; 0,\}$где

$hp\; (x,\; y,\; z)\; =\; z\; deg\; \; (p)\; p\; (xz,\; yz)\; \{\backslash \; displaystyle\; ^\; \{h\}\; p\; (x,\; y,\; z)\; =\; z\; ^\; \{\backslash \; deg\; (p)\}\; p\; (\{\backslash \; tfrac\; \{x\}\; \{z\}\},\; \{\backslash \; tfrac\; \{y\}\; \{z\}\})\}$

является результатом гомогенизация по п. Наоборот, если P (x, y, z) = 0 - однородное уравнение проективной кривой, то P (x, y, 1) = 0 - уравнение аффинной кривой, состоящей из точек проективной кривой третья проективная координата которого не равна нулю. Эти две операции взаимны друг с другом, так как $hp\; (x,\; y,\; 1)\; =\; p\; (x,\; y)\; \{\backslash \; displaystyle\; ^\; \{h\}\; p\; (x,\; y,\; 1)\; =\; p\; (x,\; y)\}$и, если p определяется как $p\; (x,\; y)\; =\; P\; (x,\; y,\; 1)\; \{\backslash \; displaystyle\; p\; (x,\; y)\; =\; P\; (x,\; y,\; 1)\}$, тогда $hp\; (x,\; y,\; z)\; =\; P\; (x,\; y,\; z),\; \{\backslash \; displaystyle\; ^\; \{h\}\; p\; (x,\; y,\; z)\; =\; P\; (x,\; y,\; z),\}$, поскольку однородный многочлен P не делится на z.

Например, проективная кривая уравнения x + y - z является проективным завершением единичной окружности уравнения x + y - 1 = 0.

Это означает, что аффинная кривая и ее проективное пополнение являются одними и теми же кривыми, или, точнее, что аффинная кривая является частью проективной кривой, которая достаточно велика, чтобы хорошо определить «полную» кривую. Эта точка зрения обычно выражается, называя «бесконечно удаленными точками» аффинной кривой точки (в конечном числе) проективного пополнения, не принадлежащие аффинной части.

Проективные кривые часто исследуют сами по себе. Они также полезны для изучения аффинных кривых. Например, если p (x, y) - полином, определяющий аффинную кривую, помимо частных производных $px\; \prime \; \{\backslash \; displaystyle\; p\; \text{'}\_\; \{x\}\}$и $py\; \prime \; \{\; \backslash \; displaystyle\; p\; \text{'}\_\; \{y\}\}$, полезно рассмотреть производную на бесконечности

$p\; \infty \; \prime \; (x,\; y)\; =\; hpz\; \prime \; (x,\; y,\; 1).\; \{\backslash \; displaystyle\; p\; \text{'}\_\; \{\backslash \; infty\}\; (x,\; y)\; =\; \{^\; \{h\}\; p\text{'}\; \_\; \{z\}\; (x,\; y,\; 1)\}.\}$

Например, уравнение касательной к аффинная кривая уравнения p (x, y) = 0 в точке (a, b) равна

$xpx\; \prime \; (a,\; b)\; +\; ypy\; \prime \; (a,\; b)\; +\; p\; \infty \; \prime \; (a,\; b)\; =\; 0.\; \{\backslash \; displaystyle\; xp\; \text{'}\_\; \{x\}\; (a,\; b)\; +\; yp\text{'}\; \_\; \{y\}\; (a,\; b)\; +\; p\; \text{'}\_\; \{\backslash \; infty\}\; (a,\; b)\; =\; 0.\}$

В этом разделе мы рассматриваем плоскую алгебраическую кривую, определяемую двумерным многочленом p (x, y), и ее проективное пополнение, определяемое гомогенизацией $P\; (x,\; y,\; z)\; знак\; равно\; hp\; (x,\; y,\; z)\; \{\backslash \; displaystyle\; P\; (x,\; y,\; z)\; =\; \{\}\; ^\; \{h\}\; p\; (x,\; y,\; z)\}$из р.

Пересечение с линией

Часто бывает полезно знать точки пересечения кривой с данной линией. Пересечение с осями координат и асимптоты полезны для построения кривой. Пересечение линией, параллельной осям, позволяет найти хотя бы точку на каждой ветви кривой. Если доступен эффективный алгоритм поиска корня , он позволяет рисовать кривую, нанося точку пересечения со всеми линиями, параллельными оси y и проходящими через каждый пиксель на ось абсцисс.

Если полином, определяющий кривую, имеет степень d, любая линия разрезает кривую не более чем на d точек. Теорема Безу утверждает, что это число точно равно d, если точки ищутся на проективной плоскости над алгебраически замкнутым полем (например, комплексные числа ), и считали с их кратностью. Следующий метод вычислений еще раз доказывает эту теорему в этом простом случае.

Чтобы вычислить пересечение кривой, определяемой полиномом p, с линией уравнения ax + by + c = 0, решается уравнение прямой для x (или для y, если a = 0). Подставляя результат в p, получаем одномерное уравнение q (y) = 0 (или q (x) = 0, если уравнение прямой было решено относительно y), каждый из корней которого является одной координатой точки пересечения. Другая координата выводится из уравнения линии. Кратность точки пересечения - это кратность соответствующего корня. Точка пересечения находится на бесконечности, если степень q меньше степени p; кратность такой бесконечно удаленной точки пересечения равна разности степеней p и q.

Касательная в точке

Касательная в точке (a, b) кривой - это линия уравнения $(x\; -\; a)\; px\; \prime \; (a,\; b)\; +\; (Y\; -\; b)\; py\; \prime \; (a,\; b)\; =\; 0\; \{\backslash \; displaystyle\; (xa)\; p\; \text{'}\_\; \{x\}\; (a,\; b)\; +\; (yb)\; p\text{'}\; \_\; \{y\}\; (a,\; b)\; =\; 0\}$, как и для каждой дифференцируемой кривой, определенной неявным уравнением. В случае полиномов другая формула касательной имеет более простой постоянный член и более симметрична:

$xpx\; \prime \; (a,\; b)\; +\; ypy\; \prime \; (a,\; b)\; +\; p\; \infty \; \prime \; (a,\; b)\; =\; 0,\; \{\backslash \; displaystyle\; xp\; \text{'}\_\; \{x\}\; (a,\; b)\; +\; yp\text{'}\; \_\; \{y\}\; (a,\; b)\; +\; p\; \text{'}\_\; \{\backslash \; infty\}\; (a,\; b)\; =\; 0,\}$

где $п\; \infty \; \prime \; (x,\; y)\; =\; п\; z\; \prime \; (x,\; y,\; 1)\; \{\backslash \; displaystyle\; p\; \text{'}\_\; \{\backslash \; infty\}\; (x,\; y)\; =\; P\text{'}\; \_\; \{z\}\; (x,\; y,\; 1)\}$- производная на бесконечности. Эквивалентность двух уравнений вытекает из теоремы Эйлера об однородной функции, примененной к P.

Если $px\; \prime \; (a,\; b)\; =\; py\; \prime \; (a,\; b)\; =\; 0,\; \{\backslash \; displaystyle\; p\; \text{'}\_\; \{x\}\; (a,\; b)\; =\; p\text{'}\; \_\; \{y\}\; (a,\; b)\; =\; 0,\}$касательная не определена, а точка является особой точка .

Это немедленно распространяется на проективный случай: Уравнение касательной к в точке проективных координат (a: b: c) проективной кривой уравнения P (x, y, z) = 0 равно

$x\; P\; x\; \prime \; (a,\; b,\; c)\; +\; y\; P\; y\; \prime \; (a,\; b,\; c)\; +\; z\; P\; z\; \prime \; (a,\; b,\; c)\; =\; 0,\; \{\backslash \; displaystyle\; xP\; \text{'}\; \_\; \{x\}\; (a,\; b,\; c)\; +\; yP\; \text{'}\_\; \{y\}\; (a,\; b,\; c)\; +\; zP\text{'}\; \_\; \{z\}\; (a,\; b,\; c)\; =\; 0,\}$

и точки особые кривые - это такие точки, что

$P\; x\; \prime \; (a,\; b,\; c)\; =\; P\; y\; \prime \; (a,\; b,\; c)\; =\; P\; z\; \prime \; (a,\; b,\; c)\; =\; 0.\; \{\backslash \; displaystyle\; P\; \text{'}\_\; \{x\}\; (a,\; b,\; c)\; =\; P\text{'}\; \_\; \{y\}\; (a,\; b,\; c)\; =\; P\; \text{'}\_\; \{z\}\; (a,\; b,\; c)\; =\; 0.\}$

( Условие P (a, b, c) = 0 подразумевается из этих условий по теореме Эйлера об однородной функции.)

Асимптоты

Каждая бесконечная ветвь алгебраической кривой соответствует бесконечно удаленной точке кривой, то есть точке проективного пополнения кривой, не принадлежащей ее аффинной части. Соответствующая асимптота является касательной к кривой в этой точке. Может применяться общая формула касательной к проективной кривой, но в этом случае стоит сделать ее явной.

Пусть $p\; =\; pd\; +\; \cdots \; +\; p\; 0\; \{\backslash \; displaystyle\; p\; =\; p\_\; \{d\}\; +\; \backslash \; cdots\; +\; p\_\; \{0\}\}$будет разложением полинома, определяющего кривую на однородные части, где p i - сумма мономов p степени i. Отсюда следует, что

$P\; =\; hp\; =\; pd\; +\; zpd\; -\; 1\; +\; \cdots \; +\; zdp\; 0\; \{\backslash \; displaystyle\; P\; =\; \{^\; \{h\}\; p\}\; =\; p\_\; \{d\}\; +\; zp\_\; \{d-1\}\; +\; \backslash \; cdots\; +\; z\; ^\; \{d\}\; p\_\; \{0\}\}$

и

$P\; z\; \prime \; (a,\; b,\; 0)\; =\; pd\; -\; 1\; (a,\; b).\; \{\backslash \; displaystyle\; P\; \text{'}\_\; \{z\}\; (a,\; b,\; 0)\; =\; p\_\; \{d-1\}\; (a,\; b).\}$

Бесконечная точка кривой является нулем p в форме (a, б, 0). Эквивалентно, (a, b) является нулем p d. Из фундаментальной теоремы алгебры следует, что над алгебраически замкнутым полем (обычно полем комплексных чисел) p d разлагается на произведение линейных множителей. Каждый фактор определяет бесконечно удаленную точку на кривой: если bx - ay является таким фактором, то он определяет бесконечно удаленную точку (a, b, 0). В действительных числах p d делится на линейные и квадратичные множители. неприводимые квадратичные множители определяют нереальные точки на бесконечности, а действительные точки задаются линейными множителями. Если (a, b, 0) - бесконечно удаленная точка кривой, говорят, что (a, b) - это асимптотическое направление . Положив q = p d, уравнение соответствующей асимптоты будет

$xqx\; \prime \; (a,\; b)\; +\; yqy\; \prime \; (a,\; b)\; +\; pd\; -\; 1\; (a,\; b)\; =\; 0.\; \{\backslash \; displaystyle\; xq\; \text{'}\_\; \{x\}\; (a,\; b)\; +\; yq\text{'}\; \_\; \{y\}\; (a,\; b)\; +\; p\_\; \{d-1\}\; (a,\; b)\; =\; 0.\}$

Если $qx\; \prime \; (\; a,\; b)\; =\; qy\; \prime \; (a,\; b)\; =\; 0\; \{\backslash \; displaystyle\; q\; \text{'}\_\; \{x\}\; (a,\; b)\; =\; q\text{'}\; \_\; \{y\}\; (a,\; b)\; =\; 0\}$и $pd\; -\; 1\; (a,\; b)\; \ne \; 0,\; \{\backslash \; displaystyle\; p\_\; \{d-1\}\; (a,\; b)\; \backslash \; neq\; 0,\}$асимптота - это линия на бесконечности, а в В реальном случае кривая имеет ответвление, которое выглядит как парабола . В этом случае говорят, что кривая имеет параболическую ветвь. Если

$qx\; \prime \; (a,\; b)\; =\; qy\; \prime \; (a,\; b)\; =\; pd\; -\; 1\; (a,\; b)\; =\; 0,\; \{\backslash \; displaystyle\; q\; \text{'}\_\; \{x\}\; (a,\; b)\; =\; q\text{'}\; \_\; \{\; y\}\; (a,\; b)\; =\; p\_\; \{d-1\}\; (a,\; b)\; =\; 0,\}$

кривая имеет особую точку на бесконечности и может иметь несколько асимптот. Их можно вычислить методом вычисления касательного конуса особой точки.

Особые точки

Особые точки кривой степени d, определяемой полиномом p (x, y) степени d, являются решениями системы уравнений :

$px\; \prime \; (x,\; y)\; =\; py\; \prime \; (x,\; y)\; =\; p\; (x,\; y)\; =\; 0.\; \{\backslash \; displaystyle\; p\; \text{'}\_\; \{x\}\; (x,\; y)\; =\; p\text{'}\; \_\; \{y\}\; (x,\; y)\; =\; p\; (x,\; y)\; =\; 0.\}$

В нулевой характеристике эта система эквивалентна

$px\; \prime \; (x,\; y)\; =\; py\; \prime \; (x,\; y)\; знак\; равно\; п\; \infty \; \prime \; (x,\; y)\; =\; 0,\; \{\backslash \; displaystyle\; p\; \text{'}\_\; \{x\}\; (x,\; y)\; =\; p\text{'}\; \_\; \{y\}\; (x,\; y)\; =\; p\; \text{'}\_\; \{\backslash \; infty\}\; (x,\; y)\; =\; 0,\}$

где, используя обозначения из предыдущего раздела, $p\; \infty \; \prime \; (x,\; y)\; =\; P\; z\; \prime \; (x,\; y,\; 1).\; \{\backslash \; displaystyle\; p\; \text{'}\_\; \{\backslash \; infty\}\; (x,\; y)\; =\; P\text{'}\; \_\; \{z\}\; (x,\; y,\; 1).\}$Системы эквивалентны из-за теоремы Эйлера об однородных функциях. Последняя система имеет то преимущество, что у нее третий многочлен степени d-1 вместо d.

Аналогично, для проективной кривой, задаваемой однородным многочленом P (x, y, z) степени d, особые точки имеют решения системы

$P\; x\; \prime \; (x,\; y,\; z)\; =\; П\; Y\; \prime \; (Икс,\; Y,\; Z)\; =\; П\; Z\; \prime \; (Икс,\; Y,\; Z)\; =\; 0\; \{\backslash \; Displaystyle\; P\; \text{'}\_\; \{x\}\; (x,\; y,\; z)\; =\; P\text{'}\; \_\; \{y\}\; (x,\; y,\; z)\; =\; P\; \text{'}\_\; \{z\}\; (x,\; y,\; z)\; =\; 0\}$

как однородные координаты. (В положительной характеристике в систему необходимо добавить уравнение $P\; (x,\; y,\; z)\; \{\backslash \; displaystyle\; P\; (x,\; y,\; z)\}$.)

Это означает, что количество особых точек конечно до тех пор, пока p (x, y) или P (x, y, z) не содержит квадратов. Теорема Безу означает, таким образом, что количество особых точек не превосходит (d − 1), но эта граница не точна, поскольку система уравнений переопределена. Если приводимые многочлены разрешены, точная граница равна d (d − 1) / 2, это значение достигается, когда полином множится в линейные множители, то есть если кривая представляет собой объединение d прямых. Для неприводимых кривых и многочленов количество особых точек не превосходит (d − 1) (d − 2) / 2 из-за формулы, выражающей род через особенности (см. Ниже). Максимума достигают кривые рода нуль, все особенности которых имеют кратность два и различные касательные (см. Ниже).

Уравнение касательных в особой точке задается ненулевой однородной частью младшей степени в ряду Тейлора многочлена в особой точке. Когда вы меняете координаты, чтобы поместить особую точку в начало координат, уравнение касательных в особой точке, таким образом, является ненулевой однородной частью низшей степени полинома, а кратность особой точки является степенью этого однородного часть.

Изучение аналитической структуры алгебраической кривой в окрестности особой точки дает точную информацию о топологии особенности. Фактически, вблизи особой точки реальная алгебраическая кривая представляет собой объединение конечного числа ветвей, которые пересекаются только в особой точке и выглядят либо как куспид, либо как гладкая кривая.

Рядом с регулярной точкой одна из координат кривой может быть выражена как аналитическая функция другой координаты. Это следствие аналитической теоремы о неявной функции и подразумевает, что кривая гладкая около точки. Вблизи особой точки ситуация более сложная и включает ряд Пюизо, которые обеспечивают аналитические параметрические уравнения ветвей.

Для описания сингулярности стоит перевести кривую на наличие сингулярности в начале координат. Это состоит из изменения переменной вида $X\; =\; x\; -\; a,\; Y\; =\; y\; -\; b,\; \{\backslash \; displaystyle\; X\; =\; xa,\; Y\; =\; yb,\}$где $a,\; b\; \{\backslash \; displaystyle\; a,\; b\}$- координаты особой точки. В дальнейшем предполагается, что рассматриваемая особая точка всегда находится в начале координат.

Уравнение алгебраической кривой: $f\; (x,\; y)\; =\; 0,\; \{\backslash \; displaystyle\; f\; (x,\; y)\; =\; 0,\}$где f - многочлен от х и у. Этот многочлен можно рассматривать как многочлен от y с коэффициентами в алгебраически замкнутом поле ряда Пюизо по x. Таким образом, f можно разложить на множители вида $y\; -\; P\; (x),\; \{\backslash \; displaystyle\; y-P\; (x),\}$, где P - ряд Пюизо. Все эти коэффициенты различны, если f является неприводимым многочленом, потому что это означает, что f является бесквадратным, свойство, которое не зависит от поля коэффициентов.

Встречающиеся здесь серии Пюизо имеют вид

$P\; (x)\; =\; \sum \; n\; =\; n\; 0\; \infty \; travelling\; /\; d,\; \{\backslash \; displaystyle\; P\; (x)\; =\; \backslash \; sum\; \_\; \{n\; =\; n\_\; \{0\; \}\}\; ^\; \{\backslash \; infty\}\; a\_\; \{n\}\; x\; ^\; \{n\; /\; d\},\}$

где d - положительное целое число, а $n\; 0\; \{\backslash \; displaystyle\; n\_\; \{0\}\}$является целым числом, которое также можно считать положительным, поскольку мы рассматриваем только те ветви кривой, которые проходят через начало координат. Без ограничения общности, мы можем предположить, что d является взаимно простым с наибольшим общим делителем n, таким что $an\; \ne \; 0\; \{\backslash \; displaystyle\; a\_\; \{n\}\; \backslash \; neq\; 0\}$(в противном случае можно было бы выбрать меньший общий знаменатель для показателей степени).

Пусть $\omega \; d\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{d\}\}$будет примитивным корнем степени d из единицы. Если указанная выше серия Пюизо встречается при факторизации $f\; (x,\; y)\; =\; 0\; \{\backslash \; displaystyle\; f\; (x,\; y)\; =\; 0\}$, то серия d

$P\; i\; (\; Икс)\; знак\; равно\; \sum \; N\; знак\; равно\; N\; 0\; \infty \; и\; \omega \; dixn\; /\; d\; \{\backslash \; displaystyle\; P\_\; \{i\}\; (x)\; =\; \backslash \; sum\; \_\; \{n\; =\; n\_\; \{0\}\}\; ^\; \{\backslash \; infty\}\; a\_\; \{n\}\; \backslash \; omega\; \_\; \{d\; \}\; ^\; \{i\}\; x\; ^\; \{n\; /\; d\}\}$

встречаются также при факторизации (следствие теории Галуа ). Эти серии d называются сопряженными и рассматриваются как отдельная ветвь кривой индекса ветвления d.

В случае реальной кривой, то есть кривой, определяемой полиномом с действительными коэффициентами, могут иметь место три случая. Если ни один $P\; i\; (x)\; \{\backslash \; displaystyle\; P\_\; \{i\}\; (x)\}$не имеет действительных коэффициентов, значит, у одного есть ненастоящая ветвь. Если некий $P\; i\; (x)\; \{\backslash \; displaystyle\; P\_\; \{i\}\; (x)\}$имеет действительные коэффициенты, то его можно выбрать как $P\; 0\; (x)\; \{\backslash \; displaystyle\; P\_\; \{\; 0\}\; (x)\}$. Если d нечетно, то каждое действительное значение x дает реальное значение $P\; 0\; (x)\; \{\backslash \; displaystyle\; P\_\; \{0\}\; (x)\}$, и у одного есть реальная ветвь, которая выглядит регулярный, хотя он особенный, если d>1. Если d четно, то $P\; 0\; (x)\; \{\backslash \; displaystyle\; P\_\; \{0\}\; (x)\}$и $P\; d\; /\; 2\; (x)\; \{\backslash \; displaystyle\; P\_\; \{d\; /\; 2\; \}\; (x)\}$имеют реальные значения, но только для x ≥ 0. В этом случае реальная ветвь выглядит как куспид (или является куспидом, в зависимости от определения куспид, который используется).

Например, у обычного куспида есть только одна ветвь. Если он определяется уравнением $y\; 2\; -\; x\; 3\; =\; 0,\; \{\backslash \; displaystyle\; y\; ^\; \{2\}\; -x\; ^\; \{3\}\; =\; 0,\}$, то факторизация будет $(\; у\; -\; х\; 3/2)\; (у\; +\; х\; 3/2);\; \{\backslash \; displaystyle\; (y-x\; ^\; \{3/2\})\; (y\; +\; x\; ^\; \{3/2\});\}$индекс ветвления равен 2, и два фактора действительны и определяют каждую половину ветви. Если куспид поворачивается, уравнение принимает вид $y\; 3\; -\; x\; 2\; =\; 0,\; \{\backslash \; displaystyle\; y\; ^\; \{3\}\; -x\; ^\; \{2\}\; =\; 0,\}$и факторизация $(Y\; -\; Икс\; 2/3)\; (Y\; -\; J\; 2\; Икс\; 2/3)\; (Y\; -\; (J\; 2)\; 2\; Икс\; 2/3),\; \{\backslash \; Displaystyle\; (yx\; ^\; \{2/3\})\; (yj\; ^\; \{2\; \}\; x\; ^\; \{2/3\})\; (y-\; (j\; ^\; \{2\})\; ^\; \{2\}\; x\; ^\; \{2/3\}),\}$с $j\; =\; (1\; +\; -\; 3)\; /\; 2\; \{\backslash \; displaystyle\; j\; =\; (1\; +\; \{\backslash \; sqrt\; \{-3\}\})\; /\; 2\}$(коэффициент $(j\; 2)\; 2\; \{\backslash \; displaystyle\; (j\; ^\; \{2\})\; ^\; \{2\}\}$не был упрощен до j для демонстрации того, как приведенное выше определение $P\; i\; (x)\; \{\backslash \; displaystyle\; P\_\; \{i\}\; (x)\}$является специализированный). Здесь индекс ветвления равен 3, и действителен только один фактор; это показывает, что в первом случае два фактора должны рассматриваться как определяющие одну и ту же ветвь.

Алгебраическая кривая - это алгебраическое многообразие размерности один. Это означает, что аффинная кривая в аффинном пространстве размерности n определяется, по крайней мере, n-1 полиномами от n переменных. Чтобы определить кривую, эти многочлены должны генерировать простой идеал размерности Крулля 1. Это условие нелегко проверить на практике. Следовательно, может быть предпочтительным следующий способ представления неплоских кривых.

Пусть $f,\; g\; 0,\; g\; 3,\dots ,\; gn\; \{\backslash \; displaystyle\; f,\; g\_\; \{0\},\; g\_\; \{3\},\; \backslash \; ldots,\; g\_\; \{n\}\}$быть n полиномами от двух переменных x 1 и x 2, таких что f неприводимо.Точки в аффинном размерности n, координаты которых удовлетворяют уравнениям и неравенствам

$f\; (x\; 1,\; x\; 2)\; =\; 0\; g\; 0\; (x\; 1,\; x\; 2)\; \ne \; 0\; x\; 3\; =\; g\; 3\; (x\; 1,\; Икс\; 2)\; g\; 0\; (Икс\; 1,\; Икс\; 2)\; ⋮\; Иксn\; =\; GN\; (Икс\; 1,\; Икс\; 2)\; g\; 0\; (Икс\; 1,\; Икс\; 2)\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{Выровнено\}\; F\; (X\_\; \{1\},\; x\_\; \{2\})\; =\; 0\; \backslash \backslash \; g\_\; \{0\}\; (x\_\; \{1\},\; x\_\; \{2\})\; \backslash \; neq\; 0\; \backslash \backslash \; x\_\; \{3\}\; =\; \{\backslash \; frac\; \{g\_\; \{3\}\; (x\_\; \{1\},\; x\_\; \{2\})\; \}\; \{g\_\; \{0\}\; (x\_\; \{1\},\; x\_\; \{2\})\}\}\; \backslash \backslash \; \{\}\; \backslash \; vdots\; \backslash \backslash \; x\_\; \{n\}\; =\; \{\backslash \; frac\; \{g\_\; \{n\}\; (x\_\; \{1\},\; x\_\; \{\; 2\})\}\; \{g\_\; \{0\}\; (x\_\; \{1\},\; x\_\; \{2\})\}\}\; \backslash \; end\; \{align\}\}\}$

- все точки алгебраической кривой, в которой конечное число точек был удален. Эта кривая порождает систему образующих идеала многочленов h такой, что существует целое число k такое $g\; 0\; kh\; \{\backslash \; displaystyle\; g\_\; \{0\}\; ^\; \{k\}\; h\}$принадлежит к идеалу,ожденному $f,\; x\; 3\; g\; 0\; -\; g\; 3,\dots ,\; xng\; 0\; -\; gn\; \{\backslash \; displaystyle\; f,\; x\_\; \{3\}\; g\_\; \{0\}\; -g\_\; \{3\},\; \backslash \; ldots,\; x\_\; \{n\}\; g\_\; \{0\}\; -g\_\; \{n\}\; \}$. Это представление является бирациональной эквивалентностью между кривой и плоской кривой, определяемой f. Таким образом можно представить любую алгебраическую кривую. Однако может потребоваться линейная замена числа, чтобы почти всегда вводить проекцию на две первые переменные. Когда необходимо замена числа, почти каждое изменение удобно, если оно установлено над бесконечным полем.

Это представление позволяет нам легко вывести свойство хорошей алгебраической кривой, включая ее графическое представление, из свойств ее плоской проекции.

Для кривой, определенной ее неявными уравнениями, приведенное выше представление кривой может быть выведено из базиса Грёбнера для упорядочения блоков, так что блок меньшего переменные (x 1, x 2). Многочлен f - это единственный многочлен в базе, который зависит только от x 1 и x 2. Доли g i/g0получаются путем выбора для i = 3,..., n полинома в базисе, который является линейным по x i и зависит только от x 1, x 2 и x i. Если эти варианты невозможны, это означает, что либо уравнения определяют алгебраический набор, либо что разновидность не имеет размерности один, либо необходимо изменить координаты. Последний случай имеет место, когда f существует и уникально, и для i = 3,..., n существуют многочлены, у которых старший одночлен зависит только от x 1, x 2 и x i.

Изучение алгебраических кривых может быть сведено к изучению неприводимых алгебраических кривых: тех кривых, которые нельзя записать как объединение двух меньших кривых. До бирациональной эквивалентности неприводимых кривых над полем F являются категориально эквивалентными и полями алгебраических функций от одной переменной над F. Такое поле алгебраических функций расширение поля K из F, которое содержит элемент x, который трансцендентен над F, и такой, что K является конечным алгебраическим расширением F (x), которое является полем рациональных функций в неопределенном x над F.

Например, рассмотрим поле C комплексных чисел, через которое мы можем определить поле C (x) рациональных функций в C . Если y = x - x - 1, то поле C (x, y) является полем эллиптических функций . Элемент x не определен однозначно; поле также можно рассматривать, например, как расширение C (y). Алгебраическая кривая, соответствующая полю функции, - это просто набор точек (x, y) в C, удовлетворяющих y = x - x - 1.

Если поле F не является алгебраически замкнутым, точка точки зрения на геометрические точки, как мы включаем, например, «кривые» без точек на них. Например, если базовое поле F является полем R действительных чисел, то x + y = −1 определяет поле алгебраического расширения R (x), но соответствующая кривая как подмножество R не имеет точек. Уравнение x + y = −1 действительно определяет неприводимую алгебраическую кривую над R в смысле схемы (интеграл, разделенный одномерные схемы конечного типа над R ). В этом смысле взаимно однозначное соответствие между неприводимыми алгебраическими кривыми над F (с точностью до бирациональной эквивалентности) и полями алгебраических функций от одной модели F, вообще говоря, выполнено.

Две кривые могут быть бирационально эквивалентными (т.е. иметь изоморфные функциональные поля), не будучи изоморфными как кривые. Ситуация становится проще, когда мы имеем дело с методами не кривыми, т.е. такими, которые лишены каких-либо функций. Две неособые проективные кривые над полем изоморфны тогда и только тогда, когда их функциональные поля изоморфны.

Теорема Цена касается функционального поля алгебраической кривой над алгебраически замкнутым полем.

Комплексная проективная алгебраическая кривая находится в n-мерном комплексном проективном пространстве CP . Он комплексную размерность, но топологическую размерность, как реальное имеет обширие, 2n, и является компактным, прочным и ориентируемым. Алгебраическая кривая над C также имеет топологическую размерность два; другими словами, это поверхность .

. топологический род этой поверхности, то есть ручек или отверстий для бублика, равенство геометрическому виду алгебраическая кривая, которая может быть вычислена алгебраическими средствами. Короче говоря, если рассматривать плоскую проекцию неособой кривой, имеющей степень d и обычные особенности (особенности кратности два с различными касательными), то род равенство (d - 1) (d - 2) / 2 - k, где k - количество этих особенностей.

Компактные римановы поверхности

A Римановы поверхности - это связное комплексное аналитическое многообразие одного комплексного измерения, что делает его связным вещественным разнообразием двух измерений. Оно компактно, если компактно как топологическое пространство.

Существует тройная эквивалентность категорий между категорией гладких неприводимых проективных алгебраических кривых над C (с непостоянными регулярными отображениями как морфизмов), категории компактных римановых поверхностей (с непостоянными голоморфными отображениями в морфизмов) и противоположной категории полей алгебраических функций в одном переменная над C (с гомоморфизмами полей, которые фиксируют C как морфизмы). Это означает, что, изучая эти три предмета, мы в некотором смысле изучаем одно и то же. Он позволяет использовать сложные аналитические методы в алгебраической геометрии, а алгебро-геометрические методы - в комплексном аналитическом и теоретико-полевые методы - в обоих. Это характерно для гораздо более широкого класса задач алгебраической геометрии.

См. Также алгебраическую геометрию и аналитическую геометрию для более общей теории.

Используя внутреннюю концепцию касательного пространства, точки P на алгебраической кривой C классифицируются как гладкие (синоним: неособые), иначе единственное число. Учитывая n - 1 однородных многочленов от n + 1 числа, мы можем найти матрицу Якоби как (n - 1) × (n + 1) матрицу частных производных. Если ранг эта матрица равенство n - 1, то многочлены определяют алгебраическую кривую (в результате они определяют алгебраическое многообразие более высокой размерности). Если ранг остается n - 1, когда матрица Якоби вычисляется в точке P на кривой, то эта точка является гладкой или регулярной точкой; в случае если это особая точка. В частности, если кривая проективной плоской алгебраической кривой, заданной одним однородным полиномиальным уравнением f (x, y, z) = 0, то особые точки - это в точности точки P, в которой ранг 1 × (n + 1) матрица равна нулю, то есть где

$\partial \; f\; \partial \; x\; (P)\; =\; \partial \; f\; \partial \; y\; (P)\; =\; \partial \; f\; \partial \; z\; (P)\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\}\}\; (P)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; y\}\}\; (P)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; z\}\}\; (P)\; =\; 0.\}$

Поскольку f является полиномиальное, это определение является чисто алгебраическим и не делает никаких предположений о природе поля F, которое, в частности, не обязательно должно быть действительными или комплексными числами. Конечно, следует помнить, что (0,0,0) не является точкой кривой и, следовательно, не является особой точкой.

Аналогично, для аффинной алгебраической кривой, определенной одним полиномиальным уравнением f (x, y) = 0, то особые точки - это в точности точки P кривой, в которых ранг матрицы Якоби 1 × n равно нулю, то есть где

$f\; (P)\; =\; \partial \; f\; \partial \; x\; (P)\; =\; \partial \; f\; \partial \; y\; (P)\; =\; 0.\; \{\backslash \; displaystyle\; f\; (P)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\; \backslash \; partial\; x\}\}\; (P)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; y\}\}\; (P)\; =\; 0.\}$

Особенности кривой не являются бирациональными инвариантами. Однако определение местоположения и классификация особенностей кривой - это один из способов вычисления рода, который является бирациональным инвариантом. Чтобы это сработало, мы должны рассматривать кривую проективно и требовать, чтобы F была алгебраически замкнутой, чтобы были учтены все особенности, принадлежащие кривой.

Классификация особенностей

x = y

Особые точки включают несколько точек, в которых кривая пересекает саму себя, а также различные типы выступов, например, которые показаны кривой с уравнением x = y при (0,0).

Кривая C имеет не более конечного числа особых точек. Если его нет, его можно назвать гладким или неособым. Обычно это определение понимается над алгебраически замкнутым полем и для кривой C в проективном пространстве (т. Е. Полным в смысле алгебраической геометрии). Например, плоская кривая уравнения $y\; -\; x\; 3\; =\; 0\; \{\backslash \; displaystyle\; yx\; ^\; \{3\}\; =\; 0\}$считается сингулярной, поскольку имеет особую точку (куспид) на бесконечности.

В оставшейся части этого раздела рассматривается плоская кривая C, определенная как нулевой набор двумерного многочлена f (x, y). Некоторые из результатов, но не все, можно обобщить на неплоские кривые.

Особые точки классифицируются с помощью нескольких инвариантов. Кратность m определяется как максимальное целое число, такое, что производные f для всех порядков до m - 1 обращаются в нуль (также минимальное число пересечения между кривой и прямой в P). Интуитивно, особая точка имеет дельта-инвариант δ, если она концентрирует δ обычных двойных точек в P. Чтобы сделать это точным, процесс раздува создает так называемые бесконечно близкие точки и суммирует m (m − 1) / 2 по бесконечно близким точкам, где m - их кратность, дает δ. Для неприводимой и приведенной кривой и точки P мы можем алгебраически определить δ как длину $OP\; ~\; /\; OP\; \{\backslash \; displaystyle\; \{\backslash \; widetilde\; \{\{\backslash \; mathcal\; \{O\}\}\; \_\; \{P\}\}\}\; /\; \{\backslash \; mathcal\; \{O\}\}\; \_\; \{P\}\}$где $OP\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{O\}\}\; \_\; \{P\}\}$- локальное кольцо в P и $OP\; ~\; \{\backslash \; displaystyle\; \{\backslash \; widetilde\; \{\{\backslash \; mathcal\; \{O\}\}\; \_\; \{P\}\}\}\}$- его интегральное замыкание.

Число Милнора µ особенности - это степень отображения grad f (x, y) / | grad f (x, y) | на малой сфере радиуса ε в смысле топологической степени непрерывного отображения, где grad f - (комплексное) векторное поле градиента f. Оно связано с δ и r соотношением,

μ = 2δ - r + 1.

Здесь число ветвления r диаграммы P - это количество локально неприводимых ветвей в точке P. Например, r = 1 в точке обычный касп и r = 2 в обычной двойной точке. Кратность m не меньше r, а P сингулярна тогда и только тогда, когда m не меньше 2. Более того, δ не меньше m (m-1) / 2.

Вычисление дельта-инвариантов всех сингулярностей позволяет определить род g кривой; если d - степень, то

$g\; =\; 1\; 2\; (d\; -\; 1)\; (d\; -\; 2)\; -\; \sum \; P\; \delta \; P,\; \{\backslash \; displaystyle\; g\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (d-1)\; (d-2)\; -\; \backslash \; sum\; \_\; \{P\}\; \backslash \; delta\; \_\; \{P\},\}$

где сумма берется по всем особым точкам P комплексной проективной плоской кривой. Это называется формулой рода ..

Сопоставьте инварианты [m, δ, r] особенности, где m - кратность, δ - дельта-инвариант, а r - число ветвления. Тогда обычная куспид - это точка с инвариантами [2,1,1] и обычная двойная точка - это точка с инвариантами [2,1,2], а обычная m-кратная точка - это точка с инвариантами [m, m ( м - 1) / 2, м].

Рациональные кривые

A рациональная кривая, также называемая уникурсальной кривой, - это любая кривая, которая бирационально эквивалентна прямой, которая может принять за проективную линию; соответственно, мы можем отождествить фигурное поле кривой с полем использования функций от одной неопределенной F (x). Если F алгебраически замкнута, это эквивалентно кривой рода ноль; однако поле всех вещественных алгебраических функций, определенных на вещественном алгебраическом множестве x + y = −1, является полем нулевого рода, которое не является полем рациональных функций.

Конкретно, рациональная кривая, вложенная в аффинное пространство размерности n над F, может быть параметризована (за исключением исключительных точек) с помощью n рациональных функций от единственного параметра т; путем использования этих рациональных функций к одному и тому же знаменателю, полученному + 1 полиномы, определяют полиномиальные параметры проективного пополнения кривой в проективном пространстве. Примером может служить рациональная нормальная кривая, где все эти многочлены являются одночленами.

Любое коническое сечение, определенное над F с рациональной точкой в F - рациональная кривая. Его можно параметры, проведя линию с наклоном через рациональную точку и пересекающуюся с плоской квадратичной кривой; это дает многочлены с F-рациональными коэффициентами и одним F-рациональным корнем, следовательно, другой корень также F-рациональнленым (т.е. принадлежит F).

x + xy + y = 1

Например, рассмотрим эллипс x + xy + y = 1, где (−1, 0) - рациональная точка. Проведя линию с наклоном t из (−1,0), y = t (x + 1), подставив ее в уравнение эллипса, разложив на множители и решив относительно x, получим

$x\; =\; 1\; -\; t\; 2\; 1\; +\; т\; +\; т\; 2.\; \{\backslash \; displaystyle\; x\; =\; \{\backslash \; frac\; \{1-t\; ^\; \{2\}\}\; \{1\; +\; t\; +\; t\; ^\; \{2\}\}\}.\}$

Тогда уравнение для y имеет вид

$y\; =\; t\; (\; Икс\; +\; 1)\; знак\; равно\; Т\; (Т\; +\; 2)\; 1\; +\; Т\; +\; Т\; 2,\; \{\backslash \; Displaystyle\; у\; =\; Т\; (х\; +\; 1)\; =\; \{\backslash \; гидроразрыва\; \{т\; (т\; +\; 2)\}\; \{1\; +\; т\; +\; т\; ^\; \{2\; \}\}\}\; \backslash ,,\}$

который использует рациональную параметры эллипса и, следовательно, показывает, что эллипс является рациональной кривой. Даны все точки эллипса, кроме (−1,1), что соответствует t = ∞; поэтому всякая кривая параметров реальной проективной линией.

Такую рациональную параметры можно рассмотреть в проективном представлении, приравняв первые проективные координаты к числителям параметров, а последние - к общему знаменателю. Параметр определен в проекционной линии, многочлены параметры должны быть гомогенизированными. Например, проективная параметризация вышеуказанного эллипса:

$X\; =\; U\; 2\; -\; T\; 2,\; Y\; =\; T\; (T\; +\; 2\; U),\; Z\; =\; T\; 2\; +\; TU\; +\; U\; 2.\; \{\backslash \; Displaystyle\; X\; =\; U\; ^\; \{2\}\; -T\; ^\; \{2\},\; \backslash \; quad\; Y\; =\; T\; \backslash ,\; (T\; +\; 2\; \backslash ,\; U),\; \backslash \; quad\; Z\; =\; T\; ^\; \{2\}\; +\; TU\; +\; U\; ^\; \{2\}.\}$

Исключив T и U между этими уравнениями, мы снова получим проективное уравнение эллипса

$X\; 2\; +\; XY\; +\; Y\; 2\; =\; Z\; 2,\; \{\backslash \; displaystyle\; X\; ^\; \{2\}\; +\; X\; \backslash ,\; Y\; +\; Y\; ^\; \{2\}\; =\; Z\; ^\; \{2\},\; \}$

, которое может быть легко получено путем усреднения приведенного выше уравнения.

Многие кривые в Википедии список кривых используются рациональными и, следовательно, имеют аналогичные рациональные параметры.

Кривые рациональной плоскости

Кривые рациональной плоскости - это рациональные кривые, встроенные в $P\; 2\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{P\}\; ^\; \{2\}\}$. Даны общие разделы $s\; 1,\; s\; 2,\; s\; 2\; \in \; \Gamma \; (P\; 1,\; O\; (d))\; \{\backslash \; displaystyle\; s\_\; \{1\},\; s\_\; \{2\},\; s\_\; \{2\}\; \backslash \; in\; \backslash \; Gamma\; (\backslash \; mathbb\; \{\; P\}\; ^\; \{1\},\; \{\backslash \; mathcal\; \{O\}\}\; (d))\}$степени $d\; \{\backslash \; displaystyle\; d\}$однородные многочлены в двух координатах, $x,\; y\; \{\backslash \; displaystyle\; x,\; y\}$, есть карта

$s:\; P\; 1\; \to \; P\; 2\; \{\backslash \; displaystyle\; s:\; \backslash \; mathbb\; \{P\}\; ^\; \{1\}\; \backslash \; to\; \backslash \; mathbb\; \{P\}\; ^\; \{2\}\}$определяется как $s\; ([x:\; y])\; =\; [s\; 1\; ([x:\; y]):\; s\; 2\; ([x:\; y]):\; s\; 3\; ([\; х:\; у])]\; \{\backslash \; displaystyle\; s\; ([x:\; y])\; =\; [s\_\; \{1\}\; ([x:\; y]):\; s\_\; \{2\}\; ([x:\; y]):\; s\_\; \{3\}\; ([x\; :\; y])]\}$

, определяющая рациональную плоскую кривую степень $d\; \{\backslash \; displaystyle\; d\}$. Имеется связанное пространство модулей $M\; =\; M\; ¯\; 0,\; 0\; (P\; 2,\; d\; \cdot \; [H])\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{M\}\}\; =\; \{\backslash \; overline\; \{\backslash \; mathcal\; \{M\}\; \}\}\; \_\; \{0,0\}\; (\backslash \; mathbb\; \{P\}\; ^\; \{2\},\; d\; \backslash \; cdot\; [H])\}$(где $[H]\; \{\backslash \; displaystyle\; [H]\}$- класс гиперплоскости), параметризующий все такие устойчивые кривые. Чтобы определить размерность пространств модулей, можно сделать подсчет измерений: $d\; +\; 1\; \{\backslash \; displaystyle\; d\; +\; 1\}$параметры в $\Gamma \; (P\; 1,\; O\; (d))\; \{\backslash \; displaystyle\; \backslash \; Gamma\; (\backslash \; mathbb\; \{P\}\; ^\; \{1\},\; \{\backslash \; mathcal\; \{O\}\}\; (d))\}$, что дает $3\; d\; +\; 3\; \{\backslash \; displaystyle\; 3d\; +\; 3\}$всего параметров для каждого из разделов. Затем, как это показано с помощью до проективного частного $P\; 2\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{P\}\; ^\; \{2\}\}$, существует $1\; \{\backslash \; displaystyle\; 1\}$меньше расписания в $M\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{M\}\}\}$. Кроме того, трехмерная группа автоморфизмов $P\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{P\}\; ^\; \{1\}\}$, следовательно, $M\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{M\}\}\}$имеет размер $3\; d\; +\; 3-1\; -\; 3\; =\; 3\; d\; -\; 1\; \{\backslash \; displaystyle\; 3d\; +\; 3-1-3\; =\; 3d-1\}$. Это пространство модулей можно использовать для подсчета числа $N\; d\; \{\backslash \; displaystyle\; N\_\; \{d\}\}$степени $d\; \{\backslash \; displaystyle\; d\}$пересекающихся плоских кривых $3\; d\; -\; 1\; \{\backslash \; displaystyle\; 3d-1\}$очков с использованием теории Громова - Виттена. Он задается рекурсивным запуском

$N\; d\; =\; \sum \; d\; A\; +\; d\; B\; =\; d\; N\; d\; AN\; d\; B\; d\; A\; 2\; d\; B\; (d\; B\; (3\; d\; -\; 4\; 3\; d\; A\; -\; 2)\; -\; d\; A\; (3\; d\; -\; 4\; 3\; d\; A\; -\; 1))\; \{\backslash \; displaystyle\; N\_\; \{d\}\; =\; \backslash \; sum\; \_\; \{d\_\; \{A\}\; +\; d\_\; \{B\}\; =\; d\}\; N\_\; \{d\_\; \{A\}\}\; N\_\; \{d\_\; \{B\}\}\; d\_\; \{A\}\; ^\; \{2\}\; d\_\; \{B\}\; \backslash \; left\; (d\_\; \{B\}\; \{\backslash \; binom\; \{3d-4\}\; \{3d\_\; \{A\}\; -2\}\}\; -\; d\_\; \{A\}\; \{\backslash \; binom\; \{3d-4\}\; \{3d\_\; \{A\}\; -\; 1\}\}\; \backslash \; right)\}$

где $N\; 1\; =\; N\; 2\; =\; 1\; \{\backslash \; displaystyle\; N\_\; \{1\}\; =\; N\_\; \{2\}\; =\; 1\}$.

Эллиптические кривые

Эллиптическая кривая может быть определена как любая кривая рода с рациональной точкой : обычная модель - это неособая кубическая кривая, достаточно для моделирования любой кривой рода один. В этой модели выделенная точка обычно считается точкой перегиба на бесконечности; это равносильно требованию, чтобы кривая могла быть записана в форме Тейта-Вейерштрасса, которая в проективной версии имеет вид

$y\; 2\; z\; +\; a\; 1\; xyz\; +\; a\; 3\; yz\; 2\; =\; x\; 3\; +\; a\; 2\; x\; 2\; z\; +\; a\; 4\; xz\; 2\; +\; а\; 6\; з\; 3.\; \{\backslash \; displaystyle\; y\; ^\; \{2\}\; z\; +\; a\_\; \{1\}\; xyz\; +\; a\_\; \{3\}\; yz\; ^\; \{2\}\; =\; x\; ^\; \{3\}\; +\; a\_\; \{2\}\; x\; ^\; \{2\}\; z\; +\; a\_\; \{4\}\; xz\; ^\; \{2\}\; +\; a\_\; \{6\}\; z\; ^\; \{3\}.\}$

Если характеристика поля отличается от 2 и 3, то линейное изменение координат позволяет положить $a\; 1\; =\; a\; 2\; =\; a\; 3\; =\; 0,\; \{\backslash \; displaystyle\; a\_\; \{1\}\; =\; a\_\; \{2\}\; =\; a\_\; \{3\}\; =\; 0,\}$, что дает классическую форму Вейерштрасса

$y\; 2\; =\; x\; 3\; +\; px\; +\; q.\; \{\backslash \; displaystyle\; y\; ^\; \{2\}\; =\; x\; ^\; \{3\}\; +\; px\; +\; q.\}$

Эллиптические кривые несут потери абелевой группы с выделенной точкой как тождество группового закона. В плоской модели сумма трех точек в группе равна нулю тогда и только, когда они коллинеарны. Для группы эллиптической кривой, определенной над комплексными числами, группа изоморфна аддитивной комплексной плоскости по модулю решетки периодов соответствующих эллиптических функций.

Пересечение двух квадрик Поверхности, вообще говоря, неособая кривая, следовательно, эллиптическая кривая, если у нее есть рациональная точка. В особых случаях пересечение может быть либо рациональной формой, либо разложено на кривые малые степени, которые не всегда различны (либо кубическая кривая и линия, либо две коники, либо коника и две прямые, либо четыре прямые).

Кривые рода больше одного

Кривые рода больше одного заметно отличаются как от рациональных, так и от эллиптических кривых. Такие кривые, определенные над рациональными числами, согласно теореме Фалтингса, могут иметь только конечное число рациональных точек, и их можно рассматривать как имеющие структуру гиперболической геометрии. Примерами являются гиперэллиптические кривые, кривая четвертой степени Клейна и кривая Ферма x + y = z, когда n больше трех. Также кривые проекционной плоскости в $P\; 2\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{P\}\; ^\; \{2\}\}$и кривые в $P\; 1\; \times \; P\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{P\}\; ^\; \{\; 1\}\; \backslash \; times\; \backslash \; mathbb\; \{P\}\; ^\; \{1\}\}$дает много полезных примеров.

Проективные плоские кривые

Плоские кривые $C\; \subset \; P\; 2\; \{\backslash \; displaystyle\; C\; \backslash \; subset\; \backslash \; mathbb\; \{P\}\; ^\; \{2\}\}$степени $k\; \{\backslash \; displaystyle\; k\}$, которое может быть построено как геометрическое место исчезновения общего сечения $s\; \in \; \Gamma \; (P\; 2,\; O\; (k))\; \{\backslash \; displaystyle\; s\; \backslash \; in\; \backslash \; Gamma\; (\; \backslash \; mathbb\; \{P\}\; ^\; \{2\},\; \{\backslash \; mathcal\; \{O\}\}\; (k))\}$, имеет род

$(k\; -\; 1)\; (k\; -\; 2)\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{(k-1)\; (k-2)\}\; \{2\}\}\}$

, который может быть вычислен с использованием когомологии когерентного пучка. Вот краткое изложение родов кривых относительно их степени

$степени\; 1\; 2\; 3\; 4\; 5\; 6\; 7\; рода\; 0\; 0\; 1\; 3\; 6\; 10\; 15\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; text\; \{deg\}\}\; 1\; 2\; 3\; 4\; 5\; 6\; 7\; \backslash \backslash \; \{\backslash \; text\; \{genus\}\}\; 0\; 0\; 1\; 3\; 6\; 10\; 15\; \backslash \; end\; \{matrix\}\}\}$

Например, кривая $x\; 4\; +\; y\; 4\; +\; z\; 4\; \{\backslash \; displaystyle\; x\; ^\; \{4\}\; +\; y\; ^\; \{4\}\; +\; z\; ^\; \{4\}\}$определяет кривую рода $3\; \{\backslash \; displaystyle\; 3\}$, которая является гладкой, поскольку дифференциалы $4\; x\; 3,\; 4\; y\; 3,\; 4\; z\; 3\; \{\backslash \; displaystyle\; 4x\; ^\; \{3\},\; 4y\; ^\; \{3\},\; 4z\; ^\; \{3\}\}$не имеют общих нулей с кривой.. Не пример общего раздел - это кривая $x\; (x\; 2\; +\; y\; 2\; +\; z\; 2)\; \{\backslash \; displaystyle\; x\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; z\; ^\; \{2\})\}$которая, по теореме Безауза, должно пересекаться не более чем $2\; \{\backslash \; displaystyle\; 2\}$точек, является объединением двух рациональных кривых $C\; 1\; \cup \; C\; 2\; \{\backslash \; displaystyle\; C\_\; \{1\}\; \backslash \; cup\; C\_\; \{2\}\}$пересекаются в двух точках. Примечание $C\; 1\; \{\backslash \; displaystyle\; C\_\; \{1\}\}$задается точкой схода $x\; \{\backslash \; displaystyle\; x\}$и $C\; 2\; \{\backslash \; displaystyle\; C\_\; \{2\; \}\}$задается место исчезновения $x\; 2\; +\; y\; 2\; +\; z\; 2\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; z\; ^\; \{2\}\}$. Их можно найти явно: точка лежит в обоих, если $x\; =\; 0\; \{\backslash \; displaystyle\; x\; =\; 0\}$. Итак, два решения - это точка $[0:\; y:\; z]\; \{\backslash \; displaystyle\; [0:\; y:\; z]\}$такие, что $y\; 2\; +\; z\; 2\; =\; 0\; \{\backslash \; displaystyle\; y\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; =\; 0\}$, которые равны $[0:\; 1:\; -\; 1]\; \{\backslash \; displaystyle\; [0:\; 1:\; -1]\}$и $[0:\; 1:\; -\; 1]\; \{\backslash \; displaystyle\; [0:\; 1:\; \{\backslash \; sqrt\; \{-1\}\}]\}$.

Кривые в произведении проекционных линий

Кривая $C\; \subset \; P\; 1\; \times \; P\; 1\; \{\backslash \; displaystyle\; C\; \backslash \; subset\; \backslash \; mathbb\; \{P\}\; ^\; \{1\}\; \backslash \; times\; \backslash \; mathbb\; \{P\}\; ^\; \{1\}\}$задано исчезающим геометрическим местом $s\; \in \; \Gamma \; (п\; 1\; \times \; п\; 1,\; О\; (а,\; Ь))\; \{\backslash \; Displaystyle\; s\; \backslash \; in\; \backslash \; Gamma\; (\backslash \; mathbb\; \{P\}\; ^\; \{1\}\; \backslash \; times\; \backslash \; mathbb\; \{P\}\; ^\; \{1\},\; \{\backslash \; mathcal\; \{O\}\; \}\; (a,\; b))\}$, для $a,\; b\; \ge \; 2\; \{\backslash \; displaystyle\; a,\; b\; \backslash \; geq\; 2\}$, дайте кривые рода

$ab\; -\; a\; -\; b\; +\; 1\; \{\backslash \; displaystyle\; ab-ab\; +\; 1\}$

, который можно проверить с помощью когомологии когерентного пучка. Если $a\; =\; 2\; \{\backslash \; displaystyle\; a\; =\; 2\}$, то они определяют кривые рода $2\; b\; -\; 2\; -\; b\; +\; 1\; =\; b\; -\; 1\; \{\backslash \; displaystyle\; 2b-2-b\; +\; 1\; =\; b-1\}$, поэтому кривую любого рода можно построить как кривую в $P\; 1\; \times \; P\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{P\}\; ^\; \{1\}\; \backslash \; times\; \backslash \; mathbb\; \{P\}\; ^\; \{1\}\}$. Их роды могут быть сведены в таблицу

$bidegree\; (2,\; 2)\; (2,\; 3)\; (2,\; 4)\; (2,\; 5)\; род\; 1\; 2\; 3\; 4\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; text\; \{bidegree\; \}\}\; (2,2)\; (2,3)\; (2,4)\; (2,5)\; \backslash \backslash \; \{\backslash \; text\; \{genus\}\}\; 1\; 2\; 3\; 4\; \backslash \; end\; \{matrix\}\}\}$

и для $a\; =\; 3\; \{\backslash \; displaystyle\; a\; =\; 3\}$, это

$бистепень\; (3,\; 2)\; (3,\; 3)\; (3,\; 4)\; (3,\; 5)\; род\; 2\; 4\; 6\; 8\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{matrix\}\; \{\backslash \; text\; \{bidegree\}\}\; (3,2)\; (3,3)\; (3,4)\; (3,5)\; \backslash \backslash \; \{\backslash \; text\; \{genus\}\}\; 2\; 4\; 6\; 8\; \backslash \; end\; \{matrix\}\}\}$

Классическая алгебраическая геометрия

• Acnode
• Теорема Безу
• Теорема Крамера (алгебраические кривые)
• Crunode
• Curve
• Набросок кривой
• Якобиева размерие
• Квартика Клейна
• Список кривых
• Шестнадцатая Гильберта
• Плоская кубическая кривая
• Гиперэллиптическая кривая

Современная алгебраическая геометрия

• Бирациональная геометрия
• Коническая раздел
• Эллиптическая кривая
• Дробный идеал
• Функциональное поле алгебра алгебраического множества
• Функциональное поле (теория)
• Род (математика)
• Полиномиальная лемма niscate
• Плоская кривая четвертой степени
• Рациональная нормальная кривая
• Теорема Римана - Роха для Роха для Роха для кривых
• Теорема Вебера

Геометрия римановых поверхностей

• Формула Римана - Гурвица
• Теорема Римана - Роха для Римановы поверхности
• Римановы поверхности

На Викискладе есть материалы, связанные с Алгебраическими кривыми.

• Эгбертом Брискорном и Хорстом Кнёррером, Плоские алгебраические кривые, Джон Стилвелл, переводчик, Биркхойзер, 1986
• Клод Шевалле, Введение в теорию алгебраических функций одной, Американское математическое общество, Mathematical Surveys Number VI, 1951
• J. Л. Кулидж, Трактат об алгебраических плоских кривых, Oxford University Press, 1931, (Dover Publications 2004).
• Хершель М. Фаркас и Ирвин Кра, Римановы поверхности, Springer, 1980
• W. Фултон, Алгебраические кривые: введение в алгебраическую геометрию.
• К.Г. Гибсон, Элементарная геометрия алгебраических кривых: Введение для студентов, Cambridge University Press, 1998.
• Филип А. Гриффитс, Введение в алгебраические кривые, Кунико Велтин, пер., Американское математическое общество, Перевод тома 70 математических монографий, редакция 1985 г.
• Робин Хартсхорн, Алгебраическая геометрия, Springer, 1977
• Сигеру Иитака, Алгебраическая геометрия: введение в бирациональную геометрию алгебраических множеств, Springer, 1982
• Джон Милнор, Особые точки гиперповерхностей, Princeton University Press, 1968
• Джордж Сэлмон, Кривые на высших плоскостях, третье издание, GE Stechert Co., 1934
• Жан-Пьер Серр, Алгебраические группы и поля классов, Springer, 1988
• Эрнст Кёттер (1887). "Grundzüge einer rein geometrischen Theorie der algebraischen ebenen Kurven (Основы чисто геометрической теории алгебраических плоских кривых)". Труды Королевской академии Берлина. - получил премию Академии 1886 года

1. ^Норман Фрейзер (февраль 1888 г.). «Синтетическая геометрия алгебраических кривых Кёттера». Труды Эдинбургского математического общества. 7 : 46–61. Здесь: стр.46