Лагранжева механика

Формулировка классической механики Жозеф-Луи Лагранж (1736–1813)

Лагранжева является механика переформулировкой классической механики, введенной итальянско-французским математиком и астрономом Жозефом-Луи Лагранжем в 1788 году.

В лагранжевой механике - траектория системы. Лагранжа первого рода, которые рассматривают ограничения явно как дополнительные уравнения, часто с использованием множителей Лагранжа ; или уравнения Лагранжа второго рода, которые включают ограничения собственного разумного выбора общих координат. В каждом случае математическая функция, называемая лагранжианом, функция обобщенных координат, их производных по времени и времени и содержит информацию о динамике системы.

Никакая новая физика не обязательно вводится при применении механики Лагранжа по сравнению с механикой Ньютона. Однако он более математически сложен и систематичен. Законы Ньютона могут быть не- консервативные силы, такие как трение ; однако они явно создают ограничивающие силы и лучше всего подходят для декартовых координат. Лагранжева механика идеальна для систем с консервативными силами и для обхода ограничивающих сил в любой системе координат. Диссативные и ведомые силы могут быть учтены посредством разделения внешних сил на превышении, что приводит к набору модифицированных Эйлера - Лагранжа (EL). Обобщенные координаты могут быть выбраны для удобства, чтобы использовать ограничения симметрии в системе или геометрии, что может упростить решение для движения системы. Лагранжева механика также напрямую показывает сохраняющиеся величины и их симметрии, поскольку частный случай теоремы Нётер.

Лагранжева механика важна не только для своих широких приложений, но и из-за своей роли в продвижении глубокого понимания физика. Хотя Лагранж стремился описать только классическую механику в своем трактате Mécanique analytique, Уильям Роуэн Гамильтон позже разработал принцип Гамильтона, который можно использовать для вывести уравнение Лагранжа, которое позже было признано применимым к большей части фундаментальной теоретической физики, в частности, квантовой механики и теории относительности. Его также можно применять к другим системам по аналогии, например, для связанных электрических цепей с индуктивностями и емкостями.

Лагранжева механика широко используется для решения механических задач в физике. и когда формулировка Ньютона классической механики неудобна. Механика Лагранжа используется к динамике частиц, в то время как поля описываются с помощью плотности лагранжиана. Уравнения Лагранжа также используются в задаче оптимизации динамических систем. В механике уравнения Лагранжа второго используются гораздо чаще, чем уравнения первого рода.

• 1 Введение
• 2 От ньютоновской механики к лагранжевой
  • 2.1 Законы Ньютона
  • 2.2 Принцип Даламбера
  • 2.3 Уравнения движения на основе принципа Даламбера
  • 2.4 Эйлер– Уравнения Лагранжа и принцип Гамильтона
  • 2.5 Множители и ограничения Лагранжа
• 3 Свойства лагранжиана
  • 3.1 Неединственность
  • 3.2 Инвариантность относительно точечных преобразований
  • 3.3 Циклические координаты и сохраняющиеся импульсы
  • 3.4 Энергия
    • 3.4.1 Определение
    • 3.4.2 Инвариантность относительно преобразований координат
    • 3.4.3 Сохранение
    • 3.4.4 Кинетическая и потенциальная энергия
  • 3.5 Механическое подобие
  • 3.6 Взаимодействующие частицы
• 4 Примеры
  • 4.1 Консервативная сила
    • 4.1.1 Декартовые координаты
    • 4.1.2 Полярные координаты в 2d и 3d
  • 4.2 Маятник на подвижной опоре
  • 4.3 Задача двухчастичной центральной силы
  • 4.4 Электромагнетизм
• 5 Расширения для включения неконсервативных сил
• 6 Другие контексты и формулировки
  • 6.1 Альтернативные формулировки классическая механика
  • 6.2 Формулировка импульсного пространства
  • 6.3 Высшие производные обобщенные системы
  • 6.4 Оптика
  • 6.5 Релятивистская формулировка
  • 6.6 Квантовая механика
  • 6.7 Классическая теория поля
  • 6.8 Теорема Нётер
• 7 См. Также
• 8 Сноски
• 9 Примечания
• 10 Ссылки
• 11 Дополнительная литература
• 12 Внешние ссылки

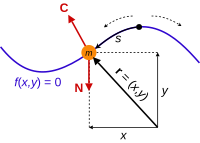Бусина вынуждена двигаться по проводу без трения. Проволока оказывает на бортик реактивную силу C, удерживая его на проволоке. Неограничивающая сила N в этом случае - это сила тяжести. Обратите внимание, что исходное положение провода может привести к различным движению. 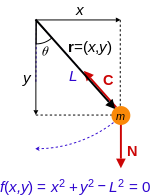Простой маятник. Шток жесткое, положение боба ограничено уравнением f (x, y) = 0, сила ограничения C представляет собой натяжение в штоке. Опять же, не ограничивающая сила N в данном случае - это сила тяжести.

Предположим, существует шарик, скользящий по проволоке, или качающийся простой маятник и т. Д. каждый из массивных объектов (бусинка, маятник и т. д.) как расчетные движения частиц с использованием механики Ньютона потребует решения своей изменяющейся во времени силы ограничения, необходимой для удержания частиц в ограниченное движение (сила реакции, оказываемая проволокой на борт, или натяжение в стержне маятника). Чтобы выбрать удобный набор независимых обобщенных координат, которые полностью используют альтернативное движение частиц, можно найти удобный набор независимых друг от друга обобщенных координат. Такой выбор избавляет от необходимости вводить ограничение в результирующую систему уравнений. Уравнений меньше, так как нельзя напрямую вычислять влияние ограничения на частицу в момент.

Для большого разнообразия физических систем, если размер и форма массивного объекта незначительно, рассматривать его как точечную частицу. Для системы из N точечных частиц с массами m1, m 2,..., m N каждая часть имеет вектор положения , обозначенных r1, r2,..., rN. декартовых координат часто бывает достаточно, поэтому r1= (x 1, y 1, z 1), r2= (x 2, y 2, z 2) и так далее. В трехмерное изображение каждый вектор положения требует трех координат для однозначного определения местоположения точки, поэтому существует 3N координат для однозначного определения системы координат. Все это точка точки в космосе, в которых можно найти частицы; общая точка в изображается r = (x, y, z). скорость каждая частица - это скорость, с которой частица движется по своему пути движения, и является производной по времени от ее положения, таким образом,

$v\; 1\; =\; dr\; 1\; dt,\; v\; 2\; =\; dr\; 2\; dt,\dots ,\; v\; N\; =\; dr\; N\; dt\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\; \_\; \{1\}\; =\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{r\}\; \_\; \{1\}\}\; \{dt\}\},\; \backslash \; mathbf\; \{v\}\; \_\; \{2\}\; =\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{r\}\; \_\; \{2\}\}\; \{dt\}\},\; \backslash \; ldots,\; \backslash \; mathbf\; \{v\}\; \_\; \{N\}\; =\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{r\; \}\; \_\; \{N\}\}\; \{dt\}\}\}$В механике Ньютона уравнения движения задаются законами Ньютона. Второй закон: "чистая сила равна массе, умноженной на ускорение ",$\sum \; F\; =\; md\; 2\; rdt\; 2\; \{\backslash \; displaystyle\; \backslash \; sum\; \backslash \; mathbf\; \{F\}\; =\; m\; \{\backslash \; frac\; \{d\; ^\; \{\; 2\}\; \backslash \; mathbf\; \{r\}\}\; \{dt\; ^\; \{2\}\}\}\}$классифицируемых частиц в 3 измерениях существует 3N обыкновенных дифференциальных уравнений второго порядка в положениях частиц,

Вместо сил в лагранжевой механике используется энергия в системе. Центральный параметр лагранжиан, функция, которая суммирует динамику всей системы в целом, лагранжиан имеет единицу. Любая функция, которая генерирует правильные уравнения движения в соответствии с физическими средствами, может быть принята как лагранжиан. Тем не менее, это возможно для построения общих выражений для больших классов приложений. частиц может быть определен как

$L\; =\; T\; -\; V\; \{\; \backslash \; displaystyle\; L\; =\; TV\}$

где

$T\; =\; 1\; 2\; \sum \; k\; =\; 1\; N\; mkvk\; 2\; \{\backslash \; displaystyle\; T\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\; \}\; m\_\; \{k\}\; v\_\; \{k\}\; ^\; \{2\}\}$

- полная кинетическая энергия системы, равная сумме Σ кинетических энергий частиц, а V - потенциальная энергия системы.

Кинетическая энергия - это энергия движения системы, а v k= vk· vk- это квадратная величина скорости, эквивалентная скалярному произведению скорости на себя. Кинетическая энергия является функцией только скоростей vk, а не положений rkили времени t, поэтому T = T (v1, v2,...).

потенциальная энергия системы энергии энергии между частями, то есть, сколько будет иметь одна часть из-за всех остальных и других внешних воздействий. Для консервативных сил (например, ньютоновской гравитации ) это функция только векторов положения частиц, поэтому V = V (r1, r2,...). Для тех неконсервативных сил, которые могут быть получены из соответствующих функций (например, электромагнитный потенциал ), скорость также появятся, V = V (r1, r2,..., v1, v2,...). Если есть какое-то внешнее поле или внешняя движущая сила, изменяющаяся со временем, поэтому будет меняться со временем, поэтому в большинстве случаев V = V (r1, r2,..., v1, v2,..., t).

Вышеупомянутая форма L не выполняется в релятивистской лагранжевой механике и должна быть заменена функция, совместимой со специальной или общей теорией относительности. Кроме того, для диссипативных сил вместе с L. должна быть введена другая функция.

Каждая из одной или нескольких подчиняться одному или нескольким голономным ограничениям ; такое ограничение описывается уравнением вида f (r, t) = 0. Если количество ограничений в системе равно C, то ограничение имеет уравнение, f 1(r, t) = 0, f 2(r, t) = 0,... f C(r, t) = 0, каждую из которых может распространяться к любой из частиц. Если части k подчиняется ограничению i, тогда f i(rk, t) = 0. В любой момент времени независимые частицы связаны друг с другом. Уравнения определяют допустимые пути, по которым частицы могут двигаться, но не то, где они находятся или как они быстро движутся в каждый момент времени. Неголономные связи зависят от скоростей частиц, ускорений или более высоких производных положений. Лагранжева механика может использовать только к системам, чьи связи, если они есть, все голономны. Три примера неголономных связей: когда уравнения отношения неинтегрируемы, когда связи имеют неравенства, или со сложными неконсервативными силами, такими как трение. Неголономные связи требуют специального рассмотрения, и, возможно, придется вернуться к механике Ньютона или использовать другие методы.

Если T или V или оба явно зависят от времени из-за изменяющихся во времени ограничений или воздействий, лагранжиан L (r1, r2,... v1, v2,... t) явно является временем- зависимый. Если ни потенциал, ни кинетическая энергия не зависит от времени, то лагранжиан L (r1, r2,... v1, v2,...) явно не зависит от времени. В любом случае лагранжиан всегда будет иметь неявную зависимость от времени обобщенные координаты.

С этими определениями уравнения Лагранжа первого рода являются

уравнениями Лагранжа (первого рода)

$\partial \; L\; \partial \; rk\; -\; ddt\; \partial \; L\; \partial \; р\; \dot{}\; К\; +\; \sum \; я\; знак\; равно\; 1\; С\; \lambda \; я\; \partial \; fi\; \partial \; rk\; знак\; равно\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\; \}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{r\}\}\}\; \_\; \{k\}\}\}\; +\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{\; C\}\; \backslash \; lambda\; \_\; \{i\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\_\; \{i\}\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\}\; =\; 0\}$

где k = 1, 2,..., N обозначает частицы, существует множитель Лагранжа λiдля каждого уравнения связи f i, и

$\partial \; \partial \; rk\; \equiv \; (\partial \; \partial \; xk,\; \partial \; \partial \; yk,\; \partial \; \partial \; zk),\; \partial \; \partial \; р\; \dot{}\; К\; \equiv \; (\partial \; \partial \; Икс\; \dot{}\; К,\; \partial \; \partial \; Y\; \dot{}\; К,\; \partial \; \partial \; Z\; \dot{}\; K)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\}\; \backslash \; Equiv\; \backslash \; слева\; (\{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; x\_\; \{k\}\}\},\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; y\_\; \{k\}\}\},\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; z\_\; \{k\}\; \}\}\; \backslash \; right)\; \backslash ,,\; \backslash \; quad\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{r\}\}\}\; \_\; \{k\}\}\}\; \backslash \; Equiv\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{x\}\}\; \_\; \{k\}\}\},\; \{\backslash \; frac\; \{\backslash \; parti\; al\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\; y\}\}\; \_\; \{k\}\}\},\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{z\}\}\; \_\; \{k\}\}\}\; \backslash \; right)\}$

каждое сокращение для времени частных производных ∂ / ∂ по указанным переменным (не производной по всему вектору). Каждая точка является сокращением для производной по времени. Эта процедура увеличивает количество решаемых уравнений по сравнению с законами Ньютона с 3N до 3N + C, поскольку существует 3N связанных между собой уравнений второго порядка в координатах положения и множителях, а также C уравнений ограничений. Однако при решении вместе с координатами частиц частицы могут дать информацию о силах связи. Координаты не нужно исключать пути решения связи.

В лагранжиане все координаты положения и компоненты скорости являются независимыми переменными, и производные лагранжиана берутся по ним отдельно в соответствии с обычными правилами дифференцирования (например, производная L по компоненту z-скорости частицы 2, v z2 = dz 2 / dt, это всего лишь; никаких неудобных цепных правил или полные производные необходимо использовать, чтобы связать компонент скорости с пространственной координатой z 2).

В каждом уравнении ограничения одна координата избыточной, потому что она определяется из двух других. Таким образом, независимым образом равно n = 3N - C.Мы можем преобразовать каждый вектор положения в общий набор n обобщенных координат, которые удобно записать как n q = (q 1, q 2,... q n), выражая каждый вектор положения и, следовательно, координаты положения, как функции обобщенных координат и времени,

$rk\; =\; rk\; (q,\; t)\; =\; (xk\; (q,\; t),\; yk\; (q,\; t),\; zk\; (q,\; t),\; t).\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\; =\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\; (\backslash \; mathbf\; \{q\},\; t)\; =\; (x\_\; \{k\}\; (\backslash \; mathbf\; \{q\},\; t),\; y\_\; \{k\; \}\; (\backslash \; mathbf\; \{q\},\; t),\; z\_\; \{k\}\; (\backslash \; mathbf\; \{q\},\; t),\; t)\; \backslash ,.\}$

Вектор q - это точка в конфигурационное пространство системы. Производные по времени от обобщенных координат называются обобщенными скоростями и для каждой частицы преобразование ее момента времени, ее положения по времени, составляет

$q\; \dot{}\; j\; =\; dqjdt,\; vk\; =\; \sum \; j\; =\; 1\; n\; \partial \; rk\; \partial \; qjq\; \dot{}\; j\; +\; \partial \; rk\; \partial \; т.\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{q\}\}\; \_\; \{j\}\; =\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; q\_\; \{j\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \backslash ,,\; \backslash \; quad\; \backslash \; mathbf\; \{v\}\; \_\; \{\; k\}\; =\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\; \{\backslash \; partial\; q\_\; \{j\}\}\}\; \{\backslash \; dot\; \{q\}\}\; \_\; \{j\; \}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\; \{\backslash \; partial\; t\}\}\; \backslash ,.\}$

Учитывая это vk, кинетическая энергия в обобщенных координатах зависит от обобщенных скоростей, обобщенных координат и время, если наклон зависит от времени из-за изменяющихся во времени ограничений, поэтому T = T (q, d q / dt, t).

С этими определениями уравнения Эйлера - Лагранжа или уравнения Лагранжа второго рода

уравнения Лагранжа (второго рода)

$ddt\; (\partial \; L\; \partial \; q\; \dot{}\; j)\; =\; \partial \; L\; \partial \; qj\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{j\}\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; q\_\; \{j\}\}\}\}$

- математические результаты из вариационное исчисление, которое также может быть использовано в механике. Подстановка в лагранжиан L (q, d q / dt, t) дает уравнения движения системы. Количество уравнений уменьшилось по сравнению с механикой Ньютона, с 3N до n = 3N - C дифференциальных уравнений второго порядка в общих координатах. Эти уравнения вообще не включают в себя следующие силы связи.

Хотя уравнения включают в себя частные производные результаты, частных производных по-прежнему являются обыкновенными дифференциальными уравнениями в координатах положения частиц. полная производная по времени, обозначенное d / dt, включает часто неявное дифференцирование. Оба уравнения линейны по лагранжиану, но, как правило, будут нелинейными связанными уравнениями по координатам.

Законы Ньютона

Исаак Ньютон (1642–1727)

Для простоты законов Ньютона можно проиллюстрировать для одной частицы без особой потери общность (для системы из N частиц все эти уравнения применимы к каждой частице в системе). Уравнение движения для частиц массы m - это второй закон Ньютона 1687 года, в современной векторной записи

$F\; =\; ma,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; =\; m\; \backslash \; mathbf\; \{\; a\}\; \backslash ,,\}$

где a - его ускорение, а F - результирующая сила, действующая на него. В трех пространственных измерениях это система трех связанных обыкновенных дифференциальных уравнений второго порядка , которые необходимо решить, поскольку в этом векторном уравнении есть три компонента. Решения заданного положения r частицы в момент времени t, при условии начальных условий из r и v, когда t = 0.

Законы Ньютона легко использовать в декартовых координатах, но декартовые координаты не всегда удобны, а для других систем координат уравнения могут стать сложными. В наборе криволинейных координат ξ= (ξ, ξ, ξ) закон в обозначении тензорного индекса является «лагранжевой формой»

$F\; a\; =\; m\; (d\; 2\; \xi \; adt\; 2\; +\; \Gamma \; abcd\; \xi \; bdtd\; \xi \; cdt)\; =\; gak\; (ddt\; \partial \; T\; \partial \; \xi \; \dot{}\; K\; -\; \partial \; T\; \partial \; \xi \; k),\; \xi \; \dot{}\; a\; \equiv \; d\; \xi \; adt,\; \{\backslash \; displaystyle\; F\; ^\; \{a\}\; =\; m\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; ^\; \{2\}\; \backslash \; xi\; ^\; \{a\}\}\; \{\backslash \; mathrm\; \{d\}\; t\; ^\; \{2\}\}\}\; +\; \backslash \; Gamma\; ^\; \{a\}\; \{\}\; \_\; \{bc\}\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; \backslash \; xi\; ^\; \{b\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; \backslash \; xi\; ^\; \{c\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \backslash \; right)\; =\; g\; ^\; \{ak\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; T\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; xi\}\}\; ^\; \{k\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; T\}\; \{\backslash \; partial\; \backslash \; xi\; ^\; \{k\}\}\}\; \backslash \; right)\; \backslash ,,\; \backslash \; quad\; \{\backslash \; dot\; \{\backslash \; xi\}\}\; ^\; \{a\}\; \backslash \; Equiv\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; \backslash \; xi\; ^\; \{a\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \backslash ,,\}$

где F - ath контравариантные компоненты результирующей силы, действующей на частицу, Γ bc - символы Кристоффеля второго рода,

$T\; =\; 1\; 2\; mgbcd\; \xi \; bdtd\; \xi \; cdt,\; \{\backslash \; displaystyle\; T\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; mg\_\; \{\; bc\}\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; \backslash \; xi\; ^\; \{b\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; \backslash \; xi\; ^\; \{c\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \backslash ,,\}$

- кинетическая энергия частицы, а g bc - ковариантные компоненты метрический тензор криволинейной системы координат. Все индексы a, b, c принимают значения 1, 2, 3. Криволинейные координаты не то же самое, что обобщенные координаты.

Приведение закона Ньютона в такую ​​форму может показаться чрезмерным усложнением, но есть преимущества. Компоненты ускорения в терминах символов Кристоффеля можно избежать, вычислив вместо этого производные кинетической энергии. Если на частицу не действует равнодействующая сила, F= 0, она не ускоряется, а движется с постоянной скоростью по прямой. Математически решения дифференциального уравнения - это геодезические, кривые экстремальной длины между двумя точками в пространстве (они могут оказаться минимальными, поэтому это кратчайшие пути, но это не обязательно). В плоском трехмерном реальном пространстве геодезические - это просто прямые линии. Итак, для свободной частицы второй закон Ньютона совпадает с уравнением геодезических, и состояния свободных частиц следуют геодезическим, экстремальным траекториям, по которым они могут двигаться. Если на частицу действуют силы, F≠ 0, частица ускоряется из-за сил, действующих на нее, и отклоняется от геодезических, если бы она была свободна. При соответствующем расширении величин, приведенных здесь в плоскомпространственное пространство до 4d искривленного пространства-времени, вышеуказанная форма закона Ньютона также переносится в общей теорию относительности Эйнштейна , и в этом случае частицы следуют геодезическим в искривленном пространстве -времени, которые больше не являются «прямыми линиями» в обычном смысле.

Однако нам все еще необходимо знать полную равнодействующую силу F, действующую на части, которая, в свою очередь, требует результирующей силы без ограничения N плюс результирующая сила ограничения C,

$F\; =\; C\; +\; N.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; =\; \backslash \; mathbf\; \{C\}\; +\; \backslash \; mathbf\; \{N\}\; \backslash ,.\}$

Силы ограничения могут быть сложными, поскольку они обычно зависят от времени. Кроме того, при наличии ограничений криволинейные координаты не связаны с независимыми ограничениями.

Силы связи могут быть либо исключены из соотношений движения, так что остаются только силы, либо включены указанные связи в уравнения движения.

Принцип Д'Аламбера

Жан Даламбер (1717–1783) 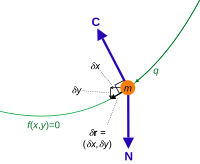Одна степень свободы. 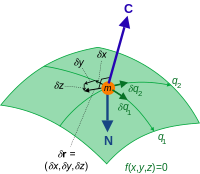Две степени свободы. Ограничивающая сила C и виртуальное смещение δ r для частиц массы m, ограниченной кривой. Результирующая сила без ограничения N.

. Фундаментальный результат в аналитической механике - это принцип Д'Аламбера, введенный в 1708 году Жаком Бернулли для понимания статическое равновесие, разработанное Даламбером в 1743 году для решения динамических задач. Принцип утверждает, что для N частиц виртуальная работа, есть работа вдоль виртуального ущерба, δ rk, равна нулю

$\sum \; k\; =\; 1\; N\; (N\; k\; +\; C\; k\; -\; mkak)\; \cdot \; \delta \; rk\; =\; 0.\; \{\backslash \; Displaystyle\; \backslash \; сумма\; \_\; \{к\; =\; 1\}\; ^\; \{N\}\; (\backslash \; mathbf\; \{N\}\; \_\; \{k\}\; +\; \backslash \; mathbf\; \{C\}\; \_\; \{k\}\; -m\_\; \{k\}\; \backslash \; mathbf\; \{a\}\; \_\; \{k\})\; \backslash \; cdot\; \backslash \; delta\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\; =\; 0\; \backslash ,.\}$

виртуальные с ущербом, δ rk, по определению, являются бесконечно малыми изменениями в конфигурации системы в соответствии с силами связи, действующие на систему в момент времени, т. е. таким образом, что силы связи ограниченное движение. Это не то же самое, что фактические факторы ущерба в системе, которые вызваны результирующими ограничивающими и не ограничивающими силами, действующими на частицу для ее ускорения и перемещения. Виртуальная работа - это работа, выполняемая вдоль сечения для любой силы (ограничения или ограничения ограничений).

Силы ограничения, действующей на систему, равна нулю;

$\sum \; k\; =\; 1\; NC\; k\; \cdot \; \delta \; рк\; знак\; равно\; 0,\; \{\backslash \; Displaystyle\; \backslash \; сумма\; \_\; \{к\; =\; 1\}\; ^\; \{N\}\; \backslash \; mathbf\; \{C\}\; \_\; \{k\}\; \backslash \; cdot\; \backslash \; delta\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\; =\; 0\; \backslash ,,\}$

, так что

$\sum \; k\; =\; 1\; N\; (N\; k\; -\; mkak)\; \cdot \; \delta \; rk\; =\; 0.\; \{\backslash \; Displaystyle\; \backslash \; сумма\; \_\; \{к\; =\; 1\}\; ^\; \{N\}\; (\backslash \; mathbf\; \{N\}\; \_\; \{k\}\; -m\_\; \{k\}\; \backslash \; mathbf\; \{a\}\; \_\; \{k\})\; \backslash \; cdot\; \backslash \; delta\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\; =\; 0\; \backslash ,.\}$

Таким образом, принцип Даламбера позволяет нам сосредоточиться только на приложенных силах, не являющихся связями, и исключить эти силы в уравнениях движения. Показанная форма также не зависит от выбора координат. Его нельзя использовать для создания системы координат в произвольной системе координат, поскольку это не позволяет нам установить отдельные слагаемые значения 0. сумма будет равна 0 тогда и только тогда, когда отдельные слагаемые равны 0. Установка каждого из слагаемых на 0 в конечном итоге даст нам наши отдельные уравнения движения.

Уравнения движения по принципу Даламбера

Если есть ограничения на частицу k, то есть, поскольку координаты позиции rk= (x k, y k, z k) связаны между собой уравнением связи, так же как и перемещение виртуальных перемещений δrk= (δx k, δy k, δz k). Мы можем избежать упрощенных координат с δ rkпутем преобразования в виртуальные координаты в обобщенных координатах. Они связаны в той же форме, что и полный дифференциал,

$\delta \; r\; k\; =\; \sum \; j\; =\; 1\; n\; \partial \; r\; k\; \partial \; q\; j\; \delta \; q\; j.\; \{\backslash \; displaystyle\; \backslash \; delta\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\; =\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\; \{\backslash \; partial\; q\_\; \{j\}\; \}\}\; \backslash \; delta\; q\_\; \{j\}\; \backslash ,.\}$

Не существует частной производной по времени по времени, умноженной на приращение времени, поскольку это виртуальное смещение, одно вдоль ограничений в момент времени.

Первый член в приведенном выше принципе Даламбера представляет собой виртуальную работу, совершаемую силами без ограничений Nkвдоль виртуальных смещений δ rk, и может без общих потерь преобразоваться в обобщенные аналоги по определению обобщенными сил

$Q\; J\; знак\; равно\; \sum \; К\; знак\; равно\; 1\; NN\; К\; \cdot \; \partial \; rk\; \partial \; qj,\; \{\backslash \; displaystyle\; Q\_\; \{j\}\; =\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\}\; \backslash \; mathbf\; \{N\}\; \_\; \{k\}\; \backslash \; cdot\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\; \{\backslash \; partial\; q\_\; \{j\}\}\}\; \backslash ,,\}$

так что

$\sum \; k\; =\; 1\; NN\; k\; \cdot \; \delta \; rk\; =\; \sum \; k\; =\; 1\; NN\; k\; \cdot \; \sum \; j\; знак\; равно\; 1\; n\; \partial \; rk\; \partial \; qj\; \delta \; qj\; =\; \sum \; j\; =\; 1\; n\; Q\; j\; \delta \; qj.\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\}\; \backslash \; mathbf\; \{N\}\; \_\; \{k\}\; \backslash \; cdot\; \backslash \; delta\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\; =\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\}\; \backslash \; mathbf\; \{N\}\; \_\; \{k\}\; \backslash \; cdot\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\; \{\backslash \; partial\; q\_\; \{j\}\}\}\; \backslash \; delta\; q\_\; \{j\}\; =\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; Q\_\; \{j\}\; \backslash \; delta\; q\_\; \{j\}\; \backslash ,.\}$

Это половина преобразования в обобщенные координаты. Осталось преобразовать ускорения в обобщенные координаты, что не сразу очевидно. Вспоминая форму Лагранжа второго закона Ньютона, можно найти частные производные кинетической энергии по обобщенным координатам и скоростям, чтобы получить желаемый результат;

$k\; =\; 1\; N\; mkak\; \cdot \; \partial \; rk\; \partial \; qj\; =\; ddt\; \partial \; Т\; \partial \; q\; \dot{}\; j\; -\; \partial \; T\; \partial \; qj.\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\}\; m\_\; \{k\}\; \backslash \; mathbf\; \{a\}\; \_\; \{k\}\; \backslash \; cdot\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\; \{\backslash \; partial\; q\_\; \{j\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; T\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{j\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; T\}\; \{\backslash \; partial\; q\_\; \{j\}\}\}\; \backslash ,.\}$

Теперь принцип Д'Аламбера находится в обобщенных координатах, как и требуется,

$\sum \; j\; =\; 1\; n\; [Q\; j\; -\; (ddt\; \partial \; T\; \partial \; q\; \dot{}\; j\; -\; \partial \; T\; \partial \; qj)]\; \delta \; qj\; =\; 0,\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; \backslash \; left\; [Q\_\; \{j\}\; -\; \backslash \; left\; (\{\backslash \; frac\; \{\; \backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; T\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{j\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; T\}\; \{\backslash \; частичный\; q\_\; \{j\}\}\}\; \backslash \; right)\; \backslash \; right]\; \backslash \; delta\; q\_\; \{j\}\; =\; 0\; \backslash ,,\}$

, и поскольку эти виртуальные с ущербом δq j независимы и не равны нулю, коэффициенты можно приравнять к нулю, что приводит к уравнениям Лагранжа или обобщенным уравнениям движения,

$Q\; j\; =\; ddt\; \partial \; T\; \partial \; q\; \dot{}\; j\; -\; \partial \; T\; \partial \; qj\; \{\backslash \; displaystyle\; Q\_\; \{j\}\; =\; \{\backslash \; гидроразрыв\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; T\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{j\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; T\}\; \{\backslash \; partial\; q\_\; \{j\}\}\}\}$

Эти уравнения a re эквивалентно законам Ньютона для сил, не являющихся связями. Обобщенные силы в этом уравнении выводятся только из сил, не связанных с ограничениями - силы связи исключены из принципа Даламбера, и их нет необходимости находить. Обобщенные силы могут быть неконсервативными, если они удовлетворяют принципу Даламбера.

Уравнения Эйлера - Лагранжа и принцип Гамильтона

По мере развития системы q прокладывает путь через конфигурационное пространство (показаны только некоторые). Путь, пройденный системой (красный), имеет стационарное действие (δS = 0) при небольших изменениях конфигурации системы (δ q).

Для неконсервативной силы, которая зависит от скорости, может быть возможно найти функцию потенциальной энергии V, которая зависит от положения и скорости. Если обобщенные силы Q я могут быть получены из дополнительного V, такое что

$Q\; j\; =\; ddt\; \partial \; V\; \partial \; q\; \dot{}\; j\; -\; \partial \; V\; \partial \; qj,\; \{\backslash \; displaystyle\; Q\_\; \{j\}\; =\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{j\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; q\_\; \{j\}\}\}\; \backslash ,,\}$

приравнивая к уравнениям Лагранжа и расчетя лагранжиан как L = T - V, получаем уравнения Лагранжа второго вида или уравнения Эйлера - Лагранжа движение

$\partial \; L\; \partial \; qj\; -\; ddt\; \partial \; L\; \partial \; q\; \dot{}\; j\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; q\_\; \{j\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\; \}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{j\}\}\}\; =\; 0\; \backslash ,.\}$

Однако уравнения Эйлера - Лагранжа мог утвердите только неконсервативные пять сил, если можно найти потенциал, как показано. Это не всегда возможно для неконсервативных сил, и уравнения Лагранжа не включает никаких никаких сил, а только обобщенные силы; поэтому они более общие, чем уравнения Эйлера - Лагранжа.

Уравнения Эйлера - Лагранжа также следуют из вариационного исчисления. Вариация лагранжиана

$\delta \; L\; =\; \sum \; j\; =\; 1\; n\; (\partial \; L\; \partial \; qj\; \delta \; qj\; +\; \partial \; L\; \partial \; q\; \dot{}\; j\; \delta \; q\; \dot{}\; j),\; \delta \; q\; \dot{}\; j\; \equiv \; \delta \; dqjdt\; \equiv \; d\; (\delta \; qj)\; dt,\; \{\backslash \; displaystyle\; \backslash \; delta\; L\; =\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; q\_\; \{j\}\}\}\; \backslash \; delta\; q\_\; \{j\}\; +\; \{\backslash \; frac\; \{\backslash \; partial)\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{j\}\}\}\; \backslash \; delta\; \{\backslash \; dot\; \{q\}\}\; \_\; \{j\}\; \backslash \; right)\; \backslash ,,\; \backslash \; quad\; \backslash \; delta\; \{\backslash \; dot\; \{q\}\}\; \_\; \{\; j\}\; \backslash \; Equiv\; \backslash \; delta\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; q\_\; \{j\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \backslash \; Equiv\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; (\backslash \; delta\; q\_\; \{j\})\}\; \{\; \backslash \; mathrm\; \{d\}\; t\}\}\; \backslash ,,\}$

который имеет форму, аналогичную полному дифференциалу L, но виртуальный ущерб и их производные по времени заменяют дифференциалы, и там нет приращения времени в соответствии с определением виртуальных перемещений. интегрирование по частям по времени может передать производную по времени δq j в ∂L / ∂ (dq j / dt) в процессе заменяя d (δq j) / dt на δq j, что позволяет факторизовать независимый виртуальный ущерб из производных лагранжиана,

$∫ t 1 t 2 δ L dt = ∫ t 1 t 2 ∑ j = 1 n ( ∂ L ∂ qj δ qj + ddt (∂ L ∂ q ˙ j δ qj) - ddt ∂ L ∂ q ˙ j δ qj) dt = ∑ j = 1 n [∂ L ∂ q ˙ j δ qj] t 1 t 2 + ∫ t 1 t 2 ∑ j знак равно 1 n (∂ L ∂ qj - ddt ∂ L ∂ qj) δ qjdt. {\ displaystyle \ int _ {t_ {1}} ^ {t_ {2}} \ delta L \, \ mathrm {d} t = \ int _ {t_ {1}} ^ {t_ {2}} \ sum _ {j = 1} ^ {n} \ left ({\ frac {\ partial L} {\ partial q_ {j}}} \ delta q_ {j} + {\ frac {\ mathrm {d}} {\ mathrm { d} t}} \ left ({\ frac {\ partial L} {\ partial {\ dot {q}} _ {j}}} \ delta q_ {j} \ right) - {\ frac {\ mathrm {d }} {\ mathrm {d} t}} {\ frac {\ partial L} {\ partial {\ dot {q}} _ {j}}} \ delta q_ {j} \ right) \, \ mathrm {d } t \, = \ sum _ {j = 1} ^ {n} \ left [{\ frac {\ partial L} {\ partial {\ dot {q}} _ {j}}} \ delta q_ {j} \ right] _ {t_ {1}} ^ {t_ {2}} + \ int _ {t_ {1}} ^ {t_ {2}} \ sum _ {j = 1} ^ {n} \ left ({ \ frac {\ partial L} {\ partial q_ {j}}} - {\ frac {\ mathrm {d}} {\ mathrm {d} t}} {\ frac {\ partial L} {\ partial {\ dot {q}} _ {j}}} \ right) \ delta q_ {j} \, \ mathrm {d} t \,.}$

Теперь, если условие δq j(t1) = δq j(t2) = 0 выполняется для всех j, неинтегрированные члены равны нулю. Если вдобавок весь интеграл по времени от δL равен нулю, то, поскольку δq j независимы, и единственный способ обнулить определенный интеграл - это если подынтегральное выражение равно нулю, каждый из коэффициентов δq j также должен быть равен нулю. Тогда получаем уравнения движения. Это можно резюмировать с помощью принципа Гамильтона ;

$\int \; t\; 1\; t\; 2\; \delta \; L\; d\; t\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{t\_\; \{1\}\}\; ^\; \{t\_\; \{2\}\}\; \backslash \; delta\; L\; \backslash ,\; \backslash \; mathrm\; \{d\}\; t\; =\; 0\; \backslash ,.\}$

Интеграл по времени от лагранжиана - это еще одна величина, называемая действие, определенное как

$S\; =\; \int \; t\; 1\; t\; 2\; L\; dt,\; \{\backslash \; displaystyle\; S\; =\; \backslash \; int\; \_\; \{t\_\; \{1\}\}\; ^\; \{t\_\; \{2\}\}\; L\; \backslash ,\; \backslash \; mathrm\; \{\; d\}\; t\; \backslash ,,\}$

, который является функционалом ; он принимает функцию Лагранжа все время между t 1 и t 2 и возвращает скалярное значение. Его размеры такие же, как [угловой момент ], [энергия] · [время] или [длина] · [импульс]. С этим определением принцип Гамильтона

$\delta \; S\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; delta\; S\; =\; 0\; \backslash ,.\}$

Таким образом, вместо того, чтобы думать о частицах, ускоряющихся в ответ на приложенные силы, можно подумать о том, что они выбирают путь стационарным действием с конечными точками пути в конфигурационном пространстве фиксируется в начальное и конечное время. Принцип Гамильтона иногда называют принципом наименьшего действия, однако функционал действия должен быть только стационарным, не обязательно максимальным или минимальным значением. Любая вариация функционала дает увеличение функционального интеграла действия.

Исторически идея найти кратчайший путь, по которому частица может пройти при наличии силы, послужила причиной первых применений вариационного исчисления к механическим проблемам, таким как проблема Брахистохрона. решено Жаном Бернулли в 1696 году, а также Лейбницем, Даниэлем Бернулли, L'Hôpital примерно в то же время, и Ньютон в следующем году. Сам Ньютон мыслил в духе вариационного исчисления, но не опубликовал. Эти идеи, в свою очередь, приводят к вариационным принципам механики, Ферма, Мопертюи, Эйлеру, Гамильтону, и другие.

Принцип Гамильтона может быть применен к неголономным связям, если уравнения связи могут быть представлены в определенной форме, линейной комбинации дифференциалов первого порядка по координатам. Полученное уравнение связи можно преобразовать в дифференциальное уравнение первого порядка. Здесь это не приводится.

Множители и ограничения Лагранжа

Лагранжиан L можно изменять в декартовых координатах rkдля N частиц,

$\int \; t\; 1\; t\; 2\; \sum \; k\; =\; 1\; N\; (\partial \; L\; \partial \; rk\; -\; ddt\; \partial \; L\; \partial \; r\; \dot{}\; k)\; \cdot \; \delta \; rkdt\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{t\_\; \{1\}\}\; ^\; \{t\_\; \{2\}\}\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\})\; \_\; \{k\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{r\}\}\}\; \_\; \{\; k\}\}\}\; \backslash \; right)\; \backslash \; cdot\; \backslash \; delta\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\; \backslash ,\; \backslash \; mathrm\; \{d\}\; t\; =\; 0\; \backslash ,.\}$

Принцип Гамильтона остается в силе, даже если координаты L выражены в не являются независимыми, здесь rk, но ограничения по-прежнему считаются голономными. Как всегда, конечные точки фиксированы δ rk(t1) = δ rk(t2) = 0 для всех k. Что нельзя сделать, так это просто приравнять коэффициенты δ rkк нулю, потому что δ rkне являются независимыми. Вместо этого можно использовать метод множителей Лагранжа для включения ограничений. Умножение каждого уравнения ограничения f i(rk, t) = 0 на множитель Лагранжа λ i для i = 1, 2,..., C и добавление результатов к исходному лагранжиану дает новый Лагранжиан

$L\; \prime \; =\; L\; (r\; 1,\; r\; 2,\dots ,\; r\; \dot{}\; 1,\; r\; \dot{}\; 2,\dots ,\; t)\; +\; \sum \; i\; =\; 1\; C\; \lambda \; i\; (t)\; fi\; (rk,\; t).\; \{\backslash \; displaystyle\; L\; \text{'}=\; L\; (\backslash \; mathbf\; \{r\}\; \_\; \{1\},\; \backslash \; mathbf\; \{r\}\; \_\; \{2\},\; \backslash \; ldots,\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{r\}\}\}\; \_\; \{1\},\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{r\}\}\}\; \_\; \{2\},\; \backslash \; ldots,\; t)\; +\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{C\}\; \backslash \; lambda\; \_\; \{i\}\; (t)\; f\_\; \{i\}\; (\backslash \; mathbf\; \{r\}\; \_\; \{k\},\; t)\; \backslash ,.\}$

Множители Лагранжа - это произвольные функции времени t, но не функции координат rk, поэтому множители приравнены к координатам положения. Варьируя этот новый лагранжиан и интегрируя по времени, получаем

$\int \; t\; 1\; t\; 2\; \delta \; L\; \prime \; dt\; =\; \int \; t\; 1\; t\; 2\; \sum \; k\; =\; 1\; N\; (\partial \; L\; \partial \; rk\; -\; ddt\; \partial \; L\; \partial \; r\; \dot{}\; k\; +\; \sum \; i\; =\; 1\; С\; \lambda \; я\; \partial \; fi\; \partial \; rk)\; \cdot \; \delta \; rkdt\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{t\_\; \{1\}\}\; ^\; \{t\_\; \{2\}\}\; \backslash \; delta\; L\; \text{'}\backslash \; mathrm\; \{d\}\; t\; =\; \backslash \; int\; \_\; \{t\_\; \{1\}\}\; ^\; \{t\_\; \{2\}\}\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\}\; -\; \{\; \backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{r\}\}\}\; \_\; \{k\}\}\}\; +\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{C\}\; \backslash \; lambda\; \_\; \{i\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\_\; \{i\}\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\}\; \backslash \; right)\; \backslash \; cdot\; \backslash \; delta\; \backslash \; mathbf\; \{\; r\}\; \_\; \{k\}\; \backslash ,\; \backslash \; mathrm\; \{d\}\; t\; =\; 0\; \backslash ,.\}$

Введенные множители могут быть найдены так, что коэффициенты δ rkравны нулю, даже если rkне являются независимыми. Уравнения движения следуют. Из предыдущего анализа принятия решения этого интеграла эквивалентно утверждению

$\partial \; L\; \prime \; \partial \; rk\; -\; ddt\; \partial \; L\; \prime \; \partial \; r\; \dot{}\; k\; =\; 0\; \Rightarrow \; \partial \; L\; \partial \; rk\; -\; ddt\; \partial \; L\; \partial \; r\; \dot{}\; k\; +\; \sum \; я\; знак\; равно\; 1\; С\; \lambda \; я\; \partial \; fi\; \partial \; rk\; знак\; равно\; 0,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; L\; \text{'}\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\; \}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; L\; \text{'}\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{r\}\}\}\; \_\; \{k\}\}\}\; =\; 0\; \backslash \; quad\; \backslash \; Rightarrow\; \backslash \; quad\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\; \backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{r\}\}\}\; \_\; \{k\}\}\}\; +\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{C\}\; \backslash \; lambda\; \_\; \{i\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\_\; \{i\}\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\}\; =\; 0\; \backslash ,,\}$

, которые представляют собой уравнениями Лагранжа первого рода . Кроме того, λ i уравнения Эйлера-Лагранжа для нового лагранжиана возвращают уравнения связи

$\partial \; L\; \prime \; \partial \; \lambda \; i\; -\; ddt\; \partial \; L\; \prime \; \partial \; \lambda \; \dot{}\; i\; =\; 0\; \Rightarrow \; fi\; (rk,\; t)\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; L\; \text{'}\}\; \{\backslash \; partial\; \backslash \; lambda\; \_\; \{i\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; L\; \text{'}\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; lambda\}\}\; \_\; \{i\}\}\}\; =\; 0\; \backslash \; quad\; \backslash \; Rightarrow\; \backslash \; quad\; f\_\; \{i\}\; (\backslash \; mathbf\; \{r\}\; \_\; \{k\},\; t)\; =\; 0\; \backslash ,.\; \}$

Для случая консервативной силы, заданной градиентой потенциальной энергии V, функция только координат rk, замена лагранжиана L = T - V дает

$\partial \; T\; \partial \; rk\; -\; ddt\; \partial \; T\; \partial \; р\; \dot{}\; К\; ⏟\; -\; FK\; +\; -\; \partial \; В\; \partial \; rk\; ⏟\; NK\; +\; \sum \; я\; знак\; равно\; 1\; C\; \lambda \; я\; \partial \; fi\; \partial \; rk\; =\; 0,\; \{\backslash \; displaystyle\; \backslash \; underbrace\; \{\{\backslash \; frac\; \{\backslash \; partial\; T\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; T\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{r\})\}\}\; \_\; \{k\}\}\}\; \_\; \{\; -\; \backslash \; mathbf\; \{F\}\; \_\; \{k\}\}\; +\; \backslash \; underbrace\; \{-\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\}\}\; \_\; \{\backslash \; mathbf\; \{N\}\; \_\; \{k\}\; \}\; +\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{C\}\; \backslash \; lambda\; \_\; \{i\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\_\; \{i\}\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{r\}\; \_\; \{k\}\}\}\; =\; 0\; \backslash ,,\; \}$

и идентифицирующая производная энергия как (отрицательные) равнодействующей силы, С k = ∑ я = 1 C λ я ∂ fi ∂ rk, {\ displaystyle \ mathbf {C} _ {k} = \ sum _ {i = 1} ^ {C} \ lambda _ {i} {\ frac {\ partial f_ {i}} {\ partial \ mathbf {r} _ {k}}} \,,}

, таким образом, давая сила ограничения явно в терминах уравнения св язи и множители Лагранжа.

Неединственность

Лагранжиан системы не уникален. Лагранжиан L можно умножить на ненулевую константу a, можно добавить произвольную константу b, и новый лагранжиан aL + b будет описывать точно то же движение, что и L. Если, кроме того, мы ограничимся, как мы делали выше, к траекториям $q\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{q\}\}$, ограниченным заданным временным интервалом $[t\; st,\; t\; fin]\; \{\backslash \; displaystyle\; [t\; \_\; \{\backslash \; text\; \{st\}\},\; t\; \_\; \{\backslash \; text\; \{fin\}\}]\}$и имеющие свои конечные точки $P\; st\; =\; q\; (t\; st)\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; text\; \{st\}\}\; =\; \backslash \; mathbf\; \{q\}\; (t\; \_\; \{\; \backslash \; text\; \{st\}\})\}$и $P\; fin\; =\; q\; (t\; fin)\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; text\; \{fin\}\}\; =\; \backslash \; mathbf\; \{q\}\; (t\; \_\; \{\backslash \; text\; \{fin\}\})\}$исправлено, тогда два лагранжиана, описывающие одну и ту же систему, могут отличаться «полной производной по времени» функции $f\; (q,\; t)\; \{\backslash \; displaystyle\; f\; (\backslash \; mathbf\; \{q\},\; t)\}$, т.е.

$L\; \prime \; (q,\; q\; \dot{},\; t)\; знак\; равно\; L\; (q,\; q\; \dot{},\; t)\; +\; df\; (q,\; t)\; dt,\; \{\backslash \; displaystyle\; L\; \text{'}(\backslash \; mathbf\; \{q\},\; \{\backslash \; dot\; \{\backslash \; mathbf)\; \{q\}\}\},\; t)\; =\; L\; (\backslash \; mathbf\; \{q\},\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\},\; t)\; +\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; f\; (\backslash \; mathbf\; \{q\},\; т)\}\; \{\backslash \; mathrm\; \{d\}\; t\}\},\}$

где $df\; (q,\; t)\; dt\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; f\; (\backslash \; mathbf\; \{q\},\; t)\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\}$- это сокращение от $\partial \; f\; (q,\; t)\; \partial \; t\; +\; \sum \; i\; \partial \; f\; (q,\; t)\; \partial \; qiq\; \dot{}\; i.\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \{\backslash \; frac\; \{\backslash \; partial\; f\; (\backslash \; mathbf\; \{q\},\; t)\}\; \{\backslash \; partial\; t\}\}\; +\; \backslash \; sum\; \_\; \{i\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\; (\backslash \; mathbf\; \{q\},\; t)\}\; \{\backslash \; partial\; q\_\; \{i\}\}\}\; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}.\}$

Оба лагранжиана $L\; \{\backslash \; displaystyle\; L\}$и $L\; \prime \; \{\backslash \; displaystyle\; L\; \text{'}\}$наши те же уравнения движения, соответствующие действия $S\; \{\backslash \; displaystyle\; S\}$и $S\; \prime \; \{\backslash \; displaystyle\; S\text{'}\}$связаны посредством

$S\; \prime \; [q]\; =\; \int \; t\; st\; t\; fin\; L\; \prime \; (q\; (t),\; q\; \dot{}\; (t),\; t)\; dt\; =\; \int \; t\; st\; t\; fin\; L\; (q\; (t),\; q\; \dot{}\; (\; t),\; t)\; dt\; +\; \int \; t\; st\; t\; fin\; df\; (q\; (t),\; t)\; dtdt\; =\; S\; [q]\; +\; f\; (P\; fin,\; t\; fin)\; -\; f\; (P\; st,\; t\; st),\; \{\; \backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; S\; \text{'}[\backslash \; mathbf\; \{q\}]\; =\; \backslash \; int\; \backslash \; limits\; \_\; \{t\; \_\; \{\backslash \; text\; \{st\}\}\}\; ^\; \{t\; \_\; \{\backslash \; text\; \{fin\}\}\}\; L\text{'}\; (\backslash \; mathbf\; \{q\}\; (t),\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\}\; (t),\; t)\; \backslash ,\; dt\; =\; \backslash \; int\; \backslash \; limits\; \_\; \{t\; \_\; \{\backslash \; text\; \{st\}\}\}\; ^\; \{t\; \_\; \{\; \backslash \; text\; \{fin\}\}\}\; L\; (\backslash \; mathbf\; \{q\}\; (t),\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\}\; (t),\; t)\; \backslash ,\; dt\; +\; \backslash \; int\; \_\; \{t\; \_\; \{\backslash \; text\; \{st\; \}\}\}\; ^\; \{t\; \_\; \{\backslash \; text\; \{fin\}\}\}\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; f\; (\backslash \; mathbf\; \{q\}\; (t),\; t)\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \backslash ,\; dt\; \backslash \backslash \; =\; S\; [\backslash \; mathbf\; \{q\}]\; +\; f\; (P\; \_\; \{\backslash \; text\; \{fin\}\},\; t\; \_\; \{\backslash \; text\; \{fin\}\})\; -\; f\; (P\; \_\; \{\backslash \; text\; \{st\}\},\; t\; \_\; \{\backslash \; text\; \{st\}\}),\; \backslash \; end\; \{align\}\}\}$

с двумя последними компонентами $f\; (P\; плавник,\; t\; плавник)\; \{\backslash \; Displaystyle\; f\; (P\; \_\; \{\backslash \; text\; \{fin\}\},\; t\; \_\; \{\backslash \; text\; \{fin\}\})\}$и $f\; (P\; st,\; t\; st)\; \{\; \backslash \; displaystyle\; f\; (P\; \_\; \{\backslash \; text\; \{st\}\},\; t\; \_\; \{\backslash \; text\; \{st\}\})\}$независимо от $q.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{q\}.\}$

Инвариантность относительно точечных преобразований

Учитывая набор обобщенных координат q, если мы изменим эти переменные на новый набор общих координат s согласно точечному преобразованию q= q(s, t) новый лагранжиан L ′ является функцией новых координат

$L\; (q\; (s,\; t),\; q\; \dot{}\; (s,\; s\; \dot{},\; t),\; t)\; знак\; равно\; L\; \text{'}(s,\; s\; \dot{},\; t),\; \{\backslash \; displaystyle\; L\; (\backslash \; mathbf\; \{q\}\; (\backslash \; mathbf\; \{s\},\; t),\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\}\; (\backslash \; mathbf\; \{s\},\; \{\backslash \; точка\; \{\backslash \; mathbf\; \{s\}\}\},\; t),\; t)\; =\; L\; \text{'}(\backslash \; mathbf\; \{s\},\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{s\}\}\},\; t)\; \backslash ,,\}$

и по цепному правиламу для частичного дифференцирования уравнения Лагранжа инвариантны относительно этого преобразования;

$ddt\; \partial \; L\; \prime \; \partial \; s\; \dot{}\; i\; =\; \partial \; L\; \prime \; \partial \; si.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; L\; \text{'}\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{s\}\}\; \_\; \{i\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\; \text{'}\}\; \{\backslash \; partial\; s\_\; \{i\}\}\}\; \backslash ,.\}$

Это может упростить уравнения движения.

Циклические координаты и сохраняющиеся моменты

Важным своим лагранжиана является то, что сохраняющиеся величины могут быть легко считаны из него. Обобщенный импульс, «канонически сопряженный» координаты q i, как определяется

$p\; i\; =\; \partial \; L\; \partial \; q\; \dot{}\; i.\; \{\backslash \; displaystyle\; p\_\; \{i\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}\}\}.\}$

Если лагранжиан L не зависит от некоторой координаты q i, из соотношений Эйлера - Лагранжа сразу следует, что

$p\; \dot{}\; i\; =\; ddt\; \partial \; L\; \partial \; q\; \dot{}\; i\; =\; \partial \; L\; \partial \; qi\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{p\}\}\; \_\; \{i\}\; =\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; q\_\; \{i\}\}\}\; =\; 0\; \backslash ,.\}$

и интегрирование показывает, что соответствующий импульс равен константе, сохраняющейся величине. Это частный случай теоремы Нётер. Такие координаты называются «циклическими» или «игнорируемыми».

Например, система может иметь лагранжиан

$L\; (r,\; \theta ,\; s\; \dot{},\; z\; \dot{},\; r\; \dot{},\; \theta \; \dot{},\; \varphi \; \dot{},\; t),\; \{\backslash \; displaystyle\; L\; (r,\; \backslash \; theta,\; \{\; \backslash \; dot\; \{s\}\},\; \{\backslash \; dot\; \{z\}\},\; \{\backslash \; dot\; \{r\}\},\; \{\backslash \; dot\; \{\backslash \; theta\}\},\; \{\backslash \; dot\; \{\backslash \; phi\}\},\; t)\; \backslash ,,\}$

где r и z - длина вдоль прямых линий, s - длина дуги вдоль некоторой кривой, а θ и φ - углы. Обратите внимание, что z, s и φ отсутствуют в лагранжиане, хотя их скорости отсутствуют. Тогда импульсы

$pz\; =\; \partial \; L\; \partial \; z\; \dot{},\; ps\; =\; \partial \; L\; \partial \; s\; \dot{},\; p\; \varphi \; =\; \partial \; L\; \partial \; \varphi \; \dot{},\; \{\backslash \; displaystyle\; p\_\; \{z\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\; \backslash \; dot\; \{z\}\}\}\}\; \backslash ,,\; \backslash \; quad\; p\_\; \{s\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{s\}\}\}\}\; \backslash ,,\; \backslash \; quad\; p\; \_\; \{\backslash \; phi\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; phi\}\}\}\}\; \backslash ,,\}$

- все сохраняющиеся величины. Единицы и характер обобщенного напряжения будут зависеть от электрических координат; в этом случае p z представляет собой поступательный импульс в направлении z, p s также является измеренным поступательным моментом вдоль кривой s, а p φ равен угловой момент в плоскости, в которой измеряется угол φ. Каким бы ни было движение системы, все координаты и скорости изменяются таким образом, что эти импульсы сохраняются.

Энергия

Определение

Для лагранжиана $L,\; \{\backslash \; displaystyle\; L,\}$энергия формы механической системы равна по определению,

$E\; знак\; равно\; \sum \; я\; знак\; равно\; 1\; nq\; \dot{}\; я\; \partial \; L\; \partial \; q\; \dot{}\; я\; -\; L.\; \{\backslash \; displaystyle\; E\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}\; \{\backslash \; frac\; \{\; \backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}\}\}\; -\; L.\}$

Инвариантность относительно преобразований координат

В каждый момент времени $t,\; \{\backslash \; displaystyle\; t,\}$энергия инвариантна относительно конфигурационного пространства изменение координат $q\; \to \; Q\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{q\}\; \backslash \; to\; \backslash \; mathbf\; \{Q\}\}$, т.е.

$E\; (q,\; q\; \dot{},\; t)\; =\; E\; (Q,\; Q\; \dot{},\; t).\; \{\backslash \; displaystyle\; E\; (\backslash \; mathbf\; \{q\},\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\},\; t)\; =\; E\; (\backslash \; mathbf\; \{Q\},\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{Q\}\}\},\; t).\}$

Помимо этого результата, приведенное ниже доказательство показывает, что при таком изменении координат производные $\partial \; L\; /\; \partial \; q\; \dot{}\; i\; \{\backslash \; displaystyle\; \backslash \; partial\; L\; /\; \backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}\}$изменяются как коэффициенты линейной формы.

Доказательство

Для преобразования координат $Q\; =\; F\; (q),\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{Q\}\; =\; F\; (\backslash \; mathbf\; \{q\}),\}$мы имеем $d\; Q\; =\; F\; *\; (q)\; dq,\; \{\backslash \; displaystyle\; d\; \backslash \; mathbf\; \{Q\}\; =\; F\; \_\; \{*\}\; (\backslash \; mathbf\; \{q\})\; d\; \backslash \; mathbf\; \{q\},\}$ где $F\; *\; (\; q)\; \{\backslash \; displaystyle\; F\; \_\; \{*\}\; (\backslash \; mathbf\; \{q\})\}$- это касательная карта пространство $\{\sum \; i\; =\; 1\; nq\; \dot{}\; i\; \cdot \; (\partial \; /\; \partial \; qi\; |\; q)\; |\; q\; \dot{}\; я\; \in \; R\}\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}\; \backslash \; cdot\; \backslash \; left\; (\backslash \; partial\; /\; \backslash \; partial\; q\_\; \{i\}\; \{\backslash \; Bigl\; |\}\; \_\; \{\backslash \; mathbf\; \{q\}\}\; \backslash \; right)\; \backslash \; \{\backslash \; biggl\; |\}\; \backslash \; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}\; \backslash \; in\; \backslash \; mathbb\; \{R\}\; \backslash \; right\; \backslash \}\}$ на векторное пространство $\{\sum \; i\; =\; 1\; n\; Q\; \dot{}\; i\; \cdot \; (\partial \; /\; \partial \; Q\; i\; |\; F\; (q))\; |\; Q\; \dot{}\; я\; \in \; R\},\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; dot\; \{Q\}\}\; \_\; \{i\}\; \backslash \; cdot\; \backslash \; left\; (\backslash \; partial\; /\; \backslash \; partial\; Q\_\; \{i\; \}\; \{\backslash \; Bigl\; |\}\; \_\; \{F\; (\backslash \; mathbf\; \{q\})\}\; \backslash \; right)\; \backslash \; \{\backslash \; biggl\; |\}\; \backslash \; \{\backslash \; dot\; \{Q\}\}\; \_\; \{i\}\; \backslash \; in\; \backslash \; mathbb\; \{R\}\; \backslash \; right\; \backslash \},\; \}$ и $F\; \ast \; (q)\; =\; (\partial \; F\; i\; /\; \partial \; qj\; |\; q)\; i,\; j\; =\; 1\; n\; \{\backslash \; displaystyle\; \backslash \; textstyle\; F\; \_\; \{*\}\; (\backslash \; mathbf\; \{q\})\; =\; \{\backslash \; bigl\; (\}\; \backslash \; partial\; F\_\; \{i\}\; /\; \backslash \; partial\; q\_\; \{j\}\; \{\backslash \; bigl\; |\}\; \_\; \{\backslash \; mathbf\; \{q\}\}\; \{\backslash \; bigr)\}\; \_\; \{i,\; j\; =\; 1\}\; ^\; \{n\}\}$ якобиан. В координатах $q\; \dot{}\; я\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}\}$и $Q\; \dot{}\; i,\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{Q\}\}\; \_\; \{i\; \},\}$предыдущая формула для $d\; Q\; \{\backslash \; displaystyle\; d\; \backslash \; mathbf\; \{Q\}\}$имеет вид $Q\; \dot{}\; =\; F\; \ast \; (q)\; q\; \dot{}.\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{Q\}\}\}\; =\; F\; \_\; \{*\}\; (\backslash \; mathbf\; \{q\})\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\}.\}$После дифференциации с участием продукт правило, $d\; Q\; \dot{}\; знак\; равно\; G\; (q,\; q\; \dot{})\; dq\; +\; F\; \ast \; (q)\; dq\; \dot{},\; \{\backslash \; displaystyle\; d\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{Q\}\}\}\; =\; G\; (\backslash \; mathbf\; \{q\; \},\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\})\; d\; \backslash \; mathbf\; \{q\}\; +\; F\; \_\; \{*\}\; (\backslash \; mathbf\; \{q\})\; d\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\},\}$ где $G (q, q ˙) dq = def d (F ∗ (q)) q ˙ = (∑ k = 1 n ∂ 2 F i ∂ qj ∂ qk | qdqk) i, j = 1 nq ˙ = (∑ j = 1 nq ˙ j ∑ k = 1 n ∂ 2 F i ∂ qj ∂ qk | qdqk) i = 1,…, n T = (∑ k = 1 ndqk ∑ j = 1 n ∂ 2 F i ∂ qj ∂ qk | qq ˙ j) i = 1,…, n T = (∑ j = 1 n ∂ 2 F i ∂ qj ∂ qk | qq ˙ j) i, k = 1 ndq. {\ displaystyle {\ begin {align} G (\ mathbf {q}, {\ dot {\ mathbf {q}}}) d \ mathbf {q} \, {\ stackrel {\ text {def}} {= }} \, d (F _ {*} (\ mathbf {q})) {\ dot {\ mathbf {q}}} = \ left (\ sum _ {k = 1} ^ {n} {\ frac { \ частичный ^ {2} F_ {i}} {\ partial q_ {j} \ partial q_ {k}}} {\ biggl |} _ {\ mathbf {q}} dq_ {k} \ right) _ {i, j = 1} ^ {n} {\ dot {\ mathbf {q}}} = \ left (\ sum _ {j = 1} ^ {n} {\ dot {q}} _ {j} \ sum _ { k = 1} ^ {n} {\ frac {\ partial ^ {2} F_ {i}} {\ partial q_ {j} \ partial q_ {k}}} {\ biggl |} _ {\ mathbf {q} } dq_ {k} \ right) _ {i = 1, \ ldots, n} ^ {T} \\ = \ left (\ sum _ {k = 1} ^ {n} dq_ {k} \ sum _ { j = 1} ^ {n} {\ frac {\ partial ^ {2} F_ {i}} {\ partial q_ {j} \ partial q_ {k}}} {\ biggl |} _ {\ mathbf {q} } {\ dot {q}} _ {j} \ right) _ {i = 1, \ ldots, n} ^ {T} = \ left (\ sum _ {j = 1} ^ {n} {\ frac { \ частичный ^ {2} F_ {i}} {\ partial q_ {j} \ partial q_ {k}}} {\ biggl |} _ {\ mathbf {q}} {\ dot {q}} _ {j} \ справа) _ {i, k = 1} ^ {n} d \ mathbf {q}. \ end {align}}}$ В векторных обозначениях $d\; L\; (Q,\; Q\; \dot{},\; t)\; =\; \partial \; L\; \partial \; Q\; d\; Q\; +\; \partial \; L\; \partial \; Q\; \dot{}\; d\; Q\; \dot{}\; +\; \partial \; L\; \partial \; tdt\; =\; (\partial \; L\; \partial \; QF\; \ast \; (q)\; +\; \partial \; L\; \partial \; Q\; \dot{}\; G\; (q,\; q\; \dot{}))\; dq\; +\; \partial \; L\; \partial \; Q\; \dot{}\; F\; \ast \; (q)\; dq\; \dot{}\; +\; \partial \; L\; \partial \; т.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; dL\; (\backslash \; mathbf\; \{Q\},\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{Q\}\}\},\; t)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{Q\}\}\; \}\; d\; \backslash \; mathbf\; \{Q\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{Q\}\}\}\}\}\; d\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{Q\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; частичное\; L\}\; \{\backslash \; partial\; t\}\}\; dt\; \backslash \backslash \; =\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{Q\}\}\}\; F\; \_\; \{*\}\; (\backslash \; mathbf\; \{q\})\; +\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{Q\}\}\}\}\}\; G\; (\backslash \; mathbf\; \{q\},\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\})\; \backslash \; right)\; d\; \backslash \; mathbf\; \{q\; \}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{Q\}\}\}\}\}\; F\; \_\; \{*\}\; (\backslash \; mathbf\; \{q\})\; d\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; t\}\}.\; \backslash \; end\; \{align\}\}\}$ С другой стороны, $d\; L\; (q,\; q\; \dot{},\; t)\; =\; \partial \; L\; \partial \; qdq\; +\; \partial \; L\; \partial \; q\; \dot{}\; dq\; \dot{}\; +\; \partial \; L\; \partial \; tdt.\; \{\backslash \; displaystyle\; dL\; (\backslash \; mathbf\; \{q\},\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\},\; t)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{q\}\}\}\; d\; \backslash \; mathbf\; \{q\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\}\}\}\; d\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; t\; \}\}\; dt.\}$ Ранее упоминалось, что лагранжианы не зависят от выбора координатного пространства, т.е. $L\; (Q,\; Q\; \dot{},\; t)\; =\; L\; (q,\; q\; \dot{},\; t).\; \{\backslash \; displaystyle\; L\; (\backslash \; mathbf\; \{Q\},\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{Q\}\}\},\; t)\; =\; L\; (\backslash \; mathbf\; \{q\},\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\},\; t).\}$Одно из следствий этого состоит в том, что $d\; L\; (Q,\; Q\; \dot{},\; t)\; =\; d\; L\; (q,\; q\; \dot{},\; t),\; \{\backslash \; displaystyle\; dL\; (\backslash \; mathbf\; \{Q\},\; \{\backslash \; точка\; \{\backslash \; mathbf\; \{Q\}\}\},\; t)\; =\; dL\; (\backslash \; mathbf\; \{q\},\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\},\; t),\}$и $\partial \; L\; \partial \; Q\; \dot{}\; F\; \ast \; (q)\; =\; \partial \; L\; \partial \; q\; \dot{}.\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{Q\}\}\}\}\}\; F\; \_\; \{*\}\; (\backslash \; mathbf\; \{q\})\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; частичное\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\}\}\}.\}$ Это демонстрирует, что для каждого $q,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{q\},\}$$q\; \dot{},\; \{\backslash \; displaystyle\; \{\; \backslash \; точка\; \{\backslash \; mathbf\; \{q\}\}\},\}$и $t,\; \{\backslash \; displaystyle\; t,\}$$\sum \; i\; =\; 1\; n\; \partial \; L\; \partial \; q\; \dot{}\; idq\; \dot{}\; i\; \{\backslash \; displaystyle\; \backslash \; стиль\; текста\; \backslash \; сумма\; \backslash \; пределы\; \_\; \{я\; =\; 1\}\; ^\; \{п\}\; \{\backslash \; гидроразрыва\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{я\}\}\}\; d\; \{\backslash \; dot\; \{q\}\}\; \_\; \{я\; \}\}$- четко определенная линейная форма, коэффициенты которой $\partial \; L\; \partial \; q\; \dot{}\; i\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{\; i\}\}\}\}$- контравариантные 1-тензоры. Применяя обе части уравнения к $q\; \dot{}\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\}\}$и используя приведенную выше формулу для $Q\; \dot{}\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{Q\}\}\}\}$дает $Q\; \dot{}\; \partial \; L\; \partial \; Q\; \dot{}\; =\; q\; \dot{}\; \partial \; L\; \partial \; q\; \dot{}.\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{Q\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{Q\}\}\}\}\}\; =\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\}\}\}.\}$ Инвариантность энергии $E\; \{\backslash \; displaystyle\; E\}$следует.

Сохранение

В лагранжой механике система замкнута тогда и только тогда, когда ее лагранжиан $L\; \{\backslash \; displaystyle\; L\}$явно не зависит от времени. Закон сохранения энергии утверждает, что энергия $E\; \{\backslash \; displaystyle\; E\}$замкнутой системы является интегралом движения.

Точнее, пусть $q\; =\; q\; (t)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{q\}\; =\; \backslash \; mathbf\; \{q\}\; (t)\}$быть экстремальным. (Другими словами, $q\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{q\}\}$удовлетворяет применению Эйлера-Лагранжа). Взяв полную производную по времени от $L\; \{\backslash \; displaystyle\; L\}$вдоль этой экстремали и используя уравнения EL, получаем

$-\; \partial \; L\; \partial \; t\; |\; q\; (t)\; =\; d\; d\; t\; [E\; |\; q\; (t)].\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; t\}\}\; \{\backslash \; biggl\; |\}\; \_\; \{\backslash \; mathbf\; \{q\}\; (t)\}\; =\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\; \}\; t\}\}\; \backslash \; left\; [E\; \{\backslash \; biggl\; |\}\; \_\; \{\backslash \; mathbf\; \{q\}\; (t)\}\; \backslash \; right].\}$

Если лагранжиан $L\; \{\backslash \; displaystyle\; L\}$не явно зависит от времени, то $\partial \; L\; /\; \partial \; t\; =\; 0,\; \{\backslash \; displaystyle\; \backslash \; partial\; L\; /\; \backslash \; partial\; t\; =\; 0,\}$поэтому $E\; \{\backslash \; displaystyle\; E\}$действительно является интегралом движения, что означает, что

$E\; (q\; (t),\; q\; \dot{}\; (t),\; t)\; =\; const.\; \{\backslash \; displaystyle\; E\; (\backslash \; mathbf\; \{q\}\; (t),\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{q\}\}\}\; (t),\; t)\; =\; \{\backslash \; text\; \{const\}\}.\}$

Следовательно, энергия сохраняется.

Кинетическая и потенциальная энергия

Также следует, что кинетическая энергия однородной функции степени 2 в общих скоростях. Если, кроме того, потенциал V является только функцией координат и не зависит от скоростей, то прямым вычислением или использованием теоремы Эйлера для однородных функций, что

$\sum \; i\; =\; 1\; nq\; \dot{}\; i\; \partial \; L\; \partial \; q\; \dot{}\; я\; знак\; равно\; \sum \; я\; знак\; равно\; 1\; nq\; \dot{}\; я\; \partial \; T\; \partial \; q\; \dot{}\; я\; =\; 2\; т.\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{я\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}\}\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}\; \{\backslash \; frac\; \{\backslash \; partial\; T\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}\}\}\; =\; 2T\; \backslash ,.\}$

При всех этих обстоятельствах константа

$E\; =\; T\; +\; V\; \{\backslash \; displaystyle\; E\; =\; T\; +\; V\}$

представляет собой полную энергию системы. Кинетическая и потенциальная энергия все еще изменяются по мере развития, но движение системы будет таким, что их сумма, полная энергия, будет постоянной системы. Это ценное упрощение, поскольку энергия E - это постоянная интегрированная интегрированная система, которая считается произвольной константой для задачи. В случае, если скорость или кинетическая энергия или и то, и другое зависит от времени, энергия не сохраняется.

Механическое подобие

Возможная потенциальная функция однородной функцией координат и не зависит от времени, и все положения положения находятся одной той же ненулевой константой α, rk′ знак равно α rk, так что

$V\; (\alpha \; r\; 1,\; \alpha \; r\; 2,\dots ,\; \alpha \; r\; N)\; =\; \alpha \; NV\; (r\; 1,\; r\; 2,\dots ,\; r\; N)\; \{\backslash \; displaystyle\; V\; (\backslash \; alpha\; \backslash \; mathbf\; \{r\}\; \_\; \{1\},\; \backslash \; alpha\; \backslash \; mathbf\; \{r\}\; \_\; \{2\},\; \backslash \; ldots,\; \backslash \; alpha\; \backslash \; mathbf\; \{r\}\; \_\; \{N\})\; =\; \backslash \; alpha\; ^\; \{N\}\; V\; (\backslash \; mathbf\; \{r\}\; \_\; \{1\},\; \backslash \; mathbf\; \{r\}\; \_\; \{2\},\; \backslash \; ldots,\; \backslash \; mathbf\; \{r\}\; \_\; \{N\})\}$

и время масштабируется на коэффициент β, t ′ = βt, тогда скорости vkмасштабируются на коэффициент α / β, а кинетическая энергия T - на (α / β). Весь лагранжиан был масштабирован с тем же коэффициентом, если

$\alpha \; 2\; \beta \; 2\; =\; \alpha \; N\; \Rightarrow \; \beta \; =\; \alpha \; 1\; -\; N\; 2.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; alpha\; ^\; \{2\}\}\; \{\backslash \; beta\; ^\; \{2\}\; \}\}\; =\; \backslash \; alpha\; ^\; \{N\}\; \backslash \; quad\; \backslash \; Rightarrow\; \backslash \; quad\; \backslash \; beta\; =\; \backslash \; alpha\; ^\; \{1\; -\; \{\backslash \; frac\; \{N\}\}\; \{2\}\}\}\; \backslash ,.\}$

Временная длина и время были масштабированы, траектории частиц в системе следуют геометрически подобным путям, различающимся по размеру. Длина l, пройденная за время t на исходной траектории, соответствует новой длине l ′, пройденной за время t ′ на новой траектории, заданной соотношениями

$t\; \prime \; t\; =\; (l\; \prime \; l)\; 1\; -\; N\; 2.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{t\; \text{'}\}\; \{t\}\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{l\text{'}\}\; \{l\}\}\; \backslash \; right)\; ^\; \{1\; -\; \{\backslash \; frac\; \{N\}\; \{2\}\}\}\; \backslash ,.\; \}$

Взаимодействующие частицы

Для данной системы, если две подсистемы A и B не взаимодействуют, лагранжиан L всей системы является суммой лагранжианов L A и L B для подсистема:

$L\; =\; LA\; +\; LB.\; \{\backslash \; displaystyle\; L\; =\; L\_\; \{A\}\; +\; L\_\; \{B\}\; \backslash ,.\}$

Если они действительно взаимодействуют, это невозможно. В некоторых ситуациях может оказаться возможным разделить лагранжиан системы L на сумму невзаимодействующих лагранжианов плюс еще один лагранжиан L AB, предоставив информацию о взаимодействии,

$L\; =\; LA\; +\; LB\; +\; LAB.\; \{\backslash \; displaystyle\; L\; =\; L\_\; \{A\}\; +\; L\_\; \{B\}\; +\; L\_\; \{AB\}\; \backslash ,.\}$

Это может быть физически мотивировано принятием невзаимодействующих лагранжианов только за кинетические энергии, в то время как лагранжиан взаимодействует полная потенциальная энергия системы. Кроме того, в предельном случае пренебрежимо малого взаимодействия L AB стремится к нулю, что приводит к отсутствию взаимодействия, описанному выше.

Расширение до более чем двух невзаимодействующих подсистем является общим - общим лагранжиан представляет собой сумму отдельных лагранжианов для каждой подсистемы. Если есть встречи, то можно добавить лагранжианы встречи.

В следующих примерах уравнения Лагранжа второго рода применяются к механическим задачам.

Консервативная сила

Частица массы m движется под действием консервативной силы, полученной из градиента ∇ скаляра потенциал,

$F\; =\; -\; \nabla \; V\; (г).\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; =\; -\; \backslash \; nabla\; V\; (\backslash \; mathbf\; \{r\})\; \backslash ,.\}$

Если частиц больше, в соответствии с приведенными выше результатами, полная кинетическая энергия является суммой по всем кинетическая энергия частиц, а потенциал является функцией всех координат.

Декартовы координаты

Лагранжиан частицы можно записать в виде

$L\; (x,\; y,\; z,\; x\; \dot{},\; y\; \dot{},\; z)\; =\; 1\; 2\; m\; (x\; \dot{}\; 2\; +\; y\; \dot{}\; 2\; +\; z\; \dot{}\; 2)\; -\; V\; (x,\; y,\; z).\; \{\backslash \; displaystyle\; L\; (x,\; y,\; z,\; \{\backslash \; dot\; \{x\}\},\; \{\backslash \; dot\; \{y\}\},\; \{\backslash \; dot\; \{z\}\})\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; m\; (\{\backslash \; точка\; \{x\}\}\; ^\; \{2\}\; +\; \{\backslash \; dot\; \{y\}\}\; ^\; \{2\}\; +\; \{\backslash \; dot\; \{z\}\}\; ^\; \{2\})\; -\; V\; (x,\; y,\; z)\; \backslash ,.\}$

Уравнения движения частиц находятся с помощью уравнения Эйлера - Лагранжа для координат x

$ddt\; (\partial \; L\; \partial \; x\; \dot{})\; =\; \partial \; L\; \partial \; x,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\; \backslash \; mathrm\; \{d\}\; t\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{x\}\}\}\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; x\}\}\; \backslash ,,\}$

с производными

$\partial \; L\; \partial \; x\; =\; -\; \partial \; V\; \partial \; x,\; \partial \; L\; \partial \; x\; \dot{}\; =\; mx\; \dot{},\; ddt\; (\partial \; L\; \partial \; x\; \dot{})\; =\; mx\; ¨,\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; x\}\}\; =\; -\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; x\}\}\; \backslash ,,\; \backslash \; quad\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{x\}\}\; \}\}\; =\; m\; \{\backslash \; dot\; \{x\}\}\; \backslash ,,\; \backslash \; quad\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; частичное\; L\}\; \{\backslash \; partial\; \{\; \backslash \; dot\; \{x\}\}\}\}\; \backslash \; right)\; =\; m\; \{\backslash \; ddot\; \{x\}\}\; \backslash ,,\}$

, следовательно,

$mx\; ¨\; =\; -\; \partial \; V\; \partial \; x,\; \{\backslash \; displaystyle\; m\; \{\backslash \; ddot\; \{\; x\}\}\; =\; -\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; x\}\}\; \backslash ,,\}$

и аналогично для координат y и z. Собирая уравнения в векторной форме, мы находим

$mr\; ¨\; =\; -\; \nabla \; V\; \{\backslash \; displaystyle\; m\; \{\backslash \; ddot\; \{\backslash \; mathbf\; \{r\}\}\}\; =\; -\; \backslash \; nabla\; V\}$

, который является вторым законом Ньютона движение для частицы, подверженной консервативной силе.

Полярные координаты в 2d и 3d

Лагранжиан для вышеуказанной задачи в сферических координатах (2d полярные координаты можно восстановить, установив $\theta \; =\; \pi \; /\; 2\; \{\backslash \; displaystyle\; \backslash \; theta\; =\; \backslash \; pi\; /\; 2\}$) с центральным потенциалом равно

$L\; =\; m\; 2\; (r\; \dot{}\; 2\; +\; r\; 2\; \theta \; \dot{}\; 2\; +\; r\; 2\; sin\; 2\; \; \theta \; \phi \; \dot{}\; 2)\; -\; V\; (г),\; \{\backslash \; displaystyle\; L\; =\; \{\backslash \; frac\; \{m\}\; \{2\}\}\; (\{\backslash \; dot\; \{r\}\}\; ^\; \{2\}\; +\; r\; ^\; \{2\}\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; ^\; \{2\}\; +\; r\; ^\; \{2\}\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\; \backslash ,\; \{\backslash \; dot\; \{\backslash \; varphi\}\}\; ^\; \{2\})\; -\; V\; (r)\; \backslash ,,\}$

так что уравнение Эйлера – Лагранжа уравнения:

$г-н\; ¨\; -\; г-н\; (\theta \; \dot{}\; 2\; +\; sin\; 2\; \; \theta \; \phi \; \dot{}\; 2)\; +\; \partial \; V\; \partial \; r\; =\; 0,\; \{\backslash \; displaystyle\; m\; \{\backslash \; ddot\; \{r\}\}\; -\; mr\; (\{\backslash \; dot\; \{\backslash \; theta\; \}\}\; ^\; \{2\}\; +\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\; \backslash ,\; \{\backslash \; dot\; \{\backslash \; varphi\}\}\; ^\; \{2\})\; +\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; r\}\}\; =\; 0\; \backslash ,,\; \}$

$ddt\; (mr\; 2\; \theta \; \dot{})\; -\; mr\; 2\; sin\; \; \theta \; cos\; \; \theta \; \phi \; \dot{}\; 2\; =\; 0,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; (mr\; ^\; \{2\}\; \{\backslash \; dot\; \{\backslash \; theta\}\})\; -\; г-н\; ^\; \{2\}\; \backslash \; sin\; \backslash \; theta\; \backslash \; cos\; \backslash \; theta\; \backslash ,\; \{\backslash \; dot\; \{\backslash \; varphi\}\}\; ^\; \{2\}\; =\; 0\; \backslash ,,\}$

$ddt\; (M\; R\; 2\; sin\; 2\; \; \theta \; \phi \; \dot{})\; знак\; равно\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; (мистер\; ^\; \{2\}\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\; \backslash ,\; \{\backslash \; dot\; \{\backslash \; varphi\}\})\; =\; 0\; \backslash ,.\}$

Координата φ является циклической, поскольку она не входит в лагранжиан, поэтому сохраняющийся импульс в системе - это угловой момент

$p\; \phi \; =\; \partial \; L\; \partial \; \phi \; \dot{}\; =\; mr\; 2\; sin\; 2\; \; \theta \; \phi \; \dot{},\; \{\backslash \; displaystyle\; p\; \_\; \{\backslash \; varphi\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; varphi\}\}\}\}\; =\; mr\; ^\; \{2\}\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\; \{\backslash \; dot\; \{\; \backslash \; varphi\}\}\; \backslash ,,\}$

, в котором r, θ и dφ / dt могут изменяться со временем, но только таким образом, чтобы p φ было постоянным.

Маятник на подвижной опоре

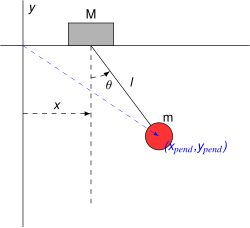Набросок ситуации с определением координат (нажмите, чтобы увеличить)

Рассмотрим маятник массы m и длины ℓ, который прикреплен к опоре массой M, который может двигаться вдоль линии в направлении оси x. Пусть x - координата вдоль линии опоры, и обозначим положение маятника углом θ от вертикали. Координаты и компоненты скорости маятника bobравны

$xpend\; =\; x\; +\; \ell \; sin\; \; \theta \; \Rightarrow \; x\; \dot{}\; pend\; =\; x\; \dot{}\; +\; \ell \; \theta \; \dot{}\; cos\; \; \theta \; ypend\; =\; -\; cos\; \; \theta \; \Rightarrow \; y\; \dot{}\; pend\; =\; \ell \; \theta \; \dot{}\; грех\; \; \theta \; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{rll\}\; x\; \_\; \{\backslash \; mathrm\; \{pend\}\}\; =\; x\; +\; \backslash \; ell\; \backslash \; sin\; \backslash \; theta\; \backslash \; quad\; \backslash \; Rightarrow\; \backslash \; quad\; \{\backslash \; dot\; \{x\}\}\; \_\; \{\backslash \; mathrm\; \{pend\}\}\; =\; \{\backslash \; точка\; \{x\}\}\; +\; \backslash \; ell\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; \backslash \; cos\; \backslash \; theta\; \backslash \backslash \; y\; \_\; \{\backslash \; mathrm\; \{pend\}\}\; =\; -\; \backslash \; ell\; \backslash \; cos\; \backslash \; theta\; \backslash \; quad\; \backslash \; Rightarrow\; \backslash \; quad\; \{\backslash \; dot\; \{y\}\}\; \_\; \{\backslash \; mathrm\; \{pend\}\}\; =\; \backslash \; ell\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; \backslash \; sin\; \backslash \; theta\; \backslash \; end\; \{array\}\}$

В качестве обобщенных координат можно принять x и θ. Тогда кинетическая система равна

$T\; =\; 1\; 2\; M\; x\; \dot{}\; 2\; +\; 1\; 2\; m\; (x\; \dot{}\; pend\; 2\; +\; y\; \dot{}\; pend\; 2)\; \{\backslash \; displaystyle\; T\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; M\; \{\backslash \; dot\; \{x\}\}\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; m\; \backslash \; left\; (\{\backslash \; dot\; \{x\}\}\; \_\; \{\backslash \; mathrm\; \{pend\}\}\; ^\; \{2\}\; +\; \{\backslash \; dot\; \{y\}\}\; \_\; \{\backslash \; mathrm\; \{pend\}\}\; ^\; \{2\}\; \backslash \; right)\}$

и потенциальная энергия

$V\; =\; mgypend\; \{\backslash \; displaystyle\; V\; =\; mgy\; \_\; \{\backslash \; mathrm\; \{pend\}\}\}$

давая лагранжиан

$L\; =\; T\; -\; V\; =\; 1\; 2\; M\; x\; \dot{}\; 2\; +\; 1\; 2\; m\; [(x\; \dot{}\; +\; \ell \; \theta \; \dot{}\; cos\; \; \theta )\; 2\; +\; (\ell \; \theta \; \dot{}\; sin\; \; \theta )\; 2]\; +\; mg\; \ell \; cos\; \; \theta \; =\; 1\; 2\; (M\; +\; m)\; x\; \dot{}\; 2\; +\; mx\; \dot{}\; \ell \; \theta \; \dot{}\; cos\; \; \theta \; +\; 1\; 2\; m\; \ell \; 2\; \theta \; \dot{}\; 2\; +\; mg\; \ell \; cos\; \; \theta \; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{rcl\}\; L\; =\; TV\; \backslash \; \backslash \; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; M\; \{\backslash \; dot\; \{x\}\}\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; m\; \backslash \; left\; [\backslash \; left\; (\{\backslash \; dot\; \{x\}\; \}\; +\; \backslash \; ell\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; \backslash \; cos\; \backslash \; theta\; \backslash \; right)\; ^\; \{2\}\; +\; \backslash \; left\; (\backslash \; ell\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; \backslash \; sin\; \backslash \; theta\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right\; ]\; +\; mg\; \backslash \; ell\; \backslash \; cos\; \backslash \; theta\; \backslash \backslash \; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; (M\; +\; m\; \backslash \; right)\; \{\backslash \; dot\; \{x\}\}\; ^\; \{2\}\; +\; m\; \{\backslash \; dot\; \{\; x\}\}\; \backslash \; ell\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; \backslash \; cos\; \backslash \; theta\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; m\; \backslash \; e\; ll\; ^\; \{2\}\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; ^\; \{2\}\; +\; mg\; \backslash \; ell\; \backslash \; cos\; \backslash \; theta\; \backslash \; end\; \{array\}\}\}$

Времена x отсутствует в лагранге, это циклическая координата. Сохраняющийся импульс равен

$p\; x\; =\; \partial \; L\; \partial \; x\; \dot{}\; =\; (M\; +\; m)\; x\; \dot{}\; +\; m\; \ell \; \theta \; \dot{}\; cos\; \; \theta .\; \{\backslash \; displaystyle\; p\_\; \{x\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{x\}\}\}\}\; =\; (M\; +\; m)\; \{\backslash \; dot\; \{x\}\}\; +\; m\; \backslash \; ell\; \{\backslash \; dot\; \{\backslash \; тета\}\}\; \backslash \; сов\; \backslash \; тета\; \backslash ,.\}$

и уравнение Лагранжа для поддержки координат х

$(м\; +\; м)\; х\; °\; +\; \ell \; м\; thetas\; ¨\; сов\; \; \theta \; -\; \ell \; м\; 2\; thetas\; \dot{}\; грех\; \; \theta \; знак\; равно\; 0\; \{\backslash \; displaystyle\; (M\; +\; m)\; \{\backslash \; ddot\; \{x\}\}\; +\; m\; \backslash \; ell\; \{\backslash \; ddot\; \{\backslash \; theta\}\}\; \backslash \; cos\; \backslash \; theta\; -m\; \backslash \; ell\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; ^\; \{2\}\; \backslash \; sin\; \backslash \; theta\; =\; 0\}$

Уравнение Лагранжа для угла θ:

$ddt\; [m\; (x\; \dot{}\; \ell \; cos\; \; \theta \; +\; \ell \; 2\; \theta \; \dot{})]\; +\; m\; \ell \; (x\; \dot{}\; \theta \; \dot{}\; +\; g)\; sin\; \; \theta \; =\; 0;\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \backslash \; left\; [m\; (\{\backslash \; dot\; \{x\}\}\; \backslash \; ell\; \backslash \; cos\; \backslash \; theta\; +\; \backslash \; ell\; ^\; \{2\}\; \{\backslash \; dot\; \{\backslash \; theta\}\})\; \backslash \; right]\; +\; m\; \backslash \; ell\; (\{\backslash \; dot\; \{x\}\}\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; +\; g)\; \backslash \; sin\; \backslash \; theta\; =\; 0;\}$

и упрощая

$\theta \; ¨\; +\; Икс\; ¨\; \ell \; соз\; \; \theta \; +\; g\; грех\; \; \theta \; =\; 0.\; \{\backslash \; Displaystyle\; \{\backslash \; ddot\; \{\backslash \; theta\}\}\; +\; \{\backslash \; frac\; \{\backslash \; ddot\; \{x\}\}\; \{\backslash \; ell\}\}\; \backslash \; cos\; \backslash \; theta\; +\; \{\backslash \; frac\; \{g\}\; \{\backslash \; ell\}\}\; \backslash \; sin\; \backslash \; theta\; =\; 0.\}$

Эти уравнения могут показаться довольно сложными, но потребовало их с помощью Ньютона потребовало бы тщательного определения всех сил, что было намного труднее и опаснее к ошибкам. Рассматривая предельные случаи, можно проверить правильность этой системы: например, $x\; ¨\; \to \; 0\; \{\backslash \; displaystyle\; \{\backslash \; ddot\; \{x\}\}\; \backslash \; to\; 0\}$должен давать уравнения движения для простого маятника, который покоится в некоторой инерциальной системе отсчета, в то время как $\theta \; ¨\; \to \; 0\; \{\backslash \; displaystyle\; \{\backslash \; ddot\; \{\backslash \; theta\}\}\; \backslash \; to\; 0\}$должен давать уравнения для маятника в постоянно ускоряющейся системе и т. Д. Кроме того, легко получить результаты численно, при подходе начальных условиях и выбранном временном шаге, новых просматриваемых результатов.

Задача двух тел с центральной силой

Два тела масс m 1 и m 2 с векторами положения r1и r2находятся на орбите вокруг каждого другого из-за привлекательного центрального V. Мы можем установить лагранжиан в терминах координат положения, как они есть, но это установленная процедура преобразования задачи двух тел в задачу одного тела следующим образом. Введите координаты Якоби ; разделение тел r= r2− r1и положение центра масс R= (m 1r1+ m 2r2) / (m 1 + m 2). Тогда лагранжиан равен

$L\; =\; 1\; 2\; MR\; \dot{}\; 2\; ⏟\; L\; см\; +\; 1\; 2\; \mu \; r\; \dot{}\; 2\; -\; V\; (|\; r\; |)\; ⏟\; L\; rel\; \{\backslash \; displaystyle\; L\; =\; \backslash \; underbrace\; \{\{\backslash \; frac\; \{1\}\; \{2\}\; \}\; M\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{R\}\}\}\; ^\; \{2\}\}\; \_\; \{L\; \_\; \{\backslash \; text\; \{cm\}\}\}\; +\; \backslash \; underbrace\; \{\{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; mu\; \{\backslash \; dot\; \{\; \backslash \; mathbf\; \{r\}\}\}\; ^\; \{2\}\; -V\; (|\; \backslash \; mathbf\; \{r\}\; |)\}\; \_\; \{L\; \_\; \{\backslash \; text\; \{rel\}\}\}\}$

где M = m 1 + m 2 - общая масса, μ = m 1m2/ (m 1 + m 2) - приведенная масса, и V - потенциал радиальной силы, который зависит только от величины расстояния | r | = | r2− r1|. Лагранжиан разбивается на член центра масс L см и член относительного движения L rel.

Уравнение Эйлера - Лагранжа для R просто

$MR\; ¨\; =\; 0,\; \{\backslash \; displaystyle\; M\; \{\backslash \; ddot\; \{\backslash \; mathbf\; \{R\}\}\}\; =\; 0\; \backslash ,,\}$

, в котором говорится, что центр масс движется по прямой с постоянной скоростью.

вертикальное движение зависит только от разделения, идеально использовать полярные координаты (r, θ) и принимать r = | r |,

$L\; отн.\; Знак\; равно\; 1\; 2\; \mu \; (р\; \dot{}\; 2\; +\; r\; 2\; \theta \; \dot{}\; 2)\; -\; V\; (r),\; \{\backslash \; displaystyle\; L\; \_\; \{\backslash \; text\; \{rel\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; mu\; (\{\backslash \; dot\; \{r\}\}\; ^\; \{2\}\; +\; r\; ^\; \{2\}\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; ^\; \{2\})\; -\; V\; (r)\; \backslash ,,\}$

, так что θ - циклическая координата с действующей (угловой) импульс

$p\; \theta \; =\; \partial \; L\; rel\; \partial \; \theta \; \dot{}\; =\; \mu \; r\; 2\; \theta \; \dot{}\; =\; \ell .\; \{\backslash \; displaystyle\; p\; \_\; \{\backslash \; theta\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\; \_\; \{\backslash \; text\; \{rel\}\}\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; theta\}\}\}\}\; =\; \backslash \; mu\; r\; ^\; \{2\}\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; =\; \backslash \; ell\; \backslash ,.\}$

Радиальная координата r и угловая скорость dθ / dt могут изменяться со временем, но только таким образом, чтобы ℓ было постоянным. Уравнение Лагранжа для r:

$\mu \; r\; \theta \; \dot{}\; 2\; -\; d\; V\; d\; r\; =\; \mu \; r\; ¨.\; \{\backslash \; displaystyle\; \backslash \; mu\; r\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{dV\}\; \{dr\}\}\; =\; \backslash \; mu\; \{\backslash \; ddot\; \{r\}\}\; \backslash ,.\}$

Это уравнение идентично к Согласно этой системе, вращающейся через вращающуюся систему. Исключая угловую скорость dθ / dt из этого радиального уравнения,

$\mu \; r\; ¨\; =\; -\; d\; V\; dr\; +\; \ell \; 2\; \mu \; r\; 3.\; \{\backslash \; displaystyle\; \backslash \; mu\; \{\backslash \; ddot\; \{r\}\}\; =\; -\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{\; d\}\; V\}\; \{\backslash \; mathrm\; \{d\}\; r\}\}\; +\; \{\backslash \; frac\; \{\backslash \; ell\; ^\; \{2\}\}\; \{\backslash \; mu\; r\; ^\; \{3\}\}\}\; \backslash ,.\}$

, которое является уравнением движения для одномерной задачи, в которой частица массы μ подвергается действию центральной внутренней силы - dV / dr и вторая внешняя сила, называемая в этом контексте центробежная сила

$F\; cf\; =\; \mu \; r\; \theta \; 2\; =\; \ell \; 2\; \mu \; r\; 3.\; \{\backslash \; Displaystyle\; F\; \_\; \{\backslash \; mathrm\; \{cf\}\}\; =\; \backslash \; mu\; r\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{\backslash \; ell\; ^\; \{2\}\}\; \{\backslash \; mu\; r\; ^\; \{3\}\}\}\; \backslash ,.\}$

Конечно, если оставаться полностью в рамках одномерной формулировки, входит только как некоторый навязанный параметр внешней внешней силы, и его интерпретация как угловой момент зависит от более общей двумерной задачи, из которой одно- возникла проблема размерности.

Если прийти к этому уравнению, используя механику Ньютона в совместно вращающейся системе отсчета, интерпретация очевидна как центробежная сила в этой системе координат из-за вращения самой рамы. Если прийти к этому уравнению напрямую, используя обобщенные координаты (r, θ) и просто следуя формулировке Лагранжа, вообще не думая о системе отсчета, интерпретация такова, что центробежная сила является результатом использования полярных координат. Как говорит Хильдебранд:

«Поскольку такие величины не являются истинными физическими силами, их часто называют силами инерции. Их присутствие или отсутствие зависит не от конкретной проблемы, а от выбранной системы координат». В частности, если выбраны декартовы координаты, центробежная сила исчезает, и формулировка включает только центральную силу, которая обеспечивает центростремительную силу для криволинейного движения.

Эта точка зрения, что фиктивные силы возникают в выборе координат, часто высказывается пользователями лагранжевого метода. Эта точка зрения естественным образом возникает в лагранжевом подходе, потому что система отсчета (возможно, неосознанно) выбирается путем выбора координат. Например, см. Сравнение лагранжианов в инерциальной и неинерциальной системе отсчета. См. Также обсуждение «полной» и «обновленной» формулировок Лагранжа в. К сожалению, такое использование «силы инерции» противоречит ньютоновской идее силы инерции. С точки зрения Ньютона, сила инерции возникает в ускорении системы наблюдения (тот факт, что она не является инерциальной системой отсчета ), а не в выборе системы координат. Для ясности, безопаснее всего называть лагранжевые силы инерции обобщенными силами инерции, чтобы отличать их от векторных сил инерции Ньютона. То есть, следует избегать следовать за Хильдебрандом, когда он говорит (стр. 155) «мы всегда имеем дело с обобщенными силами, скоростями, ускорениями и импульсами. Для краткости прилагательное« обобщенный »будет часто опускается».

Известно, что лагранжиан системы не уникален. В рамках оранжевого формализма ньютоновские фиктивные силы могут быть идентифицированы по существованию альтернативных лагранжианов, которые иногда используются симметрию системы.

Электромагнетизм

Пробная частица - это части, масса и заряд считаются настолько малыми, что ее влияние на внешнюю систему незначительно. Часто это гипотетическая упрощенная точечная части, не имеющая других свойств, кроме массы и заряда. Реальные частицы, такие как электроны и верхние кварки, более сложные и дополнительные компоненты в их лагранжианах.

Лагранжиан для заряженной частицы с электрическим зарядом q, использующей электромагнитным полем, является типичным примером потенциала, зависящий от скорости. Электрический скалярный потенциал ϕ = ϕ (r, t) и d магнитный вектор потенциала A= A(r, t) сопротивление из электрического поля E= E(r, t) и магнитного поля B= B(r, т) следующим образом;

$E\; =\; -\; \nabla \; \varphi \; -\; \partial \; A\; \partial \; T,\; B\; =\; \nabla \; \times \; A.\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{E\}\; =\; -\; \backslash \; nabla\; \backslash \; phi\; -\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{A\}\}\; \{\backslash \; partial\; t\}\}\; \backslash ,,\; \backslash \; quad\; \backslash \; mathbf\; \{B\}\; =\; \backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{A\}\; \backslash ,.\}$

Лагранжиан массивной заряженной пробной частицы в электромагнитном поле

$L\; =\; 1\; 2\; mr\; \dot{}\; 2\; +\; qr\; \dot{}\; \cdot \; A\; -\; q\; \varphi ,\; \{\backslash \; Displaystyle\; L\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; m\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{r\}\}\}\; ^\; \{2\}\; +\; q\; \backslash ,\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{r\; \}\}\}\; \backslash \; cdot\; \backslash \; mathbf\; \{A\}\; -q\; \backslash \; phi\; \backslash ,,\}$

называется минимальной связью. В сочетании с уравнением Эйлера-Лагранжа, он дает закон силы Лоренца

$mr\; ¨\; =\; q\; E\; +\; qr\; \dot{}\; \times \; B\; \{\backslash \; displaystyle\; m\; \{\backslash \; ddot\; \{\backslash \; mathbf\; \{r\; \}\}\}\; =\; q\; \backslash \; mathbf\; \{E\}\; +\; q\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{r\}\}\}\; \backslash \; times\; \backslash \; mathbf\; \{B\}\}$

При преобразовании шкалы :

$A\; \to \; A\; +\; \nabla \; f,\; \varphi \; \to \; \varphi \; -\; е\; \dot{},\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{A\}\; \backslash \; rightarrow\; \backslash \; mathbf\; \{A\}\; +\; \backslash \; nabla\; f\; \backslash ,,\; \backslash \; quad\; \backslash \; phi\; \backslash \; rightarrow\; \backslash \; phi\; -\; \{\backslash \; dot\; \{f\}\}\; \backslash ,,\}$

где f (r, t) - любая скалярная функция пространства и времени, вышеупомянутый лагранжиан преобразуется как:

$L\; \to \; L\; +\; q\; (r\; \dot{}\; \cdot \; \nabla \; +\; \partial \; \partial \; t)\; f\; =\; L\; +\; qdfdt,\; \{\backslash \; displaystyle\; L\; \backslash \; rightarrow\; L\; +\; q\; (\{\backslash \; dot\; \{\backslash \; mathbf\; \{r\}\}\}\; \backslash \; cdot\; \backslash \; nabla\; +\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; t\}\})\; f\; =\; L\; +\; q\; \{\backslash \; frac\; \{df\}\; \{dt\}\}\; \backslash ,,\}$

который по-прежнему дает тот же закон силы Лоренца.

Обратите внимание, что канонический импульс (сопряженный с положением r ) - это кинетический импульс плюс вклад от A поле (известное как потенциальный импульс):

$p\; =\; \partial \; L\; \partial \; r\; \dot{}\; =\; mr\; \dot{}\; +\; q\; A.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{p\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{r\}\}\}\}\}\; =\; m\; \{\backslash \; dot\; \{\backslash \; mathbf\; \{r\}\}\}\; +\; q\; \backslash \; mathbf\; \{A\}\; \backslash ,.\}$

Это соотношение также используется в предписании минимальной связи в квантовой механике и квантовой теории поля. Из этого выражения мы можем видеть, что канонический импульс pне является калибровочно-инвариантным, следовательно, не является измеримой физической величиной; Однако, если r является циклическим (т.е. лагранжиан не зависит от положения r), что происходит, если поля ϕ и A однородны, тогда этот канонический импульс p, приведенный здесь, представляет собой сохраняющийся импульс, в то время как измеряемый физический кинетический импульс m v - нет.

Диссипация (т.е. неконсервативные системы) также можно рассматривать с помощью эффективного лагранжиана, выработанного посредством определенного удвоения степеней свободы.

В более общей формулировке силы могут быть как консервативными, так и вязкими. Если подходящее преобразование может быть найдено из Fi, , Рэлей предлагает использовать функцию рассеяния , D в следующей форме:

$D\; =\; 1\; 2\; \sum \; j\; =\; 1\; m\; \sum \; k\; =\; 1\; m\; C\; jkq\; \dot{}\; jq\; \dot{}\; k.\; \{\backslash \; displaystyle\; D\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{m\}\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{m\}\; C\_\; \{jk\}\; \{\backslash \; dot\; \{q\}\}\; \_\; \{j\}\; \{\backslash \; dot\; \{q\}\}\; \_\; \{k\}\; \backslash ,.\}$

где C jk - константы, которые связаны с коэффициентами демпфирования в физической системе, хотя и не обязательно равны их. Если D определено таким образом, то

$Q\; j\; =\; -\; \partial \; V\; \partial \; qj\; -\; \partial \; D\; \partial \; q\; \dot{}\; j\; \{\backslash \; displaystyle\; Q\_\; \{j\}\; =\; -\; \{\backslash \; frac\; \{\backslash \; partial\; V\}\; \{\backslash \; partial\; q\_\; \{j\}\}\; \}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; D\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{j\}\}\}\}$

и

$ddt\; (\partial \; L\; \partial \; q\; \dot{}\; j)\; -\; \partial \; L\; \partial \; qj\; +\; \partial \; D\; \partial \; qj\; знак\; равно\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}))\; \_\; \{j\}\}\}\; \backslash \; справа)\; -\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; q\_\; \{j\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; D\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{j\; \}\}\}\; =\; 0\; \backslash ,.\; \}$

Идеи лагранжевой механики находят множество приложений в других областях физики и могут принимать обобщенные результаты вариационного исчисления.

Альтернативные формулировки классической механики

Близко родственная формулировка классической механики - гамильтонова механика. Гамильтониан определяется как

$H\; =\; \sum \; i\; =\; 1\; nq\; \dot{}\; i\; \partial \; L\; \partial \; q\; \dot{}\; i\; -\; L.\; \{\backslash \; displaystyle\; H\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; dot\; \{q\}\}\; \_\; \{\; i\}\; \{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}\}\}\; -\; L\; \backslash ,.\}$

и может быть получен путем выполнения преобразования Лежандра на лагранжиане, вводит новые переменные , канонически сопряженные с исходными переменными. Например, для данного набора обобщенных координат переменные , канонически сопряженные, обобщенные импульсами. Это удваивает количество чисел, но делает дифференциальные уравнения первого порядка. Гамильтониан является особенно распространенной величиной в квантовой механике (см. Гамильтониан (квантовая механика) ).

Рутова механика - это эффективная формулировка лагранжевой и гамильтоновой механики, которая часто используется на практике, но эффективная формулировка для циклических координат.

Формулировка в визуальных впечатсов

Уравнения Эйлера - Лагранжа также могут быть сформулированы в терминах обобщенных измеренийсов, не обобщенных координат. Выполнение преобразования Лежандра над обобщенным координатным лагранжианом L (q, d q / dt, t) дает обобщенный импульсный лагранжиан L ′ (p, d p / dt, t) в терминах исходного лагранжиана, а также уравнения ЭЛ в терминах обобщенных импульсов. Оба лагранжи предоставят знакомую информацию. На практике обобщенные координаты удобнее использовать и интерпретировать, чем обобщенные импульсы.

Высшие производные обобщенные координаты

Нет ограничивать производные общие координаты только первым порядком. Можно вывести модифицированные уравнения EL для лагранжиана, содержащего производные более порядка, подробности см. В уравнении Эйлера - Лагранжа.

Оптика

Лагранжева механика может быть применена к геометрической оптике путем применения вариационных принципов к лучам света в среде, а решение EL дает уравнения пути следуют лучи света.

Релятивистская формулировка

лагранжевую механику можно сформулировать в специальной теории относительности и общей теории относительности. Некоторые черты лагранжевой механики сохраняются в релятивистских теориях, но быстро возникают трудности в других отношениях. В частности, уравнения EL принимают ту же форму, и связь между циклическими координатами и сохраняемыми импульсами все еще применима, однако лагранжи должны быть изменены, и это не просто кинетическая минусая энергия частиц. Кроме того, нелегко обрабатывать многочастичные системы явно ковариантным способом, это может быть возможным, если конкретную систему отсчета.

Квантовая механика

В квантовой механике, действие и квантово-механическая фаза связаны через постоянную Планка, а принцип стационарного действия можно понять в терминах конструктивной интерференции волновых функций.

. В 1948 году Фейнман открыл формулировку интеграла по путям, расширяющая принцип наименьшего действия до квантовой механики для электронов и фотонов. В этой формулировке частиц возникают все возможные пути между начальным и конечным состояниями; вероятность конкретного конечного состояния получается суммированием всех траекторий, ведущего к нему. В классическом режиме формулировка интеграла по путям четко воспроизводит принцип Гамильтона и принцип Ферма в оптике.

Классическая теория поля

В оранжевой механике обобщенные координаты образуют дискретный набор данных, определяющих конфигурацию системы. В классической теории физическая система представляет собой не набор дискретных частиц, а, скорее, непрерывное поле ϕ (r, t), определенное в области трехмерного пространства. С полем связями плотность лагранжиана

$L\; (\varphi ,\; \nabla \; \varphi ,\; \partial \; \varphi \; /\; \partial \; t,\; r,\; t)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; phi,\; \backslash \; nabla\; \backslash \; phi,\; \backslash \; partial\; \backslash \; phi\; /\; \backslash \; partial\; t,\; \backslash \; mathbf\; \{r\},\; t)\}$

определить в терминах поля и его пространственных и временных производных в реализации r и времени t. Как и в случае с частями, для нерелятивистской плотности лагранжи также является плотностью кинетической энергии за вычет его плотности потенциальной энергии (в общем случае это неверно, и плотность лагранжиана должна быть «реконструирована»). Тогда лагранжиан является интегралом объема лагранжиана в трехмерном пространстве

$L\; (t)\; =\; \int \; L\; d\; 3\; r\; \{\backslash \; displaystyle\; L\; (t)\; =\; \backslash \; int\; \{\backslash \; mathcal\; \{L\}\}\; \backslash ,\; \backslash \; mathrm\; \{\; d\}\; ^\; \{3\}\; \backslash \; mathbf\; \{r\}\}$

где d r - это трехмерный дифференциальный элемент объема. Лагранжи представляет собой функцию времени, поскольку она неявная пространственная зависимость через поля и может иметь явную пространственную зависимость.

Теорема Нётер

Принцип действия и формализм Лагранжа связаны с теоремой Нётер, которая связывает физические сохраняющиеся величины с непрерывными симметрий физической системы.

Если лагранжиан инвариантен относительно симметрии, то результирующие уравнения движения также инвариантны относительно этой симметрии. Эта характеристика очень полезна для демонстрации того, что теории согласуются либо с специальной теорией относительности, либо с общей теорией относительности.

• Астрономический портал

• Фундаментальная лемма вариационного исчисления
• Канонические координаты
• Функциональная производная
• Обобщенные координаты
• Гамильтонова механика
• Гамильтонова оптика
• Лагранжева и эййлерова оптика
• Лагранжева и эййлерова оптика
• спецификация поля Лагранжева точка
• Лагранжева система
• Неавтономная механика
• Ограниченная задача трех тел
• Проблема Плато
• Обратная задача для лагранжевой механики, общая тема поиска лагранжиана для системы, заданной уравнениями движения.

• Гупта, Киран Чандра, Классическая механика частиц и твердого тел (Wiley, 1988).
• Кассель, Кевин (2013). Вариационные методы с приложениями в науке и технике. Кембридж: Издательство Кембриджского университета. ISBN 978-1-107-02258-4. CS1 maint: ref = harv (ссылка )
• Goldstein, Herbert, et al. Классическая механика. 3-е изд., Pearson, 2002.

• Дэвид Тонг. «Кембриджские лекции по классической динамике». DAMTP. Проверено 2017-06-08.
• Принцип наименьшего действия в интерактивном режиме Превосходное интерактивное объяснение / веб-страница
• Joseph Louis de Lagrange - uvres complete (Gallica-Math)
• Ограниченное движение и обобщенные координаты, стр.