Геометрическая оптика

редактировать

Геометрическая оптика, или лучевая оптика, является моделью оптики который описывает распространение света в терминах лучей. Луч в геометрической оптике - это абстракция, полезная для аппроксимации путей, по которым распространяется свет при определенных обстоятельствах.

Упрощающие допущения геометрической оптики включают в себя то, что световые лучи:

распространяются по прямолинейным путям, поскольку они проходят в однородной среде
изгибе, и в частности обстоятельства могут разделиться на две части, в интерфейсе между двумя разнородными средами
следуют изогнутые траектории в среде, в которой показатель преломления изменяется
может быть поглощенными или отраженными.

Геометрическая оптика не учитывает определенные оптические эффекты, такие как дифракция и интерференция. Это упрощение полезно на практике; это отличное приближение, когда длина волны мала по сравнению с размером структур, с которыми взаимодействует свет. Эти методы особенно полезны при описании геометрических аспектов визуализации, включая оптических аберраций.

Содержание

1 Пояснение
2 Отражение
3 Рефракция
4 Основы математики
- 4.1 Метод Зоммерфельда – Рунге
- 4.2 Метод Люнебурга
- 4.3 Общее уравнение с использованием четырехвекторной записи
5 См. Также
6 Ссылки
7 Дополнительная литература
- 7.1 Английские переводы некоторых ранних книги и статьи
8 Внешние ссылки

Пояснение

Когда свет распространяется в пространстве, он колеблется с амплитудой . На этом изображении каждый пик максимальной амплитуды отмечен плоскостью для иллюстрации волнового фронта. Луч - это стрелка , перпендикулярная этим параллельным поверхностям.

Луч света - это линия или кривая, который находится перпендикулярно к волновым фронтам света (и, следовательно, коллинеарен с волновым вектором ). Чуть более строгое определение светового луча следует из принципа Ферма, который гласит, что путь, пройденный лучом света между двумя точками, - это путь, который можно пройти за наименьшее время.

Геометрическую оптику часто упрощают, делая параксиальное приближение или «приближение малых углов». Затем математическое поведение становится линейным, что позволяет описывать оптические компоненты и системы с помощью простых матриц. Это приводит к методам гауссовой оптики и параксиальной трассировки лучей, которые используются для определения основных свойств оптических систем, таких как приблизительное изображение и положения объектов и увеличения.

Отражение

Диаграмма зеркального отражения

Глянцевые поверхности, такие как зеркала, просто и предсказуемо отражают свет. Это позволяет создавать отраженные изображения, которые могут быть связаны с фактическим (реальным ) или экстраполированным (виртуальным ) местоположением в пространстве.

На таких поверхностях направление отраженного луча определяется углом, под которым падающий луч образует нормаль поверхности, линию, перпендикулярную поверхности в точке, где луч падает. Падающий и отраженный лучи лежат в одной плоскости, а угол между отраженным лучом и нормалью к поверхности такой же, как и между падающим лучом и нормалью. Это известно как Закон отражения.

Для плоских зеркал закон отражения подразумевает, что изображения объектов находятся в вертикальном положении и на таком же расстоянии позади зеркала, как и объекты перед ним. зеркало. Размер изображения такой же, как и размер объекта. (увеличение плоского зеркала равно единице.) Закон также подразумевает, что зеркальные изображения имеют инвертированную четность, что воспринимается как лево-правое инверсия.

Зеркала с криволинейными поверхностями можно моделировать с помощью трассировки лучей и использования закона отражения в каждой точке на поверхности. Для зеркал с параболическими поверхностями параллельные лучи, падающие на зеркало, создают отраженные лучи, которые сходятся в общем фокусе . Другие изогнутые поверхности также могут фокусировать свет, но с аберрациями из-за расходящейся формы, вызывающей размытие фокуса в пространстве. В частности, сферические зеркала демонстрируют сферическую аберрацию. Изогнутые зеркала могут формировать изображения с увеличением больше или меньше единицы, а изображение может быть вертикальным или перевернутым. Вертикальное изображение, образованное отражением в зеркале, всегда виртуально, в то время как перевернутое изображение реально и может проецироваться на экран.

Преломление

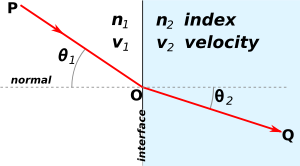
Иллюстрация закона Снеллиуса

Преломление возникает, когда свет проходит через область пространства с изменяющимся показателем преломления. Простейший случай преломления возникает, когда существует граница между однородной средой с показателем преломления $n 1 {\ displaystyle n_ {1}}$ $n_{1}$ и другой средой с показателем преломления $n 2 {\ displaystyle n_ {2}}$ $n_{2}$ . В таких ситуациях закон Снеллиуса описывает результирующее отклонение светового луча:

n 1 sin ⁡ θ 1 = n 2 sin ⁡ θ 2 {\ displaystyle n_ {1} \ sin \ theta _ { 1} = n_ {2} \ sin \ theta _ {2} \}

n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}\

, где $θ 1 {\ displaystyle \ theta _ {1}}$ $\theta _{1}$ и $θ 2 {\ displaystyle \ theta _ {2}}$ $\theta _{2}$ - это углы между нормалью (к границе раздела) и падающей и преломленной волнами соответственно. Это явление также связано с изменением скорости света, как видно из определения показателя преломления, приведенного выше, которое подразумевает:

v 1 sin ⁡ θ 2 = v 2 sin ⁡ θ 1 {\ displaystyle v_ {1} \ sin \ theta _ {2} \ = v_ {2} \ sin \ theta _ {1}}

v_1\sin\theta_2\ = v_2\sin\theta_1

, где $v 1 {\ displaystyle v_ {1}}$ $v_{1}$ и $v 2 {\ displaystyle v_ {2}}$ $v_{2}$ - скорости волн через соответствующие среды.

Различные следствия закона Снеллиуса включают тот факт, что для световых лучей, идущих от материала с высоким индексом преломления к материалу с низким показателем преломления, взаимодействие с границей раздела может привести к нулевому пропусканию. Это явление называется полным внутренним отражением и позволяет использовать технологию волоконной оптики. Когда световые сигналы проходят по оптоволоконному кабелю, они подвергаются полному внутреннему отражению, что позволяет практически не терять свет по длине кабеля. Также возможно создавать поляризованные световые лучи, используя комбинацию отражения и преломления: когда преломленный луч и отраженный луч образуют прямой угол, отраженный луч имеет свойство « плоская поляризация ». Угол падения, необходимый для такого сценария, известен как угол Брюстера..

Закон Снеллиуса может быть использован для прогнозирования отклонения световых лучей, когда они проходят через «линейную среду», при условии, что показатели преломления и геометрия СМИ известны. Например, распространение света через призму приводит к тому, что луч света отклоняется в зависимости от формы и ориентации призмы. Кроме того, поскольку разные частоты света имеют немного разные показатели преломления в большинстве материалов, преломление можно использовать для получения спектров дисперсии , которые выглядят как радуги. Открытие этого явления при прохождении света через призму, как известно, приписывают Исааку Ньютону.

Некоторые среды имеют показатель преломления, который постепенно изменяется в зависимости от положения, и, таким образом, световые лучи изгибаются сквозь среду, а не движутся по прямой. линий. Этот эффект является причиной миражей, наблюдаемых в жаркие дни, когда изменяющийся показатель преломления воздуха заставляет световые лучи изгибаться, создавая видимость зеркальных отражений на расстоянии (как если бы на поверхности бассейн с водой). Материал с переменным показателем преломления называется материалом с градиентным показателем преломления (GRIN) и имеет множество полезных свойств, используемых в современных технологиях оптического сканирования, включая копировальные аппараты и сканеры. Это явление изучается в области оптики с градиентным показателем преломления.

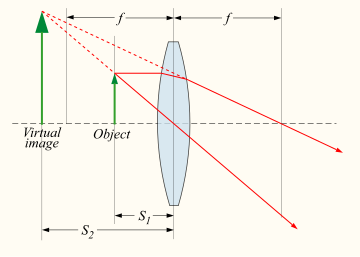
Диаграмма трассировки лучей для простой собирающей линзы.

Устройство, которое генерирует сходящиеся или расходящиеся световые лучи из-за преломления, известно как линза. Тонкие линзы создают точки фокусировки с обеих сторон, которые можно смоделировать с помощью уравнения производителя линз. В общем, существует два типа линз: выпуклые линзы, которые заставляют параллельные световые лучи сходиться, и вогнутые линзы, которые заставляют параллельные световые лучи расходиться. Подробный прогноз того, как эти линзы создают изображения, можно сделать с помощью трассировки лучей, аналогичной изогнутым зеркалам. Подобно изогнутым зеркалам, тонкие линзы подчиняются простому уравнению, которое определяет расположение изображений при определенном фокусном расстоянии ( $f {\ displaystyle f}$ $f$ ) и расстоянии до объекта ( $S 1 { \ displaystyle S_ {1}}$ $S_{1}$ ):

1 S 1 + 1 S 2 = 1 f {\ displaystyle {\ frac {1} {S_ {1}}} + {\ frac {1 } {S_ {2}}} = {\ frac {1} {f}}}

\frac{1}{S_1} + \frac{1}{S_2} = \frac{1}{f}

где $S 2 {\ displaystyle S_ {2}}$ $S_{2}$ - расстояние, связанное с изображением и считается по соглашению отрицательным, если на той же стороне линзы, что и объект, и положительным, если на противоположной стороне линзы. Фокусное расстояние f считается отрицательным для вогнутых линз.

Входящие параллельные лучи фокусируются выпуклой линзой в перевернутое реальное изображение на расстоянии одного фокусного расстояния от линзы, на дальней стороне линзы.

Входящие параллельные лучи фокусируются выпуклой линзой в перевернутое реальное изображение на расстоянии одного фокусного расстояния от линзы, на дальней стороне линзы

Лучи от объекта на конечном расстоянии фокусируются дальше от линзы, чем фокус расстояние; чем ближе объект к объективу, тем дальше изображение от объектива. В вогнутых линзах входящие параллельные лучи расходятся после прохождения через линзу таким образом, что кажется, что они возникли на вертикальном виртуальном изображении на расстоянии одного фокусного расстояния от линзы, на той же стороне линзы, к которой приближаются параллельные лучи..

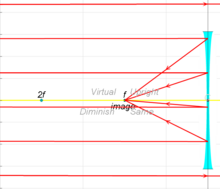
В вогнутых линзах входящие параллельные лучи расходятся после прохождения через линзу таким образом, что кажется, что они возникли на вертикальном виртуальном изображении на расстоянии одного фокусного расстояния от линзы, на той же стороне линзы, что и параллельные лучи.

Лучи от объекта, находящегося на конечном расстоянии, связаны с виртуальным изображением, которое находится ближе к линзе, чем фокусное расстояние, и на той же стороне линзы, что и объект. Чем ближе объект к объективу, тем ближе виртуальное изображение к объективу.

Лучи от объекта на конечном расстоянии связаны с виртуальным изображением, которое находится ближе к линзе, чем фокусное расстояние, и на той же стороне линзы, что и объект.

Аналогично, увеличение линзы равно задается

M = - S 2 S 1 = ff - S 1 {\ displaystyle M = - {\ frac {S_ {2}} {S_ {1}}} = {\ frac {f} {f-S_ {1}}}}

M = - \frac{S_2}{S_1} = \frac{f}{f - S_1}

где отрицательный знак по соглашению используется для обозначения вертикального объекта для положительных значений и перевернутого объекта для отрицательных значений. Подобно зеркалам, вертикальные изображения, создаваемые одиночными линзами, являются виртуальными, в то время как перевернутые изображения реальны.

Линзы страдают от аберраций, которые искажают изображения и точки фокусировки. Это происходит как из-за геометрических несовершенств, так и из-за изменяющегося показателя преломления для разных длин волн света (хроматическая аберрация ).

Основная математика

Как математическое исследование, геометрическая оптика представляет собой короткое длина волны предел для решений гиперболических уравнений в частных производных (метод Зоммерфельда – Рунге) или как свойство распространения разрывов поля в соответствии с уравнениями Максвелла (метод Люнебурга). В этой коротковолновой области предел, можно аппроксимировать решение локально следующим образом:

u (t, x) ≈ a (t, x) ei (k ⋅ x - ω t) {\ displaystyle u (t, x) \ приблизительно a (t, x) e ^ {i (k \ cdot x- \ omega t)}}

u(t,x) \approx a(t,x)e^{i(k\c dot x - \omega t)}

где $k, ω {\ displaystyle k, \ omega}$ $k, \omega$ удовлетворяют дисперсионному соотношению, а амплитуда $a (t, x) {\ displaystyle a (t, x)}$ $a(t,x)$ изменяется медленно. Точнее, решение ведущего порядка принимает форма

a 0 (t, x) ei φ (t, x) / ε. {\ displaystyle a_ {0} (t, x) e ^ {я \ varphi (t, x) / \ varepsilon}.}

a_0(t,x) e^{i\varphi(t,x)/\varepsilon}.

Фаза $φ (t, x) / ε {\ displaystyle \ varphi (t, x) / \ varepsilon}$ $\varphi(t,x)/\varepsilon$ можно линеаризовать для восстановления большого волнового числа $k: = ∇ x φ {\ displaystyle k: = \ nabla _ {x} \ varphi}$ $k:= \nabla_x \varphi$ и частоты $ω: = - ∂ t φ {\ displaystyle \ omega: = - \ partial _ {t} \ varphi}$ $\omega := -\partial_t \varphi$ . Амплитуда $a 0 {\ displaystyle a_ {0}}$ $a_{0}$ удовлетворяет уравнению переноса. Небольшой параметр $ε {\ displaystyle \ varepsilon \,}$ $\varepsilon\,$ входит в сцену из-за сильно колеблющихся начальных условий. Таким образом, когда начальные условия колеблются намного быстрее, чем коэффициенты дифференциального уравнения, решения будут сильно колебаться и переноситься вдоль лучей. Если предположить, что коэффициенты в дифференциальном уравнении гладкие, лучи тоже будут. Другими словами, преломления не происходит. Мотивация для этого метода исходит из изучения типичного сценария распространения света, когда свет с короткой длиной волны распространяется вдоль лучей, что минимизирует (более или менее) время его прохождения. Для его полного применения требуются инструменты из микролокального анализа.

метода Зоммерфельда – Рунге

Метод получения уравнений геометрической оптики с использованием предела нулевой длины волны был впервые описан Арнольдом Зоммерфельдом и Дж. Рунге в 1911 году. Их вывод был основан на устном замечании Питера Дебая. Рассмотрим монохроматическое скалярное поле $ψ (r, t) = ϕ (r) ei ω t {\ displaystyle \ psi (\ mathbf {r}, t) = \ phi (\ mathbf {r}) e ^ {i \ omega t}}$ $\psi (\mathbf {r},t)=\phi (\mathbf {r})e^{i\omega t}$ , где $ψ {\ displaystyle \ psi}$ $\psi$ может быть любой из составляющих электрического или магнитного поля и, следовательно, функция $ϕ {\ displaystyle \ phi}$ $\phi$ удовлетворяет волновому уравнению

∇ 2 ϕ + ko 2 n (r) ϕ = 0 {\ displaystyle \ nabla ^ {2 } \ phi + k_ {o} ^ {2} n (\ mathbf {r}) \ phi = 0}

\nabla ^{2}\phi +k_{o}^{2}n(\mathbf {r})\phi =0

где $ko = ω / c = 2 π / λ o {\ displaystyle k_ {o} = \ omega / c = 2 \ pi / \ lambda _ {o}}$ $k_{o}=\omega /c=2\pi /\lambda _{o}$ , где $c {\ displaystyle c}$ $c$ - скорость света в вакууме. Здесь $n (r) {\ displaystyle n (\ mathbf {r})}$ $n(\mathbf {r})$ - показатель преломления среды. Без ограничения общности введем $ϕ = A (ko, r) eiko S (r) {\ displaystyle \ phi = A (k_ {o}, \ mathbf {r}) e ^ {ik_ {o} S (\ mathbf {r})}}$ $\phi =A(k_{o},\mathbf {r})e^{ik_{o}S(\mathbf {r})}$ для преобразования уравнения в

- ko 2 A [(∇ S) 2 - n 2] + 2 iko (∇ S ⋅ ∇ A) + iko A ∇ 2 S + ∇ 2 A = 0. {\ displaystyle -k_ {o} ^ {2} A [(\ nabla S) ^ {2} -n ^ {2}] + 2ik_ {o} (\ nabla S \ cdot \ nabla A) + ik_ {o} A \ nabla ^ {2} S + \ nabla ^ {2} A = 0.}

-k_{o}^{2}A[(\nabla S)^{2}-n^{2}]+2ik_{o}(\nabla S\cdot \nabla A)+ik_{o}A\nabla ^{2}S+\nabla ^{2}A=0.

Поскольку основной принцип геометрической оптики лежит в пределе $λ o ∼ ko - 1 → 0 {\ displaystyle \ lambda _ {o} \ sim k_ {o} ^ {- 1} \ rightarrow 0}$ $\lambda _{o}\sim k_{o}^{-1}\rightarrow 0$ , предполагается следующий асимптотический ряд,

A (ko, р) знак равно ∑ м знак равно 0 ∞ A м (г) (iko) m {\ displaystyle A (k_ {o}, \ mathbf {r}) = \ sum _ {m = 0} ^ {\ infty} {\ frac {A_ {m} (\ mathbf {r})} {(ik_ {o}) ^ {m}}}}

A(k_{o},\mathbf {r})=\sum _{m=0}^{\infty }{\frac {A_{m}(\mathbf {r})}{(ik_{o})^{m}}}

Для большого, но конечного значения $ko {\ displaystyle k_ {o}}$ $k_{o}$ , ряды расходятся, и нужно соблюдать осторожность, сохраняя только соответствующие первые несколько членов. Для каждого значения $k o {\ displaystyle k_ {o}}$ $k_{o}$ можно найти оптимальное количество терминов, которые нужно сохранить, и добавление большего количества терминов, чем это оптимальное количество, может привести к худшей аппроксимации. Подставляя ряд в уравнение и собирая члены разного порядка, находим

O (ko 2): (∇ S) 2 = n 2, O (ko): 2 ∇ S ⋅ ∇ A 0 + A 0 ∇ 2 S = 0, O (1): 2 ∇ S ⋅ ∇ A 1 + A 1 ∇ 2 S = - ∇ 2 A 0, {\ displaystyle {\ begin {align} O (k_ {o} ^ {2}): \ quad (\ nabla S) ^ {2} = n ^ {2}, \\ O (k_ {o}): \ quad 2 \ nabla S \ cdot \ nabla A_ {0} + A_ {0} \ nabla ^ {2} S = 0, \\ O (1): \ quad 2 \ nabla S \ cdot \ nabla A_ {1} + A_ {1} \ nabla ^ {2} S = - \ nabla ^ {2 } A_ {0}, \ end {align}}}

{\begin{aligned}O(k_{o}^{2}):\quad (\nabla S)^{2}=n^{2},\\O(k_{o}):\quad 2\nabla S\cdot \nabla A_{0}+A_{0}\nabla ^{2}S=0,\\O(1):\quad 2\nabla S\cdot \nabla A_{1}+A_{1}\nabla ^{2}S=-\nabla ^{2}A_{0},\end{aligned}}

в общем,

O (ko 1 - m): 2 ∇ S ⋅ ∇ A m + A m ∇ 2 S = - ∇ 2 A m - 1. {\ Displaystyle O (к_ {о} ^ {1-м}): \ quad 2 \ nabla S \ cdot \ nabla A_ {m} + A_ {m} \ nabla ^ {2} S = - \ nabla ^ {2 } A_ {m-1}.}

O(k_{o}^{1-m}):\quad 2\nabla S\cdot \nabla A_{m}+A_{m}\nabla ^{2}S=-\nabla ^{2}A_{m-1}.

Первое уравнение известно как уравнение эйконала, которое определяет эйконал $S (r) {\ displaystyle S ( \ mathbf {r})}$ $S(\mathbf {r})$ - это уравнение Гамильтона – Якоби, записанное, например, в декартовых координатах, становится

(∂ S ∂ x) 2 + (∂ S ∂ y) 2 + (∂ S ∂ z) 2 знак равно N 2. {\ displaystyle \ left ({\ frac {\ partial S} {\ partial x}} \ right) ^ {2} + \ left ({\ frac {\ partial S} {\ partial y}} \ right) ^ { 2} + \ left ({\ frac {\ partial S} {\ partial z}} \ right) ^ {2} = n ^ {2}.}

\left({\frac {\partial S}{\partial x}}\right)^{2}+\left({\frac {\partial S}{\partial y}}\right)^{2}+\left({\frac {\partial S}{\partial z}}\right)^ {2}=n^{2}.

Остальные уравнения определяют функции $A m ( r) {\ displaystyle A_ {m} (\ mathbf {r})}$ $A_{m}(\mathbf {r})$ .

Метод Люнебурга

Метод получения уравнений геометрической оптики путем анализа поверхностей разрывов решений уравнений Максвелла был впервые описан Рудольф Карл Люнебург в 1944 году. Он не ограничивает электромагнитное поле специальной формой (в методе Зоммерфельда-Рунге не ясно, что поле, амплитуда которого $ϕ {\ displaystyle \ phi}$ $\phi$ зависит от $ω (\ displaystyle \ omega}$ $\omega$ все равно дает уравнение эйконала, т. Е. Фронт волны геометрической оптики). Главный вывод этого подхода:

Теорема. Предположим, что поля $E → (x, y, z, t) {\ displaystyle \ mathbf {\ vec {E}} (x, y, z, t)}$ $\mathbf {\vec {E}} (x,y,z,t)$ и $H → (x, y, z, t) {\ displaystyle \ mathbf {\ vec {H}} (x, y, z, t)}$ $\mathbf {\vec {H}} (x,y,z,t)$ (в линейной изотропной среде, описываемой диэлектрическими постоянными $ε (x, y, z) {\ displaystyle \ varepsilon (x, y, z)}$ $\varepsilon (x,y,z)$ и $μ (x, y, z) {\ displaystyle \ mu (x, y, z)}$ $\mu (x,y,z)$ ) имеют конечные разрывы вдоль поверхности, описываемой уравнением $ψ (x, y, z) - ct знак равно 0 {\ displaystyle \ psi (x, y, z) -ct = 0}$ $\psi (x,y,z)-ct=0$ . Тогда уравнения Максвелла в интегральной форме подразумевают, что $ψ {\ displaystyle \ psi}$ $\psi$ удовлетворяет уравнению эйконала:

ψ x 2 + ψ y 2 + ψ z 2 = ε μ = n 2 {\ Displaystyle \ psi _ {x} ^ {2} + \ psi _ {y} ^ {2} + \ psi _ {z} ^ {2} = \ varepsilon \ mu = n ^ {2}}

\psi _{x}^{2}+\psi _{y}^{2}+\psi _{z}^{2}=\varepsilon \mu =n^{2}

где $n {\ displaystyle n}$ $n$ - показатель преломления среды (гауссовы единицы).

Примером такой поверхности разрыва является начальный волновой фронт, исходящий от источника, который начинает излучать в определенный момент времени.

Поверхности неоднородности поля, таким образом, становятся волновыми фронтами геометрической оптики с соответствующими полями геометрической оптики, определяемыми как:

E → ∗ (x, y, z) = E → (x, y, z, ψ (Икс, Y, Z) / с) {\ Displaystyle \ mathbf {\ vec {E}} ^ {*} (x, y, z) = \ mathbf {\ vec {E}} (x, y, z, \ psi (x, y, z) / c)}

\mathbf {\vec {E}} ^{*}(x,y,z)=\mathbf {\vec {E}} (x,y,z,\psi (x,y,z)/c)

H → ∗ (x, y, z) = H → (x, y, z, ψ (x, y, z) / c) {\ displaystyle \ mathbf {\ vec {H}} ^ {*} (x, y, z) = \ mathbf {\ vec {H}} (x, y, z, \ psi (x, y, z) / c)}

\mathbf {\vec {H}} ^{*}(x,y,z)=\mathbf {\vec {H}} (x,y,z,\psi (x,y,z)/c)

Эти поля подчиняются уравнениям переноса, согласующимся с уравнениями переноса подхода Зоммерфельда-Рунге. Световые лучи в теории Люнебурга определяются как траектории, ортогональные поверхности разрыва, и при правильной параметризации можно показать, что они подчиняются принципу наименьшего времени Ферма, тем самым устанавливая тождество этих лучей со световыми лучами стандартной оптики.

Вышеупомянутые разработки могут быть обобщены на анизотропные среды.

Доказательство теоремы Люнебурга основано на исследовании того, как уравнения Максвелла управляют распространением разрывов решений. Основная техническая лемма выглядит следующим образом:

Техническая лемма. Пусть $φ (x, y, z, t) = 0 {\ displaystyle \ varphi (x, y, z, t) = 0 }$ $\varphi (x,y,z,t)=0$ быть поверхностью (трехмерным многообразием) в пространстве-времени $R 4 {\ displaystyle \ mathbf {R} ^ {4}}$ $\mathbf {R} ^{4}$ , на которой один или несколько из: $E → (x, y, z, t) {\ displaystyle \ mathbf {\ vec {E}} (x, y, z, t)}$ $\mathbf {\vec {E}} (x,y,z,t)$ , $H → (x, y, z, t) {\ displaystyle \ mathbf {\ vec {H}} (x, y, z, t)}$ $\mathbf {\vec {H}} (x,y,z,t)$ , $ε (x, y, z) {\ displaystyle \ varepsilon (x, y, z)}$ $\varepsilon (x,y,z)$ , $μ (x, y, z) {\ displaystyle \ mu (x, y, z)}$ $\mu (x,y,z)$ , имеют конечный разрыв. Тогда в каждой точке поверхности верны следующие формулы:

∇ φ × [H →] - 1 c φ t [ε E →] = 0 {\ displaystyle \ nabla \ varphi \ times [\ mathbf {\ vec { H}}] - {1 \ over c} \, \ varphi _ {t} \, [\ varepsilon \ mathbf {\ vec {E}}] = 0}

\nabla \varphi \times [\mathbf {\vec {H}} ]-{1 \over c}\,\varphi _{t}\,[\varepsilon \mathbf {\vec {E}} ]=0

∇ φ × [E →] + 1 c φ T [μ H →] знак равно 0 {\ displaystyle \ nabla \ varphi \ times [\ mathbf {\ vec {E}}] + {1 \ over c} \, \ varphi _ {t} \, [\ mu \ mathbf {\ vec {H}}] = 0}

\nabla \varphi \times [\mathbf {\vec {E}} ]+{1 \over c}\,\varphi _{t}\,[\mu \mathbf {\vec {H}} ]=0

∇ ⋅ [ε E →] = 0 {\ displaystyle \ nabla \ cdot [\ varepsilon \ mathbf {\ vec {E}}] = 0}

\nabla \cdot [\varepsilon \mathbf {\vec {E}} ]=0

∇ ⋅ [μ H →] = 0 {\ displaystyle \ nabla \ cdot [\ mu \ mathbf {\ vec {H}}] = 0}

\nabla \cdot [\mu \mathbf {\vec {H}} ]=0

, где $∇ {\ displaystyle \ nabla}$ Оператор $\nabla$ действует в пространстве $xyz {\ displaystyle xyz}$ $xyz$ (для каждого фиксированного $t {\ displaystyle t}$ $t$ ), а квадратные скобки обозначают разница в значениях по обе стороны от поверхности разрыва (настраивается в соответствии с произвольным, но фиксированным соглашением, например, градиент $∇ φ {\ displaystyle \ nabla \ varphi}$ $\nabla \varphi$ , указывающий в направлении количества s вычитается из).

Набросок доказательства. Начните с уравнений Максвелла вдали от источников (гауссовские единицы):

∇ ⋅ ε E → = 0 {\ displaystyle \ nabla \ cdot \ varepsilon \ mathbf {\ vec {E} } = 0}

\nabla \cdot \varepsilon \mathbf {\vec {E}} =0

∇ ⋅ μ H → знак равно 0 {\ displaystyle \ nabla \ cdot \ mu \ mathbf {\ vec {H}} = 0}

\nabla \cdot \mu \mathbf {\vec {H}} =0

∇ × E → + μ c H → t = 0 {\ displaystyle \ nabla \ times \ mathbf {\ vec {E}} + {\ mu \ over c} \, \ mathbf {\ vec {H}} _ {t} = 0}

{\displayst yle \nabla \times \mathbf {\vec {E}} +{\mu \over c}\,\mathbf {\vec {H}} _{t}=0}

∇ × H → - ε с E → T знак равно 0 {\ Displaystyle \ набла \ раз \ mathbf {\ vec {H}} - {\ varepsilon \ over c} \, \ mathbf {\ vec {E}} _ {t} = 0}

\nabla \times \mathbf {\vec {H}} -{\varepsilon \over c}\,\mathbf {\vec {E}} _{t}=0

Используя теорему Стокса в $R 4 {\ displaystyle \ mathbf {R} ^ {4}}$ $\mathbf {R} ^{4}$ , из первого из приведенных выше уравнений можно сделать вывод, что для любой области $D { \ displaystyle D}$ $D$ в $R 4 {\ displaystyle \ mathbf {R} ^ {4}}$ $\mathbf {R} ^{4}$ с кусочно-гладкой границей $Γ {\ displaystyle \ Gamma}$ $\Gamma$ верно следующее:

∮ Γ (M → ⋅ ε E →) d S = 0 {\ displaystyle \ oint _ {\ Gamma} (\ mathbf {\ vec {M}} \ cdot \ varepsilon \ mathbf {\ vec {E}}) \, dS = 0}

\oint _{\Gamma }(\mathbf {\vec {M}} \cdot \varepsilon \mathbf {\vec {E}})\,dS=0

, где $M → {\ dis playstyle \ mathbf {\ vec {M}}}$ $\mathbf {\vec {M}}$ - это проекция единичной нормали к поверхности $φ = 0 {\ displaystyle \ varphi = 0}$ $\varphi = 0$ на 3D slice $t = const {\ displaystyle t = {\ rm {const}}}$ $t={\rm {const}}$ и $d S {\ displaystyle dS}$ $dS$ - объемная 3-форма на $Γ {\ displaystyle \ Gamma}$ $\Gamma$ . Точно так же из оставшихся уравнений Максвелла устанавливается следующее:

∮ Γ (M → ⋅ μ H →) d S = 0 {\ displaystyle \ oint _ {\ Gamma} (\ mathbf {\ vec {M}} \ cdot \ mu \ mathbf {\ vec {H}}) \, dS = 0}

\oint _{\Gamma }(\mathbf {\vec {M}} \cdot \mu \mathbf {\vec {H}})\,dS=0

∮ Γ (M → × E → + μ ct NH →) d S = 0 {\ displaystyle \ oint _ {\ Gamma} (\ mathbf {\ vec {M}} \ times \ mathbf {\ vec {E}} + {\ mu \ over c} \, t_ {N} \, \ mathbf {\ vec {H}}) \, dS Знак равно 0}

\oint _{\Gamma }(\mathbf {\vec {M}} \times \mathbf {\vec {E}} +{\mu \over c}\,t_{N}\,\mathbf {\vec {H}})\,dS=0

∮ Γ (M → × H → - ε ct NE →) d S = 0 {\ displaystyle \ oint _ {\ Gamma} (\ mathbf {\ vec {M}} \ times \ mathbf {\ vec {H}} - {\ varepsilon \ over c} \, t_ {N} \, \ mathbf {\ vec {E}}) \, dS = 0}

\oint _{\Gamma }(\mathbf {\vec {M}} \times \mathbf {\vec {H}} -{\varepsilon \over c}\,t_{N}\,\mathbf {\vec {E}})\,dS=0

где $t N {\ displaystyle t_ {N}}$ $t_{N}$ - четвертая (временная) координата нормализованного четырехмерного градиента $φ {\ displaystyle \ varphi}$ $\varphi$ :

∇ 4 D φ ‖ ∇ 4 D φ ‖ = (x N, Y N, Z N, T N) {\ Displaystyle {\ nabla ^ {4D} \ varphi \ over \ | \ nabla ^ {4D} \ varphi \ |} = (x_ {N}, y_ {N}, z_ {N}, t_ {N})}

{\nabla ^{4D}\varphi \over \|\nabla ^{4D}\varphi \|}=(x_{N},y_{N},z_{N},t_{N})

NB: Используя это обозначение, мы имеем: $M → = (x N, y N, z N) {\ displaystyle \ mathbf {\ vec {M }} = (x_ {N}, y_ {N}, z_ {N})}$ $\mathbf {\vec {M}} =(x_{N},y_{N},z_{N})$ .

Теперь по consi извлечение произвольных малых подповерхностей $Γ 0 {\ displaystyle \ Gamma _ {0}}$ $\Gamma _{0}$ из $Γ {\ displaystyle \ Gamma}$ $\Gamma$ и создание небольших окрестностей вокруг $Γ 0 {\ displaystyle \ Gamma _ {0}}$ $\Gamma _{0}$ в $R 4 {\ displaystyle \ mathbf {R} ^ {4}}$ $\mathbf {R} ^{4}$ , и вычитая выше интегралов соответственно, получаем:

∮ Γ 0 (∇ φ ⋅ [ε E →]) d S ‖ ∇ 4 D φ ‖ = 0 {\ displaystyle \ oint _ {\ Gamma _ {0}} (\ nabla \ varphi \ cdot [\ varepsilon \ mathbf {\ vec {E}}]) \, {dS \ over \ | \ nabla ^ {4D} \ varphi \ |} = 0}

\oint _{\Gamma _{0}}(\nabla \varphi \cdot [\varepsilon \mathbf {\vec {E}} ])\,{dS \over \|\nabla ^{4D}\varphi \|}=0

∮ Γ 0 (∇ φ ⋅ [μ H →]) d S ‖ ∇ 4 D φ ‖ знак равно 0 {\ displaystyle \ oint _ {\ Gamma _ {0}} (\ nabla \ varphi \ cdot [\ mu \ mathbf {\ vec {H}}]) \, {dS \ over \ | \ nabla ^ {4D} \ varphi \ |} = 0}

\oint _{\Gamma _{0}}(\nabla \varphi \cdot [\mu \mathbf {\vec {H}} ])\,{dS \over \|\nabla ^{4D}\varphi \|}=0

∮ Γ 0 (∇ φ × [H →] - 1 c φ t [ε E →]) d S ‖ ∇ 4 D φ ‖ знак равно 0 {\ displaystyle \ oint _ {\ Gamma _ {0}} \ left (\ nabla \ varphi \ times [\ mathbf {\ vec {H}}] - {1 \ over c} \, \ varphi _ {t} \, [\ varepsilon \ mathbf {\ vec {E}}] \ right) \, {dS \ over \ | \ nabla ^ {4D} \ varphi \ |} = 0}

\oint _{\Gamma _{0}}\left(\nabla \varphi \times [\mathbf {\vec {H}} ]-{1 \over c}\,\varphi _{t}\,[\varepsilon \mathbf {\vec {E}} ]\right)\,{dS \over \|\nabla ^{4D}\varphi \|}=0

∮ Γ 0 (∇ φ × [E →] + 1 c φ t [ μ H →]) d S ‖ ∇ 4 D φ ‖ знак равно 0 {\ displaystyle \ oint _ {\ Gamma _ {0}} \ left (\ nabla \ varphi \ times [\ mathbf {\ vec {E}}] + {1 \ over c} \, \ varphi _ {t} \, [\ mu \ mathbf {\ vec {H}}] \ right) \, {dS \ over \ | \ nabla ^ {4D} \ varphi \ | } = 0}

\oint _{\Gamma _{0}}\left(\nabla \varphi \times [\mathbf {\vec {E}} ]+{1 \over c}\,\varphi _{t}\,[\mu \mathbf {\vec {H}} ]\right)\,{dS \over \|\nabla ^{4D}\varphi \|}=0

Поскольку $Γ 0 {\ displaystyle \ Gamma _ {0}}$ $\Gamma _{0}$ произвольно, подынтегральные выражения должны быть равны 0, что доказывает лемму.

Теперь легко показать, что, проходя через сплошную среду, поверхности разрыва подчиняются уравнению эйконала. В частности, если $ε {\ displaystyle \ varepsilon}$ $\varepsilon$ и $μ {\ displaystyle \ mu}$ $\mu$ непрерывны, то разрывы $E → {\ displaystyle \ mathbf {\ vec {E}}}$ $\mathbf {\vec {E}}$ и $H → {\ displaystyle \ mathbf {\ vec {H}}}$ $\mathbf {\vec {H}}$ удовлетворяет: $[ε E →] = ε [E →] {\ displaystyle [\ varepsilon \ mathbf {\ vec {E}}] = \ varepsilon [\ mathbf {\ vec {E}}]}$ $[\varepsilon \mathbf {\vec {E}} ]=\varepsilon [\mathbf {\vec {E}} ]$ и $[ μ H →] = μ [H →] {\ Displaystyle [\ mu \ mathbf {\ vec {H}}] = \ mu [\ mathbf {\ vec {H}}]}$ $[\mu \mathbf {\vec {H}} ]=\mu [\mathbf {\vec {H}} ]$ . В этом случае первые два уравнения леммы можно записать как:

∇ φ × [H →] - ε c φ t [E →] = 0 {\ displaystyle \ nabla \ varphi \ times [\ mathbf {\ vec {H}}] - {\ varepsilon \ over c} \, \ varphi _ {t} \, [\ mathbf {\ vec {E}}] = 0}

\nabla \varphi \times [\mathbf {\vec {H}} ]-{\varepsilon \over c}\,\varphi _{t}\,[\mathbf {\vec {E}} ]=0

∇ φ × [E →] + μ с φ T [ЧАС →] знак равно 0 {\ Displaystyle \ nabla \ varphi \ раз [\ mathbf {\ vec {E}}] + {\ mu \ over c} \, \ varphi _ {t} \, [\ mathbf {\ vec {H}}] = 0}

\nabla \varphi \times [\mathbf {\vec {E}} ]+{\mu \over c}\,\varphi _{t}\,[\mathbf {\vec {H}} ]=0

Взяв векторное произведение первого уравнения на $∇ φ {\ displaystyle \ nabla \ varphi}$ $\nabla \varphi$ и подставив второе, получаем:

∇ φ × (∇ φ × [H →]) - ε c φ t (∇ φ × [E →]) = (∇ φ ⋅ [H →]) ∇ φ - ‖ ∇ φ ‖ 2 [H →] + ε μ с 2 φ T 2 [ЧАС →] знак равно 0 {\ displaystyle \ nabla \ varphi \ times (\ nabla \ varphi \ times [\ mathbf {\ vec {H}}]) - {\ varepsilon \ over c} \, \ varphi _ {t} \, (\ nabla \ varphi \ times [\ mathbf {\ vec {E}}]) = (\ nabla \ varphi \ cdot [\ mathbf {\ vec {H}}]) \, \ nabla \ varphi - \ | \ nabla \ varphi \ | ^ {2} \, [\ mathbf {\ vec {H}}] + {\ varepsilon \ mu \ over c ^ {2}} \ varphi _ {t} ^ {2} \, [\ mathbf {\ vec {H}}] = 0}

\nabla \varphi \times (\nabla \varphi \times [\mathbf {\vec {H}} ])-{\varepsilon \over c}\,\varphi _{t}\,(\nabla \varphi \times [\mathbf {\vec {E}} ])=(\nabla \varphi \cdot [\mathbf {\vec {H}} ])\,\nabla \varphi -\|\nabla \varphi \|^{2}\,[\mathbf {\vec {H}} ]+{\varepsilon \mu \over c^{2}}\varphi _{t}^{2}\,[\mathbf {\vec {H}} ]=0

По второму уравнению Максвелла, $∇ φ ⋅ [H →] = 0 {\ displaystyle \ nabla \ varphi \ cdot [\ mathbf {\ vec {H}}] = 0}$ $\nabla \varphi \cdot [\mathbf {\vec {H}} ]=0$ , следовательно, только для точек, лежащих на поверхности $φ = 0 {\ displaystyle \ varphi = 0}$ $\varphi = 0$ :

‖ ∇ φ ‖ 2 = ε μ c 2 φ t 2 {\ displaystyle \ | \ nabla \ varphi \ | ^ {2} = {\ varepsilon \ mu \ over c ^ {2}} \ varphi _ {t} ^ {2}}

\|\nabla \varphi \|^{2}={\varepsilon \mu \over c^{2}}\varphi _{t}^{2}

(Обратите внимание на наличие разрыва на этом шаге, поскольку в противном случае мы бы делили на ноль.)

Из физических соображений можно без ограничения общности предположить, что $φ {\ displaystyle \ varphi}$ $\varphi$ равно имеет следующий вид: $φ (x, y, z, t) = ψ (x, y, z) - ct {\ displaystyle \ varphi (x, y, z, t) = \ psi (x, y, z) -ct}$ $\varphi (x,y,z,t)=\psi (x,y,z)-ct$ , т.е. двумерная поверхность, движущаяся в пространстве, смоделированная как поверхности уровня $ψ {\ displaystyle \ psi}$ $\psi$ . (Математически $ψ {\ displaystyle \ psi}$ $\psi$ существует, если $φ t ≠ 0 {\ displaystyle \ varphi _ {t} \ neq 0}$ $\varphi _{t}\neq 0$ на теорема о неявной функции.) Вышеупомянутое уравнение, записанное в терминах $ψ {\ displaystyle \ psi}$ $\psi$ , принимает следующий вид:

‖ ∇ ψ ‖ 2 = ε μ c 2 (- c) 2 знак равно ε μ знак равно N 2 {\ Displaystyle \ | \ набла \ psi \ | ^ {2} = {\ varepsilon \ mu \ over c ^ {2}} \, (- c) ^ {2} = \ varepsilon \ mu = n ^ {2}}

\|\nabla \psi \|^{2}={\varepsilon \mu \over c^{2}}\,(-c)^{2}=\varepsilon \mu =n^{2}

т.е.

ψ x 2 + ψ y 2 + ψ z 2 = n 2 {\ displaystyle \ psi _ {x} ^ {2} + \ psi _ {y } ^ {2} + \ psi _ {z} ^ {2} = n ^ {2}}

\psi _{x}^{2}+\psi _{y}^{2}+\psi _{z}^{2}=n^{2}

, которое является уравнением эйконала и выполняется для всех $x {\ displaystyle x}$ $x$ , $y { \ displaystyle y}$ $y$ , $z {\ displaystyle z}$ $z$ , поскольку переменная $t {\ displaystyle t}$ $t$ отсутствует. Другие законы оптики, такие как закон Снеллиуса и формулы Френеля, могут быть аналогичным образом получены с учетом разрывов в $ε {\ displaystyle \ varepsilon}$ $\varepsilon$ и $μ {\ displaystyle \ mu}$ $\mu$ .