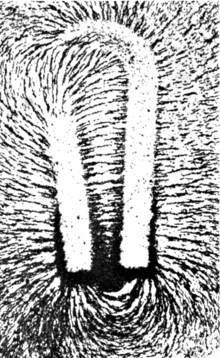
 Форма магнитного поля, создаваемого подковообразным магнитом, определяется ориентацией железных опилок, разбросанных на листе бумаги над магнитом.
Форма магнитного поля, создаваемого подковообразным магнитом, определяется ориентацией железных опилок, разбросанных на листе бумаги над магнитом. Магнитное поле представляет собой векторное поле, которое описывает магнитное воздействие на перемещение электрических зарядов, электрических токов и магнитных материалов. Движущийся заряд в магнитном поле испытывает силу, перпендикулярную его собственной скорости и магнитному полю. Постоянный магнит «S поля тянут магнитные на ферромагнитных материалах, такие как железо, и привлекает или отталкивает другие магниты. Кроме того, магнитное поле, которое изменяется в зависимости от местоположения, будет оказывать влияние на ряд немагнитных материалов, влияя на движение их внешних атомных электронов. Магнитные поля окружают намагниченные материалы и создаются электрическими токами, такими как те, которые используются в электромагнитах, и электрическими полями, меняющимися во времени. Поскольку как сила, так и направление магнитного поля могут изменяться в зависимости от местоположения, оно математически описывается функцией, присваивающей вектор каждой точке пространства, называемой векторным полем.
В электромагнетизма, термин «магнитное поле» используется для двух различных, но тесно связанных с ними векторных полей, обозначенных символами B и H. В Международной системе единиц, H, напряженности магнитного поля, измеряется в СИ базовых единицах ампер на метр (А / м). B, плотность магнитного потока, измеряется в теслах (в основных единицах СИ: килограмм в секунду 2 на ампер), что эквивалентно ньютону на метр на ампер. H и B различаются тем, как они учитывают намагниченность. В вакууме, два поля связаны через вакуум проницаемость, ; но в намагниченном материале условия различаются намагниченностью материала в каждой точке.
Магнитные поля создаются двигающейся электрические заряды и внутренние магнитные моменты из элементарных частиц, связанных с фундаментальной квантовой собственностью, их спины. Магнитные поля и электрические поля взаимосвязаны и являются компонентами электромагнитной силы, одной из четырех фундаментальных сил природы.
Магнитные поля используются в современной технике, особенно в электротехнике и электромеханике. Вращающиеся магнитные поля используются как в электродвигателях, так и в генераторах. Взаимодействие магнитных полей в электрических устройствах, таких как трансформаторы, рассматривается и исследуется как магнитные цепи. Магнитные силы дают информацию о носителях заряда в материале через эффект Холла. Земля создает собственное магнитное поле, которое защищает озоновый слой Земли от солнечного ветра и играет важную роль в навигации с использованием компаса.
Сила, действующая на электрический заряд, зависит от его местоположения, скорости и направления; два векторных поля используются для описания этой силы. Первое - это электрическое поле, которое описывает силу, действующую на неподвижный заряд, и дает составляющую силы, не зависящую от движения. Магнитное поле, напротив, описывает компонент силы, который пропорционален скорости и направлению заряженных частиц. Поле определяется законом силы Лоренца и в каждый момент времени перпендикулярно как движению заряда, так и силе, которую он испытывает.
Есть два различных, но тесно связанных векторных полей, которые иногда называют как «магнитное поле», написанной Б и Н. Хотя как лучшие названия для этих полей, так и точная интерпретация того, что они представляют, были предметом длительных дискуссий, существует широкое согласие относительно того, как работает лежащая в основе физика. Исторически сложилось, что термин «магнитное поле» было зарезервировано для H во время использования других терминов для B, но многие недавние учебники используют термин «магнитное поле», чтобы описать B, а также или вместо H. Для обоих есть много альтернативных имен (см. Врезку).
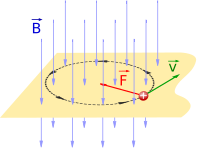 Заряженная частица, которая движется со скоростью V в магнитном поле B будет чувствовать магнитную силу F. Поскольку магнитная сила всегда тянет боком к направлению движения, частица движется по кругу.
Заряженная частица, которая движется со скоростью V в магнитном поле B будет чувствовать магнитную силу F. Поскольку магнитная сила всегда тянет боком к направлению движения, частица движется по кругу.  Поскольку эти три вектора связаны друг с другом перекрестным произведением, направление этой силы можно найти с помощью правила правой руки.
Поскольку эти три вектора связаны друг с другом перекрестным произведением, направление этой силы можно найти с помощью правила правой руки. | Альтернативные названия для B |
|---|
|
Вектор магнитного поля B в любой точке может быть определен как вектор, который при использовании в законе силы Лоренца правильно предсказывает силу, действующую на заряженную частицу в этой точке:
Закон силы Лоренца ( векторная форма, единицы СИ )
Здесь F - сила, действующая на частицу, q - электрический заряд частицы, v - скорость частицы, а × обозначает перекрестное произведение. Направление силы, действующей на заряд, можно определить с помощью мнемоники, известной как правило правой руки (см. Рисунок). Используя правую руку, указывая большим пальцем в направлении тока, а пальцами в направлении магнитного поля, результирующая сила, действующая на заряд, направлена наружу от ладони. Сила, действующая на отрицательно заряженную частицу, находится в противоположном направлении. Если и скорость, и заряд меняются местами, то направление силы остается прежним. По этой причине измерение магнитного поля (само по себе) не может различить, есть ли положительный заряд, движущийся вправо, или отрицательный заряд, движущийся влево. (Оба этих случая производят один и тот же ток.) С другой стороны, магнитное поле в сочетании с электрическим полем может различать их, см. Эффект Холла ниже.
Первый член в уравнении Лоренца взят из теории электростатики и говорит, что частица с зарядом q в электрическом поле E испытывает электрическую силу:
Второй член - магнитная сила:
Используя определение перекрестного произведения, магнитную силу также можно записать в виде скалярного уравнения:
где Р магнитное, V, и B являются скалярная величина их соответствующих векторов, и θ представляет собой угол между скоростью частицы и магнитным полем. Вектор В это определяется как поле вектора, необходимого, чтобы сделать закон силы Лоренца правильно описывают движение заряженной частицы. Другими словами,
[Эта] команда «Измерьте направление и величину вектора B в таком-то месте» требует следующих операций: Возьмите частицу с известным зарядом q. Измерьте усилие на д в покое, чтобы определить E. Затем измерьте силу, действующую на частицу, когда ее скорость равна v ; повторите с v в другом направлении. Теперь найдите B, при котором закон силы Лоренца соответствует всем этим результатам - это магнитное поле в рассматриваемом месте.
Поле B также может быть определено крутящим моментом на магнитном диполе, м.
Магнитный момент ( векторная форма, единицы СИ )
В единицах СИ B измеряется в теслах (обозначение: T). В гауссовых-СГС, B измеряется в гаусс (символ: G). (Преобразование составляет 1 Т = 10000 Гс.) Одна нанотесла эквивалентна 1 гамме (символ: γ).
| Альтернативные названия для H |
|---|
|
Магнитное поле H определяется:
Определение H поля ( вектор формы, единицы СИ )
Где - проницаемость вакуума, а M - вектор намагниченности. В вакууме B и H пропорциональны друг другу. Внутри материала они разные (см. H и B внутри и снаружи магнитных материалов). Поле H измеряется в амперах на метр (А / м) в единицах СИ и в эрстедах (Э) в единицах сгс.
Инструмент, используемый для измерения местного магнитного поля, известен как магнитометр. Важные классов магнитометров включают в себя использование индукционных магнитометров (или поиск-катушке магнитометров), которые измеряют только изменение магнитных полей, вращающиеся магнитометры катушки, эффект Холл магнитометры, ЯМР магнитометры, СКВИД магнитометры и индукционные магнитометры. Магнитные поля далеких астрономических объектов измеряются по их влиянию на местные заряженные частицы. Например, электроны, вращающиеся вокруг силовой линии, производят синхротронное излучение, которое можно обнаружить в радиоволнах. Наивысшая точность измерения магнитного поля была достигнута гравитационным зондом B при 5 ат (5 × 10 −18 Тл).
 Направление силовых линий магнитного поля представлено железными опилками, посыпанными на бумагу, помещенную над стержневым магнитом.
Направление силовых линий магнитного поля представлено железными опилками, посыпанными на бумагу, помещенную над стержневым магнитом.  Стрелки компаса указывают в направлении местного магнитного поля, к южному полюсу магнита и от его северного полюса.
Стрелки компаса указывают в направлении местного магнитного поля, к южному полюсу магнита и от его северного полюса. Поле можно визуализировать с помощью набора линий магнитного поля, которые следуют за направлением поля в каждой точке. Линии могут быть построены путем измерения силы и направления магнитного поля в большом количестве точек (или в каждой точке пространства). Затем отметьте каждое местоположение стрелкой (называемой вектором ), указывающей в направлении местного магнитного поля, величина которого пропорциональна силе магнитного поля. Соединение этих стрелок образует набор линий магнитного поля. Направление магнитного поля в любой точке параллельно направлению близлежащих силовых линий, и локальная плотность силовых линий может быть сделана пропорциональной ее напряженности. Линии магнитного поля подобны линиям тока в потоке жидкости в том смысле, что они представляют непрерывное распределение, а при другом разрешении будет отображаться больше или меньше линий.
Преимущество использования силовых линий магнитного поля в качестве представления состоит в том, что многие законы магнетизма (и электромагнетизма) могут быть изложены полностью и кратко с использованием простых понятий, таких как «количество» силовых линий, проходящих через поверхность. Эти концепции можно быстро «перевести» в их математическую форму. Например, количество силовых линий, проходящих через данную поверхность, является поверхностным интегралом магнитного поля.
Различные явления «отображают» силовые линии магнитного поля, как если бы силовые линии были физическим явлением. Например, железные опилки, помещенные в магнитное поле, образуют линии, которые соответствуют «силовым линиям». «Линии» магнитного поля также визуально отображаются в полярных сияниях, в которых дипольные взаимодействия частиц плазмы создают видимые полосы света, совпадающие с локальным направлением магнитного поля Земли.
Силовые линии можно использовать как качественный инструмент для визуализации магнитных сил. В ферромагнитных веществах, таких как железо, и в плазме, магнитные силы можно понять, представив, что силовые линии создают напряжение (как резинка) по своей длине и давление, перпендикулярное их длине, на соседние силовые линии. «В отличие от» полюса магнитов притягиваются, потому что они связаны множеством силовых линий; «подобные» полюса отталкиваются, потому что их силовые линии не пересекаются, а проходят параллельно, давя друг на друга.
Постоянные магниты - это объекты, которые создают свои собственные постоянные магнитные поля. Они сделаны из ферромагнитных материалов, таких как железо и никель, которые намагничены и имеют как северный, так и южный полюс.
Магнитное поле постоянных магнитов может быть довольно сложным, особенно вблизи магнита. Магнитное поле небольшого прямого магнита пропорционально силе магнита (называемой его магнитным дипольным моментом m). Эти уравнения являются нетривиальными, а также зависеть от расстояния от магнита и ориентации магнита. Для простых магнитов m указывает в направлении линии, проведенной от южного к северному полюсу магнита. Переворачивание стержневого магнита эквивалентно повороту его метра на 180 градусов.
Магнитное поле больших магнитов можно получить, моделируя их как совокупность большого количества маленьких магнитов, называемых диполями, каждый из которых имеет собственное значение m. Магнитное поле, создаваемое магнитом, тогда является чистым магнитным полем этих диполей; любая результирующая сила, действующая на магнит, является результатом суммирования сил на отдельных диполях.
Существовали две упрощенные модели природы этих диполей. Эти две модели производят два различных магнитных полей, H и B. Однако вне материала они идентичны (для мультипликативной константы), так что во многих случаях различие можно игнорировать. Это особенно верно для магнитных полей, например, создаваемых электрическими токами, которые не создаются магнитными материалами.
Реалистичная модель магнетизма сложнее любой из этих моделей; ни одна из моделей полностью не объясняет, почему материалы являются магнитными. Модель монополя не имеет экспериментального подтверждения. Модель Ампера объясняет некоторые, но не все, магнитный момент материала. Как предсказывает модель Ампера, движение электронов внутри атома связано с орбитальным магнитным дипольным моментом этих электронов, и эти орбитальные моменты действительно вносят вклад в магнетизм, наблюдаемый на макроскопическом уровне. Однако движение электронов не является классическим, и спиновый магнитный момент электронов (который не объясняется ни одной из моделей) также является значительным вкладом в общий момент магнитов.
 Модель магнитного полюса: два противоположных полюса, Северный (+) и Южный (-), разделенные расстоянием d, создают H- поле (линии).
Модель магнитного полюса: два противоположных полюса, Северный (+) и Южный (-), разделенные расстоянием d, создают H- поле (линии). Исторически сложилось так, что в ранних учебниках физики сила и крутящий момент между двумя магнитами моделировались как из-за отталкивания или притяжения друг друга магнитных полюсов так же, как кулоновская сила между электрическими зарядами. На микроскопическом уровне эта модель противоречит экспериментальным данным, и полюсная модель магнетизма больше не является типичным способом представления этой концепции. Однако его до сих пор иногда используют в качестве макроскопической модели ферромагнетизма из-за его математической простоты.
В этой модели магнитное H- поле создается фиктивными магнитными зарядами, которые распределены по поверхности каждого полюса. Эти магнитные заряды в действительности связано с полем намагниченности М. Следовательно, H- поле аналогично электрическому полю E, которое начинается с положительного электрического заряда и заканчивается отрицательным электрическим зарядом. Таким образом, около северного полюса все линии H- поля направлены от северного полюса (внутри магнита или снаружи), в то время как около южного полюса все линии H- поля указывают на южный полюс (внутри магнита или снаружи). Кроме того, северный полюс чувствует силу в направлении H- поля, в то время как сила на южном полюсе противоположна H- полю.
В модели магнитного полюса элементарный магнитный диполь m образован двумя противоположными магнитными полюсами с силой полюса q m, разделенными вектором небольшого расстояния d, так что m = q m d. Модель магнитного полюса правильно предсказывает поле H как внутри, так и снаружи магнитных материалов, в частности тот факт, что H противоположно полю намагничивания M внутри постоянного магнита.
Поскольку она основана на фиктивной идее плотности магнитного заряда, у полюсной модели есть ограничения. Магнитные полюса не могут существовать отдельно друг от друга, как электрические заряды, но всегда идут парами север-юг. Если намагниченный объект разделен пополам, на поверхности каждой части появляется новый полюс, поэтому у каждого есть пара дополнительных полюсов. Модель магнитного полюса не учитывает ни магнетизм, создаваемый электрическими токами, ни внутреннюю связь между угловым моментом и магнетизмом.
В модели полюса магнитный заряд обычно рассматривается как математическая абстракция, а не как физическое свойство частиц. Однако магнитный монополь - это гипотетическая частица (или класс частиц), которая физически имеет только один магнитный полюс (либо северный полюс, либо южный полюс). Другими словами, он обладал бы «магнитным зарядом», аналогичным электрическому заряду. Линии магнитного поля начинаются или заканчиваются на магнитных монополях, поэтому, если они существуют, они будут давать исключения из правила, согласно которому силовые линии магнитного поля не начинаются и не заканчиваются. Некоторые теории (например, теории Великого Объединения ) предсказывали существование магнитных монополей, но до сих пор ни одна из них не наблюдалась.

 Текущий цикл (кольцо), который переходит на страницу в точке x и выходит в точке, создает поле B (линии). По мере уменьшения радиуса токовой петли создаваемые поля становятся идентичными абстрактному «магнитостатическому диполю» (представленному стрелкой, указывающей вправо).
Текущий цикл (кольцо), который переходит на страницу в точке x и выходит в точке, создает поле B (линии). По мере уменьшения радиуса токовой петли создаваемые поля становятся идентичными абстрактному «магнитостатическому диполю» (представленному стрелкой, указывающей вправо). В модели, разработанной Ампером, элементарный магнитный диполь, из которого состоят все магниты, представляет собой достаточно малую амперовскую петлю тока I. Дипольный момент этой петли равен m = IA, где A - площадь петли.
Эти магнитные диполи создают магнитное B- поле.
Магнитное поле магнитного диполя изображено на рисунке. Снаружи идеальный магнитный диполь идентичен идеальному электрическому диполю такой же силы. В отличие от электрического диполя, магнитный диполь правильно моделируется как токовая петля, имеющая ток I и площадь a. Такая токовая петля имеет магнитный момент:
где направление m перпендикулярно области петли и зависит от направления тока с использованием правила правой руки. Идеальный магнитный диполь моделируется как реальный магнитный диполь, площадь которого a была уменьшена до нуля, а его ток I увеличен до бесконечности, так что произведение m = Ia является конечным. Эта модель проясняет связь между угловым моментом и магнитным моментом, который лежит в основе вращения эффекта Эйнштейна – де Гааза за счет намагничивания и его обратного эффекта, эффекта Барнетта или намагничивания за счет вращения. Более быстрое вращение петли (в том же направлении) увеличивает, например, ток и, следовательно, магнитный момент.
Определение силы между двумя маленькими магнитами довольно сложно, потому что она зависит от силы и ориентации обоих магнитов, а также их расстояния и направления относительно друг друга. Сила особенно чувствительна к вращению магнитов из-за магнитного момента. Сила, действующая на каждый магнит, зависит от его магнитного момента и магнитного поля другого.
Чтобы понять силу между магнитами, полезно изучить модель магнитного полюса, приведенную выше. В этой модели H- поле одного магнита толкает и притягивает оба полюса второго магнита. Если это H- поле одинаково на обоих полюсах второго магнита, то на этот магнит нет результирующей силы, поскольку сила противоположна для противоположных полюсов. Однако, если магнитное поле первого магнита неоднородно (например, H около одного из его полюсов), каждый полюс второго магнита видит другое поле и подвергается действию другой силы. Эта разница в двух силах перемещает магнит в направлении увеличения магнитного поля и может также вызвать чистый крутящий момент.
Это конкретный пример общего правила, согласно которому магниты притягиваются (или отталкиваются в зависимости от ориентации магнита) в области с более высоким магнитным полем. Любое неоднородное магнитное поле, вызванное постоянными магнитами или электрическим током, воздействует на небольшой магнит таким образом.
Детали модели петли Ампера различны и более сложны, но дают один и тот же результат: магнитные диполи притягиваются / отталкиваются в области более высокого магнитного поля. Математически сила, действующая на небольшой магнит с магнитным моментом m из-за магнитного поля B, равна:
где градиент ∇ является изменение величины м B на единицу расстояния и направления является то, что максимальное увеличение м B. Скалярное произведение м B = М.Б. соз ( amp; thetas ;), где т и В представляют собой величину из м и B векторов и θ представляет собой угол между ними. Если m находится в том же направлении, что и B, то скалярное произведение положительно, и точки градиента «поднимаются вверх», втягивая магнит в области более высокого поля B (более строго большего m B). Это уравнение действительно только для магнитов нулевого размера, но часто является хорошим приближением для не слишком больших магнитов. Магнитная сила на больших магнитах определяется путем их разделения на более мелкие области, каждая из которых имеет свой собственный m, а затем суммирования сил на каждой из этих очень маленьких областей.
Если два одинаковых полюса двух отдельных магнитов приблизить друг к другу и одному из магнитов дать возможность повернуться, он быстро повернется, чтобы выровняться с первым. В этом примере магнитное поле неподвижного магнита создает магнитный момент на магните, который может свободно вращаться. Этот магнитный момент τ стремится выровнять полюса магнита с силовыми линиями магнитного поля. Компас, таким образом, поворачивается, чтобы выровняться с магнитным полем Земли.
Крутящий момент на диполе В полюсной модели диполя поле H (справа) вызывает равные, но противоположные силы на полюсе N ( + q) и полюсе S ( - q), создавая крутящий момент.
В полюсной модели диполя поле H (справа) вызывает равные, но противоположные силы на полюсе N ( + q) и полюсе S ( - q), создавая крутящий момент.  Эквивалентно, поле B индуцирует тот же крутящий момент в токовой петле с тем же магнитным дипольным моментом.
Эквивалентно, поле B индуцирует тот же крутящий момент в токовой петле с тем же магнитным дипольным моментом. С точки зрения модели полюса, два равных и противоположных магнитных заряда, испытывающих одинаковую H, также испытывают равные и противоположные силы. Поскольку эти равные и противоположные силы находятся в разных местах, это создает крутящий момент, пропорциональный расстоянию (перпендикулярному силе) между ними. С определением m как силы полюса, умноженной на расстояние между полюсами, это приводит к τ = μ 0 m H sin θ, где μ 0 - постоянная, называемая проницаемостью вакуума, измеряющая4π × 10 -7 В с / ( А м ), а θ - угол между Н и м.
Математически крутящий момент τ на маленьком магните пропорционален приложенному магнитному полю и магнитному моменту m магнита:
где × представляет векторное векторное произведение. Это уравнение включает всю качественную информацию, включенную выше. На магните нет крутящего момента, если m находится в том же направлении, что и магнитное поле, поскольку перекрестное произведение равно нулю для двух векторов, находящихся в одном направлении. Кроме того, все остальные ориентации ощущают крутящий момент, который скручивает их в направлении магнитного поля.
Токи электрических зарядов создают магнитное поле и ощущают силу, обусловленную магнитными B-полями.
 Правило захвата правой рукой : ток, текущий в направлении белой стрелки, создает магнитное поле, показанное красными стрелками.
Правило захвата правой рукой : ток, текущий в направлении белой стрелки, создает магнитное поле, показанное красными стрелками. Все движущиеся заряженные частицы создают магнитные поля. Движущиеся точечные заряды, такие как электроны, создают сложные, но хорошо известные магнитные поля, которые зависят от заряда, скорости и ускорения частиц.
Силовые линии магнитного поля образуют концентрические круги вокруг цилиндрического проводника с током, такого как кусок провода. Направление такого магнитного поля можно определить с помощью « правила правого захвата » (см. Рисунок справа). Сила магнитного поля уменьшается с удалением от провода. (Для проволоки бесконечной длины сила обратно пропорциональна расстоянию.)
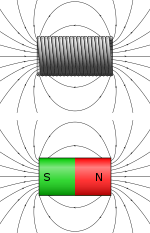 Соленоид с электрическим током, протекающим через он ведет себя как магнит.
Соленоид с электрическим током, протекающим через он ведет себя как магнит. Сгибание токоведущего провода в петлю концентрирует магнитное поле внутри петли, ослабляя его снаружи. Сгибание провода в несколько близко расположенных петель с образованием катушки или « соленоида » усиливает этот эффект. Устройство, сформированное таким образом вокруг железного сердечника, может действовать как электромагнит, создавая сильное, хорошо контролируемое магнитное поле. Бесконечно длинный цилиндрический электромагнит имеет однородное магнитное поле внутри и не имеет магнитного поля снаружи. Электромагнит конечной длины создает магнитное поле, которое похоже на то, которое создается однородным постоянным магнитом, его сила и полярность определяются током, протекающим через катушку.
Магнитное поле, создаваемое постоянным током I (постоянный поток электрических зарядов, в котором заряд не накапливается и не истощается в любой точке) описывается законом Био – Савара :
где интегральная сумма по длине провода, где вектор d ℓ - это элемент векторной линии с направлением в том же смысле, что и ток I, μ 0 - магнитная постоянная, r - расстояние между местоположением d ℓ и местом, где магнитное поле вычисляется, а r̂ - единичный вектор в направлении r. Например, в случае достаточно длинного прямого провода это будет: где r = | г |. Направление касается круга, перпендикулярного проводу, согласно правилу правой руки.Несколько более общий способ соотнести ток с
B- полем - через закон Ампера : где линейный интеграл берется по любому произвольному циклу, а enc - ток, заключенный в этом цикле. Закон Ампера всегда справедлив для установившихся токов и может использоваться для расчета B- поля для определенных высокосимметричных ситуаций, таких как бесконечный провод или бесконечный соленоид.В модифицированной форме, которая учитывает изменяющиеся во времени электрические поля, закон Ампера является одним из четырех уравнений Максвелла, описывающих электричество и магнетизм.
Заряженные частицы, двигающиеся в B - поле испытывает боковое усилие, которое пропорционально силе магнитного поля, составляющая скорости, перпендикулярные к магнитному полю и заряду частицы. Эта сила известна как сила Лоренца и определяется выражением
где F - сила, q - электрический заряд частицы, v - мгновенная скорость частицы, а B - магнитное поле (в теслах ).Сила Лоренца всегда перпендикулярна как скорости частицы, так и магнитному полю, создавшему ее. Когда заряженная частица движется в постоянном магнитном поле, она движется по спиральной траектории, ось спирали которой параллельна магнитному полю, а скорость частицы остается постоянной. Поскольку магнитная сила всегда перпендикулярна движению, магнитное поле не может работать с изолированным зарядом. Он может работать только косвенно, через электрическое поле, создаваемое изменяющимся магнитным полем. Часто утверждают, что магнитная сила может работать с неэлементарным магнитным диполем или с заряженными частицами, движение которых ограничено другими силами, но это неверно, потому что в этих случаях работа выполняется электрическими силами зарядов. отклоняется магнитным полем.
Сила, действующая на провод с током, аналогична силе движущегося заряда, как и ожидалось, поскольку провод с током представляет собой совокупность движущихся зарядов. Токоведущий провод чувствует силу в присутствии магнитного поля. Сила Лоренца на макроскопическом токе часто называется силой Лапласа. Рассмотрим проводник длины л, сечения А и заряда д за счет электрического тока I. Если этот проводник поместить в магнитное поле величиной B, которое составляет угол θ со скоростью зарядов в проводнике, сила, действующая на отдельный заряд q, равна
Итак, для N зарядов где сила, действующая на проводник, равна где i = nqvA.Выведенные выше формулы для магнитного поля верны при работе со всем током. Однако магнитный материал, помещенный в магнитное поле, генерирует собственный связанный ток, который может быть сложной задачей для расчета. (Этот связанный ток возникает из-за суммы токовых петель атомного размера и спина субатомных частиц, таких как электроны, составляющие материал.) H- поле, как определено выше, помогает выделить этот связанный ток; но чтобы увидеть, как это сделать, сначала полезно познакомиться с концепцией
намагничивания.Намагниченность векторное поле М представляет собой, как сильно намагничивается область материала. Он определяется как чистый магнитный дипольный момент на единицу объема этой области. Таким образом, намагниченность однородного магнита является материальной постоянной, равной магнитному моменту m магнита, деленному на его объем. Поскольку единица измерения магнитного момента в системе СИ - А м 2, единица измерения намагниченности M в системе СИ - это ампер на метр, что совпадает с единицей измерения H- поля.
Поле намагниченности M области указывает направление среднего магнитного дипольного момента в этой области. Поэтому силовые линии намагничивания начинаются около южного магнитного полюса и заканчиваются около северного магнитного полюса. (Намагниченности вне магнита нет.)
В модели петли Ампера намагниченность возникает из-за объединения множества крошечных петель Ампера, чтобы сформировать результирующий ток, называемый связанным током. Этот связанный ток является источником магнитного поля B, создаваемого магнитом. Учитывая определение магнитного диполя, поле намагничивания подчиняется закону, аналогичному закону Ампера:
где интеграл - это линейный интеграл по любому замкнутому контуру, а I b - связанный ток, заключенный в этом замкнутом контуре.
В модели магнитного полюса намагничивание начинается и заканчивается на магнитных полюсах. Следовательно, если данная область имеет чистую положительную «силу магнитного полюса» (соответствующую северному полюсу), тогда в нее входит больше силовых линий намагничивания, чем выходит из нее. Математически это эквивалентно:
,где интеграл представляет собой замкнутый поверхностный интеграл по замкнутой поверхности S и д М является «магнитным зарядом» (в единицах магнитного потока ), вложенных S. (Замкнутая поверхность полностью окружает область без отверстий, позволяющую выходить силовым линиям.) Отрицательный знак возникает из-за того, что поле намагничивания перемещается с юга на север.
 Сравнение B, H и M внутри и снаружи цилиндрического стержневого магнита. См. Также: Размагничивающее поле
Сравнение B, H и M внутри и снаружи цилиндрического стержневого магнита. См. Также: Размагничивающее поле В единицах СИ H-поле связано с B-полем соотношением
В терминах H-поля закон Ампера имеет вид
где I f представляет собой «свободный ток», заключенный в контур, так что линейный интеграл H вообще не зависит от связанных токов.Для дифференциального эквивалента этого уравнения см. Уравнения Максвелла. Закон Ампера приводит к граничному условию
где K f - поверхностная плотность свободного тока, а единичная нормаль указывает в направлении от среды 2 к среде 1.Аналогичным образом, поверхностный интеграл от Н над любой замкнутой поверхности не зависит от свободных токов и выбирает из «магнитных зарядов» внутри этой замкнутой поверхности:
которое не зависит от свободных токов.
Следовательно, H- поле можно разделить на две независимые части:
где H 0 - приложенное магнитное поле, создаваемое только свободными токами, а H d - размагничивающее поле, обусловленное только связанными токами.
Следовательно, магнитное H- поле повторно факторизует связанный ток с точки зрения «магнитных зарядов». Н силовые линии контура только вокруг «свободный ток», и, в отличие от магнитного B поля, начинается и заканчивается рядом магнитных полюсов, а также.
Большинство материалов реагируют на приложенное B- поле, создавая свою собственную намагниченность M и, следовательно, свои собственные B- поля. Обычно реакция слабая и существует только при приложении магнитного поля. Термин магнетизм описывает, как материалы реагируют на микроскопическом уровне на приложенное магнитное поле, и используется для классификации магнитной фазы материала. Материалы делятся на группы в зависимости от их магнитных свойств:
В случае парамагнетизма и диамагнетизма намагниченность M часто пропорциональна приложенному магнитному полю, так что:
где μ - параметр, зависящий от материала, называемый проницаемостью. В некоторых случаях проницаемость может быть второго ранга тензор так, что Н может не указывать в том же направлении, что и B. Эти отношения между B и H являются примерами определяющих уравнений. Однако, сверхпроводники и ферромагнетиков имеют более сложную B -До- H отношению; см. магнитный гистерезис.Энергия необходима для создания магнитного поля как для работы против электрического поля, создаваемого изменяющимся магнитным полем, так и для изменения намагниченности любого материала в магнитном поле. Для недисперсионных материалов эта же энергия высвобождается при разрушении магнитного поля, так что энергия может быть смоделирована как хранимая в магнитном поле.
Для линейных, недисперсионных материалов (таких, что B = μ H, где μ не зависит от частоты), плотность энергии равна:
Если поблизости нет магнитных материалов, то μ можно заменить на μ 0. Однако приведенное выше уравнение нельзя использовать для нелинейных материалов; необходимо использовать более общее выражение, приведенное ниже.
В общем, дополнительная работа на единицу объема δW, необходимая для того, чтобы вызвать небольшое изменение магнитного поля δ B, равна:
Как только связь между H и B известна, это уравнение используется для определения работы, необходимой для достижения заданного магнитного состояния. Для гистерезисных материалов, таких как ферромагнетики и сверхпроводники, необходимая работа также зависит от того, как создается магнитное поле. Однако для линейных недисперсионных материалов общее уравнение приводит непосредственно к более простому уравнению плотности энергии, приведенному выше.
Как и все векторные поля, магнитное поле имеет два важных математических свойства, которые связывают его с его источниками. (Для B на источниках тока и изменение электрических полей.) Эти два свойство, наряду с двумя соответствующих свойствами электрического поля, составляют уравнения Максвелла. Уравнения Максвелла вместе с законом силы Лоренца образуют полное описание классической электродинамики, включая электричество и магнетизм.
Первое свойство - это дивергенция векторного поля A, ∇ A, которое представляет, как A «течет» наружу из данной точки. Как обсуждалось выше, линия B- поля никогда не начинается и не заканчивается в точке, а вместо этого образует полный цикл. Это математически эквивалентно тому, что дивергенция B равна нулю. (Такие векторные поля называются соленоидальными векторными полями. ) Это свойство называется законом Гаусса для магнетизма и эквивалентно утверждению об отсутствии изолированных магнитных полюсов или магнитных монополей.
Второе математическое свойство называется изгибом, так что ∇ × A представляет, как A изгибается или «циркулирует» вокруг данной точки. Результат завивки называется «источником циркуляции». Уравнения для ротора B и E называются уравнением Ампера – Максвелла и законом Фарадея соответственно.
Одним из важных свойств создаваемого таким образом B- поля является то, что линии магнитного B- поля не начинаются и не заканчиваются (математически B - соленоидальное векторное поле ); линия поля может простираться только до бесконечности, или закругляться, образуя замкнутую кривую, или следовать бесконечному (возможно, хаотическому) пути. Линии магнитного поля выходят из магнита около его северного полюса и входят около его южного полюса, но внутри магнита линии B- поля проходят через магнит от южного полюса обратно на север. Если линия B- поля попадает куда-то в магнит, она должна куда-то уходить; не допускается иметь конечную точку.
Более формально, поскольку все силовые линии магнитного поля, которые входят в любую заданную область, должны также покидать эту область, вычитание «количества» силовых линий, которые входят в область, из числа, выходящего из нее, дает идентичный ноль. Математически это эквивалентно закону Гаусса для магнетизма :
где интеграл является поверхностным интегралом по замкнутой поверхности S (замкнутая поверхность - это поверхность, которая полностью окружает область без отверстий, позволяющую выйти любым силовым линиям). Поскольку d A указывает наружу, скалярное произведение в интеграле положительно для указывающего B- поля и отрицательно для B- поля, указывающего внутрь.
Изменяющееся магнитное поле, такое как магнит, движущийся через проводящую катушку, создает электрическое поле (и, следовательно, имеет тенденцию управлять током в такой катушке). Это известно как закон Фарадея и лежит в основе многих электрических генераторов и электродвигателей. Математически закон Фарадея:
где -
электродвижущая сила (или ЭДС, напряжение, генерируемое вокруг замкнутого контура), а Φ - магнитный поток - произведение площади на магнитное поле, перпендикулярное этой области. (Это определение магнитного потока почему Б часто называют плотностью магнитного потока.) Отрицательный знак представляет тот факт, что любой ток, генерируемый в переменном магнитном поле в катушке создает магнитное поле, которое противодействует по изменению в магнитном поле, вызвал это. Это явление известно как закон Ленца. Эта интегральная формулировка закона Фарадея может быть преобразована в дифференциальную форму, которая применяется при несколько иных условиях.Подобно тому, как изменяющееся магнитное поле создает электрическое поле, изменяющееся электрическое поле создает магнитное поле. Этот факт известен как поправка Максвелла к закону Ампера и применяется как дополнительный член к закону Ампера, как указано выше. Этот дополнительный член пропорционален скорости изменения электрического потока во времени и аналогичен приведенному выше закону Фарадея, но с другой положительной константой спереди. (Электрический поток через площадь пропорционален площади, умноженной на перпендикулярную часть электрического поля.)
Полный закон, включая поправочный член, известен как уравнение Максвелла – Ампера. Обычно он не дается в интегральной форме, потому что эффект настолько мал, что его обычно можно игнорировать в большинстве случаев, когда используется интегральная форма.
Термин Максвелла является критически важным в создании и распространении электромагнитных волн. Поправка Максвелла к закону Ампера вместе с законом индукции Фарадея описывает, как взаимно изменяющиеся электрические и магнитные поля взаимодействуют, поддерживая друг друга и, таким образом, формируя электромагнитные волны, такие как свет: изменяющееся электрическое поле порождает изменяющееся магнитное поле, которое генерирует изменяющееся электрическое поле. снова поле. Однако они обычно описываются с использованием приведенной ниже дифференциальной формы этого уравнения.
где J - полная микроскопическая плотность тока.
Как обсуждалось выше, материалы реагируют на приложенное электрическое поле E и магнитное поле B, создавая свои собственные внутренние «связанные» распределения заряда и тока, которые вносят вклад в E и B, но их трудно вычислить. Чтобы обойти эту проблему, поля H и D используются для повторного факторизации уравнений Максвелла с точки зрения плотности свободного тока J f:
Эти уравнения не более общие, чем исходные уравнения (если известны «связанные» заряды и токи в материале). Кроме того, они должны быть дополнены соотношением между B и H, а также, что между Е и D. С другой стороны, для простых соотношений между этими величинами эта форма уравнений Максвелла может обойти необходимость вычисления связанных зарядов и токов.
Согласно специальной теории относительности, разделение электромагнитной силы на отдельные электрические и магнитные компоненты не является фундаментальным, но изменяется в зависимости от системы отсчета наблюдения : электрическая сила, воспринимаемая одним наблюдателем, может восприниматься другим (в другой системе координат). ссылки) как магнитная сила или смесь электрических и магнитных сил.
Формально специальная теория относительности объединяет электрическое и магнитное поля в тензор второго ранга, называемый электромагнитным тензором. Изменение опорных кадров смешивает эти компоненты. Это аналогично тому, как специальная теория относительности смешивает пространство и время с пространством-временем, а массу, импульс и энергию - с четырьмя импульсами. Точно так же энергия, запасенная в магнитном поле, смешивается с энергией, запасенной в электрическом поле, в электромагнитном тензоре энергии-импульса.
В продвинутых темах, таких как квантовая механика и теория относительности, часто легче работать с потенциальной формулировкой электродинамики, чем с терминами электрического и магнитного полей. В этом представлении магнитный векторный потенциал A и электрический скалярный потенциал φ определены так, что:
Векторный потенциал A можно интерпретировать как обобщенный потенциальный импульс на единицу заряда, так же как φ интерпретируется как обобщенная потенциальная энергия на единицу заряда.
Уравнения Максвелла, выраженные в терминах потенциалов, можно без особых усилий привести в форму, согласующуюся со
специальной теорией относительности. В теории относительности A вместе с φ образует четырехмерный потенциал, аналогичный четырехмерному импульсу, который объединяет импульс и энергию частицы. Использование четырехпотенциала вместо электромагнитного тензора имеет то преимущество, что намного проще - и его можно легко модифицировать для работы с квантовой механикой.В современной физике, электромагнитное поле понимаются не классическое поле, а скорее квантовое поле ; он представлен не как вектор из трех чисел в каждой точке, а как вектор из трех квантовых операторов в каждой точке. Наиболее точное современное описание электромагнитного взаимодействия (и многого другого) - это квантовая электродинамика (КЭД), которая включена в более полную теорию, известную как Стандартная модель физики элементарных частиц.
В КЭД величина электромагнитных взаимодействий между заряженными частицами (и их античастицами ) вычисляется с использованием теории возмущений. Эти довольно сложные формулы создают замечательное графическое представление в виде диаграмм Фейнмана, в которых происходит обмен виртуальными фотонами.
Предсказания QED согласуются с экспериментами с чрезвычайно высокой степенью точности: в настоящее время около 10 −12 (и ограничено экспериментальными ошибками); подробности см. в прецизионных тестах QED. Это делает КЭД одной из наиболее точных физических теорий, построенных на данный момент.
Все уравнения в этой статье находятся в классическом приближении, которое менее точно, чем упомянутое здесь квантовое описание. Однако в большинстве повседневных обстоятельств разница между двумя теориями незначительна.
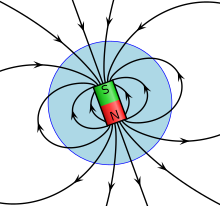 Эскиз магнитного поля Земли, представляющий источник поля в виде магнита. Южный полюс магнитного поля находится рядом с географическим северным полюсом Земли.
Эскиз магнитного поля Земли, представляющий источник поля в виде магнита. Южный полюс магнитного поля находится рядом с географическим северным полюсом Земли. Магнитное поле Земли создается конвекцией жидкого сплава железа во внешнем ядре. В динамо-процессе движения запускают процесс обратной связи, в котором электрические токи создают электрические и магнитные поля, которые, в свою очередь, действуют на токи.
Поле на поверхности Земли примерно такое же, как если бы гигантский стержневой магнит был расположен в центре Земли и наклонен под углом примерно 11 ° от оси вращения Земли (см. Рисунок). Северный полюс стрелки магнитного компаса указывает примерно на север, к Северному магнитному полюсу. Однако, поскольку магнитный полюс притягивается к своей противоположности, Северный магнитный полюс на самом деле является южным полюсом геомагнитного поля. Эта путаница в терминологии возникает из-за того, что полюс магнита определяется географическим направлением, на которое он указывает.
Магнитное поле Земли непостоянно - сила поля и положение его полюсов различаются. Более того, полюса периодически меняют свою ориентацию в процессе, называемом геомагнитным разворотом. Последний поворот произошел 780.000 лет назад.
Вращающееся магнитное поле является ключевым принципом в работе переменного тока двигателей. Постоянный магнит в таком поле вращается, чтобы поддерживать свое выравнивание с внешним полем. Этот эффект был концептуализирован Николой Тесла, а затем использовался в его и других ранних электродвигателях переменного тока.
Магнитный момент используется для привода электродвигателей. В одной простой конструкции двигателя магнит прикреплен к свободно вращающемуся валу и подвергается воздействию магнитного поля от множества электромагнитов. Постоянно переключая электрический ток через каждый из электромагнитов, меняя полярность их магнитных полей, подобные полюса сохраняются рядом с ротором; результирующий крутящий момент передается на вал.
Вращающееся магнитное поле может быть создано с использованием двух ортогональных катушек с разностью фаз переменного тока 90 градусов. Однако на практике такая система будет питаться по трехпроводной схеме с неравными токами.
Это неравенство вызовет серьезные проблемы при стандартизации сечения проводника, поэтому для его преодоления используются трехфазные системы, в которых три тока равны по величине и имеют разность фаз 120 градусов. В этом случае вращающееся магнитное поле создают три одинаковые катушки, имеющие взаимные геометрические углы 120 градусов. Способность трехфазной системы для создания вращающегося поля, используемое в электрических двигателях, является одной из главных причин, почему трехфазные системы доминируют в мире электрической мощности систем водоснабжения.
В синхронных двигателях используются обмотки ротора, питаемые постоянным напряжением, что позволяет управлять возбуждением машины, а в асинхронных двигателях используются короткозамкнутые роторы (вместо магнита), которые следуют за вращающимся магнитным полем многослойного статора. Короткозамкнутые витки ротора создают вихревые токи во вращающемся поле статора, и эти токи, в свою очередь, перемещают ротор под действием силы Лоренца.
В 1882 году Никола Тесла определил концепцию вращающегося магнитного поля. В 1885 году Галилео Феррарис независимо исследовал эту концепцию. В 1888 году Тесла получил патент США 381968 за свою работу. Также в 1888 году Феррарис опубликовал свое исследование в докладе Королевской академии наук в Турине.
Носители заряда проводника с током, помещенного в поперечное магнитное поле, испытывают боковую силу Лоренца; это приводит к разделению зарядов в направлении, перпендикулярном току и магнитному полю. Результирующее напряжение в этом направлении пропорционально приложенному магнитному полю. Это известно как эффект Холла.
Эффект Холла часто используется для измерения величины магнитного поля. Он также используется для определения знака доминирующих носителей заряда в таких материалах, как полупроводники (отрицательные электроны или положительные дырки).
Важное применение H - в магнитных цепях, где B = μ H внутри линейного материала. Здесь μ - магнитная проницаемость материала. Этот результат аналогичен по форме закону Ома J = σ E, где J - плотность тока, σ - проводимость, а E - электрическое поле. Продолжая эту аналогию, аналог макроскопического закона Ома ( I = V ⁄ R):
где - магнитный поток в цепи, -
магнитодвижущая сила, приложенная к цепи, а R m - сопротивление цепи. Здесь магнитное сопротивление R m представляет собой величину, аналогичную по своей природе сопротивлению для магнитного потока. Используя эту аналогию, легко вычислить магнитный поток сложной геометрии магнитного поля, используя все доступные методы теории цепей.По состоянию на октябрь 2018 года максимальное магнитное поле, создаваемое в макроскопическом объеме за пределами лаборатории, составляет 2,8 кТл ( ВНИИЭФ в Сарове, Россия, 1998). По состоянию на октябрь 2018 года наибольшее магнитное поле, созданное в лаборатории в макроскопическом объеме, составило 1,2 кТл исследователями из Токийского университета в 2018 году. Самые большие магнитные поля, создаваемые в лаборатории, возникают в ускорителях частиц, таких как RHIC, внутри столкновений. тяжелых ионов, где микроскопические поля достигают 10 14 Тл. Магнитары имеют самые сильные известные магнитные поля среди всех естественных объектов, в диапазоне от 0,1 до 100 ГТ (от 10 8 до 10 11 Тл).
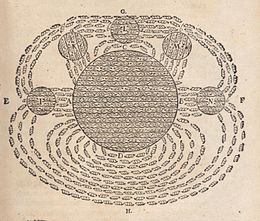 Один из первых рисунков магнитного поля, сделанный Рене Декартом в 1644 году, показывающий, что Земля притягивает магниты. Это проиллюстрировало его теорию о том, что магнетизм был вызван циркуляцией крошечных спиральных частиц, «частей с резьбой», через поры с резьбой в магнитах.
Один из первых рисунков магнитного поля, сделанный Рене Декартом в 1644 году, показывающий, что Земля притягивает магниты. Это проиллюстрировало его теорию о том, что магнетизм был вызван циркуляцией крошечных спиральных частиц, «частей с резьбой», через поры с резьбой в магнитах. Хотя магниты и некоторые свойства магнетизма были известны древним обществам, исследование магнитных полей началось в 1269 году, когда французский ученый Петрус Перегринус де Марикур с помощью железных игл нанес на карту магнитное поле на поверхности сферического магнита. Отметив, что линии поля пересекаются в двух точках, он назвал эти точки «полюсами» по аналогии с полюсами Земли. Он также сформулировал принцип, согласно которому магниты всегда имеют как северный, так и южный полюс, независимо от того, насколько тонко их разрезают.
Почти три столетия спустя Уильям Гилберт из Колчестера повторил работу Петруса Перегринуса и был первым, кто прямо заявил, что Земля является магнитом. Опубликованная в 1600 году работа Гилберта « Де Магнете» помогла утвердить магнетизм как науку.
 Ганс Кристиан Эрстед, Der Geist in der Natur, 1854 г.
Ганс Кристиан Эрстед, Der Geist in der Natur, 1854 г. В 1750 году Джон Мичелл заявил, что магнитные полюса притягиваются и отталкиваются в соответствии с законом обратных квадратов. Шарль-Огюстен де Кулон экспериментально подтвердил это в 1785 году и прямо заявил, что северный и южный полюса не могут быть разделены. Основываясь на этой силе между полюсами, Симеон Дени Пуассон (1781–1840) создал первую успешную модель магнитного поля, которую он представил в 1824 году. В этой модели магнитное H- поле создается магнитными полюсами, а магнетизм обусловлен небольшие пары северно-южных магнитных полюсов.
Три открытия 1820 года поставили под сомнение эти основы магнетизма. Ганс Кристиан Эрстед продемонстрировал, что токоведущий провод окружен круговым магнитным полем. Затем Андре-Мари Ампер показал, что параллельные провода с токами притягиваются друг к другу, если токи идут в одном направлении, и отталкиваются, если они в противоположных направлениях. Наконец, Жан-Батист Био и Феликс Савар объявили эмпирические результаты о силах, которые длинный прямой провод с током действовал на небольшой магнит, определив, что силы были обратно пропорциональны перпендикулярному расстоянию от провода до магнита. Позже Лаплас вывел закон силы, основанный на дифференциальном действии дифференциального участка провода, который стал известен как закон Био-Савара, поскольку Лаплас не опубликовал свои выводы.
Расширяя эти эксперименты, Ампер опубликовал свою успешную модель магнетизма в 1825 году. В ней он показал эквивалентность электрических токов магнитам и предположил, что магнетизм возникает из-за постоянно протекающих контуров тока вместо диполей магнитного заряда в модели Пуассона. Кроме того, Ампер вывел как силовой закон Ампера, описывающий силу между двумя токами, так и закон Ампера, который, как и закон Био-Савара, правильно описывает магнитное поле, создаваемое постоянным током. Также в этой работе Ампер ввел термин электродинамика для описания взаимосвязи между электричеством и магнетизмом.
В 1831 году Майкл Фарадей открыл электромагнитную индукцию, когда он обнаружил, что изменяющееся магнитное поле генерирует окружающее электрическое поле, сформулировав то, что теперь известно как закон индукции Фарадея. Позже Франц Эрнст Нойман доказал, что для движущегося проводника в магнитном поле индукция является следствием закона силы Ампера. В процессе он ввел магнитный векторный потенциал, который, как позже было показано, эквивалентен лежащему в основе механизму, предложенному Фарадеем.
В 1850, Лорд Кельвин, тогда известный как William Thomson, различие между двумя магнитными полями сейчас обозначают H и B. Первая применима к модели Пуассона, а вторая - к модели Ампера и индукции. Кроме того, он выяснил, как H и B соотносятся друг с другом, и ввел термин проницаемость.
Между 1861 и 1865 годами Джеймс Клерк Максвелл разработал и опубликовал уравнения Максвелла, которые объяснили и объединили все классическое электричество и магнетизм. Первый набор этих уравнений был опубликован в статье, озаглавленной « О физических силовых линиях» в 1861 году. Эти уравнения были действительными, но неполными. Максвелл завершил свою систему уравнений в своей более поздней статье 1865 года «Динамическая теория электромагнитного поля» и продемонстрировал тот факт, что свет является электромагнитной волной. Генрих Герц опубликовал в 1887 и 1888 годах работы, экспериментально подтверждающие этот факт.
В 1887 году Тесла разработал асинхронный двигатель, работающий на переменном токе. В двигателе использовался многофазный ток, который генерировал вращающееся магнитное поле для вращения двигателя (принцип, который, по утверждениям Теслы, был изобретен в 1882 году). Тесла получил патент на свой электродвигатель в мае 1888 года. В 1885 году Галилео Феррарис независимо исследовал вращающиеся магнитные поля и впоследствии опубликовал свое исследование в документе для Королевской академии наук в Турине, всего за два месяца до того, как Тесла получил свой патент, в Март 1888 г.
Двадцатый век показал, что классическая электродинамика уже согласуется со специальной теорией относительности, и расширил классическую электродинамику для работы с квантовой механикой. Альберт Эйнштейн в своей статье 1905 года, в которой была установлена теория относительности, показал, что и электрическое, и магнитное поля являются частью одного и того же явления, наблюдаемого из разных систем отсчета. Наконец, возникшая область квантовой механики была объединена с электродинамикой, чтобы сформировать квантовую электродинамику, которая впервые формализовала представление о квантовании энергии электромагнитного поля в форме фотонов.
|