Диполь

редактировать

Электромагнитное явление

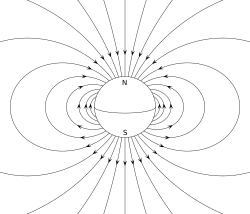
Магнитное поле сферы с северным магнитным полюсом вверху и южным магнитным полюсом внизу. Для сравнения: Земля имеет южный магнитный полюс около своего северного географического полюса и северный магнитный полюс около южного полюса.

В электромагнетизме существует два вида диполи :

электрический диполь имеет дело с разделением положительных и отрицательных зарядов, обнаруженных в любой электромагнитной системе. Простым примером этой системы является пара электрических зарядов равной величины, но противоположного знака, разделенных некоторым типично небольшим расстоянием. (Постоянный электрический диполь называется электрет.)
A магнитный диполь - это замкнутая циркуляция системы электрического тока. Простым примером является одиночный контур провода с постоянным током через него.. стержневой магнит представляет собой пример магнита с постоянным магнитным дипольным моментом.

Электрический или магнитный диполи можно охарактеризовать их дипольным моментом, векторной величиной. диполь, электрический дипольный момент направлен от отрицательного заряда к положительному и имеет величину, равную силе каждого заряда, умноженной на расстояние между зарядами (чтобы быть точным: для определения дипольный момент, всегда следует учитывать «дипольный предел», когда, например, расстояние генерирующих зарядов должно сходиться к 0, в то время как одновременно сила заряда должна расходиться до бесконечности таким образом, чтобы произведение оставалось положительной константой.)

Для магнитной (дипольной) тока Если взять петлю, то магнитный дипольный момент проходит через нее (согласно правилу захвата правой рукой ) с величиной, равной току в петле, умноженному на площадь петли.

Подобно петлям магнитного тока, электронная частица и некоторые другие фундаментальные частицы имеют магнитные дипольные моменты, поскольку электрон генерирует магнитное поле идентично тому, что генерируется очень маленькой токовой петлей. Однако магнитный дипольный момент электрона возникает не из-за токовой петли, а из-за внутреннего свойства электрона. Электрон может также иметь электрический дипольный момент, хотя он еще не наблюдался (см. электрический дипольный момент электрона ).

Контурная диаграмма электростатического потенциала горизонтально ориентированного электрического диполя бесконечно малого размера. Яркие цвета указывают на самый высокий и самый низкий потенциал (где расположены противоположные заряды диполя).

Постоянный магнит, такой как стержневой магнит, обязан своим магнетизмом собственному магнитному дипольному моменту электрона. Два конца стержневого магнита называются полюсами - не путать с монополями, см. Классификация ниже) - и могут быть помечены как «север» и «юг». С точки зрения магнитного поля Земли, они являются полюсами, направленными на север и на юг, соответственно: если бы магнит был свободно подвешен в магнитном поле Земли, полюс, направленный на север, был бы направлен на север, а на юг. полюс поиска будет указывать на юг. Дипольный момент стержневого магнита направлен от его магнитного юга к его магнитному северному полюсу. В магнитном компасе северный полюс стержневого магнита указывает на север. Однако это означает, что северный геомагнитный полюс Земли является южным полюсом (полюсом, направленным на юг) ее дипольного момента, и наоборот.

Единственными известными механизмами создания магнитных диполей являются токовые петли или квантово-механический спин, поскольку существование магнитных монополей никогда не было экспериментально продемонстрировано.

Термин происходит от греческого δίς (дис), «дважды» и πόλος (полос), «ось».

Содержание

1 Классификация
2 Молекулярный диполи
3 Оператор квантово-механического диполя
4 Атомные диполи
5 Поле статического магнитного диполя
- 5.1 Величина
- 5.2 Векторная форма
- 5.3 Магнитный векторный потенциал
6 Поле от электрический диполь
7 Крутящий момент на диполе
8 Дипольное излучение
9 См. также
10 Примечания
11 Ссылки
12 Внешние ссылки

Классификация

Линии электрического поля из двух противоположные заряды, разделенные конечным расстоянием.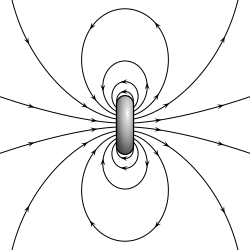

Силовые линии магнитного поля кольцевого тока конечного диаметра.

Силовые линии точечного диполя любого типа, электрического, магнитного, акустического и т. д.

Физический диполь состоит из двух равных и противоположных точечных зарядов: в буквальном смысле - двух полюсов. Его поле на больших расстояниях (т.е. на расстояниях, больших по сравнению с разделением полюсов) почти полностью зависит от дипольного момента, как определено выше. Точечный (электрический) диполь - это предел, достигаемый за счет стремления расстояния к 0 при сохранении фиксированного дипольного момента. Поле точечного диполя имеет особенно простую форму, и член порядка 1 в мультипольном разложении в точности является полем точечного диполя.

Хотя в природе не существует известных магнитных монополей, существуют магнитные диполи в форме квантово-механического спина, связанные с такими частицами, как электроны. (хотя точное описание таких эффектов выходит за рамки классического электромагнетизма). Теоретический точечный магнитный диполь имеет магнитное поле точно такой же формы, что и электрическое поле точечного электрического диполя. Очень маленькая токоведущая петля - это примерно точечный магнитный диполь; магнитный дипольный момент такой петли является произведением тока, протекающего в петле, и (векторной) площади петли.

Любая конфигурация зарядов или токов имеет «дипольный момент», который описывает диполь, поле которого на больших расстояниях является наилучшим приближением к полю данной конфигурации. Это просто один член в мультипольном разложении, когда полный заряд («момент монополя») равен 0 - как это всегда бывает в магнитном случае, поскольку магнитных монополей нет. Дипольный член является доминирующим на больших расстояниях: его поле спадает пропорционально 1 / r по сравнению с 1 / r для следующего (квадрупольного ) члена и более высокими степенями 1 / r для более высоких члены, или 1 / r для монопольного члена.

Молекулярные диполи

Многие молекулы имеют такие дипольные моменты из-за неоднородного распределения положительных и отрицательных зарядов на различных атомах. Так обстоит дело с полярными соединениями, такими как фтороводород (HF), где электронная плотность распределяется между атомами неравномерно. Следовательно, диполь молекулы - это электрический диполь с собственным электрическим полем, которое не следует путать с магнитным диполем, который генерирует магнитное поле.

Физик-химик Питер Дж. В. Дебай был первым ученым, широко изучившим молекулярные диполи, и, как следствие, дипольные моменты измеряются в единицах, названных дебай в его честь.

Для молекул существует три типа диполей:

Постоянные диполи: Они возникают, когда два атома в молекуле имеют существенно разную электроотрицательность : один атом притягивает электроны больше чем другой, становится более отрицательным, тогда как другой атом становится более положительным. Молекула с постоянным дипольным моментом называется полярной молекулой. См. диполь-дипольное притяжение.
Мгновенные диполи: Это происходит случайно, когда электроны оказываются более концентрированными в одном месте, чем другие в молекуле , создав временный диполь. Эти диполи меньше по величине, чем постоянные диполи, но все же играют большую роль в химии и биохимии из-за их распространенности. См. мгновенный диполь.
Индуцированные диполи: Это может произойти, когда одна молекула с постоянным диполем отталкивает электроны другой молекулы, вызывая дипольный момент в этой молекуле. Молекула поляризована, когда она несет индуцированный диполь. См. индуцированное дипольное притяжение..

В более общем смысле, индуцированный диполь любого поляризуемого распределения заряда ρ (помните, что молекула имеет распределение заряда) вызывается электрическим полем, внешним по отношению к ρ. Это поле может, например, возникать из иона или полярной молекулы вблизи ρ или может быть макроскопическим (например, молекула между пластинами заряженного конденсатора ). Величина наведенного дипольного момента равна произведению силы внешнего поля и дипольной поляризуемости ρ.

Значения дипольного момента могут быть получены путем измерения диэлектрической проницаемости. Вот некоторые типичные значения газовой фазы в единицах дебай :

Линейная молекула CO 2 имеет нулевой диполь, поскольку два диполя связи аннулируются.

Бромид калия (KBr) имеет один из самых высоких дипольных моментов, потому что это ионное соединение, который существует в виде молекулы в газовой фазе.

Изогнутая молекула H 2 O имеет чистый диполь. Два диполя связи не отменяются.

Общий дипольный момент молекулы может быть аппроксимирован как векторная сумма дипольных моментов связей. В виде векторной суммы он зависит от относительной ориентации связей, так что из дипольного момента можно вывести информацию о геометрии молекулы.

Например, нулевой диполь CO 2 подразумевает что два дипольных момента связи C = O сокращаются, так что молекула должна быть линейной. Для H 2 O моменты связи O-H не сокращаются, потому что молекула изогнута. Для озона (O 3), который также является изогнутой молекулой, дипольные моменты связей не равны нулю, даже если связи O-O находятся между подобными атомами. Это согласуется со структурами Льюиса для резонансных форм озона, которые показывают положительный заряд на центральном атоме кислорода.

Резонансные структуры Льюиса молекулы озона

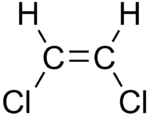Цис-изомер, дипольный момент 1,90 D

Транс-изомер, нулевой дипольный момент

Примером в органической химии роли геометрии в определении дипольного момента являются цис- и транс-изомеры 1,2-дихлорэтен. В цис-изомере две полярные связи C-Cl находятся на одной стороне от двойной связи C = C, а молекулярный дипольный момент равен 1,90 D. В транс-изомере дипольный момент равен нулю, поскольку две связи C-Cl являются на противоположных сторонах C = C и сокращаются (и два момента связи для гораздо менее полярных связей C-H также сокращаются).

Другим примером роли геометрии молекулы является трифторид бора, который имеет три полярные связи с разницей в электроотрицательности, превышающей традиционно цитируемый порог 1,7 для ионная связь. Однако из-за равностороннего треугольного распределения фторид-ионов вокруг катионного центра бора молекула в целом не имеет какого-либо идентифицируемого полюса: невозможно построить плоскость, которая разделяет молекулу на чистую отрицательную часть. и чистая положительная часть.

Квантово-механический дипольный оператор

Рассмотрим набор из N частиц с зарядами q i и векторами положения ri. Например, этот набор может быть молекулой, состоящей из электронов, все с зарядом −e, и ядер с зарядом eZ i, где Z i - это атомный номер i-го ядра. Наблюдаемая дипольная величина (физическая величина) имеет квантовомеханический оператор диполя :

p = ∑ i = 1 N q i r i. {\ displaystyle {\ mathfrak {p}} = \ sum _ {i = 1} ^ {N} \, q_ {i} \, \ mathbf {r} _ {i} \,.}

{\ mathfrak {p}} = \ sum _ {i = 1} ^ {N} \, q_ {i} \, \ mathbf {r} _ {i} \,.

Обратите внимание, что это определение действительно только для нейтральных атомов или молекул, т.е. полный заряд равен нулю. В ионизированном случае

p = ∑ я = 1 N qi (ri - rc), {\ displaystyle {\ mathfrak {p}} = \ sum _ {i = 1} ^ {N} \, q_ {i} \, (\ mathbf {r} _ {i} - \ mathbf {r} _ {c}),}

{\ displaystyle {\ mathfrak {p}} = \ sum _ {i = 1} ^ {N} \, q_ {i} \, (\ mathbf {r} _ {i} - \ mathbf {r} _ { c}),}

где $rc {\ displaystyle \ mathbf {r} _ {c}}$ $\ mathbf {r} _ {c}$ - центр масс молекулы / группы частиц.

Атомные диполи

Невырожденный (S-состояние) атом может иметь только нулевой постоянный диполь. Этот факт квантово-механически следует из инверсионной симметрии атомов. Все три компонента дипольного оператора антисимметричны относительно инверсии относительно ядра,

I p I - 1 = - p, {\ displaystyle {\ mathfrak {I}} \; {\ mathfrak {p}} \; {\ mathfrak {I}} ^ {- 1} = - {\ mathfrak {p}},}

{\ displaystyle {\ mathfrak {I}} \; { \ mathfrak {p}} \; {\ mathfrak {I}} ^ {- 1} = - {\ mathfrak {p}},}

где $p {\ displaystyle {\ mathfrak {p}}}$ ${\ mathfrak {p}}$ - оператор диполя, а $I {\ displaystyle {\ mathfrak {I}}}$ ${\ mathfrak {I}}$ - оператор инверсии.

Постоянный дипольный момент атома в невырожденном состоянии (см. вырожденный уровень энергии ) задается как математическое ожидание (среднее) значение дипольного оператора,

⟨p ⟩ = ⟨S | p | S⟩, {\ displaystyle \ left \ langle {\ mathfrak {p}} \ right \ rangle = \ left \ langle \, S \, | {\ mathfrak {p}} | \, S \, \ right \ rangle, }

{\ displaystyle \ left \ langle {\ mathfrak {p} } \ right \ rangle = \ left \ langle \, S \, | {\ mathfrak {p}} | \, S \, \ right \ rangle,}

где $| S⟩ {\ displaystyle | \, S \, \ rangle}$ $| \, S \, \ rangle$ - невырожденная волновая функция в S-состоянии, которая является симметричной или антисимметричной относительно инверсии: $I | S⟩ = ± | S⟩ {\ Displaystyle {\ mathfrak {I}} \, | \, S \, \ rangle = \ pm | \, S \, \ rangle}$ ${\ displaystyle {\ mathfrak {I}} \, | \, S \, \ rangle = \ pm | \, S \, \ rangle}$ . Поскольку произведение волновой функции (в кет) и ее комплексно сопряженной (в бюстгальтере) всегда симметрично относительно инверсии и обратной,

⟨p⟩ = ⟨I - 1 S | p | I - 1 S⟩ = ⟨S | I p I - 1 | S⟩ знак равно - ⟨п⟩ {\ Displaystyle \ left \ langle {\ mathfrak {p}} \ right \ rangle = \ left \ langle \, {\ mathfrak {I}} ^ {- 1} \, S \, | {\ mathfrak {p}} | \, {\ mathfrak {I}} ^ {- 1} \, S \, \ right \ rangle = \ left \ langle \, S \, | {\ mathfrak {I}} \, {\ mathfrak {p}} \, {\ mathfrak {I}} ^ {- 1} | \, S \, \ right \ rangle = - \ left \ langle {\ mathfrak {p}} \ right \ rangle}

{\ displaystyle \ left \ langle {\ mathfrak { p}} \ right \ rangle = \ left \ langle \, {\ mathfrak {I}} ^ {- 1} \, S \, | {\ mathfrak {p}} | \, {\ mathfrak {I}} ^ {-1} \, S \, \ right \ rangle = \ left \ langle \, S \, | {\ mathfrak {I}} \, {\ mathfrak {p}} \, {\ mathfrak {I}} ^ {-1} | \, S \, \ right \ rangle = - \ left \ langle {\ mathfrak {p}} \ right \ rangle}

следует, что математическое ожидание меняет знак при инверсии. Мы использовали здесь тот факт, что $I {\ displaystyle {\ mathfrak {I}}}$ ${\ displaystyle {\ mathfrak {I}}}$ , будучи оператором симметрии, является унитарным : $I - 1 = I ∗ {\ displaystyle {\ mathfrak {I}} ^ {- 1} = {\ mathfrak {I}} ^ {*} \,}$ ${\ mathfrak {I}} ^ { -1} = {\ mathfrak {I}} ^ {*} \,$ и по определению эрмитово сопряженное $I ∗ {\ displaystyle {\ mathfrak {I}} ^ {*} \,}$ ${\ mathfrak {I}} ^ {*} \,$ можно переместить с бюстгальтера на кет, и тогда он станет $I ∗ ∗ = I {\ displaystyle {\ mathfrak {I}} ^ {**} = {\ mathfrak {I}} \,}$ ${\ displaystyle {\ mathfrak {I}} ^ {**} = {\ mathfrak {I}} \,}$ . Поскольку единственная величина, которая равна самому минусу, - это ноль, математическое ожидание обращается в нуль,

⟨p⟩ = 0. {\ displaystyle \ left \ langle {\ mathfrak {p}} \ right \ rangle = 0.}

{\ displaystyle \ left \ langle {\ mathfrak {p}} \ right \ rangle = 0.}

В случае атомов с открытой оболочкой с вырожденными уровнями энергии можно определить дипольный момент с помощью эффекта Штарка первого порядка. Это дает ненулевой диполь (по определению пропорциональный ненулевому сдвигу Штарка первого порядка), только если некоторые из волновых функций, принадлежащих вырожденным энергиям, имеют противоположную четность ; т.е. иметь другое поведение при инверсии. Это редкое явление, но случается с возбужденным атомом водорода, где состояния 2s и 2p "случайно" вырождены (происхождение этого вырождения см. В статье вектор Лапласа – Рунге – Ленца ) и имеют противоположные четность (2s - четное, 2p - нечетное).

Поле статического магнитного диполя

Величина

Напряженность дальнего поля B дипольного магнитного поля определяется как

B (m, r, λ) знак равно μ 0 4 π mr 3 1 + 3 грех 2 ⁡ (λ), {\ displaystyle B (m, r, \ lambda) = {\ frac {\ mu _ {0}} {4 \ pi}} { \ frac {m} {r ^ {3}}} {\ sqrt {1 + 3 \ sin ^ {2} (\ lambda)}} \,,}

{\ displaystyle B (m, r, \ lambda) = {\ frac {\ mu _ {0}} {4 \ pi}} {\ frac { m} {г ^ {3}}} {\ sqrt {1 + 3 \ sin ^ {2} (\ lambda)}} \,,}

где

B - напряженность поля, измеряется в теслах

r - расстояние от центра, измеряется в метрах

λ - магнитная широта (равная 90 ° - θ), где θ - магнитная широта, измеренная в радиан или градусов от оси диполя

м - дипольный момент, измеренный в амперах -квадратных метрах или джоулях на тесла

μ0- проницаемость свободного пространства, измеренная в генри на метр.

Преобразование в цилиндрические координаты достигается с использованием r = z + ρ и

λ знак равно arcsin ⁡ (zz 2 + ρ 2) {\ displaystyle \ lambda = \ arcsin \ left ({\ frac {z} {\ sqrt {z ^ {2} + \ rho ^ {2}}}} \ right)}

{\ displaystyle \ lambda = \ arcsin \ left ({\ frac {z} {\ sqrt {z ^ {2} + \ rho ^ {2}}}} \ right)}

где ρ - перпендикулярное расстояние от оси z. Тогда

В (ρ, z) = μ 0 м 4 π (z 2 + ρ 2) 3 2 1 + 3 z 2 z 2 + ρ 2 {\ displaystyle B (\ rho, z) = {\ frac {\ mu _ {0} m} ​​{4 \ pi \ left (z ^ {2} + \ rho ^ {2} \ right) ^ {\ frac {3} {2}}}} {\ sqrt {1+ {\ frac {3z ^ {2}} {z ^ {2} + \ rho ^ {2}}}}}}

{\ displaystyle B (\ rho, z) = {\ frac {\ mu _ {0} m} ​​{4 \ pi \ left (z ^ {2} + \ rho ^ {2} \ right) ^ {\ frac {3} {2}}}} {\ sqrt {1 + {\ frac {3z ^ {2}} {z ^ { 2} + \ rho ^ {2}}}}}}

Векторная форма

Само поле является векторной величиной:

В (т, г) знак равно μ 0 4 π 3 (м ⋅ р ^) р ^ - г-н 3 {\ Displaystyle \ mathbf {B} (\ mathbf {m}, \ mathbf {r}) = {\ гидроразрыва {\ mu _ {0}} {4 \ pi}} \ {\ frac {3 (\ mathbf {m} \ cdot {\ hat {\ mathbf {r}}}) {\ hat {\ mathbf {r}}} - \ mathbf {m}} {r ^ {3}}}}

{\ displaystyle \ mathbf {B} (\ mathbf {m}, \ mathbf {r}) = {\ frac {\ mu _ {0}} {4 \ pi}} \ {\ frac {3 (\ mathbf {m} \ cdot {\ hat {\ mathbf {r}}}) {\ hat {\ mathbf {r}}} - \ mathbf {m}} {r ^ {3} }}}

где

B- поле,

r- вектор от положения диполя до положения, в котором поле измеряется

r - абсолютное значение r : расстояние от диполя

r̂= r/ r - единичный вектор, параллельный r;

m- (векторный) дипольный момент;

μ0- проницаемость свободного space

Это в точности поле точечного диполя, в точности дипольный член в мультипольном разложении произвольного поля и приблизительно поле любого дипольоподобного контура. фигурация на больших расстояниях.

Магнитный векторный потенциал

векторный потенциал Aмагнитного диполя равен

A (r) = μ 0 4 π m × r ^ r 2 {\ displaystyle \ mathbf {A} (\ mathbf {r}) = {\ frac {\ mu _ {0}} {4 \ pi}} {\ frac {\ mathbf {m} \ times {\ hat {\ mathbf {r}) }}} {r ^ {2}}}}

{\ displaystyle \ mathbf {A} ( \ mathbf {r}) = {\ frac {\ mu _ {0}} {4 \ pi}} {\ frac {\ mathbf {m} \ times {\ hat {\ mathbf {r}}}} {r ^ {2}}} }

с теми же определениями, что и выше.

Поле электрического диполя

электростатический потенциал в позиции r, обусловленный электрическим диполем в начале координат, определяется как

Φ (г) знак равно 1 4 π ϵ 0 п ⋅ р ^ р 2 {\ displaystyle \ Phi (\ mathbf {r}) = {\ frac {1} {4 \ pi \ epsilon _ {0}}} \, { \ frac {\ mathbf {p} \ cdot {\ hat {\ mathbf {r}}}} {r ^ {2}}}}

{\ displaystyle \ Phi ( \ mathbf {r}) = {\ frac {1} {4 \ pi \ epsilon _ {0}}} \, {\ frac {\ mathbf {p} \ cdot {\ hat {\ mathbf {r}}}} {г ^ {2}}}}

где p - (вектор) дипольный момент, а є 0 - диэлектрическая проницаемость свободного пространства.

Этот член появляется как второй член в мультипольном разложении произвольного электростатического потенциала Φ (г ). Если источником Φ (r ) является диполь, как это предполагается здесь, этот член является единственным ненулевым членом в мультипольном разложении Φ (r ). электрическое поле от диполя можно найти по градиенту этого потенциала:

E = - ∇ Φ = 1 4 π ϵ 0 3 (p ⋅ r ^) r ^ - пр 3. {\ displaystyle \ mathbf {E} = - \ nabla \ Phi = {\ frac {1} {4 \ pi \ epsilon _ {0}}} \ {\ frac {3 (\ mathbf {p} \ cdot {\ hat {\ mathbf {r}}}) {\ hat {\ mathbf {r}}} - \ mathbf {p}} {r ^ {3}}}.}

{\ displaystyle \ mathbf {E} = - \ nabla \ Phi = {\ frac {1} {4 \ pi \ epsilon _ {0}}} \ {\ гидроразрыв {3 (\ mathbf {p} \ cdot {\ hat {\ mathbf {r}}}) {\ hat {\ mathbf {r}}} - \ mathbf {p}} {r ^ {3}}}. }

Это формально идентично выражению для магнитного поле точечного магнитного диполя изменилось лишь с несколькими названиями. Однако в реальном диполе, где заряды физически разделены, «внутренние» силовые линии разные, так как силовые линии магнитного поля непрерывны, а силовые линии электрического поля расходятся или сходятся от точечных зарядов. Для дальнейшего обсуждения внутреннего поля диполей см. Или Магнитный момент # Внутреннее магнитное поле диполя.

Крутящий момент на диполе

Поскольку направление электрического поля определяется как направление силы на положительный заряд, силовые линии электрического поля направлены от положительного заряда в сторону отрицательного заряда.

При помещении в однородное электрическое или магнитное поле равные, но противоположные силы возникают с каждой стороны диполя, создавая крутящий момент τ}:

τ = p × E {\ displaystyle {\ boldsymbol {\ tau}} = \ mathbf {p} \ times \ mathbf {E}}

{\ boldsymbol {\ tau}} = \ mathbf {p} \ times \ mathbf {E}

для электрического дипольного момента p(в кулонах-метрах) или

τ = m × B {\ displaystyle {\ boldsymbol {\ tau}} = \ mathbf {m} \ times \ mathbf {B}}

{\ boldsymbol {\ tau}} = \ mathbf {m} \ times \ mathbf {B}

для магнитный дипольный момент m(в ампер-квадратных метрах).

Результирующий крутящий момент будет стремиться выровнять диполь с приложенным полем, что в случае электрического диполя дает потенциальную энергию

U = - p ⋅ E {\ displaystyle U = - \ mathbf {p} \ cdot \ mathbf {E}}

U = - \ mathbf {p} \ cdot \ mathbf {E}

Энергия магнитного диполя аналогичным образом

U = - m ⋅ B {\ displaystyle U = - \ mathbf {m} \ cdot \ mathbf {B} }

U = - \ mathbf {m} \ cdot \ mathbf {B}

Дипольное излучение

Модуль вектора Пойнтинга для колеблющегося электрического диполя (точное решение). Два заряда показаны в виде двух маленьких черных точек.

В дополнение к диполям в электростатике также принято рассматривать электрический или магнитный диполь, который колеблется во времени. Это расширение или более физический следующий шаг к излучению сферической волны.

В частности, рассмотрим гармонически колеблющийся электрический диполь с угловой частотой ω и дипольным моментом p 0 вдоль направления ẑ Форма

p (r, t) = p (r) e - i ω t = p 0 z ^ e - i ω t. {\ Displaystyle \ mathbf {p} (\ mathbf {r}, t) = \ mathbf {p} (\ mathbf {r}) e ^ {- я \ omega t} = p_ {0} {\ hat {\ mathbf {z}}} e ^ {- i \ omega t}.}

{\ displaystyle \ mathbf {p} (\ mathbf {r}, t) = \ mathbf {p} (\ mathbf {r}) e ^ {- я \ omega t} = p_ {0} {\ hat {\ mathbf {z}}} e ^ {- i \ omega t}.}

В вакууме точное поле, создаваемое этим колеблющимся диполем, можно получить, используя формулировку запаздывающего потенциала как:

E = 1 4 π ε 0 {ω 2 c 2 r (r ^ × p) × r ^ + (1 r 3 - i ω cr 2) (3 r ^ [r ^ ⋅ p] - p)} ei ω rce - i ω t B знак равно ω 2 4 π ε 0 c 3 (r ^ × p) (1 - ci ω r) ei ω r / cre - i ω t. {\ displaystyle {\ begin {align} \ mathbf {E} = {\ frac {1} {4 \ pi \ varepsilon _ {0}}} \ left \ {{\ frac {\ omega ^ {2}} { c ^ {2} r}} \ left ({\ hat {\ mathbf {r}}} \ times \ mathbf {p} \ right) \ times {\ hat {\ mathbf {r}}} + \ left ({ \ frac {1} {r ^ {3}}} - {\ frac {i \ omega} {cr ^ {2}}} \ right) \ left (3 {\ hat {\ mathbf {r}}} \ left [{\ hat {\ mathbf {r}}} \ cdot \ mathbf {p} \ right] - \ mathbf {p} \ right) \ right \} e ^ {\ frac {i \ omega r} {c}} e ^ {- i \ omega t} \\\ mathbf {B} = {\ frac {\ omega ^ {2}} {4 \ pi \ varepsilon _ {0} c ^ {3}}} ({\ hat {\ mathbf {r}}} \ times \ mathbf {p}) \ left (1 - {\ frac {c} {i \ omega r}} \ right) {\ frac {e ^ {i \ omega r / c }} {r}} e ^ {- i \ omega t}. \ end {align}}}

{\ displaystyle {\ begin {align} \ mathbf {E } = {\ frac {1} {4 \ pi \ varepsilon _ {0}}} \ left \ {{\ frac {\ omega ^ {2}} {c ^ {2} r}} \ left ({\ шляпа {\ mathbf {r}}} \ times \ mathbf {p} \ right) \ times {\ hat {\ mathbf {r}}} + \ left ({\ frac {1} {r ^ {3}}} - {\ frac {i \ omega} {cr ^ {2}}} \ right) \ left (3 {\ hat {\ mathbf {r}}} \ left [{\ hat {\ mathbf {r}}} \ cdot \ mathbf {p} \ right] - \ mathbf {p} \ right) \ right \} e ^ {\ frac {i \ omega r} {c}} e ^ {- i \ omega t} \\\ mathbf {B} = {\ frac {\ omega ^ {2}} {4 \ pi \ varepsilon _ {0} c ^ {3}}} ({\ hat {\ mathbf {r}}} \ times \ mathbf { p}) \ left (1 - {\ frac {c} {i \ omega r}} \ right) {\ frac {e ^ {i \ omega r / c}} {r}} e ^ {- i \ omega t}. \ end {align}}}

При rω / c ≫ 1 дальнее поле принимает более простую форму излучающей "сферической" волны, но с угловой зависимостью, заложенной в перекрестное произведение:

B = ω 2 4 π ε 0 c 3 (r ^ × p) ei ω (r / c - t) r = ω 2 μ 0 p 0 4 π c ( r ^ × z ^) ei ω (r / c - t) r = - ω 2 μ 0 p 0 4 π c sin ⁡ (θ) ei ω (r / c - t) r ϕ ^ E = c B × r ^ = - ω 2 μ 0 p 0 4 π sin ⁡ (θ) (ϕ ^ × r ^) ei ω (r / c - t) r = - ω 2 μ 0 p 0 4 π sin ⁡ (θ) e i ω (r / c - t) r θ ^. {\ displaystyle {\ begin {align} \ mathbf {B} = {\ frac {\ omega ^ {2}} {4 \ pi \ varepsilon _ {0} c ^ {3}}} ({\ hat {\ mathbf {r}}} \ times \ mathbf {p}) {\ frac {e ^ {i \ omega (r / ct)}} {r}} = {\ frac {\ omega ^ {2} \ mu _ { 0} p_ {0}} {4 \ pi c}} ({\ hat {\ mathbf {r}}} \ times {\ hat {\ mathbf {z}}}) {\ frac {e ^ {i \ omega (r / ct)}} {r}} = - {\ frac {\ omega ^ {2} \ mu _ {0} p_ {0}} {4 \ pi c}} \ sin (\ theta) {\ frac {e ^ {i \ omega (r / ct)}} {r}} \ mathbf {\ hat {\ phi}} \\\ mathbf {E} = c \ mathbf {B} \ times {\ hat {\ mathbf {r}}} = - {\ frac {\ omega ^ {2} \ mu _ {0} p_ {0}} {4 \ pi}} \ sin (\ theta) \ left ({\ hat {\ phi }} \ times \ mathbf {\ hat {r}} \ right) {\ frac {e ^ {i \ omega (r / ct)}} {r}} = - {\ frac {\ omega ^ {2} \ му _ {0} p_ {0}} {4 \ pi}} \ sin (\ theta) {\ frac {e ^ {i \ omega (r / ct)}} {r}} {\ hat {\ theta} }. \ end {align}}}

{\ displaystyle {\ begin {align} \ mathbf {B} = {\ frac {\ omega ^ {2}} {4 \ pi \ varepsilon _ {0} c ^ {3}}} ({\ hat {\ mathbf {r}}} \ times \ mathbf {p}) {\ frac {e ^ {i \ omega (r / ct)}} {r}} = {\ frac {\ omega ^ {2} \ mu _ {0} p_ {0}} {4 \ pi c}} ({\ hat {\ mathbf { r}}} \ times {\ hat {\ mathbf {z}}}) {\ frac {e ^ {i \ omega (r / ct)}} {r}} = - {\ frac {\ omega ^ {2 } \ mu _ {0} p_ {0}} {4 \ pi c}} \ sin (\ theta) {\ frac {e ^ {i \ omega (r / ct)}} {r}} \ mathbf {\ шляпа {\ phi}} \\\ mathbf {E} = c \ mathbf {B} \ times {\ hat {\ mathbf {r}}} = - {\ frac {\ omega ^ {2} \ mu _ { 0} p_ {0}} {4 \ pi}} \ sin (\ theta) \ left ({\ hat {\ phi}} \ times \ mathbf {\ hat {r}} \ справа) {\ frac {e ^ {i \ omega (r / ct)}} {r}} = - {\ frac {\ omega ^ {2} \ mu _ {0} p_ {0}} {4 \ pi }} \ sin (\ theta) {\ frac {e ^ {i \ omega (r / ct)}} {r}} {\ hat {\ theta}}. \ end {align}}}

Усредненный по времени вектор Пойнтинга

⟨S⟩ = (μ 0 p 0 2 ω 4 32 π 2 c) sin 2 ⁡ (θ) r 2 r ^ {\ displaystyle \ langle \ mathbf {S} \ rangle = \ left ({\ frac {\ mu _ {0} p_ {0} ^ {2} \ omega ^ {4}} {32 \ pi ^ {2}) c}} \ right) {\ frac {\ sin ^ {2} (\ theta)} {r ^ {2}}} \ mathbf {\ hat {r}}}

{\ displaystyle \ langle \ mathbf {S} \ rangle = \ left ({\ frac {\ mu _ {0} p_ {0} ^ {2} \ omega ^ {4}} {32 \ pi ^ {2} c}} \ right) {\ frac {\ sin ^ {2} (\ theta)} {r ^ {2}}} \ mathbf {\ hat {r}}}

я s не распределены изотропно, а сосредоточены вокруг направлений, лежащих перпендикулярно дипольному моменту, в результате несферических электрических и магнитных волн. Фактически, функция сферической гармоники (sin θ), отвечающая за такое тороидальное угловое распределение, в точности является волной l = 1 "p".

Полная средняя по времени мощность, излучаемая полем, затем может быть получена из вектора Пойнтинга как

P = μ 0 ω 4 p 0 2 12 π c. {\ displaystyle P = {\ frac {\ mu _ {0} \ omega ^ {4} p_ {0} ^ {2}} {12 \ pi c}}.}

P = {\ frac {\ mu _ {0} \ omega ^ {4} p_ {0} ^ {2}} {12 \ пи c}}.

Обратите внимание, что зависимость мощности от четвертая степень частоты излучения соответствует рэлеевскому рассеянию и лежащим в основе эффектам, почему небо состоит в основном из синего цвета.

Диполь с круговой поляризацией описывается как суперпозиция двух линейных диполей.

См. Также

Примечания

Ссылки

Внешние ссылки

Программа Геомагнетизма Геологической службы США
Области Сила : глава из онлайн-учебника
Электрический дипольный потенциал Стивена Вольфрама и Плотность энергии магнитного диполя Франца Краффта. Wolfram Demonstrations Project.