Вектор Лапласа – Рунге – Ленца

Вектор, используемый в астрономии

В классической механике, Вектор Лапласа – Рунге – Ленца (LRL) - это вектор , используемый в основном для описания формы и ориентации орбиты одного астрономического тела вокруг другого, например планеты. вращается вокруг звезды. Для двух тел, взаимодействующих с помощью ньютоновской гравитации, вектор LRL является константой движения, что означает, что он одинаков независимо от того, где он рассчитывается на орбите; эквивалентно, вектор LRL называется сохраняющимся. В более общем смысле, вектор LRL сохраняется во всех задачах, в которых два тела взаимодействуют посредством центральной силы, которая изменяется как обратный квадрат расстояния между ними; такие проблемы называются проблемами Кеплера.

атом водорода является проблемой Кеплера, поскольку он состоит из двух заряженных частиц, взаимодействующих по закону Кулона из электростатики, другой обратный квадрат центральная сила. Вектор LRL был существенным в первом квантовомеханическом выводе спектра атома водорода до разработки уравнения Шредингера. Однако сегодня такой подход используется редко.

В классической и квантовой механике сохраняющиеся величины обычно соответствуют симметрии системы. Сохранение вектора LRL соответствует необычной симметрии; задача Кеплера математически эквивалентна частице, свободно движущейся по поверхности четырехмерной (гипер-) сферы, так что вся проблема симметрична при определенных поворотах четырехмерного пространства. Эта более высокая симметрия является результатом двух свойств задачи Кеплера: вектор скорости всегда движется по идеальной окружности и для данной общей энергии все такие скоростные окружности пересекаются друг с другом в те же две точки.

Вектор Лапласа – Рунге – Ленца назван в честь Пьера-Симона де Лапласа, Карла Рунге и Вильгельма Ленца. Он также известен как вектор Лапласа, вектор Рунге – Ленца и вектор Ленца . По иронии судьбы, никто из этих ученых этого не обнаружил. Вектор LRL был повторно открыт несколько раз и также эквивалентен безразмерному вектору эксцентриситета из небесной механики. Были определены различные обобщения вектора LRL, которые включают эффекты специальной теории относительности, электромагнитных полей и даже различных типов центральных сил.

Содержание

• 1 Контекст
• 2 История повторных открытий
• 3 Математическое определение
• 4 Выведение орбит Кеплера
• 5 Годографы кругового импульса
• 6 Константы движения и суперинтегрируемость
• 7 Эволюция при возмущенных потенциалах
• 8 Скобки Пуассона
  • 8.1 Немасштабированные функции
  • 8.2 Масштабированные функции
  • 8.3 Инварианты Казимира и уровни энергии
• 9 Квантовая механика атома водорода
• 10 Сохранение и симметрия
• 11 Вращательная симметрия в четырех измерениях
• 12 Обобщения на другие потенциалы и относительность
• 13 Доказательства того, что вектор Лапласа – Рунге – Ленца сохраняется в задачах Кеплера
  • 13.1 Прямое доказательство сохранения
  • 13.2 Уравнение Гамильтона – Якоби в параболических координатах
  • 13.3 Теорема Нётер
  • 13.4 Преобразование Ли n
• 14 Альтернативные вычисления, символы и формулировки
• 15 См. также
• 16 Ссылки
• 17 Дополнительная литература

Контекст

Отдельная частица, движущаяся под любым консервативным центральная сила имеет по крайней мере четыре константы движения, общую энергию E и три декартовых компонента углового импульс вектор Lотносительно начала координат. Орбита частицы ограничена плоскостью, определяемой начальным импульсом pчастицы (или, что эквивалентно, ее скоростью v) и вектором r между частицей и центром. силы (см. рисунок 1 ниже).

Как определено ниже (см. Математическое определение), вектор Лапласа – Рунге – Ленца (вектор LRL) A всегда лежит в плоскости движения для любого центральная сила. Однако A постоянно только для центральной силы, обратной квадрату. Однако для большинства центральных сил этот вектор Aне постоянен, но изменяется как по длине, так и по направлению; если центральная сила приблизительно равна закону обратных квадратов, вектор A приблизительно постоянен по длине, но медленно вращает свое направление. Обобщенный сохраняющийся вектор LRL $A\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\}\}\}$можно определить для всех центральных сил, но этот обобщенный вектор является сложной функцией положения и обычно не выражается в замкнутой форме.

Плоскость движения перпендикулярна вектору углового момента L, который постоянен; это может быть выражено математически векторным скалярным произведением уравнением r⋅ L= 0; аналогично, поскольку A лежит в этой плоскости, A⋅ L= 0.

Вектор LRL отличается от других сохраняемых величин следующим свойством. В то время как для типичных сохраняющихся величин существует соответствующая циклическая координата в трехмерном лагранжиане системы, такой координаты для вектора LRL не существует. Таким образом, сохранение вектора LRL должно быть получено напрямую, например, методом скобок Пуассона, как описано ниже. Такие сохраняющиеся величины называются «динамическими», в отличие от обычных «геометрических» законов сохранения, например, углового момента.

История повторного открытия

Вектор LRL A является константой движения важной проблемы Кеплера и полезен при описании астрономические орбиты, такие как движение планет. Тем не менее, он никогда не был хорошо известен среди физиков, возможно, потому, что он менее интуитивен, чем импульс и угловой момент. Следовательно, за последние три столетия он был независимо открыт повторно несколько раз.

Якоб Херманн был первым, кто показал, что A сохраняется для частного случая обратного квадрата центральную силу, и выяснил ее связь с эксцентриситетом орбитального эллипса . Работа Германа была обобщена до ее современной формы Иоганном Бернулли в 1710 году. В конце века Пьер-Симон де Лаплас заново открыл сохранение A, выводя его аналитически, а не геометрически. В середине девятнадцатого века Уильям Роуэн Гамильтон вывел эквивалентный вектор эксцентриситета, определенный ниже, используя его, чтобы показать, что вектор импульса p движется по окружности для движения под действием обратной квадрата центральной силы (рис. 3).

В начале двадцатого века Джозайя Уиллард Гиббс вывел тот же вектор с помощью векторного анализа. Вывод Гиббса был использован в качестве примера Карлом Рунге в популярном немецком учебнике векторов, на который ссылался Вильгельм Ленц в своей статье о (стар.) квантово-механическая обработка атома водорода . В 1926 году вектор был использован Вольфгангом Паули для получения спектра водорода водорода с использованием современной квантовой механики, но не Уравнение Шредингера ; после публикации Паули он стал известен в основном как вектор Рунге – Ленца.

Математическое определение

Для одиночной частицы, на которую действует обратный квадрат центральная сила, описываемая уравнением

$F\; (r)\; =\; -\; kr\; 2\; r\; ^,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; (r)\; =\; \{\backslash \; frac\; \{-k\}\; \{r\; ^\; \{2\}\}\}\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\},\}$

LRL вектор A математически определяется формулой

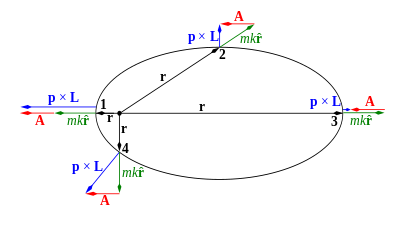Рисунок 1: Вектор LRL A (показан красным) в четырех точках (обозначенных 1, 2, 3 и 4) на эллиптическая орбита связанной точечной частицы, движущейся под действием центральной силы, обратной квадрату . Центр притяжения показан в виде небольшого черного кружка, из которого исходят векторы положения (также черные). Вектор углового момента L перпендикулярен орбите. Копланарные векторы p× Lи (mk / r) r показаны синим и зеленым цветом соответственно; эти переменные определены ниже. Вектор A постоянен по направлению и величине.

$A\; =\; p\; \times \; L\; -\; mkr\; ^,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{A\}\; =\; \backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; -\; mk\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\},\}$

где

• m - масса точечной частицы, движущейся под центральной силой,,
• p- ее импульс вектор,
• L= r× p- это его вектор углового момента,
• k - параметр, описывающий силу центральной силы,,
• r- вектор положения частицы (рис. 1), а
• $r\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\}\}$- соответствующий единичный вектор, т. е. $r\; ^\; =\; rr\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\}\; =\; \{\backslash \; frac\; \{\backslash \; mathbf\; \{r\}\}\; \{r\}\}\}$, где r - величина r.

. сила консервативна, общая энергия E представляет собой константу движения,

$E\; =\; p\; 2\; 2\; m\; -\; kr\; =\; 1\; 2\; mv\; 2\; -\; kr.\; \{\backslash \; displaystyle\; E\; =\; \{\backslash \; frac\; \{p\; ^\; \{2\}\}\; \{2m\}\}\; -\; \{\backslash \; frac\; \{k\}\; \{r\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; mv\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{k\}\; \{r\}\}.\}$

Кроме того, предполагаемая сила является центральной силой, и, таким образом, вектор углового момента L также сохраняется и определяет плоскость, в которой частица путешествует. Вектор LRL A перпендикулярен вектору углового момента L, потому что оба p× Lи r перпендикулярны L . Отсюда следует, что A лежит в плоскости орбиты .

. Это определение вектора LRL A относится к единственной точечной частице массы м движется под действием фиксированной силы. Однако то же определение можно расширить до задач двух тел, таких как проблема Кеплера, приняв m как приведенную массу двух тел и r как вектор между двумя телами.

Также могут использоваться различные альтернативные формулировки для одной и той же постоянной движения. Наиболее распространенным является масштабирование с помощью mk для определения вектора эксцентриситета (который является вектором с тем же направлением, что и большая полуось, и модуль которого равен эксцентриситету коники):

$e\; =\; A\; mk\; =\; 1\; mk\; (p\; \times \; L)\; -\; r\; ^.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; =\; \{\backslash \; frac\; \{\backslash \; mathbf\; \{A\}\}\; \{mk\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{mk\}\}\; (\backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{L\})\; -\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\}.\}$

Получение орбит Кеплера

Рисунок 2: Упрощенная версия рисунка 1, определяющая угол θ между A и r в одной точке орбиты.

Форма и ориентация орбит задачи Кеплера могут быть определены из вектора LRL следующим образом. Взяв скалярное произведение из A с вектором положения r, получаем уравнение

$A\; \cdot \; r\; =\; A\; r\; cos\; \; \theta \; =\; r\; \cdot \; (p\; \times \; L)\; -\; мкр,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{A\}\; \backslash \; cdot\; \backslash \; mathbf\; \{r\}\; =\; Ar\; \backslash \; cos\; \backslash \; theta\; =\; \backslash \; mathbf\; \{r\}\; \backslash \; cdot\; \backslash \; left\; (\backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; \backslash \; справа)\; -mkr,\}$

где θ - это угол между r и A (рисунок 2). Переставляя тройное скалярное произведение

$r\; \cdot \; (p\; \times \; L)\; =\; (r\; \times \; p)\; \cdot \; L\; =\; L\; \cdot \; L\; =\; L\; 2\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{r\}\; \backslash \; cdot\; \backslash \; left\; (\backslash \; mathbf\; \{p\; \}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; \backslash \; right)\; =\; \backslash \; left\; (\backslash \; mathbf\; \{r\}\; \backslash \; times\; \backslash \; mathbf\; \{p\}\; \backslash \; right)\; \backslash \; cdot\; \backslash \; mathbf\; \{L\}\; =\; \backslash \; mathbf\; \{L\}\; \backslash \; cdot\; \backslash \; mathbf\; \{L\}\; =\; L\; ^\; \{2\}\}$

и перестановка дает определяющую формулу для конического сечения , при условии, что A является константой, что имеет место для закона силы обратных квадратов,

$1\; r\; знак\; равно\; mk\; L\; 2\; (1\; +\; A\; mk\; cos\; \; \theta )\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{r\}\}\; =\; \{\backslash \; frac\; \{mk\}\; \{L\; ^\; \{2\}\}\}\; \backslash \; left\; (1\; +\; \{\backslash \; frac\; \{\; A\}\; \{mk\}\}\; \backslash \; cos\; \backslash \; theta\; \backslash \; right)\}$

из эксцентриситета e,

$e\; =\; A\; mk\; =\; |\; А\; |\; mk\; \{\backslash \; displaystyle\; e\; =\; \{\backslash \; frac\; \{A\}\; \{mk\}\}\; =\; \{\backslash \; frac\; \{\backslash \; left\; |\; \backslash \; mathbf\; \{A\}\; \backslash \; right\; |\}\; \{mk\}\}\}$

и прямая кишка

$|\; 2\; \ell \; |\; =\; 2\; L\; 2\; м\; k.\; \{\backslash \; displaystyle\; \backslash \; left\; |\; 2\; \backslash \; ell\; \backslash \; right\; |\; =\; \{\backslash \; frac\; \{2L\; ^\; \{2\}\}\; \{mk\}\}.\}$

Большая полуось a конического сечения может быть определена с помощью прямой кишки и эксцентриситета

$a\; (1\; \pm \; e\; 2)\; =\; \ell \; =\; L\; 2\; mk,\; \{\backslash \; displaystyle\; a\; \backslash \; left\; (1\; \backslash \; pm\; e\; ^\; \{2\}\; \backslash \; right)\; =\; \backslash \; ell\; =\; \{\backslash \; frac\; \{L\; ^\; \{2\}\}\; \{\; mk\}\},\}$

где знак минус относится к эллипсам, а знак плюс к гиперболам.

Взяв скалярное произведение A на себя, получаем уравнение с энергией E,

$A\; 2\; =\; m\; 2\; k\; 2\; +\; 2\; m\; EL\; 2,\; \{\backslash \; displaystyle\; A\; ^\; \{2\}\; =\; m\; ^\; \{2\}\; k\; ^\; \{2\}\; +\; 2mEL\; ^\; \{2\},\}$

, которое можно переписать в терминах эксцентриситета,

$e\; 2\; -\; 1\; =\; 2\; L\; 2\; mk\; 2\; E.\; \{\backslash \; displaystyle\; e\; ^\; \{2\}\; -1\; =\; \{\backslash \; frac\; \{2L\; ^\; \{2\}\}\; \{mk\; ^\; \{2\}\}\}\; E.\}$

Таким образом, если энергия E отрицательна (связанные орбиты), эксцентриситет меньше единицы, а орбита представляет собой эллипс . И наоборот, если энергия положительна (несвязанные орбиты, также называемые «рассеянными орбитами»), эксцентриситет больше единицы, а орбита представляет собой гиперболу. Наконец, если энергия точно равна нулю, эксцентриситет равен единице, а орбита представляет собой параболу. Во всех случаях направление A лежит вдоль оси симметрии конического сечения и указывает от центра силы к перицентру , точке наибольшего сближения.

Годографы кругового импульса

Рис. 3. Вектор импульса p (показан синим) движется по окружности, как частица движется по эллипсу. Четыре отмеченные точки соответствуют точкам на рисунке 1. Круг с центром на оси y в позиции A / L (показан пурпурным) с радиусом mk / L (показан зеленым). Угол η определяет эксцентриситет e эллиптической орбиты (cos η = e). По теореме о вписанном угле для окружностей, η также является углом между любой точкой окружности и двумя точками пересечения с осью p x, p x = ± p 0, которые зависят только от E, но не L.

Сохранение вектора LRL A и вектора углового момента L полезен для демонстрации того, что вектор импульса p движется по окружности под действием центральной силы, обратной квадрату.

Взяв скалярное произведение

$mkr\; ^\; =\; p\; \times \; L\; -\; A\; \{\backslash \; displaystyle\; mk\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{r\}\}\}\; =\; \backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; -\; \backslash \; mathbf\; \{A\}\}$

с собой дает

$(mk)\; 2\; =\; A\; 2\; +\; p\; 2\; L\; 2\; +\; 2\; L\; \cdot \; (p\; \times \; A).\; \{\backslash \; displaystyle\; (mk)\; ^\; \{2\}\; =\; A\; ^\; \{2\}\; +\; p\; ^\; \{2\}\; L\; ^\; \{2\}\; +2\; \backslash \; mathbf\; \{L\}\; \backslash \; cdot\; (\backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{A\}).\}$

Далее выбирая L вдоль оси z и большую полуось в качестве оси x, получаем уравнение геометрического места для p,

$px\; 2\; +\; (py\; -\; AL)\; 2\; =\; (mk\; L)\; 2.\; \{\backslash \; displaystyle\; p\_\; \{x\}\; ^\; \{2\}\; +\; \backslash \; left\; (p\_\; \{y\}\; -\; \{\backslash \; frac\; \{A\}\; \{L\}\}\; \backslash \; right)\; ^\; \{2\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{mk\}\; \{L\})\; \}\; \backslash \; right)\; ^\; \{2\}.\}$

Другими словами, вектор импульса p ограничен кругом радиуса mk / L = L / ℓ с центром в (0, A / L). Эксцентриситет e соответствует косинусу угла η, показанного на рисунке 3.

В вырожденном пределе круговых орбит и, таким образом, исчезающем A, окружность центрируется в начале координат (0, 0). Для краткости также полезно ввести переменную $p\; 0\; =\; 2\; m\; |\; E\; |\; \{\backslash \; displaystyle\; p\_\; \{0\}\; =\; \{\backslash \; sqrt\; \{2m\; |\; E\; |\}\}\}$.

Этот круговой годограф полезен для иллюстрации симметрии проблемы Кеплера.

Константы движения и суперинтегрируемость

Семь скалярных величин E, A и L (будучи векторами, последние две вносят по три сохраняющиеся величины каждая) связаны двумя уравнениями, A⋅ L= 0 и A = mk + 2 mEL, что дает пять независимых констант движения. (Поскольку величина A, следовательно, эксцентриситет e орбиты, может быть определена из полного углового момента L и энергии E, только направление A сохраняется независимо; кроме того, поскольку A должен быть перпендикулярен L, он вносит только одну дополнительную сохраняемую величину.)

Это согласуется с шестью начальными условиями (начальное положение частицы и векторы скорости , каждый с тремя компонентами), которые определяют орбиту частицы, поскольку начальное время не определяется постоянной движения. Таким образом, полученная 1-мерная орбита в 6-мерном фазовом пространстве полностью определена.

Механическая система с d степенями свободы может иметь не более 2d - 1 констант движения, так как есть 2d начальных условий, и начальное время не может быть определено константой движения. Система с более чем d константами движения называется суперинтегрируемой, а система с 2d - 1 константами называется максимально суперинтегрируемой. Поскольку решение уравнения Гамильтона – Якоби в одной системе координат может дать только d констант движения, суперинтегрируемые системы должны быть разделимы более чем в одной системе координат. Задача Кеплера максимально суперинтегрируема, поскольку имеет три степени свободы (d = 3) и пять независимых констант движения ; его уравнение Гамильтона – Якоби разделимо как в сферических координатах, так и в параболических координатах, как описано ниже.

Максимально суперинтегрируемые системы движутся по замкнутым одномерным орбитам в фазовое пространство, поскольку орбита является пересечением фазового пространства изоповерхностей их постоянных движения. Следовательно, орбиты перпендикулярны всем градиентам всех этих независимых изоповерхностей, пяти в этой конкретной задаче, и, следовательно, определяются обобщенными перекрестными произведениями всех этих градиентов. В результате все суперинтегрируемые системы автоматически описываются механикой Намбу, альтернативно и эквивалентно гамильтоновой механике.

Максимально суперинтегрируемые системы могут быть квантованы с использованием коммутационных соотношений, как показано ниже. Тем не менее, эквивалентным образом, они также квантованы в рамках Намбу, например, в этой классической проблеме Кеплера в квантовый атом водорода.

Эволюция при возмущенных потенциалах

Рис. 5: Постепенно прецессирующая эллиптическая орбита с эксцентриситетом e = 0,667. Такая прецессия возникает в задаче Кеплера, если притягивающая центральная сила немного отклоняется от закона обратных квадратов. Скорость прецессии может быть рассчитана с использованием формул в тексте.

Вектор Лапласа – Рунге – Ленца A сохраняется только для идеального обратного квадрата центрального сила. Однако в большинстве практических задач, таких как движение планет, взаимодействие потенциальной энергии между двумя телами не является в точности законом обратных квадратов, но может включать в себя дополнительную центральную силу, так называемую возмущение, описываемое потенциальной энергией h (r). В таких случаях вектор LRL медленно вращается в плоскости орбиты, что соответствует медленной апсидальной прецессии орбиты.

По предположению, возмущающий потенциал h (r) является консервативной центральной силой, что подразумевает, что полная энергия E и угловой момент вектор L сохранены. Таким образом, движение все еще находится в плоскости, перпендикулярной L, и величина A сохраняется из уравнения A = mk + 2mEL. Потенциал возмущения h (r) может быть функцией любого вида, но должен быть значительно слабее, чем основная сила обратного квадрата между двумя телами.

Скорость, с которой вектор LRL вращается, предоставляет информацию о возмущающем потенциале h (r). Используя каноническую теорию возмущений и координаты действие-угол, легко показать, что A вращается со скоростью

$\partial \; \partial \; L\; ⟨h\; (r)⟩\; =\; \partial \; \partial \; L\; \{1\; T\; \int \; 0\; T\; час\; (r)\; dt\}\; знак\; равно\; \partial \; \partial \; L\; \{м\; L\; 2\; \int \; 0\; 2\; \pi \; r\; 2\; час\; (r)\; d\; \theta \},\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; frac\; \{\backslash \; partial\; \}\; \{\backslash \; partial\; L\}\}\; \backslash \; langle\; h\; (r)\; \backslash \; rangle\; =\; \backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; L\}\}\; \backslash \; left\; \backslash \; \{\{\backslash \; frac\; \{1\}\; \{T\}\}\; \backslash \; int\; \_\; \{\; 0\}\; ^\; \{T\}\; час\; (г)\; \backslash ,\; dt\; \backslash \; right\; \backslash \}\; \backslash \backslash \; [1em]\; =\; \backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; L\}\}\; \backslash \; left\; \backslash \; \{\{\backslash \; frac\; \{m\}\; \{\; L\; ^\; \{2\}\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{2\; \backslash \; pi\}\; r\; ^\; \{2\}\; h\; (r)\; \backslash ,\; d\; \backslash \; theta\; \backslash \; right\; \backslash \},\; \backslash \; end\; \{align\}\}\}$

где T - период обращения, и тождество L dt = mr dθ использовалось для преобразования интеграла по времени в угловой интеграл (рисунок 5). Выражение в угловых скобках, ⟨h (r)⟩, представляет возмущающий потенциал, но усредненный за один полный период; то есть усредненное значение за один полный проход тела по орбите. Математически это среднее по времени соответствует следующей величине в фигурных скобках. Это усреднение помогает подавить колебания скорости вращения.

Этот подход использовался для проверки теории общей теории относительности Эйнштейна, которая добавляет небольшое эффективное обратнокубическое возмущение к нормальному ньютоновскому гравитационному потенциалу,

$h\; (r)\; =\; k\; L\; 2\; м\; 2\; c\; 2\; (1\; r\; 3).\; \{\backslash \; displaystyle\; h\; (r)\; =\; \{\backslash \; frac\; \{kL\; ^\; \{2\}\}\; \{m\; ^\; \{2\}\; c\; ^\; \{2\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{r\; ^\; \{3\}\}\}\; \backslash \; right).\}$

Подставляя эту функцию в интеграл и используя уравнение

$1\; r\; =\; mk\; L\; 2\; (1\; +\; A\; mk\; cos\; \; \theta )\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{r\}\}\; =\; \{\backslash \; frac\; \{mk\}\; \{L\; ^\; \{2\}\}\}\; \backslash \; left\; (1\; +\; \{\backslash \; frac\; \{A\}\; \{mk\}\}\; \backslash \; cos\; \backslash \; theta\; \backslash \; right)\}$

, чтобы выразить r через θ, скорость прецессии перицентра , вызванная этим неньютоновским возмущением, вычисляется как

$6\; \pi \; k\; 2\; TL\; 2\; c\; 2,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{6\; \backslash \; pi\; k\; ^\; \{\; 2\}\}\; \{TL\; ^\; \{2\}\; c\; ^\; \{2\}\}\},\}$

, что близко соответствует наблюдаемой аномальной прецессии Меркурия и бинарных пульсаров. Это согласие с экспериментом является убедительным доказательством общей теории относительности.

скобок Пуассона

Немасштабированных функций

Алгебраическая структура проблемы, как объясняется в последующих разделах, такова: SO (4) / 2 ~ SO (3) × SO (3). Три компонента L i вектора углового момента L имеют скобки Пуассона

$\{L\; i,\; L\; j\}\; =\; \sum \; s\; =\; 1\; 3\; \epsilon \; ijs\; L\; s,\; \{\backslash \; displaystyle\; \backslash \; \{L\_\; \{i\},\; L\_\; \{j\}\; \backslash \}\; =\; \backslash \; sum\; \_\; \{s\; =\; 1\}\; ^\; \{3\}\; \backslash \; varepsilon\; \_\; \{ijs\}\; L\_\; \{s\},\}$

где i = 1, 2, 3 и ϵ ijs - полностью антисимметричный тензор, то есть символ Леви-Чивита ; здесь используется индекс суммирования s, чтобы избежать путаницы с параметром силы k, определенным выше. Тогда, поскольку вектор LRL A преобразуется как вектор, мы имеем следующие отношения скобок Пуассона между A и L:

$\{A\; i,\; L\; j\}\; =\; \sum \; s\; =\; 1\; 3\; \epsilon \; ijs\; A\; s.\; \{\backslash \; displaystyle\; \backslash \; \{A\_\; \{i\},\; L\_\; \{j\}\; \backslash \}\; =\; \backslash \; sum\; \_\; \{s\; =\; 1\}\; ^\; \{3\}\; \backslash \; varepsilon\; \_\; \{ijs\}\; A\_\; \{s\}.\}$

Наконец, скобки Пуассона между различными компонентами A следующие:

$\{A\; i,\; A\; j\}\; =\; -\; 2\; m\; \sum \; s\; =\; 1\; 3\; \epsilon \; ijs\; L\; s\; H,\; \{\backslash \; displaystyle\; \backslash \; \{A\_\; \{i\},\; A\_\; \{j\}\; \backslash \}\; =\; -\; 2m\; \backslash \; sum\; \_\; \{s\; =\; 1\}\; ^\; \{3\}\; \backslash \; varepsilon\; \_\; \{ijs\}\; L\_\; \{s\}\; H,\}$

где $H\; \{\backslash \; displaystyle\; H\}$- гамильтониан. Обратите внимание, что диапазон компонентов A и компонентов L не закрыт скобками Пуассона из-за множителя $H\; \{\backslash \; displaystyle\; H\}$в правой части этого последнего соотношения.

Наконец, поскольку и L, и A являются константами движения, мы имеем

$\{A\; i,\; H\}\; =\; \{L\; i,\; H\}\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; \{A\_\; \{i\},\; H\; \backslash \}\; =\; \backslash \; \{L\_\; \{i\},\; H\; \backslash \}\; =\; 0.\}$

Скобки Пуассона будут расширены до квантово-механического коммутационные отношения в следующем разделе и скобки в следующем разделе.

Масштабированные функции

Как отмечено ниже масштабированный вектор Лапласа – Рунге – Ленца D может быть определен в тех же единицах, что и угловой момент, путем деления A на $p\; 0\; =\; 2\; м\; |\; H\; |\; \{\backslash \; displaystyle\; p\_\; \{0\}\; =\; \{\backslash \; sqrt\; \{2m\; |\; H\; |\}\}\}$. Поскольку D по-прежнему преобразуется как вектор, скобки Пуассона для D с вектором углового момента L могут быть записаны в аналогичном форма

$\{D\; i,\; L\; j\}\; =\; \sum \; s\; =\; 1\; 3\; \epsilon \; ijs\; D\; s.\; \{\backslash \; displaystyle\; \backslash \; \{D\_\; \{i\},\; L\_\; \{j\}\; \backslash \}\; =\; \backslash \; sum\; \_\; \{s\; =\; 1\}\; ^\; \{3\}\; \backslash \; varepsilon\; \_\; \{ijs\}\; D\_\; \{s\}.\}$

скобки Пуассона из D с самим собой зависят от знака H, то есть от того, является ли энергия отрицательной (создавая замкнутые эллиптические орбиты при обратном квадратная центральная сила) или положительная (создавая открытые гиперболические орбиты под действием центральной силы, обратной квадрату). Для отрицательных энергий, то есть для связанных систем, скобки Пуассона равны

$\{D\; i,\; D\; j\}\; =\; \sum \; s\; =\; 1\; 3\; \epsilon \; i\; j\; s\; L\; s.\; \{\backslash \; displaystyle\; \backslash \; \{D\_\; \{i\},\; D\_\; \{j\}\; \backslash \}\; =\; \backslash \; sum\; \_\; \{s\; =\; 1\}\; ^\; \{3\}\; \backslash \; varepsilon\; \_\; \{ijs\}\; L\_\; \{s\}.\}$

Теперь мы можем оценить мотивацию для выбранного масштабирования D : При таком масштабировании гамильтониан больше не появляется в правой части предыдущего соотношения. Таким образом, диапазон трех компонентов L и трех компонентов D образует шестимерную алгебру Ли под скобкой Пуассона. Эта алгебра Ли изоморфна so (4), алгебре Ли 4-мерной группы вращений SO (4).

Напротив, для положительной энергии скобки Пуассона имеют противоположный знак,

$\{D\; i,\; D\; j\}\; =\; -\; \sum \; s\; =\; 1\; 3\; \epsilon \; ijs\; L\; s.\; \{\backslash \; displaystyle\; \backslash \; \{D\_\; \{i\},\; D\_\; \{j\}\; \backslash \}\; =\; -\; \backslash \; sum\; \_\; \{s\; =\; 1\}\; ^\; \{3\}\; \backslash \; varepsilon\; \_\; \{ijs\}\; L\_\; \{s\}.\}$

В этом случае Алгебра Ли изоморфна so (3,1).

Различие между положительной и отрицательной энергиями возникает из-за того, что желаемое масштабирование - то, которое исключает гамильтониан из правой части скобок Пуассона между компонентами масштабированного вектора LRL - включает квадратный корень из гамильтониан. Чтобы получить функции с действительными значениями, мы должны затем взять абсолютное значение гамильтониана, который различает положительные значения (где $|\; H\; |\; =\; H\; \{\backslash \; displaystyle\; |\; H\; |\; =\; H\}$) и отрицательные значения (где $|\; H\; |\; =\; -\; H\; \{\backslash \; displaystyle\; |\; H\; |\; =\; -H\}$).

Инварианты Казимира и уровни энергии

Инварианты Казимира для отрицательных энергий равны

$C\; 1\; =\; D\; \cdot \; D\; +\; L\; \cdot \; L\; =\; m\; k\; 2\; 2\; |\; E\; |,\; \{\backslash \; displaystyle\; C\_\; \{1\}\; =\; \backslash \; mathbf\; \{D\}\; \backslash \; cdot\; \backslash \; mathbf\; \{D\}\; +\; \backslash \; mathbf\; \{L\}\; \backslash \; cdot\; \backslash \; mathbf\; \{L\}\; =\; \{\backslash \; frac\; \{mk\; ^\; \{2\}\}\; \{2\; |\; E\; |\; \}\},\}$

$C\; 2\; =\; D\; \cdot \; L\; =\; 0,\; \{\backslash \; displaystyle\; C\_\; \{2\}\; =\; \backslash \; mathbf\; \{D\}\; \backslash \; cdot\; \backslash \; mathbf\; \{L\}\; =\; 0,\}$

и имеют исчезающие скобки Пуассона со всеми компоненты D и L,

$\{C\; 1,\; L\; i\}\; =\; \{C\; 1,\; D\; i\}\; =\; \{C\; 2,\; L\; i\}\; =\; \{C\; 2,\; D\; i\}\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; \{C\_\; \{1\},\; L\_\; \{i\}\; \backslash \}\; =\; \backslash \; \{C\_\; \{1\},\; D\_\; \{i\}\; \backslash \}\; =\; \backslash \; \{C\_\; \{2\},\; L\_\; \{i\}\; \backslash \}\; =\; \backslash \; \{C\_\; \{2\},\; D\_\; \{i\}\; \backslash \}\; =\; 0.\}$

C2тривиально равно нулю, поскольку два вектора всегда перпендикулярны.

Однако другой инвариант, C 1, нетривиален и зависит только от m, k и E.При каноническом квантовании этот инвариант допускает уровни энергии водорода -подобные атомы должны быть получены с использованием только квантово-механических канонических коммутационных соотношений вместо обычного решения уравнения Шредингера. Этот вывод подробно обсуждается в следующем разделе.

Квантовая механика атома водорода

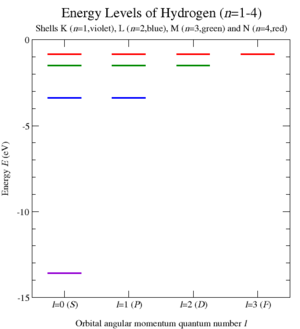Рис. 6. Уровни энергии атома водорода, предсказанные из коммутационных соотношений углового момента и векторных операторов Лапласа – Рунге – Ленца; эти уровни энергии были проверены экспериментально.

Скобки Пуассона предоставляют простое руководство для квантования большинства классических систем : соотношение коммутации двух квантово-механических операторы задаются скобкой Пуассона соответствующих классических переменных, умноженной на iħ.

Путем выполнения этого квантования и вычисления собственных значений C 1 Оператор Казимира для задачи Кеплера, Вольфганг Паули смог получить уровни энергии водородоподобных атомов (рис. 6) и, таким образом, их спектр атомного излучения. Этот элегантный вывод 1926 года был получен до разработки уравнения Шредингера.

Тонкость квантово-механического оператора для вектора LRL A заключается в том, что операторы импульса и момента количества движения не коммутируют; следовательно, квантовый оператор перекрестное произведение из p и L должен быть определен тщательно. Обычно операторы для декартовых компонентов Asопределяются с использованием симметризованного (эрмитова) произведения,

$A\; s\; =\; -\; mkr\; ^\; s\; +\; 1\; 2\; \sum \; i\; =\; 1\; 3\; \sum \; j\; =\; 1\; 3\; \epsilon \; sij\; (\; пи\; \ell \; j\; +\; \ell \; jpi),\; \{\backslash \; displaystyle\; A\_\; \{s\}\; =\; -\; mk\; \{\backslash \; hat\; \{r\}\}\; \_\; \{s\}\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{\; 3\}\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{3\}\; \backslash \; varepsilon\; \_\; \{sij\}\; (p\_\; \{i\}\; \backslash \; ell\; \_\; \{j\}\; +\; \backslash \; ell\; \_\; \{j\}\; p\_\; \{i\}),\}$

После этого сделано, можно показать, что квантовые операторы LRL удовлетворяют соотношениям коммутации, точно аналогичным отношениям скобок Пуассона из предыдущего раздела - просто заменив скобку Пуассона на $1\; /\; (i\; \hslash )\; \{\backslash \; displaystyle\; 1\; /\; (i\; \backslash \; hbar)\}$, умноженное на коммутатор.

Из этих операторов можно определить дополнительные лестничные операторы для L,

$J\; 0\; =\; A\; 3,\; \{\backslash \; displaystyle\; J\_\; \{0\}\; =\; A\_\; \{3\},\}$

$J\; \pm \; 1\; =\; \mp \; 1\; 2\; (A\; 1\; \pm \; i\; A\; 2).\; \{\backslash \; displaystyle\; J\; \_\; \{\backslash \; pm\; 1\}\; =\; \backslash \; mp\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\}\}\}\; \backslash \; left\; (A\_\; \{1\}\; \backslash \; pm\; iA\_\; \{2\}\; \backslash \; right).\}$

Эти дополнительные соединения разные собственные состояния L, поэтому разные спиновые мультиплеты между собой.

Нормализованный первый инвариантный оператор Казимира, квантовый аналог описанного выше, может быть определен аналогичным образом,

$C\; 1\; =\; -\; mk\; 2\; 2\; \hslash \; 2\; H\; -\; 1\; -\; I,\; \{\backslash \; displaystyle\; C\_\; \{1\}\; =\; -\; \{\backslash \; frac\; \{mk\; ^\; \{2\}\}\; \{2\; \backslash \; hbar\; ^\; \{2\}\}\}\; H\; ^\; \{-\; 1\}\; -I,\}$

где H является обратным к гамильтонову оператору энергии, а I - тождественный оператор .

. Применяя эти лестничные операторы к собственным состояниям | ℓmn〉 полного углового момента, азимутального углового момента и операторов энергии, собственных значений первого оператора Казимира, C 1, как видно, квантованы, n - 1. Важно отметить, что из-за исчезновения C 2 они не зависят от квантовых чисел ℓ и m, что делает уровни энергии вырождаются.

Следовательно, уровни энергии задаются следующим образом:

$E\; n\; =\; -\; mk\; 2\; 2\; \hslash \; 2\; n\; 2,\; \{\backslash \; displaystyle\; E\_\; \{n\}\; =\; -\; \{\backslash \; frac\; \{mk\; ^\; \{2\}\}\; \{2\; \backslash \; hbar\; ^\; \{2\}\; n\; ^\; \{2\}\}\},\}$

, что совпадает с формулой Ридберга для водородоподобных атомов (рисунок 6). Дополнительные операторы симметрии A соединили разные ℓ мультиплеты между собой для заданной энергии (и C 1), определяя n состояний на каждом уровне. Фактически они увеличили группу углового момента SO (3) до SO (4) /ℤ2~ SO (3) × SO (3).

Сохранение и симметрия

Сохранение вектора LRL соответствует тонкой симметрии системы. В классической механике симметрии - это непрерывные операции, которые отображают одну орбиту на другую без изменения энергии системы; в квантовой механике симметрии - это непрерывные операции, которые «смешивают» электронные орбитали с одинаковой энергией, то есть вырожденные уровни энергии. С такими симметриями обычно связывают сохраняющуюся величину. Например, каждая центральная сила симметрична относительно группы вращения SO (3), что приводит к сохранению углового момента L. Обычно полное вращение системы не влияет на энергию орбиты; квантово-механически, вращения смешивают сферические гармоники одного и того же квантового числа l без изменения энергии.

Рис. 7. Семейство годографов кругового импульса для заданной энергии E. Все круги проходят через одни и те же две точки $\pm \; p\; 0\; =\; \pm \; 2\; м\; |\; E\; |\; \{\backslash \; displaystyle\; \backslash \; pm\; p\_\; \{0\}\; =\; \backslash \; pm\; \{\backslash \; sqrt\; \{2m\; |\; E\; |\}\}\}$на оси p x (см. рисунок 3). Это семейство годографов соответствует одному семейству аполлоновских кругов и σ-изоповерхностям биполярных координат.

. Симметрия для центральной силы обратного квадрата выше и тоньше. Своеобразная симметрия задачи Кеплера приводит к сохранению как вектора углового момента L, так и вектора LRL A (как определено выше) и квантово-механически, гарантирует, что уровни энергии водорода не зависят от квантовых чисел углового момента l и m. Однако симметрия более тонкая, потому что операция симметрии должна иметь место в многомерном пространстве ; такие симметрии часто называют «скрытыми симметриями».

Классически более высокая симметрия проблемы Кеплера допускает непрерывные изменения орбит, которые сохраняют энергию, но не угловой момент; Другими словами, орбиты с одинаковой энергией, но с различным угловым моментом (эксцентриситетом) могут непрерывно преобразовываться друг в друга. Квантово-механически это соответствует смешиванию орбиталей, которые различаются квантовыми числами l и m , например s (l = 0) и p (l = 1) атомными орбиталями. Такое смешивание не может быть выполнено с помощью обычных трехмерных перемещений или вращений, но эквивалентно вращению в более высоком измерении.

Для отрицательных энергий, т.е. для связанных систем, группа высшей симметрии SO (4), которая сохраняет длину четырехмерных векторов

$|\; е\; |\; 2\; =\; е\; 1\; 2\; +\; е\; 2\; 2\; +\; е\; 3\; 2\; +\; е\; 4\; 2.\; \{\backslash \; displaystyle\; |\; \backslash \; mathbf\; \{e\}\; |\; ^\; \{2\}\; =\; e\_\; \{1\}\; ^\; \{2\}\; +\; e\_\; \{2\}\; ^\; \{2\}\; +\; e\_\; \{3\}\; ^\; \{2\}\; +\; e\_\; \{4\}\; ^\; \{2\}.\}$

В 1935 году Владимир Фок показал, что квантово-механическая ограниченная проблема Кеплера эквивалентна проблеме свободной частицы, ограниченной трехмерной единичной сферой . в четырехмерном пространстве. В частности, Фок показал, что волновая функция Шредингера в импульсном пространстве для задачи Кеплера была стереографической проекцией сферических гармоник на сфера. Вращение сферы и повторное проецирование приводят к непрерывному отображению эллиптических орбит без изменения энергии; квантово-механически это соответствует смешиванию всех орбиталей с одинаковым квантовым числом энергии n. Валентин Баргманн впоследствии заметил, что скобки Пуассона для вектора углового момента L и масштабированный вектор LRL D образуют алгебру Ли для SO (4). Проще говоря, шесть величин D и L соответствуют шести сохраняющимся угловым моментам в четырех измерениях, связанных с шестью возможными простыми вращениями в этом пространстве (там шесть способов выбора двух осей из четырех). Этот вывод не означает, что наша вселенная представляет собой трехмерную сферу; это просто означает, что эта конкретная физическая проблема (задача двух тел для обратных квадратов центральных сил ) математически эквивалентна свободной частице на трехмерной сфере.

Для положительных энергий - т. Е. Для несвязанных, «рассеянных» систем - группа высшей симметрии SO (3,1), которая сохраняет длину Минковского 4-вектора

$ds\; 2\; =\; e\; 1\; 2\; +\; e\; 2\; 2\; +\; e\; 3\; 2\; -\; e\; 4\; 2.\; \{\backslash \; displaystyle\; ds\; ^\; \{2\}\; =\; e\_\; \{1\}\; ^\; \{2\}\; +\; e\_\; \{2\}\; ^\; \{2\}\; +\; e\_\; \{3\}\; ^\; \{2\}\; -e\_\; \{4\}\; ^\; \{2\}.\}$

Оба случаи отрицательной и положительной энергии были рассмотрены Фоком и Баргманном и энциклопедически рассмотрены Бандером и Ициксоном.

Орбиты систем с центральной силой и орбиты проблемы Кеплера в частности - также симметричны под отражением. Следовательно, указанные выше группы SO (3), SO (4) и SO (3,1) не являются полными группами симметрии своих орбит; полные группы: O (3), O (4) и O (3,1), соответственно. Тем не менее, только связанные подгруппы, SO (3), SO (4) и SO (3,1) необходимы для демонстрации сохранения углового момента и векторы LRL; симметрия отражения не имеет отношения к сохранению, что может быть получено из алгебры Ли группы.

Вращательная симметрия в четырех измерениях

Рисунок 8: Годографы импульса на рисунке 7 соответствуют стереографическим проекциям больших кругов на трехмерной единичной сфере η. Все большие круги пересекают ось η x, которая перпендикулярна странице; проекция идет от северного полюса (единичный вектор w ) на плоскость η x−ηy, как показано здесь для пурпурного годографа пунктирными черными линиями. Большой круг на широте α соответствует эксцентриситету e = sin α. Цвета больших кругов, показанные здесь, соответствуют соответствующим им годографам на рисунке 7.

Связь между проблемой Кеплера и четырехмерной симметрией вращения SO (4) может быть легко визуализируется. Обозначим четырехмерные декартовы координаты (w, x, y, z), где (x, y, z) представляют собой декартовы координаты вектора нормального положения r. Трехмерный вектор импульса p связан с четырехмерным вектором $\eta \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; eta\}\}\}$на трехмерной единичной сфере.

$\eta \; знак\; равно\; п\; 2\; -\; p\; 0\; 2\; p\; 2\; +\; p\; 0\; 2\; w\; ^\; +\; 2\; p\; 0\; p\; 2\; +\; p\; 0\; 2\; p\; =\; mk\; -\; rp\; 0\; 2\; mkw\; ^\; +\; rp\; 0\; mkp,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{\; выровнено\}\; \{\backslash \; boldsymbol\; \{\backslash \; eta\}\}\; =\; \backslash \; displaystyle\; \{\backslash \; frac\; \{p\; ^\; \{2\}\; -p\_\; \{0\}\; ^\; \{2\}\}\; \{p\; ^\; \{2\}\; +\; p\_\; \{0\}\; ^\; \{2\}\}\}\; \backslash \; mathbf\; \{\backslash \; hat\; \{w\}\}\; +\; \{\backslash \; frac\; \{2p\_\; \{0\}\}\; \{p\; ^\; \{2\}\; +\; p\_\; \{0\}\; ^\; \{2\}\}\}\; \backslash \; mathbf\; \{p\}\; \backslash \backslash \; [1em]\; =\; \backslash \; displaystyle\; \{\backslash \; frac\; \{mk-rp\_\; \{0\}\; ^\; \{2\}\}\; \{mk\}\}\; \backslash \; mathbf\; \{\backslash \; hat\; \{w\}\}\; +\; \{\backslash \; frac\; \{rp\_\; \{0\}\}\; \{mk\}\}\; \backslash \; mathbf\; \{p\},\; \backslash \; end\; \{align\}\}\}$

где $w\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{w\}\}\}$- единичный вектор вдоль новой оси w. Преобразование p в η может быть однозначно инвертировано; например, компонент импульса x равен

$px\; =\; p\; 0\; \eta \; x\; 1\; -\; \eta \; w,\; \{\backslash \; displaystyle\; p\_\; \{x\}\; =\; p\_\; \{0\}\; \{\backslash \; frac\; \{\backslash \; eta\; \_\; \{x\}\}\; \{1-\; \backslash \; eta\; \_\; \{w\}\}\},\}$

и аналогично для p y и p z. Другими словами, трехмерный вектор p является стереографической проекцией четырехмерного $\eta \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; eta\}\}\}$вектор, масштабированный на p 0 (рисунок 8).

Без потери общности, мы можем исключить нормальную вращательную симметрию, выбрав декартовы координаты так, чтобы ось z была выровнена с вектором углового момента L и Годографы импульса выровнены, как на рисунке 7, с центрами кружков на оси y. Поскольку движение является плоским, а p и L перпендикулярны, p z = η z = 0 и внимание может быть ограничено трехмерный вектор $\eta \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; eta\}\}\}$= (η w, η x, η y). Семейство аполлонических кругов годографов импульса (рис. 7) соответствует семейству больших кругов на трехмерном $\eta \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; eta\}\; \}\}$сфера, каждая из которых пересекает ось η x в двух фокусах η x = ± 1, соответствующих фокусам годографа импульса при p <391.>x = ± p 0. Эти большие круги связаны простым вращением вокруг оси η x (рисунок 8). Эта вращательная симметрия преобразует все орбиты с одинаковой энергией друг в друга; однако такой поворот ортогонален обычным трехмерным поворотам, поскольку он преобразует четвертое измерение η w. Эта более высокая симметрия характерна для задачи Кеплера и соответствует сохранению вектора LRL.

Элегантное переменные действие-угол решение проблемы Кеплера может быть получено путем исключения избыточных четырехмерных координат $\eta \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; eta\}\}\}$в пользу эллиптических цилиндрических координат (χ, ψ, φ)

$\eta \; w\; =\; cn\; \; \chi \; cn\; \; \psi ,\; \{\backslash \; displaystyle\; \backslash \; eta\; \_\; \{w\}\; =\; \backslash \; operatorname\; \{cn\}\; \backslash \; chi\; \backslash \; имя\; оператора\; \{cn\}\; \backslash \; psi,\}$

$\eta \; x\; =\; sn\; \chi \; dn\; \; \psi \; cos\; \; \varphi ,\; \{\backslash \; displaystyle\; \backslash \; eta\; \_\; \{x\}\; =\; \backslash \; operatorname\; \{sn\}\; \backslash ,\; \backslash \; chi\; \backslash \; operatorname\; \{dn\}\; \backslash \; psi\; \backslash ,\; \backslash \; соз\; \backslash \; фи,\}$

$\eta \; y\; =\; sn\; \; \chi \; dn\; \; \psi \; sin\; \; \varphi ,\; \{\backslash \; displaystyle\; \backslash \; eta\; \_\; \{y\}\; =\; \backslash \; operatorname\; \{sn\}\; \backslash \; chi\; \backslash \; operatorname\; \{dn\}\; \backslash \; psi\; \backslash \; sin\; \backslash \; фи,\}$

$\eta \; z\; =\; dn\; \; \chi \; sn\; \; \psi ,\; \{\backslash \; displaystyle\; \backslash \; eta\; \_\; \{z\}\; =\; \backslash \; operatorname\; \{dn\}\; \backslash \; chi\; \backslash \; operatorname\; \{sn\}\; \backslash \; psi,\}$

где sn, cn и dn - это эллиптические функции Якоби..

Обобщения для других потенциалов и теории относительности.

Вектор Лапласа – Рунге – Ленца также можно обобщить для определения сохраняющихся величин, применимых к другим ситуациям.

В присутствии однородного электрического поля E обобщенный вектор Лапласа – Рунге – Ленца $A\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\}\}\}$is

$A\; =\; A\; +\; mq\; 2\; [(r\; \times \; E)\; \times \; r],\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\}\}\; =\; \backslash \; mathbf\; \{A\}\; +\; \{\backslash \; frac\; \{mq\}\; \{2\}\}\; \backslash \; left\; [\backslash \; left\; (\backslash \; mathbf\; \{\; r\}\; \backslash \; times\; \backslash \; mathbf\; \{E\}\; \backslash \; right)\; \backslash \; times\; \backslash \; mathbf\; \{r\}\; \backslash \; right],\}$

где q - заряд движущейся по орбите частицы. Хотя $A\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\}\}\}$не сохраняется, оно приводит к сохранению величины, а именно $A\; \cdot \; E\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\}\; \}\; \backslash \; cdot\; \backslash \; mathbf\; \{E\}\}$.

Далее обобщая вектор Лапласа – Рунге – Ленца на другие потенциалы и специальную теорию относительности, наиболее общую форму можно записать как

$A\; =\; (\partial \; \xi \; \partial \; u)\; (п\; \times \; L)\; +\; [\xi \; -\; u\; (\partial \; \xi \; \partial \; u)]\; L\; 2\; r\; ^,\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\}\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; \backslash \; xi\}\; \{\backslash \; частичный\; u\}\}\; \backslash \; right)\; \backslash \; left\; (\backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; \backslash \; right)\; +\; \backslash \; left\; [\backslash \; xi\; -u\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; \backslash \; xi\}\; \{\backslash \; partial\; u\}\; \}\; \backslash \; right)\; \backslash \; right]\; L\; ^\; \{2\}\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\},\}$

где u = 1 / r (см. теорему Бертрана ) и ξ = cos θ, с угол θ, определяемый формулой

$\theta \; =\; L\; \int \; udum\; 2\; c\; 2\; (\gamma \; 2-1)\; -\; L\; 2\; u\; 2,\; \{\backslash \; displaystyle\; \backslash \; theta\; =\; L\; \backslash \; int\; ^\; \{u\}\; \{\backslash \; frac\; \{du\}\; \{\backslash \; sqrt\; \{m\; ^\; \{2\}\; c\; ^\; \{2\}\; (\backslash \; gamma\; ^\; \{2\}\; -1)\; -L\; ^\; \{2\}\; u\; ^\; \{2\}\}\}\},\}$

и γ - фактор Лоренца. Как и раньше, мы можем получить сохраняющийся бинормальный вектор B, взяв векторное произведение с сохраняющимся вектором углового момента

$B\; =\; L\; \times \; A.\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{B\}\}\; =\; \backslash \; mathbf\; \{L\}\; \backslash \; times\; \{\backslash \; mathcal\; \{A\}\}.\}$

Эти два вектора можно аналогичным образом объединить в сохраняющийся диадический тензор W,

$W\; =\; \alpha \; A\; \otimes \; A\; +\; \beta \; B\; \otimes \; B.\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{W\}\}\; =\; \backslash \; alpha\; \{\backslash \; mathcal\; \{A\}\}\; \backslash \; otimes\; \{\backslash \; mathcal\; \{A\}\}\; +\; \backslash \; beta\; \backslash ,\; \{\backslash \; mathcal\; \{B\}\}\; \backslash \; otimes\; \{\backslash \; mathcal\; \{B\}\}.\}$

На иллюстрации можно вычислить вектор LRL для нерелятивистского изотропного гармонического осциллятора. Поскольку сила центральная,

$F\; (r)\; =\; -\; kr,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; (r)\; =\; -\; k\; \backslash \; mathbf\; \{r\},\}$

, угловой момент вектор сохраняется, и движение лежит в плоскости.

Сохраняющийся диадический тензор можно записать в простой форме

$W\; =\; 1\; 2\; mp\; \otimes \; p\; +\; k\; 2\; r\; \otimes \; r,\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{W\}\}\; =\; \{\backslash \; frac\; \{1\; \}\; \{2m\}\}\; \backslash \; mathbf\; \{p\}\; \backslash \; otimes\; \backslash \; mathbf\; \{p\}\; +\; \{\backslash \; frac\; \{k\}\; \{2\}\}\; \backslash ,\; \backslash \; mathbf\; \{r\}\; \backslash \; otimes\; \backslash \; mathbf\; \{r\},\}$

хотя p и r не обязательно перпендикулярны.

Соответствующий вектор Рунге – Ленца более сложен,

$A\; =\; 1\; mr\; 2\; \omega \; 0\; A\; -\; mr\; 2\; E\; +\; L\; 2\; \{(p\; \times \; L)\; +\; (mr\; \omega \; 0\; A\; -\; mr\; E)\; г\; ^\},\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{mr\; ^\; \{2\}\; \backslash \; omega\; \_\; \{0\}\; A-mr\; ^\; \{2\}\; E\; +\; L\; ^\; \{2\}\; \}\}\}\; \backslash \; left\; \backslash \; \{\backslash \; left\; (\backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; \backslash \; right)\; +\; \backslash \; left\; (mr\; \backslash \; omega\; \_\; \{0\}\; A-mrE\; \backslash \; right)\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\; \}\; \backslash \; right\; \backslash \},\}$

где

$\omega \; 0\; =\; km\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{0\}\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{k\}\; \{m\}\}\}\}$

- собственное колебание частота, и

$A\; =\; (E\; 2\; -\; \omega \; 2\; L\; 2)\; 1/2\; /\; \omega .\; \{\backslash \; displaystyle\; A\; =\; (E\; ^\; \{2\}\; -\; \backslash \; omega\; ^\; \{2\}\; L\; ^\; \{2\})\; ^\; \{1/2\}\; /\; \backslash \; omega.\}$

Доказательства того, что вектор Лапласа – Рунге – Ленца сохраняется в Задачи Кеплера

Следующие аргументы показывают, что вектор LRL сохраняется при центральных силах, которые подчиняются закону обратных квадратов.

Прямое доказательство сохранения

Центральная сила $F\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\}$, действующая на частицу, равна

$F\; =\; dpdt\; =\; е\; (г)\; рр\; знак\; равно\; е\; (г)\; р\; ^\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{F\}\; =\; \{\backslash \; гидроразрыва\; \{d\; \backslash \; mathbf\; \{p\}\}\; \{dt\}\}\; =\; f\; (г)\; \{\backslash \; гидроразрыва\; \{\backslash \; mathbf\; \{г\}\; \}\; \{r\}\}\; =\; f\; (r)\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\}\}$

для некоторой функции $f\; (r)\; \{\backslash \; displaystyle\; f\; (r)\}$радиуса $р\; \{\backslash \; displaystyle\; r\}$. Поскольку угловой момент $L\; =\; r\; \times \; p\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{L\}\; =\; \backslash \; mathbf\; \{r\}\; \backslash \; times\; \backslash \; mathbf\; \{p\}\}$сохраняется при центральном силы, $ddt\; L\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; mathbf\; \{L\}\; =\; 0\}$и

$ddt\; (p\; \times \; L)\; =\; dpdt\; \times \; L\; знак\; равно\; е\; (г)\; р\; ^\; \times \; (г\; \times \; mdrdt)\; =\; е\; (г)\; MR\; [г\; (г\; \cdot \; drdt)\; -\; r\; 2\; drdt],\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; left\; (\backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{p\}\}\; \{dt\}\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; =\; f\; (r)\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\}\; \backslash \; times\; \backslash \; left\; (\backslash \; mathbf\; \{r\}\; \backslash \; times\; m\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{r\}\}\; \{dt\}\}\; \backslash \; right)\; =\; f\; (r)\; \{\backslash \; frac\; \{m\}\; \{r\}\}\; \backslash \; left\; [\backslash \; mathbf\; \{r\}\; \backslash \; left\; (\backslash \; mathbf\; \{r\}\; \backslash \; cdot\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{r\}\}\; \{dt\}\}\; \backslash \; right)\; -r\; ^\; \{2\}\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{r\}\}\; \{\; dt\}\}\; \backslash \; right],\}$

где momentum $p\; =\; mdrdt\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{p\}\; =\; m\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{r\}\}\; \{dt\}\; \}\}$и где тройное векторное произведение было упрощено с использованием формулы Лагранжа

$r\; \times \; (r\; \times \; drdt)\; =\; r\; (r\; \cdot \; drdt)\; -\; r\; 2\; drdt.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{r\}\; \backslash \; times\; \backslash \; left\; (\backslash \; mathbf\; \{r\}\; \backslash \; times\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{r\}\}\; \{dt\}\}\; \backslash \; right)\; =\; \backslash \; mathbf\; \{r\}\; \backslash \; left\; (\backslash \; mathbf\; \{\; r\}\; \backslash \; cdot\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{r\}\}\; \{dt\}\}\; \backslash \; right)\; -r\; ^\; \{2\}\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{r\}\}\; \{dt\}\}.\}$

Тождество

$ddt\; (r\; \cdot \; r)\; =\; 2\; r\; \cdot \; drdt\; =\; ddt\; (r\; 2)\; =\; 2\; rdrdt\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; left\; (\backslash \; mathbf\; \{r\}\; \backslash \; cdot\; \backslash \; mathbf\; \{r\; \}\; \backslash \; right)\; =\; 2\; \backslash \; mathbf\; \{r\}\; \backslash \; cdot\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{r\}\}\; \{dt\}\}\; =\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; (r\; ^\; \{2\})\; =\; 2r\; \{\backslash \; frac\; \{dr\}\; \{dt\}\}\}$

дает уравнение

$ddt\; (p\; \times \; L)\; =\; -\; mf\; (r)\; r\; 2\; [1\; rdrdt\; -\; rr\; 2\; drdt]\; =\; -\; mf\; (r)\; r\; 2\; ddt\; (\; р-р).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; left\; (\backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; \backslash \; right)\; =\; -\; mf\; (r)\; r\; ^\; \{2\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\; \}\; \{r\}\}\; \{\backslash \; frac\; \{d\; \backslash \; mathbf\; \{r\}\}\; \{dt\}\}\; -\; \{\backslash \; frac\; \{\backslash \; mathbf\; \{r\}\}\; \{r\; ^\; \{2\}\}\}\; \{\backslash \; frac\; \{dr\}\; \{dt\}\}\; \backslash \; right]\; =\; -\; mf\; (r)\; r\; ^\; \{2\}\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; mathbf\; \{r\}\}\; \{r\}\}\; \backslash \; right).\}$

Для частный случай центральной силы, обратной квадрату $f\; (r)\; =\; -\; kr\; 2\; \{\backslash \; displaystyle\; f\; (r)\; =\; \{\backslash \; frac\; \{-k\}\; \{r\; ^\; \{2\}\}\}\}$, это равно

$ddt\; (p\; \times \; L)\; =\; mkddt\; (rr)\; =\; ddt\; (mkr\; ^).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; left\; (\backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; \backslash \; right)\; =\; mk\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\; \backslash \; mathbf\; \{r\}\}\; \{r\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; (mk\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\}).\}$

Следовательно, A сохраняется для центральных сил, обратных квадрату

$ddt\; A\; =\; ddt\; (p\; \times \; L)\; -\; ddt\; (mkr\; ^)\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; mathbf\; \{A\}\; =\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; left\; (\backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; \backslash \; right)\; -\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; left\; (mk\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\}\; \backslash \; right)\; =\; \backslash \; mathbf\; \{0\}.\}$

Более короткое доказательство получается при использовании отношения углового момента к угловой скорости $L\; =\; mr\; 2\; \omega \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{L\}\; =\; mr\; ^\; \{2\}\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}\}$, что справедливо для частицы, движущейся в плоскости, перпендикулярной $L\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{L\}\}$. Если задать обратные квадраты центральных сил, производная по времени от $p\; \times \; L\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\}$равна

$ddtp\; \times \; L\; =\; (-\; kr\; 2\; r\; ^)\; \times \; (mr\; 2\; \omega )\; знак\; равно\; mk\; \omega \; \times \; r\; ^\; =\; mkddtr\; ^,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; =\; \backslash \; left\; (\; \{\backslash \; frac\; \{-k\}\; \{r\; ^\; \{2\}\}\}\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\}\; \backslash \; right)\; \backslash \; times\; \backslash \; left\; (mr\; ^\; \{2\}\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}\; \backslash \; right)\; =\; mk\; \backslash ,\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}\; \backslash \; times\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\}\; =\; mk\; \backslash ,\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\},\}$

где последнее равенство выполняется, потому что единичный вектор может изменяться только вращением, и $\omega \; \times \; r\; ^\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}\; \backslash \; times\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\}\}$- орбитальная скорость вращающегося вектора. Таким образом, A рассматривается как разность двух векторов с равными производными по времени.

Как описано в другом месте этой статьи, этот вектор LRL A является частным случаем общего сохраняемого вектора $A\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\; \}\}\}$, который может быть определен для всех центральных сил. Однако, поскольку большинство центральных сил не создают замкнутых орбит (см. теорему Бертрана ), аналогичный вектор $A\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\}\}\}$редко имеет простое определение и обычно является многозначной функцией угла θ между r и $A\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\}\}\}$.

уравнением Гамильтона – Якоби в параболические координаты

Постоянство вектора LRL также может быть получено из уравнения Гамильтона – Якоби в параболических координатах (ξ, η), которые определяются уравнения

$\xi \; =\; r\; +\; x,\; \{\backslash \; displaystyle\; \backslash \; xi\; =\; r\; +\; x,\}$

$\eta \; =\; r\; -\; x,\; \{\backslash \; displaystyle\; \backslash \; eta\; =\; rx,\}$

где r представляет радиус в плоскости орбиты

$r\; =\; x\; 2\; +\; y\; 2.\; \{\backslash \; displaystyle\; r\; =\; \{\backslash \; sqrt\; \{x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\}\}.\}$

Инверсия этих координат:

$x\; =\; 1\; 2\; (\xi \; -\; \eta ),\; \{\backslash \; displaystyle\; x\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (\backslash \; xi\; -\; \backslash \; eta),\}$

$y\; =\; \xi \; \eta ,\; \{\backslash \; displaystyle\; y\; =\; \{\backslash \; sqrt\; \{\backslash \; xi\; \backslash \; eta\}\},\}$

Разделение уравнение Гамильтона – Якоби в этих координатах дает два эквивалентных уравнения

$2\; \xi \; p\; \xi \; 2\; -\; mk\; -\; m\; E\; \xi \; =\; -\; \Gamma ,\; \{\backslash \; displaystyle\; 2\; \backslash \; xi\; p\; \_\; \{\backslash \; xi\}\; ^\; \{2\}\; -mk-mE\; \backslash \; xi\; =\; -\; \backslash \; Gamma,\}$

$2\; \eta \; p\; \eta \; 2\; -\; mk\; -\; m\; E\; \eta \; =\; \Gamma ,\; \{\backslash \; displaystyle\; 2\; \backslash \; eta\; p\; \_\; \{\backslash \; eta\}\; ^\; \{2\}\; -mk-mE\; \backslash \; eta\; =\; \backslash \; Gamma,\; \}$

где Γ - постоянная движения. Вычитание и повторное выражение с точки зрения декартовых импульсов p x и p y показывает, что Γ эквивалентно вектору LRL

$\Gamma \; =\; py\; (xpy\; -\; ypx)\; -\; mkxr\; =\; А\; х.\; \{\backslash \; displaystyle\; \backslash \; Gamma\; =\; p\_\; \{y\}\; (xp\_\; \{y\}\; -yp\_\; \{x\})\; -\; mk\; \{\backslash \; frac\; \{x\}\; \{r\}\}\; =\; A\_\; \{x\}.\}$

Теорема Нётер

Связь между вращательной симметрией, описанной выше, и сохранением вектора LRL может быть сделана количественной посредством теоремы Нётер. Эта теорема, которая используется для нахождения постоянных движения, утверждает, что любое бесконечно малое изменение обобщенных координат физической системы

$\delta \; qi\; =\; \epsilon \; gi\; (q,\; q\; \dot{},\; t)\; \{\backslash \; displaystyle\; \backslash \; delta\; q\_\; \{i\}\; =\; \backslash \; varepsilon\; g\_\; \{i\}\; (\backslash \; mathbf\; \{q\},\; \backslash \; mathbf\; \{\backslash \; dot\; \{q\}\},\; t)\}$

, который заставляет лагранжиан изменяться первым упорядочить по полной производной по времени

$\delta \; L\; =\; \epsilon \; ddt\; G\; (q,\; t)\; \{\backslash \; displaystyle\; \backslash \; delta\; L\; =\; \backslash \; varepsilon\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; G\; (\backslash \; mathbf\; \{q\},\; t)\}$

соответствует сохраняющейся величине Γ

$\Gamma \; =\; -\; G\; +\; \sum \; igi\; (\partial \; L\; \partial \; q\; \dot{}\; i).\; \{\backslash \; displaystyle\; \backslash \; Gamma\; =\; -G\; +\; \backslash \; sum\; \_\; \{i\}\; g\_\; \{i\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; L\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{q\}\}\; \_\; \{i\}\}\}\; \backslash \; right).\}$

В частности, сохраняющаяся компонента вектора LRL A ​​s соответствует изменению координат

$\delta \; xi\; =\; \epsilon \; 2\; [2\; пикселя\; -\; xips\; -\; \delta \; равно\; (r\; \cdot \; p)],\; \{\; \backslash \; displaystyle\; \backslash \; delta\; x\_\; \{i\}\; =\; \{\backslash \; frac\; \{\backslash \; varepsilon\}\; \{2\}\}\; \backslash \; left\; [2p\_\; \{i\}\; x\_\; \{s\}\; -x\_\; \{i\}\; p\_\; \{s\}\; -\; \backslash \; delta\; \_\; \{is\}\; \backslash \; left\; (\; \backslash \; mathbf\; \{r\}\; \backslash \; cdot\; \backslash \; mathbf\; \{p\}\; \backslash \; right)\; \backslash \; right],\}$

где i равно 1, 2 и 3, с x i и p i являющиеся i-ми компонентами векторов положения и импульса r и p, соответственно; как обычно, δ is представляет собой дельту Кронекера. Результирующее изменение первого порядка в лагранжиане составляет

$\delta \; L\; =\; 1\; 2\; \epsilon \; m\; k\; d\; d\; t\; (x\; s\; r).\; \{\backslash \; displaystyle\; \backslash \; delta\; L\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; varepsilon\; mk\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{x\_\; \{s\}\}\; \{r\}\}\; \backslash \; right).\; \}$

Подстановка в общую формулу для сохраняющейся величины Γ дает сохраняющуюся компоненту A s вектора LRL,

$A\; s\; =\; [p\; 2\; xs\; -\; ps\; (r\; \cdot \; p)]\; -\; mk\; (xsr)\; =\; [p\; \times \; (r\; \times \; p)]\; s\; -\; mk\; (xsr).\; \{\backslash \; Displaystyle\; A\_\; \{s\}\; =\; \backslash \; left\; [p\; ^\; \{2\}\; x\_\; \{s\}\; -p\_\; \{s\}\; \backslash \; left\; (\backslash \; mathbf\; \{r\}\; \backslash \; cdot\; \backslash \; mathbf\; \{p\}\; \backslash \; right)\; \backslash \; right]\; -mk\; \backslash \; left\; (\{\backslash \; frac\; \{x\_\; \{s\}\}\; \{r\}\}\; \backslash \; right)\; =\; \backslash \; left\; [\backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; left\; (\backslash \; mathbf\; \{r\}\; \backslash \; times\; \backslash \; mathbf\; \{p\}\; \backslash \; right)\; \backslash \; right]\; \_\; \{s\}\; -mk\; \backslash \; left\; (\{\backslash \; frac\; \{x\_\; \{s\}\}\; \{r\}\}\; \backslash \; right).\}$

Преобразование Ли

Рис. 9: Преобразование Ли, из которого выполняется сохранение вектора LRL A выводится. При изменении масштабного параметра λ энергия и угловой момент изменяются, но эксцентриситет e, величина и направление A - нет.

Теорема Нётер вывод сохранения вектора LRL A элегантно, но имеет один недостаток: изменение координат δx i включает не только положение r, но и импульс p или, что то же самое, скорость v . Этот недостаток может быть устранен путем получения сохранения A с использованием подхода, впервые предложенного Sophus Lie. В частности, можно определить преобразование Ли, в котором координаты r и время t масштабируются с помощью различных степеней параметра λ (рисунок 9),

$t\; \to \; \lambda \; 3\; t,\; r\; \to \; \lambda \; 2\; r,\; p\; \to \; 1\; \lambda \; p.\; \{\backslash \; displaystyle\; t\; \backslash \; rightarrow\; \backslash \; lambda\; ^\; \{3\}\; t,\; \backslash \; qquad\; \backslash \; mathbf\; \{r\}\; \backslash \; rightarrow\; \backslash \; lambda\; ^\; \{2\}\; \backslash \; mathbf\; \{r\},\; \backslash \; qquad\; \backslash \; mathbf\; \{p\}\; \backslash \; rightarrow\; \{\backslash \; frac\; \{1\}\; \{\backslash \; lambda\}\}\; \backslash \; mathbf\; \{p\}.\}$

Это преобразование изменяет полный угловой момент L и энергию E,

$L\; \to \; \lambda \; L,\; E\; \to \; 1\; \lambda \; 2\; E,\; \{\backslash \; displaystyle\; L\; \backslash \; rightarrow\; \backslash \; lambda\; L,\; \backslash \; qquad\; E\; \backslash \; rightarrow\; \{\backslash \; frac\; \{1\}\; \{\backslash \; lambda\; ^\; \{2\}\}\}\; E,\}$

, но сохраняет их произведение EL. Следовательно, эксцентриситет e и величина A сохраняются, как можно видеть из уравнения для A

$A\; 2\; =\; m\; 2\; k\; 2\; e\; 2\; =\; m\; 2\; k\; 2\; +\; 2\; m\; E\; L\; 2.\; \{\backslash \; displaystyle\; A\; ^\; \{2\}\; =\; m\; ^\; \{2\}\; k\; ^\; \{2\}\; e\; ^\; \{2\}\; =\; m\; ^\; \{2\}\; k\; ^\; \{2\}\; +\; 2mEL\; ^\; \{2\}.\}$

Направление A также сохраняется, поскольку полуоси не изменяются глобальным масштабированием. Это преобразование также сохраняет третий закон Кеплера, а именно, что полуось a и период T образуют постоянную T / a.

Альтернативные вычисления, символы и формулировки

В отличие от импульса и углового момента векторов pи L общепринятого определения вектора Лапласа – Рунге – Ленца не существует; В научной литературе используется несколько различных коэффициентов масштабирования и символов. Наиболее распространенное определение дается выше, но другой распространенной альтернативой является деление на константу mk для получения безразмерного сохраненного вектора эксцентриситета

$e\; =\; 1\; mk\; (p\; \times \; L)\; -\; r\; ^\; знак\; равно\; mk\; (v\; \times \; (r\; \times \; v))\; -\; r\; ^,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; =\; \{\backslash \; frac\; \{1\}\; \{mk\}\}\; \backslash \; left\; (\backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; \backslash \; справа)\; -\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\}\; =\; \{\backslash \; frac\; \{m\}\; \{k\}\}\; \backslash \; left\; (\backslash \; mathbf\; \{v\}\; \backslash \; times\; \backslash \; left\; (\backslash \; mathbf\; \{r\}\; \backslash \; times\; \backslash \; mathbf\; \{v\}\; \backslash \; right)\; \backslash \; right)\; -\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\},\}$

где v - вектор скорости. Этот масштабированный вектор e имеет то же направление, что и A, и его величина равна эксцентриситету орбиты и, таким образом, исчезает для круговых орбит.

Возможны и другие масштабированные версии, например, разделив A только на m

$M\; =\; v\; \times \; L\; -\; kr\; ^,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; =\; \backslash \; mathbf\; \{v\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; -k\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\},\}$

или на p 0

$D\; =\; A\; p\; 0\; =\; 1\; 2\; m\; |\; E\; |\; \{p\; \times \; L\; -\; mkr\; ^\},\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{D\}\; =\; \{\backslash \; frac\; \{\backslash \; mathbf\; \{A\}\}\; \{p\_\; \{0\}\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2m\; |\; E\; |\; \}\}\}\; \backslash \; left\; \backslash \; \{\backslash \; mathbf\; \{p\}\; \backslash \; times\; \backslash \; mathbf\; \{L\}\; -mk\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\}\}\; \backslash \; right\; \backslash \},\}$

который имеет те же единицы измерения, что и angular импульс вектор L.

В редких случаях знак вектора LRL может быть изменен на противоположный, т. е. масштабироваться на -1. Другие общие символы для вектора LRL включают a, R, F, Jи V . Однако выбор масштаба и символа для вектора LRL не влияет на его сохранение.

Рисунок 4: Вектор углового момента L, вектор LRL A и Гамильтон вектор, бинормаль B, взаимно перпендикулярны; A и B точки вдоль большой и малой осей, соответственно, эллиптической орбиты задачи Кеплера.

Альтернативным сохраняющимся вектором является бинормаль вектор B, изученный Уильямом Роуэном Гамильтоном,

$B\; =\; p\; -\; (mk\; L\; 2\; r)\; (L\; \times \; r),\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; =\; \backslash \; mathbf\; \{p\}\; -\; \backslash \; left\; (\{\backslash \; frac\; \{mk\}\; \{L\; ^\; \{2\}\; r\}\}\; \backslash \; right)\; \backslash \; \backslash \; left\; (\backslash \; mathbf\; \{L\}\; \backslash \; times\; \backslash \; mathbf\; \{r\}\; \backslash \; right),\}$

который сохраняется и указывает по малой полуоси эллипса. (Он не определен для исчезающего эксцентриситета.)

Вектор LRL A= B× Lпредставляет собой векторное произведение из B и L (рисунок 4). На годографе импульса в соответствующем разделе выше легко увидеть, что B связывает начало импульсов с центром кругового годографа и имеет величину A / L. В перигелии он указывает в направлении импульса.

Вектор B обозначается как «бинормальный», поскольку он перпендикулярен как A, так и L . Подобно самому вектору LRL, бинормальный вектор может быть определен с различными масштабами и символами.

Два консервативных вектора, A и B, могут быть объединены, чтобы сформировать консервативный диадический тензор W,

$W\; =\; \alpha \; A\; \otimes \; A\; +\; \beta \; B\; \otimes \; В,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{W\}\; =\; \backslash \; alpha\; \backslash \; mathbf\; \{A\}\; \backslash \; otimes\; \backslash \; mathbf\; \{A\}\; +\; \backslash \; beta\; \backslash ,\; \backslash \; mathbf\; \{B\}\; \backslash \; otimes\; \backslash \; mathbf\; \{B\},\}$

где α и β - произвольные константы масштабирования, а $\otimes \; \{\backslash \; displaystyle\; \backslash \; otimes\}$представляет тензорное произведение (которое не связано с векторным перекрестным произведением , несмотря на их похожий символ). Написанное в явных компонентах, это уравнение имеет вид

$W\; i\; j\; =\; \alpha \; A\; i\; A\; j\; +\; \beta \; B\; i\; B\; j.\; \{\backslash \; displaystyle\; W\_\; \{ij\}\; =\; \backslash \; alpha\; A\_\; \{i\}\; A\_\; \{j\}\; +\; \backslash \; beta\; B\_\; \{i\}\; B\_\; \{j\}.\}$

Будучи перпендикулярными друг другу, векторы A и B можно рассматривать как главные оси сохраняющегося тензора W, то есть его масштабированные собственные векторы. Wперпендикулярны L,

$L\; \cdot \; W\; знак\; равно\; \alpha \; (L\; \cdot \; A)\; A\; +\; \beta \; (L\; \cdot \; B)\; B\; знак\; равно\; 0,\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{L\}\; \backslash \; cdot\; \backslash \; mathbf\; \{W\}\; =\; \backslash \; alpha\; \backslash \; left\; (\backslash \; mathbf\; \{L\}\; \backslash \; cdot\; \backslash \; mathbf\; \{A\}\; \backslash \; right)\; \backslash \; mathbf\; \{A\}\; +\; \backslash \; beta\; \backslash \; left\; (\backslash \; mathbf\; \{L\}\; \backslash \; cdot\; \backslash \; mathbf\; \{B\}\; \backslash \; right)\; \backslash \; mathbf\; \{B\}\; =\; 0,\}$

поскольку A и B также перпендикулярны L, L⋅ A= L⋅ B= 0.

Более конкретно, это уравнение в явных компонентах читается как

$(L\; \cdot \; W)\; J\; знак\; равно\; \alpha \; (\sum \; я\; знак\; равно\; 1\; 3\; L\; я\; A\; я)\; A\; J\; +\; \beta \; (\sum \; я\; =\; 1\; 3\; L\; я\; В\; я)\; B\; J\; знак\; равно\; 0.\; \{\backslash \; Displaystyle\; \backslash \; left\; (\backslash \; mathbf\; \{L\}\; \backslash \; cdot\; \backslash \; mathbf\; \{W\}\; \backslash \; right)\; \_\; \{j\}\; =\; \backslash \; alpha\; \backslash \; left\; (\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{3\}\; L\_\; \{i\}\; A\_\; \{i\}\; \backslash \; right)\; A\_\; \{j\}\; +\; \backslash \; beta\; \backslash \; left\; (\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{3\}\; L\_\; \{i\}\; B\_\; \{i\}\; \backslash \; right)\; B\_\; \{j\}\; =\; 0.\}$

См. также

• Астродинамика : Орбита, Вектор эксцентриситета, Орбитальные элементы
• Теорема Бертрана
• Уравнение Бине
• Задача двух тел

Ссылки

Дополнительная литература

• Баез, Джон. «Тайны гравитационной задачи двух тел». Архивировано с оригинального 21.10.2008. Проверено 11 декабря 2004 г.
• Д'Элизео, М. М. (2007). «Орбитальное уравнение первого порядка». Американский журнал физики. 75 (4): 352–355. Bibcode : 2007AmJPh..75..352D. doi : 10.1119 / 1.2432126.
• Холл, Брайан К. (2013), Квантовая теория для математиков, Тексты для выпускников по математике, 267, Springer, ISBN 978-1461471158.
• выщелачивание, PGL; Г. П. Флессас (2003). «Обобщения вектора Лапласа – Рунге – Ленца». J. Нелинейная математика. Phys. 10 (3): 340–423. arXiv : math-ph / 0403028. Bibcode : 2003JNMP... 10..340L. doi :10.2991/jnmp.2003.10.3.6.