Плотность электронов

редактировать

Плотность вероятности того, что электроны где-то находятся

В квантовой химии плотность электронов или электронная плотность - это мера вероятности присутствия электрона в бесконечно малом элементе пространства, окружающем любую заданную точку. Это скалярная величина, зависящая от трех пространственных переменных, и обычно обозначается как $ρ (r) {\ displaystyle \ rho ({\ textbf {r}})}$ ${\ displaystyle \ rho ({\ textbf {r}})}$ или $n ( r) {\ displaystyle n ({\ textbf {r}})}$ ${\ displaystyle n ({\ textbf {r}})}$ . Плотность определяется посредством определения нормированной волновой функцией $N {\ displaystyle N}$ $N$ -электрона , которая сама зависит от $4 N {\ displaystyle 4N}$ $4N$ переменные ( $3 N {\ textstyle 3N}$ ${\ textstyle 3N}$ пространственные и $N {\ displaystyle N}$ $N$ координаты вращения ). И наоборот, плотность определяет волновую функцию по модулю с точностью до фазового фактора, обеспечивая формальную основу теории функционала плотности.

Согласно квантовой механике, из-за принципа неопределенности в атомном масштабе невозможно предсказать точное местоположение электрона, только вероятность его нахождения в данном положении; поэтому электроны в атомах и молекулах действуют так, как будто они «размазаны» в пространстве. Для одноэлектронных систем концентрация электронов в любой точке пропорциональна квадрату величины волновой функции .

Содержание

1 Определение
2 Общие свойства
3 Топология
- 3.1 Ядерный куспид условие
- 3.2 Асимптотическое поведение
4 Плотность отклика
5 Обзор
6 Эксперименты
7 Плотность вращения
8 См. также
9 Ссылки

Определение

Электронная плотность, соответствующая нормированной волновой функции $N {\ displaystyle N}$ $N$ -электрона $Ψ {\ displaystyle \ Psi}$ $\ Psi$ (с $r {\ displaystyle {\ textbf {r}}}$ ${\ displaystyle {\ textbf {r}}}$ и $s {\ displaystyle s}$ $s$ , обозначающие пространственные и спиновые переменные соответственно) определяется как

ρ (r) = ⟨Ψ | р ^ (г) | Ψ⟩, {\ displaystyle \ rho (\ mathbf {r}) = \ langle \ Psi | {\ hat {\ rho}} (\ mathbf {r}) | \ Psi \ rangle,}

{\ displaystyle \ rho (\ mathbf {r}) = \ langle \ Пси | {\ hat {\ rho}} (\ mathbf {r}) | \ Psi \ rangle,}

где оператор, соответствующий к наблюдаемой плотности

ρ ^ (r) = ∑ i = 1 N δ (r - ri). {\ Displaystyle {\ шляпа {\ rho}} (\ mathbf {r}) = \ сумма _ {я = 1} ^ {N} \ \ delta (\ mathbf {r} - \ mathbf {r} _ {i}).}

{\ displaystyle {\ hat {\ rho}} (\ mathbf {r}) = \ sum _ {i = 1} ^ {N} \ \ delta (\ mathbf {r} - \ mathbf {r} _ {i}).}

Вычисление $ρ (r) {\ displaystyle \ rho (\ mathbf {r})}$ ${\ displaystyle \ rho (\ mathbf {r})}$ , как определено выше, мы можем упростить выражение следующим образом.

$ρ (r) = s 1 ⋯ ∑ s N ∫ d r 1 ⋯ ∫ d r N (∑ i = 1 N δ (r - r i)) | Ψ (r 1, s 1, r 2, s 2,..., R N, s N) | 2 = N ∑ s 1 ⋯ ∑ s N ∫ d r 2 ⋯ ∫ d r N | Ψ (r, s 1, r 2, s 2,...., R N, s N) | 2 {\ displaystyle {\ begin {align} \ rho (\ mathbf {r}) = \ sum _ {{s} _ {1}} \ cdots \ sum _ {{s} _ {N}} \ int \ \ mathrm {d} \ mathbf {r} _ {1} \ \ cdots \ int \ \ mathrm {d} \ mathbf {r} _ {N} \ \ left (\ sum _ {i = 1} ^ {N} \ delta (\ mathbf {r} - \ mathbf {r} _ {i}) \ right) | \ Psi (\ mathbf {r} _ {1}, s_ {1}, \ mathbf {r} _ {2}, s_ {2},..., \ mathbf {r} _ {N}, s_ {N}) | ^ {2} \\ = N \ sum _ {{s} _ {1}} \ cdots \ сумма _ {{s} _ {N}} \ int \ \ mathrm {d} \ mathbf {r} _ {2} \ \ cdots \ int \ \ mathrm {d} \ mathbf {r} _ {N} \ | \ Psi (\ mathbf {r}, s_ {1}, \ mathbf {r} _ {2}, s_ {2},..., \ mathbf {r} _ {N}, s_ {N}) | ^ {2} \ end {align}}}$ ${\ displaystyle {\ begin {align} \ rho (\ mathbf {r}) = \ sum _ {s} _ {1}} \ cdots \ sum _ {{s } _ {N}} \ int \ \ mathrm {d} \ mathbf {r} _ {1} \ \ cdots \ int \ \ mathrm {d} \ mathbf {r} _ {N} \ \ left (\ sum _ {i = 1} ^ {N} \ delta (\ mathbf {r} - \ mathbf {r} _ {i}) \ right) | \ Psi (\ mathbf {r} _ {1}, s_ {1}, \ mathbf {r} _ {2}, s_ {2},..., \ mathbf {r} _ {N}, s_ {N}) | ^ {2} \\ = N \ sum _ {{s } _ {1}} \ cdots \ sum _ {{s} _ {N}} \ int \ \ mathrm {d} \ mathbf {r} _ {2} \ \ cdots \ int \ \ mathrm {d} \ mathbf {r} _ {N} \ | \ Psi (\ mathbf {r}, s_ {1}, \ mathbf {r} _ {2}, s_ {2},..., \ mathbf { r} _ {N}, s_ {N}) | ^ {2} \ end {align}}}$

Словами: удерживая единственный электрон в позиции $r {\ displaystyle {\ textbf {r}}}$ ${\ displaystyle {\ textbf {r}}}$ , мы суммируем по всем возможным расположениям других электронов.

В теориях Хартри – Фока и функционала плотности волновая функция обычно представлена как один определитель Слейтера, построенный из $N { \ displaystyle N}$ $N$ орбитали, $φ k {\ displaystyle \ varphi _ {k}}$ $\ varphi _ {k}$ , с соответствующими занятиями $nk {\ displaystyle n_ {k}}$ $n_ {k}$ . В этих ситуациях плотность упрощается до

ρ (r) = ∑ k = 1 N n k | φ k (r) | 2. {\ displaystyle \ rho (\ mathbf {r}) = \ sum _ {k = 1} ^ {N} n_ {k} | \ varphi _ {k} (\ mathbf {r}) | ^ {2}.}

\ rho ({\ mathbf {r}}) = \ sum _ {{k = 1 }} ^ {N} n _ {{k}} | \ varphi _ {k} ({\ mathbf {r}}) | ^ {2}.

Общие свойства

По определению, электронная плотность является неотрицательной функцией, интегрируемой с общим числом электронов. Далее, для системы с кинетической энергией T плотность удовлетворяет неравенствам

1 2 ∫ d r (∇ ρ (r)) 2 ≤ T. {\ displaystyle {\ frac {1} {2}} \ int \ mathrm {d} \ mathbf {r} \ {\ big (} \ nabla {\ sqrt {\ rho (\ mathbf {r})}} {\ большой)} ^ {2} \ leq T.}

{\ frac {1} {2}} \ int {\ mathrm {d}} {\ mathbf {r}} \ {\ big (} \ nabla {\ sqrt {\ rho ({\ mathbf {r}})}} {\ big)} ^ {{2}} \ leq T.

3 2 (π 2) 4/3 (∫ dr ρ 3 (r)) 1/3 ≤ T. {\ displaystyle {\ frac {3} {2}} \ left ({\ frac {\ pi} {2}} \ right) ^ {4/3} \ left (\ int \ mathrm {d} \ mathbf {r } \ \ rho ^ {3} (\ mathbf {r}) \ right) ^ {1/3} \ leq T.}

{\ frac {3} {2 }} \ left ({\ frac {\ pi} {2}} \ right) ^ {{4/3}} \ left (\ int {\ mathrm {d}} {\ mathbf {r}} \ \ rho ^ {{3}} ({\ mathbf {r}}) \ right) ^ {{1/3}} \ leq T.

Для конечных кинетических энергий первое (более сильное) неравенство помещает квадратный корень из плотности в пространстве Соболева $H 1 (R 3) {\ displaystyle H ^ {1} (\ mathbb {R} ^ {3})}$ ${\ displaystyle H ^ {1} (\ mathbb {R} ^ {3})}$ . Вместе с нормализацией и неотрицательностью это определяет пространство, содержащее физически приемлемые плотности как

J N = {ρ | ρ (r) ≥ 0, ρ 1/2 (r) ∈ H 1 (R 3), ∫ d r ρ (r) = N}. {\ Displaystyle {\ mathcal {J}} _ {N} = \ left \ {\ rho \ left | \ rho (\ mathbf {r}) \ geq 0, \ \ rho ^ {1/2} (\ mathbf { r}) \ in H ^ {1} (\ mathbf {R} ^ {3}), \ \ int \ mathrm {d} \ mathbf {r} \ \ rho (\ mathbf {r}) = N \ right. \ right \}.}

\ mathcal {J} _ {N} = \ left \ {\ rho \ left | \ rho (\ mathbf {r}) \ geq 0, \ \ rho ^ {1/2} (\ mathbf {r}) \ in H ^ {1} (\ mathbf {R} ^ {3}), \ \ int \ mathrm {d} \ mathbf {r} \ \ rho (\ mathbf {r}) = N \ right. \ right \}.

Второе неравенство помещает плотность в пространство L. Вместе со свойством нормализации допустимые плотности помещаются на пересечении L и L - надмножество $JN {\ displaystyle {\ mathcal {J}} _ {N}}$ ${\ mathcal {J}} _ {{N} }$ .

Топология

основное состояние электронная плотность атома предположительно является монотонно затухающей функцией расстояния от ядра.

Ядерного каспа

Электронная плотность отображает каспы на каждом ядре в молекуле в результате неограниченного кулоновского электрон-ядерного потенциала. Это поведение количественно выражается условием каспа Като, сформулированным в терминах сферически усредненной плотности, $ρ ¯ {\ displaystyle {\ bar {\ rho}}}$ ${\ bar {\ rho}}$ , относительно любого заданного ядра как

∂ ∂ r α ρ ¯ (r α) | r α = 0 = - 2 Z α ρ ¯ (0). {\ displaystyle \ left. {\ frac {\ partial} {\ partial r _ {\ alpha}}} {\ bar {\ rho}} (r _ {\ alpha}) \ right | _ {r _ {\ alpha} = 0 } = - 2Z _ {\ alpha} {\ bar {\ rho}} (0).}

\ left. {\ frac {\ partial} {\ partial r _ {\ alpha}}}} {\ bar {\ rho}} (r _ {{\ alpha}}) \ right | _ {{r _ {{\ alpha}} = 0}} = - 2Z _ {{\ alpha}} {\ bar {\ rho}} (0).

То есть, радиальная производная сферически усредненной плотности, вычисленная в любом ядре, равна удвоенной плотности в этом ядре. умножается на отрицательное значение атомного номера ( $Z {\ displaystyle Z}$ $Z$ ).

Асимптотическое поведение

Условие ядерного каспа обеспечивает поведение плотности, близкое к ядерному (малое $r {\ displaystyle r}$ $r$ ) как

ρ (r) ∼ e - 2 Z α r. {\ displaystyle \ rho (r) \ sim e ^ {- 2Z _ {\ alpha} r} \,.}

\ rho (r) \ sim e ^ {{- 2Z _ {{\ alpha}} r }} \,.

Дальний (большой $r {\ displaystyle r}$ $r$ ) также известно поведение плотности, имеющее вид

ρ (r) ∼ e - 2 2 I r. {\ displaystyle \ rho (r) \ sim e ^ {- 2 {\ sqrt {2 \ mathrm {I}}} r} \,.}

\ rho (r) \ sim e ^ {{- 2 {\ sqrt {2 {\ mathrm {I}}}} r}} \,.

, где I - энергия ионизации система.

Плотность отклика

Другим более общим определением плотности является «плотность линейного отклика». Это плотность, которая в сочетании с любым бесспиновым одноэлектронным оператором дает соответствующее свойство, определяемое как производная энергии. Например, дипольный момент является производной энергии по внешнему магнитному полю и не является математическим ожиданием оператора над волновой функцией. Для некоторых теорий они одинаковы, когда волновая функция сходится. Числа заполнения не ограничиваются диапазоном от нуля до двух, и поэтому иногда даже плотность отклика может быть отрицательной в определенных областях пространства.

Обзор

В молекулах, области с высокой электронной плотностью обычно находятся вокруг атома и его связей. В делокализованных или сопряженных системах, таких как фенол, бензол и соединениях, таких как гемоглобин и хлорофилл электронная плотность значительна во всей области, т. е. в бензоле они находятся выше и ниже плоского кольца. Иногда это изображают схематически как серию чередующихся одинарных и двойных связей. В случае фенола и бензола кружок внутри шестиугольника показывает делокализованную природу соединения. Это показано ниже:

В соединениях с множественными кольцевыми системами, которые связаны между собой, это уже неточно, поэтому используются чередующиеся одинарные и двойные связи. В таких соединениях, как хлорофилл и фенол, на некоторых диаграммах показана пунктирная или пунктирная линия, обозначающая делокализацию областей, где электронная плотность выше рядом с одинарными связями. Сопряженные системы иногда могут представлять области, где электромагнитное излучение поглощается на разных длинах волн, что приводит к окрашиванию соединений. В полимерах эти области известны как хромофоры.

В квантово-химических расчетах плотность электронов ρ (r ) является функцией координат r, определенных так ρ ( r)dr- число электронов в малом объеме d r . Для молекул с закрытой оболочкой $ρ (r) {\ displaystyle \ rho (\ mathbf {r })}$ $\ rho ({\ mathbf {r}})$ можно записать в терминах суммы произведений базисных функций, φ:

ρ (r) = ∑ μ ∑ ν P μ ν ϕ μ (r) ϕ ν (r) {\ displaystyle \ rho (\ mathbf {r}) = \ sum _ {\ mu} \ sum _ {\ nu} P _ {\ mu \ nu} \ phi _ {\ mu} (\ mathbf {r}) \ phi _ {\ nu} (\ mathbf {r})}

\ rho ({ \ mathbf {r}}) = \ sum _ {\ mu} \ sum _ {\ nu} P _ {{\ mu \ nu}} \ phi _ {\ mu} ({\ mathbf {r}}) \ phi _ {\ nu} ({\ mathbf {r}})

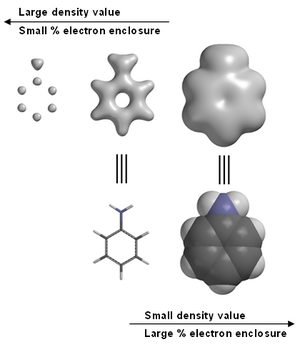Электронная плотность рассчитана для анилина, высокие значения плотности указывают на положение атомов, промежуточные значения плотности подчеркивают связь, низкие значения обеспечивают информация о форме и размере молекулы.

где P - матрица плотности . Плотность электронов часто отображается в виде изоповерхности (поверхности изоплотности) с размером и формой поверхности, определяемыми значение выбранной плотности, или в единицах процент всех заключенных электронов.

Программное обеспечение для молекулярного моделирования часто предоставляет графические изображения электронной плотности. Например, в анилин (см. Изображение справа). Графические модели, в том числе электронная плотность, широко используются в химическом образовании. Обратите внимание, что на крайнем левом изображении анилина высокие концентрации электронов связаны с атомами углерода и азотом, но с атомами водорода только с одним протоном в ядрах, не видны. Это причина того, что дифракция рентгеновских лучей затрудняет определение местоположения водорода.

Большинство пакетов программного обеспечения для молекулярного моделирования позволяют пользователю выбирать значение электронной плотности, часто называемое изозначением. Некоторое программное обеспечение также позволяет указывать электронную плотность в процентах от общего количества заключенных электронов. В зависимости от изозначения (типичными единицами измерения являются электроны на кубический бор ) или процента от общего количества заключенных электронов, поверхность электронной плотности может использоваться для определения местоположения атомов, подчеркивая электронные плотности, связанные с химическими связями, или для обозначения общего размера и формы молекулы.

Графически поверхность электронной плотности также служит холстом, на котором могут отображаться другие электронные свойства. Карта электростатического потенциала (свойство электростатического потенциала, отображаемое на электронной плотности) обеспечивает индикатор распределения заряда в молекуле. Карта потенциала локальной ионизации (свойство потенциала локальной ионизации, отображаемое на электронную плотность) обеспечивает индикатор электрофильности. А карта LUMO (самая низкая незанятая молекулярная орбиталь, отображаемая на основе электронной плотности) может служить индикатором нуклеофильности.

Эксперименты

Многие экспериментальные методы могут измерять электронную плотность. Например, от квантовой кристаллографии до сканирования дифракции рентгеновских лучей, где рентгеновские лучи подходящей длины волны нацелены на образец, а измерения выполняются с течением времени, дает вероятностное представление расположение электронов. С этих позиций для кристаллизованных систем часто можно определить молекулярные структуры, а также точное распределение плотности заряда. Квантовая электродинамика и некоторые разделы квантовой теории также изучают и анализируют электронное суперпозицию и другие связанные явления, такие как индекс NCI, который позволяет изучение нековалентных взаимодействий с использованием электронной плотности. Анализ населения по Малликену основан на плотности электронов в молекулах и представляет собой способ деления плотности между атомами для оценки зарядов атомов.

В просвечивающей электронной микроскопии (TEM) и глубоконеупругом рассеянии, а также в других экспериментах с частицами высоких энергий электроны высоких энергий взаимодействуют с электронное облако, чтобы дать прямое представление о электронной плотности. ПЭМ, сканирующая туннельная микроскопия (СТМ) и атомно-силовая микроскопия (АСМ) могут использоваться для исследования электронной плотности отдельных отдельных атомов.

Спиновая плотность

Спиновая плотность - это электронная плотность, приложенная к свободным радикалам. Он определяется как полная электронная плотность электронов одного спина за вычетом общей электронной плотности электронов другого спина. Один из способов его экспериментального измерения - с помощью электронного спинового резонанса, нейтронная дифракция позволяет напрямую отображать спиновую плотность в 3D-пространстве.