Войти
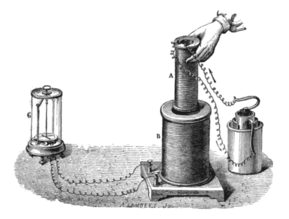
Эксперимент Фарадея, показывающий индукцию между витками проволоки: жидкая батарея (справа) обеспечивает ток, который течет через небольшую катушку ( A), создавая магнитное поле. Когда катушки неподвижны, ток не индуцируется. Но когда малая катушка перемещается внутрь или из большой катушки ( B), магнитный поток через большую катушку изменяется, вызывая ток, который регистрируется гальванометром ( G). Закон индукции Фарадея (кратко, закон Фарадея) - это основной закон электромагнетизма, предсказывающий, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС) - явление, известное как электромагнитная индукция. Это основной принцип работы трансформаторов, дросселей и многих типов электрических двигателей, генераторов и соленоидов.
Уравнение Максвелла-Фарадея (указанное как одно из уравнений Максвелла ) описывает тот факт, что пространственно изменяющееся (а также, возможно, изменяющееся во времени, в зависимости от того, как магнитное поле изменяется во времени) электрическое поле всегда сопровождает изменяющееся во времени магнитное поле, в то время как Закон Фарадея гласит, что существует ЭДС (электродвижущая сила, определяемая как электромагнитная работа, совершаемая над единичным зарядом, когда он прошел один виток проводящей петли) в проводящей петле, когда магнитный поток через поверхность, заключенную петлей, изменяется во времени.
Был открыт закон Фарадея, и один из его аспектов (трансформаторная ЭДС) был позже сформулирован как уравнение Максвелла – Фарадея. Уравнение закона Фарадея может быть получено с помощью уравнения Максвелла – Фарадея (описывающего ЭДС трансформатора) и силы Лоренца (описывающей ЭДС движения). Интегральная форма уравнения Максвелла – Фарадея описывает только ЭДС трансформатора, в то время как уравнение закона Фарадея описывает как ЭДС трансформатора, так и ЭДС движения.
Схема железного кольцевого аппарата Фарадея. Изменяющийся магнитный поток левой катушки индуцирует ток в правой катушке. Электромагнитная индукция была независимо открыта Майклом Фарадеем в 1831 году и Джозефом Генри в 1832 году. Фарадей был первым, кто опубликовал результаты своих экспериментов. В первой экспериментальной демонстрации электромагнитной индукции Фарадеем (29 августа 1831 г.) он намотал два провода на противоположные стороны железного кольца ( тора ) (устройство, подобное современному тороидальному трансформатору ). Основываясь на своей оценке недавно обнаруженных свойств электромагнитов, он ожидал, что, когда ток начнет течь по одному проводу, своего рода волна пройдет через кольцо и вызовет некоторый электрический эффект на противоположной стороне. Он подключил один провод к гальванометру и наблюдал, как подсоединяет другой провод к батарее. Действительно, он видел переходный ток (который он назвал «волной электричества»), когда подключал провод к батарее, и другой, когда он отключал его. Эта индукция была вызвана изменением магнитного потока, которое происходило при подключении и отключении батареи. В течение двух месяцев Фарадей обнаружил несколько других проявлений электромагнитной индукции. Например, он видел переходные токи, когда быстро вставлял стержневой магнит в катушку проводов и из нее, и генерировал постоянный ( постоянный ) ток, вращая медный диск возле стержневого магнита с помощью скользящего электрического провода («диск Фарадея» ").
Диск Фарадея, первый электрический генератор, разновидность униполярного генератора. Майкл Фарадей объяснил электромагнитную индукцию, используя концепцию, которую он назвал силовыми линиями. Однако ученые в то время широко отвергали его теоретические идеи, главным образом потому, что они не были сформулированы математически. Исключением был Джеймс Клерк Максвелл, который в 1861–1862 гг. Использовал идеи Фарадея как основу своей количественной теории электромагнитного поля. В статьях Максвелла изменяющийся во времени аспект электромагнитной индукции выражается как дифференциальное уравнение, которое Оливер Хевисайд назвал законом Фарадея, хотя он отличается от исходной версии закона Фарадея и не описывает ЭДС движения. Версия Хевисайда (см. Уравнение Максвелла – Фарадея ниже) - это форма, признанная сегодня в группе уравнений, известной как уравнения Максвелла.
Закон Ленца, сформулированный Эмилем Ленцем в 1834 году, описывает «поток через цепь» и дает направление наведенной ЭДС и тока, возникающего в результате электромагнитной индукции (подробно описанных в примерах ниже).
Переменный электрический ток течет через соленоид слева, создавая изменяющееся магнитное поле. Это поле вызывает за счет электромагнитной индукции электрический ток, протекающий в проволочной петле справа. Наиболее распространенная версия закона Фарадея гласит:
Электродвижущая сила вокруг замкнутого пути равна отрицательной скорости изменения магнитного потока, заключенного на пути, во времени.
Определение поверхностного интеграла основывается на разбиении поверхности Σ на мелкие элементы поверхности. Каждому элементу соответствует вектор d A, величина которого равна площади элемента и имеет направление, нормальное к элементу и указывающее «наружу» (относительно ориентации поверхности). Для петли проволоки в магнитном поле, то магнитный поток Φ B определяются для любой поверхности Е, чья граница находится данный цикл. Поскольку проволочная петля может двигаться, обозначим поверхность Σ ( t). Магнитный поток - это поверхностный интеграл :
где d представляет собой элемент площади поверхности двигающейся поверхности Е ( т), B является магнитным полем, а B д является скалярным произведением вектора, представляющее элемент потока через д А. Проще говоря, магнитный поток через проволочную петлю пропорционален количеству силовых линий магнитного поля, которые проходят через петлю.
Когда поток изменяется - из-за изменения B, или из-за того, что проволочная петля перемещается или деформируется, или и то, и другое - закон индукции Фарадея гласит, что проволочная петля приобретает ЭДС, определяемую как энергия, доступная от единичного заряда, который один раз прошел вокруг петля. (В некоторых источниках определение приводится по-другому. Это выражение было выбрано для совместимости с уравнениями специальной теории относительности.) Эквивалентно, это напряжение, которое можно было бы измерить, перерезав провод для создания разомкнутой цепи и прикрепив вольтметр к проводам.
Закон Фарадея гласит, что ЭДС также определяется скоростью изменения магнитного потока:
где - электродвижущая сила (ЭДС), а Φ B - магнитный поток.
Направление электродвижущей силы задается законом Ленца.
Законы индукции электрических токов в математической форме были установлены Францем Эрнстом Нойманом в 1845 году.
Закон Фарадея содержит информацию о соотношении как величин, так и направлений его переменных. Однако отношения между направлениями не являются явными; они скрыты в математической формуле.
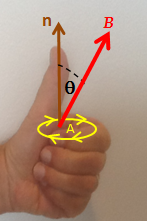Правило левой руки для закона Фарадея. Знак ΔΦ B, изменение магнитного потока, определяется на основе соотношения между магнитным полем B, площадью петли A и нормалью n к этой области, как показано пальцами левой руки. Если ΔΦ B положительно, направление ЭДС совпадает с направлением изогнутых пальцев (желтые стрелки). Если ΔΦ B отрицательно, ЭДС направлена против стрелок. Направление электродвижущей силы (ЭДС) можно определить непосредственно из закона Фарадея, не прибегая к закону Ленца. Правило левой руки помогает в этом, а именно:
Для плотно намотанной катушки с проволокой, состоящей из N одинаковых витков, каждый с одинаковым Φ B, закон индукции Фарадея гласит, что
где N - количество витков провода, а Φ B - магнитный поток, проходящий через одиночный контур.
Иллюстрация теоремы Кельвина – Стокса с поверхностью Σ, ее границей ∂ Σ и ориентацией n, заданной правилом правой руки. Уравнение Максвелла – Фарадея утверждает, что изменяющееся во времени магнитное поле всегда сопровождает изменяющееся в пространстве (также возможно изменяющееся во времени) неконсервативное электрическое поле, и наоборот. Уравнение Максвелла – Фарадея имеет вид
(в единицах СИ ), где ∇ × - оператор ротора, и снова E ( r, t) - электрическое поле, а B ( r, t) - магнитное поле. Эти поля обычно могут быть функциями положения r и времени t.
Уравнение Максвелла – Фарадея является одним из четырех уравнений Максвелла и поэтому играет фундаментальную роль в теории классического электромагнетизма. Его также можно записать в интегральной форме по теореме Кельвина – Стокса, воспроизводя тем самым закон Фарадея:
где, как показано на рисунке, Σ - поверхность, ограниченная замкнутым контуром ∂ Σ, d l - бесконечно малый векторный элемент контура ∂Σ, а d A - бесконечно малый векторный элемент поверхности Σ. Его направление ортогонально этому участку поверхности, величина - это площадь бесконечно малого участка поверхности.
И d l, и d A имеют двусмысленность знака; чтобы получить правильный знак, используется правило правой руки, как описано в статье « Теорема Кельвина – Стокса». Для плоской поверхности Σ положительный элемент пути d l кривой ∂ Σ определяется правилом правой руки как тот, который указывает пальцами правой руки, когда большой палец указывает в направлении нормали n к поверхности Σ..
Криволинейный интеграл вокруг ∂ Е называется циркуляцией. Ненулевая циркуляция E отличается от поведения электрического поля, создаваемого статическими зарядами. Генерируемое зарядом E- поле может быть выражено как градиент скалярного поля, которое является решением уравнения Пуассона и имеет нулевой интеграл по путям. См. Теорему о градиенте.
Интегральное уравнение верно для любого пути ∂ Σ через пространство и любой поверхности Σ, для которой этот путь является границей.
Если поверхность Σ не меняется во времени, уравнение можно переписать:
Поверхностный интеграл в правой стороне представляет собой явное выражение для магнитного потока Φ B через Е.
Векторное электрическое поле, индуцированное изменяющимся магнитным потоком, соленоидальная составляющая общего электрического поля, может быть аппроксимировано в нерелятивистском пределе объемным интегральным уравнением
Четыре уравнения Максвелла (включая уравнение Максвелла – Фарадея) вместе с законом силы Лоренца являются достаточным основанием для вывода всего, что связано с классическим электромагнетизмом. Следовательно, можно «доказать» закон Фарадея, исходя из этих уравнений.
Отправной точкой является производная по времени от потока через произвольную поверхность Σ (которая может перемещаться или деформироваться) в пространстве:
(по определению). Эта полная производная по времени может быть вычислена и упрощена с помощью уравнения Максвелла – Фарадея и некоторых векторных тождеств; подробности находятся в поле ниже:
| Рассмотрим производную по времени магнитного потока через замкнутую границу (петлю), которая может перемещаться или деформироваться. Площадь, ограниченная петлей, обозначается как Σ ( t)), тогда производная по времени может быть выражена как Интеграл может изменяться со временем по двум причинам: подынтегральное выражение может измениться или область интегрирования может измениться. Таким образом, они складываются линейно: где t 0 - любое заданное фиксированное время. Мы покажем, что первый член в правой части соответствует ЭДС трансформатора, второй - ЭДС движения (от магнитной силы Лоренца на носителях заряда из-за движения или деформации проводящей петли в магнитном поле). Первый член в правой части можно переписать, используя интегральную форму уравнения Максвелла – Фарадея: Далее мы анализируем второй член в правой части: 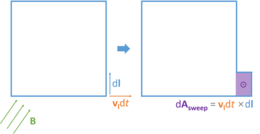 Область, заметаемая векторным элементом d l петли ∂ Σ за время d t, когда он перемещался со скоростью v l. Доказательство этого немного сложнее, чем первый член; более подробную информацию и альтернативные подходы к доказательству можно найти в ссылках. По мере того как петля перемещается и / или деформируется, она выметает поверхность (см. Рисунок справа). Поскольку небольшая часть петли d l движется со скоростью v l за короткое время d t, она выметает область, вектор которой равен d A sweep = v l d t × d l (обратите внимание, что этот вектор направлен наружу от дисплей на правом рисунке). Следовательно, изменение магнитного потока через петлю из-за деформации или перемещения петли за время d t равно Здесь используются тождества тройных скалярных произведений. Следовательно, где v l - скорость части петли ∂ Σ. Их объединение приводит к следующему: |
Результат:
где ∂Σ - граница (петля) поверхности Σ, а v l - скорость части границы.
В случае проводящей петли ЭДС (электродвижущая сила) - это электромагнитная работа, совершаемая над единичным зарядом, когда он один раз прошел вокруг петли, и эта работа выполняется силой Лоренца. Следовательно, ЭДС выражается как
где - ЭДС, а v - единичная скорость заряда.
С макроскопической точки зрения для зарядов на участке петли v состоит в среднем из двух компонентов; один - скорость заряда на отрезке v t, а другой - скорость отрезка v l (петля деформируется или перемещается). v t не влияет на работу, совершаемую над зарядом, поскольку направление v t совпадает с направлением. Математически,
поскольку перпендикулярно as и проходят в одном направлении. Теперь мы можем видеть, что для проводящей петли ЭДС совпадает с производной по времени магнитного потока, проходящего через петлю, за исключением знака на ней. Следовательно, теперь мы приходим к уравнению закона Фарадея (для проводящей петли) как
где. При нарушении этого интеграла, это ЭДС трансформатора (из-за изменяющегося во времени магнитного поля) и для ЭДС движения (из-за магнитной силы Лоренца, действующей на заряды из-за движения или деформации петли в магнитном поле).
Возникает соблазн обобщить закон Фарадея, чтобы заявить: если ∂Σ - это любой произвольный замкнутый контур в пространстве, то полная производная по времени магнитного потока через Σ равна ЭДС вокруг ∂Σ. Это утверждение, однако, не всегда верно, и причина заключается не только в очевидной причине, что ЭДС не определена в пустом пространстве, когда нет проводника. Как отмечалось в предыдущем разделе, закон Фарадея не гарантированно работает, если скорость абстрактной кривой ∂Σ не совпадает с фактической скоростью материала, проводящего электричество. Два примера, проиллюстрированные ниже, показывают, что часто можно получить неверные результаты, когда движение ∂Σ отделено от движения материала.
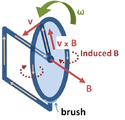
Униполярный генератор Фарадея. Диск вращается с угловой скоростью ω, охватывая проводящий радиус по кругу в статическом магнитном поле B (направление вдоль нормали к поверхности диска). Магнитная сила Лоренца v × B запускает ток по радиусу проводимости к проводящему ободу, и оттуда цепь замыкается через нижнюю щетку и ось, поддерживающую диск. Это устройство генерирует ЭДС и ток, хотя форма «цепи» постоянна и, таким образом, поток через цепь не изменяется со временем.
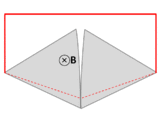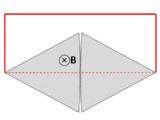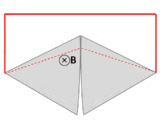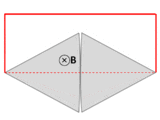
Провод (сплошные красные линии) соединяется с двумя соприкасающимися металлическими пластинами (серебряными), образуя цепь. Вся система находится в однородном магнитном поле, перпендикулярном странице. Если абстрактный путь ∂Σ следует по первичному пути прохождения тока (отмечен красным), то магнитный поток через этот путь резко меняется при вращении пластин, но ЭДС почти равна нулю. После лекций Фейнмана по физике
Можно проанализировать подобные примеры, позаботившись о том, чтобы путь ∂Σ двигался с той же скоростью, что и материал. В качестве альтернативы всегда можно правильно рассчитать ЭДС, объединив закон силы Лоренца с уравнением Максвелла – Фарадея:
где «очень важно отметить, что (1) [ v m ] - это скорость проводника... не скорость элемента пути d l и (2) в целом, частная производная по времени не может быть перемещается за пределы интеграла, поскольку площадь является функцией времени ".
Закон Фарадея представляет собой единое уравнение, описывающее два разных явления: ЭДС движения, создаваемую магнитной силой на движущемся проводе (см. Силу Лоренца ), и ЭДС трансформатора, создаваемую электрической силой из-за изменяющегося магнитного поля (описанную Максвеллом –Уравнение Фарадея).
Джеймс Клерк Максвелл обратил внимание на этот факт в своей статье 1861 года « О физических силовых линиях». Во второй половине Части II этой статьи Максвелл дает отдельное физическое объяснение каждому из двух явлений.
Ссылки на эти два аспекта электромагнитной индукции есть в некоторых современных учебниках. Как утверждает Ричард Фейнман:
Таким образом, "правило потока", согласно которому ЭДС в цепи равна скорости изменения магнитного потока в цепи, применяется независимо от того, изменяется ли магнитный поток из-за изменения поля или из-за того, что цепь движется (или и то, и другое)...
Тем не менее, в нашем объяснении правила мы использовали два совершенно разных закона для двух случаев - v × B для «движений схемы» и ∇ × E = −∂ t B для «изменений поля».
Мы не знаем другого места в физике, где такой простой и точный общий принцип требует для своего реального понимания анализа в терминах двух различных явлений.
- Ричард П. Фейнман, Лекции Фейнмана по физикеВ общем случае объяснение возникновения двигательной ЭДС действием магнитной силы на заряды в движущемся проводе или в цепи, изменяющей его площадь, неудовлетворительно. На самом деле заряды в проводе или в цепи могут полностью отсутствовать, исчезнет ли тогда эффект электромагнитной индукции в этом случае? Данная ситуация анализируется в статье, в которой при записи интегральных уравнений электромагнитного поля в четырехмерной ковариантной форме в законе Фарадея вместо частной производной по времени появляется полная производная магнитного потока, проходящего через контур.. Таким образом, электромагнитная индукция возникает либо при изменении магнитного поля с течением времени, либо при изменении площади цепи. С физической точки зрения лучше говорить не об ЭДС индукции, а о напряженности индуцированного электрического поля, возникающего в цепи при изменении магнитного потока. В этом случае вклад в изменение магнитного поля вносится слагаемым, где - векторный потенциал. Если площадь контура изменяется в случае постоянного магнитного поля, то некоторая часть контура неизбежно движется, и электрическое поле возникает в этой части контура в сопутствующей системе отсчета K 'в результате преобразования Лоренца магнитное поле, присутствующее в неподвижной системе отсчета K, которое проходит через контур. Наличие поля в K 'считается результатом эффекта индукции в движущейся цепи, независимо от того, присутствуют ли в цепи заряды или нет. В проводящей цепи поле вызывает движение зарядов. В системе отсчета K это выглядит как появление ЭДС индукции, градиент которой, взятый по контуру, кажется, порождает поле.
Размышления об этой очевидной дихотомии были одним из основных путей, которые привели Альберта Эйнштейна к разработке специальной теории относительности :
Известно, что электродинамика Максвелла - как обычно понимается в настоящее время - применительно к движущимся телам приводит к асимметриям, которые, по-видимому, не присущи явлениям. Возьмем, например, взаимное электродинамическое действие магнита и проводника.
Наблюдаемое явление здесь зависит только от относительного движения проводника и магнита, в то время как обычный взгляд проводит резкое различие между двумя случаями, когда одно или другое из этих тел находится в движении. Ведь если магнит находится в движении, а проводник покоится, в окрестности магнита возникает электрическое поле с определенной энергией, производящее ток в местах, где расположены части проводника.
Но если магнит неподвижен, а проводник движется, электрическое поле поблизости от магнита не возникает. В проводнике, однако, мы находим электродвижущую силу, которой сама по себе не соответствует энергия, но которая вызывает - при условии равенства относительного движения в двух рассмотренных случаях - электрические токи того же пути и силы, что и создаваемые электрическими силами в первом случае.
Примеры такого рода, вместе с безуспешными попытками обнаружить какое-либо движение Земли относительно «легкой среды», предполагают, что явления электродинамики, как и механики, не обладают свойствами, соответствующими идее абсолютного покоя.
- Альберт Эйнштейн, Электродинамика движущихся тел.трактат об электричестве и магнетизме.
СМИ, связанные с законом индукции Фарадея на Викискладе?
