Работа (физика)

редактировать

Процесс передачи энергии объекту посредством приложения силы посредством ущерба

Работа
A бейсбол питчер выполняет функцию положения, которая движется, находясь в положении, в котором оно перемещается.
Общие символы	W
единица СИ	джоуль (Дж)
Другие единицы	Фут-фунт, Эрг
В базовых единицах СИ	1 kg ⋅m ⋅s
Производные от. других величин	W = F ⋅ s. W = τ θ
Размер	MLT

В физике, работа - это энергия, передаваемая объекту или от объекта посредством приложения силы при перемещении. В простейшей форме его часто представляют как произведение силы и с ущербом. Считается, что сила совершает положительную работу, если (при приложении) она имеет компонент в направлении с ущербом точки приложения. Сила совершает отрицательную работу, если ее составляющая противоположна направление с точки в точке приложения силы.

Например, когда мяч удерживается над землей, а затем падает, работа, выполняемая гравитационной силой на мяч при его падении, равна весу мяча (сила), умноженному на расстояние на землю (смещение). Когда сила F постоянна, а угол между силой и смещением s равен θ, то проделанная работа определяется следующим образом:

W = F s cos ⁡ θ {\ displaystyle W = Fs \ cos {\ theta}}

{\ displaystyle W = Fs \ cos {\ theta}}

Работа - это скалярная величина, поэтому она имеет только значение и не имеет направления. Работа передает энергию из одного места в другое или из одной формы в другую. единица СИ работы - это джоуль (Дж).

Содержание

1 Этимология
2 Единицы
3 Работа и энергия
4 Ограничивающие силы
5 Математический расчет
- 5.1 Работа, совершаемая с помощью использования силы
- 5.2 Крутящий момент и вращение
6 Работа и потенциальная энергия
- 6.1 Зависимость от пути
- 6.2 Независимость от пути
- 6.3 Работа под воздействием силы тяжести
- 6.4 Работа под силой тяжести в пространстве
- 6.5 Работа пружиной
- 6.6 Работа за счет газа
7 Принцип работы - энергии
- 7.1 Вывод для частиц, движущейся по прямому
- 7.2 Общий вывод теоремы о работе - энергии для частиц
- 7.3 Вывод для частиц в ограниченном движении
  - 7.3.1 Векторная формулировка
  - 7.3.2 Тангенциальные и нормальные компоненты
- 7.4 Движение по прямому (занос до остановки)
- 7.5 Выбег по горной дороге (гравитационные гонки)
8 Работа сил, действ на твердое тело
9 Ссылки
10 Библиография
11 Внешние ссылки

Этимология

Согласно Джаммер у, термин «работа» введен в 1826 году французским математиком Гаспар-Гюстав Кориолис как «вес, поднимаемый на высоту», основанный на использовании первых паровых двигателей для подъема ведер с водой из затопленных рудников. По словам Рене Дюга, французского инженера и историка, именно Соломону Ко «мы обязаны термину работа в том смысле, в каком он сейчас используется в механике».

Единицы

Единицей работы СИ джоуль (Дж), названный в честь английской физика 19 века Джеймса Прескотта Джоуля, который определяется как работа, необходимая для приложения силы в одном ньютон через смещение на один метр.

Эквивалент ньютон-метр (Н · м) иногда используется в качестве единица измерения для работы, но ее можно спутать с единиц измерения крутящего момента. Орган SI не рекомендует использовать Н · м, поскольку это может привести к путанице относительно того, является ли величина, выраженная в ньютон-метр, измерением крутящего момента или измерением работы.

Единицы работы вне системы СИ ньютон-метр, эрг, фут-фунт, фут-фунтал, киловатт-час, и лошадиных сил в час. Из-за того, что работа имеет тот же физический размер , что и heat, иногда единицы измерения обычно зарезервированы для содержания тепла или энергии, например therm, БТЕ и калория используются в качестве единицы измерения.

Работа и энергия

Работа W, используемая постоянная величина F в точке, которая перемещает смещение по прямой линии в направлении силы, является произведением

W = F s {\ displaystyle W = Fs}

{\ displaystyle W = Fs}

Например, если сила в 10 ньютонов (F = 10 Н) действует вдоль точки, которая проходит 2 метра (s = 2 м), то есть W = Fs = (10 Н) (2 м) = 20 Дж.. Это примерно работа, выполняемая при поднятии предмета весом 1 кг с уровня земли на голову человека против силы тяжести.

Работа удваивается либо путем подъема удвоенного веса на такое же расстояние, либо путем подъема того же груза на удвоенное расстояние.

Работа связана с энергией. Принцип работы-энергии гласит, увеличение кинетической энергии твердого тела вызывается равным объемом положительной работы, совершенной на равнодействующей силой, действующей на это тело. И наоборот, уменьшение кинетической энергии вызывается равным образом отрицательной работы, совершенной равнодействующей силой. Таким образом, если чистая работа положительна, кинетическая энергия частиц увеличивается на работу. Если чистая проделанная работа отрицательна, то кинетическая энергия частицы уменьшается на работу.

Из закона второго Ньютона можно показать, что работают на свободном (без полей), твердое (без внутренних степеней свободы) тело, равно изменению кинетической энергии KE, соответствующей линейной скорости и угловой скорости этого тела,

W = Δ KE. {\ displaystyle W = \ Delta KE.}

{\ displaystyle W = \ Delta KE.}

Работа сил, генерируемых потенциальной функцией, известна как потенциальная энергия, а силы называются консервативными. Следовательно, работа над объектом, просто перемещается в консервативном силовом поле который, без изменения скорости или вращения, равна минус изменению потенциальной энергии PE объекта,

W = - Δ ЧП. {\ displaystyle W = - \ Delta PE.}

{\ displaystyle W = - \ Delta PE.}

Эти формулы показывают, что работа - это энергия, связанная с силой, работа обладает физическими размерами и единицами энергии. Обсуждаемые принципы здесь принципы работы / энергии идентичны работы / энергии.

Ограничивающие силы

Ограничивающие силы определяют смещение объекта в системе, ограничивая его в пределах диапазона. Например, в случае прикрепления к уклона , плюс сила тяжести, объект прилипает к склону, будучи прикрепленным к натянутой струне, не может двигаться наружу, чтобы сделать струну более «тугой». Он устраняет все ограничения в этом направлении, что есть скорость в ограничении, ограничена до 0, так что ограничения не работают с системой.

Для механической системы ограничения устраняют перемещение в направлениях, которые характеризуют ограничение. Таким образом, виртуальная работа, выполняемая ограничения сил, равна нулю, результат, который верен только в том случае, если силы трения исключены.

Фиксированные силы ограничения без трения не хватает работы в системе, поскольку движением и силами связи всегда составляет 90 °. Примеры неработающих ограничений: жесткие взаимосвязи между частями, скользящее движение по поверхности без трения и контакт качения без скольжения.

Например, в системе шкивов, такой как машина Атвуда, внутреннее силы, действующие на трос и опорный шкив, не влияет на систему. Поэтому нужно рассчитывать только для гравитационных сил, действующих на тела. Другой пример - центростремительная сила, оказываемая внутрь струной на шар при равномерном круговом движении вбок, заставляет шар совершать круговое движение, ограничивая его от центра круга. Эта сила нулевую работу, потому что она перпендикулярна скорости мяча.

Магнитная сила , действующая на заряженную частицу, равна F = q v× B, где q - заряд, v - скорость частица, а B - магнитное поле . Результат перекрестного произведения всегда перпендикулярен обоим исходным векторм, поэтому F⊥ v. скалярное произведение двух перпендикулярных векторов всегда равно нулю, поэтому работа W = F⋅ v= 0, и магнитная сила не действует. Он может изменить направление движения, но никогда не изменит скорость.

Математический расчет

Для движущихся объектов количество работы / времени (мощность) интегрируется по траектории точки приложения силы. Таким образом, в любой момент скорости работы, совершенной силой (измеряемая в джоулях в секунду, или ватт ), является скалярным произведением силы (вектором) и вектором скорости точки приложения. Это скалярное произведение силы и скорости известно как мгновенная мощность. Интегралом по времени мгновенной мощности, приложенной вдоль траектории точки

, является интегралом по времени мгновенной мощности. Работа - это результат воздействия силы на точку, которая следует кривой X со скоростью v в каждый момент времени. Небольшой объем работы δW, который происходит за момент времени dt, рассчитывается как

δ W = F ⋅ ds = F ⋅ vdt {\ displaystyle \ delta W = \ mathbf {F} \ cdot d \ mathbf {s} = \ mathbf {F} \ cdot \ mathbf {v} dt}

\ delta W = \ mathbf {F} \ cdot d \ mathbf {s} = \ mathbf {F} \ cdot \ mathbf {v} dt

где F⋅ v- мощность над моментом dt. Сумма этих малых объемов работы по траектории точки работы,

W = ∫ t 1 t 2 F ⋅ vdt = ∫ t 1 t 2 F ⋅ dsdtdt = ∫ CF ⋅ ds, {\ displaystyle W = \ int _ {t_ { 1}} ^ {t_ {2}} \ mathbf {F} \ cdot \ mathbf {v} dt = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F} \ cdot {\ tfrac {d \ mathbf {s}} {dt}} dt = \ int _ {C} \ mathbf {F} \ cdot d \ mathbf {s},}

{\ displaystyle W = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F} \ cdot \ mathbf {v} dt = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F} \ cdot {\ tfrac {d \ mathbf {s}} {dt}} dt = \ int _ {C} \ mathbf {F} \ cdot d \ mathbf {s},}

где C - траектория от x(t1) до x(t2). Этот интеграл вычисляется вдоль траектории частиц и поэтому считается зависимым от пути.

Если сила всегда направлена вдоль этой линии, величина силы равна F, то этот интеграл упрощается до

W = ∫ CF ds {\ displaystyle W = \ int _ {C} F \, ds }

{\ displaystyle W = \ int _ {C} F \, ds}

где s - смещение по линии. Если F является постоянным, помимо того, что он направлен вдоль линии, интеграл дополнительно упрощается до

W = ∫ CF ds = F ∫ C ds = F s {\ displaystyle W = \ int _ {C } F \, ds = F \ int _ {C} ds = Fs}

{\ displaystyle W = \ int _ {C} F \, ds = F \ int _ {C} ds = Fs}

где s - смещение точки вдоль линии.

Этот расчет можно обобщить для постоянной силы, которая не направлена вдоль линии, за которой следует частица. В этом случае скалярное векторное произведение F⋅ d s = F cos θ ds, где θ - угол между силой и направлением движения, то есть

W = ∫ CF ⋅ ds = F s cos ⁡ θ. {\ displaystyle W = \ int _ {C} \ mathbf {F} \ cdot d \ mathbf {s} = Fs \ cos \ theta.}

W = \ int _ {C} \ mathbf {F} \ cdot d \ mathbf {s} = Fs \ cos \ theta.

Когда компонент силы перпендикулярен смещению объекта (например, когда тело движется по круговой траектории под действие центральной силы ), работа не выполняется, так как косинус 90 ° равенство нулю. Таким образом, гравитация не может совершать никаких действий на планете с круговой орбитой (это идеальный вариант, поскольку все орбиты имеют слегка эллиптическую форму). Кроме того, никакая работа не выполняется с телом, например, движущимся с постоянной скоростью в идеальной центрифуге без трения.

Работа, выполняемая используемая сила

Вычисление работы как «сила, умноженная на отрезке прямой траектории», применимо только в самых простых обстоятельствах, как принято выше. Если сила изменяется или если тело движется по криволинейной траектории, возможно вращаясь и не обязательно жестко, то только путь приложения силы имеет значение для выполненной работы, и только составляющая сила параллельна точка приложения скорость выполняет работу (положительная работа, когда в том же направлении, и отрицательная, когда в противоположном направлении скорости). Эту составляющую силу можно описать скалярной величиной, называемой скалярной тангенциальной составляющей (F cos (θ), где θ - угол между силой и скоростью). И тогда самое общее определение работы можно определить следующим образом:

Работа силы - это линейный интеграл ее скалярной тангенциальной составляющей вдоль пути ее точки приложения.

Если сила изменяется (например, сжатие пружины) нам нужно использовать исчисление, чтобы найти проделанную работу. Если сила задается как F (x) (функция x), то работа совершенной силой вдоль оси x от a до b, равна:

W = ∫ ab F (s) ⋅ ds {\ displaystyle W = \ int _ { a} ^ {b} \ mathbf {F (s)} \ cdot d \ mathbf {s}}

{\ displaystyle W = \ int _ {a} ^ {b} \ mathbf {F (s)} \ cdot d \ mathbf {s}}

Крутящий момент и вращение

A пара сил возникает в результате равных и противоположных сил, действует на две разные точки твердого тела. Сумма (равнодействующая) этих сил может уравновешиваться, но их воздействие на тело - это пара или крутящий момент T . Работа крутящего момента рассчитывается как

d W = T ⋅ ω → dt, {\ displaystyle dW = \ mathbf {T} \ cdot {\ vec {\ omega}} dt,}

{\ displaystyle dW = \ mathbf {T} \ cdot {\ vec {\ omega}} dt,}

где T⋅ ω- мощность над моментом δt. Сумма малых объемов твердого тела дает работу,

W = ∫ t 1 t 2 T ⋅ ω → d t. {\ displaystyle W = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {T} \ cdot {\ vec {\ omega}} dt.}

{\ displaystyle W = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {T} \ cdot {\ vec {\ omega}} dt.}

Этот интеграл вычисляется вдоль траектории твердого тела с угловой скоростью ω, которая изменяется со временем и поэтому называется зависимой от пути.

Если вектор угловой скорости сохраняет постоянное направление, то он принимает форму

ω → = ϕ ˙ S, {\ displaystyle {\ vec {\ omega}} = {\ dot {\ phi}} \ mathbf {S},}

{\ vec {\ omega}} = {\ dot {\ phi}} \ mathbf {S },

где φ - угол поворота вокруг постоянного единичного вектора S . В этом случае происходит работа крутящего момента,

W = ∫ t 1 t 2 T ⋅ ω → dt = ∫ t 1 t 2 T ⋅ S d ϕ dtdt = ∫ CT ⋅ S d ϕ, {\ displaystyle W = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {T} \ cdot {\ vec {\ omega}} dt = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf { T} \ cdot \ mathbf {S} {\ frac {d \ phi} {dt}} dt = \ int _ {C} \ mathbf {T} \ cdot \ mathbf {S} d \ phi,}

W = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {T} \ cdot {\ vec {\ omega}} dt = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {T} \ cdot \ mathbf {S} {\ frac {d \ phi} {dt}} dt = \ int _ {C} \ mathbf {T} \ cdot \ mathbf {S } d \ phi,

, где C - траектория от φ (t 1) до φ (t 2). Этот интеграл зависит от траектории вращения φ (t) и, следовательно, зависит от пути.

Если крутящий момент T выровнен с вектором угловой скорости так, что

T = τ S, {\ displaystyle \ mathbf {T} = \ tau \ mathbf {S},}

\ mathbf {T} = \ tau \ mathbf {S},

и крутящий момент и угловая скорость постоянны, тогда работа принимает вид

W = ∫ t 1 t 2 τ ϕ ˙ dt = τ (ϕ 2 - ϕ 1). {\ displaystyle W = \ int _ {t_ {1}} ^ {t_ {2}} \ tau {\ dot {\ phi}} dt = \ tau (\ phi _ {2} - \ phi _ {1}).}

W = \ int _ {t_ {1}} ^ { t_ {2}} \ tau {\ dot {\ phi}} dt = \ tau (\ phi _ {2} - \ phi _ {1}).

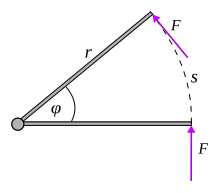Сила постоянной величины, перпендикулярная плечу рычага

Этот результат можно понять проще, если рассматривать крутящий момент как результат силы величины F, приложенной перпендикулярно плечу рычага на расстоянии r, как показано на рисунке. Эта сила будет действовать через расстояние по окружности s = rφ, поэтому проделанная работа будет

W = F s = F r ϕ. {\ displaystyle W = Fs = Fr \ phi.}

{\ displaystyle W = Fs = Fr \ phi.}

Введите крутящий момент τ = Fr, чтобы получить

W = F r ϕ = τ ϕ, {\ displaystyle W = Fr \ phi = \ tau \ phi, }

W = Fr \ phi = \ tau \ phi,

, как указано выше.

Обратите внимание, что только составляющая крутящего момента в направлении угловой скорости вносит вклад в работу.

Работа и потенциальная энергия

Скалярное произведение силы F и скорость v точки ее приложения определяют мощность ввод в систему в определенный момент времени. Интеграция этой мощности в траектории точки приложения, C = x (t), определяет работу, вводимую в систему силой.

Зависимость от пути

Следовательно, работа, совершенная сила F на объект, который движется по кривой C, определяется как линейный интеграл :

W = ∫ CF ⋅ dx = ∫ T 1 T 2 F ⋅ vdt, {\ displaystyle W = \ int _ {C} \ mathbf {F} \ cdot d \ mathbf {x} = \ int _ {t_ { 1}} ^ {t_ {2}} \ mathbf {F} \ cdot \ mathbf {v} dt,}

{\ displaystyle W = \ int _ {C} \ mathbf {F} \ cdot d \ mathbf {x} = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F } \ cdot \ mathbf {v} dt,}

где dx (t) определяет траекторию C, а v - это скорость по этой траектории. Как правило, этот интеграл требует пути, по которому определяется скорость, поэтому считается, что оценка работы зависит от пути.

Производная интеграла по работе по времени дает мгновенную мощность,

d W dt = P (t) = F v. {\ Displaystyle {\ frac {dW} {dt}} = P (t) = \ mathbf {F} \ cdot \ mathbf {v}.}

{\ frac {dW} {dt}} = P (t) = \ mathbf {F} \ cdot \ mathbf {v}.

Независимость от пути

Если работа для прикладной силы не зависит от пути, тогда работа, выполняемая сила, по теореме градиента определяет потенциальную функцию, которая оценивается в начале и в конце траектории точки приложения. Это означает, что возможная функция U (x ), которую можно оценить в двух точках x(t1) и x(t2) для получения работы по любой траектории между этими двумя точками. Традиционно эту функцию определяют с отрицательным знаком, чтобы положительная работа была уменьшением, то есть

W = ∫ CF ⋅ dx = ∫ x (t 1) x (t 2) F ⋅ dx = U (x (t 1)) - U (x (t 2)). {\ Displaystyle W = \ int _ {C} \ mathbf {F} \ cdot \ mathrm {d} \ mathbf {x} = \ int _ {\ mathbf {x} (t_ {1})} ^ {\ mathbf { x} (t_ {2})} \ mathbf {F} \ cdot \ mathrm {d} \ mathbf {x} = U (\ mathbf {x} (t_ {1})) - U (\ mathbf {x} ( t_ {2})).}

{\ Displaystyle W = \ int _ {C} \ mathbf {F} \ cdot \ mathrm {d} \ mathbf {x} = \ int _ {\ mathbf {x} (t_ {1})} ^ {\ mathbf { x} (t_ {2})} \ mathbf {F} \ cdot \ mathrm {d} \ mathbf {х} = U (\ mathbf {x} (t _ {1})) - U (\ mathbf {x} (t_ {2})).}

Функция U (x ) называется потенциальной энергией, не с приложенной силой. Сила, полученная из такой потенциальной функции, называется консервативной. Примерами сил, потенциальную энергию, обладают силой тяжести и силы пружины.

В этом случае градиент работы дает

∇ W = - ∇ U = - (∂ U ∂ x, ∂ U ∂ y, ∂ U ∂ z) = F, {\ displaystyle \ nabla W = - \ nabla U = - \ left ({\ frac {\ partial U} {\ partial x}}, {\ frac {\ partial U} {\ partial y}}, {\ frac {\ partial U} {\ partial z}} \ right) = \ mathbf {F},}

{\ displaystyle \ nabla W = - \ nabla U = - \ left ({\ frac {\ partial U} {\ partial x}}, {\ frac {\ partial U} {\ partial y} }, {\ frac {\ partial U} {\ partial z}} \ right) = \ mathbf {F},}

, а сила F называется "производной от потенциала"

Временный потенциал U определяет силу F в каждой точке x в зоне, набор сил называется силовым полем. Мощность, приложенная к телу силовым полем, получается из градиента работы или в направлении скорости V тела, то есть

P (t) = - ∇ U ⋅ v = F ⋅ v. {\ Displaystyle P (t) = - \ nabla U \ cdot \ mathbf {v} = \ mathbf {F} \ cdot \ mathbf {v}.}

{\ displaystyle P (t) = - \ nabla U \ cdot \ mathbf {v} = \ mathbf {F} \ cdot \ mathbf {v}.}

Работа под воздействием силы тяжести

Гравитация F = mg действительно работает W = mgh вдоль любого нисходящего пути

отсутствие других силитация приводит к постоянному ускорению вниз каждого движущегося объекта. У поверхности Земли ускорение свободного падения g = 9,8 м⋅с, а сила тяжести на объекте массы m Fg= mg. Удобно представить себе эту гравитационную силу, сосредоточенную в центре масс объекта.

Если объект смещен вверх или вниз на вертикальное расстояние y 2 - y 1, работа W, выполненная над объектом его весом mg, будет:

W = F g (y 2 - y 1) = F g Δ y = - mg Δ y {\ displaystyle W = F_ {g} (y_ {2} -y_ {1}) = F_ {g} \ Delta y = -mg \ Delta y}

W = F_ {g} (y_ {2} -y_ {1 }) = F_ {g} \ Delta y = -mg \ Delta y

где F g - это вес (фунты в имперских единицах и ньютоны в единицах СИ), а Δy - изменение высоты y. Обратите внимание, что работа, выполняемая силой тяжести, зависит только от вертикального движения объекта. Наличие трения не влияет на работу, выполняемую с объектом его весом.

Работа под действием силы тяжести в космосе

Сила тяжести, действующая на массу M на другую массу m, определяется как

F = - GM mr 3 r, {\ displaystyle \ mathbf { F} = - {\ frac {GMm} {r ^ {3}}} \ mathbf {r},}

\ mathbf {F} = - {\ frac {GMm} {r ^ {3}}} \ mathbf {r},

где r - вектор положения от M до m.

Пусть масса m движется со скоростью v , тогда работа силы тяжести над этой массой, когда она перемещается из положения r(t1) в r(t2), определяется как

W = - ∫ r (t 1) r (t 2) GM mr 3 r ⋅ dr = - t 1 t 2 GM mr 3 r ⋅ vdt. {\ displaystyle W = - \ int _ {\ mathbf {r} (t_ {1})} ^ {\ mathbf {r} (t_ {2})} {\ frac {GMm} {r ^ {3}}} \ mathbf {r} \ cdot d \ mathbf {r} = - \ int _ {t_ {1}} ^ {t_ {2}} {\ frac {GMm} {r ^ {3}}} \ mathbf {r} \ cdot \ mathbf {v} dt.}

W = - \ int _ {\ mathbf {r} (t_ {1})} ^ {\ mathbf {r} (t_ {2})} {\ frac {GMm} {r ^ {3}}} \ mathbf {r} \ cdot d \ mathbf {r} = - \ int _ {t_ {1}} ^ {t_ {2}} {\ frac {GMm} {r ^ {3}}} \ mathbf {r} \ cdot \ mathbf {v} dt.

Обратите внимание, что положение и скорость массы m задаются как

r = rer, v = r ˙ er + r θ ˙ et,{\ displaystyle \ mathbf {r} = r \ mathbf {e} _ {r}, \ qquad \ mathbf {v} = {\ dot {r}} \ mathbf {e} _ {r} + r {\ dot { \ theta}} \ mathbf {e} _ {t},

\ mathbf {r} = r \ mathbf {e} _ {r}, \ qquad \ mathbf {v} = {\ dot {r}} \ mathbf {e} _ {r} + r {\ dot {\ theta}} \ mathbf {e} _ {t},

где erи et- радиальный и тангенциальный единичные конструкции, направленное относительно вектора от М к м. Используйте это, чтобы упростить формулу работы силы тяжести до,

W = - t 1 t 2 G m M r 3 (rer) ⋅ (r ˙ er + r θ ˙ et) dt = - ∫ t 1 t 2 G m M r 3 rr ˙ dt = GM mr (t 2) - GM mr (t 1). {\ displaystyle W = - \ int _ {t_ {1}} ^ {t_ {2}} {\ frac {GmM} {r ^ {3}}} (r \ mathbf {e} _ {r}) \ cdot ({\ dot {r}} \ mathbf {e} _ {r} + r {\ dot {\ theta}} \ mathbf {e} _ {t}) dt = - \ int _ {t_ {1}} ^ {t_ {2}} {\ frac {GmM} {r ^ {3}}} r {\ dot {r}} dt = {\ frac {GMm} {r (t_ {2})}} - {\ frac {GMm} {r (t_ {1})}}.}

W = - \ int _ {t_ {1}} ^ {t_ {2}} {\ frac {GmM} {r ^ {3}}} (r \ mathbf {e} _ {r}) \ cdot ({\ dot { r}} \ mathbf {e} _ {r} + r {\ dot {\ theta}} \ mathbf {e} _ {t}) dt = - \ int _ {t_ {1}} ^ {t_ {2} } {\ frac {GmM} {r ^ {3}}} r {\ dot {r}} dt = {\ frac {GMm} {r (t_ {2})}} - {\ frac {GMm} {r (t_ {1})}}.

В этом вычислении используется тот факт, что

ddtr - 1 = - r - 2 r ˙ = - r ˙ r 2. {\ displaystyle { \ frac {d} {dt}} r ^ {- 1} = - r ^ {- 2} {\ dot {r}} = - {\ frac {\ dot {r}} {r ^ {2}}}.}

{\ frac {d} {dt}} r ^ {- 1} = - r ^ {- 2} {\ dot {r}} = - {\ frac {\ dot {r} } {г ^ {2}}}.

Функция

U = - GM mr, {\ displaystyle U = - {\ frac {GMm} {r}},}

U = - {\ frac {GMm} {r}},

- это функция гравитационного потенциала, также известная как гравитационная потенциальная энергия. Отрицательный знак следует за условием, что работа достигается за счет потенциальной энергии.

Работа пружины

Силы в пружинах, собранных отклонений

Рассмотрим пружину, которая оказывает горизонтальное усилие F = (−kx, 0, 0), которое пропорционально егоение в направлении x независимо от того, как движется тело. Работа этой пружины по телу, движущемуся по пространству с кривой X (t) = (x (t), y (t), z (t)), вычисляется с использованием его скорости, v = (v x, v y, v z), чтобы получить

W = ∫ 0 t F ⋅ vdt = - ∫ 0 tkxvxdt = - 1 2 kx 2. {\ Displaystyle W = \ int _ {0} ^ {t} \ mathbf {F} \ cdot \ mathbf {v} dt = - \ int _ {0} ^ {t} kxv_ {x} dt = - {\ frac {1} {2}} kx ^ {2}.}

{\ displaystyle W = \ int _ {0} ^ {t} \ mathbf {F} \ cdot \ mathbf {v} dt = - \ int _ {0} ^ {t} kxv_ {x} dt = - {\ frac {1} {2}} kx ^ {2}.}

Для удобства рассмотрим, что контакт с пружиной происходит при t = 0, тогда интеграл от расстояния x и скорости x, xv x, равно (1/2) x. Скорость здесь не имеет значения. Работа - это действие на усилие пружины, которое также зависит от расстояния; отсюда результат x.

Работа газа

W = ∫ ab P d V {\ displaystyle W = \ int _ {a} ^ {b} {P} dV}

{\ displaystyle W = \ int _ {a} ^ {b} {P} dV}

где P - давление, V - объем, а a и b - начальный и конечный объемы.

Принцип работы-энергии

Принцип работы и кинетическая энергия (также известный как принцип работы-энергии ) утверждает, что выполненная работа все силы, действующие на частицу (работа равнодействующей силы), равны изменению кинетической энергии частиц. То есть работа W, совершенная равнодействующей силой на частице, равна изменению кинетической энергии частиц $E k {\ displaystyle E_ {k}}$ $E_ {k}$ ,

W = Δ E К знак равно 1 2 mv 2 2 - 1 2 mv 1 2 {\ displaystyle W = \ Delta E_ {k} = {\ tfrac {1} {2}} mv_ {2} ^ {2} - {\ tfrac {1} { 2}} mv_ {1} ^ {2}}

{\ displaystyle W = \ Delta E_ {k} = {\ tfrac {1} {2}} mv_ {2} ^ {2} - {\ tfrac {1} {2}} mv_ {1} ^ {2}}

где $v 1 {\ displaystyle v_ {1}}$ $v_ {1}$ и $v 2 {\ displaystyle v_ {2}}$ $v_ {2}$ - скорость частиц до и после выполнения работы, а м - ее масса.

. Начало вывода принципа работа - энергия. с вторым законом движения Ньютона и равнодействующей силой, действующей на частицу. Вычисление скалярного произведения сил на скорость частиц позволяет оценить мгновенную мощность, добавленную к системе.

Ограничения определяют направление движения частиц, гарантируя отсутствие компонента скорости в направлении движения. Это также означает, что ограничения не прибавляют к мгновенной мощности. Интеграл по времени этого скалярного уравнения дает работу из мгновенной мощности, а кинетическую энергию - из скалярного произведения скорости и ускорения. Тот факт, что принцип работы-энергии устраняет ограничивающие силы, лежит в основе лагранжевой механики.

В этом разделе уделяется внимание принципу работы-энергии, поскольку он применяет к динамике частиц. В более общих системах работа может быть потенциальную энергию механического устройства, тепловую энергию в тепловой системе или электрическую энергию в электрическом устройстве. Работа передает энергию из одного места в другое или из одной формы в другую.

Вывод для частиц, движущейся по прямой линии

В случае, если результирующая сила Fпостоянна как по величине, так и по направлению и параллельна скорости частиц, частица движется с постоянным ускорением а по прямой. Связь между результирующей силой и ускорением уравнением F = ma (второй закон Ньютона ), а смещение частиц s может быть выражено уравнением

s = v 2 2 - v 1 2 2 a {\ displaystyle s = {\ frac {v_ {2} ^ {2} -v_ {1} ^ {2}} {2a}}}

s = {\ frac {v_ { 2} ^ {2} -v_ {1} ^ {2}} {2a}}

что следует из $v 2 2 = v 1 2 + 2 как {\ displaystyle v_ {2} ^ {2} = v_ {1} ^ {2} + 2as}$ $v_ {2} ^ {2} = v_ {1} ^ {2 } + 2as$ (см. Уравнения движения ).

Работа чистой силы рассчитывается как произведение ее величины и размера частиц. Подставляя приведенные выше уравнения, получаем:

W = F s = mas = ma (v 2 2 - v 1 2 2 a) = mv 2 2 2 - mv 1 2 2 = Δ E k {\ displaystyle W = Fs = mas = ma \ left ({\ frac {v_ {2} ^ {2} -v_ {1} ^ {2}} {2a}} \ right) = {\ frac {mv_ {2} ^ {2}} { 2}} - {\ frac {mv_ {1} ^ {2}} {2}} = \ Delta {E _ {\ mathrm {k}}}}

{\ displaystyle W = Fs = mas = ma \ left ({\ frac {v_ {2} ^ {2} -v_ {1} ^ {2}} {2a}} \ справа) = {\ frac {mv_ {2} ^ { 2}} {2}} - {\ frac {mv_ {1} ^ {2}} {2}} = \ Delta {E _ {\ mathrm {k}}}}

Другой вывод:

W = F s = mas = m (v 2 2 - v 1 2 2 s) s = 1 2 mv 2 2 - 1 2 mv 1 2 = Δ E K {\ displaystyle W = Fs = mas = m \ left ({\ frac {v_ { 2} ^ {2} -v_ {1} ^ {2}} {2s}} \ right) s = {\ frac {1} {2}} mv_ {2} ^ {2} - {\ frac {1} {2}} mv_ {1} ^ {2} = \ Delta {E _ {\ mathrm {k}}}}

{\ displaystyle W = Fs = mas = m \ left ({\ frac {v_ {2} ^ {2} - v_ {1} ^ {2}} {2s}} \ right) s = {\ frac {1} {2}} mv_ {2} ^ {2} - {\ frac {1} {2}} mv_ {1} ^ {2} = \ Delta {E _ {\ mathrm {k }}}}

В общем случае прямолинейного движения, когда чистая сила F не постоянная по величине, но постоянная по направлению и параллельная скорости частицы, работа должна быть проинтегрирована вдоль пути частиц:

W = ∫ t 1 t 2 F ⋅ vdt = ∫ t 1 t 2 F vdt = ∫ t 1 t 2 mavdt = m ∫ t 1 t 2 vdvdtdt = m ∫ v 1 v 2 vdv = 1 2 м (v 2 2 - v 1 2). {\ Displaystyle W = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F} \ cdot \ mathbf {v} dt = \ int _ {t_ {1}} ^ {t_ {2} } F \, vdt = \ int _ {t_ {1}} ^ {t_ {2}} ma \, vdt = m \ int _ {t_ {1}} ^ {t_ {2}} v \, {dv \ над dt} \, dt = m \ int _ {v_ {1}} ^ {v_ {2}} v \, dv = {\ tfrac {1} {2}} m (v_ {2} ^ {2} - v_ {1} ^ {2}).}

{\ displaystyle W = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F} \ cdot \ mathbf { v} dt = \ int _ {t_ {1}} ^ {t_ {2}} F \, vdt = \ int _ {t_ {1}} ^ {t_ {2}} ma \, vdt = m \ int _ {t_ {1}} ^ {t_ {2}} v \, {dv \ over dt} \, dt = m \ int _ {v_ {1}} ^ {v_ {2}} v \, dv = {\ tfrac {1} {2}} m (v_ {2} ^ {2} -v_ {1} ^ {2}).}

Общий вывод теоремы работы - энергии для частиц

Для любой чистой силы, действующей на частицу, движущуюся по любой криволинейной траектории, можно показать, что его работа равна Использование простого вывода, аналогичного приведенному выше уравнению работы кинетической энергии частиц. Некоторые авторы называют этот результат принципом работа-энергия, но он более известен как теорема работа-энергия :

W = ∫ t 1 t 2 F ⋅ vdt = m ∫ t 1 t 2 a ⋅ vdt = m 2 ∫ T 1 T 2 дв 2 dtdt знак равно м 2 ∫ v 1 2 v 2 2 dv 2 = mv 2 2 2 - mv 1 2 2 = Δ E k {\ displaystyle W = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F} \ cdot \ mathbf {v} dt = m \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {a} \ cdot \ mathbf {v} dt = { \ frac {m} {2}} \ int _ {t_ {1}} ^ {t_ {2}} {\ frac {dv ^ {2}} {dt}} \, dt = {\ frac {m} { 2}} \ int _ {v_ {1} ^ {2}} ^ {v_ {2} ^ {2}} dv ^ {2} = {\ frac {mv_ {2} ^ {2}} {2}} - {\ frac {mv_ {1} ^ {2}} {2}} = \ Delta {E_ {k}}}

{\ displaystyle W = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F} \ cdot \ mathbf {v} dt = m \ int _ {t_ {1} } ^ {t_ {2}} \ mathbf {a} \ cdot \ mathbf {v} dt = {\ frac {m} {2}} \ int _ {t_ {1}} ^ {t_ {2}} {\ гидроразрыв {dv ^ {2}} {dt}} \, dt = {\ frac {m} {2}} \ int _ {v_ {1} ^ {2}} ^ {v_ {2} ^ {2}} dv ^ {2} = {\ frac {mv_ {2} ^ {2}} {2}} - {\ frac {mv_ {1} ^ {2}} {2}} = \ Delta {E_ {k}} }

Идентификатор $a ⋅ v = 1 2 dv 2 dt {\ displaystyle \ textstyle \ mathbf {a} \ cdot \ mathbf {v} = {\ frac {1} {2}} {\ frac {dv ^ {2}} {dt}}}$ $\ textstyle \ mathbf {a} \ cdot \ mathbf {v} = {\ frac {1} {2 }} {\ frac {dv ^ {2}} {dt}}$ требует некоторой алгебры. Из обозначатора $v 2 = v ⋅ v {\ displaystyle \ textstyle v ^ {2} = \ mathbf {v} \ cdot \ mathbf {v}}$ $\ textstyle v ^ {2} = \ mathbf {v} \ cdot \ mathbf {v}$ и определение $a = dvdt { \ displaystyle \ textstyle \ mathbf {a} = {\ frac {d \ mathbf {v}} {dt}}}$ $\ textstyle \ mathbf {a} = {\ frac {d \ mathbf {v}} {dt}}$ следует

dv 2 dt = d (v ⋅ v) dt = dvdt ⋅ v + v ⋅ dvdt = 2 dvdt ⋅ v = 2 a ⋅ v {\ displaystyle {\ frac {dv ^ {2}} {dt}} = {\ frac {d (\ mathbf {v} \ cdot \ mathbf) { v})} {dt}} = {\ frac {d \ mathbf {v}} {dt}} \ cdot \ mathbf {v} + \ mathbf {v} \ cdot {\ frac {d \ mathbf {v}} {dt}} = 2 {\ frac {d \ mathbf {v}} {dt}} \ cdot \ mathbf {v} = 2 \ mathbf {a} \ cdot \ mathbf {v}}

{\ frac {dv ^ {2}} {dt}} = {\ frac {d (\ mathbf {v} \ cdot \ mathbf {v})} {dt}} = {\ frac { d \ mathbf {v}} {dt}} \ cdot \ mathbf {v} + \ mathbf {v} \ cdot {\ frac {d \ mathbf {v}} {dt}} = 2 {\ frac {d \ mathbf {v}} {dt}} \ cdot \ mathbf {v} = 2 \ mathbf {a} \ cdot \ mathbf {v}

Оставшаяся часть приведенного выше вывод - это просто простое исчисление, такое же, как и в предыдущем прямолинейном случае.

Вывод для частиц в ограниченном движении

В динамике частиц формула, приравнивающая работу, приложенную к системе, к ее изменению кинетической энергии, получается как первый интеграл второго закона Ньютона движения. Полезно отметить, что результирующая сила, используемая в законах Ньютона, может быть разделена на силы, приложенные к частице, и силы, налагаемые ограничениями на движение частиц. Примечательно, что работа сдерживающей силы равна нулю, поэтому в принципе работа - энергия должна учитывать только работа приложенных сил.

Чтобы убедиться в этом, рассмотрим частицу P, которая следует траектории X (t) с действующей на нее силой F . Изолируйте частицу окружающей среды, чтобы обнажить силы R, тогда закон Ньютона принимает форму

F + R = m X ¨, {\ displaystyle \ mathbf {F} + \ mathbf {R} = m {\ ddot {\ mathbf {X}}},}

\ mathbf {F} + \ mathbf {R} = m {\ ddot {\ mathbf {X}}},

где m - масса частиц.

Векторная формулировка

Обратите внимание, что n точек над вектором указывает его n-ю производную по времени. скалярное произведение каждой стороны закона Ньютона на вектор скорости дает

F ⋅ X ˙ = m X ¨ ⋅ X ˙, {\ displaystyle \ mathbf {F} \ cdot {\ dot {\ mathbf {X} }} = m {\ ddot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}},}

\ mathbf {F} \ cdot {\ dot {\ mathbf {X }}} = м {\ ddot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}},

, потому что ограничения перпендикулярны скорости частиц. Проинтегрируйте это уравнение вдоль его траектории от точки X(t1) до точки X(t2), чтобы получить

∫ t 1 t 2 F ⋅ X ˙ d t = m ∫ t 1 t 2 X ¨ ⋅ X ˙ d t. {\ displaystyle \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F} \ cdot {\ dot {\ mathbf {X}}} dt = m \ int _ {t_ {1}} ^ {t_ {2}} {\ ddot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}} dt.}

\ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F} \ cdot {\ dot {\ mathbf {X }}} dt = m \ int _ {t_ {1}} ^ {t_ {2}} {\ d точка {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}} dt.

Левая часть этого уравнения - это работа приложенной силы как он действует на частицу вдоль траектории от момента времени t 1 до момента времени t 2. Это также можно записать как

W = ∫ t 1 t 2 F ⋅ X ˙ dt = ∫ X (t 1) X (t 2) F ⋅ d X. {\ Displaystyle W = \ int _ {t_ {1} } ^ {t_ {2}} \ mathbf {F} \ cdot {\ dot {\ mathbf {X}}} dt = \ int _ {\ mathbf {X} (t_ {1})} ^ {\ mathbf {X } (t_ {2})} \ mathbf {F} \ cdot d \ mathbf {X}.}

W = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F} \ cdot {\ dot {\ mathbf {X}}} dt = \ int _ {\ mathbf {X} (t_ {1})} ^ {\ mathbf {X} (t_ {2})} \ mathbf {F} \ cdot d \ mathbf {X}.

Этот интеграл вычисляется по траектории X (t) частиц и, следовательно, зависит от пути.

Правую часть первого интеграла уравнения Ньютона можно упростить, используя следующее тождество:

1 2 ddt (X ˙ ⋅ X ˙) = X ¨ ⋅ X ˙, {\ displaystyle {\ frac {1} {2 }} {\ frac {d} {dt}} ({\ dot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}}) = {\ ddot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}},}

{\ frac {1} {2}} {\ frac {d} {dt}} ({\ dot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}) }) = {\ ddot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}},

(см. правило продукта для получения). Теперь он явно проинтегрирован для получения изменения кинетической энергии,

Δ K = m ∫ t 1 t 2 X ¨ ⋅ X ˙ dt = m 2 ∫ t 1 t 2 ddt (X ˙ ⋅ X ˙) dt = m 2 Икс ˙ ⋅ Икс ˙ (T 2) - м 2 Икс ˙ ⋅ Икс ˙ (t 1) = 1 2 м Δ v 2, {\ displaystyle \ Delta K = m \ int _ {t_ {1}} ^ {t_ {2}} {\ ddot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}} dt = {\ frac {m} {2}} \ int _ {t_ {1}} ^ {t_ {2}} {\ frac {d} {dt}} ({\ dot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}}) dt = {\ frac {m} {2}} {\ dot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}} (t_ {2}) - {\ frac {m} {2}} {\ dot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}} (t_ {1}) = {\ frac {1} {2}} m \ Delta \ mathbf {v ^ {2}},}

\ Delta K = m \ int _ {t_ {1}} ^ {t_ {2}} {\ ddot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}} dt = {\ frac {m} {2}} \ int _ {t_ {1}} ^ {t_ {2}} {\ frac {d} {dt}} ({\ dot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X})}}) dt = {\ frac {m } {2}} {\ dot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}} (t_ {2}) - {\ frac {m} {2}} {\ dot { \ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}} (t_ {1}) = {\ frac {1} {2}} m \ Delta \ mathbf {v ^ {2}},

где кинетическая энергия частицы определяется скалярной величиной,

K = m 2 X ˙ ⋅ X ˙ = 1 2 mv 2 {\ displaystyle K = {\ frac {m} {2}} { \ dot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}} = {\ frac {1} {2}} m {\ mathbf {v ^ {2}}}}

K = {\ frac {m} {2 }} {\ dot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}} = {\ frac {1} {2}} m {\ mathbf {v ^ {2}}}

Тангенциальная и нормальная составляющие

Полезно разделить векторы скорости и ускорения на тангенциальную и нормальную составляющие вдоль траектории Икс (t), такой, что

Икс ˙ = v T и X ¨ = v ˙ T + v 2 κ N, {\ displaystyle {\ dot {\ mathbf {X}}} = v \ mathbf { T} \ quad {\ t_dv {and}} \ quad {\ ddot {\ mathbf {X}}} = {\ dot {v}} \ mathbf {T} + v ^ {2} \ kappa \ mathbf {N},}

{\ displaystyle {\ dot {\ mathbf {X}}} = v \ mathbf {T} \ quad {\ t_dv {и}} \ q uad {\ ddot {\ mathbf {X}}} = {\ точка {v}} \ mathbf {T} + v ^ {2} \ kappa \ mathbf {N},}

где

v = | X ˙ | = X ˙ ⋅ X ˙. {\ displaystyle v = | {\ dot {\ mathbf {X}}} | = {\ sqrt {{\ dot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}}}}. }

v = | {\ dot {\ mathbf {X}}} | = {\ sqrt {{\ dot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}}}}.

Тогда скалярное произведение скорости с ускорением во втором законе Ньютона принимает вид

Δ K = m ∫ t 1 t 2 v ˙ vdt = m 2 ∫ t 1 t 2 ddtv 2 dt знак равно м 2 v 2 (T 2) - м 2 v 2 (t 1), {\ displaystyle \ Delta K = m \ int _ {t_ {1}} ^ {t_ {2}} {\ dot {v }} vdt = {\ frac {m} {2}} \ int _ {t_ {1}} ^ {t_ {2}} {\ frac {d} {dt}} v ^ {2} dt = {\ frac {m} {2}} v ^ {2} (t_ {2}) - {\ frac {m} {2}} v ^ {2} (t_ {1}),}

{\ displaystyle \ Delta K = m \ int _ {t_ {1}} ^ {t_ {2}} {\ dot {v}} vdt = {\ frac {m} {2}} \ int _ {t_ {1}} ^ {t_ {2}} {\ frac {d} {dt}} v ^ {2} dt = {\ frac {m} {2}} v ^ {2} (t_ { 2}) - {\ frac {m} {2}} v ^ {2} (t_ {1}),}

где кинетическая энергия частица определяется скалярной величиной,

K = m 2 v 2 = m 2 X ˙ ⋅ X ˙. {\ Displaystyle К = {\ гидроразрыва {м} {2}} v ^ {2} = {\ гидроразрыва {м} {2}} {\ точка {\ mathbf {X}}} \ cdot {\ точка {\ mathbf {X}}}.}

K = {\ frac {m} {2}} v ^ {2} = {\ frac {m} {2}} {\ dot {\ mathbf {X}}} \ cdot {\ dot {\ mathbf {X}}}.

Результатом является принцип работа – энергия для динамики частиц,

W = Δ K. {\ displaystyle W = \ Delta K. \!}

W = \ Delta K. \!

Этот вывод можно обобщить на произвольные системы твердого тела.

Движение по прямой (занос до остановки)

Рассмотрим случай, когда транспортное средство движется по прямой горизонтальной траектории под действием движущей силы и силы тяжести, которые в сумме равны Ф . Силы связи между транспортным средством и дорогой определяют R, и мы имеем

F + R = m X ¨. {\ displaystyle \ mathbf {F} + \ mathbf {R} = m {\ ddot {\ mathbf {X}}}.}

\ mathbf {F} + \ mathbf {R} = m {\ ddot {\ mathbf {X}}}.

Для удобства пусть траектория будет вдоль оси X, поэтому X = (d, 0) и скорость V = (v, 0), тогда R⋅ V= 0 и F⋅ V= F x v, где F x - это составляющая F вдоль оси X, поэтому

F xv = mv ˙ v. {\ displaystyle F_ {x} v = m {\ dot {v}} v.}

F_ {x} v = m {\ dot {v}} v.

Интегрирование обеих сторон дает

∫ t 1 t 2 F xvdt = m 2 v 2 (t 2) - m 2 v 2 (t 1). {\ displaystyle \ int _ {t_ {1}} ^ {t_ {2}} F_ {x} vdt = {\ frac {m} {2}} v ^ {2} (t_ {2}) - {\ frac {m} {2}} v ^ {2} (t_ {1}).}

\ int _ {t_ {1}} ^ {t_ {2}} F_ {x} vdt = {\ frac {m} {2}} v ^ {2} (t_ { 2}) - {\ frac {m} {2}} v ^ {2} (t_ {1}).

Если F x постоянно вдоль траектории, то интеграл скорости равен расстоянию, поэтому

F x (d (t 2) - d (t 1)) = m 2 v 2 (t 2) - m 2 v 2 (t 1). {\ displaystyle F_ {x} (d (t_ {2}) - d (t_ {1})) = {\ frac {m} {2}} v ^ {2} (t_ {2}) - {\ frac {m} {2}} v ^ {2} (t_ {1}).}

F_ {x} (d (t_ {2}) - d (t_ {1})) = {\ frac {m} {2}} v ^ {2} (t_ {2}) - {\ frac {m} {2}} v ^ {2} (t_ {1}).

В качестве примера рассмотрим занос автомобиля до остановки, где k - коэффициент трения, а W - вес автомобиля. Тогда сила вдоль траектории равна F x = −kW. Скорость v автомобиля можно определить по длине s t он скользит по принципу работа - энергия,

k W s = W 2 g v 2, или v = 2 k s g. {\ displaystyle kWs = {\ frac {W} {2g}} v ^ {2}, \ quad {\ t_dv {or}} \ quad v = {\ sqrt {2ksg}}.}

кВт = {\ frac {W} {2g}} v ^ {2}, \ quad {\ t_dv {или}} \ quad v = {\ sqrt {2ksg}}.

Обратите внимание, что эта формула использует тот факт, что масса автомобиля равна m = Вт / г.

Гравитационный гонщик Lotus тип 119Б на праздновании 60-летия Lotus.

Чемпионат по гравитационным гонкам в Кампос-Новос, Санта-Катарина, Бразилия, 8 сентября 2010 года. Рассмотрим случай транспортного средства, которое трогается с места и едет по горной дороге, принцип работы-энергии помогает вычислить минимальное расстояние, которое транспортное средство преодолевает, чтобы достичь скорости V, скажем, 60 миль в час (88 кадров в секунду). Сопротивление качению и сопротивление воздуха замедляет транспортное средство, поэтому фактическое расстояние будет больше, чем если бы этими силами пренебречь.

Пусть траектория транспортных средств следующего за дорогой, будет X (t). Сила, действующая на транспортное средство, представляет собой постоянную силу тяжести F = (0, 0, W), в то время как сила дороги на транспортное средство является сдерживающей силой R . Второй закон Ньютона дает

F + R = m X ¨. {\ displaystyle \ mathbf {F} + \ mathbf {R} = m {\ ddot {\ mathbf {X}}}.}

\ mathbf {F} + \ mathbf {R} = m {\ ddot {\ mathbf {X}}}.

скалярное произведение этого уравнения со скоростью, V = (v x, v y, v z), дает

W vz = m V ˙ V, {\ displaystyle Wv_ {z } = m {\ dot {V}} V,}

Wv_ {z} = m {\ dot {V}} V,

, где V - величина V . Силы связи между транспортным средством и дорогой исключаются из этого уравнения, поскольку R⋅ V= 0, что они не работают. Интегрируйте обе стороны, чтобы получить

∫ t 1 t 2 W v z d t = m 2 V 2 (t 2) - m 2 V 2 (t 1). {\ displaystyle \ int _ {t_ {1}} ^ {t_ {2}} Wv_ {z} dt = {\ frac {m} {2}} V ^ {2} (t_ {2}) - {\ frac {m} {2}} V ^ {2} (t_ {1}).}

\ int _ {t_ {1}} ^ {t_ {2}} Wv_ {z} dt = {\ frac {m} {2}} V ^ {2} (t_ {2}) - {\ frac {m} {2}} V ^ {2} (t_ {1}).

Весовая сила W постоянна вдоль траектории, а интеграл вертикальной скорости представляет собой вертикальное расстояние, поэтому

W Δ z = м 2 В 2. {\ displaystyle W \ Delta z = {\ frac {m} {2}} V ^ {2}.}

W \ Delta z = {\ frac {m} {2}} V ^ {2}.

Напомним, что V (t 1) = 0. Обратите внимание, что этот результат не зависит от формы дороги, по которой следует транспортное средство.

Чтобы определить расстояние вдоль предположим, что снижение составляет 6%, что соответствует крутой дороге. Это означает, что высота уменьшается на 6 футов на 100 футов пройденного пути - для таких малых углов функции sin и tan примерно равны. Следовательно, s в футах при уклоне 6% для достижения скорости V составляет не менее

s = Δ z 0,06 = 8,3 В 2 г, или s = 8,3 88 2 32,2 ≈ 2000 футов. {\ displaystyle s = {\ frac {\ Delta z} {0.06}} = 8.3 {\ frac {V ^ {2}} {g}}, \ quad {\ t_dv {или}} \ quad s = 8.3 {\ frac {88 ^ {2}} {32.2}} \ приблизительно 2000 {\ t_dv {ft}}.}

s = {\ frac {\ Delta z} {0.06}} = 8.3 {\ frac {V ^ {2}} {g}}, \ quad {\ t_dv {или}} \ quad s = 8.3 {\ frac {88 ^ {2}} {32.2}} \ приблизительно 2000 {\ t_dv {ft}}.

В формуле используется тот факт, что массовые транспортные средства W = мг.

Работа сил, действующих на твердое тело

Работа сил, действующих в различных точках на одно твердое тело, может быть вычислена на основе работы равнодействующей силы и крутящего момента. Чтобы убедиться, пусть силы F1, F2... Fnна точки X1, X2... Xnтвердого тела.

Траектории Xi, i = 1,..., решающим движением твердого тела. Это движение задается набором поворотов [A (t)] и траекторией d (t) контрольной точки в теле. Пусть координаты xii = 1,..., n определяют эти точки в системе отсчета M движущегося твердого тела, так что траектории, отслеживаемые в фиксированной системе F, задаются как

X i (t) = [A (t)] xi + d (t) i = 1,…, n. {\ displaystyle \ mathbf {X} _ {i} (t) = [A (t)] \ mathbf {x} _ {i} + \ mathbf {d} (t) \ quad i = 1, \ ldots, n.}

\ mathbf {X} _ {i} (t) = [A (t)] \ mathbf {x} _ {i} + \ mathbf {d} (t) \ quad i = 1, \ ldots, n.

Скорость точек Xiвдоль их траекторий равна

V i = ω → × (X i - d) + d ˙, {\ displaystyle \ mathbf {V} _ {i} = {\ vec { \ omega}} \ times (\ mathbf {X} _ {i} - \ mathbf {d}) + {\ dot {\ mathbf {d}}},}

\ mathbf {V} _ {i} = {\ vec {\ omega}} \ times (\ mathbf {X} _ {i} - \ mathbf {d}) + {\ dot {\ mathbf {d }}},

где ω - вектор угловой скорости, полученный из кососимметричной матрицы

[Ω] = A ˙ AT, {\ displaystyle [\ Omega] = {\ dot {A}} A ^ {\ mathrm {T}},}

[\ Omega] = {\ dot {A}} A ^ {\ mathrm {T}},

известная как матрица угловой скорости.

Небольшую работу сил при малых смещениях δ riможно определить, аппроксимируя смещение величиной δ r= vδt, поэтому

δ W = F 1 ⋅ V 1 δ t + F 2 ⋅ В 2 δ T +… + FN ⋅ В N δ T {\ Displaystyle \ delta W = \ mathbf {F} _ {1} \ cdot \ mathbf {V} _ {1} \ delta t + \ mathbf {F} _ {2} \ cdot \ mathbf {V} _ {2} \ delta t + \ ldots + \ mathbf {F} _ {n} \ cdot \ mathbf {V} _ {n} \ delta t}

\ delta W = \ mathbf {F} _ {1} \ cdot \ mathbf {V} _ {1} \ delta t + \ mathbf {F} _ {2} \ cdot \ mathbf {V} _ {2} \ delta t + \ ldots + \ mathbf {F} _ {n} \ c точка \ mathbf {V} _ {n} \ delta t

или

δ W Знак равно ∑ я знак равно 1 NF я ⋅ (ω → × (X - d) + d ˙) δ т. {\ displaystyle \ delta W = \ sum _ {i = 1} ^ {n} \ mathbf {F} _ {i} \ cdot ({\ vec {\ omega}} \ times (\ mathbf {X} _ {i } - \ mathbf {d}) + {\ dot {\ mathbf {d}}}) \ delta t.}

\ delta W = \ sum _ {i = 1} ^ {n} \ mathbf {F} _ {i} \ cdot ( {\ vec {\ omega}} \ times (\ mathbf {X} _ {i} - \ mathbf {d}) + {\ dot {\ mathbf {d}}}) \ дельта т.

Эту формулу можно переписать, чтобы получить

δ W = (∑ i = 1 n F i) ⋅ d ˙ δ T + (∑ я знак равно 1 N (Икс я - d) × F я) ⋅ ω → δ T = (F ⋅ d ˙ + T ⋅ ω →) δ T, {\ Displaystyle \ delta W = \ left (\ sum _ {i = 1} ^ {n} \ mathbf {F} _ {i} \ right) \ cdot {\ dot {\ mathbf {d}}} \ delta t + \ left (\ sum _ {i = 1} ^ {n} \ left (\ mathbf {X} _ {i} - \ mathbf {d} \ right) \ times \ mathbf {F} _ {i} \ right) \ cdot {\ vec {\ omega}} \ delta t = \ left (\ mathbf {F} \ cdot {\ dot {\ mathbf {d}}} + \ mathbf {T} \ cdot {\ vec {\ omega}} \ right) \ Т} Дельта

{\ displaystyle \ delta W = \ left (\ sum _ {i = 1} ^ {n} \ mathbf {F} _ {i} \ right) \ cdot {\ dot {\ mathbf {d }}} \ delta t + \ left (\ sum _ {i = 1} ^ {n} \ left (\ mathbf {X} _ {i} - \ mathbf {d} \ right) \ times \ mathbf {F} _ {i} \ right) \ cdot {\ vec {\ omega}} \ delta t = \ left (\ mathbf {F} \ cdot {\ dot {\ mathbf {d}}} + \ mathbf {T} \ cdot {\ vec {\ omega}} \ right) \ delta t,}

где F и Т являются результирующая сила и крутящий момент применяется в опорной точке д подвижной рамы М в твердом теле.

Ссылки

Библиография

Serway, Raymond A.; Джуэтт, Джон В. (2004). Физика для ученых и инженеров (6-е изд.). Брукс / Коул. ISBN 0-534-40842-7.
Типлер, Пол (1991). Физика для ученых и инженеров: механика (3-е изд. Расширенная версия). В. Х. Фриман. ISBN 0-87901-432-6.

Внешние ссылки

Принцип работы - энергия