 A луч преломляемого света в пластиковом блоке
A луч преломляемого света в пластиковом блоке В оптике, показатель преломления (также известный как показатель преломления или показатель преломления ) материала - это безразмерное число , которое имеет качество быстро свет проходит через материал. Он определяется как

, где c - скорость света в вакууме, а v - света фазовая скорость в среде. Например, показатель преломления воды равен 1,333, что означает, что означает свет в вакууме в 1,333 раза быстрее, чем в воде. Увеличение показателя преломления соответствует уменьшению скорости света в материале.
 Преломление светового луча
Преломление светового луча Показатель преломления определяет, насколько световой путь искривляется или преломляется при входе в материал. Это описывается законом Снеллиуса преломления, n 1 sinθ 1 = n 2 sinθ 2, где θ 1 и θ 2 - углы падения и преломления, соответственно, луча, пересекающего границу раздела двух сред с показателями преломления n 1 и n 2. Показатели преломления также определяют количество света, которое отражается при достижении границы раздела, а также критический угол для полного внутреннего отражения, их интенсивность (уравнения Френеля ) и Брюстера.
Показатель преломления можно рассматривать как коэффициент, на который скорость и длина волны уменьшаются по сравнению с их значениями вакуума: скорость света в среде v = c / n, и аналогично длина волны в этой скорости среде λ = λ 0 / n, где λ 0 - длина волны этого света в вакууме. Это, что означает, что показатель имеет показатель преломления, равный 1, и что частота (f = v / λ) волны не зависит от показателя преломления. В результате воспринимаемого человеческим глазом цвет преломленного света, который зависит от частоты, не зависит от преломления или показателя преломления среды.
Показатель преломления зависит от длины волны, поэтому белый свет преломлении расщепляется на составляющие цвета. Это называется дисперсией. Это можно наблюдать в призмах и радугах, а также как хроматическая аберрация в линзах. Распространение света в поглощающих материаловх можно описать с помощью комплексного -значного показателя преломления. Затем мнимая часть обрабатывает затухание , а действующая часть учитывает преломление. Для огромного показателя преломления изменяется длина волны на несколько процентов. Использование единственного значения, обычно измеряемого при 633 нм.
Концепция показателя преломления используется в пределах всего электромагнитного излучения, от рентгеновских лучей до радиоволн. Его также можно применить к явлениям волны, таким как звук. В этом случае используется скорость звука, и необходимо выбрать эталонную среду, отличную от вакуума.
Показатель преломления n оптической среды определяется как отношение скорости света в вакууме c = 299792458 м / с и фазовой скорости v света в среде,

Фазовая скорость - это скорость, с которой движутся гребни или фаза волны волны, которая может отличаться от групповой скорости , скорости, с которой движется импульс света или огибающая волны.
Приведенное выше определение иногда называют абсолютным показателем преломления или абсолютным показателем преломления, чтобы отличить его от определений, в которых используется абсолютная скорость света в других эталонных средах, чем используется вакуум. Исторически воздух при стандартизированном давлении и температуре был обычным методом сравнения.
 Томас Янг ввел термин «индекс преломления».
Томас Янг ввел термин «индекс преломления». Томас Янг предположительно был человеком, который первым использовал и изобрел название «индекс преломления» в 1807. В то же время он изменил это значение преломляющей силы на одно число вместо традиционного отношения двух чисел. У этого соотношения был недостаток, заключающийся в различии внешнего вида. Ньютон, назвавший это «пропорцией синусов падения и преломления», записал это как отношение двух чисел, например «529 к 396» (или «почти 4 к 3»; для воды). Хоксби, назвавший это «коэффициентом преломления», записал его как отношение с фиксированным числителем, например «10000 к 7451,9» (для мочи). Хаттон записал это как отношение с фиксированным знаменателем, например 1,3358 к 1 (вода).
Янг не использовал символ для показателя преломления в 1807 году. В последующие годы начали использовать другие символы: n, m, и µ. Символ n постепенно возобладал.
 Алмазы имеют очень высокий показатель преломления 2,417. У него самый высокий показатель преломления среди всех прозрачных материалов.
Алмазы имеют очень высокий показатель преломления 2,417. У него самый высокий показатель преломления среди всех прозрачных материалов. Показатель преломления также зависит от длины волны света, как это определяется уравнением Коши:
Наиболее общая форма уравнения Коши -

где n - показатель преломления, λ - длина волны, A, B, C и т. Д. - коэффициенты, которые могут быть использованы для материалов с помощью подгонка уравнения к измеренным показателям преломления на известных длинах волн. Коэффициенты обычно указываются для λ как длина волны вакуума в микрометрах.
Обычно достаточно использовать двухчленную форму уравнения:

где коэффициенты A и адаптированные B специально для этой формы уравнения.
| Материал | n |
|---|---|
| Вакуум | 1 |
| Газы при 0 ° C и 1 атм. | |
| Воздух | 1.000293 |
| Гелий | 1.000036 |
| Водород | 1.000132 |
| Двуокись углерода | 1.00045 |
| Жидкости при 20 ° C | |
| Вода | 1,333 |
| Этанол | 1,36 |
| Оливковое масло | 1,47 |
| Твердые вещества | |
| Лед | 1,31 |
| Плавленый кварц (кварц) | 1,46 |
| ПММА (акрил, оргстекло, люцит, плексиглас) | 1,49 |
| Оконное стекло | 1,52 |
| Поликарбонат (Lexan ™) | 1,58 |
| Флинт-стекло (типовое) | 1,69 |
| Сапфир | 1,77 |
| Цирконий | 2,15 |
| Алмаз | 2,42 |
| Муассанит | 2,65 |
Для видимого света Большинство прозрачных носителей имеют показатели преломления от 1 до 2. Несколько примеров приведены в таблице рядом. Эти значения измеряются на желтом дублете D-линии натрия длиной волны 589 нанометров, как это обычно делается. Газы при атмосферном давлении имеют показатель преломления, близкий к 1, из-за их низкой плотности. Почти все твердые тела и жидкости имеют показатель преломления выше 1,3, за исключением аэрогеля. Аэрогель представляет собой твердое тело очень низкой плотности, которое может печатать с показателем преломления в диапазоне от 1 002 1,265. Муассанит находится в конце диапазона с показателем преломления до 2,65. Большинство пластиков имеют некоторые показатели преломления в диапазоне от 1,3 до 1,7, но имеют высокие показатели преломления имеют значения до 1,76.
Для инфракрасного света показатели преломления могут быть значительно выше. Германий прозрачен в диапазоне волн от 2 до 14 мкм и имеет показатель преломления около 4. Недавно был обнаружен тип новых материалов, называемые «топологические изоляторы», которые имеют высокий показатель преломления до 6 в ближнем и среднем инфракрасном диапазоне частот. Более того, топологические изоляторы прозрачны, когда они имеют наноразмерную толщину. Эти свойства важны для приложений в инфракрасной оптике.
Согласно теории относительности, никакая информация не может перемещаться быстрее скорости света в вакууме, но это не означает, что показатель преломления не может быть меньше 1. Показатель преломления измеряет фазовую скорость света, которая не несет информации . Фазовая скорость - это скорость, с которой движутся гребни волны, и она может быть быстрее света в вакууме и таким образом, дать показатель преломления ниже 1. Это может происходить вблизи резонансных частот , для поглощающих сред, в плазме и для рентгеновских лучей. В рентгеновском режиме преломления ниже, но очень близки к 1 (исключения, близкие к некоторым резонансным частотам). Например, вода имеет показатель преломления 0,99999974 = 1 - 2,6 × 10 для рентгеновского излучения с энергией фотонов 30 кэВ (длина волны 0,04).
Пример плазма с показателем преломления меньше единицы - это ионосфера Земли. Среда преломления ионосферы (плазма ) меньше показателя электромагнитные волны, распространяющиеся через плазму, отклоняются «от нормали» (см. Геометрическая оптика ), что позволяет Радиоволна преломляется обратно на Землю, что обеспечивает возможность радиосвязи на большие расстояния. См. Распространение радиоволн и Skywave.
 A Разъемный кольцевой резонатор, устроенный так, чтобы произвести отрицательный показатель преломления для микроволн
A Разъемный кольцевой резонатор, устроенный так, чтобы произвести отрицательный показатель преломления для микроволн Недавние исследования также применил нет материала с отрицательным показателем преломления, которое может иметь место, если диэлектрическая проницаемость и проницаемость имеют одновременно отрицательные значения. Этого можно достичь с помощью периодически создаваемых метаматериалов. Получающееся в результате отрицательное преломление (т. Е. Обращение закона Снеллиуса ) предлагает возможность суперлинзы и других новых явлений, которые будут активно развиваться с помощью метаматериалы. Три концепции - среда Веселаго с отрицательным показателем преломления, суперленза Пендри и неотражающий кристалл Ефимова являются основами теории метаматериалов с интересными свойствами отражения.
 В оптической минералогии, шлифы использованы для изучения горных пород. Метод основан на различных показателях преломления минералов.
В оптической минералогии, шлифы использованы для изучения горных пород. Метод основан на различных показателях преломления минералов.В атомном масштабе фазовая скорость электромагнитной волны в материале замедлена, поскольку электрическое поле создаущение в зарядах каждый атом (в первую очередь электроны ) пропорционален электрической восприимчивости среды. (Точно так же магнитное поле возбущение, пропорциональное магнитной восприимчивости.) Когда электромагнитные поля колеблются в достаточно, заряды в материале будут "качаться" взад и вперед. на той же частот. Таким образом, заряды излучают электромагнитную волну той же частоты, но обычно с фазовой задержкой , так как заряды могут двигаться не в фазе с движущей их силой (см. гармонический осциллятор с синусоидальным приводом ). Световая волна, распространяющаяся в среде, представляет собой макроскопическую суперпозицию (сумма) всех такихов в материал: исходная волна плюс волны, излучаемые всеми движущимися зарядами. Эта волна обычно представляет собой волну с той же длиной волны, чем исходная, что приводит к замедлению фазовой скорости волны. Большая часть колеблющихся зарядов материала будет изменяющая волну, изменяя ее скорость. Однако некоторая чистая энергия будет излучаться в других направлениях или даже на других частотах (см. рассеяние ).
В зависимости от относительной фазы исходной движущейся волны и волн, излучаемых движением заряда, существует несколько возможностей:
Для распространения информации на частотах видимого света находится где-то между 90 ° и 180 °, что соответствует комбинации преломления и фаз..
 Свет разных имеет несколько разных показателей преломления в воде и, следовательно, проявляется в разных положениях в радуге.
Свет разных имеет несколько разных показателей преломления в воде и, следовательно, проявляется в разных положениях в радуге.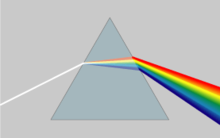 В призме из-за дисперсии разные цвета преломляются под разными углами, расщепляя белый свет на радугу цветов.
В призме из-за дисперсии разные цвета преломляются под разными углами, расщепляя белый свет на радугу цветов. 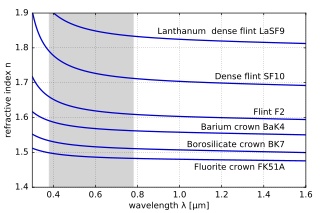 Изменение показателя преломления в зависимости от длины волны для различных очков. Заштрихованная зона диапазон диапазона видимого света.
Изменение показателя преломления в зависимости от длины волны для различных очков. Заштрихованная зона диапазон диапазона видимого света. Показатель преломления материала изменяется в зависимости от длины (и частоты ) света. Это называется дисперсией и приводит к тому, что призмы и радуги разделяют белый свет на составляющие его спектральные цвета. Показатель преломления зависит от длины волны, изменяется и угол преломления при переходе света от одного материала к другому. Дисперсия также приводит к тому, что фокусное расстояние линз зависит от длины волны. Это тип хроматической аберрации, которую часто необходимо корректировать в системах визуализации. В области распространения, где материал не поглощает свет, показатель преломления движения увеличивается с увеличением длины волны и, следовательно, увеличивается скорость распространения частоты. Это называется «нормальной дисперсией», в отличие от «аномальной дисперсии». Для видимого нормальная дисперсия означает, что показатель преломления синего света выше, чем красного.
Для оптики в видимом диапазоне количества дисперсии материала линзы часто определяется число с помощью Аббе :

Для более точного описания Для показателя показателя преломления от длины волны можно использовать уравнение Селлмейера. Это эмпирическая формула, которая хорошо подходит для описания дисперсии. В таблицах вместо показателя преломления часто указываются коэффициенты Селлмейера.
Из-за дисперсии обычно важно указать длину волны света в вакууме, для которой измеряется показатель преломления. Как правило, проводят различные спектральные линии х , излучения ; например, n D обычно обозначает показатель преломления на линии Фраунгофера "D", в центре двойной эмиссии желтого натрия на 589,29 нм. длина волны.
Когда свет проходит через среду, некоторая ее часть всегда будет ослаблена. Это может быть удобно учесть, задав комплексный показатель преломления

Здесь действительная часть n является показателем преломления и указывает фазовую скорость, а мнимая часть κ называется коэффициент ослабления - хотя κ может также относиться к массовому коэффициенту ослабления - и указывает величину ослабления, когда электромагнитная волна распространяется через материал.
Это κ соответствует затуханию, можно увидеть, вставив этот показатель преломления в выражение для электрического поля плоской электромагнитной волны, распространяющейся в z-направлении. Это можно сделать, связав комплексное волновое число k с комплексным показателем преломления от n до k = 2π n/λ0, с λ 0 - длина волны вакуума; это можно вставить в выражение плоской волны как
![\mathbf {E} (z,t)=\operatorname {Re} \!\left[\mathbf {E} _{0}e^{i({\underline {k}}z-\omega t)}\right]=\operatorname {Re} \!\left[\mathbf {E} _{0}e^{i(2\pi (n+i\kappa)z/\lambda _{0}-\omega t)}\right]=e^{-2\pi \kappa z/\lambda _{0}}\operatorname {Re} \!\left[\mathbf {E} _{0}e^{i(kz-\omega t)}\right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/430eaede5060d08b487bb940c99144d125a0fa0f)
Здесь мы видим, что κ дает экспоненциальное затухание, как и ожидалось из закона Бера – Ламберта. Поскольку напряженность пропорциональна квадрату электрического поля, она будет зависеть от глубины в материале как exp (−4πκz / λ 0), а коэффициент затухания станет α = 4πκ / λ 0. Это также относится к глубине проникновения, расстоянию, после которого интенсивность уменьшается до 1 / e, δ p = 1 / α = λ 0 / (4πκ).
И n, и κ зависят от частоты. В большинстве случаев κ>0 (свет поглощается) или κ = 0 (свет распространяется бесконечно без потерь). Вв особых ситуациях, особенно в среде усиления из лазеров, также возможно, что κ < 0, corresponding to an amplification of the light.
В альтернативном соглашении используется n = n - iκ вместо n = n + iκ, но где κ>0 по-прежнему соответствует потерям. Следовательно, эти два соглашения несовместимы, и их не следует путать. Разница с определением синусоидальной зависимости от времени как Re [exp (−iωt)] по сравнению с Re [exp (+ iωt)]. См. Математическое описание непрозрачности..
Диэлектрические проводимости и ненулевая способность по постоянному току в материалах вызывает поглощение. Хорошие диэлектрические материалы, такие как стекло, очень низкую проводимость по постоянному току, а на низких частотах диэлектрические потери также незначительны, что приводит к почти отсутствию поглощения. Однако на более высоких частотах (например, в видимом свете) диэлектрические потери могут значительно увеличить поглощение, уменьшая ность материала до этих частот.
Действующая и мнимая части комплексного показателя преломления связаны посредством новых Крамерса - Кронига. В 1986 году А. Форухи и И. Блумер вывели уравнение , описывающее κ функцию энергии фотона E, применимое к аморфным материалам. Затем выведите уравнение для n как функции E, чтобы вывести уравнение для ситуации Крамерса - Кронига. Тот же самый формализм был применен к кристаллическим материалам Форухи и Блумером в 1988 году.
Показатели преломления и экстинкции n и κ не могут быть измерены напрямую. Они должны определяться косвенно из измеряемых величин, которые зависят от них, таких как коэффициент отражения, R или коэффициент пропускания, T, или эллипсометрические параметры, ψ и δ. Определение n и κ из таких измеренных величин потребинует разработки теоретического выражения для R или T, или ψ и δ в терминах действующей физической модели для n и κ. Подгоняя теоретическую модель к измеренным R или T, или ψ и δ с помощью регрессионного анализа, можно вывести n и κ.
Для рентгеновского и крайнего ультрафиолетового излучения комплексный показатель преломления незначительно отклоняется от единицы и обычно имеет действительную часть меньше 1. Поэтому обычно записывается как n = 1 - δ + iβ (или n = 1 - δ - iβ с альтернативным соглашением, указанным выше). Значительно выше дельта частоты атомного резонанса может быть задана как

где 





с 

 Цвета мыльного пузыря ограниченным оптическим образом . длина пути через тонкую мыльную пленку в определении, называемом тонкопленочной интерференцией.
Цвета мыльного пузыря ограниченным оптическим образом . длина пути через тонкую мыльную пленку в определении, называемом тонкопленочной интерференцией.Длина оптического пути (OPL) - это геометрической длины d пути света, проходящего через систему, и показатель преломления среды, в которой распространяется,

Это важное понятие в оптике, поскольку оно определяет фазу света и управляет помехами и дифракция света при его распространении. Согласно принципу Ферма, световые лучи можно охарактеризовать как те кривые, которые оптимизируют длину оптического пути.
 Refraction света в интерфейсе между двумя средами с разными показателями преломления, с n 2>n1. Так фазовая скорость ниже во второй среде (v 2< v1), угол преломления θ 2 меньше угла падения θ 1 ; что есть лучшими в среде с более высоким показателем преломления ближе к нормали.
Refraction света в интерфейсе между двумя средами с разными показателями преломления, с n 2>n1. Так фазовая скорость ниже во второй среде (v 2< v1), угол преломления θ 2 меньше угла падения θ 1 ; что есть лучшими в среде с более высоким показателем преломления ближе к нормали. Когда свет перемещается из одной среды в другую, он меняет направление, то есть преломляется. Если он перемещается из среды с показателем преломления n 1 в среду с показателем преломления n 2, с углом падения на нормаль поверхности от θ 1, угол преломления θ 2 может быть вычислен по закону Снеллиуса :

Когда свет попадает в материал с более высоким преломлением, преломление будет меньше, чем угол падения, и свет будет преломляться по нормали к поверхности. Чем выше показатель преломления, тем ближе к нормальному направлению распространяется свет. При переходе в среду с более низким показателем преломления свет вместо этого будет преломляться от нормыли к поверхности.
 Полное внутреннее отражение можно увидеть на границе воздух-вода.
Полное внутреннее отражение можно увидеть на границе воздух-вода. Если нет угла θ 2, удовлетворяющего закону Снеллиуса, т. Е.

свет не может будут передаваться и вместо этого будут подвергаться полному внутреннему отражению. Это происходит только при переходе к менее оптически плотному материалу, чтобы получить полное внутреннее отражение, углы падения θ 1 должен быть больше критического угла

Помимо прошедшего света есть также отраженная часть. а количество отраженного света определяется коэффициентом отражения поверхности. ажения может быть рассчитан из показателя преломления и угла падения с помощью соотношений Френеля, которые для нормального падения уменьшаются до

Для обычного стекла в воздухе n 1 = 1 и n 2 = 1,5, и, таким образом, около 4% падающей мощности отражается. При других углах падения коэффициент отражения также будет зависеть от поляризации входящего света. Под определенным углом, называемым углом Брюстера, p-поляризованный свет (свет с электрическим полем в плоскости падения ) будет полностью проходить. Угол Брюстера может быть вычислен из двух показателей преломления границы раздела как

 оптическая сила линзы увеличенного стекла Система и показателем преломления линзы.
оптическая сила линзы увеличенного стекла Система и показателем преломления линзы. Фокусное расстояние линзы определяет его показателем преломления n и радиусами кривизны R1и R 2 его поверхностей. Сила тонкой линзы в окружении по формуле производитель линз :

где f - фокусное расстояние объектива.
Разрешение хорошего оптического микроскопа в основном определяется числовой апертурой (NA) его линза объектива. Числовая апертура, в свою очередь, определяется показателем преломления среды, заполняющим пространство между образцом и линзой, и половинным углом сбора света θ в соответствии с

По этой причине масляная иммерсия обычно используется для получения высокого разрешения в микроскопии. В этом методе объектив погружается в каплю иммерсионного масла с высоким показателем преломления на исследуемом образце.
Показатель преломления электромагнитного излучения равен

где ε r - относительная диэлектрическая проницаемость материала, а μ r - его относительная проницаемость. Показатель преломления используется для оптики в уравнениях Френеля и законе Снеллиуса ; в то время как относительная диэлектрическая проницаемость и магнитная проницаемость используются в уравнениях Максвелла и в электронике. Большинство встречающихся в природе немагнитны на оптических частотах, то есть μ r очень близко к 1, поэтому n приблизительно равно √ε r. В этом конкретном случае комплексная относительная диэлектрическая проницаемость εr, с действующей и мнимой частями ε r и ̃ r, и комплексный показатель преломления n, с действующими и мнимые части n и κ (последний называется «коэффициентом ослабления») подчиняются подчинению

и их компоненты связаны с помощью:


и:


где 
Волновое сопротивление плоской электромагнитной волны в непроводящей среде имеет вид

где 
в немагнитных средах с 


Таким образом, показатель преломления в немагнитной среде - это отношение волнового сопротивления вакуума к волновому сопротивлению среды.
Отражательная способность 

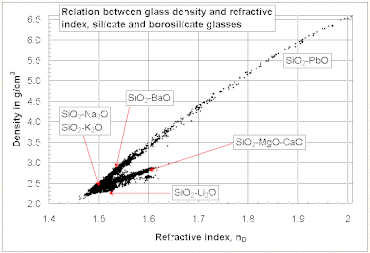 Отношение между преломляющими индекс и плотность силикатного и боросиликатного стекла
Отношение между преломляющими индекс и плотность силикатного и боросиликатного стекла Как правило, показатель преломления стекла увеличивается с его плотностью . Однако не существует общей линейной зависимости между показателем преломления и плотностью для всех силикатных и боросиликатных стекол. Относительно высокий показатель преломления и низкая плотность могут быть получены для стекол, содержащих оксиды легких металлов, таких как Li2O и MgO, тогда как противоположная тенденция наблюдается для стекол, содержащих PbO и BaO, как показано на диаграмме справа.
Многие масла (например, оливковое масло ) и этанол являются примерами жидкостей, которые обладают большей преломляющей способностью, но менее плотной, чем вода, вопреки общей корреляции между плотность и показатель преломления.
Для воздуха n - 1 пропорционально плотности газа до тех пор, пока химический состав не изменяется. Это означает, что он также пропорционален давлению и обратно пропорционален температуре для идеальных газов.
Иногда определяется «показатель преломления групповой скорости», обычно называемый групповым индексом. :

где v g - это групповая скорость. Это значение не следует путать с n, которое всегда определяется относительно фазовой скорости . Когда дисперсия мала, групповая скорость может быть связана с фазовой скоростью соотношением

где λ - длина волны в среде. В th