Пространство вещественных координат

редактировать

Пространство, образованное кортежами из n действительных чисел

Декартова структура произведения R на Декартова плоскость из упорядоченных пар (x, y). Синие линии обозначают оси координат, горизонтальные зеленые линии - это целое число y, вертикальные голубые линии - это целое число x, коричнево-оранжевые линии показывают полуцелое число x или y, пурпурный и его оттенок кратны одной десятой (лучше всего видно при увеличении)

В математике, реальное координатное пространство с размерностью n, записанное R() или ℝ, представляет собой координатное пространство над вещественными числами. Это означает, что это набор n-кортежей вещественных чисел (последовательностей n действительных чисел). При покомпонентном сложении и скалярном умножении это вещественное векторное пространство.

Как правило, декартовы координаты элементов евклидова пространства образуют реальные координатные пространства. Это объясняет название координатного пространства и тот факт, что термины геометрические часто используются при работе с координатными пространствами. Например, R представляет собой плоскость .

Координатные пространства широко используются в геометрии и физике, поскольку их элементы позволяют размещать точки в евклидовых пространствах., и вычисления с ними.

Содержание

1 Определение и структуры
2 Область определения функции нескольких переменных
3 Векторное пространство
- 3.1 Матричная запись
- 3.2 Стандартный базис
4 Геометрические свойства и использование
- 4.1 Ориентация
- 4.2 Аффинное пространство
- 4.3 Выпуклость
- 4.4 Евклидово пространство
- 4.5 В алгебраической и дифференциальной геометрии
- 4.6 Другие проявления
- 4.7 Многогранники в R
5 Топологические свойства
6 Примеры
- 6,1 n ≤ 1
- 6,2 n = 2
- 6,3 n = 3
- 6,4 n = 4
7 Нормы на R
8 См. Также
9 Сноски
10 Ссылки

Определение и структуры

Для любого натурального числа n набор Rсостоит из всех n- кортежей из действительные числа (R). Его называют «n-мерным реальным пространством» или «реальным n-пространством».

Элемент R, таким образом, является кортежем из n и записывается

(x 1, x 2,…, xn) {\ displaystyle (x_ {1}, x_ {2}, \ ldots, x_ {n})}

(x_1, x_2, \ldots, x_n)

, где каждый x i является действительным числом. Итак, в исчислении с несколькими переменными область функции нескольких действительных переменных и область значений реальной векторнозначной функции равны подмножества из R для некоторого n.

Реальное n-пространство имеет несколько дополнительных свойств, а именно:

С покомпонентным сложением и скалярным умножением, это реальное векторное пространство. Каждое n-мерное реальное векторное пространство изоморфно ему.
С скалярным произведением (сумма посланцевого произведения компонентов) это внутреннее пространство продукта. Каждое n-мерное реальное внутреннее пространство продукта изоморфно ему.
Как и любое внутреннее пространство продукта, это топологическое пространство и топологическое векторное пространство.
. евклидово пространство и реальное аффинное пространство, и каждое евклидово или аффинное пространство изоморфно ему.
Это аналитическое многообразие, и может рассматриваться как прототип всех многообразий, поскольку, по определению, многообразие вблизи каждой точки изоморфно открытому подмножеству из R.
Это алгебраическое разнообразие, и каждое реальное алгебраическое многообразие является подмножеством R.

. Эти свойства и структуры R делают его фундаментальным почти во всех областях математики и областях их применения., например, статистика, теория вероятностей и многие части физики.

Область определения функции нескольких переменных

Любая функция f (x 1, x 2,…, x n) из n вещественных переменных можно рассматривать как функция на R (то есть с R в качестве домена ). Использование реального n-пространства вместо нескольких переменных, рассматриваемых по отдельности, может упростить обозначения и предложить разумные определения. Рассмотрим для n = 2 функцию композиция следующего вида:

F (t) = f (g 1 (t), g 2 (t)), {\ displaystyle F (t) = f (g_ {1} (t), g_ {2} (t)),}

F (t) = f (g_ {1} (t), g_ {2 } (t)),

где функции g 1 и g 2 являются непрерывными. Если

∀x1∈ R: f (x 1, ·) непрерывно (на x 2)

∀x2∈ R: f (·, x 2) непрерывно (на x 1)

, то F не обязательно непрерывна. Непрерывность является более сильным условием: непрерывность f в естественной топологии R (обсуждается ниже), также называемой многомерной непрерывностью, которая достаточна для непрерывности композиции F.

Векторное пространство

Координатное пространство R образует n-мерное векторное пространство над полем вещественного числа с добавлением структуры линейности, и часто все еще обозначается R . Операции с R как с векторным пространством обычно определяются

Икс + Y знак равно (Икс 1 + Y 1, Икс 2 + Y 2,…, xn + yn) {\ displaystyle \ mathbf {x} + \ mathbf {y} = (x_ {1} + y_ {1}, x_ {2} + y_ {2}, \ ldots, x_ {n} + y_ {n})}

{\mathbf x}+{\mathbf y}=(x_{1}+y_{1},x_{2}+y_{2},\ldots,x_{n}+y_{n})

α x = (α x 1, α x 2,…, α xn). {\ Displaystyle \ alpha \ mathbf {x} = (\ alpha x_ {1}, \ alpha x_ {2}, \ ldots, \ alpha x_ {n}).}

\alpha {\mathbf x}=(\alpha x_{1},\alpha x_{2},\ldots,\alpha x_{n}).

Нулевой вектор задается как

0 = (0, 0,…, 0) {\ displaystyle \ mathbf {0} = (0,0, \ ldots, 0)}

{ \ mathbf 0} = (0,0, \ ldots, 0)

, а аддитивный обратный вектора x равен задается как

- x = (- x 1, - x 2,…, - xn). {\ displaystyle - \ mathbf {x} = (- x_ {1}, - x_ {2}, \ ldots, -x_ {n}).}

- {\ mathbf x} = (- x_ {1}, - x_ {2}, \ ldots, -x_ {n}).

Эта структура важна, потому что любое n-мерное реальное векторное пространство изоморфен векторному пространству R.

Матричная нотация

В стандартной нотации matrix каждый элемент R обычно записывается как вектор-столбец

Икс = [Икс 1 Икс 2 ⋮ Xn] {\ Displaystyle \ mathbf {x} = {\ begin {bmatrix} x_ {1} \\ x_ {2} \\\ vdots \\ x_ {n} \ end {bmatrix} }}

{\ mathbf x} = {\ begin {bmatrix} x_ {1} \\ x_ {2} \\\ vdots \\ x_ {n} \ end {bmatrix}}

и иногда как вектор-строку :

x = [x 1 x 2… xn]. {\ displaystyle \ mathbf {x} = {\ begin {bmatrix} x_ {1} x_ {2} \ dots x_ {n} \ end {bmatrix}}.}

{\mathbf x}={\begin{bmatrix}x_{1}x_{2}\dots x_{n}\end{ bmatrix}}.

Координатное пространство R может затем интерпретироваться как пространство всех n × 1 векторов-столбцов или всех 1 × n векторов-строк с помощью обычных матричных операций сложения и скалярного умножения.

Линейные преобразования из R в R затем могут быть записаны как матрицы m × n, которые действуют на элементы R через left умножение (когда элементы R являются векторами-столбцами) и на элементы R посредством правого умножения (когда они являются векторами-строками). Формула умножения слева, особый случай умножения матриц , выглядит следующим образом:

(A x) k = ∑ l = 1 n A klxl {\ displaystyle (A {\ mathbf {x}}) _ {k} = \ sum \ limits _ {l = 1} ^ {n} A_ {kl} x_ {l}}

(A{{\mathbf x}})_{k}=\sum \limits _{{l=1}} ^{n}A_{{kl}}x_{l}

Любое линейное преобразование является непрерывной функцией (см. ниже). Кроме того, матрица определяет открытую карту от R до R тогда и только тогда, когда ранг матрицы равен m.

Стандартный базис

Координатное пространство R имеет стандартный базис:

e 1 = (1, 0,…, 0) e 2 = (0, 1,…, 0) ⋮ en = (0, 0,…, 1) {\ displaystyle {\ begin {align} \ mathbf {e} _ {1} = (1,0, \ ldots, 0) \ \\ mathbf {e} _ {2} = (0,1, \ ldots, 0) \\ {} \ \ vdots \\\ mathbf {e} _ {n} = (0,0, \ ldots, 1) \ end {align}}}

{\begin{aligned}{\mathbf e}_{1}=(1,0, \ldots,0)\\{\mathbf e}_{2}=(0,1,\ldots,0)\\{}\ \vdots \\{\mathbf e}_{n}=(0,0,\ldots,1)\end{aligned}}

Чтобы увидеть, что это базис, обратите внимание, что произвольный вектор в R может быть записан однозначно в виде

x = ∑ i = 1 nxiei. {\ displaystyle \ mathbf {x} = \ sum _ {i = 1} ^ {n} x_ {i} \ mathbf {e} _ {i}.}

{\mathbf x}=\sum _{{i=1}}^{n}x_{i}{\mathbf {e}}_{i}.

Геометрические свойства и использует

ориентацию

Тот факт, что вещественные числа, в отличие от многих других полей, составляют упорядоченное поле, дает структуру ориентации на R . Любая полноранговая линейная карта R на себя либо сохраняет, либо меняет ориентацию пространства в зависимости от знака детерминанта его матрица. Если один переставляет координаты (или, другими словами, элементы базиса), результирующая ориентация будет зависеть от четности перестановки.

диффеоморфизмов R или в нем, благодаря своей способности избегать нулевого якобиана, также классифицируются на сохраняющие ориентацию и меняющие ориентацию. Это имеет важные последствия для теории дифференциальных форм, приложения которой включают электродинамику.

Еще одним проявлением этой структуры является то, что точечное отражение в R имеет разные свойства в зависимости от четности n. Для четного n он сохраняет ориентацию, а для нечетного n - наоборот (см. Также неправильное вращение ).

Аффинное пространство

R, понимаемое как аффинное пространство, является тем же пространством, где R как векторное пространство действует посредством переводов. И наоборот, вектор следует понимать как «разность между двумя точками», обычно иллюстрируемую направленным отрезком линии, соединяющим две точки. Различие говорит о том, что не существует канонического выбора места origin в аффинном n-пространстве, потому что он может быть переведен куда угодно.

Выпуклость

n-симплекс (см. ниже) - это стандартное выпуклое множество, которое отображается на каждый многогранник и является пересечением стандартной (n + 1) аффинной гиперплоскости. (стандартное аффинное пространство) и стандартный (n + 1) ортант (стандартный конус).

В реальном векторном пространстве, таком как R, можно определить выпуклый конус, который содержит все неотрицательные линейные комбинации своих векторов. Соответствующим понятием в аффинном пространстве является выпуклое множество, которое допускает только выпуклые комбинации (неотрицательные линейные комбинации, сумма которых равна 1).

На языке универсальной алгебры векторное пространство - это алгебра над универсальным векторным пространством R конечных последовательностей коэффициентов, соответствующих конечным суммам векторов, в то время как аффинное пространство - это алгебра над универсальной аффинной гиперплоскостью в этом пространстве (конечных последовательностей, суммирующих до 1), конус - это алгебра над универсальным ортантом (конечных последовательностей неотрицательных чисел) и выпуклое множество - это алгебра над универсальным симплексом (конечных последовательностей неотрицательных чисел в сумме до 1). Это геометризует аксиомы в терминах «сумм с (возможными) ограничениями на координаты».

Другая концепция выпуклого анализа - это выпуклая функция от R до действительных чисел, которая определяется посредством неравенства между ее значениями на выпуклая комбинация точек и сумма значений в этих точках с одинаковыми коэффициентами.

Евклидово пространство

скалярное произведение

x ⋅ y = ∑ i = 1 nxiyi = x 1 y 1 + x 2 y 2 + ⋯ + xnyn {\ displaystyle \ mathbf {x} \ cdot \ mathbf {y} = \ sum _ {i = 1} ^ {n} x_ {i} y_ {i} = x_ {1} y_ {1} + x_ {2} y_ {2} + \ cdots + x_ {n} y_ {n}}

{\ mathbf {x}} \ cdot {\ mathbf {y}} = \ sum _ {{i = 1}} ^ {n} x_ {i} y_ {i} = x_ {1} y_ {1} + x_ {2} y_ {2} + \ cdots + x_ {n} y_ {n}

определяет норму |x| = √ x⋅ xв векторном пространстве R . Если каждый вектор имеет свою евклидову норму, то для любой пары точек расстояние

d (x, y) = ‖ x - y ‖ = ∑ i = 1 n (xi - yi) 2 { \ Displaystyle d (\ mathbf {x}, \ mathbf {y}) = \ | \ mathbf {x} - \ mathbf {y} \ | = {\ sqrt {\ sum _ {i = 1} ^ {n} ( x_ {i} -y_ {i}) ^ {2}}}}

d ({\ mathbf {x}}, {\ mathbf {y}}) = \ | {\ mathbf {x}} - {\ mathbf {y}} \ | = {\ sqrt {\ сумма _ {{я = 1}} ^ {n} (x_ {i} -y_ {i}) ^ {2}}}

определен, обеспечивая структуру метрического пространства на R в дополнение к его аффинной структуре.

Что касается структуры векторного пространства, то обычно предполагается, что скалярное произведение и евклидово расстояние существуют в R без специальных пояснений. Однако, строго говоря, реальное n-пространство и евклидово n-пространство - это разные объекты. Любое евклидово n-пространство имеет систему координат , где скалярное произведение и евклидово расстояние имеют показанную выше форму, называемую декартовой. Но в евклидовом пространстве существует множество декартовых систем координат.

И наоборот, приведенная выше формула для евклидовой метрики определяет стандартную евклидову структуру на R, но не единственно возможная. На самом деле, любая положительно определенная квадратичная форма q определяет свое собственное «расстояние» √q (x− y), но оно не сильно отличается от евклидовой в том смысле, что

∃ C 1>0, C 2>0, ∀ x, y ∈ R n: C 1 d (x, y) ≤ q (x - y) ≤ C 2 d (x, y). {\ Displaystyle \ существует C_ {1}>0, \ \ существует C_ {2}>0, \ \ forall \ mathbf {x}, \ mathbf {y} \ in \ mathbb {R} ^ {n}: C_ { 1} d (\ mathbf {x}, \ mathbf {y}) \ leq {\ sqrt {q (\ mathbf {x} - \ mathbf {y})}} \ leq C_ {2} d (\ mathbf {x }, \ mathbf {y}).}

\exists C_{1}>0, \ \ exists C_ {2}>0, \ \ forall {\ mathbf {x}}, {\ mathbf {y}} \ in {\ mathbb {R}} ^ {n}: C_ {1} d ({\ mathbf {x}}, {\ mathbf {y}}) \ leq {\ sqrt {q ({\ mathbf {x}} - {\ mathbf {y}})}} \ leq C_ {2} d ({\ mathbf {x}}, {\ mathbf {y}}).

Такое изменение показателя сохраняет некоторые его свойства, например свойство быть полным метрическое пространство. Это также означает, что любое линейное преобразование полного ранга R или его аффинное преобразование не увеличивает расстояния больше, чем на некоторый фиксированный C 2, и не делает расстояния меньше 1 1 C 1 раз, фиксированное конечное число раз меньше.

Вышеупомянутая эквивалентность метрических функций остается в силе, если √q (x− y) заменить на M (x− y), где M - любая выпуклая положительная однородная функция степени 1, то есть a векторная норма (полезные примеры см. в разделе Расстояние Минковского ). Из-за того факта, что любая «естественная» метрика на R не особо отличается от евклидовой метрики, R не всегда отличается от евклидова n-пространства даже в профессиональных математических работах.

В алгебраической и дифференциальной геометрии

Хотя определение многообразия не требует, чтобы его пространство модели было R, этот выбор является наиболее распространенное и почти исключительное в дифференциальной геометрии.

С другой стороны, теоремы вложения Уитни утверждают, что любое реальное дифференцируемое m-мерное многообразие может быть встроенный в R.

Другие виды

Другие структуры, рассматриваемые в R, включают в себя псевдоевклидово пространство, симплектическая структура (четное n) и контактная структура (нечетное n). Все эти структуры, хотя и могут быть определены безкоординатным образом, допускают стандартные (и достаточно простые) формы в координатах.

Rтакже является вещественным векторным подпространством C, которое инвариантно для комплексного сопряжения ; см. также комплексификация.

Многогранники в R

Есть три семейства многогранников , которые имеют простые представления в пространствах R для любого n и могут использоваться для визуализации любой аффинной системы координат в реальном n-пространстве. Вершины гиперкуба имеют координаты (x 1, x 2,…, x n), где каждая x k принимает одно из двух значений, обычно 0 или 1. Однако можно выбрать любые два числа вместо 0 и 1, например −1 и 1. Можно представить себе n-гиперкуб. как декартово произведение n идентичных интервалов (таких как единичный интервал [0,1]) на действительной прямой. Как n-мерное подмножество его можно описать с помощью системы 2n неравенств :

0 ≤ x 1 ≤ 1 ⋮ 0 ≤ xn ≤ 1 {\ displaystyle \ displaystyle {\ begin {matrix} 0 \ leq x_ { 1} \ leq 1 \\\ vdots \\ 0 \ leq x_ {n} \ leq 1 \ end {matrix}}}

\ displaystyle {\ begin {matrix} 0 \ leq x_ {1} \ leq 1 \\\ vdots \\ 0 \ leq x_ {n} \ leq 1 \ end {matrix}}

(для [0,1])

| х 1 | ≤ 1 ⋮ | х п | ≤ 1 {\ displaystyle \ displaystyle {\ begin {matrix} | x_ {1} | \ leq 1 \\\ vdots \\ | x_ {n} | \ leq 1 \ end {matrix}}}

\ displaystyle {\ begin {matrix } | x_ {1} | \ leq 1 \\\ vdots \\ | x_ {n} | \ leq 1 \ end {matrix}}

(для [−1,1])

Каждая вершина кросс-многогранника имеет для некоторого k координату x k, равную, а все остальные координаты равны 0 (таким образом, что это k-й стандартный базисный вектор от до знака ). Это двойственный многогранник гиперкуба. Как n-мерное подмножество его можно описать с помощью одного неравенства, в котором используется операция абсолютного значения :

∑ k = 1 n | х к | ≤ 1, {\ displaystyle \ sum \ limits _ {k = 1} ^ {n} | x_ {k} | \ leq 1 \,,}

\ sum \ limits _ {{k = 1}} ^ {n} | x_ {k} | \ leq 1 \,,

, но это можно выразить с помощью системы 2 линейные неравенства.

Третий многогранник с просто перечисляемыми координатами - это стандартный симплекс, вершинами которого являются n стандартных базисных векторов и начало координат (0, 0,…, 0). Как n-мерное подмножество оно описывается системой из n + 1 линейных неравенств:

0 ≤ x 1 ⋮ 0 ≤ xn ∑ k = 1 nxk ≤ 1 {\ displaystyle {\ begin {matrix} 0 \ leq x_ {1} \\\ vdots \\ 0 \ leq x_ {n} \\\ sum \ limits _ {k = 1} ^ {n} x_ {k} \ leq 1 \ end {matrix}}}

{\begin{matrix}0\leq x_{1}\\\vdots \\0\leq x_{n}\\\sum \limits _{{k=1}}^{n}x_{k}\leq 1\end{matrix}}

Замена всех «≤» с «<" gives interiors of these polytopes.

Топологические свойства

Топологическая структура из R (называемая стандартной топологией, Евклидова топология, или обычная топология ) может быть получена не только из декартова произведения. Она также идентична естественной топологии, вызванной Евклидова метрика, описанная выше : множество открыто в евклидовой топологии тогда и только тогда, когда содержит открытый шар вокруг каждой из своих точек Кроме того, R является линейным топологическим пространством (см. непрерывность линейных отображений выше), и существует только одна возможная (нетривиальная) топология, совместимая с его линейная структура. Поскольку существует много открытых линейных отображений m R, которые не являются изометриями, может быть много евклидовых структур на R, которые соответствуют одной и той же топологии. Фактически, это не сильно зависит даже от линейной структуры: существует множество нелинейных диффеоморфизмов (и других гомеоморфизмов) R на себя или на его части, такие как евклидово открытое мяч или внутренность гиперкуба).

Rимеет топологическое измерение n. Важным результатом по топологии R, который далеко не поверхностен, является инвариантность Брауэра домена. Любое подмножество R (с его топологией подпространства ), которое гомеоморфно другому открытому подмножеству R, само открыто. Непосредственным следствием этого является то, что R не гомеоморфен R, если m ≠ n - интуитивно «очевидный» результат, который, тем не менее, трудно доказать.

Несмотря на различие в топологической размерности и вопреки наивному восприятию, можно отображать менее размерное реальное пространство непрерывно и сюръективно на R . Возможна непрерывная (хотя и не гладкая) кривая заполнения пространства (изображение R ).

Примеры

Пустой вектор-столбец,. единственный элемент R

n ≤ 1

Случаи 0 ≤ n ≤ 1 не предлагают ничего нового: R - это вещественная линия, тогда как R (пространство, содержащее пустой вектор-столбец) - это синглтон, понимаемый как нулевое векторное пространство. Однако полезно включить их как тривиальные случаи теорий, которые описывают различные n.

n = 2

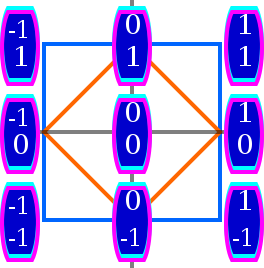И гиперкуб, и кросс-многогранник в R являются квадратами, но координаты вершин расположены иначе

n = 3

Куб (гиперкуб) и октаэдр (кросс-многогранник) R . Координаты не показаны

n = 4

Rможно представить, используя тот факт, что 16 точек (x 1, x 2, x 3, x 4), где каждый x k равен 0 или 1, являются вершинами тессеракта (на фото), 4- гиперкуб (см. выше).

Первое основное использование R - это модель пространство-время : три пространственные координаты плюс одна временная. Обычно это связывают с теорией относительности, хотя с Галилея для таких моделей использовались четыре измерения. Однако выбор теории приводит к иной структуре: в теории относительности Галилея координата t является привилегированной, а в теории относительности Эйнштейна - нет. Специальная теория относительности установлена в пространстве Минковского. Общая теория относительности использует искривленные пространства, которые для большинства практических целей можно представить как R с изогнутой метрикой. Ни одна из этих структур не обеспечивает (положительно-определенную) метрику на R.

евклидовом R, также привлекает внимание математиков, например, из-за его связи с кватернионами, 4-мерную действительную алгебру сами по себе. См. вращения в 4-мерном евклидовом пространстве для получения дополнительной информации.

В дифференциальной геометрии n = 4 - единственный случай, когда R допускает нестандартную дифференциальную структуру : см. экзотический R.

Нормы на R

В векторном пространстве Rможно определить множество норм. Некоторые общие примеры:

p-norm, определяемый $| | х | | p: = ∑ i = 1 n | х я | pp {\ displaystyle || {\ textbf {x}} || _ {p}: = {\ sqrt [{p}] {\ sum _ {i = 1} ^ {n} | x_ {i} | ^ { p}}}}$ $||{\textbf {x}}||_{p}:={\sqrt[{p}]{\sum _{i=1}^{n}|x_{i}|^{p}}}$ для всех $x ∈ {\ displaystyle {\ textbf {x}} \ in}$ ${\ displaystyle {\ textbf {x}} \ in}$ Rгде $p {\ displaystyle p}$ $p$ положительное целое число. Случай $p = 2 {\ displaystyle p = 2}$ $p=2$ очень важен, потому что это точно евклидова норма.
$∞ {\ displaystyle \ infty}$ $\ infty$ -норма или максимальная норма, определяемая $| | х | | ∞: = max {x 1,…, xn} {\ displaystyle || {\ textbf {x}} || _ {\ infty}: = \ max \ {x_ {1}, \ dots, x_ {n} \ }}$ ${\ displaystyle || {\ textbf {x}} || _ {\ infty}: = \ max \ {x_ {1}, \ dots, x_ {n} \}}$ для всех $x ∈ {\ displaystyle {\ textbf {x}} \ in}$ ${\ displaystyle {\ textbf {x}} \ in}$ R. Это предел всех p-норм : $| | х | | ∞ = lim p → ∞ ∑ i = 1 n | х я | pp {\ displaystyle || {\ textbf {x}} || _ {\ infty} = \ lim \ limits _ {p \ to \ infty} {\ sqrt [{p}] {\ sum _ {i = 1} ^ {n} | x_ {i} | ^ {p}}}}$ ${\ displaystyle || {\ textbf {x}} || _ {\ inft y} = \ lim \ limits _ {p \ to \ infty} {\ sqrt [{p}] {\ sum _ {i = 1} ^ {n} | x_ {i} | ^ {p}}}}$ .

Действительно удивительный и полезный результат состоит в том, что каждая норма, определенная в R, эквивалентна. Это означает для двух произвольных норм $| | ⋅ | | {\ displaystyle || \ cdot ||}$ $|| \ cdot ||$ и $| | ⋅ | | ′ {\ Displaystyle || \ cdot || ^ {\ prime}}$ $||\cdot ||^{\prime }$ на R вы всегда можете найти положительные действительные числа $α, β>0 {\ displaystyle \ alpha, \ beta>0}$ $\alpha,\beta>0$ , такое что

$α ⋅ | | x | | ≤ | | x | | ′ ≤ β ⋅ | | x | | | {\ displaystyle \ alpha \ cdot || {\ textbf {x}} | | \ leq || {\ textbf {x}} || ^ {\ prime} \ leq \ beta \ cdot || {\ textbf {x}} ||}$ ${\ displaystyle \ alpha \ cdot || {\ textbf {x}} || \ leq || {\ textbf {x}} || ^ {\ prime} \ leq \ beta \ cdot || {\ textbf {x}} ||}$ для всех $x ∈ {\ displaystyle {\ textbf {x}} \ in}$ ${\ displaystyle {\ textbf {x}} \ in}$ R.

Это определяет отношение эквивалентности на множестве всех норм на R . С помощью этого результата вы можете проверить, что последовательность векторов в R сходится с $| | ⋅ | | {\ displaystyle || \ cdot ||}$ $|| \ cdot ||$ тогда и только тогда, когда она сходится с $| | ⋅ | | ′ {\ Displaystyle || \ cdot || ^ {\ prime}}$ $||\cdot ||^{\prime }$ .

Вот набросок того, как может выглядеть доказательство этого результата:

Из-за отношения эквивалентности достаточно s как эта каждая норма на R эквивалентна евклидовой норме $| | ⋅ | | 2 {\ Displaystyle || \ cdot || _ {2}}$ $|| \ cdot || _ {2}$ . Пусть $| | ⋅ | | {\ displaystyle || \ cdot ||}$ $|| \ cdot ||$ - произвольная норма на R . Доказательство делится на два этапа:

Мы показываем, что существует $β>0 {\ displaystyle \ beta>0}$ $\beta>0$ , так что $| | x | | ≤ β ⋅ | | x | | 2 { \ displaystyle || {\ textbf {x}} || \ leq \ beta \ cdot || {\ textbf {x}} || _ {2}}$ $||{\textbf {x }}||\leq \beta \cdot ||{\textbf {x}}||_{2}$ для всех $x ∈ {\ displaystyle {\ textbf {x}} \ in}$ ${\ displaystyle {\ textbf {x}} \ in}$ R. На этом этапе вы используете тот факт, что каждый $x = (x 1,…, xn) ∈ {\ displaystyle {\ textbf {x}} = ( x_ {1}, \ dots, x_ {n}) \ in}$ ${\textbf {x}}=(x_{1},\dots,x_{n})\in$ Rможно представить как линейную комбинацию стандартного базиса : $x = ∑ i = 1 nei ⋅ xi { \ displaystyle {\ textbf {x}} = \ sum _ {i = 1} ^ {n} e_ {i} \ cdot x_ {i}}$ ${\textbf {x}}=\sum _{i=1}^{n}e_{i}\cdot x_{i}$ . Затем с помощью неравенства Коши – Шварца $| | x | | = | | ∑ i = 1 nei ⋅ xi | | ≤ ∑ i = 1 n | | ei | | ⋅ | xi | ≤ ∑ i = 1 n | | ei | | 2 ⋅ ∑ я знак равно 1 N | xi | 2 знак равно β ⋅ | | x | | 2 {\ displaystyle || {\ textbf {x}} || = \ left | \ left | \ sum _ {i = 1} ^ {n} e_ {i} \ cdot x_ {i} \ right | \ right | \ leq \ sum _ {i = 1} ^ {n} || e_ {i} || \ cdot | x_ { i} | \ leq {\ sqrt {\ sum _ {i = 1} ^ {n} || e_ {i} || ^ {2}}} \ cdot {\ sqrt {\ sum _ {i = 1} ^ {n} | x_ {i} | ^ {2}}} = \ beta \ cdot || {\ textbf {x}} || _ {2}}$ ${\ displaystyle || {\ textbf {x} } || = \ left | \ left | \ sum _ {i = 1} ^ {n} e_ {i} \ cdot x_ {i} \ right | \ right | \ leq \ sum _ {i = 1} ^ { n} || e_ {i} || \ cdot | x_ {i} | \ leq {\ sqrt {\ sum _ {i = 1} ^ {n} || e_ {i} || ^ {2}}} \ cdot {\ sqrt {\ sum _ {i = 1} ^ {n} | x_ {i} | ^ {2}}} = \ beta \ cdot || {\ textbf {x}} || _ {2} }$ , где $β: = ∑ i = 1 n | | e i | | 2 {\ displaystyle \ beta: = {\ sqrt {\ sum _ {i = 1} ^ {n} || e_ {i} || ^ {2}}}}$ ${\ displaystyle \ beta: = {\ sqrt {\ sum _ {i = 1} ^ {n} || e_ {i} || ^ {2}}}}$ .
Теперь нам нужно найти $α>0 {\ displaystyle \ alpha>0}$ $\alpha>0$ , так что $α ⋅ | | x | | 2 ≤ | | x | | {\ displaystyle \ alpha \ cdot || {\ textbf {x}} || _ { 2} \ leq || {\ textbf {x}} ||}$ ${\ displaystyle \ alpha \ cdot || {\ textbf {x}} || _ {2} \ leq || {\ textbf {x}} ||}$ для всех $x ∈ {\ displaystyle {\ textbf {x}} \ in}$ ${\ displaystyle {\ textbf {x}} \ in}$ R. Предположим, что нет такой $α {\ displaystyle \ alpha}$ $\alpha$ . Тогда существует для каждого $k ∈ N {\ displaystyle k \ in \ mathbb {N}}$ $k \ in \ mathbb {N}$ a $xk ∈ {\ displaystyle { \ textbf {x}} _ {k} \ in}$ ${\ Displaystyle {\ т extbf {x}} _ {k} \ in}$ R, такой, что $| | xk | | 2>k ⋅ | | xk | | {\ displaystyle || {\ textbf {x}} _ { k} || _ {2}>k \ cdot || {\ textbf {x}} _ {k} ||}$ $||{\textbf {x}}_{k}||_{2}>k \ cdot || {\ textbf {x}} _ {k} ||$ . Определите вторую последовательность $(x ~ k) k ∈ N {\ displaystyle ({\ tilde {\ textbf {x}}} _ {k}) _ {k \ in \ mathbb {N}}}$ ${\ displaystyle ({\ tilde {\ textbf {x}}} _ {k}) _ {k \ in \ mathbb {N}}}$ по $x ~ k: = xk | | х к | | 2 {\ displaystyle {\ tilde {\ textbf {x}}} _ {k}: = {\ frac {{\ textbf {x}} _ {k}} {|| {\ textbf {x}} _ {k } || _ {2}}}}$ ${\tilde {\textbf {x}}}_{k}:={\frac {{\textbf {x}}_{k}}{||{\textbf {x}}_{k}||_{2}}}$ . Эта последовательность ограничена, потому что $| | х ~ к | | 2 = 1 {\ displaystyle || {\ tilde {\ textbf {x}}} _ {k} || _ {2} = 1}$ ${\ displaystyle || {\ tilde {\ textbf {x}}} _ {k} || _ {2} = 1}$ . Итак, благодаря теореме Больцано – Вейерштрасса существует сходящаяся подпоследовательность $(x ~ kj) j ∈ N {\ displaystyle ({\ tilde {\ textbf {x}}}} _ {k_ {j }}) _ {j \ in \ mathbb {N}}}$ $({\tilde {\textbf {x}}}_{k_ {j}})_{j\in \mathbb {N} }$ с ограничением $a ∈ {\ displaystyle {\ textbf {a}} \ in}$ ${\ displaystyle {\ textbf {a}} \ in}$ R. Теперь покажем, что $| | а | | 2 = 1 {\ displaystyle || {\ textbf {a}} || _ {2} = 1}$ ${\ displaystyle || {\ textbf {a}} || _ {2} = 1}$ , но $a = 0 {\ displaystyle {\ textbf {a}} = {\ textbf {0}}}$ ${\textbf {a}}={\textbf {0}}$ , что является противоречием. Это $| | а | | ≤ | | а - х ~ к j | | + | | х ~ к j | | ≤ β ⋅ | | а - х ~ к j | | 2 + | | х к j | | | | х к j | | 2 → j → ∞ 0 {\ displaystyle || {\ textbf {a}} || \ leq || {\ textbf {a}} - {\ tilde {\ textbf {x}}} _ {k_ {j}} || + || {\ tilde {\ textbf {x}}} _ {k_ {j}} || \ leq \ beta \ cdot || {\ textbf {a}} - {\ tilde {\ textbf {x} }} _ {k_ {j}} || _ {2} + {\ frac {|| {\ textbf {x}} _ {k_ {j}} ||} {|| {\ textbf {x}} _ {k_ {j}} || _ {2}}} \ {\ overset {j \ to \ infty} {\ to}} \ 0}$ ${\ displaystyle || {\ textbf {a}} || \ leq || {\ textbf {a}} - {\ tilde {\ textbf {x}}} _ {k_ {j}} || + || {\ tilde {\ textbf {x}}} _ {k_ {j }} || \ leq \ beta \ cdot || {\ textbf {a}} - {\ tilde {\ textbf {x}}} _ {k_ {j}} || _ {2} + {\ frac {| | {\ textbf {x}} _ {k_ {j}} ||} {|| {\ textbf {x}} _ {k_ {j}} || _ {2}}} \ {\ overset {j \ to \ infty} {\ to}} \ 0}$ , потому что $| | а - х ~ к j | | → 0 {\ displaystyle || {\ textbf {a}} - {\ tilde {\ textbf {x}}} _ {k_ {j}} || \ к 0}$ $||{\textbf {a}}-{\tilde {\textbf {x}}}_{k_{j}}||\to 0$ и $0 ≤ | | х к j | | | | х к j | | 2 < 1 k j {\displaystyle 0\leq {\frac {||{\textbf {x}}_{k_{j}}||}{||{\textbf {x}}_{k_{j}}||_{2}}}<{\frac {1}{k_{j}}}}$ $0\leq {\frac {||{\textbf { x}}_{k_{j}}||}{||{\textbf {x}}_{k_{j}}||_{2}}}<{\frac {1}{k_{j} }}$ , поэтому $| | х к j | | | | х к j | | 2 → 0 {\ displaystyle {\ frac {|| {\ textbf {x}} _ {k_ {j}} ||} {|| {\ textbf {x}} _ {k_ {j}} || _ { 2}}} \ на 0}$ ${\ displaystyle {\ frac {|| {\ textbf {x} } _ {k_ {j}} ||} {|| {\ textbf {x}} _ {k_ {j}} || _ {2}}} \ to 0}$ . Отсюда следует $| | а | | = 0 {\ displaystyle || {\ textbf {a}} || = 0}$ ${\ displaystyle || {\ textbf {a}} || = 0}$ , поэтому $a = 0 {\ displaystyle {\ textbf {a}} = {\ textbf {0} }}$ ${\textbf {a}}={\textbf {0}}$ . С другой стороны $| | а | | 2 = 1 {\ displaystyle || {\ textbf {a}} || _ {2} = 1}$ ${\ displaystyle || {\ textbf {a}} || _ {2} = 1}$ , потому что $| | а | | 2 = | | lim j → ∞ x ~ k j | | 2 = lim j → ∞ | | х ~ к j | | 2 = 1 {\ displaystyle || {\ textbf {a}} || _ {2} = || \ lim \ limits _ {j \ to \ infty} {\ tilde {\ textbf {x}}} _ {k_ {j}} || _ {2} = \ lim \ limits _ {j \ to \ infty} || {\ tilde {\ textbf {x}}} _ {k_ {j}} || _ {2} = 1}$ $||{\textbf {a}}||_{2}=||\lim \limits _{j\to \infty }{\tilde {\textbf {x}}}_{k_{j}}||_{2}=\lim \limits _{j\to \infty }||{\tilde {\textbf {x}}}_{k_{j}}||_{2}=1$ . Это никогда не может быть правдой, поэтому предположение было ложным и существует такое $α>0 {\ displaystyle \ alpha>0}$ $\alpha>0$ .