Псевдоевклидово пространство

В математике и теоретической физике, псевдоевклидовом пространстве пространство является конечным мерным реальным n-пространством вместе с невырожденной квадратичной формой q. Такая квадратичная форма при соответствующем выборе базиса (e1,..., e n) может быть применена к вектору x = x 1e1+... + x nen, что дает

$q\; (x)\; =\; (x\; 1\; 2\; +\dots \; +\; xk\; 2)\; -\; (xk\; +\; 1\; 2\; +\dots \; +\; xn\; 2)\; \{\backslash \; displaystyle\; q\; (x)\; =\; \backslash \; left\; (x\_\; \{1\}\; ^\; \{2\}\; +\; \backslash \; ldots\; +\; x\_\; \{k\}\; ^\; \{2\}\; \backslash \; right)\; -\; \backslash \; left\; (x\_\; \{k\; +\; 1\}\; ^\; \{2\}\; +\; \backslash \; ldots\; +\; x\_\; \{n\}\; ^\; \{2\}\; \backslash \; right)\}$, который называется скалярным квадратом вектора x.

Для евклидовых пространств, k = n, что означает, что квадратичная форма положительно определена. Когда 0 ≠ k ≠ n, q представляет собой изотропную квадратичную форму . Обратите внимание, что если 1 ≤ i ≤ k и k < j ≤ n, then q(ei + e j) = 0, так что e i + e j равно нулевой вектор. В псевдоевклидовом пространстве с k ≠ n, в отличие от евклидова пространства, существуют векторы с отрицательным скалярным квадратом.

Как и в случае с термином «евклидово пространство», термин «псевдоевклидово пространство» может использоваться для обозначения аффинного пространства или векторного пространства в зависимости от автора, с последнее альтернативно упоминается как псевдоевклидово векторное пространство (см. раздел точка-вектор ).

• 1 Геометрия
  • 1.1 Положительные, нулевые и отрицательные скалярные квадраты
  • 1.2 Интервал
  • 1.3 Вращения и сферы
  • 1.4 Симметричная билинейная форма
  • 1.5 Подпространства и ортогональность
  • 1.6 Закон параллелограмма и теорема Пифагора
  • 1.7 Угол
• 2 Алгебра и тензорное исчисление
• 3 Примеры
• 4 См. Также
• 5 Сноски
• 6 Ссылки
• 7 Внешние ссылки

Геометрия псевдоевклидова пространства согласована, несмотря на то, что некоторые свойства евклидова пространства не применяются, в первую очередь то, что это не метрическое пространство, как объясняется ниже. аффинная структура не изменилась, и, следовательно, также концепции строка, плоскость и, как правило, аффинное подпространство (плоский ), а также отрезки.

Положительные, нулевые и отрицательные скалярные квадраты

n = 3, k равно 1 или 2 в зависимости от выбора знака of q

A нулевой вектор - это вектор, для которого квадратичная форма равна нулю. В отличие от евклидова пространства, такой вектор может быть ненулевым, и в этом случае он само- ортогонален. Если квадратичная форма не определена, псевдоевклидово пространство имеет линейный конус нулевых векторов, заданных как {x: q (x) = 0}. Когда псевдоевклидово пространство обеспечивает модель для пространства-времени (см. ниже), нулевой конус называется световым конусом начала координат.

Нулевой конус разделяет два открытых набора, соответственно, для которых q (x)>0 и q (x) < 0. If k ≥ 2, then the set of vectors for which q(x)>0 связаны. Если k = 1, то он состоит из двух непересекающихся частей, одна с x 1>0, а другая с x 1< 0. Similar statements can be made for vectors for which q(x) < 0 if k is replaced with n − k.

Interval

Квадратичная форма q соответствует квадрату вектора в евклидовом случае. Чтобы определить векторную норму (и расстояние) в инвариантной манере, нужно получить квадратные корни из скалярных квадратов, что, возможно, приводит к мнимым расстояния; см. квадратный корень из отрицательных чисел. Но даже для треугольника с положительными скалярными квадратами всех трех сторон (чьи квадратные корни действительны и положительны) неравенство треугольника в общем случае не выполняется.

Следовательно, термины норма и расстояние избегаются в псевдоевклидовой геометрии, которые могут быть заменены скалярным квадратом и интервалом соответственно.

Хотя для кривой , все касательные векторы которой имеют скалярные квадраты одного знака, длина дуги определена. У него есть важные приложения: например, см. собственное время.

Вращения и сферы

Группа вращений такого пространства - это неопределенная ортогональная группа O (q), также обозначаемая как O ( k, n - k) без ссылки на конкретную квадратичную форму. Такие «вращения» сохраняют форму q и, следовательно, скалярный квадрат каждого вектора, включая положительный, нулевой или отрицательный он.

В то время как евклидово пространство имеет единичную сферу, псевдоевклидово пространство имеет гиперповерхности {x: q (x) = 1} и {x: q (x) = −1}. Такая гиперповерхность, называемая квазисферой, сохраняется соответствующей неопределенной ортогональной группой.

Симметричная билинейная форма

Квадратичная форма q приводит к симметричной билинейной форме, определяемой следующим образом:

$⟨x,\; y⟩\; =\; 1\; 2\; [q\; (\; x\; +\; y)\; -\; q\; (x)\; -\; q\; (y)]\; =\; (x\; 1\; y\; 1\; +\dots \; +\; xkyk)\; -\; (xk\; +\; 1\; yk\; +\; 1\; +\dots \; +\; xnyn).\; \{\backslash \; displaystyle\; \backslash \; langle\; x,\; y\; \backslash \; rangle\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; [q\; (x\; +\; y)\; -q\; (x)\; -q\; (y)]\; =\; \backslash \; left\; (x\_\; \{1\}\; y\_\; \{1)\; \}\; +\; \backslash \; ldots\; +\; x\_\; \{k\}\; y\_\; \{k\}\; \backslash \; right)\; -\; \backslash \; left\; (x\_\; \{k\; +\; 1\}\; y\_\; \{k\; +\; 1\}\; +\; \backslash \; ldots\; +\; x\_\; \{n\}\; y\_\; \{n\}\; \backslash \; right).\}$

Квадратичная форма может быть выражена через билинейную форму: q (x) = ⟨x, x⟩.

Когда ⟨x, y⟩ = 0, тогда x и y являются ортогональными векторами псевдоевклидова пространства.

Эту билинейную форму часто называют скалярным произведением, а иногда и «внутренним произведением» или «скалярным произведением», но она не определяет пространство внутреннего произведения и не обладает свойствами скалярного произведения евклидовых векторов.

Если x и y ортогональны, а q (x) q (y) < 0, then x is гиперболо-ортогональны относительно y.

Стандартный базис реального n-пространства - ортогональный. Не существует ортонормированных базисов в псевдоевклидовом пространстве, для которого билинейная форма является неопределенной, поскольку ее нельзя использовать для определения векторной нормы.

Подпространства и ортогональность

Для (положительно-размерного) подпространство U псевдоевклидова пространства, когда квадратичная форма q ограничена до U, возможны следующие три случая:

1. q|Uлибо положительно, либо отрицательно определено. Тогда U по существу евклидово (с точностью до знака q).
2. q|Uнеопределенно, но невырождено. Тогда U само по себе псевдоевклидово. Возможно, только если dim U ≥ 2; если dim U = 2, что означает, что U является плоскостью , то она называется гиперболической плоскостью.
3. q|Uвырожденной.

Одно из самых неприятных свойств (для евклидовой интуиции) псевдоевклидовых векторов и плоскостей является их ортогональностью. Когда два ненулевых евклидовых вектора ортогональны, они не коллинеарны. Пересечения любого евклидова линейного подпространства с его ортогональным дополнением - это {0} подпространство. Но из определения из предыдущего пункта сразу следует, что любой вектор ν нулевого скалярного квадрата ортогонален сам себе. Следовательно, изотропная линия N = ⟨ν⟩, генерируемая нулевым вектором ν, является подмножеством его ортогонального дополнения N.

Формальное определение ортогонального дополнения к векторное подпространство в псевдоевклидовом пространстве дает совершенно четко определенный результат, который удовлетворяет равенству dim U + dim U = n из-за невырожденности квадратичной формы. Это просто условие

U ∩ U = {0} или, эквивалентно, U + U = все пространство,

, которое может быть нарушено, если подпространство U содержит нулевое направление. Хотя подпространства образуют решетку, как и в любом векторном пространстве, эта операция ⊥ не является ортодополнением, в отличие от внутренних пространств продукта.

Для подпространства N, составленного полностью нулевых векторов (что означает, что скалярный квадрат q, ограниченный до N, равен 0), всегда выполняется:

N ⊂ N или, что то же самое, N ∩ N = N.

Такое подпространство может иметь до min (k, n - k) размерности.

Для (положительного) евклидова k-подпространства его ортогональным дополнением является (n - k) -мерное отрицательное «евклидово» подпространство, и наоборот. Как правило, для (d + + d - + d 0) -мерного подпространства U, состоящего из d + положительных и d - отрицательные размеры (см. закон инерции Сильвестра для пояснения), его ортогональное "дополнение" U имеет (k - d + - d 0) положительные и (n - k - d - - d 0) отрицательные измерения, а остальные d 0 вырождены и образуют U ∩ U пересечение.

Закон параллелограмма и теорема Пифагора

Закон параллелограмма принимает форму

$q\; (x)\; +\; q\; (y)\; =\; 1\; 2\; (q\; (x\; +\; y)\; +\; q\; (x\; -\; y)).\; \{\backslash \; displaystyle\; q\; (x)\; +\; q\; (y)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (q\; (x\; +\; y)\; +\; q\; (xy)).\}$

Использование квадрата суммы тождество, для произвольного треугольника можно выразить скалярный квадрат третьей стороны из скалярных квадратов двух сторон и их билинейного произведения:

$q\; (x\; +\; y)\; =\; q\; (x)\; +\; q\; (y)\; +\; 2\; ⟨х,\; у⟩.\; \{\backslash \; displaystyle\; q\; (x\; +\; y)\; =\; q\; (x)\; +\; q\; (y)\; +2\; \backslash \; langle\; x,\; y\; \backslash \; rangle.\}$

Это демонстрирует, что для ортогональных векторов псевдоевклидов аналог Верна теорема Пифагора :

$⟨x,\; y⟩\; =\; 0\; \Rightarrow \; q\; (x)\; +\; q\; (y)\; =\; q\; (x\; +\; y).\; \{\backslash \; displaystyle\; \backslash \; langle\; x,\; y\; \backslash \; rangle\; =\; 0\; \backslash \; Rightarrow\; q\; (x)\; +\; q\; (y)\; =\; q\; (x\; +\; y).\}$

Угол

Как правило, абсолютное значение | ⟨x, y⟩ | билинейной формы на двух векторах может быть больше √ | q (x) q (y) |, равно ему или меньше. Это вызывает аналогичные проблемы с определением угла (см. Точечное произведение § Геометрическое определение ), поскольку появился выше для расстояний.

Если k = 1 (только один положительный член в q), то для векторов положительного скалярного квадрата:

$|\; ⟨X,\; y⟩\; |\; \ge \; q\; (x)\; q\; (y),\; \{\backslash \; displaystyle\; |\; \backslash \; langle\; x,\; y\; \backslash \; rangle\; |\; \backslash \; geq\; \{\backslash \; sqrt\; \{q\; (x)\; q\; (y)\}\}\; \backslash ,,\}$

, что позволяет определять гиперболический угол, аналог угла между этими векторами через обратный гиперболический косинус :

$arccosh\; \; |\; ⟨X,\; y⟩\; |\; д\; (х)\; д\; (у).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{arccosh\}\; \{\backslash \; frac\; \{|\; \backslash \; langle\; x,\; y\; \backslash \; rangle\; |\}\; \{\backslash \; sqrt\; \{q\; (x)\; q\; (y)\}\}\}\; \backslash ,.\}$

Это соответствует расстоянию на (n - 1) -мерное гиперболическое пространство. Это известно как быстрота в контексте теории относительности, обсуждаемой ниже. В отличие от евклидова угла, он принимает значения из [0, + ∞) и равен 0 для антипараллельных векторов.

Нет разумного определения угла между нулевым вектором и другим вектором (нулевым или ненулевым).

Как и евклидовы пространства, каждое псевдоевклидово векторное пространство порождает алгебру Клиффорда. В отличие от свойств выше, где замена q на -q изменяла числа, но не геометрию, изменение знака квадратичной формы приводит к отдельной алгебре Клиффорда, так, например, Cl 1,2 (R) и Cl 2,1 (R) не изоморфны.

Как и в любом векторном пространстве, существуют псевдоевклидовы тензоры. Как и в случае с евклидовой структурой, есть операторы повышения и понижения индексов, но, в отличие от случая с евклидовыми тензорами, нет базисов, где эти операции не изменяют значения компонентов. Если существует вектор v, соответствующий ковариантный вектор равен:

$v\; \alpha \; =\; q\; \alpha \; \beta \; v\; \beta ,\; \{\backslash \; displaystyle\; v\; \_\; \{\backslash \; alpha\}\; =\; q\; \_\; \{\backslash \; alpha\; \backslash \; beta\}\; v\; ^\; \{\; \backslash \; beta\}\; \backslash ,,\}$

и стандартной формы

$q\; \alpha \; \beta \; =\; (I\; k\; \times \; k\; 0\; 0\; -\; I\; (n\; -\; k)\; \times \; (n\; -\; k))\; \{\backslash \; displaystyle\; q\; \_\; \{\backslash \; alpha\; \backslash \; beta\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; I\_\; \{k\; \backslash \; times\; k\}\; 0\; \backslash \backslash \; 0\; -I\; \_\; \{(nk)\; \backslash \; times\; (nk)\}\; \backslash \; end\; \{pmatrix\}\}\}$

первые k компонентов v α численно такие же, как у v, но остальные n - k имеют противоположные знаки.

Соответствие между контравариантным и ковариантным тензорами составляет тензорное исчисление на псевдоримановы многообразия являются обобщением одного на римановых многообразиях.

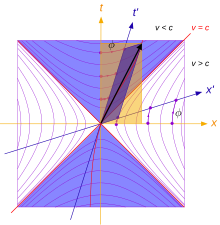
Очень важным псевдоевклидовым пространством является пространство Минковского, которое представляет собой математическую среду, в которой теория Альберта Эйнштейна сформулирована специальная теория относительности. Для пространства Минковского n = 4 и k = 3, так что

$q\; (x)\; =\; x\; 1\; 2\; +\; x\; 2\; 2\; +\; x\; 3\; 2\; -\; x\; 4\; 2,\; \{\backslash \; displaystyle\; q\; (x)\; =\; x\_\; \{1\}\; ^\; \{2\}\; +\; x\_\; \{2\}\; ^\; \{2\}\; +\; x\_\; \{3\}\; ^\; \{2\}\; -x\_\; \{4\}\; ^\; \{2\},\}$

Геометрия, связанная с этой псевдометрикой, была исследована Пуанкаре. Его группа вращения - это группа Лоренца. Группа Пуанкаре включает также переводы и играет ту же роль, что и евклидовы группы обычных евклидовых пространств.

Еще одно псевдоевклидово пространство - это плоскость z = x + yj, состоящая из комплексных чисел с разбиением, снабженная квадратичной формой

$\Vert \; z\; \Vert \; =\; zz\; \ast \; =\; z\; \ast \; z\; =\; x\; 2\; -\; y\; 2.\; \{\backslash \; displaystyle\; \backslash \; lVert\; z\; \backslash \; rVert\; =\; zz\; ^\; \{*\}\; =\; z\; ^\; \{*\}\; z\; =\; x\; ^\; \{2\}\; -y\; ^\; \{2\}.\}$

Это простейший случай неопределенного псевдоевклидова пространства. (n = 2, k = 1) и единственный, где нулевой конус делит пространство на четыре открытых множества. Группа SO (1, 1) состоит из так называемых гиперболических вращений.

• Псевдориманово многообразие
• Гиперболическое уравнение
• Модель гиперболоида
• Paravector

• Картан Эли (1981) [1938], Теория спиноров, Нью-Йорк: Dover Publications, стр. 3, ISBN 978-0-486-64070-9, MR 0631850
• Вернер Гройб (1963) Линейная алгебра, 2-е издание, §12.4 Псевдоевклидовы пространства, стр. 237– 49, Springer-Verlag.
• Уолтер Нолл (1964) «Евклидова геометрия и хронометрия Минковского», American Mathematical Monthly 71: 129–44.
• Новиков, СП; Фоменко, А.Т.; [перевод с русского М. Цаплиной] (1990). Основные элементы дифференциальной геометрии и топологии. Дордрехт; Бостон: Kluwer Academic Publishers. ISBN 0-7923-1009-8.
• Секерес, Питер (2004). Курс современной математической физики: группы, гильбертово пространство и дифференциальная геометрия. Издательство Кембриджского университета. ISBN 0-521-82960-7.
• Шафаревич И.Р. ; Ремизов А.О. (2012). Линейная алгебра и геометрия. Спрингер. ISBN 978-3-642-30993-9.

• D.D. Соколов (составитель), Псевдоевклидово пространство, Математическая энциклопедия