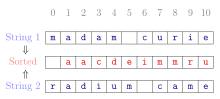Войти
Алгоритмический тест анаграммы с использованием мультимножеств в качестве канонических форм: Строки «мадам Кюри"и" пришел радий"даны как массивы C. Каждый преобразуется в каноническую форму путем сортировки. Поскольку обе отсортированные строки буквально совпадают, исходные строки были анаграммами друг друга. В математике и информатике канонический, нормальный или стандартная форма математического объекта - это стандартный способ представления этого объекта в виде математического выражения. Часто это тот, который обеспечивает простейшее представление объекта и позволяет его уникальным образом идентифицировать. Различие между «канонической» и «нормальной» формами варьируется от подполя к подполю. В большинстве полей каноническая форма определяет уникальное представление для каждого объекта, в то время как нормальная форма просто определяет его форму без требования уникальности.
Каноническая форма положительного целого числа в десятичное представление - это конечная последовательность цифр, которая не начинается с нуля. В более общем смысле, для класса объектов, для которого определено отношение эквивалентности, каноническая форма состоит в выборе конкретного объекта в каждом классе. Например:
В информатике, а точнее в компьютерной алгебре, при представлении математических объектов на компьютере обычно существует много разных способов представления одного и того же объекта. В этом контексте каноническая форма - это такое представление, в котором каждый объект имеет уникальное представление (с канонической формой - это процесс, посредством которого представление переводится в его каноническую форму). Таким образом, равенство двух объектов легко проверить, проверив равенство их канонических форм.
Несмотря на это преимущество, канонические формы часто зависят от произвольного выбора (например, порядка переменных), что создает трудности при проверке равенства двух объектов в результате независимых вычислений. Следовательно, в компьютерной алгебре нормальная форма - более слабое понятие: нормальная форма - это представление, в котором ноль представлен однозначно. Это позволяет проверять равенство, переводя разницу двух объектов в нормальную форму.
Каноническая форма может также означать дифференциальную форму, которая определяется естественным (каноническим) способом.
Дан набор S объектов с отношение эквивалентности R на S, каноническая форма задается путем обозначения некоторых объектов S как «в канонической форме», так что каждый рассматриваемый объект эквивалентен ровно одному объекту в канонической форме. форма. Другими словами, канонические формы в S представляют классы эквивалентности один раз и только один раз. Чтобы проверить, эквивалентны ли два объекта, достаточно проверить равенство их канонических форм. Таким образом, каноническая форма обеспечивает теорему классификации и многое другое, поскольку она не только классифицирует каждый класс, но также дает выделенного (канонического) представителя для каждого объекта в классе.
Формально, канонизация отношения эквивалентности R на множестве S - это отображение c: S → S такое, что для всех s, s 1, s 2 ∈ S:
Свойство 3 является избыточным; это следует из применения 2 к 1.
С практической точки зрения часто бывает выгодно иметь возможность распознавать канонические формы. Существует также практический, алгоритмический вопрос, который следует рассмотреть: как перейти от данного объекта s в S к его канонической форме s * • Канонические формы обычно используются для повышения эффективности работы с классами эквивалентности. Например, в модульной арифметике каноническая форма для класса остатка обычно принимается как наименьшее неотрицательное целое число в нем. Операции над классы выполняются путем объединения этих представителей и последующего сведения результата к наименьшему неотрицательному остатку. Требование ss иногда смягчается, позволяя формам быть уникальными с точностью до некоторого более тонкого отношения эквивалентности, например, позволяя переупорядочивать термины (если нет естественного упорядочения терминов).
Каноническая форма может быть просто соглашением или глубокой теоремой. Например, полиномы обычно записываются с помощью убывающих степеней: обычно пишут x + x + 30, чем x + 30 + x, хотя эти две формы определяют один и тот же многочлен. Напротив, существование жордановой канонической формы для матрицы - глубокая теорема.
Примечание: в этом разделе «от до » некоторое отношение эквивалентности E означает, что каноническая форма не уникальна в целом, но если один объект имеет две разные канонические формы, они E-эквивалентны.
Стандартная форма используется многими математиками и учеными для записи чрезвычайно больших чисел более кратким и понятным способом, наиболее заметным из которых является научная запись.
| Объекты | A эквивалентно B, если: | Нормальная форма | Примечания |
|---|---|---|---|
| Нормальные матрицы над комплексными числами |  для некоторой унитарной матрицы U | Диагональные матрицы (до переупорядочения) | Это Спектральная теорема |
| Матрицы над комплексом числа |  для некоторых унитарных матриц U и V | Диагональные матрицы с вещественными положительными элементами (в порядке убывания) | Разложение по сингулярным числам |
| Матрицы над алгебраически замкнутым полем |  для некоторой обратимой матрицы P | нормальной формы Джордана (с точностью до переупорядочения блоков) | |
| Матрицы над алгебраически замкнутым полем | для некоторой обратимой матрицы P | Каноническая форма Вейра (с точностью до переупорядочивания блоков) | |
| Матрицы над полем | для некоторых обратимая матрица P | нормальная форма Фробениуса | |
| Матрицы в области главных идеалов |  для некоторых обратимых матриц P и Q | нормальная форма Смита | Эквивалентность аналогична разрешению обратимых преобразований элементарных строк и столбцов |
| Матрицы над целыми числами |  для некоторой унимодулярной матрицы U | нормальной формы Эрмита | |
| Конечномерные векторные пространства над полем K | A и B изоморфны как векторные пространства |  , na неотрицательное целое число |
| Объекты | A эквивалентно B, если: | Нормальная форма |
|---|---|---|
| Конечно порожденные R-модули с R a область главных идеалов | A и B изоморфны как R-модули | Первичная декомпозиция (с точностью до переупорядочения) или инвариантная факторная декомпозиция |
Напротив, существуют альтернативные формы записи уравнения. Например, уравнение прямой может быть записано как линейное уравнение в точка-наклон и наклон-пересечение в форме.
Выпуклые многогранники могут быть записаны в каноническую форму, такую что:
Каждое дифференцируемое многообразие имеет котангенсный пучок. Этому пакету всегда может быть присвоена определенная дифференциальная форма, называемая канонической однократной формой. Эта форма придает кокасательному расслоению структуру симплектического многообразия и позволяет интегрировать векторные поля на многообразии с помощью уравнений Эйлера-Лагранжа или с помощью Гамильтонова механика. Такие системы интегрируемых дифференциальных уравнений называются интегрируемыми системами.
Изучение динамических систем частично совпадает с изучением интегрируемых систем. ; там есть идея нормальной формы (динамических систем).
При изучении многообразий в трех измерениях, каждый имеет первую фундаментальную форму, вторая фундаментальная форма и третья фундаментальная форма.
| Объекты | A эквивалентно B, если: | Нормальная форма |
|---|---|---|
| Гильбертовы пространства | Если A и B являются гильбертовыми пространствами бесконечной размерности, то A и B изометрически изоморфны. |  пробелы последовательности (вплоть до замены индексного набора I другим индексным набором той же мощности ) |
Коммутативная  -алгебры с единицей | A и B изоморфны как -алгебры | Алгебра  непрерывных функций на компакте пространство Хаусдорфа, до гомеоморфизма базового пространства. |
The символическое преобразование формулы из одной формы в другую называется «переписыванием» этой формулы. Можно изучить абстрактные свойства переписывания общих формул, изучив набор правил, с помощью которых можно корректно манипулировать формулами. Это «правила перезаписи» - неотъемлемая часть абстрактной системы перезаписи. Часто возникает вопрос, можно ли привести какое-то общее выражение к единой общей форме, нормальной форме. Если разные последовательности перезаписей по-прежнему приводят к одной и той же форме, то эту форму можно назвать нормальной формой, а перезапись - конфлюэнтной. Не всегда удается получить нормальную форму.
не имеет нормальной формы. В типизированном лямбда-исчислении каждый правильно сформированный термин можно переписать в его нормальную форму.В теории графов, раздел математики, канонизация графов - это задача нахождения канонической формы данного графа G. Каноническая форма - это помеченный граф Canon (G), который изоморфен G, так что каждый граф который изоморфен G, имеет ту же каноническую форму, что и G. Таким образом, из решения проблемы канонизации графа, можно также решить проблему изоморфизма графов : проверить, изоморфны ли два графа G и H, вычислить их канонические формы Canon (G) и Canon (H) и проверить, идентичны ли эти две канонические формы.
В вычислении приведение данных к любому виду канонической формы обычно называется нормализацией данных.
Например, нормализация базы данных - это процесс организации полей и таблиц в реляционной базе данных для минимизации избыточность и зависимость.
В области безопасности программного обеспечения обычная уязвимость не отмечена вредоносным вводом (см. Внедрение кода ). Смягчением этой проблемы является правильная проверка ввода. Перед выполнением проверки ввода, ввод обычно нормализуется путем исключения кодировки (например, кодировка HTML ) и сокращения входных данных до одного общего набора символов .
Другие формы данных, обычно связанные с помощью обработки сигналов (включая аудио и визуализации ) или машинного обучения, можно нормализовать, чтобы обеспечить ограниченный диапазон значений.
