Расстояние Минковского

редактировать

расстояние Минковского или метрика Минковского - это метрика в нормированном векторном пространстве, которое можно рассматривать как обобщение как евклидова расстояния, так и манхэттенского расстояния. Он назван в честь немецкого математика Германа Минковского.

Определение

Расстояние Минковского порядка $p {\ displaystyle p}$ $p$ (где $p {\ displaystyle p}$ $p$ является целым числом) между двумя точками

X = (x 1, x 2,…, xn) и Y = (y 1, y 2,…, yn) ∈ R n { \ Displaystyle X = (x_ {1}, x_ {2}, \ ldots, x_ {n}) {\ text {и}} Y = (y_ {1}, y_ {2}, \ ldots, y_ {n}) \ in \ mathbb {R} ^ {n}}

X = (x_ {1}, x_ {2}, \ ldots, x_ {n}) {\ text {и}} Y = (y_ {1}, y_ {2}, \ ldots, y_ {n}) \ in {\ mathbb {R}} ^ {n}

определяется как:

D (X, Y) = (∑ я = 1 n | xi - yi | p) 1 p {\ displaystyle D \ left (X, Y \ right) = \ left (\ sum _ {i = 1} ^ {n} | x_ {i} -y_ {i} | ^ {p} \ right) ^ {\ frac {1} { p}}}

{\ displaystyle D \ left (X, Y \ right) = \ left (\ sum _ {i = 1} ^ {n} | x_ {i} -y_ {i} | ^ { p} \ right) ^ {\ frac {1} {p}}}

Для $p ≥ 1 {\ displaystyle p \ geq 1}$ $p \ geq 1$ расстояние Минковского является метрикой в результате Минковского неравенство. Когда $p < 1 {\displaystyle p<1}$ $p <1$ , расстояние между (0,0) и (1,1) равно $2 1 / p>2 {\ displaystyle 2 ^ {1 / p}>2}$ $2^{1/p}>2$ , но точка (0,1) на расстоянии 1 от обеих этих точек. Поскольку это нарушает неравенство треугольника , для $p < 1 {\displaystyle p<1}$ $p <1$ это не метрика. Однако для этих значений можно получить метрику, просто удалив показатель степени $1 / p {\ displaystyle 1 / p}$ $1 / p$ . Результирующая метрика также является F-нормой.

расстояние Минковского обычно используется с $p {\ displaystyle p}$ $p$ равно 1 или 2, что соответствует Манхэттенскому расстоянию и Евклидову расстоянию соответственно. В предельном случае $p {\ displaystyle p}$ $p$ достигая бесконечности, получаем расстояние Чебышева :

lim p → ∞ (∑ i = 1 n | xi - yi | p) 1 p = max i = 1 n | xi - yi |. {\ displaystyle \ lim _ {p \ to \ infty} {\ left (\ sum _ {i = 1} ^ {n } | x_ {i} -y_ {i} | ^ {p} \ right) ^ {\ frac {1} {p}}} = \ max _ {i = 1} ^ {n} | x_ {i} - y_ {i} |. \,}

\ lim_ {p \ to \ infty} {\ left (\ sum_ {i = 1} ^ n | x_i-y_i | ^ p \ right) ^ \ frac {1} {p}} = \ max_ {i = 1} ^ n | x_i-y_i |. \,

Аналогично, для $p {\ displaystyle p}$ $p$ достижения отрицательной бесконечности, мы имеем:

lim p → - ∞ (∑ i = 1 п | х я - у я | p) 1 p = min i = 1 n | х я - у я |. {\ displaystyle \ lim _ {p \ to - \ infty} {\ left (\ sum _ {i = 1} ^ {n} | x_ {i} -y_ {i} | ^ {p} \ right) ^ { \ frac {1} {p}}} = \ min _ {i = 1} ^ {n} | x_ {i} -y_ {i} |. \,}

\ lim_ {p \ to- \ infty} {\ left (\ sum_ {i = 1} ^ n | x_i-y_i | ^ p \ right) ^ \ frac {1} {p}} = \ min_ {i = 1} ^ n | x_i-y_i |. \,

Расстояние Минковского также можно рассматривать как кратное среднему значению покомпонентных разностей между P и Q.

На следующем рисунке показаны единичные круги (набор всех точек, которые находятся на единичном расстоянии от центра) с различными значениями $p {\ displaystyle p}$ $p$ :

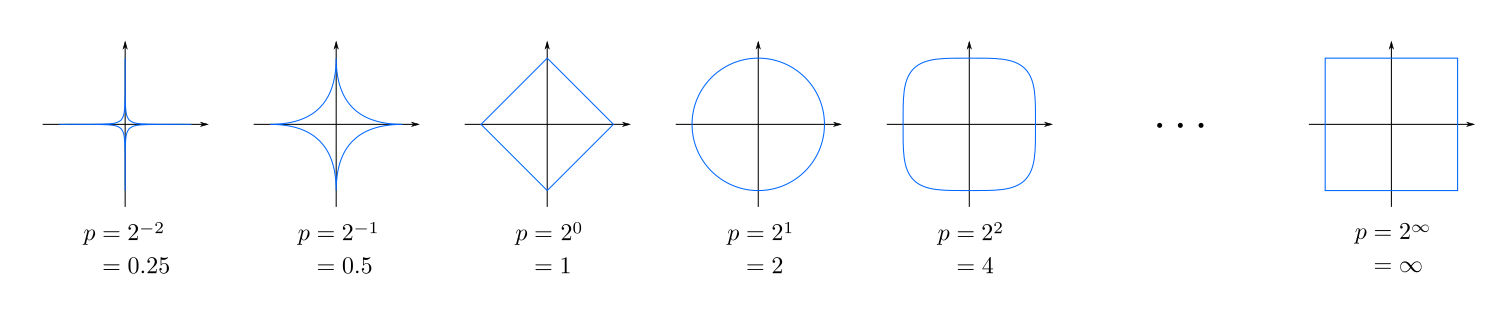
См. также

Внешние ссылки

Простая реализация IEEE 754 на C ++

Пакет / модуль JavaScript NPM