Лемма Шепли – Фолкмана

Лемма Шепли – Фолкмана иллюстрируется сложением Минковского четырех множеств. Точка (+) в выпуклой оболочке суммы Минковского четырех невыпуклых множеств (справа) является суммой четырех точек (+) из (слева) множества - две точки в двух невыпуклых множествах плюс две точки в выпуклой оболочке двух множеств. Выпуклые корпуса окрашены в розовый цвет. Каждый исходный набор имеет ровно две точки (показаны красными точками).

Лемма Шепли – Фолкмана является результатом выпуклой геометрии с приложениями в математическая экономика, которая описывает сложение Минковского из , устанавливает в векторное пространство. Сложение Минковского определяется как сложение элементов наборов: например, добавление набора, состоящего из целых чисел ноль и единица, к самому себе дает набор, состоящий из нуля, единицы и два:

{0, 1} + {0, 1} = {0 + 0, 0 + 1, 1 + 0, 1 + 1} = {0, 1, 2}.

Шепли – Фолкман Лемма и связанные с ней результаты дают утвердительный ответ на вопрос: «Близка ли сумма многих множеств к выпуклой ?» Набор определяется как выпуклый, если каждый отрезок линии, соединяющий две его точки, является подмножеством в наборе: например, твердый диск $\bullet \; \{\backslash \; displaystyle\; \backslash \; bullet\}$- выпуклый набор, а круг $\circ \; \{\backslash \; displaystyle\; \backslash \; circ\}$- нет, потому что отрезок линии, соединяющий две отдельные точки $\oslash \; \{\backslash \; displaystyle\; \backslash \; oslash\; \}$не является частью круга. Лемма Шепли – Фолкмана предполагает, что если количество суммированных множеств превышает размерность векторного пространства, то их сумма Минковского будет приблизительно выпуклой.

Лемма Шепли – Фолкмана была введена как шаг в доказательстве теоремы Шепли – Фолкмана теоремы, которая устанавливает верхнюю границу на расстоянии между сумма Минковского и ее выпуклая оболочка. Выпуклая оболочка множества Q - это наименьшее выпуклое множество, которое содержит Q. Это расстояние равно нулю тогда и только тогда, когда сумма выпукла. Оценка теоремы на расстояние зависит от размерности D и формы множеств слагаемых, но не от количества множеств слагаемых N, когда N>D. Формы подколлекции, состоящей только из D наборов слагаемых, определяют границу расстояния между средним значением Минковского из N наборов

​⁄N(Q1+ Q 2 +... + Q N)

и его выпуклая оболочка. Когда N увеличивается до бесконечности, граница уменьшается до нуля (для наборов слагаемых равномерно ограниченного размера). Верхняя граница теоремы Шепли – Фолкмана была уменьшена на следствие Старра (альтернативно теорема Шепли – Фолкмана – Старра ).

Лемма Ллойда Шепли и Джона Фолкмана была впервые опубликована экономистом Россом М. Старром, который исследовал существование экономическое равновесие во время обучения у Кеннета Эрроу. В своей статье Старр изучал выпуклую экономику, в которой невыпуклые множества заменены их выпуклыми оболочками; Старр доказал, что выпуклая экономика имеет равновесия, которые близко аппроксимируются «квазиравновесиями» исходной экономики; кроме того, он доказал, что каждое квазиравновесие обладает многими из оптимальных свойств истинного равновесия, существование которых доказано для выпуклой экономики. После статьи Старра 1969 года результаты Шепли – Фолкмана – Старра широко использовались, чтобы показать, что основные результаты (выпуклой) экономической теории являются хорошим приближением к крупным экономикам с невыпуклостями; например, квазиравновесия близко аппроксимируют равновесия выпуклой экономики. «Получение этих результатов в общей форме было одним из главных достижений послевоенной экономической теории», - писал Роджер Геснери. Тема невыпуклых множеств в экономике изучалась многими нобелевскими лауреатами, помимо Ллойда Шепли, получившего премию в 2012 году: Arrow (1972), Роберт Ауман (2005), Жерар Дебре (1983), Тьяллинг Купманс (1975), Пол Кругман (2008) и Пол Самуэльсон (1970); дополнительная тема выпуклых множеств в экономике была подчеркнута этими лауреатами, наряду с Леонидом Гурвичем, Леонидом Канторовичем (1975) и Робертом Солоу. (1987).

Лемма Шепли – Фолкмана имеет приложения также в оптимизации и теории вероятностей. В теории оптимизации лемма Шепли – Фолкмана использовалась для объяснения успешного решения задач минимизации, которые являются суммами многих функций. Лемма Шепли – Фолкмана также использовалась в доказательствах «закона средних значений» для случайных множеств, теоремы, которая была доказана только для выпуклых множеств..

• 1 Вводный пример
• 2 Предварительные сведения
  • 2.1 Вещественные векторные пространства
  • 2.2 Выпуклые множества
  • 2.3 Выпуклая оболочка
  • 2.4 сложение Минковского
  • 2.5 Выпуклые оболочки сумм Минковского
• 3 утверждения
  • 3.1 Лемма Шепли и Фолкмана
    • 3.1.1 Размерность реального векторного пространства
  • 3.2 Теорема Шепли – Фолкмана и следствие Старра
  • 3.3 Доказательства и вычисления
• 4 Приложения
  • 4.1 Экономика
    • 4.1.1 Невыпуклые предпочтения
    • 4.1.2 Статья Старра 1969 года и современная экономика
  • 4.2 Математическая оптимизация
    • 4.2.1 Предварительные сведения о теории оптимизации
    • 4.2.2 Аддитивная оптимизация задачи
  • 4.3 Теория вероятностей и меры
• 5 Примечания
• 6 Ссылки
• 7 Внешние ссылки

Например, подмножество целых чисел {0, 1, 2 } содержится в inte rval из вещественных чисел [0, 2], которое является выпуклым. Из леммы Шепли – Фолкмана следует, что каждая точка в [0, 2] является суммой целого числа из {0, 1} и действительного числа из [0, 1].

Расстояние между выпуклым интервалом [0, 2] и невыпуклое множество {0, 1, 2} равно половине

1/2 = | 1 - 1/2 | = | 0 - 1/2 | = | 2 - 3/2 | = | 1 - 3/2 |.

Однако расстояние между средним суммой Минковского

1/2 ({0, 1} + {0, 1}) = {0, 1/2, 1}

и его выпуклая оболочка [0, 1] составляет только 1/4, что составляет половину расстояния (1/2) между его слагаемым {0, 1} и [0, 1]. По мере того, как все больше наборов складываются вместе, среднее от их суммы «заполняет» его выпуклую оболочку: максимальное расстояние между средним и его выпуклой оболочкой приближается к нулю, поскольку среднее включает больше слагаемых.

Лемма Шепли – Фолкмана зависит от следующих определений и является результатом выпуклой геометрии.

вещественных векторных пространств

A вещественных векторных пространств двух измерений. быть задана декартовой системой координат, в которой каждая точка идентифицируется упорядоченной парой действительных чисел, называемых «координатами», которые обычно обозначаются x и y. Две точки на декартовой плоскости могут быть сложены по координатам

(x1, y 1) + (x 2, y 2) = (x 1+x2, y 1+y2);

далее точка может быть умножена на каждое действительное число λ по координатам

λ (x, y) = (λx, λy).

В более общем смысле, любое реальное векторное пространство (конечной) размерности D можно рассматривать как набор всех D-кортежей вещественных чисел D {(v 1, v 2,..., V D)}, для которых определены две операции : сложение вектора и умножение на действительное число. Для конечномерных векторных пространств операции сложения векторов и умножения действительных чисел могут быть определены по координатам, следуя примеру декартовой плоскости.

Выпуклое наборы

В выпуклом наборе Q отрезок линии, соединяющий любые две его точки, является подмножеством Q. В невыпуклом множестве Q, точка в некотором отрезке линии, соединяющем две его точки, не является членом Q. отрезок линии ents проверяет, является ли подмножество выпуклым.

В реальном векторном пространстве непустой набор Q определяется как выпуклый if, для каждой пары точек, каждая точка на отрезке линии, который соединяет их, является подмножеством Q. Например, сплошной диск $\bullet \; \{\backslash \; displaystyle\; \backslash \; bullet\}$выпуклый, а круг $\circ \; \{\backslash \; displaystyle\; \backslash \; circ\}$- нет, потому что он не содержит отрезка линии, соединяющего его точки $\oslash \; \{\backslash \; displaystyle\; \backslash \; oslash\}$; невыпуклый набор из трех целых чисел {0, 1, 2} содержится в интервале [0, 2], который является выпуклым. Например, твердый куб выпуклый; однако все, что является полым или помятым, например форма полумесяца, не является выпуклым. пустое множество выпукло по определению или пусто, в зависимости от автора.

Более формально набор Q является выпуклым, если для всех точек v 0 и v 1 в Q и для каждого действительного числа λ в блоке interval [0,1], точка

(1 - λ) v 0 + λv 1

является членом Q.

Согласно математической индукции, множество Q является выпуклым тогда и только тогда, когда каждая выпуклая комбинация членов Q также принадлежит Q. По определению, выпуклая комбинация индексированного подмножества {v 0, v 1,..., v D } векторного пространства - это любое средневзвешенное значение λ 0v0+ λ 1v1+... + λ DvDдля некоторого индексированного набора неотрицательных действительных чисел {λ d }, удовлетворяющего уравнению λ 0 + λ 1 +... + λ D = 1.

Определение выпуклого множества подразумевает, что пересечение двух выпуклых множеств является выпуклым множеством. В более общем смысле, пересечение семейства выпуклых множеств является выпуклым множеством. В частности, пересечение двух непересекающихся множеств является пустым множеством, которое является выпуклым.

Выпуклая оболочка

В выпуклой оболочке красного множества, каждая синяя точка - это выпуклая комбинация некоторых красных точек.

Для каждого подмножества Q реального векторного пространства его выпуклая оболочка Conv (Q) является минимальной выпуклое множество, содержащее Q. Таким образом, Conv (Q) является пересечением всех выпуклых множеств, которые покрывают Q. Выпуклая оболочка множества может быть эквивалентно определена как множество всех выпуклых комбинаций точек в Q. Например, выпуклая оболочка множества целых чисел {0,1} является замкнутым интервал из вещественных чисел [0,1], который содержит целые конечные точки. Выпуклая оболочка единичной окружности является замкнутым единичным кругом, который содержит единичную окружность.

Минковский сложение

Минковски сложение наборов. Сумма квадратов $Q\; 1\; =\; [0,\; 1]\; 2\; \{\backslash \; displaystyle\; Q\_\; \{1\}\; =\; [0,1]\; ^\; \{2\}\}$и $Q\; 2\; =\; [1,\; 2]\; 2\; \{\backslash \; displaystyle\; Q\_\; \{2\}\; =\; [1,2]\; ^\; \{2\}\}$- квадрат $Q\; 1\; +\; Q\; 2\; =\; [1,\; 3]\; 2\; 2\; \{\backslash \; displaystyle\; Q\_\; \{1\}\; +\; Q\_\; \{2\}\; =\; [1,3]\; ^\; \{2\}\; 2\}$.

В любом векторном пространстве (или алгебраической структуре с добавлением) $X\; \{\backslash \; displaystyle\; X\}$, сумма Минковского двух непустых наборов $A,\; B\; \subseteq \; X\; \{\backslash \; displaystyle\; A,\; B\; \backslash \; substeq\; X\}$определяется как - поэлементная операция $A\; +\; B:\; =\; \{x\; +\; y\; \mid \; x\; \in \; A,\; y\; \in \; B\}.\; \{\backslash \; displaystyle\; A\; +\; B:\; =\; \backslash \; \{x\; +\; y\; \backslash \; mid\; x\; \backslash \; in\; A,\; ~\; y\; \backslash \; in\; B\; \backslash \}.\}$(см. также.) Например,

$\{0,\; 1\}\; +\; \{0,\; 1\}\; =\; \{0\; +\; 0,\; 0\; +\; 1,\; 1\; +\; 0,\; 1\; +\; 1\}\; =\; \{0,\; 1,\; 2\}\; \{\backslash \; displaystyle\; \backslash \; \{0,1\; \backslash \}\; +\; \backslash \; \{0,1\; \backslash \}\; =\; \backslash \; \{0\; +\; 0,0\; +\; 1,1\; +\; 0,1\; +\; 1\; \backslash \}\; =\; \backslash \; \{0,1,2\; \backslash \}\}$

Очевидно, что эта операция коммутативна и ассоциативна для набора непустых множеств. Все такие операции четко определенным образом распространяются до рекурсивных форм $\sum \; n\; =\; 1\; N\; Q\; n\; =\; Q\; 1\; +\; Q\; 2\; +\dots \; +\; Q\; N.\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{N\}\; Q\_\; \{n\}\; =\; Q\_\; \{1\}\; +\; Q\_\; \{2\}\; +\; \backslash \; ldots\; +\; Q\_\; \{N\}.\}$По принципу индукции легко видеть, что

$\sum \; n\; =\; 1\; NQ\; n\; =\; \{\sum \; n\; =\; 1\; N\; qn\; \mid \; qn\; \in \; Q\; n,\; 1\; \le \; n\; \le \; N\}.\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{N\}\; Q\_\; \{n\}\; =\; \backslash \; \{\backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{N\}\; q\_\; \{n\}\; \backslash \; mid\; q\_\; \{n\}\; \backslash \; in\; Q\_\; \{n\},\; ~\; 1\; \backslash \; leq\; n\; \backslash \; leq\; N\; \backslash \}.\}$

Выпуклые оболочки сумм Минковского

Сложение Минковского хорошо ведет себя относительно взятия выпуклых оболочек. В частности, для всех подмножеств $A,\; B\; \subseteq \; X\; \{\backslash \; displaystyle\; A,\; B\; \backslash \; substeq\; X\}$реального векторного пространства $X\; \{\backslash \; displaystyle\; X\}$, выпуклая оболочка их суммы Минковского является суммой Минковского их выпуклых оболочек. То есть

$C\; o\; n\; v\; (A\; +\; B)\; =\; C\; o\; n\; v\; (A)\; +\; C\; o\; n\; v\; (B).\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{Conv\}\; (A\; +\; B)\; =\; \backslash \; mathrm\; \{Conv\}\; (A)\; +\; \backslash \; mathrm\; \{Conv\}\; (B).\}$

И по индукции следует, что

$C\; onv\; (\sum \; n\; Знак\; равно\; 1\; NQ\; n)\; знак\; равно\; \sum \; N\; =\; 1\; NC\; onv\; (Q\; n)\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{Conv\}\; (\backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{N\}\; Q\_\; \{n\})\; =\; \backslash \; sum\; \_\; \{n\; =\; 1\; \}\; ^\; \{N\}\; \backslash \; mathrm\; \{Conv\}\; (Q\_\; \{n\})\}$

для любого $N\; \in \; N\; \{\backslash \; displaystyle\; N\; \backslash \; in\; \backslash \; mathbb\; \{N\}\}$и непустого подмножества $Q\; N\; \subseteq \; X\; \{\backslash \; displaystyle\; Q\_\; \{n\}\; \backslash \; substeq\; X\}$, $1\; \le \; n\; \le \; N\; \{\backslash \; displaystyle\; 1\; \backslash \; leq\; n\; \backslash \; leq\; N\}$.

сложение Минковского и выпуклые оболочки. Шестнадцать темно-красных точек (справа) образуют сумму Минковского четырех невыпуклых множеств (слева), каждое из которых состоит из пары красных точек. Их выпуклые оболочки (заштрихованные розовым цветом) содержат знаки плюса (+): правый знак плюса - это сумма левых знаков плюса.

Согласно предыдущему тождеству для каждой точки $x\; \in \; C\; onv\; (\sum \; n\; =\; 1\; NQ\; n)\; \{\backslash \; displaystyle\; x\; \backslash \; in\; \backslash \; mathrm\; \{Conv\}\; (\backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{N\}\; Q\_\; \{n\})\}$в выпуклой оболочке есть элементы, $qn\; (x)\; \in \; C\; onv\; (Q\; n)\; \{\backslash \; displaystyle\; q\_\; \{n\}\; (x)\; \backslash \; in\; \backslash \; mathrm\; \{Conv\}\; (Q\_\; \{n\})\}$для $1\; \le \; n\; \le \; N\; \{\backslash \; displaystyle\; 1\; \backslash \; leq\; n\; \backslash \; leq\; N\}$, зависит от $x\; \{\backslash \; displaystyle\; x\}$и так, что $\sum \; n\; =\; 1\; N\; qn\; (x)\; =\; x\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{N\}\; q\_\; \{n\}\; (x)\; =\; x\}$.

Лемма Шепли и Фолкмана

Лауреат Нобелевской премии 2012 г. Economics, Ллойд Шепли доказал лемму Шепли – Фолкмана с помощью Джона Фолкмана.

. Работая с вышеуказанной схемой, лемма Шепли – Фолкмана утверждает, что в приведенном выше представлении

$Икс\; =\; \sum \; N\; =\; 1\; N\; qn\; (x)\; \{\backslash \; displaystyle\; x\; =\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{N\}\; q\_\; \{n\}\; (x)\}$

не более $D\; \{\backslash \; displaystyle\; D\; \}$резюме ds $q\; n\; (x)\; \{\backslash \; displaystyle\; q\_\; \{n\}\; (x)\}$нужно брать строго из выпуклой оболочки. То есть существует представление указанной выше формы, такое что $|\; \{l\; \le \; n\; \le \; N\; \mid \; q\; n\; (x)\; \in \; C\; o\; n\; v\; (Q\; n)\; \setminus \; Q\; n\}\; |\; \le \; D\; \{\backslash \; displaystyle\; |\; \backslash \; \{l\; \backslash \; leq\; n\; \backslash \; leq\; N\; \backslash \; mid\; q\_\; \{n\}\; (x)\; \backslash \; in\; \backslash \; mathrm\; \{Conv\}\; (Q\_\; \{n\})\; \backslash \; setminus\; Q\_\; \{n\}\; \backslash \}\; |\; \backslash \; leq\; D\}$. При необходимости перестановка индексов означает, что точка имеет представление

$x\; =\; \sum \; n\; =\; 1\; D\; qn\; (x)\; +\; \sum \; n\; =\; D\; +\; 1\; N\; qn\; (x)\; \{\backslash \; displaystyle\; x\; =\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{D\}\; q\_\; \{n\}\; (x)\; +\; \backslash \; sum\; \_\; \{n\; =\; D\; +\; 1\}\; ^\; \{N\}\; q\_\; \{n\}\; (x)\}$

где $qn\; \in \; C\; onv\; (Q\; n)\; \{\backslash \; displaystyle\; q\_\; \{n\}\; \backslash \; in\; \backslash \; mathrm\; \{Conv\}\; (Q\_\; \{n\})\}$для $1\; \le \; n\; \le \; D\; \{\backslash \; displaystyle\; 1\; \backslash \; leq\; n\; \backslash \; leq\; D\}$и $qn\; \in \; Q\; n\; \{\backslash \; displaystyle\; q\_\; \{n\}\; \backslash \; in\; Q\_\; \{n\}\}$для $D\; +\; 1\; \le \; n\; \le \; N\; \{\backslash \; displaystyle\; D\; +\; 1\; \backslash \; leq\; n\; \backslash \; leq\; N\}$. Обратите внимание, что повторная индексация зависит от точки. Более сжато, лемма Шепли – Фолкмана утверждает, что

$C\; o\; n\; v\; (\sum \; n\; =\; 1\; N\; Q\; n)\; \subseteq \; \bigcup \; I\; \subseteq \; \{1,\; 2,\dots \; N\}:\; |\; Я\; |\; =\; D\; \sum \; n\; \in \; I\; C\; o\; n\; v\; (Q\; n)\; +\; \sum \; n\; \notin \; I\; Q\; n.\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{Conv\}\; (\backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{N\}\; Q\_\; \{n\})\; \backslash \; substeq\; \backslash \; bigcup\; \_\; \{I\; \backslash \; substeq\; \backslash \; \{1,2,\; \backslash \; ldots\; N\; \backslash \}:\; ~\; |\; I\; |\; =\; D\}\; \backslash \; sum\; \_\; \{n\; \backslash \; in\; I\}\; \backslash \; mathrm\; \{Conv\}\; (Q\_\; \{n\})\; +\; \backslash \; sum\; \_\; \{n\; \backslash \; notin\; I\}\; Q\_\; \{n\}.\}$

Например, каждая точка в $[0,\; 2]\; =\; [0,\; 1]\; +\; [0,\; 1]\; =\; C\; onv\; (\{0,\; 1\})\; +\; C\; onv\; (\{0,\; 1\})\; \{\backslash \; displaystyle\; [0,2]\; =\; [\; 0,1]\; +\; [0,1]\; =\; \backslash \; mathrm\; \{Conv\}\; (\backslash \; \{0,1\; \backslash \})\; +\; \backslash \; mathrm\; \{Conv\}\; (\backslash \; \{0,1\; \backslash \})\}$согласно лемма - сумма элемента в $\{0,\; 1\}\; \{\backslash \; displaystyle\; \backslash \; \{0,1\; \backslash \}\}$и элемента в $[0,\; 1]\; \{\backslash \; displaystyle\; [0,\; 1]\}$.

Размерность реального векторного пространства

И наоборот, лемма Шепли – Фолкмана характеризует размерность конечномерных вещественных векторных пространств. То есть, если векторное пространство подчиняется лемме Шепли – Фолкмана для натурального числа D и не для числа меньше D, то его размерность равна D; лемма Шепли – Фолкмана верна только для конечномерных векторных пространств.

Теорема Шепли – Фолкмана и следствие Старра

Описанный радиус (синий) и внутренний радиус (зеленый) множества точек (темно-красный, с его выпуклый корпус показан более светлыми красными пунктирными линиями). Внутренний радиус меньше описанного радиуса, за исключением подмножеств одной окружности, для которых они равны.

Шепли и Фолкман использовали свою лемму для доказательства своей теоремы, которая ограничивает расстояние между суммой Минковского и ее выпуклой оболочкой, «выпуклая» сумма:

• Теорема Шепли – Фолкмана утверждает, что квадрат евклидова расстояния от любой точки выпуклой суммы Conv (∑ Q n) до исходной (невыпуклой) сумма ∑ Q n ограничена суммой квадратов D наибольших описанных радиусов множеств Q n (радиусы наименьших сфер, охватывающих эти множества ). Эта оценка не зависит от количества слагаемых N (если N>D).

Теорема Шепли – Фолкмана устанавливает ограничение на расстояние между суммой Минковского и ее выпуклой оболочкой; это расстояние равно нулю тогда и только тогда, когда сумма выпукла. Их оценка на расстояние зависит от размерности D и формы наборов слагаемых, но не от количества наборов слагаемых N, когда N>D.

Радиус описанной окружности часто превышает (и не может быть меньше) внутреннего радиуса:

• Внутренний радиус набора Q n определяется как наименьшее число r такое, что для любой точки q в выпуклой оболочке Q n, существует сфера радиуса r, которая содержит подмножество Q n, выпуклая оболочка которого содержит q.

Старр использовал внутренний радиус для уменьшения верхней границы, указанной в теорема Шепли – Фолкмана:

• Следствие Старра к теореме Шепли – Фолкмана утверждает, что квадрат евклидова расстояния от любой точки x в выпуклой сумме Conv (∑ Q n) до исходной (невыпукленной) суммы ∑ Q n ограничено суммой квадратов D наибольших внутренних радиусов множеств Q n.

Следствие Старра устанавливает верхнюю границу евклидова расстояния между метками Минковского. сумма N множеств и выпуклая оболочка Сумма Минковского; это расстояние между суммой и ее выпуклой оболочкой является мерой невыпуклости множества. Для простоты это расстояние называется «невыпуклостью» набора (по отношению к измерению Старра). Таким образом, оценка Старра невыпуклости суммы зависит только от D наибольших внутренних радиусов множеств слагаемых; однако оценка Старра не зависит от числа слагаемых N, когда N>D. Например, расстояние между выпуклым интервалом [0, 2] и невыпуклым множеством {0, 1, 2} равно половине

1/2 = | 1 - 1/2 | = | 0 - 1/2 | = | 2 - 3/2 | = | 1 - 3/2 |.

Таким образом, оценка Старра на невыпуклость среднего

​⁄N∑ Q n

уменьшается с увеличением числа слагаемых N. Например, расстояние между усредненным набором

1/2 ({0, 1} + {0, 1}) = {0, 1/2, 1}

и его выпуклой оболочкой [0, 1] составляет всего 1/4, что составляет половину расстояния (1/2) между его слагаемым {0, 1} и [0, 1]. Формы подколлекции, состоящей только из D наборов слагаемых, определяют границу расстояния между средним набором и его выпуклой оболочкой; таким образом, когда количество слагаемых увеличивается до бесконечности, граница уменьшается до нуля (для наборов слагаемых равномерно ограниченного размера). Фактически, оценка Старра невыпуклости этого среднего множества уменьшается до нуля по мере увеличения числа слагаемых N до бесконечности (когда внутренние радиусы всех слагаемых ограничены то же число).

Доказательства и вычисления

Первоначальное доказательство леммы Шепли – Фолкмана установило только существование представления, но не предоставило алгоритм для вычисления представления: аналогичные доказательства были предоставлены, среди прочих, Эрроу и Ханом, Касселсом и Шнайдером. Абстрактное и элегантное доказательство Экеланда было расширено Арстейном. Различные доказательства появлялись и в неопубликованных работах. В 1981 году Старр опубликовал итерационный метод для вычисления представления заданной точки суммы; однако его вычислительное доказательство дает более слабую оценку, чем исходный результат. Элементарное доказательство леммы Шепли – Фолкмана в конечномерном пространстве можно найти в книге Берцекаса вместе с приложениями к оценке разрыва двойственности в сепарабельных задачах оптимизации и играх с нулевой суммой.

Лемма Шепли – Фолкмана позволяет исследователям распространить результаты для сумм Минковского выпуклых множеств на суммы общих множеств, которые не обязательно должны быть выпуклыми. Такие суммы множеств возникают в экономике, в математической оптимизации и в теории вероятностей ; в каждой из этих трех математических наук невыпуклость является важной особенностью приложений.

Экономика

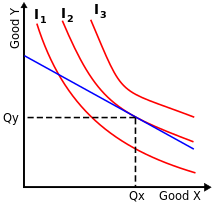Потребитель предпочитает каждую корзину товаров на кривой безразличия I3каждой корзине на I 2. Корзина (Q x, Q y), где бюджетная строка (показана синим) поддерживает I2, является оптимальной и выполнимой, в отличие от любой корзины, лежащей на I 3, что является предпочтительным, но невыполнимым.

В экономике предпочтения потребителя определяются по всем «корзинам» товаров. Каждая корзина представлена ​​в виде неотрицательного вектора, координаты которого представляют количество товаров. В этом наборе корзин для каждого потребителя определена кривая безразличия ; кривая безразличия потребителя включает все корзины товаров, которые потребитель считает эквивалентными: то есть для каждой пары корзин на одной кривой безразличия потребитель не предпочитает одну корзину другой. Через каждую товарную корзину проходит одна кривая безразличия. Набор предпочтений потребителя (относительно кривой безразличия) - это объединение кривой безразличия и всех товарных корзин, которые потребитель предпочитает кривой безразличия. Предпочтения потребителя являются выпуклыми, если все такие наборы предпочтений являются выпуклыми.

Оптимальная корзина товаров возникает там, где строка бюджета поддерживает набор предпочтений потребителя, как показано на диаграмме. Это означает, что оптимальная корзина находится на максимально возможной кривой безразличия с учетом линии бюджета, которая определяется в терминах вектора цен и дохода потребителя (вектора обеспеченности). Таким образом, набор оптимальных корзин - это функция цен, и эта функция называется потребительским спросом. Если набор предпочтений является выпуклым, то при каждой цене спрос потребителя представляет собой выпуклый набор, например, уникальную оптимальную корзину или линейный сегмент корзин.

Невыпуклые предпочтения

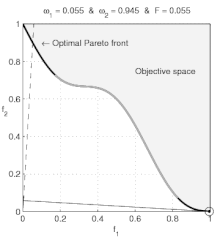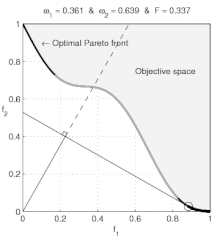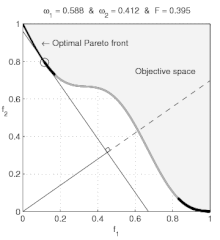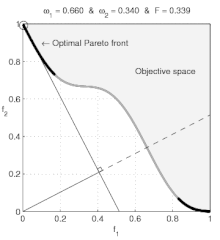Когда потребительские предпочтения предпочтения имеют вогнутость, потребитель может перепрыгивать между двумя отдельными оптимальными корзинами.

Однако, если набор предпочтений невыпуклый, то некоторые цены определяют линию бюджета, которая поддерживает две отдельные оптимальные корзины. Например, мы можем представить, что для зоопарков лев стоит столько же, сколько орел, и, кроме того, бюджета зоопарка хватит на одного орла или одного льва. Можно также предположить, что смотритель зоопарка считает любое животное равноценным. В этом случае зоопарк покупал либо одного льва, либо одного орла. Конечно, современный зоопарк не захочет покупать половину орла и половину льва (или грифона )! Таким образом, предпочтения хранителя зоопарка невыпуклые: хранитель зоопарка предпочитает иметь любое животное любой строго выпуклой комбинации обоих.

Когда набор предпочтений потребителя невыпуклый, то (для некоторых цен) спрос потребителя не связан ; несвязанный спрос подразумевает некоторое прерывистое поведение потребителя, как это обсуждалось Гарольдом Хотеллингом :

Если рассматривать кривые безразличия к покупкам как имеющие волнообразный характер, выпуклые в некоторых регионах и вогнутые в других, мы вынужден сделать вывод, что только части, выпуклые к началу координат, могут считаться имеющими какое-либо значение, поскольку остальные по существу ненаблюдаемы. Их можно обнаружить только по скачкам спроса, которые могут возникнуть при изменении соотношений цен, что приводит к резкому скачку точки касания через пропасть при повороте прямой линии. Но, хотя такие разрывы могут указывать на существование пропастей, они никогда не могут измерить их глубину. Вогнутые части кривых безразличия и их многомерные обобщения, если они существуют, должны навсегда остаться в неизмеримой безвестности.

Трудности изучения невыпуклых предпочтений подчеркивали Герман Вольд и снова Пол Самуэльсон, который писал, что невыпуклости «окутаны вечной тьмой...», согласно Диверту.

Тем не менее, с 1959 по 1961 год предпочтения невыпуклых тел были освещены последовательность статей в Журнале политической экономии (JPE). Основными участниками были Фаррелл, Батор, Купманс и Ротенберг. В частности, в статье Ротенберга обсуждалась приближенная выпуклость сумм невыпуклых множеств. Эти документы JPE стимулировали публикацию статьи Ллойда Шепли и Мартина Шубика, в которых рассматривались выпуклые предпочтения потребителей и вводилась концепция «приблизительного равновесия». Статьи JPE и статья Шепли-Шубика повлияли на другое понятие «квазиравновесия», благодаря Роберту Ауманну.

статье 1969 года Старра и современной экономике

Кеннету Эрроу (1972 Нобель лауреат ) помог Россу М. Старру изучить невыпуклость экономику.

Были собраны предыдущие публикации по невыпуклости и экономике в аннотированной библиографии Kenneth Arrow. Он дал библиографию Старру, который в то время был студентом и поступил на продвинутый курс математической экономики Эрроу. В своей курсовой работе Старр изучал общие равновесия искусственной экономики, в которой невыпуклые предпочтения были заменены их выпуклой оболочкой. В выпуклой экономике при каждой цене совокупный спрос был суммой выпуклой оболочки требований потребителей. Идеи Старра заинтересовали математиков Ллойда Шепли и Джона Фолкмана, которые доказали свою одноименную лемму и теорему в «частной переписке», о чем сообщалось в опубликованной статье Старра 1969.

В своей публикации 1969 года Старр применил теорему Шепли – Фолкмана – Старра. Старр доказал, что «выпуклая» экономика имеет общее равновесие, которое может быть близко аппроксимировано «квазиравновесием» исходной экономики, когда количество агентов превышает размер товаров: Конкретно, Старр доказал, что существует по крайней мере один квазиравновесие. -равновесие цен p opt со следующими свойствами:

• Для каждой квазиравновесной цены p opt все потребители могут выбрать оптимальные корзины (максимально предпочтительные и соответствующие их бюджетным ограничениям).
• При квазиравновесных ценах p opt в выпуклой экономике рынок каждого товара находится в равновесии: его предложение равно его спросу.
• Для каждого квазиравновесия, цены «почти очищают» рынки для исходной экономики: верхняя граница на расстоянии между множеством равновесий «выпуклой» экономики и множеством квазиравновесий исходная экономия вытекала из следствия Старра к теореме Шепли – Фолкмана.

Старр установил, что

"в совокупности несоответствие между распределением в фиктивной экономике, порожденным [взятием выпуклой оболочки всех наборов потребления и производства], и некоторым распределением в реальной экономике ограничено способом, который не зависит от количества экономических агенты. Следовательно, средний агент испытывает отклонение от намеченных действий, значение которого исчезает по мере того, как число агентов стремится к бесконечности ".

После работы Старра 1969 года результаты Шепли-Фолкмана-Старра широко использовались в экономической теории. Роджер Гезнери резюмировал их экономические последствия: «Некоторые ключевые результаты, полученные при допущении выпуклости, остаются (приблизительно) актуальными в обстоятельствах, когда выпуклость не работает. Например, в экономиках с большой стороной потребления невыпуклость предпочтений не разрушает стандартные результаты "." Получение этих результатов в общем виде было одним из главных достижений послевоенной экономической теории ", - писал Гезнери. Тема невыпуклые множества в экономике изучались многими лауреатами Нобелевской премии : Эрроу (1972), Роберт Ауманн (2005), Жерар Дебре (1983), Тьяллинг Купманс (1975), Пол Кругман (2008) и Пол Самуэльсон (1970); дополнительная тема выпуклых множеств в области экономики был отмечен этими лауреатами наряду с Леонидом Гурвичем, Леонидом Канторовичем (1975) и Робертом Солоу (1987). –Результаты Фолкмана – Старра были представлены в экономической литературе: в микроэкономике, в теории общего равновесия, в государственной экономике (включая рыночные неудачи ), так как а также в теории игр, в математико-экономической s, а в прикладная математика (для экономистов). Результаты Шепли-Фолкмана-Старра также повлияли на экономические исследования с использованием меры и теории интеграции.

Математическая оптимизация

A функция является выпуклой, если область выше его граф является выпуклым множеством.

Лемма Шепли – Фолкмана использовалась для объяснения того, почему большие задачи минимизации с невыпуклостями могут быть почти решена (с помощью итерационных методов, доказательства сходимости которых указаны только для выпуклых задач ). Лемма Шепли – Фолкмана поощряет использование методов выпуклой минимизации в других приложениях с суммами многих функций.

Предварительные сведения о теории оптимизации

Нелинейная оптимизация опирается на следующие определения для функции :

• График функции f - это набор пар аргументов x и оценок функции f (x)

График (f) = {(x, f (x))}

• эпиграф функции с действительным знаком f - это набор точек над графиком

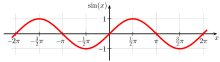синусоидальной функцией является невыпуклая.

Epi (f) = {(x, u): f (x) ≤ u }.

• Функция с действительным знаком определяется как выпуклая функция, если ее эпиграф является выпуклым множеством.

Например, квадратичная функция f (x) = x является выпуклой, как и абсолютное значение функция g ( х) = | х |. Однако синусоидальная функция (изображена) невыпуклая на интервале (0, π).

Проблемы аддитивной оптимизации

Во многих задачах оптимизации целевая функция f является разделимой: то есть f является суммой многих слагаемых-функций, каждая из которых имеет собственный аргумент:

f (x) = f ((x1,..., x N))= ∑fn(xn).

Например, задачи линейной оптимизации разделимы. Для разделяемой задачи с оптимальным решением мы фиксируем оптимальное решение

xmin = (x 1,..., x N)min

с минимальным значением f ( x min). Для этой разделяемой задачи мы также рассматриваем оптимальное решение (xmin, f (x min))«выпуклой задачи», где выпуклые оболочки взятых из графиков функций слагаемых.Таким оптимальным решением является предел последовательности точек в выпуклой задаче

(xj, f (x j))∈ ∑Conv (Graph (f n)).

Конечно, данная оптимальная точка представляет собой сумму точек на графиках исходных слагаемых и небольшого числа выпуклых слагаемых по лемме Шепли – Фолкмана.

Этот анализ был опубликовано Иваром Экеландом в 1974 г., чтобы объяснить очевидную выпуклость разделимых задач со многими слагаемыми, несмотря на невыпуклость задач слагаемых. В 1973 г. молодой математик Клод Лемарешаль был удивлен благодаря его успеху с выпуклой минимизацией методом ds о задачах, которые заведомо невыпуклые; для минимизации нелинейных задач решение двойной задачи не должно предоставлять полезную информацию для решения основной задачи, если только основная задача не является выпуклой и не удовлетворяет квалификационным ограничениям . Проблема Лемарешала была аддитивно отделимой, и каждая функция слагаемого была невыпуклой; тем не менее, решение двойственной задачи обеспечивает близкое приближение к оптимальному значению прямой задачи. Анализ Экланда объяснил успех методов выпуклой минимизации для больших и разделимых задач, несмотря на невыпуклость слагаемых функций. Экеланд и более поздние авторы утверждали, что аддитивная отделимость создает приблизительно выпуклую совокупную проблему, даже несмотря на то, что слагаемые функции невыпуклые. Решающим шагом в этих публикациях является использование леммы Шепли – Фолкмана. Лемма Шепли – Фолкмана поощряет использование методов выпуклой минимизации в других приложениях с суммами многих функций.

Теория вероятностей и меры

Выпуклые множества часто изучаются с помощью теории вероятностей.. Каждая точка в выпуклой оболочке (непустого ) подмножества Q конечномерного пространства является ожидаемым значением простого случайного вектор, который принимает свои значения в Q, как следствие леммы Каратеодори. Таким образом, для непустого множества Q набор ожидаемых значений простых Q-значных случайных векторов равен выпуклой оболочке Q; это равенство означает, что результаты Шепли – Фолкмана – Старра полезны в теории вероятностей. С другой стороны, теория вероятностей предоставляет инструменты для изучения выпуклых множеств в целом и результатов Шепли – Фолкмана – Старра в частности. Результаты Шепли – Фолкмана – Старра широко использовались в вероятностной теории случайных множеств, например, для доказательства закона больших чисел, центральной предельной теоремы, и принцип больших отклонений . Эти доказательства вероятностных предельных теорем использовали результаты Шепли – Фолкмана – Старра, чтобы избежать предположения, что все случайные множества являются выпуклыми.

A вероятностная мера - это конечная мера, и лемма Шепли – Фолкмана имеет приложения в не вероятностной теории меры, например в теориях объема и векторные меры. Лемма Шепли – Фолкмана позволяет уточнить неравенство Брунна – Минковского, которое ограничивает объем сумм в терминах объемов их множеств слагаемых. Объем набора определяется с помощью меры Лебега, которая определяется на подмножествах евклидова пространства. В продвинутой теории меры лемма Шепли – Фолкмана использовалась для доказательства теоремы Ляпунова, которая утверждает, что диапазон векторной меры выпуклый. Здесь традиционный термин «диапазон» (альтернативно «изображение») - это набор значений, производимых функцией. Векторная мера - это векторное обобщение меры; например, если p 1 и p 2 - это вероятностные меры, определенные в одном и том же измеряемом пространстве, тогда функция произведения p1p2- векторная мера, где p 1p2определяется для каждого события ω как

(p1p2)(ω) = (p1(ω), p 2 (ω)).

Теорема Ляпунова была используется в экономике, в ("bang-bang" ) теории управления и в статистической теории. Теорема Ляпунова была названа непрерывным аналогом леммы Шепли – Фолкмана, которая сама была названа дискретным аналогом теоремы Ляпунова.

• Эрроу, Кеннет Дж. ; Хан, Фрэнк Х. (1980) [1971]. Общий конкурентный анализ. Учебники по экономике. 12 (перепечатка Сан-Франциско, Калифорния: Holden-Day, Inc. Mathematical Economics Texts 6 изд.). Амстердам: Северная Голландия. ISBN 0-444-85497-5. MR 0439057. Cite имеет пустой неизвестный параметр: | 1 =() CS1 maint: ref = harv (ссылка )
• Artstein, Zvi (1980). «Дискретный и непрерывный взрыв и лицевые пространства, или: ищите крайние точки». Обзор SIAM. 22 (2): 172–185. doi : 10.1137 / 1022026. JSTOR 2029960. MR 0564562. CS1 maint: ref = harv (ссылка )
• Картер, Майкл (2001). Основы математической экономики. Кембридж, Массачусетс: MIT Press. Pp. Xx + 649. ISBN 0-262-53192-5. MR 1865841. (Сайт автора с ответами на упражнения ). Архивировано с оригинала 15 сентября 2006 г. CS1 maint: ref = harv (ссылка )
• Диверт, WE (1982). «12 двойственных подходов к микроэкономической теории». В Эрроу, Кеннет Джозеф ; Intriligator, Майкл Д. (ред.). Справочник по математической экономике, Том II . Справочники по экономике. 1 . Амстердам: North-Holla nd Publishing Co., стр. 535–599. DOI : 10.1016 / S1573-4382 (82) 02007-4. ISBN 978-0-444-86127-6. MR 0648778. CS1 maint: ref = harv (ссылка )
• Экеланд, Ивар (1999) [1976]. «Приложение I: Априорная оценка в выпуклом программировании». В Экланд, Ивар; Темам, Роджер (ред.). Выпуклый анализ и вариационные задачи. Классика прикладной математики. 28 (Исправленное переиздание изд. Северной Голландии). Филадельфия, Пенсильвания: Общество промышленной и прикладной математики (SIAM). Стр. 357–373. ISBN 0 -89871-450-8. MR 1727362. CS1 maint: ref = harv (ссылка )
• Грин, Джерри; Хеллер, Уолтер П. (1981). "1 Математический анализ и выпуклость с приложениями к экономике ". В Эрроу, Кеннет Джозеф ; Intriligator, Майкл Д. (ред.). Справочник по математической экономике, Том I . Справочники по экономике. 1 . Амстердам: North-Holland Publishing Co., стр. 15–52. doi : 10.1016 / S1573-4382 (81) 01005-9. ISBN 0-444-86126-2. MR 0634800. CS1 maint: ref = harv (ссылка )
• G uesnerie, Роджер (1989). «Первое наилучшее распределение ресурсов с невыпуклостями в производстве». В Корнете, Бернар; Тюлькенс, Генри (ред.). Вклад в исследования операций и экономику: двадцатая годовщина CORE (доклады симпозиума, проведенного в Лувен-ла-Нев, январь 1987 г.). Кембридж, Массачусетс: MIT Press. С. 99–143. ISBN 0-262-03149-3. MR 1104662. CS1 maint: ref = harv (ссылка )
• Mas-Colell, A. (1987). «Невыпуклость». В Итуэлл, Джон ; Милгейт, Мюррей ; Ньюман, Питер (ред. Новый Палгрейв: экономический словарь (первое издание). Palgrave Macmillan. Pp. 653–661. doi : 10.1057 / 9780230226203.3173. 278>ISBN 9780333786765. (PDF-файл на домашней странице Mas-Colell ). CS1 maint: ref = harv (ссылка )
• Rockafellar, R. Tyrrell (1997). Выпуклый анализ. Princeton Landmarks in Mathematics. Princeton, NJ: Princeton University Press. Pp. Xviii + 451. ISBN 0-691-01586-4. MR 1451876. CS1 maint: ref = harv (ссылка ). Перепечатка 1970 (MR 274683 ) Princeton Mathematical Series 28
• Schneider, Rolf (1993). Выпуклые тела: теория Брунна – Минковского. Энциклопедия математики и ее приложений. 44 . Кембридж: Cambridge University Press, стр. Xiv + 490. ISBN 0-521-35220-7. MR 1216521. CS1 maint: ref = harv (ссылка )
• Старр, Росс М. (1969). «Квазиравновесия на рынках с невыпуклыми предпочтениями (Приложение 2: Теорема Шепли – Фолкмана, стр. 35–37)». Econometrica. 37 (1): 25–38. doi : 10.2307 / 1909201. JSTOR 1909201. CS1 maint: ref = harv (ссылка )
• Старр, Росс М. (2008). «Теорема Шепли – Фолкмана». В Дурлауф, Стивен Н. ; Блюм, Лоуренс E (ред.). Новый экономический словарь Пэлгрейва (второе изд.). Palgrave Macmillan. Pp. 317–318 (1-е изд.). doi : 10.1057 / 9780230226203.1518. ISBN 978-0-333-78676- 5. Cite имеет пустой неизвестный параметр: | 1 =() CS1 maint: ref = harv (ссылка )

• Андерсон, Роберт М. (март 2005 г.). «1 Теорема Шепли – Фолкмана» (PDF). Economics 201B: невыпуклые предпочтения и приблизительные равновесия. Беркли, Калифорния: экономический факультет Калифорнийского университета в Беркли. pp. 1–5. Проверено 15 января 2011 г. Cite имеет пустой неизвестный параметр: | 1 =()
• Howe, Roger (ноябрь 1979 г.). О тенденции к выпуклости векторной суммы множеств (PDF) (Отчет). Дискуссионные документы фонда Cowles. 538 . Bo x 2125 Йельская станция, Нью-Хейвен, Коннектикут 06520: Фонд исследований в области экономики Коулза, Йельский университет. Проверено 15 января 2011 г. Cite имеет пустой неизвестный параметр: | 1 =() CS1 maint: location (link )
• Starr, Ross M. (сентябрь 2009 г.). «8 выпуклых множеств, теорем о разделении и невыпуклых множеств в R (раздел 8.2.3 Измерение невыпуклости, теорема Шепли – Фолкмана)» (PDF). Общая теория равновесия: введение. Стр. 3–6. doi : 10.1017 / CBO9781139174749. ISBN 9781139174749. MR 1462618. (Проект второго издания, из курса Старра на экономическом факультете Калифорнийского университета в Сан-Диего). Проверено 15 января 2011 г.
• Старр, Росс М. (май 2007 г.). 75>«Теорема Шепли – Фолкмана» (PDF). Стр. 1–3. (Черновик статьи для второго издания Экономического словаря New Palgrave). Проверено 15 января 2011 г.