 Математическая индукция может быть неформально проиллюстрирована ссылкой на последовательный эффект падения домино.
Математическая индукция может быть неформально проиллюстрирована ссылкой на последовательный эффект падения домино. Математическая индукция - это метод математического доказательства. По сути, он используется для доказательства того, что утверждение P ( n) выполняется для любого натурального числа n = 0, 1, 2, 3,... ; то есть общее утверждение представляет собой последовательность бесконечного числа случаев P (0), P (1), P (2), P (3),.... Неформальные метафоры помогают объяснить эту технику, например, падение домино или подъем по лестнице:
Математическая индукция доказывает, что мы можем подняться по лестнице сколь угодно высоко, доказывая, что мы можем подняться на нижнюю ступеньку ( основание) и что с каждой ступеньки мы можем подняться на следующую ( ступеньку).
- Конкретная математика, стр. 3 на полях.Доказательство по индукции состоит из двух корпусов. Первый, базовый случай (или базис), доказывает утверждение для n = 0 без каких-либо знаний о других случаях. Второй случай, шаг индукции, доказывает, что если утверждение верно для любого данного случая n = k, то оно должно выполняться и для следующего случая n = k + 1. Эти два шага устанавливают, что утверждение верно для любого натурального числа n.. Базовый вариант не обязательно начинать с п = 0, но часто с п = 1, и, возможно, с каким - либо фиксированное натуральное число п = N, установление истины заявления для всех натуральных чисел п ≥ N.
Метод может быть расширен для доказательства утверждений о более общих хорошо обоснованных структурах, таких как деревья ; это обобщение, известное как структурная индукция, используется в математической логике и информатике. Математическая индукция в этом расширенном смысле тесно связана с рекурсией. Математическая индукция - это правило вывода, используемое в формальных доказательствах, и это основа большинства доказательств правильности компьютерных программ.
Хотя его название может предполагать иное, математическую индукцию не следует путать с индуктивными рассуждениями, используемыми в философии (см. Проблема индукции ). Математический метод исследует бесконечно много случаев, чтобы доказать общее утверждение, но делает это с помощью конечной цепочки дедуктивных рассуждений с участием переменной n, которая может принимать бесконечно много значений.
В 370 г. до н.э. Платоновский « Парменид» мог содержать ранний пример неявного индуктивного доказательства. Противоположная итеративная техника - обратный отсчет, а не вверх - встречается в парадоксе соритов, где утверждалось, что если 1000000 песчинок образуют кучу, а удаление одной песчинки из кучи оставляет ее кучей, то одна песчинка. (или даже без зерен) образует кучу.
В Индии первые неявные доказательства с помощью математической индукции появляются в « циклическом методе » Бхаскары и в аль-Фахри, написанном аль-Караджи около 1000 г. н.э., который применил его к арифметическим последовательностям для доказательства биномиальной теоремы и свойств треугольника Паскаля..
Однако ни один из этих древних математиков явно не высказал гипотезы индукции. Другой подобный случай (вопреки тому, что написал Вакка, как тщательно показал Фройденталь) был случай Франческо Моролико в его Arithmeticorum libri duo (1575), который использовал эту технику, чтобы доказать, что сумма первых n нечетных целых чисел равна n 2.
Самым ранним строгим применением индукции был Герсонид (1288–1344). Первая явная формулировка принципа индукции была дана Паскалем в его « Арифметическом треугольнике» (1665). Другой француз, Ферма, широко использовал родственный принцип: косвенное доказательство бесконечным спуском.
Гипотеза индукции также использовалась швейцарцем Якобом Бернулли, и с тех пор она стала широко известной. Современная формальная трактовка этого принципа появилась только в XIX веке у Джорджа Буля, Августа де Моргана, Чарльза Сандерса Пирса, Джузеппе Пеано и Ричарда Дедекинда.
Простейшая и наиболее распространенная форма математической индукции предполагает, что утверждение, содержащее натуральное число n (то есть целое число n ≥ 0 или 1), выполняется для всех значений n. Доказательство состоит из двух шагов:
Гипотеза индуктивного шага о том, что утверждение верно для определенного n, называется индукционной гипотезой или индуктивной гипотезой. Чтобы доказать индуктивный шаг, нужно принять предположение индукции для n, а затем использовать это предположение, чтобы доказать, что утверждение верно для n + 1.
Авторы, которые предпочитают определять натуральные числа, начинающиеся с 0, используют это значение в базовом случае; те, кто определяет натуральные числа, чтобы начать с 1, используют это значение.
С помощью математической индукции можно доказать следующее утверждение P ( n) для всех натуральных чисел n.
Это устанавливает общую формулу для суммы натуральных чисел, меньших или равных данному числу; фактически бесконечная последовательность операторов:,, и т.д.
Предложение. Для любого,
Доказательство. Пусть P ( n) - утверждение. Доказательство проводится индукцией по n.
Базовый случай: покажите, что утверждение верно для наименьшего натурального числа n = 0.
P (0) явно верно:
Индуктивный шаг: покажите, что для любого k ≥ 0, есливыполняется P ( k), то P ( k +1) также выполняется.
Предположим предположение индукции, что для конкретного k выполняется единственный случай n = k, что означает, что P ( k) истинно:
Следует, что:
Алгебраически правая часть упрощается как:
Приравнивая крайнюю левую и правую части, мы заключаем, что:
То есть утверждение P ( k + 1) также выполняется, устанавливая индуктивный шаг.
Заключение: Поскольку и базовый случай, и индуктивный шаг были доказаны как истинные, математической индукцией утверждение P ( n) выполняется для любого натурального числа n. ∎
Индукция часто используется для доказательства неравенств. В качестве примера мы докажем это для любого действительного и натурального числа.
На первый взгляд может показаться, что более общая версия для любых действительных чисел может быть доказана без индукции; но случай показывает, что это может быть ложным для нецелых значений. Это предполагает, что мы исследуем утверждение специально для естественных значений, а индукция - самый удобный инструмент.
Предложение. Для любого,.
Доказательство. Зафиксируйте произвольное действительное число, и пусть будет утверждение. Мы вводим в курс дела.
Базовый случай: расчетподтверждается.
Индуктивный шаг: мы показываем следствиедля любого натурального числа. Предположим гипотезу индукции: для данного значенияверенединственный случай. Используя формулу сложения углов и неравенство треугольника, получаем:
Неравенство между крайними левыми и правыми величинами показывает, что это правда, что завершает индуктивный шаг.
Заключение: предложениеверно для всех натуральных чисел. ∎
На практике доказательства по индукции часто строятся по-разному, в зависимости от точного характера доказываемого свойства. Все варианты индукции являются частными случаями трансфинитной индукции; см. ниже.
Если кто-то хочет доказать утверждение не для всех натуральных чисел, а только для всех чисел n, больших или равных определенному числу b, то доказательство по индукции состоит из следующего:
Это можно использовать, например, чтобы показать, что 2 n ≥ n + 5 для n ≥ 3.
Таким образом можно доказать, что некоторое утверждение P ( n) выполняется для всех n ≥ 1 или даже для всех n ≥ −5. Эта форма математической индукции на самом деле является частным случаем предыдущей формы, потому что если доказываемое утверждение - это P ( n), то доказательство его с помощью этих двух правил эквивалентно доказательству P ( n + b) для всех натуральных чисел n с базовый случай индукции 0.
Предположим, бесконечный запас 4- и 5-долларовых монет. Индукция может быть использована для доказательства того, что любая сумма в долларах больше или равная 12 может быть образована комбинацией таких монет. Пусть S ( k) обозначает утверждение « k долларов могут быть образованы комбинацией 4- и 5-долларовых монет ». Доказательство того, что S ( k) истинно для всех k ≥ 12, может быть получено индукцией по k следующим образом:
Базовый случай: показать, что S ( k) выполняется для k = 12, просто: возьмите три 4-долларовые монеты.
Шаг индукции: учитывая, что S ( k) выполняется для некоторого значения k ≥ 12 ( предположение индукции), докажите, что S ( k + 1) также выполняется:
Следовательно, по принципу индукции S ( k) выполняется для всех k ≥ 12, и доказательство завершено.
В этом примере, хотя S ( k) также выполняется, приведенное выше доказательство не может быть изменено для замены минимальной суммы в 12 долларов на любое меньшее значение m. Для m = 11 базовый случай на самом деле неверен; при m = 10 второй случай на этапе индукции (замена трех 5-долларовых монет на четыре 4-долларовых) не сработает; не говоря уже о еще меньшем m.
Иногда желательно доказать утверждение, включающее два натуральных числа, n и m, повторяя процесс индукции. То есть доказывается базовый случай и индуктивный шаг для n, и в каждом из них доказываются базовый случай и индуктивный шаг для m. Смотрите, например, доказательство коммутативности сопровождая добавление натуральных чисел. Возможны и более сложные аргументы с участием трех и более счетчиков.
Метод бесконечного спуска - это разновидность математической индукции, которую использовал Пьер де Ферма. Он используется, чтобы показать, что некоторая инструкция Q ( n) ложна для всех натуральных чисел n. Его традиционная форма состоит в том, чтобы показать, что если Q ( n) истинно для некоторого натурального числа n, то оно также верно и для некоторого строго меньшего натурального числа m. Поскольку не существует бесконечных убывающих последовательностей натуральных чисел, эта ситуация была бы невозможна, тем самым показывая (от противного), что Q ( n) не может быть истинным ни для какого n.
Справедливость этого метода может быть проверена с помощью обычного принципа математической индукции. Используя математическую индукцию по утверждению P ( n), определенному как « Q ( m) ложно для всех натуральных чисел m, меньших или равных n », следует, что P ( n) выполняется для всех n, что означает, что Q ( n) ложно для любого натурального числа n.
Наиболее распространенная форма доказательства с помощью математической индукции требует на этапе индукции доказательства того, что
после чего принцип индукции «автоматизирует» n применений этого шага для перехода от P (0) к P ( n). Это можно было бы назвать «индукцией предшественника», потому что каждый шаг доказывает что-то о числе из чего-то о предшественнике этого числа.
Вариант, представляющий интерес с точки зрения вычислительной сложности, - это «префиксная индукция», в которой на индуктивном шаге доказывается следующее утверждение:
или эквивалентно
Затем принцип индукции «автоматизирует» log n применений этого вывода при переходе от P (0) к P ( n). Фактически, это называется «префиксной индукцией», потому что каждый шаг доказывает что-то о числе из чего-то о «префиксе» этого числа, образованном путем усечения младшего бита его двоичного представления. Его также можно рассматривать как применение традиционной индукции по длине этого двоичного представления.
Если традиционная индукция предшественника интерпретируется вычислительно как n- шаговый цикл, то префиксная индукция будет соответствовать log- n- шаговому циклу. Из-за этого доказательства, использующие префиксную индукцию, «более конструктивны», чем доказательства, использующие предшествующую индукцию.
Индукция по предшественнику может тривиально имитировать индукцию по префиксу для того же оператора. Индукция префикса может имитировать индукцию предшественника, но только за счет усложнения инструкции (добавление ограниченного универсального квантора ), поэтому интересные результаты, связывающие индукцию префикса с вычислением за полиномиальное время, зависят от полного исключения неограниченных кванторов и ограничения чередования. ограниченных универсальных и экзистенциальных кванторов, разрешенных в утверждении.
Можно пойти еще дальше: нужно доказать
после чего принцип индукции «автоматизирует» log log n приложений этого вывода при переходе от P (0) к P ( n). Эта форма индукции аналогичным образом использовалась для изучения логарифмических параллельных вычислений.
Другой вариант, называемый полной индукцией, индукцией курса значений или сильной индукцией (в отличие от которого основная форма индукции иногда называется слабой индукцией), упрощает доказательство индуктивного шага с помощью более сильной гипотезы: утверждение доказывается при предположение, которое выполняется для всех натуральных чисел меньше, чем ; напротив, основная форма только предполагает. Название «сильная индукция» не означает, что этот метод может доказать нечто большее, чем «слабая индукция», а просто относится к более сильной гипотезе, используемой в индуктивном шаге.
Фактически, можно показать, что эти два метода фактически эквивалентны, как объясняется ниже. В этой форме полной индукции все еще необходимо доказать базовый случай, и может даже потребоваться доказать дополнительные базовые случаи, например, до того, как будет применен общий аргумент, как в приведенном ниже примере числа Фибоначчи.
Хотя только что описанная форма требует доказательства базового случая, в этом нет необходимости, если можно доказать (предполагая для всех ниже) для всех. Это частный случай трансфинитной индукции, описанный ниже, хотя он больше не эквивалентен обычной индукции. В этой форме базовый случай включается в случай, когда он доказывается без каких-либо других предположений; этот случай, возможно, придется рассматривать отдельно, но иногда тот же аргумент применяется для и, что делает доказательство более простым и элегантным. В этом методе, однако, важно убедиться, что доказательство не подразумевает это неявно, например, говоря «выберите произвольный » или предполагая, что набор из m элементов имеет элемент.
Полная индукция эквивалентна обычной математической индукции, описанной выше, в том смысле, что доказательство одним методом может быть преобразовано в доказательство другим. Предположим, что имеется доказательство по полной индукции. Позвольте значить « справедливо для всех таких, что ». Тогда верно для всех тогда и только тогда, когда верно для всех, и наше доказательство легко трансформируется в доказательство с помощью (обычной) индукции. С другой стороны, если бы оно было доказано с помощью обычной индукции, доказательство уже фактически было бы доказано с помощью полной индукции: доказывается в базовом случае, без каких-либо предположений, и доказывается на этапе индукции, на котором можно предположить все более ранние случаи, но нужно использовать только случай.
Полная индукция наиболее полезна, когда для каждого индуктивного шага требуется несколько экземпляров индуктивной гипотезы. Например, полная индукция может использоваться, чтобы показать, что
где это п - го числа Фибоначчи, (далее золотое сечение ) и корни полинома. Используя тот факт, что для каждого, указанная выше идентичность может быть проверена прямым вычислением, если предполагается, что оно уже выполняется для обоих и. Для завершения доказательства идентичность должна быть проверена в двух базовых случаях: и.
Другое доказательство по полной индукции использует гипотезу, что утверждение верно для всех меньших более тщательно. Рассмотрим утверждение, что «каждое натуральное число больше 1 является произведением (одного или нескольких) простых чисел », что является частью фундаментальной теоремы арифметики о « существовании ». Для доказательства шага индукции предположение индукции состоит в том, что для данного утверждения утверждение верно для всех меньших. Если простое число, то это, безусловно, произведение простых чисел, а если нет, то по определению это произведение:, где ни один из множителей не равен 1; следовательно, ни один не равен, и поэтому оба больше 1 и меньше чем. Гипотеза индукции теперь применима к и, поэтому каждое из них является произведением простых чисел. Таким образом, это продукт произведений простых чисел и, следовательно, сам продукт простых чисел.
Мы постараемся доказать тот же пример, что и выше, на этот раз с сильной индукцией. Утверждение остается прежним:
Однако будут небольшие различия в структуре и предположениях доказательства, начиная с расширенного базового случая:
Базовый случай: покажите, что верно для.
Базовый случай верен.
Гипотеза индукции: для некоторых предположение верно для всех с.
Индуктивный шаг: Докажите, что верно.
Выбор и наблюдение, которое показывает, что это верно, с помощью индуктивной гипотезы. То есть сумма может быть образована некоторой комбинацией монет и долларов. Затем, просто добавив долларовую монету к этой комбинации, вы получите сумму. То есть держит. QED
Иногда удобнее вывести обратный вывод, доказывая утверждение для, учитывая его справедливость для. Однако доказательства действительности утверждения ни для одного числа недостаточно, чтобы установить базовый случай; вместо этого нужно доказать утверждение для бесконечного подмножества натуральных чисел. Например, Огюстен Луи Коши сначала использовал прямую (регулярную) индукцию, чтобы доказать неравенство среднего арифметического и геометрического для всех степеней двойки, а затем использовал обратную индукцию, чтобы показать это для всех натуральных чисел.
Индуктивный шаг должен быть доказан для всех значений n. Чтобы проиллюстрировать это, Джоэл Коэн предложил следующий аргумент, цель которого - доказать математической индукцией, что все лошади одного цвета :
Базовый случай тривиален (поскольку любая лошадь того же цвета, что и она сама), а индуктивный шаг верен во всех случаях. Однако логика индуктивного шага неверна из-за утверждения, что «два набора перекрываются» неверно (есть только лошади до удаления и после удаления, наборы по одной лошади не перекрываются).
В логике второго порядка можно записать « аксиому индукции» следующим образом:
где P (.) - переменная для предикатов, содержащих одно натуральное число, а k и n - переменные для натуральных чисел.
Другими словами, базовый случай P (0) и шаг индукции (а именно, что предположение индукции P ( k) влечет P ( k + 1)) вместе означают, что P ( n) для любого натурального числа n. Аксиома индукции утверждает справедливость вывода, что P ( n) выполняется для любого натурального числа n из базового случая и индуктивного шага.
Первый квантор в аксиоме распространяется на предикаты, а не на отдельные числа. Это квантор второго порядка, что означает, что эта аксиома сформулирована в логике второго порядка. Аксиоматизирующая арифметическая индукция в логике первого порядка требует схемы аксиом, содержащей отдельную аксиому для каждого возможного предиката. В статье Аксиомы Пеано содержится дальнейшее обсуждение этого вопроса.
Аксиома структурной индукции для натуральных чисел была впервые сформулирована Пеано, который использовал ее для определения натуральных чисел вместе со следующими четырьмя другими аксиомами:
В теории множеств ZFC первого порядка количественная оценка по предикатам не допускается, но все же можно выразить индукцию количественной оценкой по множествам:
A можно читать как набор, представляющий предложение и содержащий натуральные числа, для которых утверждение верно. Это не аксиома, а теорема, учитывая, что натуральные числа определяются на языке теории множеств ZFC аксиомами, аналогичными аксиомам Пеано.
Один вариант принципа полной индукции может быть обобщен для утверждений об элементах любого хорошо обоснованного множества, то есть множества с иррефлексивным отношением lt;, которое не содержит бесконечных убывающих цепочек. Каждый набор, представляющий порядковое число, хорошо обоснован, набор натуральных чисел является одним из них.
Применительно к хорошо обоснованному набору трансфинитную индукцию можно сформулировать как один шаг. Чтобы доказать, что утверждение P ( n) выполняется для каждого порядкового числа:
Эта форма индукции, применяемая к набору порядковых чисел (которые образуют хорошо упорядоченный и, следовательно, хорошо обоснованный класс), называется трансфинитной индукцией. Это важный метод доказательства в теории множеств, топологии и других областях.
Доказательства по трансфинитной индукции обычно различают три случая:
Строго говоря, в трансфинитной индукции нет необходимости доказывать базовый случай, потому что это пустой частный случай утверждения, что если P истинно для всех n lt; m, то P истинно для m. Это пусто верно именно потому, что не существует значений n lt; m, которые могли бы служить контрпримерами. Таким образом, частные случаи являются частными случаями общего случая.
Принцип математической индукции обычно формулируется как аксиома натуральных чисел; см. аксиомы Пеано. В контексте других аксиом Пеано он строго сильнее, чем принцип хорошего порядка. Предположим следующее:
Затем можно доказать, что индукция, учитывая перечисленные выше аксиомы, влечет принцип хорошего порядка. Следующее доказательство использует полную индукцию и первую и четвертую аксиомы.
Доказательство. Предположим, что существует непустое множество натуральных чисел S, в котором нет наименьшего элемента. Пусть Р ( п) является утверждение, что п не в S. Тогда Р (0) верно, так как если бы это было ложно, то 0 является наименьшим элементом S. Кроме того, пусть n - натуральное число, и предположим, что P ( m) истинно для всех натуральных чисел m, меньших n + 1. Тогда, если P ( n + 1) ложно, n + 1 находится в S, таким образом, являясь минимальным элементом в S, противоречие. Таким образом, P ( n + 1) верно. Следовательно, по принципу полной индукции P ( n) выполняется для всех натуральных чисел n ; поэтому S пусто; противоречие. QED
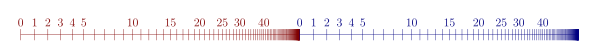 « Числовая линия » для множества {(0, n): n ∈ ℕ} ∪ {(1, n): n ∈ ℕ}. Цифры относятся ко второму компоненту пар; первый может быть получен по цвету или местоположению.
« Числовая линия » для множества {(0, n): n ∈ ℕ} ∪ {(1, n): n ∈ ℕ}. Цифры относятся ко второму компоненту пар; первый может быть получен по цвету или местоположению. С другой стороны, множество {(0, n): n ∈ ℕ} ∪ {(1, n): n ∈ ℕ}, показанное на рисунке, хорошо упорядочено лексикографическим порядком. Более того, за исключением аксиомы индукции, он удовлетворяет всем аксиомам Пеано, где константа Пеано 0 интерпретируется как пара (0,0), а функция преемника Пеано определяется на парах как succ ( x, n) = ( x, n + 1) для всех x ∈ {0,1} и n ∈ℕ. В качестве примера нарушения аксиомы индукции определим предикат P ( x, n) как ( x, n) = (0, 0) или ( x, n) = ( succ ( y, m)) для некоторого y ∈ {0,1} и m ∈ℕ. Тогда базовый случай P (0,0) тривиально верен, как и ступенчатый случай: если P ( x, n), то P ( succ ( x, n)). Однако P не верно для всех пар в наборе.
Аксиомы Пеано с принципом индукции однозначно моделируют натуральные числа. Замена принципа индукции на принцип хорошей упорядоченности позволяет создавать более экзотические модели, удовлетворяющие всем аксиомам.
В нескольких книгах и источниках ошибочно напечатано, что принцип хорошего порядка эквивалентен аксиоме индукции. В контексте других аксиом Пеано это не так, но в контексте других аксиом они эквивалентны; в частности, принцип хорошего порядка подразумевает аксиому индукции в контексте первых двух перечисленных выше аксиом и
Распространенная ошибка во многих ошибочных доказательствах - это предположение, что n - 1 - единственное и точно определенное натуральное число, свойство, которое не подразумевается другими аксиомами Пеано.