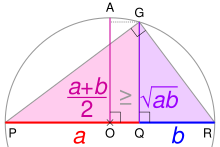
Неравенство средних арифметических и геометрических

Доказательство без слов неравенства средних арифметических и геометрических :. PR - это диаметр круга с центром в O; его радиус AO равен среднему арифметическому значений a и b. Используя теорему о среднем геометрическом, треугольник PGR высота GQ представляет собой среднее геометрическое. Для любого отношения a: b, AO ≥ GQ. 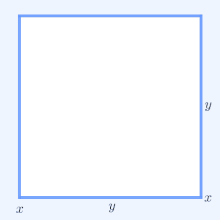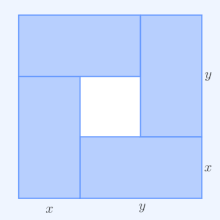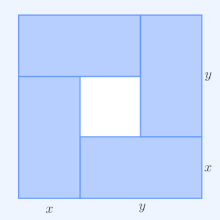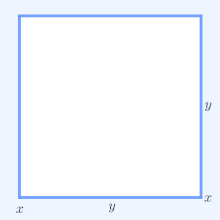Визуальное доказательство того, что (x + y) ≥ 4xy. Извлечение квадратного корня и деление на два дает неравенство AM – GM.

В математике, неравенство среднего арифметического и геометрического, или, короче, AM – GM неравенство, утверждает, что среднее арифметическое списка неотрицательных действительных чисел больше или равно среднему геометрическому того же списка ; и, кроме того, что два средних значения равны тогда и только тогда, когда все числа в списке одинаковы.

Простейший нетривиальный случай - т. Е. С более чем одной переменной - для двух неотрицательных чисел x и y - это утверждение, что

$x\; +\; y\; 2\; \ge \; xy\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\; +\; y\}\; \{2\}\}\; \backslash \; geq\; \{\backslash \; sqrt\; \{xy\}\}\}$

с равенством тогда и только тогда, когда x = y. Этот случай можно увидеть из того факта, что квадрат действительного числа всегда неотрицателен (больше или равен нулю), и из элементарного случая (a ± b) = a ± 2ab + b бинома формула :

$0\; \le \; (x\; -\; y)\; 2\; =\; x\; 2\; -\; 2\; xy\; +\; y\; 2\; =\; x\; 2\; +\; 2\; xy\; +\; y\; 2\; -\; 4\; xy\; =\; (x\; +\; y)\; 2\; -\; 4\; xy.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; 0\; \backslash \; leq\; (xy)\; ^\; \{2\}\; \backslash \backslash \; =\; x\; ^\; \{2\}\; -2xy\; +\; y\; ^\; \{2\}\; \backslash \backslash \; =\; x\; ^\; \{2\}\; +\; 2xy\; +\; y\; ^\; \{2\}\; -4xy\; \backslash \backslash \; =\; (x\; +\; y)\; ^\; \{2\}\; -4xy.\; \backslash \; End\; \{align\}\}\}$

Следовательно (x + y) ≥ 4xy, с равенством именно тогда, когда (x - y) = 0, т.е. x = y. Тогда неравенство AM – GM следует из извлечения положительного квадратного корня из обеих сторон и последующего деления обеих сторон на 2.

Для геометрической интерпретации рассмотрим прямоугольник со сторонами длиной x и y, следовательно, он имеет периметр 2x + 2y и площадь xy. Аналогично, квадрат со всеми сторонами длиной √xy имеет периметр 4√xy и такую ​​же площадь, как прямоугольник. В простейшем нетривиальном случае неравенства AM – GM для периметров следует, что 2x + 2y ≥ 4√xy и что только квадрат имеет наименьший периметр среди всех прямоугольников одинаковой площади.

Расширения неравенства AM – GM доступны для включения весов или обобщенных средних.

• 1 Предпосылки
• 2 Неравенство
• 3 Геометрические интерпретация
• 4 Пример приложения
• 5 Практическое применение
• 6 Доказательства неравенства AM – GM
  • 6.1 Доказательство с использованием неравенства Дженсена
  • 6.2 Доказательство по индукции
    • 6.2.1 Доказательство по индукции # 1
    • 6.2.2 Доказательство по индукции №2
  • 6.3 Доказательство Коши с использованием прямой-обратной индукции
    • 6.3.1 Случай, когда все члены равны
    • 6.3.2 Случай, когда не все члены равны
      • 6.3.2.1 Подслучай, где n = 2
      • 6.3.2.2 Подслучай, где n = 2
      • 6.3.2.3 Подслучай, где n < 2
  • 6.4 Доказательство индукцией с использованием основного исчисления
  • 6.5 Доказательство Полиа с использованием экспоненциальной функции
  • 6.6 Доказательство с помощью множителей Лагранжа
• 7 Обобщения
  • 7.1 Взвешенное неравенство AM – GM
  • 7.2 Доказательство с использованием неравенства Дженсена
  • 7.3 Матричная арифметика Неравенство среднего геометрического
  • 7.4 Другое обобщение ns
• 8 См. также
• 9 Примечания
• 10 Ссылки
• 11 Внешние ссылки

Среднее арифметическое или, менее точно, среднее значение список из n чисел x 1, x 2,..., x n - это сумма чисел, деленная на n:

$x\; 1\; +\; x\; 2\; +\; \cdots \; +\; x\; n\; n.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\}\; \{n\}\}.\}$

Среднее геометрическое аналогично, за исключением того, что определяется только для списка неотрицательных действительных чисел и использует умножение и корень вместо сложения и деления:

$x\; 1\; \cdot \; x\; 2\; \cdots \; xnn.\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; [\{n\}]\; \{x\_\; \{1\}\; \backslash \; cdot\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n\}\}\}.\}$

Если x 1, x 2,..., x n>0, это равно экспоненте среднего арифметического натуральных логарифмов чисел:

$exp\; \; (ln\; \; x\; 1\; +\; ln\; \; x\; 2\; +\; \cdots \; +\; ln\; \; xnn).\; \{\backslash \; displaystyle\; \backslash \; exp\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; ln\; \{x\_\; \{1\}\}\; +\; \backslash \; ln\; \{x\_\; \{2\}\}\; +\; \backslash \; cdots\; +\; \backslash \; ln\; \{x\_\; \{n\}\}\}\; \{n\}\}\; \backslash \; right).\; \}$

Повторяя неравенство с использованием математической записи, мы имеем, что для любого списка из n неотрицательных действительных чисел x 1, x 2,... Икс n,

$Икс\; 1\; +\; Икс\; 2\; +\; \cdots \; +\; Xnn\; \ge \; Икс\; 1\; \cdot \; Икс\; 2\; \cdots \; Xnn,\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\}\; \{п\; \}\}\; \backslash \; geq\; \{\backslash \; sqrt\; [\{n\}]\; \{x\_\; \{1\}\; \backslash \; cdot\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n\}\}\}\; \backslash ,,\}$

и это равенство выполняется тогда и только тогда, когда x 1 = x 2 = · · · = x n.

В двух измерениях, 2x 1 + ​​2x 2 - это периметр прямоугольника со сторонами длиной x 1 и x 2. Аналогично, 4√x 1x2- это периметр квадрата с такой же площадью , x 1x2, что и у этого прямоугольника. Таким образом, для n = 2 неравенство AM – GM утверждает, что прямоугольник заданной площади имеет наименьший периметр, если этот прямоугольник также является квадратом.

Полное неравенство - это расширение этой идеи до n измерений. Каждая вершина n-мерного бокса соединена с n ребрами. Если длины этих ребер равны x 1, x 2,..., x n, тогда x 1 + ​​x 2 + ​​· · · + x n - общая длина ребер, инцидентных вершина. Имеется 2 вершины, поэтому мы умножаем это на 2; Однако поскольку каждое ребро пересекает две вершины, каждое ребро считается дважды. Поэтому делим на 2 и заключаем, что рёбер 2n. Имеется одинаковое количество ребер каждой длины и длины n; следовательно, имеется 2 ребра каждой длины, и сумма всех длин ребер равна 2 (x 1 + ​​x 2 + ​​· · · + x n). С другой стороны,

$2\; n\; -\; 1\; (x\; 1\; +\dots \; +\; xn)\; =\; 2\; n\; -\; 1\; nx\; 1\; x\; 2\; \cdots \; xnn\; \{\backslash \; displaystyle\; 2\; ^\; \{n-1\}\; (x\_\; \{1\}\; +\; \backslash \; ldots\; +\; x\_\; \{n\})\; =\; 2\; ^\; \{n-1\}\; n\; \{\backslash \; sqrt\; [\{n\}]\; \{x\_\; \{1\}\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n\}\}\}\}$

- общая длина соединенных ребер в вершину n-мерного куба равного объема, так как в этом случае x 1 =... = x n. Поскольку неравенство гласит:

$x\; 1\; +\; x\; 2\; +\; \cdots \; +\; xnn\; \ge \; x\; 1\; x\; 2\; \cdots \; xnn,\; \{\backslash \; displaystyle\; \{x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; \backslash \; over\; n\}\; \backslash \; geq\; \{\backslash \; sqrt\; [\{n\}]\; \{x\_\; \{1\}\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n\}\}\},\}$

его можно пересчитать, умножив на n2, чтобы получить

$2\; n\; -\; 1\; (\; Икс\; 1\; +\; Икс\; 2\; +\; \cdots \; +\; Xn)\; \ge \; 2\; N\; -\; 1\; NX\; 1\; Икс\; 2\; \cdots \; Xnn\; \{\backslash \; Displaystyle\; 2\; ^\; \{n-1\}\; (x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\})\; \backslash \; geq\; 2\; ^\; \{n-1\}\; n\; \{\backslash \; sqrt\; [\{n\}]\; \{x\_\; \{1\}\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n\}\}\}\}$

с равенством тогда и только тогда, когда x 1 = x 2 = · · · = x n.

Таким образом, неравенство AM – GM утверждает, что только n-куб имеет наименьшую сумму длин ребер, соединенных с каждая вершина среди всех n-мерных блоков с одинаковым объемом.

Рассмотрим функцию

$f\; (x,\; y,\; z)\; =\; xy\; +\; yz\; +\; zx\; 3\; \{\backslash \; displaystyle\; f\; (x,\; y,\; z)\; =\; \{\backslash \; frac\; \{x\}\; \{y\}\}\; +\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{y\}\; \{z\}\}\}\; +\; \{\backslash \; sqrt\; [\{3\}]\; \{\backslash \; frac\; \{z\}\; \{x\}\}\}\}$

для всех положительных действительных чисел x, y и z. Предположим, мы хотим найти минимальное значение этой функции. Сначала немного его перепишем:

$f\; (x,\; y,\; z)\; =\; 6\; \cdot \; xy\; +\; 1\; 2\; yz\; +\; 1\; 2\; yz\; +\; 1\; 3\; zx\; 3\; +\; 1\; 3\; zx\; 3\; +\; 1\; 3\; zx\; 3\; 6\; =\; 6\; \cdot \; x\; 1\; +\; Икс\; 2\; +\; Икс\; 3\; +\; Икс\; 4\; +\; Икс\; 5\; +\; Икс\; 6\; 6\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; f\; (x,\; y,\; z)\; =\; 6\; \backslash \; cdot\; \{\backslash \; frac\; \{\{\backslash \; frac\; \{x\}\; \{\; y\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{y\}\; \{z\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{y\}\; \{z\; \}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \{\backslash \; sqrt\; [\{3\}]\; \{\backslash \; frac\; \{z\}\; \{x\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \{\backslash \; sqrt\; [\{3\; \}]\; \{\backslash \; frac\; \{z\}\; \{x\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \{\backslash \; sqrt\; [\{3\}]\; \{\backslash \; frac\; \{z\}\; \{x\}\}\}\}\; \{6\}\}\; \backslash \backslash \; =\; 6\; \backslash \; cdot\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; x\_\; \{3\}\; +\; x\_\; \{4\}\; +\; x\_\; \{5\}\; +\; x\_\; \{6\}\}\; \{6\}\}\; \backslash \; end\; \{align\}\}\}$

с

$x\; 1\; =\; xy,\; x\; 2\; =\; x\; 3\; =\; 1\; 2\; yz,\; x\; 4\; =\; x\; 5\; =\; x\; 6\; =\; 1\; 3\; zx\; 3.\; \{\backslash \; displaystyle\; x\_\; \{1\}\; =\; \{\backslash \; frac\; \{x\}\; \{y\}\},\; \backslash \; qquad\; x\_\; \{2\}\; =\; x\_\; \{3\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{y\}\; \{z\}\}\},\; \backslash \; qquad\; x\_\; \{4\}\; =\; x\_\; \{5\}\; =\; x\_\; \{6\}\; =\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \{\backslash \; sqrt\; [\{3\}]\; \{\backslash \; frac\; \{z\}\; \{x\}\; \}\}.\}$

Применяя неравенство AM – GM для n = 6, получаем

$f\; (x,\; y,\; z)\; \ge \; 6\; \cdot \; xy\; \cdot \; 1\; 2\; yz\; \cdot \; 1\; 2\; yz\; \cdot \; 1\; 3\; zx\; 3\; \cdot \; 1\; 3\; zx\; 3\; \cdot \; 1\; 3\; zx\; 3\; 6\; =\; 6\; \cdot \; 1\; 2\; \cdot \; 2\; \cdot \; 3\; \cdot \; 3\; \cdot \; 3\; xyyzzx\; 6\; =\; 2\; 2/3\; \cdot \; 3\; 1/2.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; е\; (х,\; у,\; z)\; \backslash \; geq\; 6\; \backslash \; cdot\; \{\backslash \; sqrt\; [\{6\}]\; \{\{\backslash \; frac\; \{x\}\; \{y\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{y\}\; \{z\}\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{y\}\; \{z\}\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{\; 1\}\; \{3\}\}\; \{\backslash \; sqrt\; [\{3\}]\; \{\backslash \; frac\; \{z\}\; \{x\}\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \{\backslash \; sqrt\; [\{3\}]\; \{\backslash \; frac\; \{z\; \}\; \{x\}\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \{\backslash \; sqrt\; [\{3\}]\; \{\backslash \; frac\; \{z\}\; \{x\}\}\}\}\}\; \backslash \backslash \; =\; 6\; \backslash \; cdot\; \{\backslash \; sqrt\; [\; \{6\}]\; \{\{\backslash \; frac\; \{1\}\; \{2\; \backslash \; cdot\; 2\; \backslash \; cdot\; 3\; \backslash \; cdot\; 3\; \backslash \; cdot\; 3\}\}\; \{\backslash \; frac\; \{x\}\; \{y\}\}\; \{\backslash \; frac\; \{y\}\; \{z\}\}\; \{\backslash \; frac\; \{z\}\; \{x\}\}\}\}\; \backslash \backslash \; =\; 2\; ^\; \{2/3\}\; \backslash \; cdot\; 3\; ^\; \{1/2\}.\; \backslash \; end\; \{align\}\}\}$

Кроме того, мы знаем, что две стороны равны именно тогда, когда все члены среднего равны:

$f\; (x,\; y,\; z)\; =\; 2\; 2/3\; \cdot \; 3\; 1/2,\; когда\; xy\; =\; 1\; 2\; yz\; =\; 1\; 3\; zx\; 3.\; \{\backslash \; displaystyle\; f\; (x,\; y,\; z)\; =\; 2\; ^\; \{2/3\}\; \backslash \; cdot\; 3\; ^\; \{1/2\}\; \backslash \; quad\; \{\backslash \; t\_dv\; \{when\}\}\; \backslash \; quad\; \{\backslash \; frac\; \{x\}\; \{y\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{y\}\; \{z\}\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \{\backslash \; sqrt\; [\{3\}]\; \{\backslash \; frac\; \{z\}\; \{\; x\}\}\}.\}$

Все точки (x, y, z), удовлетворяющие этим условиям, лежат на полупрямой, начинающейся в начале координат, и задаются формулой

$(x,\; y,\; z)\; =\; (t,\; 2\; 3\; 3\; t,\; 3\; 3\; 2\; t)\; при\; t>0.\; \{\backslash \; displaystyle\; (x,\; y,\; z)\; =\; \{\backslash \; biggr\; (\}\; t,\; \{\backslash \; sqrt\; [\{3\}]\; \{2\}\}\; \{\backslash \; sqrt\; \{3\}\}\; \backslash ,\; t,\; \{\backslash \; frac\; \{3\; \{\backslash \; sqrt\; \{\; 3\}\}\}\; \{2\}\}\; \backslash ,\; t\; \{\backslash \; biggr)\}\; \backslash \; quad\; \{\backslash \; t\_dv\; \{with\}\}\; \backslash \; quad\; t>0.\}$

204 Важное практическое применение в

>финансовая математика предназначена для вычисления нормы прибыли : годовая доходность, рассчитанная через среднее геометрическое, меньше средней годовой доходности, рассчитанной по среднему арифметическому ( или равны, если все доходы равны). Это важно при анализе инвестиций, поскольку средняя прибыль завышает совокупный эффект.

Доказательство с использованием неравенства Дженсена

Неравенство Дженсена утверждает, что значение вогнутой функции среднего арифметического больше или равно среднему арифметическому значений функции. Поскольку loga Функция rithm вогнута, мы имеем

$log\; \; (\sum \; i\; x\; i\; n)\; \ge \; \sum \; 1\; n\; log\; \; x\; i\; =\; \sum \; (log\; \; x\; i\; 1\; /\; n)\; =\; log\; \; (\prod \; x\; i\; 1\; /\; n).\; \{\backslash \; displaystyle\; \backslash \; log\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; sum\; \_\; \{i\}\; x\_\; \{i\}\}\; \{n\}\}\; \backslash \; right)\; \backslash \; geq\; \backslash \; sum\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; log\; x\_\; \{i\}\; =\; \backslash \; sum\; \backslash \; left\; (\backslash \; log\; x\_\; \{i\}\; ^\; \{1\; /\; n\}\; \backslash \; right)\; =\; \backslash \; log\; \backslash \; left\; (\backslash \; prod\; x\_\; \{i\}\; ^\; \{1\; /\; n\}\; \backslash \; right).\}$

Принимая antilogs крайних левых и крайних правых частей, имеем неравенство AM – GM.

Доказательства по индукции

Мы должны показать, что

$x\; 1\; +\; x\; 2\; +\; \cdots \; +\; xnn\; \ge \; x\; 1\; x\; 2\; \cdots \; xnn\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\_\; \{1\}\}\; +\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\}\; \{n\}\}\; \backslash \; geq\; \{\backslash \; sqrt\; [\{n\}]\; \{x\_\; \{1\}\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n\}\}\}\}$

с равенство только тогда, когда все числа равны. Если x i ≠ x j, то замена x i и x j на (x i + x j) / 2 оставит среднее арифметическое в левой части без изменений, но увеличит среднее геометрическое в правой части, потому что

$(xi\; +\; xj\; 2)\; 2\; -\; xixj\; =\; (xi\; -\; xj\; 2)\; 2>0.\; \{\backslash \; displaystyle\; \{\backslash \; Bigl\; (\}\; \{\backslash \; frac\; \{x\_\; \{i\}\; +\; x\_\; \{j\}\}\; \{2\}\}\; \{\backslash \; Bigr)\}\; ^\; \{2\}\; -x\_\; \{i\}\; x\_\; \{j\}\; =\; \{\backslash \; Bigl\; (\}\; \{\backslash \; frac\; \{x\_\; \{i\}\; -x\_\; \{j\}\}\; \{2\}\}\; \{\backslash \; Bigr)\}\; ^\; \{2\}>0.\}$

Таким образом, правая сторона будет наибольшей, когда все x i s равны среднему арифметическому

$\alpha \; =\; x\; 1\; +\; x\; 2\; +\; \cdots \; +\; xnn,\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\; \}\}\; \{n\}\},\}$

таким образом, поскольку это наибольшее значение правой части выражения, мы имеем

$x\; 1\; +\; x\; 2\; +\; \cdots \; +\; xnn\; =\; \alpha \; =\; \alpha \; \alpha \; \cdots \; \alpha \; n\; \ge \; Икс\; 1\; Икс\; 2\; \cdots \; xnn.\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\}\; \{n\}\}\; =\; \backslash \; alpha\; =\; \{\backslash \; sqrt\; [\{n\}]\; \{\; \backslash \; alpha\; \backslash \; alpha\; \backslash \; cdots\; \backslash \; alpha\}\}\; \backslash \; geq\; \{\backslash \; sqrt\; [\{n\}]\; \{x\_\; \{1\}\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n\}\}\}.\}$

Это действительное доказательство по делу n = 2, но процедура итеративного взятия попарных средних значений может не дать n равных чисел в случае n ≥ 3. Примером этого случая является x 1 = x 2 ≠ х 3 : усреднение двух разных чисел дает два одинаковых числа, но третье по-прежнему отличается. Следовательно, на самом деле мы никогда не получим неравенство, включающее среднее геометрическое трех равных чисел.

Следовательно, необходим дополнительный трюк или модифицированный аргумент, чтобы превратить вышеприведенную идею в действительное доказательство для случая n ≥ 3.

Доказательство по индукции №1

Из неотрицательных действительных чисел x 1,..., x n, выражение AM – GM эквивалентно

$\alpha \; n\; \ge \; x\; 1\; x\; 2\; \cdots \; xn\; \{\backslash \; displaystyle\; \backslash \; alpha\; ^\; \{n\}\; \backslash \; geq\; x\_\; \{1\}\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n\}\}$

с равенством тогда и только тогда, когда α = x i для всех i ∈ {1,..., n}.

Для следующего доказательства мы применяем математическую индукцию и только хорошо известные правила арифметики.

Основание индукции: Для n = 1 утверждение верно с равенством.

Гипотеза индукции: Предположим, что утверждение AM – GM выполняется для всех вариантов n неотрицательных действительных чисел.

Шаг индукции: Рассмотрим n + 1 неотрицательных действительных чисел x 1,..., x n + 1,. Их среднее арифметическое α удовлетворяет условию

$(n\; +\; 1)\; \alpha \; =\; x\; 1\; +\; \cdots \; +\; x\; n\; +\; x\; n\; +\; 1.\; \{\backslash \; displaystyle\; (n\; +\; 1)\; \backslash \; alpha\; =\; \backslash \; x\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; +\; x\_\; \{n\; +\; 1\}.\}$

Если все x i равны α, то мы имеем равенство в утверждении AM – GM, и все готово. В случае, когда некоторые из них не равны α, должно существовать одно число, которое больше среднего арифметического α, и другое число меньше α. Без потери общности, мы можем переупорядочить наш x i, чтобы разместить эти два конкретных элемента в конце: x n>α и x n + 1 < α. Then

$xn\; -\; \alpha >0\; \alpha \; -\; xn\; +\; 1>0\; \{\backslash \; displaystyle\; x\_\; \{n\}\; -\; \backslash \; alpha>0\; \backslash \; qquad\; \backslash \; alpha\; -x\_\; \{n\; +\; 1\}>0\}$

$⟹\; (xn\; -\; \alpha )\; (\alpha \; -\; xn\; +\; 1)>0.\; (\ast )\; \{\backslash \; displaystyle\; \backslash \; подразумевает\; (x\_\; \{n\}\; -\; \backslash \; alpha)\; (\backslash \; alpha\; -x\_\; \{n\; +\; 1\})>0\; \backslash ,.\; \backslash \; qquad\; (*)\}$

Теперь определите y с помощью

$y:\; =\; xn\; +\; xn\; +\; 1\; -\; \alpha \; \ge \; xn\; -\; \alpha >0,\; \{\backslash \; displaystyle\; y:\; =\; x\_\; \{\; n\}\; +\; x\_\; \{n\; +\; 1\}\; -\; \backslash \; alpha\; \backslash \; geq\; x\_\; \{n\}\; -\; \backslash \; alpha>0\; \backslash ,,\}$

an d рассмотрим n чисел x 1,..., x n – 1, y, которые все неотрицательны. Поскольку

$(n\; +\; 1)\; \alpha \; =\; x\; 1\; +\; \cdots \; +\; xn\; -\; 1\; +\; xn\; +\; xn\; +\; 1\; \{\backslash \; displaystyle\; (n\; +\; 1)\; \backslash \; alpha\; =\; x\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n-1\}\; +\; x\_\; \{n\}\; +\; x\_\; \{n\; +\; 1\}\}$

$n\; \alpha \; =\; x\; 1\; +\; \cdots \; +\; xn\; -\; 1\; +\; xn\; +\; xn\; +\; 1\; -\; \alpha \; ⏟\; =\; y,\; \{\backslash \; displaystyle\; n\; \backslash \; alpha\; =\; x\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n-1\}\; +\; \backslash \; underbrace\; \{x\_\; \{n\}\; +\; x\_\; \{n\; +\; 1\}\; -\; \backslash \; alpha\}\; \_\; \{=\; \backslash ,\; y\},\}$

Таким образом, α также является средним арифметическим n чисел x 1,..., x n – 1, y и предположение индукции подразумевает, что

$\alpha \; n\; +\; 1\; =\; \alpha \; n\; \cdot \; \alpha \; \ge \; x\; 1\; x\; 2\; \cdots \; x\; n\; -\; 1\; y\; \cdot \; \alpha .\; (*\; *)\; \{\backslash \; Displaystyle\; \backslash \; альфа\; ^\; \{п\; +\; 1\}\; =\; \backslash \; альфа\; ^\; \{п\}\; \backslash \; CDOT\; \backslash \; альфа\; \backslash \; geq\; x\_\; \{1\}\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n-1\}\; y\; \backslash \; cdot\; \backslash \; alpha.\; \backslash \; qquad\; (**)\}$

Благодаря (*) мы знаем, что

$(xn\; +\; xn\; +\; 1\; -\; \alpha \; ⏟\; =\; y)\; \alpha \; -\; xnxn\; +\; 1\; =\; (xn\; -\; \alpha )\; (\alpha \; -\; xn\; +\; 1)>0,\; \{\backslash \; displaystyle\; (\backslash \; underbrace\; \{x\_\; \{n\}\; +\; x\_\; \{n\; +\; 1\}\; -\; \backslash \; alpha\}\; \_\; \{=\; \backslash ,\; y\})\; \backslash \; alpha\; -x\_\; \{n\}\; x\_\; \{n\; +\; 1\}\; =\; (x\_\; \{n\}\; -\; \backslash \; alpha)\; (\backslash \; alpha\; -x\_\; \{n\; +\; 1\})>0,\}$

следовательно

$y\; \alpha >xnxn\; +\; 1,\; (\ast \; \ast \; \ast )\; \{\backslash \; displaystyle\; y\; \backslash \; alpha>x\_\; \{\backslash \; displaystyle\; y\; \backslash \; alpha>x\_\; \}\; x\_\; \{n\; +\; 1\}\; \backslash ,,\; \backslash \; qquad\; (\{*\}\; \{*\}\; \{*\})\}$

, в частности, α>0. Следовательно, если хотя бы одно из чисел x 1,..., x n – 1 равно нулю, то в (**) уже есть строгое неравенство. В противном случае правая часть (**) положительна, и строгое неравенство получается путем использования оценки (***) для получения нижней оценки правой части (**). Таким образом, в обоих случаях мы можем заменить (***) на (**), чтобы получить

$\alpha \; n\; +\; 1>x\; 1\; x\; 2\; \cdots \; xn\; -\; 1\; xnxn\; +\; 1,\; \{\backslash \; displaystyle\; \backslash \; alpha\; ^\; \{n\; +\; 1\; \}>x\_\; \{1\}\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n-1\}\; x\_\; \{n\}\; x\_\; \{n\; +\; 1\}\; \backslash ,,\}$

что завершает доказательство.

Доказательство по индукции # 2

Прежде всего мы докажем, что для действительных чисел x 1< 1 and x2>1 следует

$x\; 1\; +\; x\; 2>x\; 1\; x\; 2\; +\; 1.\; \{\backslash \; displaystyle\; x\_\; \{1\}\; +\; x\_\; \{2\}>x\_\; \{1\}\; x\_\; \{2\}\; +1.\}$

Действительно, умножение обеих частей неравенства x 2>1 на 1 - x 1, дает

$x\; 2\; -\; x\; 1\; x\; 2>1\; -\; x\; 1,\; \{\backslash \; displaystyle\; x\_\; \{2\}\; -x\_\; \{1\}\; x\_\; \{2\}>1-x\_\; \{1\},\}$

откуда сразу получается требуемое неравенство.

Теперь мы собираемся доказать, что для положительных действительных чисел x 1,..., x n, удовлетворяющее x 1... x n = 1, выполняется

$x\; 1\; +\; \cdots \; +\; x\; n\; \ge \; n.\; \{\backslash \; displaystyle\; x\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; \backslash \; geq\; n.\}$

Равенство выполняется, только если x 1 =... = x n = 1.

Базис индукции: Для n = 2 утверждение верно из-за указанного выше свойства.

Гипотеза индукции: Предположим, что утверждение верно для всех натуральных чисел до n - 1.

Шаг индукции: Рассмотрим натуральное число n, т.е. для положительных действительных чисел x 1,..., x n, содержится x 1... x n = 1. Существует по крайней мере один x k< 1, so there must be at least one xj>1. Без ограничения общности положим k = n - 1 и j = n.

Далее, равенство x 1... x n = 1 запишем в виде (x 1... x n – 2) (x n – 1 xn) = 1. Тогда предположение индукции подразумевает

$(x\; 1\; +\; \cdots \; +\; xn\; -\; 2)\; +\; (xn\; -\; 1\; xn)>n\; -\; 1.\; \{\backslash \; displaystyle\; (x\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{\; n-2\})\; +\; (x\_\; \{n-1\}\; x\_\; \{n\})>n-1.\}$

Однако с учетом индукционного базиса

$x\; 1\; +\; \cdots \; +\; xn\; -\; 2\; +\; xn\; -\; 1\; +\; xn\; знак\; равно\; (x\; 1\; +\; \cdots \; +\; xn\; -\; 2)\; +\; (xn\; -\; 1\; +\; xn)>(x\; 1\; +\; \cdots \; +\; xn\; -\; 2)\; +\; xn\; -\; 1\; xn\; +\; 1>n,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; x\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n-2\}\; +\; x\_\; \{n-1\}\; +\; x\_\; \{n\}\; =\; (x\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n-2\})\; +\; (x\_\; \{n-1\}\; +\; x\_\; \{n\})\; \backslash \backslash >(x\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n-2\})\; +\; x\_\; \{n-1\}\; x\_\; \{n\}\; +1\; \backslash \backslash >n,\; \backslash \; end\; \{align\}\}\}$

почему ch завершает доказательство.

Для положительных действительных чисел a 1,..., a n, обозначим

$x\; 1\; =\; a\; 1\; a\; 1\; \cdots \; a\; n\; n,...,\; x\; n\; =\; a\; n\; a\; 1\; \cdots \; a\; n\; n.\; \{\backslash \; displaystyle\; x\_\; \{1\}\; =\; \{\backslash \; frac\; \{a\_\; \{1\}\}\; \{\backslash \; sqrt\; [\{n\}]\; \{a\_\; \{1\}\; \backslash \; cdots\; a\_\; \{n\}\}\}\},...,\; x\_\; \{n\}\; =\; \{\; \backslash \; frac\; \{a\_\; \{n\}\}\; \{\backslash \; sqrt\; [\{n\}]\; \{a\_\; \{1\}\; \backslash \; cdots\; a\_\; \{n\}\}\}\}.\}$

Числа x 1,..., x n удовлетворяют условию x 1... x n = 1. Итак, мы имеем

$a\; 1\; a\; 1\; \cdots \; ann\; +\; \cdots \; +\; ana\; 1\; \cdots \; ann\; \ge \; n,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{a\_\; \{1\}\}\; \{\backslash \; sqrt\; [\{\; n\}]\; \{a\_\; \{1\}\; \backslash \; cdots\; a\_\; \{n\}\}\}\}\; +\; \backslash \; cdots\; +\; \{\backslash \; frac\; \{a\_\; \{n\}\}\; \{\backslash \; sqrt\; [\{n\}]\; \{a\_\; \{1\}\; \backslash \; cdots\; a\_\; \{n\}\}\; \}\}\; \backslash \; geq\; n,\}$

откуда получаем

$a\; 1\; +\; \cdots \; +\; ann\; \ge \; a\; 1\; \cdots \; ann,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{a\_\; \{1\}\; +\; \backslash \; cdots\; +\; a\_\; \{n\}\}\; \{n\; \}\}\; \backslash \; geq\; \{\backslash \; sqrt\; [\{n\}]\; \{a\_\; \{1\}\; \backslash \; cdots\; a\_\; \{n\}\}\},\}$

с равенством, сохраняющимся только для 1 =... = a n.

Доказательство Коши с использованием индукции вперед-назад

Следующее доказательство по случаям напрямую опирается на хорошо известные правила арифметики, но использует редко используемую технику прямой-обратной индукции. По сути, он взят из Огюстена Луи Коши и может быть найден в его Cours d'analyse.

Случай, когда все члены равны

Если все члены равны:

$x\; 1\; =\; x\; 2\; =\; \cdots \; =\; xn,\; \{\backslash \; displaystyle\; x\_\; \{1\}\; =\; x\_\; \{2\}\; =\; \backslash \; cdots\; =\; x\_\; \{n\},\}$

, тогда их сумма равна nx 1, поэтому их среднее арифметическое равно x 1 ; и их произведение равно x 1, поэтому их среднее геометрическое равно x 1 ; следовательно, среднее арифметическое и среднее геометрическое равны, как требуется.

Случай, когда не все члены равны

Осталось показать, что если не все члены равны, то среднее арифметическое больше, чем среднее геометрическое. Ясно, что это возможно только при n>1.

Этот случай значительно сложнее, и мы делим его на подслучая.

Подслучай, где n = 2

Если n = 2, то у нас есть два члена, x 1 и x 2, и поскольку ( по нашему предположению) не все члены равны, имеем:

$(x\; 1\; +\; x\; 2\; 2)\; 2\; -\; x\; 1\; x\; 2\; =\; 1\; 4\; (x\; 1\; 2\; +\; 2\; x\; 1\; x\; 2\; +\; x\; 2\; 2)\; -\; x\; 1\; Икс\; 2\; знак\; равно\; 1\; 4\; (Икс\; 1\; 2\; -\; 2\; Икс\; 1\; Икс\; 2\; +\; Икс\; 2\; 2)\; =\; (Икс\; 1\; -\; Икс\; 2\; 2)\; 2>0,\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{Выровнено\}\; \{\backslash \; Bigl\; (\}\; \{\backslash \; гидроразрыв\; \{x\_\; \{1\}\; +\; x\_\; \{2\}\}\; \{2\}\}\; \{\backslash \; Bigr)\}\; ^\; \{2\}\; -x\_\; \{1\}\; x\_\; \{2\}\; =\; \{\backslash \; frac\; \{1\}\; \{4\}\}\; (x\_\; \{1\; \}\; ^\; \{2\}\; +\; 2x\_\; \{1\}\; x\_\; \{2\}\; +\; x\_\; \{2\}\; ^\; \{2\})\; -\; x\_\; \{1\}\; x\_\; \{2\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{1\}\; \{4\}\}\; (x\_\; \{\; 1\}\; ^\; \{2\}\; -2x\_\; \{1\}\; x\_\; \{2\}\; +\; x\_\; \{2\}\; ^\; \{2\})\; \backslash \backslash \; =\; \{\backslash \; Bigl\; (\}\; \{\backslash \; frac\; \{x\_\; \{1\}\; -x\_\; \{2\}\}\; \{2\; \}\}\; \{\backslash \; Bigr)\}\; ^\; \{2\}>0,\; \backslash \; end\; \{align\}\}\}$

отсюда

$x\; 1\; +\; x\; 2\; 2>x\; 1\; x\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; x\_\; \{2\}\}\; \{2\}\}>\{\backslash \; sqrt\; \{x\_\; \{1\}\; x\_\; \{2\}\}\}\}$

по желанию.

Подслучай, где n = 2

Рассмотрим случай, когда n = 2, где k - положительное целое число. Действуем по математической индукции.

В базовом случае k = 1, поэтому n = 2. Мы уже показали, что неравенство выполняется при n = 2, поэтому мы закончили.

Теперь предположим, что для данного k>1 мы уже показали, что неравенство выполняется для n = 2, и мы хотим показать, что оно выполняется для n = 2. Для этого мы применяем неравенство дважды для 2 чисел и один раз для 2 чисел, чтобы получить:

$x 1 + x 2 + ⋯ + x 2 k 2 k = x 1 + x 2 + ⋯ + x 2 k - 1 2 k - 1 + x 2 k - 1 + 1 + x 2 k - 1 + 2 + ⋯ + x 2 k 2 k - 1 2 ≥ x 1 x 2 ⋯ x 2 k - 1 2 k - 1 + x 2 k - 1 + 1 x 2 k - 1 + 2 ⋯ x 2 k 2 k - 1 2 ≥ x 1 x 2 ⋯ x 2 k - 1 2 k - 1 x 2 k - 1 + 1 x 2 k - 1 + 2 ⋯ x 2 k 2 k - 1 знак равно Икс 1 Икс 2 ⋯ Икс 2 К 2 К {\ Displaystyle {\ begin {align} {\ frac {x_ {1} + x_ {2} + \ cdots + x_ {2 ^ {k}}} {2 ^ { k}}} {} = {\ frac {{\ frac {x_ {1} + x_ {2} + \ cdots + x_ {2 ^ {k-1}}} {2 ^ {k-1}}} + {\ frac {x_ {2 ^ {k-1} +1} + x_ {2 ^ {k-1} +2} + \ cdots + x_ {2 ^ {k}}} {2 ^ {k-1 }}}} {2}} \\ [7pt] \ geq {\ frac {{\ sqrt [{2 ^ {k-1}}] {x_ {1} x_ {2} \ cdots x_ {2 ^ { k-1}}}} + {\ sqrt [{2 ^ {k-1}}] {x_ {2 ^ {k-1} +1} x_ {2 ^ {k-1} +2} \ cdots x_ {2 ^ {k}}}}} {2}} \\ [7pt] \ geq {\ sqrt {{\ sqrt [{2 ^ {k-1}}] {x_ {1} x_ {2} \ cdots x_ {2 ^ {k-1}}}} {\ sqrt [{2 ^ {k-1}}] {x_ {2 ^ {k-1} +1} x_ {2 ^ {k-1} + 2} \ cdots x _ {2 ^ {k}}}}}} \\ [7pt] = {\ sqrt [{2 ^ {k}}] {x_ {1} x_ {2} \ cdots x_ {2 ^ {k}} }} \ end {align}}}$

где в первом неравенстве две стороны равны, только если

$x\; 1\; =\; x\; 2\; =\; \cdots \; =\; x\; 2\; k\; -\; 1\; \{\backslash \; displaystyle\; x\_\; \{1\}\; =\; x\_\; \{2\}\; =\; \backslash \; cdots\; =\; x\_\; \{2\; ^\; \{k-1\}\}\}$

и

$x\; 2\; k\; -\; 1\; +\; 1\; =\; x\; 2\; k\; -\; 1\; +\; 2\; =\; \cdots \; =\; x\; 2\; k\; \{\backslash \; displaystyle\; x\_\; \{2\; ^\; \{k-1\}\; +1\}\; =\; x\_\; \{2\; ^\; \{k-1\}\; +2\}\; =\; \backslash \; cdots\; =\; x\_\; \{2\; ^\; \{k\}\}\}$

(в этом случае первое среднее арифметическое и первое оба среднего геометрического равны x 1, и аналогично со вторым средним арифметическим и вторым средним геометрическим); а во втором неравенстве две стороны равны, только если два средних геометрических равны. Поскольку не все 2 числа равны, оба неравенства не могут быть равенствами, поэтому мы знаем, что:

$x\; 1\; +\; x\; 2\; +\; \cdots \; +\; x\; 2\; k\; 2\; k>x\; 1\; x\; 2\; \cdots \; x\; 2\; k\; 2\; к\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{2\; ^\; \{k\}\}\}\; \{2\; ^\; \{k\}\}\}>\{\backslash \; sqrt\; [\{2\; ^\; \{k\}\}\; ]\; \{x\_\; \{1\}\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{2\; ^\; \{k\}\}\}\}\}$

по желанию.

Подслучай, где n < 2

Если n не является естественной степенью 2, то она определенно меньше некоторой естественной степени 2, поскольку последовательность 2, 4, 8,..., 2,... неограничена сверху. Поэтому, без ограничения общности, пусть m будет некоторой естественной степенью 2, которая больше n.

Итак, если у нас есть n членов, то обозначим их среднее арифметическое через α и расширим наш список терминов следующим образом:

$xn\; +\; 1\; =\; xn\; +\; 2\; =\; \cdots \; =\; xm\; =\; \alpha .\; \{\backslash \; displaystyle\; x\_\; \{n\; +\; 1\}\; =\; x\_\; \{n\; +\; 2\}\; =\; \backslash \; cdots\; =\; x\_\; \{m\}\; =\; \backslash \; alpha.\}$

Мы т тогда есть:

$\alpha \; =\; x\; 1\; +\; x\; 2\; +\; \cdots \; +\; xnn\; =\; mn\; (x\; 1\; +\; x\; 2\; +\; \cdots \; +\; xn)\; m\; =\; x\; 1\; +\; x\; 2\; +\; \cdots \; +\; xn\; +\; m\; -\; nn\; (x\; 1\; +\; x\; 2\; +\; \cdots \; +\; xn)\; m\; =\; x\; 1\; +\; x\; 2\; +\; \cdots \; +\; xn\; +\; (m\; -\; n)\; \alpha \; m\; =\; x\; 1\; +\; x\; 2\; +\; \cdots \; +\; xn\; +\; xn\; +\; 1\; +\; \cdots \; +\; xmm>x\; 1\; x\; 2\; \cdots \; xnxn\; +\; 1\; \cdots \; xmm\; =\; x\; 1\; x\; 2\; \cdots \; xn\; \alpha \; m\; -\; nm,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; alpha\; =\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\})\; \}\; \{n\}\}\; \backslash \backslash \; [6pt]\; =\; \{\backslash \; frac\; \{\{\backslash \; frac\; \{m\}\; \{n\}\}\; \backslash \; left\; (x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; \backslash \; right)\}\; \{m\}\}\; \backslash \backslash \; [6pt]\; =\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; +\; \{\backslash \; frac\; \{mn\}\; \{n\}\}\; \backslash \; left\; (x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; \backslash \; right)\}\; \{m\}\}\; \backslash \backslash \; [6pt]\; =\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; +\; \backslash \; left\; (mn\; \backslash \; right)\; \backslash \; alpha\}\; \{m\}\}\; \backslash \backslash \; [6pt]\; =\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; +\; x\_\; \{n\; +\; 1\}\; +\; \backslash \; cdots\; +\; x\_\; \{m\}\}\; \{m\}\}\; \backslash \backslash \; [6pt]>\{\backslash \; sqrt\; [\{m\}]\; \{x\_\; \{1\}\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n\}\; x\_\; \{n\; +\; 1\}\; \backslash \; cdots\; x\_\; \{m\}\}\}\; \backslash \backslash \; [6pt]\; =\; \{\backslash \; sqrt\; [\{m\}]\; \{x\_\; \{1\}\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n\}\; \backslash \; alpha\; ^\; \{mn\}\}\}\; \backslash ,,\; \backslash \; end\; \{\; выровнено\}\}\}$

так

$\alpha \; m>x\; 1\; x\; 2\; \cdots \; xn\; \alpha \; m\; -\; n\; \{\backslash \; displaystyle\; \backslash \; alpha\; ^\; \{m\}>x\_\; \{1\}\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n\}\; \backslash \; alpha\; ^\; \{mn\}\}$

и

$\alpha >Икс\; 1\; Икс\; 2\; \cdots \; xnn\; \{\backslash \; displaystyle\; \backslash \; alpha>\{\backslash \; sqrt\; [\{n\}]\; \{x\_\; \{1\}\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n\}\}\}\}$

по желанию.

Доказательство индукцией с использованием базового исчисления

В следующем доказательстве используется математическая индукция и некоторое базовое дифференциальное исчисление.

Базис индукции : Для n = 1 утверждение верно равенство.

Индукционная гипотеза : Предположим, что утверждение AM – GM выполняется для всех вариантов n неотрицательных действительных чисел.

Шаг индукции : Чтобы доказать утверждение для n + 1 неотрицательных действительных чисел x 1,..., x n, x n + 1, нам нужно доказать, что

$x\; 1\; +\; \cdots \; +\; xn\; +\; xn\; +\; 1\; n\; +\; 1\; -\; (x\; 1\; \cdots \; xnxn\; +\; 1)\; 1\; n\; +\; 1\; \ge \; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; +\; x\_\; \{n\; +\; 1\}\}\; \{n\; +\; 1\}\}\; -\; (\{x\_\; \{1\}\; \backslash \; cdots\; x\_\; \{n\}\; x\_\; \{n\; +\; 1\}\})\; ^\; \{\backslash \; frac\; \{1\}\; \{n\; +\; 1\}\}\; \backslash \; geq\; 0\}$

с равенством, только если все числа n + 1 равны.

Если все числа равны нулю, неравенство выполняется с равенством. Если некоторые, но не все числа равны нулю, мы имеем строгое неравенство. Поэтому в дальнейшем мы можем считать, что все n + 1 числа положительны.

Мы рассматриваем последнее число x n + 1 как переменную и определяем функцию

$f\; (t)\; =\; x\; 1\; +\; \cdots \; +\; xn\; +\; tn\; +\; 1\; -\; (x\; 1\; \cdots \; xnt)\; 1\; n\; +\; 1,\; t>0.\; \{\backslash \; displaystyle\; f\; (t)\; =\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; +\; t\}\; \{n\; +\; 1\}\}\; -\; (\{x\_\; \{1\}\; \backslash \; cdots\; x\_\; \{n\}\; t\})\; ^\; \{\backslash \; frac\; \{1\}\; \{n\; +\; 1\}\},\; \backslash \; qquad\; t>0.\}$

Доказательство шага индукции эквивалентно демонстрации того, что f (t) ≥ 0 для всех t>0, при f (t) = 0 только если x 1,..., x n и t равны. Это можно сделать, проанализировав критические точки функции f с помощью некоторого базового исчисления.

Первая производная функции f определяется как

$f\; \prime \; (t)\; =\; 1\; n\; +\; 1\; -\; 1\; n\; +\; 1\; (x\; 1\; \cdots \; xn)\; 1\; n\; +\; 1\; t\; -\; nn\; +\; 1,\; t>0.\; \{\backslash \; Displaystyle\; f\; \text{'}(t)\; =\; \{\backslash \; frac\; \{1\}\; \{n\; +\; 1\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{n\; +\; 1\}\}\; (\{x\_\; \{1\}\; \backslash \; cdots\; x\_\; \{n\}\})\; ^\; \{\backslash \; frac\; \{1\}\; \{n\; +\; 1\}\}\; t\; ^\; \{-\; \{\backslash \; frac\; \{n\}\; \{n\; +\; 1\}\}\},\; \backslash \; qquad\; t>0.\}$

Критическая точка t 0 должен удовлетворять f ′ (t 0) = 0, что означает

$(x\; 1\; \cdots \; xn)\; 1\; n\; +\; 1\; t\; 0\; -\; nn\; +\; 1\; =\; 1.\; \{\backslash \; displaystyle\; (\; \{x\_\; \{1\}\; \backslash \; cdots\; x\_\; \{n\}\})\; ^\; \{\backslash \; frac\; \{1\}\; \{n\; +\; 1\}\}\; t\_\; \{0\}\; ^\; \{-\; \{\backslash \; frac\; \{n\}\; \{n\; +\; 1\}\}\}\; =\; 1.\}$

После небольшой перестановки получаем

$t\; 0\; nn\; +\; 1\; =\; (x\; 1\; \cdots \; xn)\; 1\; n\; +\; 1,\; \{\backslash \; displaystyle\; t\_\; \{0\}\; ^\; \{\backslash \; frac\; \{n\}\; \{n\; +\; 1\}\}\; =\; (\{x\_\; \{1\}\; \backslash \; cdots\; x\_\; \{n\}\})\; ^\; \{\backslash \; frac\; \{1\}\; \{n\; +\; 1\}\},\}$

и, наконец,

$t\; 0\; =\; (x\; 1\; \cdots \; xn)\; 1\; n,\; \{\; \backslash \; displaystyle\; t\_\; \{0\}\; =\; (\{x\_\; \{1\}\; \backslash \; cdots\; x\_\; \{n\}\})\; ^\; \{\backslash \; frac\; \{1\}\; \{n\}\},\}$

, которое является средним геометрическим для x 1,..., x n. Это единственная критическая точка f. Поскольку f ′ ′ (t)>0 для всех t>0, функция f является строго выпуклой и имеет строгий глобальный минимум в t 0. Затем мы вычисляем значение функции в этом глобальном минимуме:

$f\; (t\; 0)\; =\; x\; 1\; +\; \cdots \; +\; xn\; +\; (x\; 1\; \cdots \; xn)\; 1\; /\; nn\; +\; 1\; -\; (x\; 1\; \cdots \; xn)\; 1\; n\; +\; 1\; (x\; 1\; \cdots \; xn)\; 1\; n\; (n\; +\; 1)\; =\; x\; 1\; +\; \cdots \; +\; xnn\; +\; 1\; +\; 1\; n\; +\; 1\; (x\; 1\; \cdots \; xn)\; 1\; n\; -\; (x\; 1\; \cdots \; xn)\; 1\; n\; =\; x\; 1\; +\; \cdots \; +\; xnn\; +\; 1\; -\; nn\; +\; 1\; (x\; 1\; \cdots \; xn)\; 1\; n\; =\; nn\; +\; 1\; (x\; 1\; +\; \cdots \; +\; xnn\; -\; (x\; 1\; \cdots \; xn)\; 1\; n)\; \ge \; 0,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; f\; (t\_\; \{0\})\; =\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; +\; (\{x\_\; \{1\}\; \backslash \; cdots\; x\_\; \{n\}\})\; ^\; \{1\; /\; n\}\}\; \{n\; +\; 1\; \}\}\; -\; (\{x\_\; \{1\}\; \backslash \; cdots\; x\_\; \{n\}\})\; ^\; \{\backslash \; frac\; \{1\}\; \{n\; +\; 1\}\}\; (\{x\_\; \{1\}\; \backslash \; cdots\; x\_\; \{n\}\})\; ^\; \{\backslash \; frac\; \{1\; \}\; \{n\; (n\; +\; 1)\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\}\; \{n\; +\; 1\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{n\; +\; 1\}\}\; (\{x\_\; \{1\}\; \backslash \; cdots\; x\_\; \{n\}\})\; ^\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; -\; (\{x\_\; \{1\}\; \backslash \; cdots\; x\_\; \{n\}\})\; ^\; \{\backslash \; frac\; \{1\}\; \{n\}\; \}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\}\; \{n\; +\; 1\}\}\; -\; \{\backslash \; frac\; \{n\}\; \{n\; +\; 1\}\}\; (\{x\_\; \{1\}\; \backslash \; cdots\; x\_\; \{n\}\})\; ^\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{n\}\; \{n\; +\; 1\}\}\; \{\backslash \; Bigl\; (\}\; \{\backslash \; frac\; \{x\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\}\; \{n\}\}\; -\; (\{x\_\; \{1\}\; \backslash \; cdots\; x\_\; \{n\}\})\; ^\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \{\backslash \; Bigr)\}\; \backslash \backslash \; \backslash \; geq\; 0,\; \backslash \; end\; \{выровнено\; \}\}\}$

где последнее неравенство выполняется в силу предположения индукции. Гипотеза также утверждает, что мы можем иметь равенство только тогда, когда x 1,..., x n все равны. В этом случае их среднее геометрическое t 0 имеет то же значение. Следовательно, если x 1,..., x n, x n + 1 все равны, мы имеем f (x n + 1)>0. Это завершает доказательство.

This technique can be used in the same manner to prove the generalized AM–GM inequality and Cauchy–Schwarz inequality in Euclidean space R.

Proof by Pólya using the exponential function

George Pólya provided a proof similar to what follows. Let f(x) = e – x for all real x, with first derivative f′(x) = e – 1 and second derivative f′′(x) = e. Observe that f(1) = 0, f′(1) = 0 and f′′(x)>0 for all real x, hence f is strictly convex with the absolute minimum at x = 1. Hence x ≤ e for all real x with equality only for x = 1.

Consider a list of non-negative real numbers x1, x2,..., xn. If they are all zero, then the AM–GM inequality holds with equality. Hence we may assume in the following for their arithmetic mean α>0. By n-fold application of the above inequality, we obtain that

$x\; 1\; \alpha \; x\; 2\; \alpha \; \cdots \; x\; n\; \alpha \; \le \; e\; x\; 1\; \alpha \; -\; 1\; e\; x\; 2\; \alpha \; -\; 1\; \cdots \; e\; x\; n\; \alpha \; -\; 1\; =\; exp\; \; (\; x\; 1\; \alpha \; -\; 1\; +\; x\; 2\; \alpha \; -\; 1\; +\; \cdots \; +\; x\; n\; \alpha \; -\; 1),\; (\; \ast )\; \{\backslash displaystyle\; \{\backslash begin\{aligned\}\{\{\backslash frac\; \{x\_\{1\}\}\{\backslash alpha\; \}\}\{\backslash frac\; \{x\_\{2\}\}\{\backslash alpha\; \}\}\backslash cdots\; \{\backslash frac\; \{x\_\{n\}\}\{\backslash alpha\; \}\}\}\backslash leq\; \{e^\{\{\backslash frac\; \{x\_\{1\}\}\{\backslash alpha\; \}\}-1\}e^\{\{\backslash frac\; \{x\_\{2\}\}\{\backslash alpha\; \}\}-1\}\backslash cdots\; e^\{\{\backslash frac\; \{x\_\{n\}\}\{\backslash alpha\; \}\}-1\}\}\backslash \backslash =\backslash exp\; \{\backslash Bigl\; (\}\{\backslash frac\; \{x\_\{1\}\}\{\backslash alpha\; \}\}-1+\{\backslash frac\; \{x\_\{2\}\}\{\backslash alpha\; \}\}-1+\backslash cdots\; +\{\backslash frac\; \{x\_\{n\}\}\{\backslash alpha\; \}\}-1\{\backslash Bigr)\},\backslash qquad\; (*)\backslash end\{aligned\}\}\}$

with equality if and only if xi= α for every i ∈ {1,..., n}. The argument of the exponential function can be simplified:

$x\; 1\; \alpha \; -\; 1\; +\; x\; 2\; \alpha \; -\; 1\; +\; \cdots \; +\; x\; n\; \alpha \; -\; 1\; =\; x\; 1\; +\; x\; 2\; +\; \cdots \; +\; x\; n\; \alpha \; -\; n\; =\; n\; \alpha \; \alpha \; -\; n\; =\; 0.\; \{\backslash displaystyle\; \{\backslash begin\{aligned\}\{\backslash frac\; \{x\_\{1\}\}\{\backslash alpha\; \}\}-1+\{\backslash frac\; \{x\_\{2\}\}\{\backslash alpha\; \}\}-1+\backslash cdots\; +\{\backslash frac\; \{x\_\{n\}\}\{\backslash alpha\; \}\}-1=\{\backslash frac\; \{x\_\{1\}+x\_\{2\}+\backslash cdots\; +x\_\{n\}\}\{\backslash alpha\; \}\}-n\backslash \backslash =\{\backslash frac\; \{n\backslash alpha\; \}\{\backslash alpha\; \}\}-n\backslash \backslash =0.\backslash end\{aligned\}\}\}$

Returning to (*),

$x\; 1\; x\; 2\; \cdots \; x\; n\; \alpha \; n\; \le \; e\; 0\; =\; 1,\; \{\backslash displaystyle\; \{\backslash frac\; \{x\_\{1\}x\_\{2\}\backslash cdots\; x\_\{n\}\}\{\backslash alpha\; ^\{n\}\}\}\backslash leq\; e^\{0\}=1,\}$

which produces x1x2· · · xn≤ α, hence the result

$x\; 1\; x\; 2\; \cdots \; x\; n\; n\; \le \; \alpha .\; \{\backslash displaystyle\; \{\backslash sqrt[\{n\}]\{x\_\{1\}x\_\{2\}\backslash cdots\; x\_\{n\}\}\}\backslash leq\; \backslash alpha.\}$

Proof by Lagrangian Multipliers

If any of the $x\; i\; \{\backslash displaystyle\; x\_\{i\}\}$are $0\; \{\backslash displaystyle\; 0\}$, then there is nothing to prove. So we may assume all the $x\; i\; \{\backslash displaystyle\; x\_\{i\}\}$are strictly positive.

Because the arithmetic and geometric means are homogeneous of degree 1, without loss of generality assume that $\prod \; i\; =\; 1\; n\; x\; i\; =\; 1\; \{\backslash displaystyle\; \backslash prod\; \_\{i=1\}^\{n\}x\_\{i\}=1\}$. Set $G\; (\; x\; 1,\; x\; 2,\; \dots ,\; x\; n)\; =\; \prod \; i\; =\; 1\; n\; x\; i\; \{\backslash displaystyle\; G(x\_\{1\},x\_\{2\},\backslash ldots,x\_\{n\})=\backslash prod\; \_\{i=1\}^\{n\}x\_\{i\}\}$, and $F\; (\; x\; 1,\; x\; 2,\; \dots ,\; x\; n)\; =\; 1\; n\; \sum \; i\; =\; 1\; n\; x\; i\; \{\backslash displaystyle\; F(x\_\{1\},x\_\{2\},\backslash ldots,x\_\{n\})=\{\backslash frac\; \{1\}\{n\}\}\backslash sum\; \_\{i=1\}^\{n\}x\_\{i\}\}$. The inequality will be proved (together with the equality case) if we can show that the minimum of $F\; (\; x\; 1,\; x\; 2,...,\; x\; n),\; \{\backslash displaystyle\; F(x\_\{1\},x\_\{2\},...,x\_\{n\}),\}$subject to the constraint $G\; (\; x\; 1,\; x\; 2,\; \dots ,\; x\; n)\; =\; 1,\; \{\backslash displaystyle\; G(x\_\{1\},x\_\{2\},\backslash ldots,x\_\{n\})=1,\}$is equal to $1\; \{\backslash displaystyle\; 1\}$, and the minimum is only achieved when $x\; 1\; =\; x\; 2\; =\; \cdots \; =\; x\; n\; =\; 1\; \{\backslash displaystyle\; x\_\{1\}=x\_\{2\}=\backslash cdots\; =x\_\{n\}=1\}$. Let us first show that the constrained minimization problem has a global minimum.

Set $K\; =\; \{\; (\; x\; 1,\; x\; 2,\; \dots ,\; x\; n)\; :\; 0\; \le \; x\; 1,\; x\; 2,\; \dots ,\; x\; n\; \le \; n\; \}\; \{\backslash displaystyle\; K=\backslash \{(x\_\{1\},x\_\{2\},\backslash ldots,x\_\{n\})\backslash colon\; 0\backslash leq\; x\_\{1\},x\_\{2\},\backslash ldots,x\_\{n\}\backslash leq\; n\backslash \}\}$. Since the intersection $K\; \cap \; \{\; G\; =\; 1\; \}\; \{\backslash displaystyle\; K\backslash cap\; \backslash \{G=1\backslash \}\}$is compact, the extreme value theorem guarantees that the minimum of $F\; (\; x\; 1,\; x\; 2,...,\; x\; n)\; \{\backslash displaystyle\; F(x\_\{1\},x\_\{2\},...,x\_\{n\})\}$subject to the constraints $G\; (\; x\; 1,\; x\; 2,\; \dots ,\; x\; n)\; =\; 1\; \{\backslash displaystyle\; G(x\_\{1\},x\_\{2\},\backslash ldots,x\_\{n\})=1\}$and $(\; x\; 1,\; x\; 2,\; \dots ,\; x\; n)\; \in \; K\; \{\backslash displaystyle\; (x\_\{1\},x\_\{2\},\backslash ldots,x\_\{n\})\backslash in\; K\}$is attained at some point inside $K\; \{\backslash displaystyle\; K\}$. On the other hand, observe that if any of the $x\; i>n\; \{\backslash displaystyle\; x\_\{i\}>n\}$, then $F\; (\; x\; 1,\; x\; 2,\; \dots ,\; x\; n)>1\; \{\backslash displaystyle\; F(x\_\{1\},x\_\{2\},\backslash ldots,x\_\{n\})>1\}$, а $F\; (1,\; 1,\dots ,\; 1)\; =\; 1\; \{\backslash \; displaystyle\; F\; (1,1,\; \backslash \; ldots,\; 1)\; =\; 1\}$и $(1,\; 1,\dots ,\; 1)\; \in \; K\; \cap \; \{G\; =\; 1\}\; \{\backslash \; displaystyle\; (1,1,\; \backslash \; ldots,\; 1)\; \backslash \; in\; K\; \backslash \; cap\; \backslash \; \{G\; =\; 1\; \backslash \}\}$. Это означает, что минимум внутри $K\; \cap \; \{G\; =\; 1\}\; \{\backslash \; displaystyle\; K\; \backslash \; cap\; \backslash \; \{G\; =\; 1\; \backslash \}\}$фактически является глобальным минимумом, поскольку значение $F\; \{\backslash \; displaystyle\; F\}$в любой точке внутри $K\; \cap \; \{G\; =\; 1\}\; \{\backslash \; displaystyle\; K\; \backslash \; cap\; \backslash \; \{G\; =\; 1\; \backslash \}\}$определенно не меньше минимума, и значение $F\; \{\backslash \; displaystyle\; F\}$в любой точке $(y\; 1,\; y\; 2,\dots ,\; yn)\; \{\backslash \; displaystyle\; (y\_\; \{1\},\; y\_\; \{2\},\; \backslash \; ldots,\; y\_\; \{n\})\}$не внутри $K\; \{\backslash \; displaystyle\; K\}$строго больше, чем значение в $(1,\; 1,\dots ,\; 1)\; \{\backslash \; displaystyle\; (1,1,\; \backslash \; ldots,\; 1)\}$, что не меньше минимального.

Метод Множитель Лагранжа говорит, что глобальный минимум достигается в точке $(x\; 1,\; x\; 2,\dots ,\; xn)\; \{\backslash \; displaystyle\; (x\_\; \{1\},\; x\_\; \{2\},\; \backslash \; ldots,\; x\_\; \{n\})\}$где градиент $F\; (x\; 1,\; x\; 2,\dots ,\; xn)\; \{\backslash \; displaystyle\; F\; (x\_\; \{1\},\; x\_\; \{2\},\; \backslash \; ldots,\; x\_\; \{n\})\}$равно $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$умножить на градиент $G\; (x\; 1,\; x\; 2,\dots ,\; xn)\; \{\backslash \; displaystyle\; G\; (x\_\; \{1\},\; x\_\; \{2\},\; \backslash \; ldots,\; x\_\; \{n\})\}$, для некоторого $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$. Мы покажем, что это происходит только тогда, когда $x\; 1\; =\; x\; 2\; =\; \cdots \; =\; xn\; =\; 1\; \{\backslash \; displaystyle\; x\_\; \{1\}\; =\; x\_\; \{2\}\; =\; \backslash \; cdots\; =\; x\_\; \{n\}\; =\; 1\}$и $F\; (x\; 1,\; x\; 2,...,\; xn)\; =\; 1.\; \{\backslash \; displaystyle\; F\; (x\_\; \{1\},\; x\_\; \{2\},...,\; x\_\; \{n\}))\; =\; 1.\}$

Вычислить $\partial \; F\; \partial \; xi\; =\; 1\; n\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; F\}\; \{\backslash \; partial\; x\_\; \{i\}\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \}$и

$\partial \; G\; \partial \; xi\; =\; \prod \; j\; \ne \; ixj\; =\; G\; (x\; 1,\; x\; 2,\dots ,\; xn)\; xi\; =\; 1\; xi\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; G\}\; \{\backslash \; частичный\; x\_\; \{i\}\}\}\; =\; \backslash \; prod\; \_\; \{j\; \backslash \; neq\; i\}\; x\_\; \{j\}\; =\; \{\backslash \; frac\; \{G\; (x\_\; \{1\},\; x\_\; \{2\},\; \backslash \; ldots,\; x\_\; \{n\})\}\; \{x\_\; \{\; i\}\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{x\_\; \{i\}\}\}\}$

вдоль ограничения. Таким образом, установка градиентов, пропорциональных друг другу, дает для каждого $i\; \{\backslash \; displaystyle\; i\}$, что $1\; n\; =\; \lambda \; xi,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; =\; \{\backslash \; frac\; \{\backslash \; lambda\}\; \{x\_\; \{i\}\}\},\}$и поэтому $n\; \lambda \; =\; xi.\; \{\backslash \; displaystyle\; n\; \backslash \; lambda\; =\; x\_\; \{i\}.\}$Поскольку левая часть не зависит от $i\; \{\backslash \; displaystyle\; i\}$, отсюда следует, что $x\; 1\; =\; x\; 2\; =\; \cdots \; =\; xn\; \{\backslash \; displaystyle\; x\_\; \{1\}\; =\; x\_\; \{2\}\; =\; \backslash \; cdots\; =\; x\_\; \{n\}\}$, а поскольку $G\; (x\; 1,\; x\; 2,\dots ,\; Xn)\; =\; 1\; \{\backslash \; displaystyle\; G\; (x\_\; \{1\},\; x\_\; \{2\},\; \backslash \; ldots,\; x\_\; \{n\})\; =\; 1\}$, отсюда следует, что $x\; 1\; =\; x\; 2\; =\; \cdots \; =\; xn\; =\; 1\; \{\backslash \; displaystyle\; x\_\; \{1\}\; =\; x\_\; \{2\}\; =\; \backslash \; cdots\; =\; x\_\; \{n\}\; =\; 1\}$и $F\; (x\; 1,\; x\; 2,\dots ,\; xn)\; =\; 1\; \{\backslash \; displaystyle\; F\; (x\_\; \{1\},\; x\_\; \{2\},\; \backslash \; ldots,\; x\_\; \{n\})\; =\; 1\}$по желанию.

Взвешенное неравенство AM – GM

Аналогичное неравенство существует для средневзвешенного арифметического и средневзвешенного геометрического. В частности, пусть неотрицательные числа x 1, x 2,..., x n и неотрицательные веса w 1, w 2,..., w n. Установите w = w 1 + ​​w 2 + ​​· · · + w n. Если w>0, то выполняется неравенство

$w\; 1\; x\; 1\; +\; w\; 2\; x\; 2\; +\; \cdots \; +\; wnxnw\; \ge \; x\; 1\; w\; 1\; x\; 2\; w\; 2\; \cdots \; xnwnw\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{w\_\; \{1\}\; x\_\; \{1\}\; +\; w\_\; \{2\}\; x\_\; \{2\}\; +\; \backslash \; cdots\; +\; w\_\; \{n\}\; x\_\; \{n\}\}\; \{w\}\}\; \backslash \; geq\; \{\backslash \; sqrt\; [\{w\}]\; \{x\_\; \{1\}\; ^\; \{w\_\; \{1\}\}\; x\_\; \{\; 2\}\; ^\; \{w\_\; \{2\}\}\; \backslash \; cdots\; x\_\; \{n\}\; ^\; \{w\_\; \{n\}\}\}\}\}$

выполняется с равенством тогда и только тогда, когда все x k с w k>0 равны. Здесь используется соглашение 0 = 1.

Если все w k = 1, это сводится к вышеупомянутому неравенству средних арифметических и геометрических.

Доказательство с использованием неравенства Дженсена

Используя конечную форму неравенства Дженсена для натурального логарифма, мы можем доказать неравенство между взвешенным средним арифметическим и средневзвешенное геометрическое значение, указанное выше.

Поскольку x k с весом w k = 0 не влияет на неравенство, мы можем далее предполагать, что все веса положительны. Если все x k равны, то равенство выполняется. Следовательно, остается доказать строгое неравенство, если не все они равны, что мы и будем предполагать в дальнейшем. Если хотя бы один x k равен нулю (но не все), то средневзвешенное геометрическое среднее равно нулю, а средневзвешенное арифметическое положительное, следовательно, выполняется строгое неравенство. Следовательно, мы можем также считать, что все x k положительны.

Поскольку натуральный логарифм строго вогнутый, конечная форма неравенства Дженсена и функциональных уравнений натурального логарифма подразумевает

$ln\; \; (w\; 1\; x\; 1\; +\; \cdots \; +\; wnxnw)>w\; 1\; w\; ln\; \; x\; 1\; +\; \cdots \; +\; wnw\; ln\; \; xn\; =\; ln\; \; x\; 1\; w\; 1\; x\; 2\; w\; 2\; \cdots \; xnwnw.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; ln\; \{\backslash \; Bigl\; (\}\; \{\backslash \; frac\; \{w\_\; \{1\}\; x\_\; \{1\}\; +\; \backslash \; cdots\; +\; w\_\; \{n\}\; x\_\; \{n\}\}\; \{w\}\}\; \{\backslash \; Bigr)\}>\{\backslash \; frac\; \{w\_\; \{1\}\}\; \{w\}\}\; \backslash \; ln\; x\_\; \{1\}\; +\; \backslash \; cdots\; +\; \{\backslash \; frac\; \{w\_\; \{n\}\}\; \{w\}\}\; \backslash \; ln\; x\_\; \{n\}\; \backslash \backslash \; =\; \backslash \; ln\; \{\backslash \; sqrt\; [\{w\}]\; \{x\_\; \{1\}\; ^\; \{w\_\; \{1\}\}\; x\_\; \{2\}\; ^\; \{w\_\; \{2\}\}\; \backslash \; cdots\; x\_\; \{n\}\; ^\; \{w\_\; \{n\}\}\}\}.\; \backslash \; end\; \{\; выровнено\}\}\}$

Поскольку натуральный логарифм равен строго возрастающему,

$w\; 1\; x\; 1\; +\; \cdots \; +\; wnxnw>x\; 1\; w\; 1\; x\; 2\; w\; 2\; \cdots \; xnwnw.\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{w\_\; \{1\; \}\; x\_\; \{1\}\; +\; \backslash \; cdots\; +\; w\_\; \{n\}\; x\_\; \{n\}\}\; \{w\}\}>\{\backslash \; sqrt\; [\{w\}]\; \{x\_\; \{1\}\; ^\; \{w\_\; \{1\}\}\; x\_\; \{2\}\; ^\; \{w\_\; \{2\}\}\; \backslash \; cdots\; x\_\; \{n\}\; ^\; \{w\_\; \{n\}\}\}\}.\}$

Среднее арифметическое геометрическое неравенство матрицы8>

Большинство матричных обобщений неравенства среднего геометрического применяется на уровне унитарно инвариантных норм, потому что даже если матрицы $A\; \{\backslash \; displaystyle\; A\}$и $B\; \{\backslash \; displaystyle\; B\}$являются положительными полуопределенными, матрица $AB\; \{\backslash \; displaystyle\; AB\}$не может быть положительно полуопределенной и, следовательно, может не иметь канонического квадратного корня. В Бхатиа и Киттане доказали, что для любой унитарно инвариантной нормы $|\; |\; |\; \cdot \; |\; |\; |\; \{\backslash \; displaystyle\; |||\; \backslash \; cdot\; |||\}$и положительные полуопределенные матрицы $A\; \{\backslash \; displaystyle\; A\}$и $B\; \{\backslash \; displaystyle\; B\}$это случай, когда

$|\; |\; |\; A\; B\; |\; |\; |\; \le \; 1\; 2\; |\; |\; |\; A\; 2\; +\; B\; 2\; |\; |\; |\; \{\backslash \; displaystyle\; |||\; AB\; |||\; \backslash \; leq\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; |||\; A\; ^\; \{2\}\; +\; B\; ^\; \{2\}\; |||\}$

Позже у тех же авторов доказано более сильное неравенство

$|\; |\; |\; A\; B\; |\; |\; |\; \le \; 1\; 4\; |\; |\; |\; (A\; +\; B)\; 2\; |\; |\; |\; \{\backslash \; displaystyle\; |||\; AB\; |||\; \backslash \; leq\; \{\backslash \; frac\; \{1\}\; \{4\}\}\; |||\; (A\; +\; B)\; ^\; \{2\}\; |||\}$

Наконец, он известен размерностью $n\; =\; 2\; \{\backslash \; displaystyle\; n\; =\; 2\}$, что выполняется следующее самое сильное возможное матричное обобщение неравенства среднего арифметико-геометрического, и предполагается, что оно выполняется для всех $n\; \{\backslash \; displaystyle\; n\}$

$|\; |\; |\; (A\; B)\; 1\; 2\; |\; |\; |\; \le \; 1\; 2\; |\; |\; |\; A\; +\; B\; |\; |\; |\; \{\backslash \; displaystyle\; |||\; (AB)\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; |||\; \backslash \; leq\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; |||\; A\; +\; B\; |||\}$

Другие обобщения

Геометрическое доказательство без слов, что max (a, b)>среднее квадратичное или среднеквадратичное (QM)>среднее арифметическое (AM)>среднее геометрическое (GM)>среднее гармоническое (HM)>min (a, b) двух положительных чисел a и b

Другие обобщения неравенства средних арифметических и геометрических включают:

• Неравенство Мюрхеда,
• Неравенство Маклорена,
• Обобщенное среднее неравенство.

• Загадка упаковки Хоффмана
• Неравенство Ки Фана
• Неравенство Юнга для продуктов

Новое неравенства с классическими средними появились в ряде публикаций (см. [7]).

7. Флорин Ничита, О неравенстве классических средств, Энциклопедия научного сообщества, MDPI, https://encyclopedia.pub/2364 - Создано: 20 августа 2020 г.; Последнее обновление: 20 августа 2020 г.

• Артур Лоуотер (1982). «Введение в неравенство». Электронная онлайн-книга в формате PDF.