характеристика Эйлера

редактировать

В математике, а точнее в алгебраической топологии и полиэдральной комбинаторике, характеристика Эйлера (или число Эйлера, или характеристика Эйлера – Пуанкаре ) - это топологический инвариант, число, которое описывает форму или структуру топологического пространства независимо от того, как оно изгибается. Обычно его обозначают как $χ {\ displaystyle \ chi}$ $\ chi$ (греческая строчная буква chi ).

Эйлерова характеристика была первоначально определена для многогранников и использовалась для доказательства различных теорем о них, включая классификацию Платоновых тел. Это было заявлено для Платоновых тел в 1537 году в неопубликованной рукописи Франческо Моролико. Леонард Эйлер, в честь которого названо это понятие, ввел его для выпуклых многогранников в более общем смысле, но не смог строго доказать что это инвариант. В современной математике характеристика Эйлера возникает из гомологии и, более абстрактно, гомологической алгебры.

Содержание

1 Многогранники
- 1.1 Плоские графы
- 1.2 Доказательство формулы Эйлера
2 Топологическое определение
3 Свойства
- 3.1 Гомотопическая инвариантность
- 3.2 Принцип включения-исключения
- 3.3 Связанная сумма
- 3.4 Свойство продукта
- 3.5 Покрывающие пространства
- 3.6 Свойство волокна
4 Примеры
- 4.1 Поверхности
- 4.2 Футбольный мяч
- 4.3 Произвольные размеры
5 Отношения с другими инвариантами
6 Обобщения
7 См. Также
8 Ссылки
- 8.1 Примечания
- 8.2 Библиография
9 Дополнительная литература
10 Внешние ссылки

Многогранники

характеристика Эйлера $χ {\ displaystyle \ chi}$ $\ chi$ был классически определен для поверхностей многогранников по формуле

χ = V - E + F {\ displaystyle \ chi = V-E + F}

{ \ displaystyle \ chi = V-E + F}

, где V, E и F - соответственно числа из вершин (углов), ребер и граней s в данном многограннике. Поверхность любого выпуклого многогранника имеет эйлерову характеристику

V - E + F = 2. {\ displaystyle V-E + F = 2.}

{\ displaystyle V-E + F = 2.}

Это уравнение, сформулированное Леонардом Эйлер в 1758 году известен как формула многогранника Эйлера . Он соответствует эйлеровой характеристике сферы сферы (т. Е. Χ = 2) и идентично применяется к сферическим многогранникам. Ниже приводится иллюстрация формулы на некоторых многогранниках.

Имя	Вершины. V	Ребра. E	Грани. F	Эйлерова характеристика:. V - E + F
Тетраэдр	4	6	4	2
Гексахэдр или куб	8	12	6	2
Октаэдр	6	12	8	2
Додекаэдр	20	30	12	2
Икосаэдр	12	30	20	2

Поверхности невыпуклых многогранников могут иметь различные эйлеровы характеристики:

Название	Вершины. V	Ребра. E	Грани. F	эйлерова характеристика:. V - E + F
Тетрагемиоктаэдр	6	12	7	1
Октагемиоктаэдр	12	24	12	0
Кубогемиоктаэдр	12	24	10	−2
Малый звездчатый додекаэдр	12	30	12	−6
Большой звездчатый додекаэдр	20	30	12	2

Для правильных многогранников Артур Кэли вывел модифицированную форму формулы Эйлера, используя плотность D, фигура вершин плотность d v и плотность лица $df {\ displaystyle d_ {f}}$ $d_ {f}$ :

dv V - E + df F = 2 D. {\ displaystyle d_ {v} V-E + d_ {f} F = 2D.}

d_ {v} V-E + d_ {f} F = 2D.

Эта версия верна как для выпуклых многогранников (где все плотности равны единице), так и для невыпуклых многогранников Кеплера-Пуансо.

Все проективные многогранники имеют эйлерову характеристику 1, как и реальная проективная плоскость, в то время как поверхности тороидальных многогранников имеют эйлерову характеристику 0, как и тор..

Плоские графы

Эйлерова характеристика может быть определена для связанных плоских графов одним и тем же $V - E + F {\ displaystyle V-E + F}$ $V-E + F$ формула для многогранных поверхностей, где F - количество граней в графе, включая внешнюю грань.

Эйлерова характеристика любого плоского связного графа G равна 2. Это легко доказывается индукцией по количеству граней, определяемых G, начиная с дерева в качестве базового случая. Для деревьев $E = V - 1 {\ displaystyle E = V-1}$ ${\ displaystyle E = V-1 }$ и $F = 1 {\ displaystyle F = 1}$ ${\ displaystyle F = 1}$ . Если G имеет компоненты C (несвязные графы), тот же аргумент индукцией по F показывает, что $V - E + F - C = 1 {\ displaystyle V-E + F-C = 1}$ $V-E + FC = 1$ . Одна из немногих работ Коши по теории графов также доказывает этот результат.

Через стереографическую проекцию плоскость отображается в двумерную сферу, так что связный граф отображается в многоугольное разложение сферы, имеющее эйлерову характеристику 2. Эта точка зрения подразумевается в Доказательство Коши формулы Эйлера приведено ниже.

Доказательство формулы Эйлера

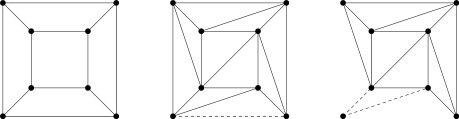Первые шаги доказательства в случае куба

Есть много доказательств формулы Эйлера. Один был дан Коши в 1811 году следующим образом. Это применимо к любому выпуклому многограннику и, в более общем смысле, к любому многограннику, граница которого топологически эквивалентна сфере, а грани топологически эквивалентны кругам.

Удалите одну грань многогранной поверхности. Оттягивая края отсутствующей грани друг от друга, деформируйте все остальные в планарный граф точек и кривых таким образом, чтобы периметр отсутствующей грани располагался снаружи, окружая полученный граф, как показано на рисунке. первый из трех графиков для частного случая куба. (Предположение, что полиэдральная поверхность гомеоморфна сфере вначале, делает это возможным.) После этой деформации правильные грани обычно перестают быть правильными. Число вершин и ребер осталось прежним, но количество граней уменьшилось на 1. Следовательно, доказательство формулы Эйлера для многогранника сводится к доказательству V - E + F = 1 для этого деформированного плоского объекта.

Если есть грань с более чем тремя сторонами, нарисуйте диагональ, то есть кривую через грань, соединяющую две вершины, которые еще не соединены. Это добавляет одно ребро и одну грань и не меняет количество вершин, поэтому не меняет количество V - E + F. (Здесь необходимо предположение, что все грани являются дисками, чтобы показать через кривую Жордана теорема о том, что эта операция увеличивает количество граней на единицу.) Продолжайте добавлять ребра таким образом, пока все грани не станут треугольными.

Повторно применяйте любое из следующих двух преобразований, сохраняя инвариант, что внешняя граница всегда является простым циклом :

Удалите треугольник только с одним ребром, смежным с внешним, как показано на втором график. Это уменьшает количество ребер и граней на единицу каждая и не меняет количество вершин, поэтому сохраняется V - E + F.
Удалите треугольник с двумя ребрами, общими для внешней части сети, как иллюстрируется третьим графиком. При каждом удалении треугольника удаляется вершина, два ребра и одна грань, поэтому сохраняется V - E + F.

Эти преобразования в конечном итоге сводят плоский граф к одному треугольнику. (Без инварианта простого цикла удаление треугольника могло бы разъединить оставшиеся треугольники, сделав недействительной остальную часть аргумента. Допустимый порядок удаления - это элементарный пример обстрела.)

При в этой точке одинокий треугольник имеет V = 3, E = 3 и F = 1, так что V - E + F = 1. Поскольку на каждом из двух вышеуказанных шагов преобразования эта величина сохраняется, мы показали, что V - E + F = 1 для деформированного плоского объекта, таким образом демонстрируя V - E + F = 2 для многогранника. Это доказывает теорему.

Дополнительные доказательства см. В разделе «Двадцать доказательств формулы Эйлера» Дэвида Эппштейна. Множественные доказательства, включая их недостатки и ограничения, используются в качестве примеров в Доказательствах и опровержениях от Имре Лакатоша.

Топологическое определение

Многогранные поверхности, описанные выше, на современном языке, двумерные конечные CW-комплексы. (Когда используются только треугольные грани, они представляют собой двумерные конечные симплициальные комплексы.) В общем, для любого конечного CW-комплекса эйлерова характеристика может быть определена как альтернированная сумма

χ знак равно К 0 - К 1 + К 2 - К 3 + ⋯, {\ Displaystyle \ chi = k_ {0} -k_ {1} + k_ {2} -k_ {3} + \ cdots,}

{\ displaystyle \ chi = k_ {0} -k_ {1} + k_ {2} -k_ {3} + \ cdots,}

, где k n обозначает количество ячеек размерности n в комплексе.

Аналогично, для симплициального комплекса характеристика Эйлера равна знакопеременной сумме

χ = k 0 - k 1 + k 2 - k 3 + ⋯, {\ displaystyle \ chi = k_ {0} -k_ {1} + k_ {2} -k_ {3} + \ cdots,}

{\ displaystyle \ chi = k_ {0} -k_ {1} + k_ {2} -k_ {3} + \ cdots,}

где k n обозначает количество n-симплексов в комплексе.

В более общем плане для любого топологического пространства мы можем определить n-е число Бетти bnкак ранг n-го группа особых гомологий. Тогда эйлерова характеристика может быть определена как знакопеременная сумма

χ = b 0 - b 1 + b 2 - b 3 + ⋯. {\ displaystyle \ chi = b_ {0} -b_ {1} + b_ {2} -b_ {3} + \ cdots.}

{\ displaystyle \ chi = b_ {0} -b_ {1} + b_ {2} -b_ {3} + \ cdots.}

Эта величина хорошо определена, если все числа Бетти конечны и если они ноль выше определенного индекса n 0. Для симплициальных комплексов это не то же определение, что и в предыдущем абзаце, но вычисление гомологии показывает, что два определения дадут одно и то же значение для $χ {\ displaystyle \ chi}$ $\ chi$ .

Properties

Эйлерова характеристика хорошо ведет себя по отношению ко многим основным операциям в топологических пространствах следующим образом.

Гомотопическая инвариантность

Гомология является топологическим инвариантом и, более того, гомотопическим инвариантом : два топологических пространства, которые гомотопически эквивалентны, имеют изоморфные группы гомологии. Отсюда следует, что эйлерова характеристика также является гомотопическим инвариантом.

Например, любое стягиваемое пространство (то есть, одна гомотопия, эквивалентная точке) имеет тривиальные гомологии, что означает, что 0-е число Бетти равно 1, а остальные 0. Следовательно, его эйлер характеристика равна 1. Этот случай включает евклидово пространство $R n {\ displaystyle \ mathbb {R} ^ {n}}$ $\ mathbb {R} ^ { n}$ любого измерения, а также единичный твердый шар в любом евклидовом пространстве - одномерном интервале, двумерном диске, трехмерном шаре и т. д.

В другом примере любой выпуклый многогранник гомеоморфен трехмерному шару, поэтому его поверхность гомеоморфна (следовательно, гомотопически эквивалентна) двумерной сфере, которая имеет эйлерову характеристику 2. Это объясняет, почему выпуклые многогранники имеют эйлерову характеристику 2.

Включение– принцип исключения

Если M и N - любые два топологических пространства, то эйлерова характеристика их непересекающегося объединения равна сумме их эйлеровых характеристик, поскольку гомологии складываются при несвязном объединении:

χ (M ⊔ N) = χ (M) + χ (N). {\ displaystyle \ chi (M \ sqcup N) = \ chi (M) + \ chi (N).}

\ chi ( M \ sqcup N) = \ chi (M) + \ chi (N).

В более общем смысле, если M и N являются подпространствами большего пространства X, то их объединение и пересечение также. В некоторых случаях эйлерова характеристика подчиняется версии принципа включения-исключения :

χ (M ∪ N) = χ (M) + χ (N) - χ (M ∩ N). {\ displaystyle \ chi (M \ cup N) = \ chi (M) + \ chi (N) - \ chi (M \ cap N).}

\ chi (M \ cup N) = \ chi (M) + \ chi (N) - \ chi (M \ cap N).

Это верно в следующих случаях:

если M и N являются. В частности, если внутренние части M и N внутри объединения все еще покрывают объединение.
, если X является локально компактным пространством, и используются характеристики Эйлера с compact поддерживает, никаких предположений относительно M или N. не требуется.
если X является стратифицированным пространством, все слои которого четномерны, принцип включения-исключения выполняется, если M и N являются объединением стратов. В частности, это применимо, если M и N являются подмногообразиями комплекса алгебраического многообразия.

В общем, принцип включения-исключения неверен. контрпример задается путем взятия X как вещественной прямой, M как подмножества, состоящего из одной точки, а N как дополнения к M.

Связанная сумма

Для двух связанных замкнутых n-образных коллекторов $M, N {\ displaystyle M, N}$ $M, N$ можно получить новый связанный коллектор $M # N {\ displaystyle M \ #N}$ ${\ displaystyle M \ #N}$ с помощью операции связанной суммы. Эйлерова характеристика связана формулой

χ (M # N) = χ (M) + χ (N) - χ (S n). {\ displaystyle \ chi (M \ #N) = \ chi (M) + \ chi (N) - \ chi (S ^ {n}).}

{\ displaystyle \ chi (M \ #N) = \ chi (M) + \ chi (N) - \ chi (S ^ { n}).}

Свойство продукта

Кроме того, Эйлер характеристика любого пространства произведения M × N равна

χ (M × N) = χ (M) ⋅ χ (N). {\ displaystyle \ chi (M \ times N) = \ chi (M) \ cdot \ chi (N).}

\ chi (M \ times N) = \ chi (M) \ cdot \ chi (N).

Эти свойства сложения и умножения также используются для мощности из наборов. Таким образом, эйлерова характеристика может рассматриваться как обобщение мощности; см. [1].

Покрывающие пространства

Аналогично, для k-листового покрывающего пространства $M ~ → M, {\ displaystyle {\ tilde {M} } \ to M,}$ ${\ tilde { M}} \ к M,$ имеет место

χ (M ~) = k χ (M). {\ displaystyle \ chi ({\ tilde {M}}) = k \ cdot \ chi (M).}

\ chi ({\ tilde {M}}) = k \ cdot \ chi (M).

В более общем смысле, для разветвленного накрывающего пространства эйлерова характеристика покрытия может вычисляется на основе вышеизложенного с поправочным коэффициентом для точек ветвления, что дает формулу Римана – Гурвица.

Свойство волокнистости

Свойство произведения выполняется в более общем случае для расслоений с определенными условиями.

Если $p: E → B {\ displaystyle p \ двоеточие E \ to B}$ $p \ двоеточие E \ to B$ - это расслоение с волокном F с базой B , связанное по путям и расслоение ориентируемо над полем K, то эйлерова характеристика с коэффициентами в поле K удовлетворяет свойству произведения:

χ (E) = χ (F) ⋅ χ (B). {\ displaystyle \ chi (E) = \ chi (F) \ cdot \ chi (B).}

\ chi (E) = \ chi (F) \ cdot \ chi (B).

Сюда входят пространства произведений и покрывающие пространства как частные случаи, и это может быть доказано с помощью спектральной последовательности Серра о гомологиях расслоения.

Для пучков волокон это также можно понять в терминах карты переноса $τ: H ∗ (B) → H ∗ (E) {\ displaystyle \ tau \ Colon H _ {*} (B) \ to H _ {*} (E)}$ $\ tau \ двоеточие H _ {*} (B) \ to H _ {*} (E)$ - обратите внимание, что это подъем и идет «не в ту сторону» - чья композиция с картой проекции $p ∗: H ∗ (E) → H ∗ (B) {\ displaystyle p _ {*} \ двоеточие H _ {*} (E) \ to H _ {*} (B)}$ $p _ {*} \ двоеточие H _ {* } (E) \ to H _ {*} (B)$ - это умножение на Класс Эйлера волокна:

p ∗ ∘ τ = χ (F) ⋅ 1. {\ displaystyle p _ {*} \ circ \ tau = \ chi (F) \ cdot 1.}

p _ {*} \ circ \ tau = \ chi (F) \ cdot 1.

Примеры

Поверхности

Эйлерову характеристику можно легко вычислить для общих поверхностей, найдя полигонизацию поверхности (то есть описание как CW-комплекс ) и используя приведенные выше определения.

Имя	Изображение	характеристика Эйлера
Интервал		1
Круг		0
Диск		1
Сфера		2
Торус. (Произведение двух кругов)		0
Двойной тор		−2
Тройной тор		−4
Реальная проективная плоскость		1
Лента Мёбиуса		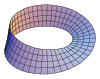0
Бутылка Клейна		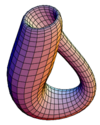0
Две сферы (не связанные). (Непересекающееся объединение двух сфер)		2 + 2 = 4
Три сферы (не связанные). (Непересекающееся объединение трех сфер)		2 + 2 + 2 = 6

Футбольный мяч

Обычно строят футбольные мячи путем сшивания пятиугольных и шестиугольных частей, при этом по три части встречаются в каждой вершине (см., например, Adidas Telstar ). Если используются P пятиугольников и H шестиугольников, то имеется F = P + H граней, V = (5 P + 6 H) / 3 вершины и E = (5 P + 6 H) / 2 ребра. Таким образом, эйлерова характеристика равна

V - E + F = 5 P + 6 H 3 - 5 P + 6 H 2 + P + H = P 6. {\ displaystyle V-E + F = {\ frac {5P + 6H} {3}} - {\ frac {5P + 6H} {2}} + P + H = {\ frac {P} {6}}. }

{\ displaystyle V-E + F = {\ frac {5P + 6H} {3}} - {\ frac {5P + 6H} {2}} + P + H = {\ frac {P} {6}}.}

Поскольку сфера имеет эйлерову характеристику 2, то P = 12. То есть футбольный мяч, построенный таким образом, всегда имеет 12 пятиугольников. В принципе, количество шестиугольников неограниченно. Этот результат применим к фуллеренам и многогранникам Гольдберга.

произвольной размерности

n-мерная сфера имеет группы сингулярных гомологий, равные

H k (S n) = {Z k = 0, n {0} в противном случае, {\ displaystyle H_ {k} (S ^ {n}) = {\ begin {cases} \ mathbb {Z} k = 0, n \\\ {0 \} {\ text {в противном случае}} \ end {cases}}}

{\ displaystyle H_ {k} (S ^ {n}) = {\ begin {cases} \ mathbb {Z} k = 0, n \\\ {0 \} {\ text {в противном случае}} \ end {cases}}}

, следовательно, имеет число Бетти 1 в размерностях 0 и n, а все остальные числа Бетти равны 0. Тогда его эйлерова характеристика равна 1 + (−1) - то есть либо 0, либо 2.

n-мерное действительное проективное пространство является частным от n-сферы по антиподальному отображению. Отсюда следует, что его эйлерова характеристика ровно вдвое меньше, чем у соответствующей сферы - либо 0, либо 1.

n-мерный тор является пространством произведения n окружностей. Его эйлерова характеристика равна 0 по свойству произведения. В более общем смысле, любое компактное параллелизуемое многообразие, включая любую компактную группу Ли, имеет эйлерову характеристику 0.

Эйлерова характеристика любого замкнутого нечетного -мерное многообразие также равно 0. Случай ориентируемых примеров является следствием двойственности Пуанкаре. Это свойство применяется в более общем плане к любому компактному слоистому пространству, все слои которого имеют нечетную размерность. Это также применимо к замкнутым нечетномерным неориентируемым многообразиям через взаимно однозначное ориентируемое двойное покрытие.

Соотношения с другими инвариантами

Эйлерова характеристика замкнутого ориентируемого поверхность может быть вычислена по ее роду g (количество торов в связной сумме разложения поверхности; интуитивно понятно, количество «ручек») как

χ = 2 - 2 г. {\ displaystyle \ chi = 2-2g.}

\ chi = 2-2g.

Эйлерова характеристика замкнутой неориентируемой поверхности может быть вычислена по ее неориентируемому роду k (количество вещественных проективных плоскостей в связной сумма разложения поверхности) как

χ = 2 - k. {\ displaystyle \ chi = 2-k.}

{\ displaystyle \ chi = 2-k.}

Для замкнутых гладких многообразий характеристика Эйлера совпадает с числом Эйлера, т. е. классом Эйлера своего касательное расслоение, вычисленное на фундаментальном классе многообразия. Класс Эйлера, в свою очередь, относится ко всем другим характеристическим классам векторных расслоений.

Для замкнутых римановых многообразий эйлерова характеристика также может быть найдена путем интегрирования кривизны ; см. теорему Гаусса – Бонне для двумерного случая и обобщенную теорему Гаусса – Бонне для общего случая.

Дискретным аналогом теоремы Гаусса – Бонне является теорема Декарта о том, что «полный дефект» многогранника, измеренный в полных окружностях, является характеристикой Эйлера. многогранника; см. дефект (геометрия).

Теорема Хадвигера характеризует эйлерову характеристику как единственное (от до скалярное умножение ) трансляционно-инвариантное, конечно аддитивное, не- функция обязательно неотрицательного множества, определенная на конечных объединениях из компактных выпуклых множеств в R, которая является «однородной степени 0».

Обобщения

Для каждого комбинаторного комплекса ячеек эйлерова характеристика определяется как количество 0-ячеек минус количество 1-ячеек плюс количество 2-клетки и т. Д., Если эта альтернированная сумма конечна. В частности, эйлерова характеристика конечного множества - это просто его мощность, а эйлерова характеристика графа - это количество вершин минус количество ребер.

В более общем плане можно Определим эйлерову характеристику любого цепного комплекса как альтернативную сумму рангов групп гомологии цепного комплекса, предполагая, что все эти ранги конечны.

Версия эйлеровой характеристики, используемая в алгебраической геометрии, выглядит следующим образом. Для любой связной связки $F {\ displaystyle {\ mathcal {F}}}$ ${\ mathcal { F}}$ на правильной схеме X, ее эйлерову характеристику определяют как

χ (F) знак равно ∑ я (- 1) ihi (X, F), {\ displaystyle \ chi ({\ mathcal {F}}) = \ sum _ {i} (- 1) ^ {i} h ^ {i} (X, {\ mathcal {F}}),}

{\ displaystyle \ chi ({\ mathcal {F}}) = \ sum _ {i} (- 1) ^ {i} h ^ {i } (Икс, {\ mathcal {F}}),}

где $привет (X, F) {\ displaystyle h ^ {i} (X, {\ mathcal {F}}) }$ ${\ displaystyle h ^ {i} (X, {\ mathcal {F}})}$ - размер i-й группы когомологий пучка $F {\ displaystyle {\ mathcal {F}}}$ ${\ mathcal { F}}$ . В этом случае все размерности конечны по теореме Гротендика о конечности. Это пример характеристики Эйлера цепного комплекса, где цепной комплекс является конечным разрешением $F {\ displaystyle {\ mathcal {F}}}$ ${\ mathcal { F}}$ по ациклическим пучкам.

Еще одно обобщение концепции эйлеровой характеристики на многообразиях происходит от орбифолдов (см. эйлерова характеристика орбифолда ). Хотя каждое многообразие имеет целочисленную эйлерову характеристику, орбифолд может иметь дробную эйлерову характеристику. Например, каплевидное орбифолд имеет эйлерову характеристику 1 + 1 / p, где p - простое число, соответствующее углу конуса 2π / p.

Концепция эйлеровой характеристики ограниченного конечного чугуна является еще одним обобщением, важным в комбинаторике. Посет считается «ограниченным», если он имеет наименьшие и наибольшие элементы; назовем их 0 и 1. Эйлерова характеристика такого чугуна определяется как целое число μ (0,1), где μ - это функция Мёбиуса в алгебре инцидентности этого чугуна.

. можно далее обобщить путем определения Q -значной эйлеровой характеристики для некоторых конечных категорий, понятия, совместимого с эйлеровыми характеристиками графов, орбифолдов и множеств, упомянутых выше. В этом случае эйлерова характеристика конечной группы или моноида G равна 1 / | G |, а эйлерова характеристика конечного группоида представляет собой сумму of 1 / | G i |, где мы выбрали одну репрезентативную группу G i для каждого компонента связности группоида.

См. также

Ссылки

Примечания

Библиография

Ричсон, Дэвид С. ; Драгоценный камень Эйлера: формула многогранника и рождение топологии. Princeton University Press 2008.

Дополнительная литература

Флегг, Х. Грэм; От геометрии к топологии, Довер 2001, стр. 40.

Внешние ссылки